| Скачать .docx |
Курсовая работа: Исследование системы передачи дискретных сообщений
Федеральное агентство связи
Поволжский Государственный Университет Телекоммуникаций
и Информатики
Кафедра ТОРС
Сдана на проверку Допустить к защите
«_____»___________2010 г. «_____»___________2010 г.
Защищена с оценкой __________
«_____»___________2010 г.
Курсовая работа по дисциплине ТЭС
«Исследование системы передачи дискретных сообщений»
Выполнила: студентка гр. БТ-81
Петухова А.С.
Проверил : Николаев Б.И.
Самара,2010
Содержание
Рецензия…………… ………………………………………………………………3
Выбор варианта ……………………………………………………………………4
Задание 1: Структурная схема системы передачи.………………………………6
Задание 2: Исследование тракта кодер-декодер источника…………………….7
Задание 3: Исследование тракта кодер-декодер канала……………………… .10
Задание 4: Исследование тракта кодер-декодер модулятор-демодулятор……12
Задание 5: Демонстрация работы системы передачи…………………………..16
Список использованной литературы…………………………………………….20
Рецензия.
Выбор варианта
№ зачетки: 08120.
a=8, b=1,c=2,d=0.
1. Выбор алгоритма кодирования источника
![]() ,
,
при ![]() выбираем код Шеннона-Фано.
выбираем код Шеннона-Фано.
1. Расчёт вероятностей символов на выходе источника сообщений (таблица 1).
Таблица 1.
| I |
Символ |
Вероятность |
| 0 |
а |
|
| 1 |
б |
|
| 2 |
в |
|
| 3 |
г |
|
| 4 |
д |
|
| 5 |
е |
|
| 6 |
з |
|
| 7 |
и |
|
| 8 |
к |
|
| 9 |
л |
|
| 10 |
м |
|
| 11 |
н |
|
| 12 |
о |
|
| 13 |
п |
|
| 14 |
р |
|
| 15 |
с |
|
2. Расчёт скорости выдачи символов источником.
![]() [симв/с].
[симв/с].
3. Выбор вида модуляции.
![]() ,
,
при ![]() выбираем ОФМ.
выбираем ОФМ.
4. Выбор вида канала.
![]() ,
,
При ![]() выбираем гауссовский канал с неопределенной фазой.
выбираем гауссовский канал с неопределенной фазой.
5. Расчёт коэффициента передачи канала.
![]() .
.
6. Расчёт спектральной плотности мощности шума.
![]()
7. Расчёт максимально допустимой вероятности ошибки на выходе демодулятора.
![]() .
.
8. Выбор текста передаваемого сообщения.
Текст сообщения состоит из 8 символов источника ![]() . Здесь
. Здесь ![]() - символ, имеющий наибольшую вероятность;
- символ, имеющий наибольшую вероятность; ![]() - символ, имеющий следующую величину вероятности после символа
- символ, имеющий следующую величину вероятности после символа ![]() ;
; ![]() - символ, имеющий следующую величину вероятности после символа
- символ, имеющий следующую величину вероятности после символа ![]() .
.
![]()
9. Выбор номеров ошибочных разрядов.

Ошибочные разряды: 4,8,10.
Задание №1.
Структурная схема системы передачи.
Составим обобщенную структурную схему системы передачи дискретных сообщений, включающую в себя источник сообщений, кодер источника, кодер канала, модулятор, канал связи, демодулятор, декодер канала, декодер источника и получателя сообщений. Дадим краткую характеристику каждого из блоков.
Источником сообщений и получателем в одних системах связи может быть человек, в других – различного рода устройства(автомат, вычислительная машина и т.д).
Устройство, преобразующее сообщение в сигнал, называют передающим, а устройство, преобразующее принятый сигнал в сообщение – приёмным.
Процедура кодирования представляет собой преобразование сообщения в последовательность кодовых символов. Устройства, осуществляющие кодирование называют кодерами .
Модулятор - устройство, преобразующее код в сигнал. Процедура модуляции представляет собой преобразование последовательности кодовых символов в сигналы, пригодные для передачи по каналу. При цифровой модуляции закодированное сообщение, представляющее собой последовательность кодовых символов, преобразуется в последовательность элементов сигнала, путём воздействия кодовых символов на переносчик. Посредством модуляции один из параметров переносчика изменяется по закону, определяемому кодом. С помощью кодирования и модуляции источник сообщения согласуется с каналом.
Аналоговый канал или канал связи - совокупность средств, обеспечивающих передачу сигнала от источника сообщений к получателю сообщений.
Процедура демодуляции представляет собой преобразование сигналов, передаваемых по каналу связи, в последовательность кодовых символов. Устройства, выполняющие такие преобразования, называют демодуляторами .
Процедура декодирования представляет собой преобразование последовательности кодовых символов в сообщение. Устройства, выполняющие такие преобразования, называют декодерами .
Кодек – совокупность устройств - кодера и декодера.
Модем – совокупность устройств – модулятора и демодулятора.
Целью передачи сообщения является доставка сообщения от источника сообщений
на передаче до получателя сообщений
на приеме. В источнике сообщений (ИС)
образуется исходное сообщение. Оно поступает в кодер
, а именно в кодер источника (КИ). Кодер
служит для преобразования первичного алфавита ![]() , во вторичный, из элементов
, во вторичный, из элементов ![]() . С кодера источника
(КИ)
сообщение поступает на кодер канала (КК)
. В кодере канала
(КК)
сообщение преобразуется в кодовую комбинацию
. С кодера источника
(КИ)
сообщение поступает на кодер канала (КК)
. В кодере канала
(КК)
сообщение преобразуется в кодовую комбинацию ![]() . Это делается для лучшего согласования источника с характером канала, упрощения передачи и обработки сигналов, и в конечном счете для увеличения эффективности передачи.
. Это делается для лучшего согласования источника с характером канала, упрощения передачи и обработки сигналов, и в конечном счете для увеличения эффективности передачи.
Далее каждый элемент кодовой комбинации ![]() в модуляторе (Мод)
преобразуется в элементарный сигнал
в модуляторе (Мод)
преобразуется в элементарный сигнал ![]() . Модуляция обеспечивает преобразование спектра низкочастотного первичного сигнала
. Модуляция обеспечивает преобразование спектра низкочастотного первичного сигнала ![]() в область частоты несущей, которую можно передать по данному каналу. Далее сигнал поступает в канал связи (КС). Канал связи (КС)
– совокупность средств, предназначенных для передачи сигналов, имеющий вход и выход. Далее с КС сигнал поступает в демодулятор (Дем).
В место приема демодулятор выдает оценку кодовых символов
в область частоты несущей, которую можно передать по данному каналу. Далее сигнал поступает в канал связи (КС). Канал связи (КС)
– совокупность средств, предназначенных для передачи сигналов, имеющий вход и выход. Далее с КС сигнал поступает в демодулятор (Дем).
В место приема демодулятор выдает оценку кодовых символов ![]() .
.
Далее сигнал поступает на декодер канала (ДК).
Преобразуется в ДК
, поступает на декодер источника (ДИ)
. В ДИ
восстанавливается исходное сообщение. На выходе декодера, несмотря на ошибки в приеме сигналов, возникающих из-за действующих в КС
шумов, должна формироваться та же последовательность, которая поступала на вход КК
. Достигается это с помощью эффективных кодов, которые исправляют ошибки, возникающие при передаче сообщения по КС
. Декодер выдает оценку сообщения ![]() . Получатель сообщения (ПС) восстанавливает сообщение по принятому сигналу и выдает нам готовое передаваемое сообщение.
. Получатель сообщения (ПС) восстанавливает сообщение по принятому сигналу и выдает нам готовое передаваемое сообщение.
Задание №2.
Исследование тракта кодер-декодер источника.
1. Найдем энтропию источника.
![]() - алфавит из 16 символов.
- алфавит из 16 символов.
Найдем избыточность источника.
Найдем производительность источника.
.
2.
Найдем минимально необходимое число разрядов кодового слова ![]() ,при условии, что производится примитивное кодирование.
,при условии, что производится примитивное кодирование.
![]()
![]()
Найдем среднее количество двоичных символов, приходящееся на один символ источника. В случае примитивного кодирования:
![]()
3. Построим кодовое дерево для кода Шеннона-Фано, при условии, что производится экономное кодирование. Запишем кодовые комбинации для представления всех 16 символов источника, найдем число разрядов каждой полученной комбинации.
|
|
|
|
|
|
|
|
|
|
||||
| а |
0,31 |
00 |
2 |
0,62 |
2 |
0,62 |
0 |
0 |
||||
| р |
0,2 |
01 |
2 |
0,4 |
1 |
0,2 |
1 |
0,2 |
||||
| м |
0,166 |
100 |
3 |
0,498 |
2 |
0,332 |
1 |
0,166 |
||||
| и |
0,135 |
101 |
3 |
0,405 |
1 |
0,135 |
2 |
0,27 |
||||
| в |
0,057 |
1100 |
4 |
0,228 |
2 |
0,114 |
2 |
0,114 |
||||
| л |
0,04 |
1101 |
4 |
0,16 |
1 |
0,04 |
3 |
0,12 |
||||
| д |
0,02 |
11100 |
5 |
0,1 |
2 |
0,04 |
3 |
0,06 |
||||
| е |
0,02 |
11101 |
5 |
0,1 |
1 |
0,02 |
4 |
0,08 |
||||
| н |
0,012 |
111100 |
6 |
0,072 |
2 |
0,024 |
4 |
0,048 |
||||
| б |
0,01 |
1111010 |
7 |
0,07 |
2 |
0,02 |
5 |
0,05 |
||||
| г |
0,0081 |
1111011 |
7 |
0,0567 |
1 |
0,0081 |
6 |
0,0486 |
||||
| к |
0,008 |
1111100 |
7 |
0,056 |
2 |
0,016 |
5 |
0,040 |
||||
| п |
0,006 |
1111101 |
7 |
0,042 |
1 |
0,006 |
6 |
0,036 |
||||
| о |
0,004 |
1111110 |
7 |
0,028 |
1 |
0,004 |
6 |
0,024 |
||||
| з |
0,002 |
11111110 |
8 |
0,016 |
1 |
0,002 |
7 |
0,014 |
||||
| с |
0,0019 |
11111111 |
8 |
0,0152 |
0 |
0 |
8 |
0,0152 |
||||
![]() - число разрядов кодовой комбинации.
- число разрядов кодовой комбинации.
![]() -вероятность
-вероятность ![]() -го символа.
-го символа.
![]() и
и ![]() - число нулей и единиц в кодовой комбинации
- число нулей и единиц в кодовой комбинации ![]() -го символа.
-го символа.
Найдем среднее количество двоичных символов, приходящееся на один символ источника.
[бит/симв]
Избыточность на выходе кодера равна:
![]() .
.
Энтропия на выходе равна:
Следовательно,
Вывод: при экономном кодирования среднее число двоичных символов, приходящееся на один символ источника меньше, чем в примитивном кодировании, это доказывает эффективность экономного кодирования. Избыточность при экономном кодировании намного меньше, чем в примитивном кодировании. Примитивный равномерный код не может обеспечить эффективного согласования источника с каналом связи.
4. Рассчитаем вероятности двоичных символов на выходе кодера источника.
Рассчитаем среднюю скорость выдачи двоичных символов на выходе кодера источника.
.
Описание процедуры кодирования и декодирования символов экономным кодом Шеннона-Фано.
При кодировании происходит процесс преобразования элементов сообщения в соответствующие им кодовые символы . Каждому элементу сообщения присваивается определённая совокупность кодовых символов, которая называется кодовой комбинацией .

Рис. Схема кодера
Совокупность кодовых комбинаций, отображающих дискретные сообщения, образует код . Правило кодирования может быть выражено кодовой таблицей, в которой приводятся алфавит кодируемых сообщений и соответствующие им кодовые комбинации. Множество возможных кодовых символов называется кодовым алфавитом , а их количество m - основанием кода.
Алгоритм кодирования Шеннона-Фано заключается в следующем. Символы алфавита источника записываются в порядке не возрастающих вероятностей. Затем они разделяются на две части так, чтобы суммы вероятностей символов, входящих в каждую из таких частей (если она содержит более одного сообщения) делится в свою очередь на две, по возможности, равновероятные части, и к ним применяется то же самое правило кодирования. Этот процесс повторяется до тех пор, пока в каждой из полученных частей не останется по одному сообщению.
Задание № 3.
Исследование тракта кодер-декор канала.
Для канального кодирования выбран код Хемминга (7,4).
1. При помехоустойчивом кодировании в сообщение целенаправленно вносится избыточность для обнаружения или исправления ошибок в канале с помехами. Кодирование осуществляется следующим образом. К 4-м информационным разрядам добавляются 3 проверочных, чтобы соблюдалось условие линейной независимости. Таким образом, получается, что каждый из 7 символов участвует хотя бы в одной проверке. Далее мы рассчитываем 3 проверочных разряда по формулам, например:
![]() ,
,
![]() ,
,
![]() .
.
Затем рассчитанные проверочные разряды дописываются после 4 информационных.
Так делается со всеми информационными разрядами и записывается готовая кодовая комбинация.
2. Определим избыточность кода.
![]() .
.
Где ![]() - общее число разрядов кодовой комбинации.
- общее число разрядов кодовой комбинации.
![]() .
.
![]() - число информационных разрядов.
- число информационных разрядов.
![]()
![]() -число проверочных разрядов.
-число проверочных разрядов.
![]() ,
,
![]() .
.
Определим скорость кода.
![]()
![]() ,
,
![]()
![]() .
.
Найдем среднее число кодированных бит, приходящееся на один символ источника.
![]()
![]()
Найдем среднюю битовую скорость на выходе кодера канала.
![]()
![]() .
.
3. Определим исправляющую и обнаруживающую способность кода.
Для начала определим исправляющую способность кода.
![]()
Где ![]() - расстояние между разрядами кодовой комбинации.
- расстояние между разрядами кодовой комбинации. ![]() .
.
![]()
Определим обнаруживающую способность кода.
![]() ,
,
![]() .
.
4. а)В режиме исправления ошибки декодер сначала вычисляет синдром,затем по таблице синдромов обнаруживает ошибочный бит, затем инвентирует его.
б)В режиме обнаружения ошибки,декодер вычисляет синдром, если в синдроме нет единиц, то кодовая комбинация является разрешенной и декодер пропускает кодовую комбинацию, а если есть хотя бы одна единица, то комбинация является запрещенной.
5. Найдем вероятность ошибки на блок, полагая, что декодер работает в режиме исправления ошибок.
![]()
![]() ,
,
Найдем вероятность ошибки на бит на выходе декодера.
![]()
Вывод: Выполнив расчеты, можно заметить следующее: вероятность того что декодер исправит ошибку в каждом блоке очень большая, это означает большую вероятность того, что переданное сообщение придет без искажений.
Найдем вероятность ошибки на блок, полагая, что декодер работает в режиме обнаружения ошибок.
![]()
![]()
Найдем вероятность ошибки на бит на выходе декодера.
![]()
Рассчитаем среднее число перезапросов на блок.
![]()
Отсюда вероятность перезапроса:
![]()
![]()
Вывод: Вероятность того, что декодер обнаружит все ошибки, довольно велика, значит, он сможет их исправить, и мы получим неискаженное сообщение.
Задание № 4.
Исследование тракта модулятор-демодулятор.
1. Определим скорость относительной фазовой модуляции:
![]()
![]() .
.
Найдем тактовый интервал передачи одного бита.
![]() ,
,
![]() .
.
Рассчитаем минимально необходимую полосу пропускания канала.
![]() .
.
Найдем частоту несущего колебания.
![]() ,
,
![]()
![]() .
.
Запишем аналитическое выражение ОФМ-сигнала в общем виде.
![]() - случайная начальная фаза, неизвестная при приеме, зависящая, в частности, от символа, передававшегося (n-2)-м элементом.
- случайная начальная фаза, неизвестная при приеме, зависящая, в частности, от символа, передававшегося (n-2)-м элементом.
2. Запишем аналитическое выражение, связывающее сигналы на входе и выходе.
Учитывая, что у нас гауссовский канал с неопределенной фазой, получаем выражения:
![]() , где
, где
![]() -сигнал на выходе,
-сигнал на выходе,
![]() - сигнал на входе,
- сигнал на входе,
![]() -шум.
-шум.

![]() и
и ![]() сигнал соответствующий приему 1 и 0 .
сигнал соответствующий приему 1 и 0 .
 .
.
 .
.
Тогда:
 .
.
Найдем амплитуду ![]() .
.
Выразим амплитуду несущего колебания из выражения для вычисления мощности единичного сигнала на передаче.
 ,
,
 .
.
![]()
Теперь найдем ![]() .
.
Так как по условию у нас некогерентный прием, то
![]()
![]()
![]()
Найдем энергию единичного сигнала из формулы.
![]() ,
,
![]()
![]() .
.
Найдем мощность единичного элемента сигнала на приеме.
![]()
![]()
![]() ,
,
![]()
![]() ,
,
![]() .
.
Отсюда:
![]() ,
,
![]()
Запишем выражение связывающее сигналы на входе и выходе.

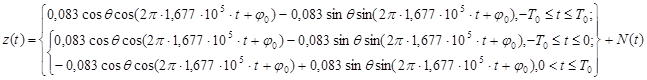 .
.
3. Запишем решающее правило и алгоритм работы демодулятора по критерию минимума средней вероятности ошибки с учетом некогерентного приема.
Оптимальный алгоритм для ОФМ:
 , i=0, 1.
, i=0, 1.
Приходящий сигнал s(t) на двух тактовых интервалах при ОФМ можно представить в зависимости от символа, передаваемого n-м элементом, так:
Для схемной реализации данный алгоритм можно упростить. Для этого подставим систему сигналов на входе алгоритм и после сокращения одинаковых слагаемых приведем алгоритм приема к виду:
![]() ,
,
где 
На рисунке показана схема реализации некогерентного приема ОФМ с согласованным фильтром и линией задержки. Приходящий сигнал поступает на фильтр СФ, согласованный с элементом сигнала ![]() длительностью Т. Отклик фильтра поступает на два входа перемножителя, на один из них непосредственно, а на другой – через линию задержки (ЛЗ), обеспечивающую задержку на время Т. Таким образом, вблизи момента отсчета на перемножитель поступают напряжения, соответствующие двум соседним элементам сигнала – только что закончившемуся и предыдущему, прошедшему через линию задержки. Можно показать, что первое из этих напряжений выражается формулой
длительностью Т. Отклик фильтра поступает на два входа перемножителя, на один из них непосредственно, а на другой – через линию задержки (ЛЗ), обеспечивающую задержку на время Т. Таким образом, вблизи момента отсчета на перемножитель поступают напряжения, соответствующие двум соседним элементам сигнала – только что закончившемуся и предыдущему, прошедшему через линию задержки. Можно показать, что первое из этих напряжений выражается формулой ![]() , а второе
, а второе ![]() . После их перемножения и фильтрации результата в ФНЧ получаем напряжение
. После их перемножения и фильтрации результата в ФНЧ получаем напряжение ![]() , которое в РУ сравнивается с нулевым порогом. Описанную схему называют схемой сравнения фаз.
, которое в РУ сравнивается с нулевым порогом. Описанную схему называют схемой сравнения фаз.
4. Найдем минимально необходимую мощность сигнала на приемной и передающей стороне.
![]()
![]()
![]() ,
,
![]() .
.
Найдем среднюю мощность сигнала на приеме.
![]() ,
,
Для ОФМ![]() , следовательно:
, следовательно:
![]()
![]() .
.
5. Определим пропускную способность непрерывного канала связи.

![]() ,
,
Для начала найдем полосу частот передаваемого сигнала ![]() .
.
При ОФМ:
![]() Гц,
Гц,

![]() .
.
Пропускная способность больше скорости модуляции, значит, расчеты были сделаны правильно, и сообщение будет проходить через декодер без задержки.
6. Определим вероятность ошибки на выходе демодулятора при использовании других видов модуляции при сохранении пиковой мощности сигнала.
 ,
,
Из проделанных выше расчетов мы видим, что у ОФМ самая маленькая вероятность появления ошибки. При АМ и ЧМ самая большая вероятность появления ошибки, это говорит о том, что самый эффективный вид модуляции – ОФМ.
Задание № 5.
Демонстрация работы системы передачи.
1. Выберем передаваемый текст в соответствии с номером варианта.
![]()
2. Закодируем буквы экономным кодом.
| а |
р |
а |
а |
м |
р |
а |
р |
| 00 |
01 |
00 |
00 |
100 |
01 |
00 |
01 |
3. Используя результаты предыдущего пункта закодируем полученную последовательность бит помехоустойчивым кодом, предварительно разбив ее на ![]() бит (недостающие разряды заполним 0 в последнем блоке).
бит (недостающие разряды заполним 0 в последнем блоке).
![]() ,
,
![]() ,
,
![]() .
.
1)
![]()
![]() ,
,
![]() ,
,
![]() ,
,
0001011
2)
![]()
![]() ,
,
![]() ,
,
![]() ,
,
0000000
3)
![]()
![]() ,
,
![]() ,
,
![]() ,
,
1000101
4)
![]()
![]() ,
,
![]() ,
,
![]() .
.
1000101
5)
![]()
![]() ,
,
![]() ,
,
![]() ,
,
1000101
Получили: 00010110000000100010110001011000101
4. Изобразим временные и спектральные диаграммы сигнала на входе и выходе модулятора. Ограничимся 10 тактовыми интервалами передачи.
0001111000 0000110001110001011000101
Временные диаграммы:
На входе:
На выходе:
Спектральные диаграммы:
На входе:
На выходе:
5. Полагая, что при демодуляции произошло 3 ошибки, запишем кодовую последовательность на выходе демодулятора (номера ошибочных разрядов выберем в соответствии с вариантом). В нашем случае это 4,8,10 бит.
00010 1100 00 000100010110001011000101
Обозначены жирным шрифтом и подчеркнуты ошибочные разряды.
Запишем кодовую комбинацию с учетом совершенных ошибок(1 заменяем на 0 и наоборот).
00011 1101 01 000100010110001011000101
6. Полагая, что демодулятор работает в режиме исправления ошибок, декодируем полученную комбинацию.
1)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Составим синдром:
![]() ,
,
![]() ,
,
![]() .
.
По таблице синдромов смотрим, какой бит исправил декодер.
| Синдром
|
Ошибочный бит |
| 000 |
- |
| 001 |
|
| 010 |
|
| 100 |
|
| 101 |
|
| 110 |
|
| 111 |
|
| 011 |
|
Декодер исправил 4 бит. Из этого мы можем сделать вывод, что декодер исправил нашу ошибку.
2)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() .
.
По таблице синдромов мы видим, что декодер не исправил ни одного бита. Видно, то что декодер вносит ошибку в 0 бит.
Восстановим текст сообщения, используя кодовую таблицу.
00010111101000100010110001011000101
Так как мы добавляли по 3 бита во время кодирования помехоустойчивым кодом - в полученной комбинации, мы тоже должны их отбросить.
0001011 1101000 1000101 1000101 1000101
Отбросим биты, подчеркнутые и выделенные жирным шрифтом.
Запишем полученную комбинацию в соответствии с кодовой таблицей и восстановим сообщение: 00011101100010001000
| а |
р |
? |
р |
м |
р |
а |
р |
| 00 |
01 |
11 |
01 |
100 |
01 |
00 |
01 |
Восстановленное сообщение:
ар?рмрар.
Вывод: полученный текст не соответствует передаваемому тексту, что характеризует неэффективную работу декодера в режиме исправления ошибок.
Литература.
1. Теория электрической связи/ Зюко А. Г., Кловский Д.Д., Коржик В.И., Назаров М.В.//под ред. Д.Д. Кловского – М.: Радио и связь, 1998.
2. Кловский Д.Д. Теория передачи сигналов – М.: Радио и связь, 1973.
3. Методическая разработка к лабораторной работе №8 по дисциплине «Теория электрической связи», «Исследование линейных блочных кодов» (для студентов 3 курса специальностей 550400, 201800, 201100, 201000, 200900), каф. ТОРС, Самара, 2004.