| Скачать .docx |
Курсовая работа: Разработка цифрового аппарата
ФГОУ ВПО Оренбургский Государственный Аграрный Университет
Кафедра Информатики и информационного обеспечения
Курсовой проект
Тема: Разработка цифрового аппарата
Оренбург – 2010
Задание на курсовой проект
Синтезировать цифровой аппарат Мура с D-триггером, используя заданный граф микропрограммы автомата (структурная схема алгоритма).
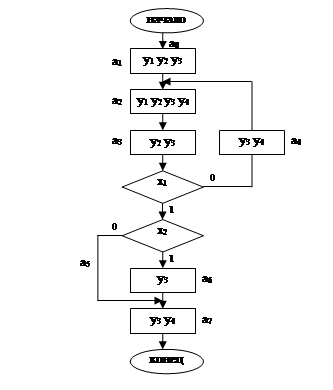
Рисунок 1 – граф микропрограммы автомата (вариант 46).
Введение
Функции цифрового аппарата (ЦА) сводятся к вводу, выводу, хранению информации, выполнению микроопераций и вычислению логических условий. Набор элементов, на основе которых строятся структуры автоматов с указанными функциями, составляет:
а) шины, обеспечивающие передачу информации;
б) регистры, обеспечивающие хранение слов и состоящие из совокупности элементов памяти (ЭП);
в) комбинационные схемы (КС), осуществляющие вычисление логических функций.
Шины обозначают совокупность цепей, где одна цепь служит для передачи одного бита информации, с целью упрощения и чтения схем.
ЭП, составляющие регистры, выбирают, как правило, с синхронной записью или с синхронной установкой.
КС по существу является перекодирующим устройством и главным объектом синтеза ЦА. Для ее реализации используется весь арсенал элементов логических функций и умение получать простые решения минимизацией составленных для КС систем уравнений логических вычислений.
Теоретической основой управляемых ЦА являются автоматы Мили (рисунок 2) и Мура (рисунок 3).
Типичным примером автомата Мили являются электронные часы с цифровым табло, где выходные функции – сегменты индикации, а входные – кнопки режимов: при нажатии одной из кнопок устанавливается действие соответствующей управляющей функции.
Главная особенность автомата Мили заключается в возможности при одном и том же состоянии ЭП задать несколько выходных функций: индикацию текущего времени, дня недели, числа месяца, номера текущего месяца и т. д.
В промышленных устройствах автоматики, как правило, не встречаются в чистом виде автоматы одного типа. Однако в их структурах доминирует автомат Мура. Поэтому в данной работе он будет являться объектом проектирования.
1. Форма представления задания
Исходной формой задания является граф микропрограммы автомата (структурная схема алгоритма), которая, как правило, является частью программы функционирования какого-либо устройства в целом и поэтому выглядит достаточно абстрактно.
Функции ЦА, согласно графу, представленному на рисунке 1:
yi - микрооперации, генерируемые ЦА (выходные функции);
хi – входные функции ЦА.
После описания входных и выходных функций можно непосредственно приступить к синтезу ЦА.
2. Технология синтеза ЦА
2.1 Эскизная часть
Для начала выявим состояния ЦА Мура на графе алгоритма и обозначим их через аi (рисунок 1).
По количеству состояний определяем необходимое количество ЭП из соотношения:
2^n-1<N<=2^n,
где N – число состояний, а n - число ЭП. Исходя из рисунка, видим, что N=8. Значит, n=3.
Здесь же делаем проверку на предмет исключения КС2 из схемы. Это эффективно в тех случаях, когда количество ЭП совпадает с числом выходных функций yi (идеальный случай), или они отличаются на несколько единиц процентном отношении. При этом обязательным условием является отсутствие последовательно следующих одинаковых комбинаций (или групп комбинаций) выходных функций ЦА в какой-либо части алгоритма работ ЦА. В это случае состояниям ЭП присваиваются состояния выходных функций, а выходные функции yi будут сниматься прямо с выходов ЭП.
В заданном алгоритме работы ЦА выполняется первое условие – нет одинаковых комбинаций yi , непосредственно следующих друг за другом. Но количество выходных функций yi (4) отличается от количества ЭП на 75%. Следовательно, синтеза КС2 не избежать. КС2 осуществляет перекодирование состояний ЭП в комбинации yi .
Теперь остается выбрать тип ЭП. Это очень непростая задача, так как в лоб она не решается. И чтобы выбрать оптимальный вариант, приходится разрабатывать синтез ЦА на разных типах ЭП. Однако, бывают очевиднее решения. Некоторые и них:
- если количество ветвлений во много раз меньше числа состояний ЦА, то предпочтительней закодировать самый длинный цикл переходов ЭП в виде последовательного набора двоичных чисел, а для реализации этого наилучшим образом подходит JK-триггер (он разработан для двоичного счета);
- если количество ветвлений во много раз больше числа состояний ЭП, то предпочтительней подбирать эти состояния между переходами так, чтобы они отличались изменением только одного заряда; в этом случае эффективнее использовать D-триггер.
В нашем случае полная неопределенность –два ветвления и три состояния ЭП. Но согласно заданию, необходимо разработать ЦА с D-триггером.
Составляем структурную схему ЦА, так как для этого есть все данные. Результат представлен на рисунке 2.

Рисунок 2 – структурная схема ЦА.
На рисунке 2 КС1 и КС2 представлены в виде черных ящиков с известными входными и выходными функциями и неизвестным содержимым.
2.2 Синтез КС2
Известны выходные функции КС2, но не установлены пока входные, которые являются состояниями ЭП. Установить их и установить соответствие между входными и выходными функциями – авторское право. Творческий подход к решению этой проблемы заключается в попытке найти наиболее простую схему КС2 методом подбора 2^n вариантов составления таблицы истинности КС2. Поскольку генерируемый ЭП код уже выбран заранее, то остается получить эти варианты только цикличным сдвигом входных кодов по отношению к выходным.
Анализ восьми вариантов таблицы истинности приведен ниже.
Таблица 1 – первый вариант таблицы истинности КС2.
| Входные функции |
Выходные функции |
Состояния |
|||||
| Q2 |
Q1 |
Q0 |
y1 |
y2 |
y3 |
y4 |
|
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
a0 |
| 0 |
0 |
1 |
1 |
1 |
1 |
0 |
a1 |
| 0 |
1 |
0 |
1 |
1 |
1 |
1 |
a2 |
| 0 |
1 |
1 |
0 |
1 |
1 |
0 |
a3 |
| 1 |
0 |
0 |
0 |
0 |
1 |
1 |
a4 |
| 1 |
0 |
1 |
0 |
1 |
1 |
0 |
a5 |
| 1 |
1 |
0 |
0 |
0 |
1 |
0 |
a6 |
| 1 |
1 |
1 |
0 |
0 |
1 |
1 |
a7 |
y1 =Q2 ’Q1 ’Q0 +Q2 ’Q1 Q0 ’;
y2 =Q2 ’Q1 ’Q0 +Q2 ’Q1 Q0 ’+Q2 ’Q1 Q0 +Q2 Q1 ’Q0 = Q1 ’Q0 +Q2 ’Q1;
y3 =Q2 ’Q1 ’Q0 +Q2 ’Q1 Q0 ’+Q2 ’Q1 Q0 +Q2 Q1 ’Q0 ’+Q2 Q1 ’Q0 +Q2 Q1 Q0 ’+Q2 Q1 Q0 = Q1 + Q2 + Q2 ’Q1 ’Q0 ;
Таблица 2 – второй вариант таблицы истинности КС2
| y4
=Q2
’Q1
Q0
’+ Q2
Q’1
Q0
’+ Q2
Q1
Q0 |
Выходные функции |
Состояния |
|||||
| Q2 |
Q1 |
Q0 |
y1 |
y2 |
y3 |
y4 |
|
| 1 |
1 |
1 |
0 |
0 |
0 |
0 |
a0 |
| 0 |
0 |
0 |
1 |
1 |
1 |
0 |
a1 |
| 0 |
0 |
1 |
1 |
1 |
1 |
1 |
a2 |
| 0 |
1 |
0 |
0 |
1 |
1 |
0 |
a3 |
| 0 |
1 |
1 |
0 |
0 |
1 |
1 |
a4 |
| 1 |
0 |
0 |
0 |
1 |
1 |
0 |
a5 |
| 1 |
0 |
1 |
0 |
0 |
1 |
0 |
a6 |
| 1 |
1 |
0 |
0 |
0 |
1 |
1 |
a7 |
y1 =Q2 ’Q1 ’Q0 ’+Q2 ’Q1 ’Q0 = Q2 ’Q1 ’;
y2 =Q2 ’Q1 ’Q0 ’+Q2 ’Q1 ’Q0 +Q2 ’Q1 Q0 ’+Q2 Q1 ’Q0 ’= Q2 ’Q1 ’+Q2 ’Q1 Q0 ’+Q2 Q1 ’Q0 ’;
y3 =Q2 ’Q1 ’Q0 ’+Q2 ’Q1 ’Q0 +Q2 ’Q1 Q0 ’+Q2 ’Q1 Q0 +Q2 Q1 ’Q0 ’+Q2 Q1 ’Q0 +Q2 Q1 Q0 ’=Q0 ’+ Q1 ’Q0 + Q2 ’Q1 Q0 ;
y4 =Q2 ’Q1 ’Q0 + Q2 ’Q1 Q0 + Q2 Q1 Q0 ’= Q2 ’Q0 + Q2 Q1 Q0 ’
Таблица 3 – третий вариант таблицы истинности КС2
| Входные функции |
Выходные функции |
Состояния |
|||||
| Q2 |
Q1 |
Q0 |
y1 |
y2 |
y3 |
y4 |
|
| 1 |
1 |
0 |
0 |
0 |
0 |
0 |
a0 |
| 1 |
1 |
1 |
1 |
1 |
1 |
0 |
a1 |
| 0 |
0 |
0 |
1 |
1 |
1 |
1 |
a2 |
| 0 |
0 |
1 |
0 |
1 |
1 |
0 |
a3 |
| 0 |
1 |
0 |
0 |
0 |
1 |
1 |
a4 |
| 0 |
1 |
1 |
0 |
1 |
1 |
0 |
a5 |
| 1 |
0 |
0 |
0 |
0 |
1 |
0 |
a6 |
| 1 |
0 |
1 |
0 |
0 |
1 |
1 |
a7 |
y1 =Q2 Q1 Q0 +Q2 ’Q1 ’Q0 ’; y2 =Q2 Q1 Q0 +Q2 ’Q1 ’Q0 ’+Q2 ’Q1 ’Q0 +Q2 ’Q1 Q0 = Q1 Q0 +Q2 ’Q1 ’; y3 =Q2 Q1 Q0 +Q2 ’Q1 ’Q0 ’+Q2 ’Q1 ’Q0 + Q2 ’Q1 Q0 ’+Q2 ’Q1 Q0 +Q2 Q1 ’Q0 ’+Q2 Q1 ’Q0 =Q0 + Q1 ’Q0 ’+ Q2 ’Q1 Q0 ’;
Таблица 4 – четвертый вариант таблицы истинности КС2
| Входные функции |
Выходные функции |
Состояния |
|||||
| Q2 |
Q1 |
Q0 |
y1 |
y2 |
y3 |
y4 |
|
| 1 |
0 |
1 |
0 |
0 |
0 |
0 |
a0 |
| 1 |
1 |
0 |
1 |
1 |
1 |
0 |
a1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
a2 |
| 0 |
0 |
0 |
0 |
1 |
1 |
0 |
a3 |
| 0 |
0 |
1 |
0 |
0 |
1 |
1 |
a4 |
| 0 |
1 |
0 |
0 |
1 |
1 |
0 |
a5 |
| 0 |
1 |
1 |
0 |
0 |
1 |
0 |
a6 |
| 1 |
0 |
0 |
0 |
0 |
1 |
1 |
a7 |
y1 =Q2 Q1 Q0 ’+Q2 Q1 Q0 =Q2 Q1 ;
y2 =Q2 Q1 Q0 ’+Q2 Q1 Q0 +Q2 ’Q1 ’Q0 ’+Q2 ’Q1 Q0 ’= Q2 Q1 +Q2 ’Q0 ’;
y3 =Q2 Q1 Q0 ’+Q2 Q1 Q0 +Q2 ’Q1 ’Q0 ’+Q2 ’Q1 ’Q0 +Q2 ’Q1 Q0 ’+Q2 ’Q1 Q0 +Q2 Q1 ’Q0 ’=Q0 ’+ Q1 Q0 + Q2 ’Q1 ’Q0 ;
y4 =Q2 Q1 Q0 + Q2 ’Q1 ’Q0 + Q2 Q1 ’Q0 ’
Таблица 5 – пятый вариант таблицы истинности КС2
| Входные функции |
Выходные функции |
Состояния |
|||||
| Q2 |
Q1 |
Q0 |
y1 |
y2 |
y3 |
y4 |
|
| 1 |
0 |
0 |
0 |
0 |
0 |
0 |
a0 |
| 1 |
0 |
1 |
1 |
1 |
1 |
0 |
a1 |
| 1 |
1 |
0 |
1 |
1 |
1 |
1 |
a2 |
| 1 |
1 |
1 |
0 |
1 |
1 |
0 |
a3 |
| 0 |
0 |
0 |
0 |
0 |
1 |
1 |
a4 |
| 0 |
0 |
1 |
0 |
1 |
1 |
0 |
a5 |
| 0 |
1 |
0 |
0 |
0 |
1 |
0 |
a6 |
| 0 |
1 |
1 |
0 |
0 |
1 |
1 |
a7 |
y1 =Q2 Q1 ’Q0 +Q2 Q1 Q0 ’;
y2 =Q2 Q1 ’Q0 +Q2 Q1 Q0 ’+Q2 Q1 Q0 +Q2 ’Q1 ’Q0 = Q2 Q1 +Q1 ’Q0;
y3 =Q2 Q1 ’Q0 +Q2 Q1 Q0 ’+Q2 Q1 Q0 +Q2 ’Q1 ’Q0 ’+Q2 ’Q1 ’Q0 +Q2 ’Q1 Q0 ’+Q2 ’Q1 Q0 =Q0 + Q1 Q0 ’+ Q2 ’Q1 ’Q0 ’;
y4 =Q2 Q1 Q0 ’+ Q2 ’Q1 ’Q0 ’+ Q2 ’Q1 Q0
Таблица 6 – шестой вариант таблицы истинности КС2
| Входные функции |
Выходные функции |
Состояния |
|||||
| Q2 |
Q1 |
Q0 |
y1 |
y2 |
y3 |
y4 |
|
| 0 |
1 |
1 |
0 |
0 |
0 |
0 |
a0 |
| 1 |
0 |
0 |
1 |
1 |
1 |
0 |
a1 |
| 1 |
0 |
1 |
1 |
1 |
1 |
1 |
a2 |
| 1 |
1 |
0 |
0 |
1 |
1 |
0 |
a3 |
| 1 |
1 |
1 |
0 |
0 |
1 |
1 |
a4 |
| 0 |
0 |
0 |
0 |
1 |
1 |
0 |
a5 |
| 0 |
0 |
1 |
0 |
0 |
1 |
0 |
a6 |
| 0 |
1 |
0 |
0 |
0 |
1 |
1 |
a7 |
y1 =Q2 Q1 ’Q0 ’+Q2 Q1 ’Q0 =Q2 Q1 ’;
y2 = Q2 Q1 ’Q0 ’+Q2 Q1 ’Q0 +Q2 Q1 Q0 ’+Q2 ’Q1 ’Q0 ’= Q2 Q1 ’+Q2 Q1 Q0 ’+Q2 ’Q1 ’Q0 ’;
y3 =Q2 Q1 ’Q0 ’+Q2 Q1 ’Q0 +Q2 Q1 Q0 ’+Q2 Q1 Q0 +Q2 ’Q1 ’Q0 ’+Q2 ’Q1 ’Q0 +Q2 ’Q1 Q0 ’=Q0 ’+ Q1 ’Q0 + Q2 Q1 Q0 ;
y4 =Q2 Q1 ’Q0 + Q2 Q1 Q0 + Q2 ’Q1 Q0 ’=Q2 Q0 ’+ Q2 ’Q1 Q0 ’
Таблица 7 – седьмой вариант таблицы истинности КС2
| Входные функции |
Выходные функции |
Состояния |
|||||
| Q2 |
Q1 |
Q0 |
y1 |
y2 |
y3 |
y4 |
|
| 0 |
1 |
0 |
0 |
0 |
0 |
0 |
a0 |
| 0 |
1 |
1 |
1 |
1 |
1 |
0 |
a1 |
| 1 |
0 |
0 |
1 |
1 |
1 |
1 |
a2 |
| 1 |
0 |
1 |
0 |
1 |
1 |
0 |
a3 |
| 1 |
1 |
0 |
0 |
0 |
1 |
1 |
a4 |
| 1 |
1 |
1 |
0 |
1 |
1 |
0 |
a5 |
| 0 |
0 |
0 |
0 |
0 |
1 |
0 |
a6 |
| 0 |
0 |
1 |
0 |
0 |
1 |
1 |
a7 |
y1 =Q2 ’Q1 Q0 +Q2 Q1 ’Q0 ’;
y2 =Q2 ’Q1 Q0 +Q2 Q1 ’Q0 ’+Q2 Q1 ’Q0 +Q2 Q1 Q0 = Q1 Q0 +Q2 Q1 ’;
y3 =Q2 ’Q1 Q0 +Q2 Q1 ’Q0 ’+Q2 Q1 ’Q0 +Q2 Q1 Q0 ’+Q2 Q1 Q0 +Q2 ’Q1 ’Q0 ’+Q2 ’Q1 ’Q0 =Q0 + Q2 Q0 ’+ Q2 ’Q1 ’Q0 ’;
y4 =Q2 Q1 ’Q0 ’+ Q2 Q1 Q0 ’+ Q2 ’Q1 ’Q0 =Q2 Q0 ’+ Q2 ’Q1 ’Q0
Таблица 8 – восьмой вариант таблицы истинности КС2
| Входные функции |
Выходные функции |
Состояния |
|||||
| Q2 |
Q1 |
Q0 |
y1 |
y2 |
y3 |
y4 |
|
| 0 |
0 |
1 |
0 |
0 |
0 |
0 |
a0 |
| 0 |
1 |
0 |
1 |
1 |
1 |
0 |
a1 |
| 0 |
1 |
1 |
1 |
1 |
1 |
1 |
a2 |
| 1 |
0 |
0 |
0 |
1 |
1 |
0 |
a3 |
| 1 |
0 |
1 |
0 |
0 |
1 |
1 |
a4 |
| 1 |
1 |
0 |
0 |
1 |
1 |
0 |
a5 |
| 1 |
1 |
1 |
0 |
0 |
1 |
0 |
a6 |
| 0 |
0 |
0 |
0 |
0 |
1 |
1 |
a7 |
y1 =Q2 ’Q1 Q0 ’+Q2 ’Q1 Q0 =Q2 ’Q1 ;
y2 =Q2 ’Q1 Q0 ’+Q2 ’Q1 Q0 +Q2 Q1 ’Q0 ’+Q2 Q1 Q0 ’= Q2 ’Q1 +Q2 Q0 ’;
y3 =Q2 ’Q1 Q0 ’+Q2 ’Q1 Q0 +Q2 Q1 ’Q0 ’+Q2 Q1 ’Q0 +Q2 Q1 Q0 ’+Q2 Q1 Q0 +Q2 ’Q1 ’Q0 ’=Q0 ’+ Q1 Q0 + Q2 Q1 ’Q0 ;
y4 =Q2 ’Q1 Q0 + Q2 Q1 ’Q0 + Q2 ’Q1 ’Q0 ’
Из рассмотренных восьми вариантов таблицы истинности следует выбрать один наиболее простой. Выберем восьмой вариант. Из его анализа следует, что для синтеза КС2 нам потребуется :
- четыре 2-х входовых элементов И;
- четыре 3-х входовых И;
- один 2-х входовый ИЛИ;
- два 3-х входовых ИЛИ.
2 .3 Синтез КС1
Теперь можно приступить к синтезу КС1. Для начала отметим, что принципиально функции КС1 ничем не отличаются от функций КС2 – такое же перекодирующее устройство. Однако, нам потребуется составить таблицу истинности для нее, а это требует знания ее функций уже в составе ЦА. Но эти функции очевидны: в соответствии с графом алгоритма ЦА комбинационная схема ЦА должна осуществлять перекодировку кода, составленного текущими состояниями ЭП Qi и комбинацией входных функций хi , в код, состоящий из управляющих функций ЭП в таком виде, который подготовит следующие состояния ЭП. И поскольку таблица истинности КС2 уже определена, то не составляет труда составить граф алгоритма ЦА уже для переходов между состояниями ЭП, заменив механически комбинации yi на Qi , откуда можно определить текущие и последующие состояния ЭП.
Процесс синтеза КС1 достаточно трудоемкий, поэтому его лучше разбить на несколько этапов.
Этап 1.
Сформируем сначала диаграмму-таблицу состояний и переходов в соответствии с графом (рисунок 1)
Таблица 9 – диаграмма состояний и переходов
| x2 ’ x1 ’ |
x2 ’ x1 |
x2 x1 ’ |
x2 x1 |
Q2 |
Q1 |
Q0 |
| a0 |
a0 |
a0 |
a0 |
0 |
0 |
1 |
| a1 |
a1 |
a1 |
a1 |
0 |
1 |
0 |
| a2 |
a2 |
a2 |
a2 |
0 |
1 |
1 |
| a3 |
a3 |
a3 |
a3 |
1 |
0 |
0 |
| a4 |
a4 |
a4 |
a4 |
1 |
0 |
1 |
| a5 |
a5 |
a5 |
a5 |
1 |
1 |
0 |
| a6 |
a6 |
a6 |
a6 |
1 |
1 |
1 |
| a7 |
a7 |
a7 |
a7 |
0 |
0 |
0 |
Составляется такая таблица легко. Приведем последовательность ее составления:
1) переход с a0 на a1 не зависит от xi , то есть он должен быть при x2 ’
x1 ’+ x2 ’ x1 + x2 x1 ’+ x2 x1 ;
2) переход с a1 на a2 не зависит от xi , то есть он должен быть при x2 ’
x1 ’+ x2 ’ x1 + x2 x1 ’+ x2 x1 ;
3) переход с a2 на a3 не зависит от xi , то есть он должен быть при x2 ’
x1 ’+ x2 ’ x1 + x2 x1 ’+ x2 x1 ;
4) переход с a3
- на a4 осуществляется при
x1 ’= x2 ’ x1 ’+ x2 x1 ’;
- на a5 при x2 ’ x1
- на a6 при x2 x1
5) переход с a5 на a7 не зависит от xi , то есть он должен быть при x2 ’
x1 ’+ x2 ’ x1 + x2 x1 ’+ x2 x1 ;
6) переход с a6 на a7 не зависит от xi , то есть он должен быть при x2 ’
x1 ’+ x2 ’ x1 + x2 x1 ’+ x2 x1 .
На этом первый этап можно считать законченным.
Этап 2.
Составляем таблицу истинности КС1, исходя из таблицы 9 и таблицы истинности D-триггера (таблица 10).
Таблица 10 – таблица истинности D-триггера
| C |
D |
Q(t) |
Q(t+1) |
Q(t)→Q(t+1) |
D |
| 0 |
0 |
0 |
0 |
0→0 |
x |
| 0 |
1 |
0 |
0 |
0→1 |
1 |
| 0 |
0 |
1 |
1 |
1→0 |
0 |
| 0 |
1 |
1 |
1 |
1→1 |
x |
| 1 |
0 |
0 |
0 |
||
| 1 |
0 |
1 |
0 |
||
| 1 |
1 |
0 |
1 |
||
| 1 |
1 |
1 |
1 |
Итак, составляем таблицу истинности КС1
Таблица 11 – таблица истинности КС1
| Входные функции |
Последующие состояния |
Выходные функции |
||||||||
| x1 |
х2 |
Q2 |
Q1 |
Q0 |
Q2 ’ |
Q1 ’ |
Q0 ’ |
D2 |
D1 |
D0 |
| 0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
x |
1 |
0 |
| 0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
x |
x |
1 |
| 0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
| 0 |
0 |
1 |
0 |
0 |
- |
- |
- |
- |
- |
- |
| 0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
x |
1 |
x |
| 0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
x |
x |
1 |
| 0 |
0 |
1 |
1 |
1 |
- |
- |
- |
- |
- |
- |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
x |
x |
1 |
| 0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
x |
1 |
0 |
| 0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
x |
x |
1 |
| 0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
| 0 |
1 |
1 |
0 |
0 |
- |
- |
- |
- |
- |
- |
| 0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
x |
1 |
x |
| 0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
x |
x |
1 |
| 0 |
1 |
1 |
1 |
1 |
- |
- |
- |
- |
- |
- |
| 0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
x |
x |
1 |
| 1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
x |
1 |
0 |
| 1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
x |
x |
1 |
| 1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1x |
| 1 |
1 |
1 |
0 |
0 |
- |
- |
- |
- |
- |
- |
| 1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
x |
1 |
x |
| 1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
x |
x |
1 |
| 1 |
1 |
1 |
1 |
1 |
- |
- |
- |
x |
x |
1 |
| 1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
|||
| 1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
x |
1 |
0 |
| 1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
x |
x |
1 |
| 1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
x |
0 |
| 1 |
0 |
1 |
0 |
0 |
- |
- |
- |
- |
- |
- |
| 1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
x |
1 |
x |
| 1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
x |
x |
1 |
| 1 |
0 |
1 |
1 |
1 |
- |
- |
- |
- |
- |
- |
| 1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
x |
x |
1 |
Теперь необходимо определить логические выражения для D-триггера – D0 , D1 и D2 .
Анализируя таблицу истинности, видим, что D2 есть логическая единица. Для составления логических выражений для D1 и D2 воспользуемся картой Карно, таким образом, будет сразу проведена минимизация ДНФ.
2 .4 Составление логической схемы ЦА
При построении логической схемы ЦА за основу принимаем структурную схему автомата (рисунок 2). Все связи между блоками уже определены в структурной схеме, остается только заполнить «черные» ящики КС1 иКС2 элементами, определенными в предыдущих пунктах и регистр ЭП представить соответствующим количеством триггеров и соединить все эти элементы в соответствии с уравнениями для y1 , y2 , y3 , y4 и D0 , D1 , D2 .
Текстовые входы (входы «С») триггеров соединяем в один узел (параллельное соединение) для того, чтобы подключить к этому входу ЦА тактовый сигнал.
Таким образом, получается схемное решение ЦА (рисунок 3).
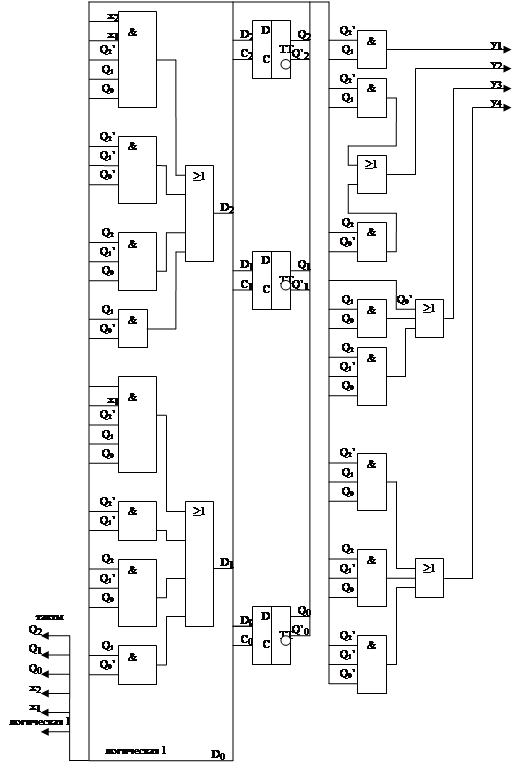
Заключение
Синтез ЦА на основе графа микропрограммы автомата состоит из двух этапов: составление логической схемы ЦА (которое в свою очередь включает эскизную часть, синтез КС2 и КС1) и непосредственно интегральной микросхемы ЦА. На первом этапе для оформления курсового проекта используются средства пакета MS Office – MS Word. На втором этапе применяются данные справочников по интегральным микросхемам для построения ее на основе логической схемы ЦА путем замены логических элементов на соответствующие цифровые микросхемы.
Список использованной литературы
1. Булатов В. Н. Дискретные преобразования и логический синтез в цифровой электронике. Методические указания; ОГУ. Оренбург, 1994
2. Тарабрин Б. В. Справочник по интегральным микросхемам; М.: «Энергия», 1977