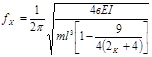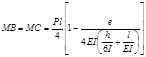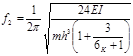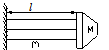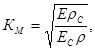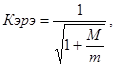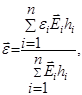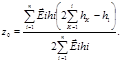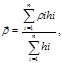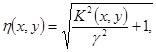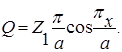| Скачать .docx |
Курсовая работа: Методика выполнения прочностных расчетов электрорадиоэлементов и элементов конструкций радиоэлектронной аппаратуры
МЕТОДИКА ВЫПОЛНЕНИЯ ПРОЧНОСТНЫХ РАСЧЕТОВ ЭЛЕКТРОРАДИОЭЛЕМЕНТОВ И ЭЛЕМЕНТОВ КОНСТРУКЦИЙ РЭА
1. Расчет прочности электрорадиэлементов
1.1 Прочность ЭРЭ, закрепленного на выводах
Большинство отказов электрорадиэлементов (ЭРЭ) обусловлено усталостными разрушениями их выводов. Усталостные разрушения обычно возникают при резонансных колебаниях ЭРЭ, закрепленных на выводах, и резонансных колебаниях монтажных плат, определяющих изгибающие моменты в выводах ЭРА.
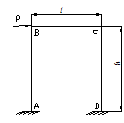
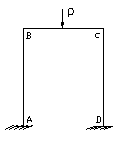
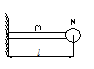
Расчетные модели ЭРЭ в этом случае студенту следует выбирать в виде рам балок. При колебаниях ЭРЭ на него действует инерционная сила Рu, которая может быть разложена на три составляющие Px, Py, Pz (рис.1).
В табл. 1 приведены расчетные соотношения для определения изгибающих моментов и собственных частот колебаний в характерных сечениях выводов ЭРЭ : места присоединения выводов к монтажной плате (точки A, D), местах изгиба выводов (токи В, С).
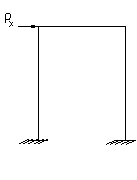
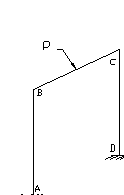
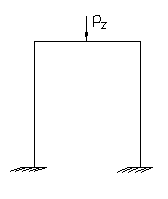
Рис. 1 Расчетная модель ЭРЭ при действии инерционной силы Рu
Таблица 1
| Схема и нагрузки |
Изгибающие моменты в характерных сечениях |
Частоты собственных колебаний |
|
|
|
|
|
|
|
|
|
|
|
|
В формулах табл.1 :
MA
, MB
, MC
, MD
, – изгибающие моменты в сечениях A, B, C, D, Н·м ; fx, fy, fz – частоты собственных колебаний ЭРЭ вдоль осей X, Y, Z, Гц ; Е – модуль упругости материала вывода ЭРЭ, Н/м2
; G – модуль сдвига материала вывода ЭРЭ, Н/м2
, ![]() где ε – коэффициент Пуассона ; I – момент инерции сечения выводы ЭРЭ, м4
; l
–– длина пролета рамы (расстояние между точками крепления выводов ЭРЭ), м ; h – высота оси ЭРЭ, м ; K – коэффициент, связывающий l
и h ;
где ε – коэффициент Пуассона ; I – момент инерции сечения выводы ЭРЭ, м4
; l
–– длина пролета рамы (расстояние между точками крепления выводов ЭРЭ), м ; h – высота оси ЭРЭ, м ; K – коэффициент, связывающий l
и h ; ![]() m – масса ЭРЭ.
m – масса ЭРЭ.
Собственные частоты изгибных колебаний ЭРЭ, описанного эквивалентной схемой балки, определяется по формуле :
|
|
(.1) |
где φ –безразмерный коэффициент, зависящий от вида конструкции и способа закрепления ЭРЭ ; l – длина вывода ЭРЭ, м ; E – модуль упругости материала вывода ЭРЭ, Н/м2 ; I – момент инерции сечения выводы ЭРЭ, м4 ; M – масса ЭРЭ без выводов, кг ; C – коэффициент, учитывающий влияние массы выводов ; m – масса одного вывода ЭРЭ, кг.
Расчетные схемы в виде балки некоторых типов ЭРЭ и соотношения для оценки частоты собственных колебаний приведены в табл. 2.
Таблица 2.2
| Тип элемента |
Эквивалентная схема |
f0 |
| Конденсатор, резистор, диод |
|
|
| Транзистор микромодуль, интегральная схема |
|
|
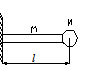
| Контакт реле |
|
|
Необходимо узнать, что выбор расчетной схемы зависит от условий внешних воздействий и колебания ЭРЭ. Модуль в виде рамы пригодна в случаях установки ЭРЭ на печатной плате при различных направлениях вибрационной нагрузки, модель в виде балки – лишь при соответствующем направлении Pu.
Пример 1. Резистор МЛТ – 0,5 установлен на печатной плате по варианту 11 а (ОСТ 4ГО.010.030) в конструкции автомобильной РЭА (группа 3 по ГОСТ 16019 – 78) ; ориентация РЭА в кабине автомобиля – произвольная.
Определить, выдержит ли испытания вибропрочность резистор, установленный по данному варианту.
Исходные данные.
Из ОСТ 4.ГО.010.030 следует, что масса резистора m = 3·10–3 кг ;
расстояние между выводами l = 1·10–2 м ;
высота установки резистора h = 5·10–3 м.
Выводы выполнены из холоднокатоной медной проволки с параметрами :
модуль упругости Е = 1,23·1011 Н/м2 ;
модуль сдвига G = 4,8·1010 Н/м2 ;
коэффициент Пуассона ε =0,28 ;
придел прочности σв = 40·105 Н/м2 ;
диаметр вывода d =1·10–3 м.
Из ГОСТ 16019 – 78 следует :
диапазон частот вибраций Δf =(10 – 70) Гц ;
коэффициент виброперегрузки nn = 4 ;
время испытаний Т =45 мин = 2700 с.
РЕШЕНИЕ. Поскольку ориентация РЭА произвольная, следует оценить все возможные варианты воздействия вибрационных нагрузок.
1. Расчет собственных частот колебаний резистора
По табл. П.2 находим, что момент инерции сечения вывода
I = 0,05·d4 = 0,05·1·10–12 =5·10–14 м4 ;
К = h/l = 5·10–3 /10·10–3 =0,5 ;
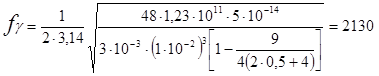 Гц ;
Гц ;
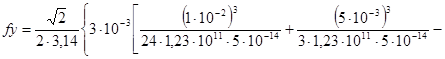
![]()
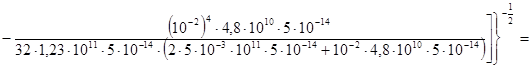
=1184 Гц ;
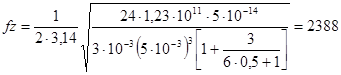 Гц.
Гц.
Выбираем частоту fy, как минимальную.
2. Расчет инерционной силы и изгибающих моментов. Определим логарифмический декремент затухания
![]()
и коэффициент динамичности по (1.9) :
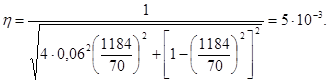
Находим инерционную силу по (1.8) :
Pu =3·10-3 ·9,8·5·10-3 ·4 = 0,6·10-3 Н.
Используя формулы табл.2.1, находим изгибающие моменты
![]() Н·м ;
Н·м ;
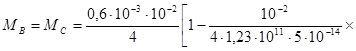
 Н·м
Н·м
3. Определяем расчетные напряжения
![]() Н/м2
;
Н/м2
;
![]() Н/м2
.
Н/м2
.
Таким образом, максимальные напряжения в местах крепления выводов к плате σ =0,15·10 Н/м2 .
4. Определяем допускаемые напряжения
Поскольку число циклов N = Тf = 3, 2·106 меньше 107 , находим придельные напряжения из (1.17) :
![]() Н/м2
;
Н/м2
;
![]() Н/м2
.
Н/м2
.
Определяем запас прочности, принимая n1 = 2, n2 = 1,3, n3 = 4. n = 2 · 1,3 · 4 = 10,4. Допускаемые напряжения
[ σ ] = σN /n = 10,7·105 /10,4 = 1,03·105 Н/м2 .
Таким образом, выбранный способ крепления резистора удовлетворяет требованиям технического задания.
1.2 Прочность ЭРЭ, прикрепленного к плате
В этом случае наиболее опасными являются резонансные колебания на основной части платы. На вывод будет действовать изгибающий момент, обусловленный поворотом сечения платы на угол θ, а также линейная сила, определяемая деформацией ΔZ = Z1 -Z2 (рис. 2).
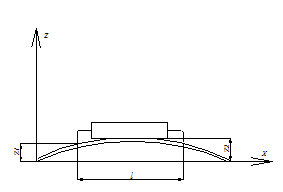
Рис.2 Изгиб выводов ЭРЭ при резонансных колебаниях платы
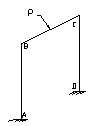
Расчетную модель можно представить в виде рамки, изображенной на рис.3
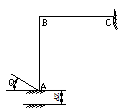
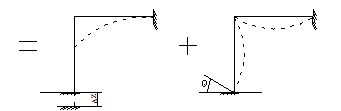
Рис.3 Расчетная модель ЭРЭ, закрепленного на плате
Изгибающие моменты для характерных сечений А, В, С определяются из соотношений :
|
|
(2) |
Таблица 3 Значение частотной постоянной
| Номер варианта схемы |
Отношение сторон платы |
||||||||
| 0,1 |
0,2 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
4 |
|
| 1 |
23,1 |
23,8 |
28,6 |
45,8 |
74,4 |
114,5 |
166,0 |
228,9 |
389,3 |
| 2 |
23,3 |
24 |
30,2 |
55 |
98,8 |
160,9 |
241,2 |
339,4 |
589,7 |
| 3 |
35,9 |
36,5 |
40,2 |
55 |
81,8 |
120,7 |
171,5 |
234,1 |
394 |
| 4 |
23,2 |
23,9 |
32,1 |
67,6 |
131,1 |
221,4 |
337,9 |
480,5 |
843,6 |
| 5 |
52 |
52,4 |
55,3 |
67,3 |
90,9 |
127,6 |
176,9 |
238,8 |
396,7 |
| 6 |
35,8 |
36,6 |
41,4 |
63,1 |
104,7 |
165,7 |
245,4 |
343,2 |
593,1 |
| 7 |
52,1 |
52,5 |
56,2 |
74,1 |
102,5 |
170,6 |
248,5 |
345,1 |
592,8 |
| 8 |
35,9 |
36,7 |
42,2 |
74,1 |
135,4 |
224,6 |
340,6 |
482,8 |
845,8 |
| 9 |
52,1 |
52,6 |
57,2 |
83,8 |
141,4 |
228,7 |
343,7 |
485,4 |
847,6 |
| 10 |
0,8 |
1,6 |
4,1 |
8,2 |
12,3 |
16,4 |
20,5 |
24,6 |
32,8 |
| 11 |
0,2 |
0,9 |
5,7 |
22,9 |
51,5 |
91,6 |
143,1 |
206,1 |
366,4 |
| 12 |
23 |
23 |
23 |
23 |
23 |
23 |
23 |
23 |
23 |
| 13 |
1,5 |
3,1 |
9,4 |
27,3 |
56,2 |
96,3 |
147,9 |
210,9 |
371,2 |
| 14 |
22,9 |
23,1 |
24,1 |
27,3 |
32 |
37,6 |
43,8 |
50,3 |
63,9 |
| 15 |
8,4 |
9,3 |
18,3 |
56,2 |
120,9 |
211,7 |
328,6 |
471,4 |
834,9 |
| 16 |
51,9 |
52,1 |
52,9 |
56,1 |
62,5 |
72,9 |
87,9 |
107,7 |
162,2 |
| 17 |
8,3 |
8,6 |
10,6 |
17,3 |
27,9 |
42,4 |
60,8 |
83,8 |
140,6 |
| 18 |
52 |
52 |
52 |
52 |
52 |
52 |
52 |
52 |
52 |
| 19 |
0,5 |
2,1 |
12,9 |
51,9 |
116,8 |
207,6 |
324,4 |
467,1 |
816,6 |
| 20 |
8,2 |
8,2 |
8,2 |
8,2 |
8,2 |
8,2 |
8,2 |
8,2 |
8,2 |
| 21 |
0,8 |
0,3 |
2,04 |
8,2 |
18,4 |
32,6 |
51 |
73,5 |
130,6 |
| 22 |
35,8 |
35,8 |
35,8 |
35,8 |
35,8 |
35,8 |
35,8 |
35,8 |
35,8 |
| 23 |
0,4 |
1,4 |
8,9 |
35,8 |
80,5 |
143,1 |
223,6 |
321,9 |
572,4 |
| 24 |
8,4 |
9,1 |
15,5 |
41,4 |
85,9 |
148,4 |
228,9 |
327,2 |
577,6 |
| 25 |
35,8 |
35,9 |
37,1 |
41,4 |
49,5 |
61,8 |
78,7 |
100,1 |
155,8 |
| 26 |
8,2 |
8,4 |
9,6 |
13,1 |
17,4 |
22,1 |
29,9 |
31,8 |
41,8 |
| 27 |
1 |
2,07 |
5,5 |
13,1 |
23,9 |
38,5 |
37,1 |
78,6 |
136,9 |
| 28 |
51,9 |
52 |
52,6 |
54,5 |
57,6 |
61,7 |
66,5 |
72 |
84,4 |
| 29 |
1,7 |
3,9 |
15,4 |
54,5 |
119,4 |
210,3 |
327,1 |
469,8 |
833,2 |
| 30 |
35,8 |
36 |
37,3 |
41,4 |
47,6 |
55,1 |
63,4 |
72,3 |
91,1 |
| 31 |
2,1 |
4,4 |
13,8 |
41,4 |
86,4 |
149,1 |
229,6 |
328,1 |
578,5 |
2. Расчет прочности печатных плат
В соответствии с общей методикой прочностных расчетов для оценки прочности печатной платы необходимо в первую очередь рассчитать основную частоту собственных колебаний платы.
Частота собственных колебаний пластин определяется соотношениями (1) – (4). Для упрощения расчета преобразуем формулу (1) к следующему виду
|
|
(3) |
где h –толщина пластин, м ; а
– длина пластины, м ; 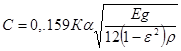 – частотная постоянная, соответствующая различным вариантам закрепление стальной пластины, изображенным в табл. П.3, при разных соотношениях сторон а/в
(табл. 3). При расчете собственной частоты пластины с соотношениями сторон а/в
, не несовпадающими с табличными, значение частотной постоянной можно найти интерполяцией табличных данных. Поскольку основание печатной платы выполняется не из стали, то в формулу (3) вводится поправочный коэффициент на материал
– частотная постоянная, соответствующая различным вариантам закрепление стальной пластины, изображенным в табл. П.3, при разных соотношениях сторон а/в
(табл. 3). При расчете собственной частоты пластины с соотношениями сторон а/в
, не несовпадающими с табличными, значение частотной постоянной можно найти интерполяцией табличных данных. Поскольку основание печатной платы выполняется не из стали, то в формулу (3) вводится поправочный коэффициент на материал
|
|
(4) |
где E и ρ – модуль упругости применяемого материала основание печатной платы ; Eс и ρс – модуль упругости и плотность стали, Eс = 2,1∙ 1011
Н/м2 ; ρс =7,85 ∙ 103 кг/м3 .
Характеристики материалов печатных плат толщиной 1 мм приведены в табл.4
Таблица 4
| Материал основания |
модуль упругости Е∙ 1010 Н/м2 |
Плотность ρ ∙ 103 кг/м3 |
Коэффициент Пуассона e |
| Гетинакс Гф –1 Стеклотекстолит СТЭ " СТЭФ " НДФ " СТЭФ–1 " СФ –2 |
2,7 3,5 3,3 3,45 3,02 5,7 |
1,45 1,98 2,47 2,32 2,05 2,67 |
0,21 0,214 0,279 0,238 0,22 0,24 |
Данные табл. 4 приведены для нагруженных пластин. Если плата равномерно нагружена, то формулу (3) вводят поправочный коэффициент на массу ЭРЭ :
|
|
(5) |
где m – масса платы ; M – масса ЭРЭ.
С учетом (4) и (5) формула для приближенного определения собственной частоты основного тона колебаний равномерно нагруженной печатной платы пример вид :
|
|
(6) |
По формуле (6) можно оценить и собственную частоту колебаний любой равномерно нагруженной пластины.
Пример 2. Определить собственную резонансную частоту печатной платы, защепленную по короткой стороне и пертую по остальным сторонам .
Исходные данные :
габаритные размеры платы, м : а = 0,1 ; в = 0,1 ; h = 1·10-3 ;
материал платы – стеклотекстолит СТЭФ – 1 с параметрами :
Е =3,02 · 1010 Н/м2 ; ρ = 2,05·103 кг/ м3 ; ε = 0,22 ;
масса элементов М = 0,1 кг.
РЕШЕНИЕ :
1. Находим массу платы
![]() кг,
кг,
2. Рассчитываем поправочный коэффициент
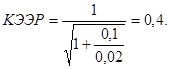
3. Из табл. 4 (вариант 3) находим С = 55 ;
4. По формуле (4) рассчитываем коэффициент
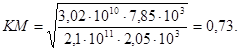
5. Подставляя полученные данные в формулу (6), определяем частоту собственных колебаний платы
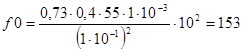 Гц.
Гц.
2.2 Расчет частот собственных колебаний многослойных печатных плат
При расчете частоты собственных колебаний многослойной печатной платы неоднородную по толщине пластину приводят к однородной следующим образом .
1. Рассчитывают коэффициент поперечного сжатия
|
|
(7) |
где ![]() – эффективный модуль упругости i
– го слоя ; Еi
– модуль упругости материала i
– го слоя ; εi
– коэффициент Пуассона i
– го слоя ; hi
– толщена i
– го слоя ; n – количество слоев многослойной платы.
– эффективный модуль упругости i
– го слоя ; Еi
– модуль упругости материала i
– го слоя ; εi
– коэффициент Пуассона i
– го слоя ; hi
– толщена i
– го слоя ; n – количество слоев многослойной платы.
2. Определяют приведенную изгибную (цилиндрическую) жесткость платы
|
|
(8) |
где z0 –расстояние нейтральной поверхности платы от верхней граничной поверхности,
|
|
(9) |
3. Определяют приведенную плотность платы
|
|
(10) |
где ρi – плотность материала i – го слоя .
4. Определяют приведенное значение модуля упругости
|
|
(11) |
где 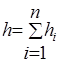 – толщина платы.
– толщина платы.
5. По (4) определяют поправочный коэффициент на материал.
6. Определяют частоту собственных колебаний платы по (6) : частотная постоянная находится для пластины с параметрами a, в,
h
коэффициент массы рассчитывается по (5) , в которой 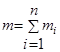 – масса платы.
– масса платы.
Пример 3. Рассчитать собственную резонансную частоту двухсторонней печатной платы, изготовленной из стеклотекстолита СФ–2–50, установленной в конструкции РЭА с замещением по короткой стороне (вариант 20).
Исходные данные :
габаритные основания платы, м : а = 0,1 ; в = 0,1 ; h2 = 9·10-4 ;
материал основания платы – стеклотекстолит СТЭ с параметрами Е2 = 3,5·1010 Н/м2 ; ρ2 = 1,98·103 кг/м3 ; ε2 = 0,214 ;
материал плакировки – медная фольга, толщиной h1 = h3 =5·10-5 м с параметрами Е 1 = Е3 = 13,2·1010 Н/м2 ; ρ1 = ρ3 = 8,9·103 кг/м3 ; ε1 = ε3 = 0,3 ; масса элементов m = 0,1 кг.
РЕШЕНИЕ
1. Рассчитаем значение эффективных модулей упругости
![]() Н/м2
;
Н/м2
;
![]() Н/м2
.
Н/м2
.
2.Приведенный коэффициент поперечного сжатия
![]()
3. Рассчитываем расстояние до нейтральной зоны, учитывая симметричность структуры
![]() м.
м.
определяем значение приведенной жесткости по (2.8) с учетом Ē1 = Ē3 и h1 = h3 :
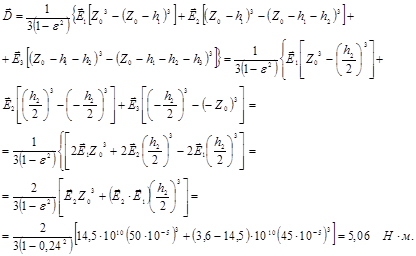
5.Определяем приведенную плотность платы по (10) :
![]() кг/м3
кг/м3
6.Определяем приведенное значение модуля упругости по (11) :
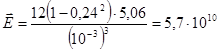 Н/м2
.
Н/м2
.
7.Определяем по (4) коэффициент
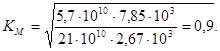
8.Определяем по (5) коэффициент
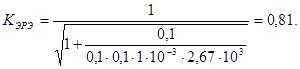
9.По табл3 (вариант 20) находим С = 8,2.
10.Рассчитываем частоту собственных колебаний платы
![]() Гц.
Гц.
2.2 Расчет механический в плате
Изгибающий момент в центре платы в режиме вибрационных колебаний
|
|
(12) |
где М – масса установленных на плате ЭРЭ, кг ; g – ускорение свободного падения –9,8 м/с2 ; ПП – коэффициент вибрационной перегрузки ;ξ – коэффициент динамичности.
Момент сопротивление изгибу ![]()
Условие вибропрочности платы
|
|
(13) |
Пример 4. Проверить условие вибропрочности печатных плат, рассмотренных в примерах 2 и 3, для условий использования в автомобильной РЭА (пример 1).
Исходные данные :
диапазон частот вибраций Δf = (10 – 70) Гц ;
коэффициент виброперегрузки ПП = 4 ;
время испытаний Т = 2700 с ;
габаритные размеры плат, м : а =0,1; в = 0,1; h = 1·10–3 ;
частоты собственных колебаний плат, Гц : f1 =153; f2 = 60;
придел упругости для стеклотекстолита σв =130·106 Н/м2 ;
логарифмический декремент затухания δ = 0,2;
запас прочности n = 10,4.
1.Рассчитаем коэффициент динамичности для обоих вариантов, при этом для первого варианта принимаем в качестве возбуждающей верхнее значение частоты fB = 70 Гц, а для второго – наихудший случай – равный частоте собственных колебаний f = 60 Гц.
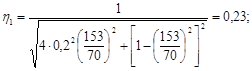 η2
= 3,14/0,2 = 15,7.
η2
= 3,14/0,2 = 15,7.
2.Допускаемые напряжения определим из соотношения (17), поскольку Tf < 107 для обоих случаев :
σ-1 = 0,3·σв = 39·106 Н/м2 ;
σN1 = 39·106 +0,167 (130·106 – 39·106 ) 16 – lg 2700 +153 = 39,1·106 Н/м2;
tN2 = 51·106 Н/м2 ; [ σ-1 ] = 3,8·106 Н/м2 ;
[ σ2 ] = 4,9·106 Н/м2 .
3.Расчетные напряжения в центре платы
![]() Н/м2 ;
Н/м2 ;
![]() Н/м2 .
Н/м2 .
Таким образом, первый вариант крепления платы удовлетворяет требованиям ТЗ, а второй – нет.
2.3 Расчет перегрузок в любой точке платы
Для определения усилий, прикладываемых к выводам ЭРЭ, необходимо знать виброперегрузки в любой точке платы с координатами х, у.
Форму колебаний платы на первой соответственной частоте в направлении осей х, у можно представить в виде
| Z (X) = Z1 sin (πx/a) ; Z (y) = Z1 sin (πy/в), |
(14) |
где Z1 – прогиб платы в центре .
Коэффициенты передачи на первой собственной частоте рассчитывается по формуле
|
|
(15) |
где γ – коэффициент механических потерь ; К (х, у) – коэффициент формы колебаний,
|
|
(16) |
здесь К (х, у) = К (ξх ) · К (ξу ),
Коэффициенты К (ξх ) · К (ξу ), определяются из табл. 5, а промежуточных точках – интерполированием.
Таблица 5 Коэффициенты формы колебаний
| Условия закрепления |
ξх = х/а, ξ = у/в |
||||||||||
| 0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
|
|
|
0 |
0,39 |
0,75 |
1,03 |
1,21 |
1,27 |
1,21 |
1,03 |
0,75 |
0,39 |
0 |
|
|
0 |
0,16 |
0,51 |
0,91 |
1,21 |
1,32 |
1,20 |
0,91 |
0,51 |
0,16 |
0 |
|
|
0 |
0,49 |
0,9 |
1,19 |
1,31 |
1,26 |
1,05 |
0,73 |
0,39 |
0,12 |
0 |
|
|
0 |
0,03 |
0,1 |
0,21 |
0,36 |
0,53 |
0,72 |
0,92 |
1,14 |
1,35 |
1,57 |
Коэффициенты механических потерь
|
|
(17) |
где f0 – первая частота собственных колебаний платы, Гц.
Угол поворота сечений платы
|
|
(18) |
Прогиб в центре платы
|
|
(19) |
где Z0 – амплитуда вибраций, передаваемая от мест крепления платы, м:
|
|
(20) |
Пример 5. Рассчитать виброускорение и вибропрочность в точках крепления резистора МЛТ – 0,5 (пример 1), установленного в центре печатной платы (пример 4).
Исходные данные :
масса резистора m =3·10-3 кг ;
длина вывода l = 2·10-3 м ;
высота установки резистора h = 1,5·10-3 м ;
модуль упругости выводов E =1,23·1011 Н/м2 ;
модуль сдвига G = 4,8·1010 Н/м2 ;
коэффициент Пуассона ε = 0,28 ;
придел прочности σв = 1·10-3 Н/м2 ;
диаметр вывода d = 1·10-3 м ;
размеры печатной платы, м : a = 0,1 ; в =0,1 ; h =1·10-3 ;
собственная частота колебаний платы f0 = 60 Гц ;
диапазон частотных вибраций Δƒ = (10 – 70) Гц .
коэффициент виброперегрузки ПП =4 ;
время испытаний Т =2700 с.
РЕШЕНИЕ.
1. По (17) находим амплитуду колебаний
![]()
2. По (17) определяем коэффициент механических потерь
![]()
3.Прогиб в центре платы находим по (19) :
![]() м.
м.
4.Коэффициент динамичности в точке с координатами х = 45·10-3 м ; у =50·10-3 м определяем по (14) :
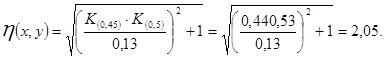
5.Виброускорение в выбранной точке
Z (x, y) = 4g·2,05 = 8,2g.
6. Угол Q определяем по (18)
![]() рад
рад
7.Определяем ΔZ как разницу перемещений
![]()
8.По (2.2) рассчитываем изгибающие моменты
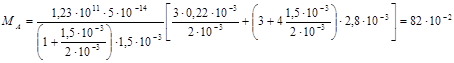 Н·м ;
Н·м ;
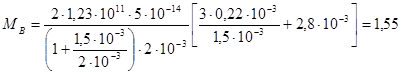 Н·м ;
Н·м ;
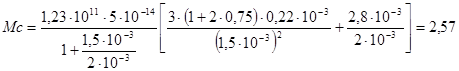 Н·м.
Н·м.
9. Для наибольшего изгибающего момента в точке С находим
![]() Н/м2
.
Н/м2
.
10.сравнивая расчетное значение σ с допускаемым [ σ ] (пример 1), приходим к выводу, что данный вариант крепления резистора не удовлетворяет требованиям ТЗ.
2.4 Проверка правильности выбора толщены стенки корпуса РЭА
Толщина стенки корпуса h, при которой выполняется прочностные требования, определяются по формуле
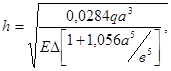
где q = P / aв – нагрузка, распределенная по площади, Н/м2 ; a, в – размеры стенки корпуса, м ; Δ – допустимый прогиб, м.
Нагрузкой Р необходимо задаваться или определять по 2 ; допустимый прогиб определяется по (5).
2.5 Расчет на прочность панели шасси
Разрушение шасси наблюдается по сечениям, ослабленным отверстиями для установки элементов конструкции. Монтажная панель шасси наиболее ослаблена в поперечном сечении рабочей длиной
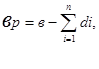
где в – ширина панели ; di – диаметр i – го отверстия, ослабляющего сечение. Высота сечения равна толщине панели Δ.
Предполагая многократный изгиб апнели под действием знакопеременной вибрационной нагрузки и, рассматривая ее как прямоугольную пластину на двух опорах, используем управление изгибной прочности
![]() .
.
Изгибающий момент в режиме резонансных колебаний
![]()
где М – масса установленных по шасси элементов конструкции ; η – коэффициент динамичности ; ПП – коэффициент вибрационной перегрузки.
Момент сопротивление изгибу ![]()
Тогда прочность панели шасси следует оценить соотношением
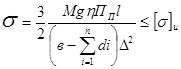
2.6Расчеты на прочность неразъемных соединений
Соединение склеиванием, пайкой и сваркой проверяют по первому уравнению прочности :
![]() ,
,
где Р – усилие, воспринимаемое соединением, Н ; S – площадь склеивания (пайкой, сварки), м2 ; [ σ ]р – допускаемое нормальное напряжение разрыва.
Условие прочности прессового соединения цилиндрических деталей номинальным диаметром d, длиной запресовки l
, нагруженного крутящим моментом М £ Мт, где Мт – момент трения в прессовочном соединении ![]() , здесь q – удельное давление на поверхности запресовки ; К – коэффициент трения.
, здесь q – удельное давление на поверхности запресовки ; К – коэффициент трения.
Удельное трение, выраженное через натяг Δ , номинальный диаметр сопряжения d , диаметр dA , dB и прочностные характеристики сопряженных деталей
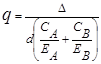 ,
,
где 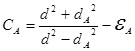 ;
; 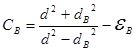 ;
;
здесь εА и εВ – коэффициенты поперечной деформации (коэффициенты Пуассона) ; ЕА и ЕВ – модуль упругости материала сопрягаемых деталей.
Следует указать, что расчет прочности соединения заклепками сводиться к совместному решению уравнения прочности для :
а) стержня заклепки, работающего на срез
![]() ;
;
б) листа, ослабленного отверстиями под заклепками и работающего на разрыв
![]()
в) листа, разрезаемого по двум параллельным плоскостям стержнем заклепки
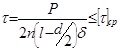 ;
;
г) листа, сминаемого стержнем заклепки
![]() .
.
В этих уравнениях : Р – растягивающее усилие, Н ; n – число заклепок ;
l – напуск листа, м ; d – диаметр заклепки, м ; t – шаг заклепок, м ; δ – толщина листа, м ; [ τ ]cp , [ σ ]р , [ σ ]см – допускаемые напряжения среза заклепки, растяжения и смятия листа, Н/м2 .
2.7Расчеты на прочность разъемных соединений
При оценке эффективности крепежных соединений (болтовых, винтовых) , можно использовать уравнение прочности для соединений заклепками. При этом чаще всего пользуются соотношением
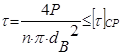 ,
,
где dВ – внутренний диаметр винта (болта), dВ = 0,8d.
Рассмотренные в методических указаниях методы оценки статической, вибро – и ударопрочности конструкций РЭА позволяют на ранних этапах проектирования оценить качество и эффективность принимаемых конструктором РЭА решений. Погрешность оценки параметров механических воздействий составляет (20 – 30)%. Если в результате расчетов механические напряжения в опасных сечениях деталей конструкций РЭА окажутся соизмеримыми, следует не упрочнять расчет, а принимать меры по повышению жесткости и прочности конструкций.
Список использованных источников
1. Основы теории цепей: Методические указания к курсовой работе для студентов – заочников специальности 23.01 "Радиотехника"/ Сост. Коваль Ю.А., Праги О.В. – Харьков: ХИРЭ, 2001. – 63 с.
2. Зернов Н.В., Карпов В.Г. "Теория электрических цепей". Издание 2-е, перераб. и доп., Л.,"Энергия",2002.