Реферат: Применение резистивных электрических цепей в радиотехнических устройствах

Академия ФСО России

Кафедра физики

Тема: "Применение резистивных электрических цепей в

радиотехнических устройствах"

Орел-2009

Содержание

Метод контурных токов (МКТ)

Решение системы контурных уравнений. Теорема взаимности

Применение резистивных цепей

Режим постоянного тока в электрических цепях

Заключение

Литература

Метод контурных токов (МКТ)

Рис. 1.1.

Число независимых контуров .

Применяя второй закон Кирхгофа, получим уравнения для контуров:

Выразим напряжения через токи и сопротивления ветвей:

Токи ветвей определим через контурные токи:

После простых преобразований получим систему трех уравнений с темя неизвестными контурными токами:

Проанализируем первое уравнение системы. Сумма называется собственным сопротивлением первого контура и обозначается . Коэффициент при токе называется взаимным сопротивлением первого и второго контура и обозначается и т. д.

По анализу полученных уравнений можно сформулировать правила составления уравнений для k-го контура:

1) В левую часть уравнения записываем со знаком "плюс" произведение контурного тока k-го контура на собственное сопротивление этого контура.

2) В левую часть записываем также слагаемые, представляющие собой произведения контурного тока другого контура на взаимное сопротивление между k-м и рассматриваемым контурами. Слагаемое входит со знаком "плюс", если k-й и рассматриваемый контурные токи совпадают по направлению во взаимном сопротивлении, в противном случае соответствующее слагаемое входит со знаком "минус".

3) В правой части уравнения записывается алгебраическая сумма ЭДС, действующих в k-м контуре, причем со знаком "плюс" входят ЭДС, направление отсчета которых совпадает с направлением контурного тока.

После определения контурных токов можно вычислить ток в любом элементе как алгебраическую сумму контурных токов. Например, ток в резисторе равен

Если электрическая цепь содержит источники тока, независимые контуры выбираются так, чтобы через источник тока проходил лишь один контурный ток.

Дерево графа не должно содержать ветви с источником тока. Контурный ток в контуре с источником тока известен: он или равен задающему току источника, или отличается от него знаком. В результате число неизвестных контурных токов и число уравнений сокращаются на количество источников тока , т. е. число уравнений .

Пример. Составим систему контурных уравнений для цепи, схема которой приведена на рис. 1.2.

Рис. 1.2.

Независимые контуры выбираем так, чтобы через источник тока проходил только один контурный ток – . При выбранном направлении контурного тока он равен задающему току источника. В схеме будут два неизвестных контурных тока и . Уравнения контурных токов:

.

Поскольку ток известен и , то окончательно получим:

.

Метод контурных токов целесообразно применять тогда, когда число контурных уравнений оказывается меньшим числа узловых уравнений.

Решение системы контурных уравнений.

Теорема взаимности

В общей форме система уравнений контурных токов, или система контурных уравнений, может быть записана в следующем виде:

Если число уравнений получилось достаточно большим, то для решения системы уравнений применяются известные из математики методы, например, метод Крамера. Все n уравнений являются линейно-независимыми и поэтому система разрешима относительно n искомых токов. В этом случае контурный ток k–го контура определяется следующим образом:

,

где – определитель системы контурных уравнений; – алгебраическое дополнение элемента определителя.

Общее решение для k-го контурного тока имеет вид:

.

Отсюда следует, что контурный ток можно найти как алгебраическую сумму частных токов, создаваемой каждой ЭДС , в отдельности. Данное соотношение есть математическая запись принципа наложения, справедливого для линейных цепей.

На основании общего решения системы контурных уравнений можно доказать следующую теорему: если источник напряжения, включенный в первый контур пассивной цепи, вызывает во втором контуре ток , то тот же источник, будучи включенным во второй контур, вызовет в первом контуре такой же ток i .

Рис. 1.3.

Дуальная формулировка этой теоремы такова: если источник тока, включенный к первой паре узлов пассивной цепи, вызывает между второй парой узлов этой цепи некоторое напряжение и, тот же источник, будучи включенным, к этой второй паре зажимов, вызывает на зажимах первой пары узлов то же самое напряжение.

Цепи, которые удовлетворяют теореме взаимности, называют взаимными или обратимыми.

Пример.

На рисунке 1.3а, показана схема цепи, для которой в чем легко убедиться, ток:

.

Требуется определить, чему будет равен ток (рис. 1.3б), если источник напряжения е перенести в ветвь с сопротивлением .

Ответ можно дать сразу же на основании теоремы взаимности:

,

а в правильности его следует убедиться, определив непосредственно из схемы (см. рис. 1.3б) традиционными методами.

Применение резистивных цепей

В электрических цепях, составленных только из резисторов, реакция цепи (ток в любой ветви или напряжение между любыми узлами цепи) связана с воздействием соотношением:

,

где А – не зависящий от времени коэффициент пропорциональности, откуда следует, что реакция резистивной цепи воспроизводит воздействие с точностью до постоянного множителя, т. е. колебания в резистивных цепях возникают в момент приложения воздействия, изменяются во времени по такому же закону, как и воздействия, и становятся равными нулю одновременно с равенством нулю воздействия.

Эти свойства резистивных цепей и определяют область их применения. В технике связи резистивные цепи применяются в качестве делителей напряжения, магазинов затуханий, измерительных мостов.

Простейший делитель напряжения представляет собой последовательное соединение двух резисторов (рис. 1.4 а). Отношение напряжений и называемое коэффициентом деления, равно:

(а) (б)

Данное соотношение справедливо, если напряжение подводится к нагрузке, сопротивление которой много больше (например, на вход усилителя). В противном случае необходимо учитывать сопротивление нагрузки (рис. 1. 4б) и тогда:

.

Магазином затухания называют высокоточный ступенчатый делитель напряжения. Он составляется из нескольких (обычно трех) звеньев, именуемых удлинителями (рис. 1.5).

Рис. 1.5.

В удлинителе сопротивления подбирают так, чтобы . Если удлинитель нагрузить на сопротивление , то его входное сопротивление также равно .

Коэффициент деления напряжения, как можно установить, применяя любой из методов анализа, равен:

По заданному значению коэффициента деления и заданной величине вычисляются значения и :

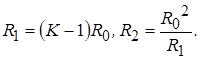
На рисунке 1.6 показано два удлинителя, соединенные так, что вход одного из них подключается к выходу другого. Последний удлинитель нагружен на сопротивление . Поэтому первый удлинитель оказывается также нагруженным на .

Коэффициент деления двух звеньев составляет:

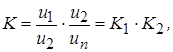
где , – коэффициенты деления звеньев.

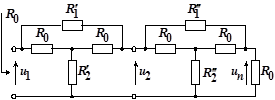
Рис. 1.6.

Значения , и можно изменять независимо друг от друга, лишь бы не нарушалось условие . Таким же способом можно соединить любое число звеньев с одинаковыми .

При большом числе звеньев коэффициент деления будет выражаться большими числами (десятки и сотни тысяч единиц). Поэтому его принято выражать в логарифмических единицах – децибелах (дБ) – по формуле:

,

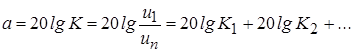и называть затуханием магазина.

Тогда вместо умножения коэффициентов деления производится сложение затуханий отдельных звеньев, выраженных в децибелах (дБ).

Так как затухание звена, например, первого,

,

то сопротивления звеньев можно вычислить по заданному затуханию звена.

Коэффициент деления (и затухание) звена можно изменять, если одновременно изменять и . Такое изменение производится обычно ступенями, через определенное число децибел.

Измерительным мостом постоянного тока называется прибор, схема которого изображена на рис. 1.7.

Рис. 1.7.

В трех плечах моста помещены резисторы, сопротивления которых известны, в четвертое плечо включается измеряемое сопротивление . В одну диагональ моста включен источник постоянного напряжения, во вторую диагональ - чувствительный индикатор.

Ток в диагонали моста (в индикаторе) равен нулю, если мост уравновешен, т. е. если выполнено условие Поэтому при равновесии моста:

С целью повышения точности измерений отношение выбирают в зависимости от порядка выбираемого значения . представляет собой набор (магазин) сопротивлений. Изменением добиваются равновесия моста.

При измерениях сопротивлений с мощностью моста может быть получена высокая точность измерения – сотых долей процента.

Режим постоянного тока в электрических цепях

Важным частным режимом работы электрической цепи является такой режим, при котором к цепи подведены только неизменные по времени воздействия в виде источников постоянного напряжения или тока.

В резистивной цепи, где реакция повторяет воздействие с точностью до постоянного множителя, в момент подведения постоянного воздействия возникают постоянные токи во всех ветвях и между всеми узлами устанавливаются постоянные напряжения, т. е. устанавливается режим постоянного тока.

В цепях общего вида, содержащих реактивные элементы, при подведении воздействия в виде источников постоянного напряжения или тока спустя некоторое время также устанавливается режим постоянного тока, т. е. все напряжения и все токи в цепи будут постоянными. Таким образом, производные тока и напряжения по времени равняются нулю. Отсюда вытекают весьма важные выводы, которые будут использоваться при рассмотрении процессов в цепях:

а) во-первых, следует заметить, что напряжения на всех емкостях в режиме постоянного тока будут представлять собой постоянные величины и поэтому через емкости токи проходить не будут. Следовательно, в данном режиме работы цепи элементы емкости представляют собой разрывы цепи;

б) во-вторых, в режиме постоянного тока через элемент индуктивности будет протекать постоянный ток. Поэтому напряжение на зажимах индуктивности будет равняться нулю тождественно. Таким образом, элемент индуктивности для режима постоянного тока будет представлять собой короткое замыкание зажимов. Одновременно следует заметить, что индуктивность с током будет определять некоторый запас энергии магнитного поля.

Из указанных особенностей реактивных элементов электрической цепи следует, что в режиме постоянного тока электрическая цепь может быть охарактеризована схемой замещения, в которой элементы емкости исключены (разрыв цепи), но напряжения на зажимах в схеме замещения указываются. Элементы индуктивности в этом случае заменяются короткозамкнутыми перемычками с известным током.

Расчет режима постоянного тока сводится к расчету резистивной цепи. При расчете или ставится задача по определению токов во всех ветвях и напряжений между всеми узлами, или, что бывает чаще, требуется найти лишь заданную реакцию цепи.

Пусть требуется определить ток в индуктивности и напряжение на емкости для цепи, изображенной на рис. 1.8 а.

(а) (б)

Рис. 1.8.

Для режима постоянного тока схема замещения цепи изображена на рис. 1.8 б.

При расчете режима постоянного тока в линейных активных цепях обычно возникает задача определения параметров резистора, обеспечивающих заданные (или выбранные) значения постоянного напряжения и тока электронной лампы или транзистора. Эта задача также сводится к расчету резистивной цепи.

Пусть, например, требуется вычислить величины сопротивлений резисторов, необходимых для обеспечения заданного режима постоянного тока транзистора (рис. 1.9).

Рис. 1.9.

Здесь читаются известными

Искомыми являются значения резисторов

Для определения составляем уравнение по второму закону Кирхгофа для контура, включающего источник, напряжение и резистор :

откуда

Определение производим на основании уравнения, составленного для контура , учитывая, что напряжение на резисторе равно :

откуда

Ток в резисторе в соответствии с первым законом Кирхгофа:

тогда

О том, как выбрать значения постоянных токов и напряжений в транзисторе, изложено в теме "Усилители электрических сигналов".

Заключение

При расчете сложных электрических цепей методами узловых напряжений или контурных токов определяют ток в любой ветви и напряжение между любыми узлами цепи. При использовании метода узловых напряжений неизвестными, подлежащими определению, являются так называемые узловые напряжения. Определив их, находят напряжение между любыми другими узлами цепи и соответственно токи в любых ветвях.

При использовании метода контурных токов неизвестными являются контурные токи. Определив их, находят токи в ветвях как алгебраическая сумма контурных токов, протекающих через данную ветвь, и соответственно напряжения между любыми узлами.

Теорема взаимности оказывается полезной в задачах анализа свойств линейных пассивных электрических цепей. При практическом использовании теоремы нужно внимательно проверить возможность и правильность ее применения.

Необходимость определения напряжений на зажимах элементов емкости и токов в элементах индуктивности объясняется тем, что эти величины при изменении режима работы цепи (при коммутациях) изменяются непрерывно. Поэтому указанные величины могут быть использованы при определении начальных условий.

Литература

Теория линейных электрических цепей. – М.: Радио и связь, 1986

Бакалов В.П. и др. Теория электрических цепей. – М.: Радио и связь, 1998.

Качанов Н.С. и др. Линейные радиотехнические устройства. М.: Воен. издат., 1974

В.П. Попов Основы теории цепей – М.: Высшая школа, 2000