| Скачать .docx |
Курсовая работа: Проектирование активного RC-фильтра нижних частот с ограниченной полосой пропускания
Содержание
Задание
Теоретические сведения
Порядок расчета и соображения по методике настройки активных фильтров
Расчет фильтра
Список литературы.
Задание №6 КП ЭБРЭ
Спроектировать активный RC - фильтр нижних частот с ограниченной полосой пропускания, удовлетворяющий следующим требованиям:
- полоса пропускания фильтра от 40 Гц до 60 кГц;
- неравномерность затухания в полосе пропускания должна быть не хуже 1,5дБ;
- полоса задерживания на частоте равной 100 Гц и выше до 500 кГц;
- относительное затухание в полосе задерживания, начиная с частоты равной 100 Гц не менее 30 дБ;
- выходное напряжение около 0,5В на высокоомной (104 Ом) нагрузке.
Теоретические сведения
Тенденция к микроминиатюризации радиоэлектронной аппаратуры в очень острой форме ставит вопрос о путях дальнейшего развития техники селективных устройств.
Уменьшение габаритов LC -фильтров ограничено тем, что добротность катушек индуктивности падает с уменьшением их размеров. Выбирая величину нагрузочного сопротивления LC- фильтра, можно уменьшить индуктивность но при этом необходимо во столько же раз увеличить емкость, т.е. это не приводит к существенному уменьшению габаритов. В то же время активный RС-фильтр можно выполнить в виде микромодульной конструкции или интегральной схемы/ Величину емкости в нем можно уменьшить, увеличивая во столько же раз сопротивление, габариты которого не зависят от номинала
Технология изготовления катушек индуктивности является специфической и вызывает ряд затруднений, особенно в тех случаях когда фильтры занимают сравнительно малый удельный вес в общем объеме аппаратуры. При использовании в фильтрах индуктивностей необходима герметизация всего фильтра или каждой катушки индуктивности в отдельности, что связано с дополнительными технологическими операциями и увеличением веса.
Первые активные RC -фильтры в которых использовались электронные лампы, были известны еще в 30-е годы. Однако их широкое применение стало возможным лишь после организации промышленного производства транзисторов. Тогда появились много численные работы по теории активных RC -цепей и по вопросам инженерного расчета и проектирования активных RC- фильтров.
Описанные в литературе активные фильтры можно подразделить, прежде всего, на линейные и нелинейные (цифровые). В первых активные элементы работают в линейном режиме, во вторых используются импульсные схемы типа мультивибраторов, триггеров и т.д.
Хотя частотные характеристики коэффициентов передачи активных фильтров описываются такими же уравнениями, как и характеристики LC-фильтров, расчеты их различны, и это представляет собой одно из серьезных затруднений при переходе к активным RC -фильтрам. Для активных RС-фильтров не существует метода, который позволял бы расчленять схему на отдельные звенья, рассчитываемые независимо одно от другого. При расчете активных RС-фильтров характеристики отдельных каскадно включаемых звеньев должны подбираться таким образом, чтобы добиться приблизительно постоянного затухания всего фильтра в пределах полосы пропускания. Поэтому, хотя активные RС-фильтры реализуются, как правило, в виде каскадного соединения звеньев, эти звенья рассчитываются все вместе, что, естественно, делает расчет значительно более сложным, хотя в то же время и более строгим, за счет использования методики синтеза по рабочим параметрам
Процесс синтеза электрической схемы можно, как известно, разделить на три этапа:
1) аппроксимацию, т.е. получение математического выражения заданной частотной зависимости затухания.
2) реализацию, т.е. составление соответствующей этому выражению идеализированной электрической схемы;
3) составление реальной электрической схемы, учитывающей неидеальность схемных элементов, наличие источников питания, цепей подачи смещения, введение дополнительных элементов с целью компенсации температурных зависимостей, целесообразный выбор величин схемных элементов с целью получения минимальных габаритов, минимальной чувствительности цепи к изменениям величин элементов и т д.
Первый этап синтеза — аппроксимация — в рассматриваемом случае активных RС-фильтров может основываться на математическом аппарате теории наилучшего приближения функций, нашедшем довольно широкое применение при решении задачи синтеза LC-фильтров по рабочим параметрам . Этот аппарат при проектировании LC-фильтров мог казаться излишней роскошью, поскольку давал довольно скромную экономию в числе схемных элементов при непропорционально большом усложнении расчетов.
При синтезе активных RC-фильтров он становится необходимостью, а использование электронных вычислительных машин и построенных с их помощью расчетных таблиц позволяет сократить трудоемкость расчета.
Второй этап синтеза — реализация --в случае активных фильтров связи со значительно большей неоднозначностью решения, чем для LC-схем.
В настоящее время существует большое количество вариантов схемных решений, которые можно сгруппировать в четыре основные вида схем на основе:
— конверторов (преобразователей) отрицательного сопротивления;
— гираторов;
— усилителей с ограниченным коэффициентом усиления (с положительной обратной связью);
— операционных усилителей.
Требования к активным RС-фильтрам в силу специфики их построения несколько отличаются от обычно предъявляемых к частотным фильтрам.
Требования к частотной характеристике фильтра.
Для LC - фильтров они определяются неравномерностью затухания в полосе пропускания и величиной относительного затухания в полосе задерживания. Поскольку в активных RС-фильтрах существует усиление сигнала в полосе пропускания, то для них можно говорить о неравномерности усиления в полосе пропускания и относительном усилении в полосе задерживания. Однако здесь используется традиционная терминология.
Входное и выходное сопротивления фильтра .
Применение активных элементов в фильтрах позволяет развязать фильтр со стороны входа и выхода без дополнительных схемных элементов. При этом, в отличие от LC-филыров, входное и выходное сопротивления могут иметь чисто активный характер, т. е. не зависеть практически от частоты, как в полосе пропускания, так и в полосе задерживания. Каскадное включение звеньев производится не по принципу согласования (равенства входного и выходного сопротивлений стыкуемых звеньев), а соединением низкоомного выходного сопротивления с высокоомным входным и наоборот.
Условия параллельной работы фильтров.
В случае активных RC-фильтров упрощаются условия параллельной работы. Поскольку фильтры с управлением по напряжению имеют большое входное сопротивление, то они должны применяться для параллельной работы со стороны входа, источником сигнала при этом должен быть генератор напряжения. Для параллельной работы со стороны выхода целесообразно использовать фильтры с управлением по току, которые имеют высокое выходное сопротивление, сопротивление нагрузки при этом должно быть значительно меньше высокоомного выходного сопротивления фильтра.
Динамические диапазон и нелинейные искажения .
При использовании активных RC-фильтров эти характеристики, по сравнению с LC-фильтрами, требуют к себе значительно большего внимания. Динамический диапазон сигналов ограничивается снизу уровнем шумов и наводок. Верхняя граница динамического диапазона зависит от типа транзистора, его режима и схемного исполнения активного элемента. В этом отношении схемы активных элементов, построенные на основе эмиттерных повторителей, обладают известными преимуществами по сравнению с усилителями тока.
Основным источником нелинейных искажений в активных RC - фильтрах являются активные элементы, построенные на основе усилителей. Поэтому в последних при высоких требованиях по нелинейности должна применяться отрицательная обратная связь.
Источники питания.
Реализация некоторых характеристик в активных RС-фильтрах накладывает специфические требования на источники питания их активных элементов. Условия стыковки по постоянному току определяют количество и полярность источников питания, а динамический диапазон — величину питающего напряжения. Кроме того, повышаются требования в отношении пульсации питающего напряжения, которые могут усиливаться в отдельных звеньях, представляя значительную помеху. Необходимо обратить внимание на внутреннее сопротивление источника питания, так как большая величина его может служить причиной недостаточного затухания в полосе задерживания фильтра.
Порядок расчета и соображения по методике настройки активных фильтров
При окончательном расчете активного RС-фильтра с целью получения практической схемы приходится учитывать большое количество факторов, которые часто противоречат друг другу. Поэтому процесс проектирования фильтра имеет несколько итеративный характер. Однако можно выделить основные этапы в расчете фильтра
Аппроксимация заданной амплитудно-частотной характеристики.
Задачей аппроксимации является определение функции передачи фильтра в виде сомножителей 1 и 2-го порядков, а именно коэффициентов b1 , b2 , br при комплексной переменной р.
Порядок п аппроксимирующей функции фильтра НЧ определяется по заданному затуханию в полосе задерживания и неравномерности передачи в полосе пропускания в зависимости от вида аппроксимации.
В заключение определяются добротности звеньев 2-го порядка и рассчитываются координаты контрольных точек характеристик соответствующих типов фильтров. По этим точкам в дальнейшем осуществляется настройка звеньев фильтра.
Выбор активного элемента и вида фильтра.
Выбор типа активного элемента определяет вид фильтра и является поэтому одним из основных этапов расчета.
Если по заданию должна обеспечиваться параллельная работа со стороны входа, то необходимо использовать фильтры с управлением по напряжению (например, фильтры на основе единичных усилителей напряжения); при параллельной работе со стороны выхода целесообразно применять фильтры с управлением по току.
Вид фильтра может определяться характером источника сигнала, а также условиями нагрузки. Низкое сопротивление источника сигнала и большое сопротивление нагрузки требуют фильтров с управлением по напряжению, а высокоомный источник сигнала и малое сопротивление нагрузки — фильтров с управлением по току. При других комбинациях условий источника сигнала и нагрузки возможно построение фильтра смешанного вида из каскадного соединения соответствующих звеньев.
При сравнительно большом динамическом диапазоне и большой величине входного сигнала преимущество имеют фильтры, активный элемент которых построен на основе эмиттерного повторителя, ибо в других схемах выполнение этих требований достигается более сложным путем.
Единичные усилители тока и напряжения (с ограниченным коэффициентом усиления) предпочтительнее других активных элементов в силу их относительной простоты, минимального числа транзисторов и достаточной стабильности (при использовании внутренней отрицательной обратной связи). Однако для построения высокодобротных звеньев эта стабильность может оказаться недостаточной, что вызовет необходимость применения звеньев с более сложными активными элементами — операционным усилителем или гиратором, где имеется возможность более стабильной реализации
После определения вида фильтра необходимо произвести выбор активных элементов для каждого звена в зависимости от его добротности, которая для многих видов звеньев определяет чувствительность реализуемой характеристики к нестабильности элементов фильтра. Для звеньев с добротностью Q<3 можно применять простейшие однотранзисторные усилители тока и напряжения. Двухтранзисторные усилители и конверторы отрицательного сопротивления могут, как правило, применяться при добротностях Q <30 – 40. Для более высокодобротных звеньев необходимо применять гираторы или операционные усилители.
Вопрос об использовании германиевых или кремниевых транзисторов в активных элементах решается в зависимости от температурных условий работы Однако, если есть возможность уменьшить сопротивления смещения (являющиеся одновременно «смысловыми» элементами фильтра) в достаточной для температурной стабилизации мере, то следует применять германиевые транзисторы, которые обеспечивают лучшее приближение параметров активных элементов к идеальным значениям.
Для выбранных активных элементов определяются параметры, особенно сопротивление, которое одновременно является «смысловым» элементом звена фильтра Обычно относительно этого сопротивления осуществляется нормирование величин элементов звена.
Оптимизация чувствительности.
Расчет соотношения величин элементов с целью оптимизации чувствительности проводится, как изложено в соответствующих разделах реализации. В случае одинаковых активных элементов оптимизацию имеет смысл проводить только для самого высокодобротного (а значит и самого нестабильного) звена.
Для низкодобротных звеньев нет необходимости проводить подобный расчет.
Порядок каскадного построения фильтра.
Способ построения фильтров из звеньев 1 и 2-го порядков определяется в основном двумя факторами максимальной величиной сигнала, проходящего через звено, и условиями стыковки звеньев.
Во избежание перегрузки активных элементов, а значит, и увеличения нелинейных искажений, следует применять каскадное построение фильтра в порядке возрастающей добротности звеньев со стороны источника сигнала, начиная фильтр звеном 1-го порядка. При этом для полосового фильтра, реализованного звеньями НЧ и ВЧ, возможны два варианта построения, каскадное соединение фильтров НЧ и ВЧ, каждый из которых составлен из своих звеньев в порядке возрастающей добротности, и каскадное соединение звеньев ПФ2 и ПФ4
Для лучшего выполнения условий стыковки непосредственно должны соединяться звенья с максимально отличающимися резонансными частотами, т. е. для полосового фильтра здесь необходимо отдать предпочтение второму варианту его построения.
Расчет величин элементов звеньев.
Расчет величин элементов производится на основе таблиц реализации коэффициентов аппроксимации. В случае полиномиальных звеньев 2-го порядка эти таблицы дают систему двух уравнений с пятью неизвестными, а для звеньев с нулями передачи имеем систему трех уравнений с восемью неизвестными. Это предоставляет большую свободу в окончательном выборе элементов. Однако не исключается и возможность наложения дополнительных условий. Например, для полиномиальных звеньев три элемента могут быть определены предварительно один - сопротивление - при расчете активного элемент, второй — из расчета оптимальной чувствительности и третий — из условий непосредственной стыковки звеньев.
Поскольку оптимизация проводится только для самого добротного звена, то величины элементов остальных звеньев могут в некоторой степени выбираться по произволу разработчика (исходя, например, из условия уменьшения общего числа номиналов элементов, меньших габаритов конденсаторов и т.п.)
В заключение обязательно необходимо проверить соответствие полученных элементов схемы условиям реализации.
Настройка фильтра.
Настройка фильтра осуществляется позвенно. Полиномиальное звено 1-го порядка, а также низкодобротные полиномиальные звенья 2-го порядка специальной настройки не требуют, если элементы подобраны с достаточной точностью (порядка 1—3%).
Однако имеется возможность более точной настройки путем непосредственной реализации коэффициентов аппроксимации b1
и b2
полиномиальных звеньев. Суть этой настройки, которую можно назвать активной, состоит в следующем. На первом этапе увеличением коэффициента передачи усилителя k
добиваемся условия b1
= 0, т. е. звено 2-го порядка вводится в режим самовозбуждения, частота которого определяется только коэффициентом аппроксимации b2
. Подбором одного из сопротивлении звена эта частота самовозбуждения устанавливается равной расчетному значению ![]() чем обеспечивается точная peaлизация коэффициента b2
. На втором этапе производится точная
чем обеспечивается точная peaлизация коэффициента b2
. На втором этапе производится точная
реализация коэффициента b1
путем уменьшения коэффициент передачи усилителя k
до величины, соответствующей координатам контрольной точки характеристики ![]() . Подобная методика настройки позволяет применять элементы с обычными допусками без специального подбора, что ускоряет процесс изготовления фильтра.
. Подобная методика настройки позволяет применять элементы с обычными допусками без специального подбора, что ускоряет процесс изготовления фильтра.
Аналогично производится настройка и дробного звена. Только здесь на первом этапе осуществляется настройка двойной Т-образной схемы по нулевой (минимальной) передаче, чем осуществляется реализация коэффициента br
. На втором этапе в режиме самовозбуждения подбором емкости, например С0
, в случае звена НЧ2—1НЗ-Д, выполняется реализация коэффициента b2
. На третьем этапе производится реализация коэффициента b1
,
как и для полиномиального звена, но по координатам своей контрольной точки ![]()
Расчет подстроенных элементов звеньев.
Методику расчете подстроечных элементов достаточно разработать для звеньев фильтров НЧ и затем распространить на остальные звенья.
В полиномиальном звене НЧ 2-го порядка необходимо иметь два регулировочных элемента: один — для установки коэффициента аппроксимации b2 (настройка по частоте), другой — для регулировки коэффициента b1 (установка заданной добротности).
Расчет фильтра
1). Аппроксимация заданной амплитудно-частотной характеристики.
Поскольку не оговорены требования к характеристике фильтра в диапазоне частот от 0 до 40 Гц, то с целью уменьшения общего числа звеньев целесообразно решать аппроксимационную задачу.
Определим нормированную частоту ограничения фильтра, как отношение
![]() =
= ![]() = 0,6666.
= 0,6666.
Нормированная частота в полосе задерживания обычного фильтра НЧ равна
![]() .
.
Эта же частота в случае фильтра НЧ с ограниченной полосой пропускания рассчитывается по формуле
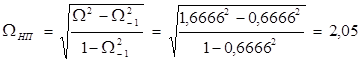
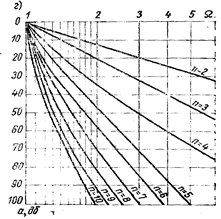
Из кривых (рис. 1.) ![]() по вычисленной
по вычисленной ![]() и заданным
и заданным ![]() и а
определим класс фильтра по затуханию: n = 4. Заметим, что в случае обычного фильтра НЧ, т. е. при использовании значения
и а
определим класс фильтра по затуханию: n = 4. Заметим, что в случае обычного фильтра НЧ, т. е. при использовании значения ![]() , необходимый класс фильтра равен 5. Таким образом, уже на этапе аппроксимации получаем очевидный выигрыш.
, необходимый класс фильтра равен 5. Таким образом, уже на этапе аппроксимации получаем очевидный выигрыш.
Из справочника выпишем коэффициент аппроксимации функции передачи НЧ прототипа ![]() n = 4
n = 4 ![]() Сомножители полиномиальной аппроксимации по Чебышеву имеют вид:
Сомножители полиномиальной аппроксимации по Чебышеву имеют вид:
![]()
По формулам:
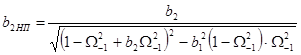
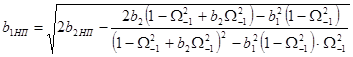
![]()
рассчитаем соответствующие коэффициенты аппроксимации искомой функции передачи фильтра НЧ с ограниченной полосой пропускания.
![]() - добротность- количественная хар-ка колебательных функций 2-го порядка
- добротность- количественная хар-ка колебательных функций 2-го порядка
Результат расчёта сведем в табл. 1.
Таблица 1.
| Звено |
b1 |
b2 |
Q |
b1 НП |
b2 НП |
QНП |
gНП |
| I |
2.41140 |
3.57906 |
1.5 |
0,44528 |
2,02 138 |
6,4 |
10 |
| II |
0,28289 |
1,01367 |
7,1 |
0,15696 |
1,01753 |
13 |
5 |
Из данной таблицы наглядно видно возрастание добротностей звеньев по сравнению с исходным НЧ прототипом. Там же показано усиление каждого звена фильтра в полосе пропускания, найденное по формуле:

В заключение решения задачи аппроксимации по ф-лам:

![]() ,
,
где индексы “Н” указывают на тип фильтра (нижних частот).
С заменой в них коэффициентов b1 и b 2 на b1НП и b 2НП , соответственно рассчитаем координаты контрольных точек характеристик звеньев (рис. 2.):
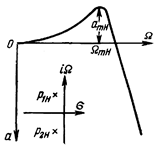
колебательный тип частотной хар-ки.
для звена I: ![]() = 0,685, а
mH
= - 10,19;
= 0,685, а
mH
= - 10,19;
для звена II ![]() = 0,985, а
mH
= - 16,18.
= 0,985, а
mH
= - 16,18.
По этим данным может осуществляться настройка звеньев фильтра.
2) Реализация фильтра и расчет величин элементов схемы.
Как видно из результатов решения аппроксимационной задачи, необходимо реализовать функции передачи 2-го порядка сравнительно низкой добротности. Поэтому для достижения заданной характеристики целесообразно использовать простейшие звенья на основе единичных усилителей, что при реализации всего фильтра каскадным соединением звеньев 2-го порядка обеспечивает минимальное число транзисторов на порядок функции передачи. Возьмем за основу звенья на основе единичных усилителей напряжения, поскольку они обладают потенциально большим динамическим диапазоном и дают возможность несколько уменьшить величины емкостей схемы за счет большей допустимой величины сопротивлений R1 и R 2 (рис 3), хотя в общем случае последнее преимущество незначительно.
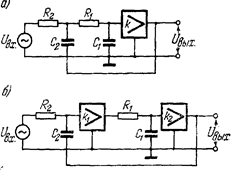
Рис. 3.. НЧ звенья 2-го порядка с усилителями напряжения" а) НЧ2-1Н1: б) НЧ2-2Н1
Расчет величин элементов звеньев в основном сводится к решению системы двух уравнении
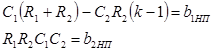
Приведенная выше система двух уравнении содержит пять неизвестных. Необходимы еще три условия. Первое из них получим, задавшись отношением сопротивлений:
![]()
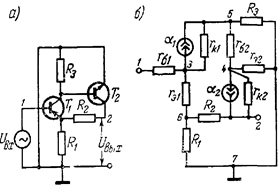
Рис. 4. Усилитель напряжения на двух транзисторах с равной проводимостью и его эквивалентная схема
Второе условие определяется выбором сопротивления в цепи базы входного транзистора усилителя напряжения (рис 4), которое представляет собой сумму сопротивлении R1 и R 2 звена фильтра
Для уменьшения величины емкостей и улучшения условии непосредственной стыковки звеньев эти сопротивления следует выбирать возможно большими однако увеличение сопротивления в цепи базы транзистора ухудшает температурную стабильность усилителя. В данном случае выберем:
![]() кОм
кОм
Это же сопротивление примем за нормирующее.
Наконец, третьим условием является выбор отношения ![]() оптимального с точки зрения чувствительности характеристики фильтра к нестабильности элементов схемы. Расчет оптимального соотношения т2
производится по следующей методике. Исходные данные для этого расчета выберем следующие: нестабильность бумажных конденсаторов типа МБМ—3% резисторов типа МЛТ—0,1%, коэффициента передачи усилителя напряжения — 0,05%. В соответствии с формулами:
оптимального с точки зрения чувствительности характеристики фильтра к нестабильности элементов схемы. Расчет оптимального соотношения т2
производится по следующей методике. Исходные данные для этого расчета выберем следующие: нестабильность бумажных конденсаторов типа МБМ—3% резисторов типа МЛТ—0,1%, коэффициента передачи усилителя напряжения — 0,05%. В соответствии с формулами:
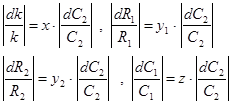
получим соотношения нестабильности элементов схемы звеньев:
х = 0,017 , y1 = y2 = 0,034 , z =1
Поскольку нестабильности пассивных элементов схемы и нестабильность коэффициента передачи усилителя отличаются более, чем на порядок, т.е. нестабильность в основном определяется пассивными элементами - конденсаторами то нецелесообразно использовать формулы для расчета оптимального соотношения элементов т2 . Как видно из выражении:
![]()

минимальная чувствительность к наиболее нестабильным элементам (конденсаторам ![]() и
и ![]() ) достигается при единичном коэффициенте усиления. Поэтому третье условие расчета элементов звена состоит в выборе величины коэффициента передачи вблизи единицы. Воспользовавшись соотношением:
) достигается при единичном коэффициенте усиления. Поэтому третье условие расчета элементов звена состоит в выборе величины коэффициента передачи вблизи единицы. Воспользовавшись соотношением:
![]() ,
,
определим коэффициент передачи усилителя из условия:
![]()
Таким образом определены все три дополнительные элемента и исходная система двух уравнений стала разрешимой. Результаты решения ее для обоих звеньев:
для звена I: ![]() = 0,0757 мкф,
= 0,0757 мкф, ![]() = 1,893 мкф,
= 1,893 мкф,
для звена II: ![]() = 0,0377 мкф,
= 0,0377 мкф, ![]() =
1,905 мкф.
=
1,905 мкф.
На основании проделанных расчетов произведем выбор величин элементов схем звеньев в соответствии с существующей шкалой номинальных значений.
Основным критерием является второе уравнение исходной системы, а неизбежный paзбpoc элементов скомпенсируем подстройкой сопротивления R 2 Результаты расчета звеньев сведем в табл. 2
Таблица 2
| Звено |
|
|
|
|
k |
| I |
0,1 |
2,0 |
8,2 |
8,61 |
1,028 |
| II |
0,05 |
2,0 |
8,2 |
8,8 |
1,022 |
Рассчитаем диапазон подстроечных сопротивлений:
Выберем исходные данные для расчета регулировки звеньев по частоте:
![]()
т.е. все этементы звена с 10 % допуском. Требуемая точность настройки зависит от добротности звена; в данном случае для первого звена имеем ![]() = 0,01, а для второго
= 0,01, а для второго ![]() = 0,005. Проверив по:
= 0,005. Проверив по:
![]()
находим что при выбранных условиях заданная настройка невозможна для обоих звенев. Наиболее простым выходом из создавшегося положения является увеличение точности подстроечного сопротивления, так как бумажныe конденсаторы не выпускаются с меньшим допуском, а использование прецизионных сопротивлений менее эффективно. Выберем для подстройки переменные сопротивления типа ППЗ — 43, которые позволяют установить необходимое значение с точностью 0,5 – 1%. Рассчитанные по формулам:

![]()
![]()
необходимый диапазон подстройки и основное сопротивлениe R 2 приведены в табл. 3
Таблица 3
| Звено |
|
|
|
| I |
5,6 |
0,4 |
7,4 |
| II |
5,6 |
0,4 |
7,5 |
В заключении рассчитаем подстроечные элементы, регулирующие коэффициент передачи усилителя (добротность звена).
Bначале по формулам:
![]()
![]()
рассчитаем диапазон коэффициента усиления к , определяемый 10% разбросом величин пассивных элементов звеньев. Получим:
для звена I: кмах = 1,0489, км in = 1,0166,
для звена II: кмах = 1,0369, км in = 1,0168.
Далее, задавшись опять 10% разбросом сопротивлений: ![]() проверим по формуле:
проверим по формуле:
![]() , (1)
, (1)
выполняется ли условие реализуемости регулировки. Для первого звена, где выбрана точность настройки ![]() = 0,03, получим, что оно не выполняется т.е. настройка при заданных разбросах элементов невозможна. При использовании элементов с 5- процентным разбросом т.е.
= 0,03, получим, что оно не выполняется т.е. настройка при заданных разбросах элементов невозможна. При использовании элементов с 5- процентным разбросом т.е. ![]() =0,05, условие (1) также не выполняется. Настройка возможна при условии выбора
=0,05, условие (1) также не выполняется. Настройка возможна при условии выбора ![]() = 0,03 т.е. практически здесь целесообразно применить переменное сопротивление. В таких же условиях находится и второе звено, которое необходимо настраивать с точностью
= 0,03 т.е. практически здесь целесообразно применить переменное сопротивление. В таких же условиях находится и второе звено, которое необходимо настраивать с точностью ![]() .
.
Таким образом задавшись окончательно: ![]() кОм
,рассчитаем необходимые элементы по формулам:
кОм
,рассчитаем необходимые элементы по формулам:
![]()
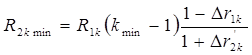
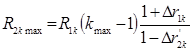
![]()
Результаты приведены в табл. 4.
Таблица 4
| Звено |
|
|
|
| I |
62 |
2 |
215 |
| II |
62 |
3 |
150 |
Полученная принципиальная схема фильтра рис. 5.
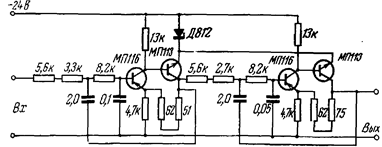
3) Настройка фильтра и результаты эксперимента.
Характеристика фильтра (рис. 6.) соответствует заданным требованиям.
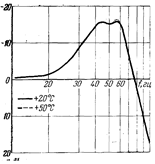
рис. 6. Хар-ка фильтра.
Список литературы
1. Пэйтон А.Дж.,Волш В. Аналоговая электроника на ОУ.–М: БИНОМ, 2004г.
2. Мошин Г., Хорн П. Проектирование активных фильтров: Пер. с англ.-М: Мир,2004г.
3. Лэм Г. Аналоговые и цифровые фильтры.-М: Мир, 2007г.
4. Свитенко В.Н. Электрорадиоэлементы. Курсовое проектирование. –М: Высш. Школа,2007г.