Главная / Рефераты / Коммуникации и связь

Курсовая работа: Проектування комбінаційних схем на мікросхемах різного ступеню інтеграції

Міністерство освіти і науки України

Херсонський національний технічний університет

Кафедра економічної кібернетики

Курсовий проект

з дисципліни:

Прикладна теорія цифрових автоматів

Проектування комбінаційних схем на мікросхемах різного ступеню інтеграції

Виконала:

студентка групи 1зКСМ Петрова К.В.

перевірив: ст. викладач Хапов Д.В.

Херсон 2006

Реферат

Тема курсового проекту: “ПРОЕКТУВАННЯ КОМБІНАЦІЙНИХ СХЕМ НА МІКРОСХЕМАХ РІЗНОГО СТУПЕНЮ ІНТЕГРАЦІЇ”.

Мета курсового проекту: вивчення методів проектування комбінаційних схем на різноманітних мікросхемах, визначення їхньої складності і швидкодії.

Логічний елемент – це електронна схема, що реалізує визначену перемикальну функцію. Сукупність логічних елементів, призначених для перетворення двійкових змінних, називається логічною схемою. Логічні схеми можна підрозділити на послідовні (последовательностные) і комбінаційні.

Комбінаційною прийнято називати схему з п входами і т виходами, у якої сукупність вихідних сигналів у даний момент часу цілком визначається сукупністю вхідних сигналів, що діють у даний момент часу, і не залежить від вхідних сигналів, що діють у попередні моменти часу. Говорять, що така схема має один стан. Отже, поводження комбінаційної схеми може бути описано системою перемикальних функцій. Розрізняють задачі аналізу і синтезу комбінаційних схем.

Задача аналізу комбінаційної схеми (КС) зводиться до знаходження системи власних логічних функцій, що відбивають логіку роботи такої схеми. У процесі аналізу з цієї схеми виключають елементи, що не впливають на логіку роботи схеми (формувачі, елементи узгодження і т.д.), а потім визначається система власних функцій.

Задача синтезу є зворотну до задачі аналізу і формулюється наступним чином. Дана перемикальна функція і дана система логічних елементів; необхідно побудувати КС, що реалізує задану функцію на заданих елементах.

Основні теоретичні положення

Синтез комбінаційної схеми на логічних елементах можна умовно розбити на три етапи.

На першому етапі, виходячи з таблиці істинності перемикальної функції, що описує роботу синтезованої комбінаційної схеми, знаходять мінімальну диз'юнктивну нормальну форму (МДНФ) функції (чи її заперечення).

Якщо функція, що описує роботу синтезованої схеми, є частково визначеною (заданою не на всіх 2ⁿ наборах), то попередньо роблять оптимальне її до визначення (таке, при якому функція буде мати більш просту МДНФ). На цьому перший етап закінчується.

На другому етапі функцію записують у так називаної операторній формі, тобто у вигляді суперпозиції операторів логічних елементів. Оператором логічного елемента називають функцію, що реалізується цим елементом. Якщо число входів в операторах досить велике, то одержання операторного запису функції зводиться до її представлення в одній зі стандартних канонічних нормальних форм. Таких форм вісім.

Рис.1.1

На прикладі МДМФ функції, заданою діаграмою Вейча на рис. 1.1,

f(x₃ , x₂ , x₁ ) = ,

покажемо метод одержання всіх нормальних форм. Позначати нормальні форми будемо шляхом указівки внутрішньої і зовнішньої функції розкладання. Так, у ДНФ внутрішньою функцією є функція І, а зовнішньої - АБО, тобто ДНФ є формою типу І/АБО.

Узявши подвійне заперечення МДНФ функції і застосувавши кілька разів правило де Моргана, послідовно одержимо наступні нормальні форми:

f(x₃ , x₂ , x₁ ) = =	форма І/АБО
== =	форма І-НІ/І-НІ
= =	форма АБО/І-НІ
=	форма АБО-НІ/АБО

Одержавши МДНФ заперечення заданої функції тобто (x₃ , x₂ , x₁ ) = , запишемо ще чотири нормальні форми:

f(x₃ , x₂ , x₁ ) = =	форма І/АБО-НІ
= =	форма І-НІ/І
= =	Форма АБО/І
=	форма АБО-НІ/АБО-НІ

Нормальні форми дозволяють одержати комбінаційну схему з двома рівнями (каскадами) логічних елементів, якщо елементи мають необхідне число входів.

Якщо ж число входів р елементів менше, ніж потрібно для реалізації отриманої нормальної форми, то змінні поєднують у групи, що містять не більш р елементів, і використовують співвідношення виду

x₁ x₂ …x_m = (x₁ …x_q )…(x_s …x_m ); - асоціативність кон’юнкції.

x₁ v x₂ v…v x_m = (x₁ v…v x_q ) v…v (x_s v…v x_m ); - асоциативність диз’юнкції.

; - правило подвійного заперечення.

Число груп змінних також не повинне перевищувати р. У протилежному випадку зазначені перетворення виконують стосовно груп змінних. Такі перетворення дозволяють представити задану функцію в операторній формі з урахуванням числа входів елементів. Отримана в цьому випадку форма не буде нормальною, тому що за рахунок додаткового каскадування елементів комбінаційна схема буде містити більш двох рівнів.

На заключному третьому етапі по операторним представленнях функцій будується комбінаційна схема. Задана система елементів дозволяє реалізувати одне чи більше операторних представлень функції. Наприклад, при наявності елементів І, АБО і І-НІ можна використовувати в якості вихідної одну з п'яти нормальних форм (І/АБО, І-НІ/І-НІ, АБО/І-НІ, І-НІ/І, АБО/І) для одержання відповідних операторних представлень з урахуванням числа входів елементів. Для вибору однієї схеми з декількох можливих необхідно порівнювати їх по заданих параметрах. Найбільше часто такими параметрами є складність і швидкодія схем.

Існують кілька способів оцінки складності:

складність по Квайну (К), обумовлена як сумарне число входів усіх логічних елементів;

складність у числі логічних елементів М;

складність у числі умовних корпусів мікросхем:

де r — число типів мікросхем; m_i — кількість мікросхем i-го типу; n_i — число висновків мікросхеми i-го типу. У якості умовного використовується корпус мікросхеми на 14 виводів.

Параметри К и М доцільно використовувати при проектуванні інтегральних схем, тому що їхня вартість залежить від площі кристала, що пропорційна числу логічних елементів і числу їхніх входів. Оцінка N зручна при порівнянні складності пристроїв, побудованих на мікросхемах.

Швидкодія КС залежить від тимчасових параметрів логічних елементів t⁰¹ і t¹⁰ , що характеризують затримку сигналів елементом (час переходу вихідного сигналу від одного логічного рівня до іншого). На практиці використовують звичайно усереднене значення часу затримки t = (t⁰¹ + t¹⁰ )/2 чи максимальне t* = max (t⁰¹ , t¹⁰ ).

Наприклад, для КС на однотипних елементах середній час затримки сигналів визначається як T = Lt, де L — рівень схеми, дорівнює числу елементів, що входять у максимальну по довжині ланцюжок елементів. Якщо використовуються елементи з різною затримкою, то в схемі визначається шлях, що вимагає максимального часу поширення сигналів.

Рис 1.2

Вибирається з декількох можливих КС, що краще інших задовольняє заданим параметрам.

Проектування КС з багатьма виходами відрізняється тим, що система перемикальних функцій піддається спільній мінімізації, а потім перетворюється до операторного представлення таким чином, щоб число використовуваних логічних елементів було мінімальним.

При реалізації перемикальних функцій у ряді випадків можна зменшити кількість корпусів мікросхем, використовуючи мікросхеми середнього ступеня інтеграції, наприклад, дешифратори і мультиплексори.

Оскільки дешифратор на п входів реалізує всі констітуенти одиниці, то для реалізації перемикальної функції від п змінних досить за допомогою АБО елемента одержати диз'юнкцію констітуент одиниці тих наборів, на яких функція приймає одиничні значення. Якщо дешифратор має інверсні виходи, то відповідно до правила де Моргана замість АБО елемента варто використовувати елемент І-НІ.

Наприклад, функцію , представлену в ДДНФ, можна реалізувати за допомогою трьох входового дешифратора з прямими (рис. 1.2, а) чи інверсними (рис. 1.2, б) виходами.

Якщо з кожної констітуенти можна винести за дужки змінну, то при наявності в дешифратора (стробуючого) входу Е знадобиться дешифратор з меншим числом інформаційних входів. Представивши останню з розглянутих функцій у вигляді , можна реалізувати її з використанням двухвходового дешифратора (рис. 1.2, в).

Дешифратори найбільше доцільно використовувати при реалізації систем перемикальних функцій. У цьому випадку для побудови схем потрібно один дешифратор і стільки логічних елементів, скільки функцій містить система.

Мультиплексор з N інформаційними входами і k = log₂ N керуючими входами дозволяє виключити k з п змінних перемикальної функції, представивши її через залишкові функції, кожна з яких залежить не більш ніж від n-k змінних.

Так, після двохкратного застосування леми про розкладення больової функції по змінній, функція y = f(x_n ,…,x₁ ) може бути представлена у формі

де f₀ , f₁ , f₂ , f₃ — залишкові функції від n–2 перемінних. Схема, що відповідає такому представленню функції, показана на рис. 1.3.

Залишкові функції можуть бути реалізовані будь-яким способом. Зокрема, кожна з них може бути представлена через свої статочне функції з використанням мультиплексоров. У кожнім конкретному випадку необхідно оцінювати складність схем при чи тім іншому способі реалізації функції. Помітимо, що складність схем залежить від того, які перемінні виключаються. Для одержання найбільш простої схеми може знадобитися перебір усіх комбінацій включаюдчи перемінних.

При реалізації функції від чотирьох перемінних з використанням мультиплексора, що має два керуючі входу (рис. 1.4), треба виключити шістьох різних пар перемінних (x₄ x₃ , x₄ x₂ , x₄ x₁ , x₃ x₂ , x₃ x₁ , x₂ x₁ ,). При виключенні кожної пари перемінних діаграму Вейча заданої функції можна розглядати як чотири самостійні діаграми для залишкових функцій f₀ , f₁ , f₂ , f₃ .

На рис. 1.5 показані всі шість варіантів визначення залишкових функцій. Виключає перемінні зазначені біля діаграм для кожного варіанта. Схеми на елементах І-НІ, що відповідають кожному варіанту, представлені на рис. 1.6. Найбільш проста реалізація заданої функції є при виключенні за допомогою мультиплексора перемінних х₁ і х₂ (рис. 1.7).

При побудові схем варто враховувати навантажувальну здатність виходів мікросхем і, при необхідності, усувати перевантаження відповідною розв'язкою.

рис. 1.7

Визначення варіанту завдання

Синтез комбінаційної схеми на логічних елементах можна умовно розбити на три етапи.

Визначаємо варіант перемикальної (больової) функції. Для цього номер варіанту переводимо у двійкову систему числення і записуємо шість його молодших розрядів у вигляді: a₆ a₅ a₄ a₃ a₂ a₁ .

54 (110110): a₆ =1, a₅ =1, a₄ =0, a₃ =1, a₂ =1, a₁ =0.

Визначивши значення a_i , підставляємо їх у таблицю 1.1.

Таблиця 1.1


0	0	0	0	1	0
1	0	0	0	0	1
0	1	0	0	0	1
1	1	0	0	1	0
0	0	1	0	1	0
1	0	1	0	1	0
0	1	1	0	0	1
1	1	1	0	0	1
0	0	0	1	1	0
1	0	0	1	0	1
0	1	0	1	1	0
1	1	0	1	0	1
0	0	1	1	0	1
1	0	1	1	1	0
0	1	1	1	1	0
1	1	1	1	1	0

Для заданої функції і для її заперечення знаходимо МДНФ за допомогою діаграми Кароно–Вейча.

МДНФ: .

МДНФ:.

Якщо функція, що описує роботу синтезованої схеми, є частково визначеною (заданою не на всіх 2n наборах), то попередньо роблять оптимальне її до визначення (таке, при якому функція буде мати більш просту МДНФ). На цьому перший етап закінчується.

Узявши подвійне заперечення МДНФ функції і затосувавши кілька разів правило ДеМоргана, одержуємо нормальні форми:

і/ні

і-ні/і-ні

або/і-ні

або-ні/або

і/або-ні

і-ні/і

або/і

або-ні/або-ні

Записуємо операторні представлення функції, що можуть бути реалізовані на елементах, заданих у табл. 1.2 та будуємо схеми:

Таблиця 1.2

Тип елементів

Число елементів у корпусі

Час затримки сигналів

2 або-ні,

2 і-ні/3 і

4/3

20/24

2 або-ні

Дивитись у додаток Схема 1.

2 і-ні / 3 і

Дивитись у додаток Схема 2.

Вибраємо операторні форми, що забезпечують одержання комбінаційної схеми з максимальною швидкодією і комбінаційною схемою з мінімальним числом умовних корпусів, тобто схему з кращим параметром T і схему з мінімальним значенням N. Усі мікросхеми мають по 14 виходів.

Знаходимо час затримки сигналу:

де – кількість елементів, що входять у максимальну по довжині ланцюжок елементів, – усереднене значення часу затримки, що знаходиться по формулі:

Розраховуємо складність схем:

де – кількість елементів у мікросхемі, – число виводів мікросхеми і-того типу, – число типів мікросхем.

4,6.

4,3.

На елементах ЗІ-НІ будуємо перетворювач кодів відповідно до таблиці 1.3. У процесі проектування використовуємо методи спільної мінімізації системи перемикальних функцій.

Таблиця 1.3


0	0	0	0	0	0	1	0
0	0	0	1	0	1	0	0
0	0	1	0	0	1	0	1
0	0	1	1	0	1	1	0
0	1	0	0	0	1	1	1
0	1	0	1	1	0	0	1
0	1	1	0	1	0	0	1
0	1	1	1	1	0	1	0
1	0	0	0	1	0	1	1
1	0	0	1	1	1	0	1
1	0	1	0	1	1	0	1
1	0	1	1	1	1	1	0
1	1	0	0	1	1	1	1
1	1	0	1	0	0	0	1
1	1	1	0	0	0	0	1
1	1	1	1	0	0	1	1

Мінімізація систем булевих функцій відбувається згідно з наступним алгоритмом, який представляє собою модифікацію алгоритму Квайна.

Будуємо повну множину елементарних кон’юнкцій отриманої системи, приписуючи в дужках після кожної констітуенти ознаку (у вигляді номеру чи номерів БФ у системі) її належності до тих чи інших БФ системи.

Виконуємо мінімізацію функції , застосовуючи модифікований алгоритм Квайна. Модифікація полягає в тому, що:

– при виконані операції неповного склеювання двох констітуент, елементарній кон’юнкції, що виникає в результаті склеювання, приписується ознака, яка складається із номерів БФ, спільних для двох констітуент (останнє також справедливо для двох елементарних кон’юнкцій, що склеюються). Якщо ознаки констітуент не містять спільних номерів, то склеювання не відбувається;

– операція поглинання відбувається тільки для елементарних кон’юнкцій з однаковими ознаками.

Отримані в результаті склеювання і поглинання елементарні кон’юнкції називаються простими імплікантами системи БФ.

Для зручності виконання операції неповного склеювання пронумеруємо кожну констітуенту із ДДНФ функції і виконуємо склеювання.

Подальші склеювання і поглинання неможливі, тобто ми отримали всі прості імпліканти системи БФ і остання форма – це скорочена ДНФ БФ .

Будуємо ІТ з тією лише відмінністю, що для кожної констітуети виділяються стільки стовпчиків, скільки різних номерів БФ містить її ознака; строчки ІТ позначаються простими імплікантами скороченої ДНФ; « * » в ІТ проставляються згідно з наступним правилом:

а) проста імпліканта і констітуента мають спільні ознаки;

б) проста імпліканта накриває констітуенту;

в) « * » проставляються лише у клітини, що знаходяться на перетині строчок (з простими імплікантами) і стовпчиків (з констітуентами 1), які мають спільні ознаки.

Далі знаходимо ядро БФ і так далі.

Дивитись у додаток Таблиця 1.

Отримана мінімальна система БФ служить основою для побудови комбінаційної схеми.

Дивитись у додаток Схема 3

Для отриманої схеми визначаємо L, Т и N.

Знаходимо час затримки сигналу:

, 100.

Розраховуємо складність схем:

де – кількість елементів у мікросхемі, – число виводів мікросхеми і-того типу, – число типів мікросхем.

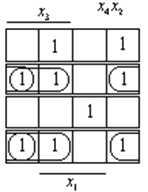
Будуємо схему для реалізації функції, заданої табл. 1.1 з використанням мультиплексорів з двома керуючими входами.

При реалізації функції від чотирьох перемінних з використанням мультиплексора, що має два керуючі входу, треба виключити шістьох різних пар перемінних (x₄ x₃ , x₄ x₂ , x₄ x₁ , x₃ x₂ , x₃ x₁ , x₂ x₁ ). При виключенні кожної пари перемінних діаграму Вейча заданої функції можна розглядати як чотири самостійні діаграми для залишкових функцій f0, f1, f2, f3.