| Скачать .docx |
Реферат: Разработка схем управления счетчиками
Проектирование синхронной пересчетной схемы
Пересчетная схема реализует следующую последовательность двоичных эквивалентов чисел: 5,4,2,0,7,6,1, (1), в которой предусмотрена возможность реверса, т.е. изменение порядка работы схемы на обратный: 1,6,7,0,2,4,5. (2)
Так как число выполняемых счетчиком операций k=2 (прямой счет и обратный), то в соответствии с с формулой
my =] log k [ (3)
my = ]log 2[ = 1
т.е. требуется одна управляющая переменная. Условимся, что при у=0 счетчик будет вырабатывать последовательность чисел (1), а при у=1 последовательность чисел (2). Описание работы счетчика представим в виде таблицы 1.
Количество разрядов счетчика определяется как
n = ]log (Nmax +1)[, (4)
где Nmax =7 – максимальное число в заданной последовательности. Следовательно, n = ]log (7+1)[=3. Обозначим выходные сигналы каждого разряда счетчика как Q1, Q2, Q3 (Q1- старший разряд, Q3- младший разряд). В столбцах Q1, Q2, Q3 таблицы 1 перечислены разрешенные комбинации выходных сигналов счетчика. Порядок следования этих комбинаций строго определен выражениями (1), (2) и значениями переменной у. В столбцах φQ 1, φQ 2, φ,Q 3 указан тип перехода, который осуществляется каждым разрядом счетчика при соответствующем изменении состояния этого счетчика.
Таблица 1
| № состояния | y | Q1 | Q2 | Q3 | φQ1 | φQ2 | φQ3 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 | β |
| 2 | 0 | 1 | 0 | 0 | β | α | 0 |
| 3 | 0 | 0 | 1 | 0 | 0 | β | 0 |
| 4 | 0 | 0 | 0 | 0 | α | α | α |
| 5 | 0 | 1 | 1 | 1 | 1 | 1 | β |
| 6 | 0 | 1 | 1 | 0 | β | β | α |
| 7 | 0 | 0 | 0 | 1 | α | 0 | 1 |
| X | X | X | X | X | X | X | X |
| 8 | 1 | 0 | 0 | 1 | α | α | β |
| 9 | 1 | 1 | 1 | 0 | 1 | 1 | α |
| 10 | 1 | 1 | 1 | 1 | β | β | β |
| 11 | 1 | 0 | 0 | 0 | 0 | α | 0 |
| 12 | 1 | 0 | 1 | 0 | α | β | 0 |
| 13 | 1 | 1 | 0 | 0 | 1 | 0 | α |
| 14 | 1 | 1 | 0 | 1 | β | 0 | 1 |
| X | X | X | X | X | X | X | X |
Используя карту Карно для четырех переменных, опишем поведение каждого разряда счетчика.
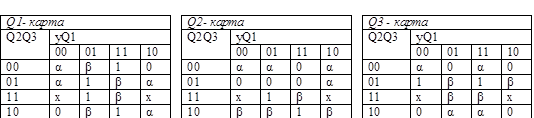
После выполнения операции подстановки в карты Карно значений входных сигналов из таблицы 2 состояние триггеров трех разрядов счетчика будут характеризоваться соответствующими картами Карно для Т-триггера и для JK – триггера.
Функции внешних переходов для Т-триггера и для JK – триггера:
Таблица 2
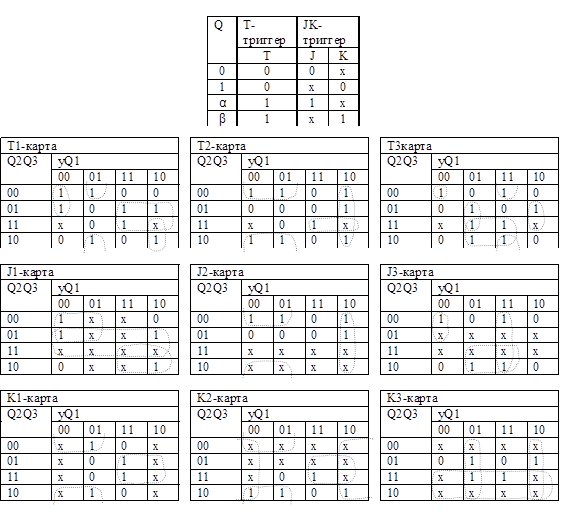
Проведя склеивание, получим следующие выражения:
Т1= yQ3 \/ y-Q1Q2 \/ -yQ1-Q3 \/ -y-Q1-Q2
T2= -y-Q3 \/ y-Q1 \/ yQ2Q3
T3= Q1Q2 \/ y-Q1Q3 \/ -y-Q1-Q2-Q3 \/ -yQ1Q3 \/ yQ1-Q3
J1= Q3 \/ yQ2 \/ -y-Q2
J2= y-Q1 \/ -y-Q3
J3= Q1Q2 \/ yQ1 \/ -y-Q1-Q2
K1= -y-Q3 \/ yQ3
K2= -y-Q3 \/ yQ3 \/ -Q1
K3= Q2 \/ -yQ1 \/ y-Q1
Преобразуем полученные функции в базис И-НЕ
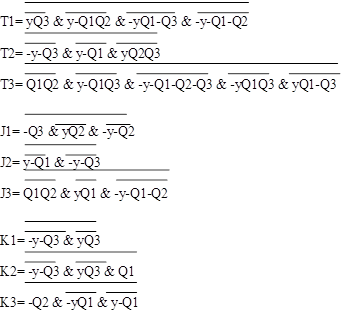
Проведем оценку сложности комбинационных схем управления в полученных счетчиках. Для счетчика, реализованного на базе JK-триггеров, сложность определяется суммой
S[JK]=1+(1+1)+(2+1)+(1+1+1)+(1+1)+(2+1)+(1+1)+(1+1)+(1+1)+(2+1+1)+(1+1+1)+(2+1)+(1+1)++(1+1)+(2+1)+(1+1)+1+(1+1+1)+1+(2+1)+(1+1)+(1+1+1)=52,
а для счетчика реализованного на базе T – триггеров, составит
S[T]=(1+1)+(1+1+1)+(2+1+1)+(2+1+1)+(1+1+1+1)+(2+1)+(1+1)+(1+1+1)+(1+1+1)+(1+1)+(1+1+1)+(2+1+1+1)+(2+1+1)+(1+1+1)+(1+1+1+1+1)=50
Сравнение оценок сложности схем показывает, что S[JK]>S[T], следовательно, для реализации пересчетной схемы целесообразно выбрать триггер T- типа.
Проектирование триггерных устройств
Функцию внешних переходов T-триггера определяет таблица 3.
Таблица 3.
| T | Qt | Qt+1 | φQi |
| 0 | 1- | 1 | 1 |
| 0 | 0- | 0 | 0 |
| 1 | 1- | 0 | β |
| 1 | 0- | 1 | α |
Условия переключения выходного сигнала триггера по отношению к синхросигналу С: изменение выходного сигнала триггера Q будет происходить при переходе С из 1 в 0, т.е. задним фронтом сигнала С.
Описание работы триггера представим в виде таблицы внутренних состояний и переходов триггерного устройства в таблице 4.
Таблица 4.
№ сост |
Состояние сигналов СТ | Q выхода | |||
| 00 | 01 | 11 | 10 | ||
| 1 | (1) | 2 | - | 4 | 0 |
| 2 | 1 | (2) | 3 | - | 0 |
| 3 | - | 6 | (3) | - | 0 |
| 4 | 1 | - | - | (4) | 0 |
| 5 | (5) | 6 | - | 8 | 1 |
| 6 | 5 | (6) | 7 | - | 1 |
| 7 | - | 2 | (7) | - | 1 |
| 8 | 5 | - | - | (8) | 1 |
Количество внутренних состояний триггера можно сократить, объединяя строки таблицы 4 по следующим правилам:
· две и более сток таблицы можно соединить, если числа в соответствующих позициях строки совпадают;
· в одной строке в данной позиции стоит "-", а в другой строке в этой же позиции стоит число
· если объединены строки, где в данной позиции стоят числа в скобках и без скобок, то в результирующей строке в данной позиции ставится число.
Минимизированная таблица внутренних состояний и переходов T – триггера имеет следующий вид:
Таблица 5.
| № состояний | СТ | Q | |||
| 00 | 01 | 11 | 10 | ||
| 1,2,4 | (1) | (2) | 3 | (4) | 0 |
| 3 | - | 6 | (3) | - | 0 |
| 5,6,8 | (5) | (6) | 7 | (8) | 1 |
| 7 | - | 2 | (7) | - | 1 |
Преобразуем таблицу 5 в соответствии с количеством новых состояний триггера в таблицу 6.
Таблица 6.
| № состояний | СТ | Q | |||
| 00 | 01 | 11 | 10 | ||
| 1,2,4 | (1) | (1) | 2 | (1) | 0 |
| 3 | - | 3 | (2) | - | 0 |
| 5,6,8 | (3) | (3) | 4 | (3) | 1 |
| 7 | - | 1 | (4) | - | 1 |
Так как число внутренних состояний уменьшилось до 4, то для кодирования этих состояний достаточно k=logS=2 внутренних переменных. Обозначим их как у1 и у2 .
Каждому внутреннему состоянию триггера поставим в соответствие набор значений переменных у1 и у2 .
Составим граф переходов, где коды 00, 01, 11, 10 – коды внутренних состояний 1,2,3,4 соответственно.
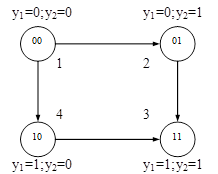
В соответствии с выбранным вариантом кодирования состояний триггера, минимизированная таблица Т – триггера (таблица 7) будет представлять собой совокупность 2 таблиц, каждая из которых определяет одну из функций у1 или у2.
Таблица 7.
| Код внутреннего состояния у1 у2 | CТ | Q | |||
| 00 | 00 | 00 | 01 | 00 | 0 |
| 01 | - | 11 | 01 | - | 0 |
| 11 | 11 | 11 | 10 | 11 | 1 |
| 10 | - | 00 | 10 | - | 1 |
Данные таблицы 7 позволяют описать поведение переменных у1 и у2 в виде карт Карно. Для устранения явления статического состязания сигналов в карты Карно кроме минимальных покрытий следует вводить избыточное покрытие, таким образом, чтобы каждая пара смежных покрытий входила бы, по меньшей мере в одно общее покрытие.

Проведя склеивание в картах Карно, определим выражения для у1 и у2 .
у1 = у2 -С \/ y1 C \/ y1 y2
y2 = y2 -C \/ y2 -T \/ -y1 CT \/ -y1 y2
Полученные уравнения позволяют построить схему проектируемого триггера. Перед построением преобразуем уравнение в базис И-НЕ, предварительно вынеся за скобки y1 и y2 .

Т-триггер имеет два входа. Т – это информационный вход, С-это разрешающий вход синхросигнала. Этот триггер работает в счетном режиме (т.к. он переключается каждый раз когда на его вход подается уровень логической единицы).
Схема проектируемого Т-триггера, построенного по полученным выражениям с использованием элементов 2И-НЕ:
