| Скачать .docx |
Курсовая работа: Разработка функциональной цифровой ячейки от функциональной логической схемы проектируемого узла до печатной платы узла
Простановка номеров цепей в соответствие с техническим заданием
Первым этапом работы является простановка номеров цепей на принципиальной схеме в соответствие с техническим заданием. В нашем случае цепи представляют собой выводы, соединенные с общей шиной, которая, в свою очередь соединена с разъемом. Всего на схеме 18 элементов. В соответствие с техническим заданием они представляют собой 6 отдельных микросхем К155ЛА4 в корпусе DIP 14 по 3 «ЗИ-НЕ» (3 секции) с 4 выводами (3 входа и один инверсный выход). Поэтому был создан элемент: символ элемента в Symbol Editor, посадочное место и тип корпуса элемента (в Pattern Editor), затем символ и посадочное место были объединены в компонент и сохранены в библиотеке с помощью Library Executive [1, 2]. В редакторе Schematic работают с принципиальной схемой. Вместо компонента на шаблоне ставится созданный элемент. Используется Place Port. Стирают цепи и номера цепей, затем элемент соединяется проводом с шиной посредством Place Wire. Затемназначаетсяномерновыхцепей (Place Wire+ Port Properties/Net Name). Номера цепей, подходящих к разъему, назначаются произвольно (из списка номеров в техническом задании). Результатом является исходная функционально-логическая схема проектируемого узла (задание на курсовой проект).
2. Компоновки логических элементов в корпуса
Компоновка типовых элементов конструкции
Компоновка – первый этап конструкторского синтеза, при котором определяется однозначное соответствие между функционально-логическим, схемотехническим и конструкторским делением проектируемого устройства. Предполагается, что конструкция разбивается на унифицированные и неунифицированные элементы нескольких уровней конструкторской иерархии.
На этапе компоновки могут решаться задачи типизации, покрытия и разрезания.
Типизация – это процедура выделения в схеме частей, повторяющих друг друга, при этом число типов может быть задано, либо определяться в процессе типизации.
Покрытие – это определение минимального числа корпусов, покрывающих логические элементы принципиальной схемы, то есть задача покрытия решается на этапе перехода от логической схемы к электрической.
Разрезание – это разбиение общей схемы на части, число которых либо задано, либо определяется в процессе разрезания, при этом стремятся обеспечить минимум суммы межблочных связей.
В курсовой работе решается задача разрезания заданной схемы устройства на подсхемы с целью определения принадлежности логических элементов отдельным микросхемам.
Алгоритм разрезания схемы состоит из двух этапов:
– предварительное разрезание (быстрое получение результата)
– окончательная компоновка (улучшение результата итерационным методом).
Последовательный алгоритм предварительной компоновки:
1. Построение матрицы смежности взвешенного графа схемы А.
2. Для каждого элемента рассчитывается его суммарная тяга к остальным элементам.
3. Выбирается элемент, имеющий максимальную локальную степень.
4. Выбранный элемент помечается меткой т. Вначале выполнения алгоритма m=0.
5. Выбираются все элементы, связанные с выбранными ранее, но непомеченные метками.
6. Увеличивается метка m=m+l. Помечаются выбранные в блоке 5 элементы метками т.
7. Выполняются блоки 5, 6, 7 пока не будут помечены все элементы.
8. Выбирается очередной модуль верхнего уровня М j для компоновки.
9. Компонуются в Mj элементы с младшими метками, не вошедшие в компоновку ранее.
10. Компоновка в Mj заканчивается, когда модуль полностью заполнен.
11. Продолжается выполнение блоков 8–11, пока не будут заполнены все модули или пока не будет исчерпан список элементов.
12. Выход из алгоритма.
Итерационный алгоритм улучшения компоновки:
Процесс оптимизации выполняется путем последовательной перестановки элементов из разных модулей.
Пусть элемент Ej установлен в модуль Ms, а элемент Ej установлен в модуль Mt.
Рассчитываем показатель качества перестановки:
Rij = R внш it + R внш jt – R внт i – R внт j – 2 Rij, где
Rвнш it – количество связей Ei с элементами в Mt, Rbhui jt количество связей Ej с элементами в Ms, R внт i – количество связей Ei внутри модуля, R внт j – количество связей Ej внутри модуля. Выбираем ту пару, для которой показатель качества перестановки максимален.
Алгоритм:
1. Ввод начальной компоновки.
2. Расчет матриц связности Cs и Cst и заполнение их.
3. Расчет матрицы эффективности перестановок Rij для всех пар модулей.
4. Выбирается из этих матриц максимальный элемент.
5. Проверка: если показатель качества перестановок отрицательный, переход к блоку 7, иначе к блоку 6.
6. Перестановка элементов Ei и Ej и возврат к блоку 2.
7. Выход из алгоритма. Дальнейшее улучшение с помощью данного
алгоритма невозможно [3].
Таким образом, 18 логических элементов размещаются в 6 микросхемах (по 3 элемента в каждой) оптимальным образом. Для этого используем программу PROG (18 элементов, 6 блоков максимальные значения входных данных для компоновки). Алгоритм работы в этой программе:
1) В соответствии со своей принципиальной электрической схемой заполняют симметричную матрицу смежности. В этой матрице у нас будет 18 строк и 18 столбцов, что соответствует количеству логических элементов. Последовательно перебирая все элементы, ищут номера повторяющихся цепей. На пересечении i-той строки и j-ro столбца ставят цифру (от 1 до 4), которая и означает количество связей, одинаковых цепей i-ro элемента с j-тым. Главная диагональ такой матрицы – нули. Заполнив матрицу, смотрят предварительную схему соединений (F2). В ней 64 внешних связей и 7 внутренних. Таким образом, на данном этапе используют последовательный алгоритм предварительной компоновки, предварительное разрезание (быстрое получение результата) в автоматическом режиме. Полученная матрица представлена ниже:
Таблица 1

Где весовой коэффициент – числовой коэффициент, параметр, отражающий значимость, относительную важность, «вес» данного фактора, показателя в сравнении с другими факторами, оказывающими влияние на изучаемый процесс.
Весовые коэффициенты равны количеству связей конкретного элемента с остальными элементами схемы.
Обозначение элементов метками:
1. Выбирается элемент с имеющий максимальную локальную степень (чей весовой коэффициент максимален) – элемент №4. Для данного элемента устанавливается метка М = 0.
2. Выбираются элементы, связанные с элементом с М = 0. Данные элементы помечаются меткой М = 1. Элементы №9, 11, 13, 14, 15, 17, 18
3. Выбираются элементы, связанные с элементами с М = 1 и не имеющими меток. Данные элементы помечаются меткой М = 2. Элементы 1, 2, 3, 5, 6, 7, 8, 10, 16.
4. Выбираются элементы, связанные с элементами с М = 2 и не имеющими меток. Данные элементы помечаются меткой М = 3. Элемент 12.
На этом этап обозначение элементов метками закончен. Далее идет первоначальная компоновка элементов.
 |
| Рис. 2. Предварительная схема соединений |
Применение этого алгоритма приводит к постепенному ослаблению внутриблочных связей от первого блока до последнего.
2) Работают с матрицами Ро. Их 15 штук (фактически, это схема соединений в матричном виде). Выбираем из матриц ту, у которой максимальное значение элемента матрицы (4,3 и т.д.). В ней меняют местами компоненты, пересечение которых и дает этот элемент матрицы. Смотрят промежуточный результат компоновки: видно, что количество внутренних связей увеличивается по сравнению с первоначальным числом (клавиша F2 для просмотра схемы соединений), а количество внешних связей уменьшается. Затем снова выбирают матрицу с максимальным значением элемента. Продолжать до тех пор, пока все элементы всех матриц не станут отрицательными, либо равными нулю. На данном этапе улучшают начальную компоновку итерационным алгоритмом. То есть основная идея этого алгоритма и этого этапа заключается в межблочных перестановках пар элементов с целью минимизации общего количества межблочных связей. Итоговый вид всех матриц Итоговый вид всех матриц:
   |
| Рис. 3. Итоговый вид всех матриц |
0 итераций (нет перестановок). Внешних связей: 64, внутренних связей: 7.
1 итерация (1-ая перестановка). Внешних связей: 59, внутренних связей: 12.
2 итерация (2-ая перестановка). Внешних связей: 54, внутренних связей: 17.
3 итерация (3-я перестановка). Внешних связей: 49, внутренних связей: 22.
4 итерация (4-ая перестановка). Внешних связей: 47, внутренних связей: 24.
5 итерация (5-ая перестановка). Внешних связей: 45, внутренних связей: 26.

Рис. 4. График зависимости числа внешних связей от числа итераций

Рис. 5. График зависимости числа внутренних связей от числа итераций
3) После работы с матрицами на экран выводится схема соединений. Это и есть оптимальное расположение (компоновка) элементов в конструкции (элементов в микросхемах и микросхем между собой).

Рис. 6. Схема соединений
Видно, что процесс оптимизации связан с увеличением внутренних связей и уменьшением внешних. После каждой перестановки число внутренних связей увеличивается, а число внешних – уменьшается. Это связано с тем, что меняются местами элементы из разных микросхем, которые являются компонентами матриц Ро. В результате задача оптимизация будет выполнена: в заданное количество блоков (микросхем) расположили с минимальным количеством внешних связей между ними по 3 элемента. Это облегчит дальнейшие этапы моделирования.
4) Осталось скомпоновать разъем с микросхемами, так как у него тоже есть электрические связи с элементами и он является частью конструкции. Фактически, повторяется п. 1 нашего алгоритма, но без заполнения матрицы смежности, так как программа не предусматривает компоновку с количеством блоков, равным 7. Для каждой микросхемы, начиная с первой, смотрят номера цепей элементов в ней, которые повторяются с номерами цепей этого разъема. На схеме соединений ставится связь от разъема к микросхеме с цифрой, которая говорит о числе совпадений цепей разъема и микросхемы. Повторять то же самое для оставшихся 5 микросхем. Соответственно, получаем схему соединений, которая будет представлять взвешенный граф с 7-ю элементами: 6 микросхем и 1 разъем. Изменяются и графики зависимостей, так как разъем увеличивает число внешних связей (в данном случае на 46).

Рис. 7. Схема соединений с учетом разъема
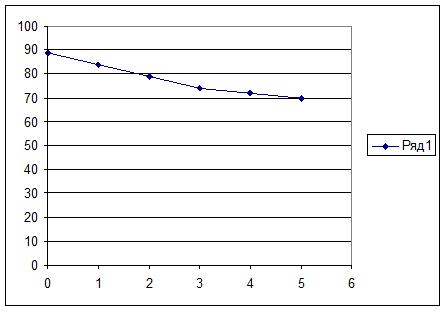 |
| Рис. 8. График зависимости числа внешних связей от числа итераций внешних связей от числа итераций с учетом разъема. |
3. Размещение элементов на коммутационных платах
Постановка задачи размещения.
Дано:
E = {e1, e2, e3, e4, e5, e6, e7} – множество элементов схемы устройства.
P = {p1, p2, p3, p4, p5, p6, p7} – множество установочных позиций на коммутационной плате для размещения элементов.
Задача размещения состоит в определение соответствия между элементами устройства и установочными позициями печатной платы. Разъем (элемент е7) может находиться только в одной конкретной позиции (позиция p7), все остальные элементы однотипны, а позиции равноправны, следовательно мы имеем 6! Вариантов размещений элементов на плате. Такая задача называется задачей дискретного размещения. Для того чтобы упростить задачу размещения и не перебирать все 6! вариантов решений используются различные комбинационные методы. В данной курсовой работе используется метод ветвей и границ.
Метод ветвей и границ.
Ход решения.
Соответствие блоков полученных в разделе 1 элементам.
| Блок | Элемент |
| 4, 9, 18 | e1 |
| 13, 1, 15 | e2 |
| 7, 11, 14 | e3 |
| 12, 6, 5 | e4 |
| 3, 17, 8 | e |
| 10, 16, 2 | e6 |
| Разъем | e7 |
1. Определение последовательности элементов.
Последовательность элементов строится исходя из оптимизированной компоновки (рис 4.), по ней определятся количество между элементами. Элемент, наиболее связанный с разъемом: е2.
Дальнейшая последовательность элементов (каждый элемент наиболее связан с предыдущими): е1, е3, е5, е6, е4.
2. Составление матрицы D и матрицы S.
Матрицы составляются исходя из оптимизированной компоновки (рис 7.).
| Матрица S | Матрица D | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
3. Расчет верхней границы – функции качества размещения.
Функция качества размещения рассчитывается следующим образом:
1. Разъем (е7) помещается в позицию (р7). Все остальные элементы остаются неразмещенными.
2. Наиболее связанный с разъемом элемент (е2) последовательно помещается в каждую возможную позицию (p1…p6), рассчитывается нижняя оценка данного размещения. Выбирается позиция, нижняя оценка размещения которого минимальна.
Нижняя оценка рассчитывается следующим образом:
F = Fн + Fнр + Fр, где:
1. Fн – оценка длины связи между не размещенными элементами
2. Fнр – оценка длины связи между не размещенными и размещенными элементами
3. Fр – значение длины связи между размещенными элементами
Для расчета нижних оценок используется программа placeing.
Минимальная нижняя оценка при размещение в позицию p6 = 4560. Элемент закрепляется в позиции p6.
3. Аналогично пункту 2 выбираются элемент наиболее связанный с размещенными элементами и разъемом. Перебираются возможные варианты размещение элемента и выбирается такое размещение, нижняя оценка которого минимальна. Элемент закрепляется в данной позиции.
4. Пункт 3 выполняется до тех пор, пока не будут размещены все элементы. Полученное размещение:
| Позиция | Элемент |
| p1 | e4 |
| p2 | e6 |
| p3 | e5 |
| p4 | e3 |
| p5 | e1 |
| p6 | e2 |
| p7 | Разъем |
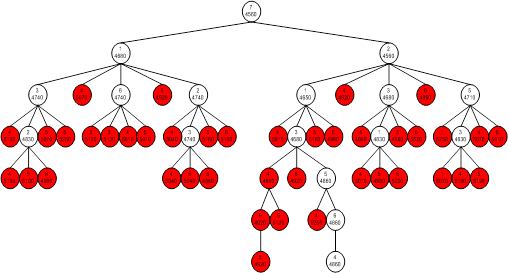
4. Дальнейшее исследование возможных вариантов размещения.
Во время исследования отсекаются бесперспективные варианты решения (те варианты, у которых нижняя оценка больше верхней границы).
Приведем полученное дерево:


4. Минимизация длины связей между контактами разъема и контактами внешних цепей
На данном этапе необходимо используя Венгерский алгоритм минимизировать длины связей между контактами разъёма и контактами внешних цепей.
Назначение осуществляется в полуавтоматическом режиме с помощью «Венгерского алгоритма» (с использованием программы VENGR.EXE).Структурная схема «венгерского алгоритма» показана на рисунке 7.
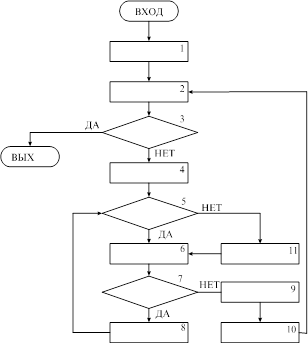
Рисунок 9 – структурная схема венгерского алгоритма.
1 блок – начальное преобразование матрицы эффективности в эквивалентную матрицу. Для этого из каждой строки вычитается минимальный элемент.
2 блок – в полученной матрице эффективности помечаются нули, образующие правильное решение, таким образом, чтобы в каждой строке и столбце было не более одного помеченного нуля.
3 блок – проверка: получен ли полный правильный выбор нулей. Выбор нулей называется полным, если помечено нулей, где – размерность матрицы. Если получен полный правильный выбор, то – к выходу, если «нет», то к блоку 4.
4 блок – помечаем «+» столбцы, в которых есть нули со «*». Таким образом помечаем все ребра, инцидентные вершинам. Каждый «+» соответствует вершине.
5 блок – проверка: есть ли в матрице незанятые нули. Нуль называется незанятым, если его строка и его столбец не помечены «+».
6 блок – помечаем незанятый нуль «/».
7 блок – проверка: есть ли в строке нуля, помеченного «/» в блоке 6 нуль со «*», если «да», то переход в блок 8.
8 блок – если в строке есть нуль со «*», то снимаем «+» со столбца, в котором он находился, а строку помечаем «+».
9 блок – если нуля со «» в строке нет, то это означает, что можно увеличить количество нулей со «*» на 1. Строится расширяющая цепочка, начиная с последнего помеченного нуля (блок 6): переходим по столбцу к нулю со «», по строке к нулю со «/», по столбцу к нулю со «*», пока цепочка не прервется. Возможно, что цепочка прервется сразу.
10 блок – в результате процедуры в блоке 9 образовалась цепочка, состоящая из нулей со «/» и нулей со «», но нулей с «/» на 1 больше. Если теперь в цепочке снять с нулей «», а «/» заменить на «*», то нулей со «*» станет на 1 больше. Снимаем все метки, кроме «» и переходим к блоку 2.
11 блок – выполняется эквивалентное преобразование матрицы с целью увеличения количества нулей. Если в блоке 5 свободных нулей не найдено, то надо их добавить – для этого в незанятых строках, не помеченных «+» находится минимальный элемент, больший нуля hmin. Вычитаем hmin из элементов всех строк, не помеченными «+» и прибавляем ко всем элементам строк столбцов, помеченных «+».
Исходными данными для работы алгоритма является матрица эффективности назначений, для ее вычисления мы должны построить матрицы R и D (связей и расстояний соответственно) и получить все элементы матрицы эффективности назначений по формуле:
Cij = ri, 1di, 1 + ri, 2di, 2 + … + ri, j-1di, j-1 + ri, jdi, j, где i, j – номера строки и столбца, на пересечении которых находится элемент. В нашем случае программа сама рассчитывает матрицу эффективности назначений. Исходными данными для нее служит матрица, отражающая координаты выводов микросхем и разъема.
Первоначальное подключение цепей к контактам разъема
Первоначальное подключение берется из задания, также вычисляется суммарная оценка длины проводников, определяющая качество данного назначения выводов разъема.
| № вывода разъема | № проводника, подключаемого к разъему |
| 1 | 4 |
| 2 | 8 |
| 3 | 12 |
| 4 | 20 |
| 5 | 16 |
| 6 | 24 |
| 7 | 28 |
| 8 | 2 |
| 9 | 27 |
| 10 | 15 |
| 11 | 7 |
| 12 | 17 |
Оценка длины проводника подключаемого к разъему – длина цепи, включающей все выводы элементов и вывод разъема с одинаковыми номерами.
Пример расчета оценки длины проводника для 1 вывода разъема.
1. Исходя из эскиза печатной платы (см Приложение 2) находятся координаты выводов подключенных к 1-му выводу разъема и координаты самого вывода разъема. Разъем: (97,5; 50), вывод 1 (0; 0) вывод 2 (12,5; 0)
2. Аналитически находится оптимальная последовательность подключения выводов к разъему. Последовательность: вывод 1 – вывод 2 – разъем.
3. Расчет оценки длины проводника
4. Аналогично рассчитываются остальные оценки длин.
Такое подключение, возможно, не является оптимальным, для оптимизации первоначального подключения цепей к разъему применяются алгоритмы линейного назначения. В данной курсовой работе используется программа, основанная на венгерском алгоритме. Для получения матрицы назначений в программе требуется заполнить следующую таблицу (см рис 6).

Рис. 10. Исходные данные программы оптимизации подключения цепей к разъему
Алгоритм заполнения таблицы.
1. Согласно имеющимся данным по микросхеме К155ЛА4 (Рис. 11 и Рис. 12) и данным по компоновке логических элементов в блоки составляется соответствие выводов каждого блока и вывода корпуса.
2. Согласно данным по размещению (Раздел 2) составляется эскиз печатной платы с размещенными на ней корпусами микросхемы (см Приложение 2). Выбирается произвольная точка, которая служит началом координат
 |
 |
| Рис. 11. Корпус микросхемы | Рис. 12. Соответствие логических выводов микросхемы выводам корпуса |
5. Согласно полученному эскизу печатной платы каждому выводу корпуса назначается своя координата относительно начала координат.
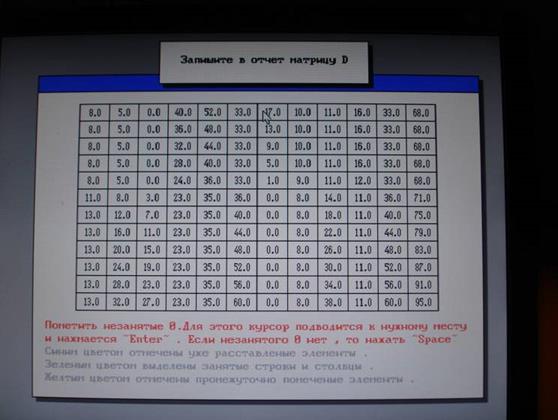
Рис. 13 Матрица D до начала выполнения алгоритма венгра

Рис. 13 Матрица D после выполнения алгоритма венгра
Результат выполнения программы – более оптимальное подключение цепей к контактам разъема.
| № вывода разъема | №Вывода разъема после переназначения |
| 1 | 17 |
| 2 | 7 |
| 3 | 27 |
| 4 | 24 |
| 5 | 12 |
| 6 | 8 |
| 7 | 15 |
| 8 | 2 |
| 9 | 28 |
| 10 | 16 |
| 11 | 20 |
| 12 | 4 |
Проведем проверку длин цепи до и после переназначения вывода разъема.
Рассмотрим цепь №17
До переназначения выводов: L=95+38=133 мм
После переназначения выводов: L=95+12=107 мм
Суммарная длина проводников уменьшилась, следовательно, найдено более оптимальное назначение выводов разъема.
5. Трассировка электрических соединений контактов элементов
Используя результаты предыдущих разделов (компоновка, минимизация расстояний), перечертим принципиальную схему используя редактор Schematic (результат представлен в приложении 3). Далее выполняем команду utils/ GenerateNetList… После чего запускаем редактор PCB, в котором чертим контур платы, подключаем нужные библиотеки, в нашем случае mai.lib, после чего выполняем команду utils/ LoadNetList… Появившиеся элементы расставляем в соответствии с результатами полученными в разделе 3. Использую команду Route/ Autorouters, в появившемся окне выбираем тип трассировки Quickroute и нажимаем кнопку Start. Результаты трассировки представлены в приложении 4.
В ходе выполнения курсовой работы был пройден весь путь разработки функциональной цифровой ячейки от функциональной логической схемы проектируемого узла до печатной платы узла. Были приобретены практические навыки применения алгоритмов и методов автоматизированного проектирования РЭС, закреплены теоретические знания.
Решение задачи компоновки позволило сократить количество внешних связей между блоками (корпусами микросхем) за счет увеличения количества внутренних (внутри блока) связей.
В результате решения задачи размещения элементов методом ветвей и границ мы получили дерево решений, отражающее оптимальный вариант размещения элементов в установочных позициях ячеек,
В результате решения задачи назначения выводов элементов схемы и разъема каждый элемент закреплен в конкретную позицию, что отображено в «схеме соединения выводов».
Результатом работы программы-трассировщика является 2-х слойная печатная плата.