| Скачать .docx |
Курсовая работа: Расчёт переходных процессов в линейных электрических цепях с сосредоточенными параметрами
Министерство Образования Украины
Кафедра электротехники
Курсовая работа
по курсу “Теория электрических и электронных цепей”
на тему “Расчёт переходных процессов в линейных электрических цепях с сосредоточенными параметрами”
Вариант № 12
Содержание курсовой работы
1. В электрической цепи, (схема которой представлена на рис.1, а параметры цепи приведены в таблице 1, причём R4 =R3 ), происходит переходной процесс. На входе цепи действует постоянное напряжение величиной Еm .
2.Классическим методом расчёта найти выражения для мгновенных значений всех токов цепи и напряжений на реактивных элементах после коммутации. Построить графики изменения этих величин в одних осях. Графики изменения построить на интервале, равном времени переходного процесса tnn .
Это время определить по следующим формулам:
![]()
![]() tnn
=
tnn
= ![]() или tnn
=
или tnn
=![]()
где λmin – наименьший из двух вещественных корней;
δ - вещественна часть комплексного корня.
3. Операторным методом расчёта найти выражение для тока в катушке индуктивности.
4. На входе цепи (рисунок 1) действует источник, напряжение которого меняется по синусоидальному закону
e(t)=Em sin(ωt +φ).
Определить выражение для мгновенного значения тока в катушке индуктивности.
Построить график переходного процесса тока катушки индуктивности.
5.На входе цепи,(рисунок 2) действует источник, напряжение которого меняется по закону(заданное графиком 1). Найти выражение для величины, указанной в 17-м столбце таблицы исходных данных (таблица 1). Построитьсовместные графики измерения заданного напряжения и искомой величины. В таблице исходных данных даны абсолютные значения напряжений U0, U1, U2, U3. Принимая значение времени: t1 =τ , t2 =1,5τ , t3 =2τ , t4 = 2,5τ .
Здесь τ – постоянная времени рассматриваемой цепи.
Таблица 1:
| Номер варианта | Номер схемы | Параметры источника |
Параметры цепи |
Параметры источника для интеграла Дюамеля |
Номер схемы по рисунку 2 | Исследуемая величина ƒ(t) |
||||||||||
Напряжение U, В |
Частота ƒ, Гц |
Нач. фаза φ,град. |
R1 Ом |
R2 Ом |
R3 Ом |
L мГн |
C мкФ |
№ графика | Uо В |
U1 В |
U2 В |
U3 В |
||||
| 12 | 12 | 70 | 30 | 75 | 26 | 10 | 10 | 100 | 25 | 12 | 20 | 5 | 10 | 0 | 4 | UR2 |
|
 |
|
|
Рисунок 2:
![]()
![]()
|
|
|
 |
|
|
|
|
 |
|
|
![]()
 |
1 этап курсовой работы
Расчет цепи с двумя реактивными элементами в переходных процессах классическим методом
 |
1 этап
Запишем начальные условия в момент времени t(-0)
![]() i2(-0)
=i1(-0)
=
i2(-0)
=i1(-0)
=![]() =
=![]() = 1.52 (A)
= 1.52 (A)
Uc(-0) = i2 . R2 =Uc(+0)
Напишем уравнения по законам Кирхгофа для цепи:
i1 -i2 -ic =0 (1)
![]() i1
.
R1
+ i2
.
R2
+L
i1
.
R1
+ i2
.
R2
+L![]() =U (2)
=U (2)
i1 . R1 + Uc =U (3)
Из (2) уравнения выразим i1
i1
= (2.1)
(2.1)
i1 из уравнения (2.1) подставим в (1) и выразим ic
ic
=![]() (1.1)
(1.1)
i1 подставим в (3) и выразим Uc
U= (3)
(3)
Uc
=U-U- i2
.
R2
-![]() (3)
(3)
Uc
=i2
.
R2
+![]() (3.1)
(3.1)
Uc
=![]()
![]() (3.2)
(3.2)
Подставим в место Uc и ic вуревнение (3.2), получим:
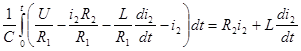 (3.3)
(3.3)
Продифференцируем уравнение (3.3) и раскроем скобки:
![]()
![]() (3.4)
(3.4)
В дифференциальном уравнении(3.4) приведём подобные слогаемые:
![]()
2 этап
Во втором этапе мы решим дифференциальное уравнение относительно i2 , для этого мы представим i2 как сумму двух составляющих i2св – свободная составляющая и i2вын – вынужденная составляющая
i2 =i2св +i2вын
i2вын найдём по схеме
i2вын
=![]()
i2св
найдём из дифференциального уравнения подставив численные значения в уравнение и заменив ![]() через l, а
через l, а ![]() через l2
получим:
через l2
получим:
Ll2
+R2
l+![]() l+
l+![]() =0 (3.5)
=0 (3.5)
Решим характеристическое уравнения (3.5) найдя его корни l1 и l2
0.1l2
+10l+![]() l+
l+![]()
15384,6+153,85l+40000+10l+0,1l2 =0
Д=b2 -4ac=(163,85)2 -4. 0,1. 55384,6=26846,82-22153,84=4692,98
![]() l1,2
=
l1,2
=![]() ;
; ![]() ;
; ![]() l1
l1
![]() l2
– вещественные
l2
– вещественные
l1
=![]()
![]()
![]()
l2
=![]()
![]()
i2св =А1 е-477t +А2 е-1162t (3.6)
i2 =1.94+ А1 е-477t +А2 е-1162t (3.7)
3 этап
Найдём А1 и А2 исходя из начальных условий, законов коммутации и на основании системы уравнений Кигхгофа записаных на 1 этапе.
Найдём ток i2 для момента времени t = +0. Для этого продифференцируем уравнение (3.6) при t=0.
i2(+0) =i2вын(+0) + А1 +А2
![]() -477 А1
-1162 А2
-477 А1
-1162 А2
Из уравнения (2) найдём ![]() для момента времени t+0
для момента времени t+0
![]() (3.8)
(3.8)
Из уравнения (3) выразим i1 для момента времени t+0 при Uc =i2 R2
i1
=![]() (3.9)
(3.9)
Найдём ![]() подставив значение i1
из уравнения (3.9) в уравнение (3.8)
подставив значение i1
из уравнения (3.9) в уравнение (3.8)
![]() (4.0)
(4.0)
Подставим значение ![]() , i2(+0)
, i2вын
в систему и найдём коэффициенты А1
и А2
, i2(+0)
, i2вын
в систему и найдём коэффициенты А1
и А2
![]() 1,52=1,94+ А1
+ А2
(4.1)
1,52=1,94+ А1
+ А2
(4.1)
2=-477 А1 -1162 А2 (4.2)
Из уравнения (4.1) выразим A1 и подставим в (4.2)
А1 =-0,42-А2
2=-477(-0,42-А2 )-1162А2 (4.3)
Из уравнения (4.3) найдём А2
2=200,34+477А2 -1162А2
2=200,34-685А2
А2
=![]()
А1 =-0,42-0,29=-0,71
Подставим найденные коэффициенты А1 и А2 в уравнение (3.7)
i2 =1,94-0,71е-477t +0,29е-1162t (А)
4 этап
Определяем остальные переменные цепи UL , Uc , ic , i1
UL
=![]() (В)
(В)
Uc
= ![]() +i2
R2
=
+i2
R2
= ![]()
=![]()
![]() (В)
(В)
ic
=![]() (А)
(А)
i1 =ic +i2 =(0,044е-477t +0,014е-1162t )+( 1,94-0,71е-477t +0,29е-1162t ) =
=1,94-0,666е-477t +0,304е-1162t (А)
Построим графики изменения найденных величин в одних осях. Графики изменения построим на интервале, равном времени переходного процесса tnn .
Это время определим по формуле:
![]()
![]() tnn
=
tnn
= ![]()
Найдём tпп время переходного процесса
tпп
=![]() (с)
(с)
Таблица переменных
| Время переходного процесса tnn (c) | Значение тока i1 (A) |
Значение тока i2 (A) |
Значение тока ic (A) |
Значение напряжения UL (B) |
Значение напряжения UC (B) |
| 0.000 | 1.578 | 1.520 | 0.058 | 0.20 | 15.22 |
| 0.001 | 1.622 | 1.590 | 0.032 | 10.49 | 16.95 |
| 0.002 | 1.713 | 1.695 | 0.018 | 9.75 | 17.92 |
| 0.003 | 1.790 | 1.779 | 0.011 | 7.07 | 18.50 |
| 0.004 | 1.844 | 1.837 | 0.006 | 4.70 | 18.84 |
| 0.005 | 1.879 | 1.875 | 0.004 | 3.02 | 19.06 |
| 0.006 | 1.902 | 1.899 | 0.0025 | 1.90 | 19.19 |
| 0.0063 | 1.907 | 1.905 | 0.0022 | 1.65 | 19.21 |
Рисунок 3 - График токов
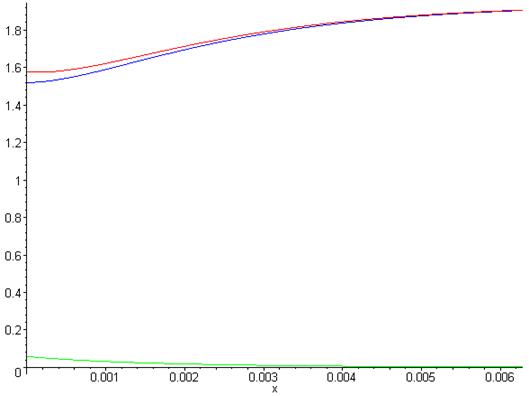
где
![]()
![]()
![]() i1
i2
ic
i1
i2
ic
Рисунок 4 – График напряжений

где
![]()
![]() UL
UC
UL
UC
2 этап курсовой работы
2. Найдём выражение для тока в катушке при действии в цепи источника синусоидального напряжения:
|
![]()
![]()
![]() R
R![]() 1
1

где Em =100 (B)
w=2pf ![]() =2 3,14 50=314 (Гц)
=2 3,14 50=314 (Гц)
j=300
R1 =R2 =10 (Ом) L=100 (мГн)
R3 =9 (Ом) С=100 (мкФ)
w=314 (Гц)
XL =wL=314. 0,1=31,4 (Ом)
XC
=![]() (Ом)
(Ом)
Найдём начальные условие:
U(t)=Um sin(wt+j)=100sin(314+30);
Um =100ej30 =86,603+j50 (В)
UC(-0) =0 (B)
Найдём полное сопротивление цепи
Zп =R1 +R3 +jXL =10+9+j31,4=19+j31,4 (Ом)
Зная сопротивление и напряжение найдём I3m
I3m
=I1m
=![]()
![]() (А)
(А)
Найдём мгновенное значение тока
i3 (t)=I3m sin(wt+j)=2.725sin(314t-28.82) (A)
Для времени t=0 ток будет равен
i3(-0) =2.725sin(-28.82)=-1.314 (A)6 (A)
Таким образом
UC(-0) =UC(+0) =0 (B)
i3(-0) = i3(+0) =-1.314 (A)
1 этап
Напишем уравнения по законам Кирхгофа для цепи:
![]() i1
-i2
-i3
=0 (1/
)
i1
-i2
-i3
=0 (1/
)
i1
.
R1
+ i3
.
R3
+L![]() =U(t) (2/
)
=U(t) (2/
)
i1 . R1 +i2 . R2 +Uc =U(t) (3/ )
Из (2/ ) уравнения выразим i1
i1
=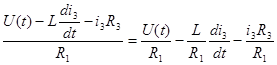 (2/
.1)
(2/
.1)
i1 из уравнения (2/ .1) подставим в (1/ ) и выразим i2
i2
=![]() (1/
.1)
(1/
.1)
U(t)=U(t)-i3
.
R3
-L![]() +R2
+R2![]()
![]()
-![]() (3.1)
(3.1)
Продифференцируем уравнение (3.1) раскроем скобки и приведём подобные слагаемые:
![]() (3.2)
(3.2)
2 этап
Вид решения для i3св при действии в цепи источников постоянного и переменного напряжений одинаков, так как в однородном дифференциальном уравнении отсутствует параметр U, а значит, вид i3св не зависит от входного напряжения.
Таким образом, выражение, которое было найдено в 1этапе, будет иметь следующий вид:
i3св =А1 е-406t +А2 е-234t
Теперь найдём вынужденную составляющую тока катушки i3вын
i3вын находим для цепи в послекоммутационном режиме. Расчёт параметров схемы при действии e(t);
Найдём вынужденную составляющую амплитудного тока I1 , а для этого найдём Zп вын сопротивление цепи:
Zп
вын
=![]() (Ом)
(Ом)
I1m
=![]() (A)
(A)
Найдём Uab вын
Uab m
= I1m
![]() (В)
(В)
I3 m
=![]()
![]() (A)
(A)
Найдём i3 вын
I3 вын = I3 m sin(wt+j)=2.607sin(314t-43.60) (A)
Таким образом
i3 =2.607sin(314t-43.60)+А1 е-406t +А2 е-234t
3/ этап
Найдём А1 и А2 исходя из начальных условий, законов коммутации и на основании системы уравнений Кигхгофа записаных на 1/ этапе.
![]() i3
=2.607sin(314t-43.60)+А1
е-406t
+А2
е-234t
i3
=2.607sin(314t-43.60)+А1
е-406t
+А2
е-234t
![]()
i3(+0) =i3(-0) =-1.314 (A)
![]() i3(+0)
=2.607sin(-43.60)+A1
+A2
=-1.798+A1
+A2
i3(+0)
=2.607sin(-43.60)+A1
+A2
=-1.798+A1
+A2
![]()
![]()
R1 i1 =U(t)-R2 i2 -UC
![]()
![]()
![]() =
=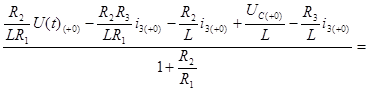
![]()
=![]()
![]()
Подставим значение ![]() , i3(+0)
, и найдём коэффициенты А1
и А2
для времени t+0
, i3(+0)
, и найдём коэффициенты А1
и А2
для времени t+0
![]() -1.314=-1.798+A1
+A2
-1.314=-1.798+A1
+A2
433.96=592/806-406A1 -234A2
A1 =-1.314+1.798-A2 =0.484- A2
433.96=592.806-406(-0.484- A2 )-234 A2
433.96-592.806+406 . 0.484= A2 (406-234)
![]() 37.658=172A2
A2
=0.219
37.658=172A2
A2
=0.219
A1 =0.265
Ток i3 будет равняться
I3 =2.607sin(314t-43.600 )+0.265е-406t +0.219е-234t (A)
Таблица переменных
| Время t, c | 0.000 | 0.001 | 0.002 | 0.003 | 0.004 | 0.005 | 0.006 | 0.0063 |
| Ток i2, A | 1.115 | 1.327 | 1.528 | 1.671 | 1.7428 | 1.7430 | 1.6745 | 1.6413 |

3 этап курсовой работы
Найдём выражение для тока катушки операторным методом:
![]()
![]()
![]() R
R![]() 1
R2
1
R2

Запишем начальные условия в момент времени t(-0)
![]() I3(-0)
=
I3(-0)
=![]() =
=![]() = 5.263 (A)
= 5.263 (A)
Uc(-0) =0 (В)
Нарисуем схему замещения цепи для расчёта тока катушки операторным методом.
В ветви с реактивными элементами добавим ЭДС, так как у нас не нулевые начальные условия. Причём в ветвь катушки по на правлению тока, а в ветвь конденсатора против тока.
 |
|
Определим операторное изображение тока катушки. Для этого составим систему уравнений по законам Кирхгофа, направление ЭДС катушки указанo на схеме.
![]() I1(p)
-I2(p)
-IC(p)
=0 (1.3)
I1(p)
-I2(p)
-IC(p)
=0 (1.3)
![]() (2.3)
(2.3)
![]() (3.3)
(3.3)
Из уравнения (2.3) выразим ток I1 (p) и подставим в уравнение (3.3):
![]()
![]()
Из уравнения (3.3)
![]() (2.3.1)
(2.3.1)
 (2.3.2)
(2.3.2)
![]()
![]()
![]()

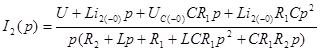
Подставим численные значения элементов
![]()
По полученному изображению найдём оригинал тока .
Операторное решение тока имеет вид правильной дроби I=![]() . Оригинал тока найдём при помощи теоремы разложения.
. Оригинал тока найдём при помощи теоремы разложения.
Определим корни знамена теля, для этого приняв его равным нулю.
p1 =0
0,000065p2 +0,1065p+36=0
![]() Д=(0б1065)2
-4.
0,000065.
36=0,0019
Д=(0б1065)2
-4.
0,000065.
36=0,0019![]()
![]()
![]()
I2
(p)=![]()
Найдём A1 A2 A3
Коэффициент An
будем искать в виде, ![]() где N(p) – числитель, а M(p) – знаменатель
где N(p) – числитель, а M(p) – знаменатель
A1
=![]()
A2
=![]()
A3
=![]()
Таким образом, i2
(t) будет равняться ![]()
i2 (t)=A1 . exp(p1 t)+ A2 . exp(p2 t)+ A3 . exp(p3 t)=1,944-0,71e-477t +0,3e-1162t
Искомый ток катушки i2 равняется :
i2 =1,944-0,71e-477t +0,3e-1162t (A)
Токи сходятся.
4 этап курсовой работы
Начертим схему для расчёта цепи интегралом Дюамеля и рассчитаем её
![]()
![]()
|
|
|
 |
|
|
|
Определим переходную характеристику h1 (t) цепи по напряжению UR2 . Для этого рассчитаем схему при подключении цепи в начальный момент t=0 к источнику единичного напряжения. Рассчитаем схему классическим методом. Так как нулевые начальные условия UC(-0) =UC(+0) =0, это значит дополнительных ЕДС не будет.
Напишем уравнения по законам Кирхгофа для цепи:
![]() i1
-i2
-ic
=0
i1
-i2
-ic
=0
i1
.
R1
+ i2
.
R2
=U iс
=![]()
iс . R3 -i2 . R1 +Uc =0 i1 =i2 +iс
![]() i1
=i2
+iс
i1
=i2
+iс
![]() i2
(R1
+R2
)+iс
R1
=U i2
=
i2
(R1
+R2
)+iс
R1
=U i2
=![]()
iс . R3 -i2 . R1 +Uc =0
iс
.
R3
+Uc
-![]() +
+![]()
ic![]() +
+![]()
![]()
![]() +
+![]()
![]() +
+![]()
![]() 0,00043l+1=0 l=-2322,58 (
0,00043l+1=0 l=-2322,58 (![]() )
)
UC св =Ae-2322,58t
UC вын
=![]() (B)
(B)
![]() UC
=UC св
+UC вын
=0,278+Ae-2322,58t
A=-0,278
UC
=UC св
+UC вын
=0,278+Ae-2322,58t
A=-0,278
UC =0,278-0,278e-2322,58t (B)
iс
=![]() =25.
10-6.
0,278.
2322,58e-2322,58t
=0,016e-2322,58t
(A)
=25.
10-6.
0,278.
2322,58e-2322,58t
=0,016e-2322,58t
(A)
Uab =ic R3 +UC =0,278-0,12e-2322,58t (B)
Таким образом переходная характеристика h1 (t) будет равна
h1 (t)=UR2 (t)=0,28-0,12. e-2322,58t (В)
t=![]() (c)
(c)
5 этап курсовой работы
 |
|
|
![]()
 |
Для расчета переходного процесса используем интеграл Дюамеля.
Переходную характеристику h1 (t) возьмем из предыдущего этапа
h1 (t)=0,28-0,12. e-2322,58t (В)
tпп
=![]() (c)
(c)
Найдёмt, t1 , t2 , U1 / (t), U2 / (t):
t=![]() (с)
(с)
t1 =t=0.00043 (c) t2 =1,5t=0.00065 (c) t3 =2t=0.00086 (c)
U0 =20 (В); U1 =-5 (B); U2 =-10 (B);
U1
/
(t)=0 (![]() ) U2
/
(t)=
) U2
/
(t)=![]() (
(![]() )
)
U3
/
(t)=![]() (
(![]() )
)
Запишем уравнение UR2 (t) для интервала :
![]()
UR2
=U0
.
h1
(t)+ (B)
(B)
| t (c) | 0 | 0.0001 | 0.0002 | 0.0003 | 0.0004 | 0.00043 |
| UR2 (B) | 3.2 | 3.697 | 4.092 | 4.404 | 4.652 | 4.716 |
Запишем уравнение UR2 (t) для интервала :
![]()
UR2
=U0
.
h1
(t)+
+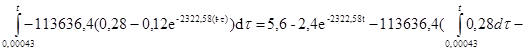
-
![]() (B)
(B)
| t (с) | 0,00043 | 0.00045 | 0.0005 | 0.00055 | 0.0006 | 0.00065 |
| UR2 (B) | 4,14 | 3,64 | 2,37 | 1,06 | -0,27 | -1,64 |
Запишем уравнение UR2 (t) для интервала :
![]()
UR2
=U0
.
h1
(t)+
+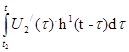 =
=![]()
-![]() )+
)+![]()
+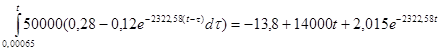 (B)
(B)
| t (c) | 0.00065 | 0.0007 | 0.00075 | 0.0008 | 0.00085 | 0.00086 |
| UR2(B) | -5,145 | -4,396 | -3,653 | -2,914 | -2,179 | -2,03 |
Запишем уравнение UR2 (t) для интервала :
![]()
UR2
=U0
.
h1
(t)+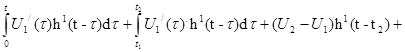
+
-![]()
+![]() (B)
(B)
| t (c) | 0.00086 | 0.0009 | 0.00095 | 0.001 | 0.0013 |
| UR2(B) | -1,97 | -1,79 | -1,60 | -1,42 | -0,707 |
Строим графики U(t) и UR2 (t) по данным таблиц.