| Скачать .docx |
Реферат: Синтез комбинационных схем (устройств)
Мурманский Государственный Технический Университет
Кафедра АиВТ
Расчетно-графическое задание
по курсу: «Основы цифровой схемотехники»
по теме:
«Синтез комбинационных схем (устройств)»
Мурманск
2008
Задание
Выполнить синтез логической схемы цифрового устройства, имеющего 4 входа и 2 выхода.
| ВХОДЫ | ВЫХОДЫ | |||||
| № | a | b | c | d | F | Q |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| 2 | 0 | 0 | 1 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 1 | 0 | 0 | 1 | 0 |
| 5 | 0 | 1 | 0 | 1 | 0 | 0 |
| 6 | 0 | 1 | 1 | 0 | 1 | 1 |
| 7 | 0 | 1 | 1 | 1 | 0 | 1 |
| 8 | 1 | 0 | 0 | 0 | 1 | 1 |
| 9 | 1 | 0 | 0 | 1 | 1 | 1 |
| 10 | 1 | 0 | 1 | 0 | 1 | 1 |
| 11 | 1 | 0 | 1 | 1 | 0 | 0 |
| 12 | 1 | 1 | 0 | 0 | 0 | 0 |
| 13 | 1 | 1 | 0 | 1 | 0 | 0 |
| 14 | 1 | 1 | 1 | 0 | 0 | 0 |
| 15 | 1 | 1 | 1 | 1 | 0 | 1 |
Для выполнения синтеза логической схемы необходимо произвести следующие действия:
1.по таблице истинности составить логические уравнения для каждого выхода в виде СДНФ и СКНФ;
2.для получения наиболее простой логической схемы выполнить минимизацию функций, записанных в СДНФ и СКНФ, используя метод непосредственных преобразований;
3.привести полученные минимизированные функции к единому базису (к базису И-НЕ);
4.выполнить минимизацию функций с помощью карт Карно и сравнить полученные результаты;
5.определить аппаратные средства, необходимые для реализации минимизированных функций как с использованием единого базиса, так и без использования единого базиса;
6.выбрать наиболее оптимальный вариант и построить для него принципиальную схему с перечнем элементов.
1. По таблице истинности составить логические уравнения для каждого выхода в виде СДНФ и СКНФ.
Совершенная дизъюнктивная логическая форма (СДНФ) представляется суммой логической простых конъюнкций, каждая из которых содержит все переменные в прямом или инверсном виде не более одного раза; в такие конъюнкции не входят суммы переменных, а также отрицания произведений двух переменных или более. Входящие в СДНФ конъюнкции называются минтермами или конституентами единиц.
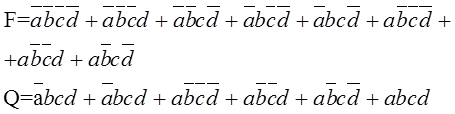
Совершенная дизъюнктивная нормальная форма (СКНФ) представляется логическим произведением дизъюнкций, каждая из которых содержит все переменные в прямом или инверсном виде не более одного раза. Входящие в произведение сомножители – дизъюнкции – называются макстермами или конституентами нулей.

2. Для получения наиболее простой логической схемы выполнить минимизацию функций, записанных в СДНФ, используя метод непосредственных преобразований.
Минимизацией называют процедуру упрощения логической функции, с тем чтобы она содержала минимальное количество членов при минимальном числе переменных.
Следует отметить, что элементарные приемы минимизации удаётся использовать не часто – при малом количестве членов функции и небольшом числе переменных. В других случаях применяются специальные методы минимизации, облегчающие поиск склеивающихся членов. К ним относится метод минимизации с помощью карт Карно.
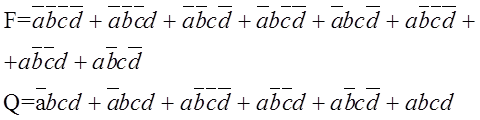
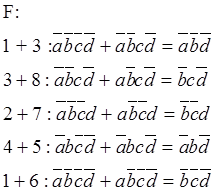

3. Привести полученные минимизированные функции к единому базису (к базису И-НЕ).

4. Выполнить минимизацию функций с помощью карт Карно и сравнить полученные результаты.
Карта Карно построена так, что в её соседние клетки попадают смежные члены функции – члены, отличающиеся значением одной переменной: в один член эта переменная входит в прямой форме, а в другой – в инверсной. Благодаря этому возникает наглядное представление о различных вариантах смежных членов.
Карта Карно имеет столько клеток, сколько комбинаций (наборов) можно составить из прямых и инверсных значений n переменных по n членов в каждой. Так, при n = 2 карта содержит четыре клетки, при n = 3 – восемь клеток, при n = 4 – шестнадцать клеток.
Наборы переменных, на которых у = 1, т.е. минтермы функции, отмечаются в соответствующих клетках карты единицами, в остальные клетки записываются нули или их оставляют пустыми. Две стоящие в соседних клетках единицы – свидетельство того, что в составе СДНФ имеются члены, отличающиеся значением одной переменной. Такие члены, как известно, склеиваются. Склеивание каждой пары минтермов уменьшает число входящих в них переменных на единицу.
Общие правила склеивания членов, занесённых в карту Карно следующие:
1) склеиваться могут 2, 4, 8, … членов; при этом соответствующие единицам клетки для наглядности охватывают контурами; каждый должен быть прямоугольником;
2) одним контуром следует объединять максимальное количество клеток;
3) одна и та же единица может охватываться разными контурами, т.е. один и тот же минтерм может склеиваться с несколькими смежными; последнее объясняется тем, что значение функции не меняется при прибавлении уже имеющихся членов;
4) крайние строки, а также крайние столбцы карты считаются смежными; их можно таковыми представить, если мысленно свернуть карту в горизонтальный или вертикальный цилиндр.
Функция, минимизированная с помощью карты Карно, состоит из суммы простых конъюнкций. Каждая из них получается в результате склеивания членов, которым соответствует охваченные контуром единицы. В такую конъюнкцию войдут только те переменные, значения которых в пределах контура не меняются.
Карта Карно для F:
| 1 | 1 | 1 |
| 1 | 1 | |
| 1 | 1 | 1 |
![]()
1 эл-т 3И-НЕ
1 эл-т 3И-НЕ
2 эл-та 2И-НЕ
4 эл-та 2И-НЕ
Карта Карно для Q:
| 1 | 1 | |
| 1 | ||
| 1 | 1 | 1 |
![]()
1 эл-т 4И-НЕ
4 эл-та 3И-НЕ
4 эл-та 2И-НЕ
Чтобы исключить низкочастотные помехи при монтаже микросхем на печатных платах, необходимо предусмотреть вблизи разъёма установку развязывающих конденсаторов из расчета не менее 0,1 мкФ на 1 м/с.
Для исключения высокочастотных помех, развязывающие ёмкости (не менее 0,002 мкФ на 1 м/с) рекомендуется размещать по площади печатной платы из расчета один конденсатор на группу не более, чем 10 м/с.
Список использованной литературы
1. Кучинский Г.С. Электролитические конденсаторы и конденсаторные установки: справочник. – М.: Энергоатомиздат, 2007.
2. Шило В.Л. Популярные цифровые микросхемы: справочник. – М.: Радио и связь, 2002.
3. Резисторы: (справочник)\ Ю.Н. Андреев, А.И. Антонян, Д.М. Иванов и др.: под ред. И.И. Четверткова – М.: Энергоатомиздат, 2001. 312с., ил.