Главная / Рефераты / Коммуникации и связь

Реферат: Систематична похибка опосередкованих вимірювань

Підкреслимо одну важливу особливість результатів опосередкованих вимірювань при нелінійній залежності у порівнянні з результатами прямих багаторазових вимірювань. Якщо в результатах одноразових спостережень систематичні похибки вилучені, то математичне сподівання середнього арифметичного ряду прямих рівнорозсіяних спостережень дорівнює істинному значенню вимірюваної величини, тобто результати прямих виправлених спостережень вільні від систематичних похибок. На відміну від цього, математичне сподівання похибки результату опосередкованих вимірювань при нелінійній залежності, яка визначається певною формулою, не дорівнює нулю, тобто похибка результату такого опосередкованого вимірювання, поряд з випадковою складовою, має і систематичну складову. А це означає, що математичне сподівання результату опосередкованих вимірювань при нелінійній залежності не дорівнює істинному значенню вимірюваної величини, або інакше, що оцінка є зміщеною, якщо хоча будь-яка одна серед других похідних в не дорівнює нулю. Покажемо це.

Обчислимо математичне сподівання абсолютної похибки опосередкованих вимірювань Y з урахуванням:

У цьому виразі перша сума дорівнює нулю, оскільки за умовою проведення експерименту, а друга сума визначає систематичну похибку. Отже, якщо вимірювані величини корельовані між собою, то, враховуючи рівність

для систематичної похибки результату опосередкованих вимірювань дістаємо

Оцінку коефіцієнта кореляції або визначають за експериментальними даними, або задають функціональною залежністю чи у вигляді матриці.

За умови, що вимірювані величини не корельовані, маємо

Тоді систематична похибка результату опосередкованих вимірювань

Отже, опосередковані вимірювання при нелінійній залежності мають специфічну систематичну похибку, яка обумовлена ненульовими частинними похідними .

Щоб вилучити цю систематичну похибку, треба в результат опосередкованих вимірювань, обчислений за формулою, ввести поправку П, яка дорівнює систематичній похибці за значенням і обернена їй за знаком, тобто .

Опосередковані вимірювання при лінійній залежності вказаної вище специфічної систематичної похибки не мають, тому що для них .

Результат і похибка опосередкованих вимірювань

Довірчі границі випадкової похибки і границі не вилученої систематичної похибки результату опосередкованого вимірювання з нелінійною залежністю визначають за певними формулами, підставляючи в останні замість коефіцієнтів відповідно перші похідні .

Довірчу повну похибку результату опосередкованого вимірювання обчислюють певним чином.

Остаточний результат опосередкованих вимірювань записується у вигляді

при , (4.35)

де- границі допустимої випадкової похибки опосередкованих вимірювань.

Формули для оцінки СКВ і результату опосередкованих вимірювань справедливі за умови, що відомі оцінки дисперсії (і СКВ) початкових величин. Значення коефіцієнта визначається для заданої довірчої ймовірності P, виходячи із закону розподілу результату опосередкованого вимірювання. Якщо закон розподілу результату опосередкованих вимірювань можна вважати нормальним, то для визначення (і довірчих границь ) використовується інтегральна функція нормованого нормального розподілу при великому числі вимірювань . При малому числі нормально розподілених результатів спостережень слід користуватися розподілом Стьюдента з “ефективним” числом степенів вільності, що визначається виразом

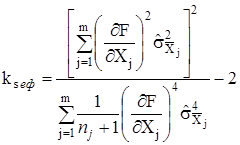Якщо числа спостережень усіх аргументів однакові , то

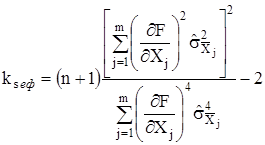При лінійній функціональній залежності опосередкованих вимірювань маємо і одержуємо приведені раніше формули для ефективного числа степенів вільності .

Оскільки число звичайно є дробовим, то для пошуку величини за таблицею розподілу Стьюдента необхідно використовувати інтерполяцію.

Довірчі границі повної похибки опосередкованих вимірювань (з урахуванням випадкової і не вилученої систематичної складових похибки вимірювань) знаходять за відповідною методикою.

Отже, загальна методика статистичної обробки результатів опосередкованих вимірювань передбачає такий алгоритм:

1) вилучення відомих (виявлених) систематичних похибок з результатів вимірювань кожного аргументу;

2) перевірку відповідності реального розподілу результатів прямих вимірювань кожного аргументу нормальному закону за одним із критеріїв згоди. Якщо така відповідність підтверджується, то проводять перевірку надмірних похибок і їх вилучення з результатів вимірювань;

3) обчислення оцінок аргументів та їх похибок;

4) перевірку відсутності кореляції між результатами вимірювань аргументів попарно, при її наявності обчислюють відповідні коефіцієнти кореляції;

5) обчислення результату опосередкованого вимірювання;

6) обчислення довірчої випадкової похибки і загальної похибки результату опосередкованого вимірювання; при нелінійній залежності знаходять систематичну похибку опосередкованих вимірювань, обумовлену перехресними членами у рівнянні.

При прямих одноразових вимірюваннях початкових величин процедура визначення результату Y опосередкованих вимірювань зберігається такою самою, як і при багаторазових вимірюваннях. Проте при прямих одноразових вимірюваннях початкових величин для оцінки характеристик похибки опосередкованих вимірювань широко використовуються абсолютні і відносні значення похибок. Для визначення абсолютної похибки результату опосередкованих вимірювань використовують співвідношення, аналогічне за формою виразу без залишкового члена, а за абсолютною похибкою знаходять відповідні відносні похибки з рівності.

Формули обчислення абсолютних і відносних похибок опосередкованих вимірювань для тих функціональних залежностей, які часто зустрічаються в практиці, наведені в табл. 1. Якщо похибки є систематичними, то формули в табл. 1. використовують з урахуванням знаків похибок. Для випадкових похибок здійснюється підсумовування за модулем, тобто арифметичне підсумовування, причому за величину беруть границі допустимих похибок (максимальні значення).

Табл. 1. свідчить, що піднесення аргументу до цілого степеня значно збільшує, а добування цілого степеня аргументу зменшує похибки результату. Тому вимірювання величин, які у формулу входять у вигляді - ціле додатне число), необхідно виконувати з більшою точністю, а вимірювання величин, які входять у формулу (1.6) у вигляді , може здійснюватися з меншою точністю. Якщо результат опосередкованих вимірювань виражається через степеневу функцію аргументів, наприклад,

то для відносної систематичної похибки одержимо

а для оцінки “зверху”, тобто максимального значення відносної випадкової похибки

Таблиця 1.

Функції Y	П о х и б к и
Функції Y	Абсолютна,	Відносна,

Проте така оцінка дає завищені результати і її застосування доцільно при 2 або 3 складових похибки. При більшому числі складових випадкової похибки опосередкованих вимірювань (за числом аргументів m), абсолютну випадкову похибку результату опосередкованих вимірювань слід обчислювати за правилами підсумовування незалежних випадкових величин, тобто геометрично

Величину називають середнім квадратичним значенням абсолютної випадкової похибки опосередкованих вимірювань.

Тоді СКЗ відносної випадкової похибки опосередкованих вимірювань

При роздільній оцінці систематичних і випадкових похибок результату опосередкованих вимірювань необхідно мати на увазі таке. Очевидно, що оцінити систематичну похибку результату опосередкованих вимірювань неможливо, не знаючи оцінок систематичних похибок початкових величин . Але якщо вони відомі, то їх необхідно вилучити з результатів прямих вимірювань , а потім оцінити результат опосередкованого вимірювання за цими виправленими значеннями . Водночас така оцінка систематичної похибки може бути проведена після закінчення експерименту. Тоді її у вигляді поправки необхідно врахувати в остаточному результаті опосередкованого вимірювання. Оцінка систематичної похибки може використовуватися також під час підготовки до експерименту, як орієнтовна оцінка. Наприклад, якщо припустити, що похибка результату опосередкованого вимірювання визначається тільки похибкою ЗВТ при вимірюванні величин , причому в цих ЗВТ переважаючою є систематична похибка (випадковою похибкою можна знехтувати), то на підставі оцінки систематичної похибки за певною формулою при (провівши формальну заміну , ) можна вибрати ЗВТ з такими границями допустимих систематичних похибок, щоб похибка результату опосередкованих вимірювань величини Y не перевищувала заданого значення.

Оцінка результатів і похибок сумісних та сукупних вимірювань

Загальною ознакою сумісних і сукупних вимірювань, відповідно до їх визначення (див. § 1.5), є те, що значення шуканих величин визначають, розв’язуючи систему рівнянь, які зв’язують шукані величини з деякими іншими величинами, вимірюваними прямими або опосередкованими методами, причому вимірюють декілька комбінацій значень цих величин. Вимірювання, проведені для кожної комбінації, дозволяють одержати одне рівняння, а сукупність цих рівнянь для всіх комбінацій являє собою систему рівнянь, в яку входять також усі значення шуканих величин. Цю систему рівнянь, відповідно до (1.7), запишемо для стислості записів у вигляді

, (4.36)

де- значення шуканих величин, ;

- значення величин, вимірюваних прямими або опосередкованими методами в q-му досліді, ;

n - число дослідів;

k - число величин, які вимірюються в кожному досліді;

m - число шуканих величин.

Рівняння, як і рівняння, за формою однакові для сумісних і сукупних вимірювань. Їх відмінністю є тільки фізична суть шуканих величин.

Якщо є значеннями тієї самої фізичної величини (наприклад, масами гир певного набору або довжинами лінійних мір), то вимірювання сукупні. Якщо ж - значення різних фізичних величин (наприклад, опору і температури), то вимірювання сумісні. Ще раз підкреслимо, що такий поділ вимірювань дуже умовний, але він традиційно існує.

Після проведення n дослідів одержують n комбінацій значень вимірюваних величин . Підставляючи у початкову систему і проводячи необхідні перетворення, одержимо систему рівнянь

Рівняння (4.37) містять у собі шукані величини і числові коефіцієнти . Для визначення m невідомих значень шуканих величин необхідно мати m рівнянь. Тоді результати вимірювань величин і довірчі границі їх похибок можна знайти за методиками обробки результатів опосередкованих вимірювань. Проте, з метою зменшення похибок результатів вимірювань, дослідів проводять дещо більше, ніж число m невідомих величин, тобто .

Оскільки точність вимірювання величин обмежена, то умовні рівняння одночасно не перетворюються в тотожності при жодних значеннях шуканих величин , а отже, не виникає можливості визначення їх істинних значень. Тому задача зводиться до знаходження оцінок шуканих величин , найбільш наближених до істинних значень. Позначимо такі оцінки . Якщо значення підставити в умовні рівняння, то їх ліві частини, в загальному випадку, будуть відрізнятися від правих частин. Такі рівняння і названі умовними. Для одержання тотожності введемо в праві частини умовних рівнянь деякі величини , які називають залишковими похибками умовних рівнянь або відхилами. Звідси маємо

. (4.38)

Для розв’язання системи умовних рівнянь застосовується метод найменших квадратів (МНК), згідно з яким оцінки вибирають так, щоб мінімізувати суму квадратів відхилів

Розв’язання задачі в самому загальному випадку, коли умовні рівняння нелінійні, а результати окремих вимірювань корельовані, дещо утруднено. Тому розглянемо окремий випадок, коли умовні рівняння лінійні або приведені до лінійного вигляду, а результати вимірювань величин рівноточні і некорельовані. Тоді оцінки, одержані методом найменших квадратів, будуть обґрунтованими і незміщеними, а при нормальному розподілі результатів вимірювань ще й ефективними. У цьому випадку система рівнянь може бути приведена до вигляду

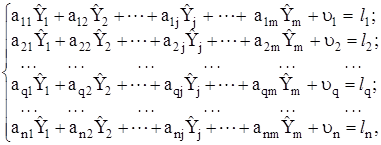(4.39)

де- коефіцієнти, одержані із системи рівнянь після її лінеаризації (якщо вона нелінійна) і підстановки значень величин , причому q - рядок, j - стовпчик;

- постійна величина.

Сума квадратів відхилів визначається із системи рівнянь

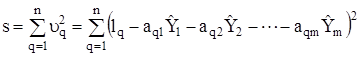
Як відомо, необхідною умовою мінімуму диференціальної функції багатьох змінних, у даному випадку , є виконання рівнянь:

Їх можна розглядати як рівняння відносно величин у математичній статистиці вони називаються нормальними рівняннями.

Використовуючи рівність, знайдемо частинні похідні і прирівняємо їх до нуля:

Запишемо одержану систему рівнянь у компактному вигляді

Ця система рівнянь є лінійною відносно шкали величин . Внаслідок розв’язання системи нормальних рівнянь одержують m невідомих величин . Для спрощення запису цієї моделі використовують позначення Гаусса для сум:

; ; .

З урахуванням цих позначень система нормальних рівнянь набуває вигляду

Як відомо, розв’язання такої лінійної системи є лінійними комбінаціями величин :

де коефіцієнти знаходять, розв’язуючи систему рівнянь (4.44) за допомогою визначника для кожної з шуканих величин:

де ;

Визначник одержаний заміною у визначнику j-го стовпця стовпцем вільних членів у (4.44).

Отже, .

Визначивши з відхили і підставивши їх у рівняння (4.42), одержимо такі рівності:

що виражають властивості відхилів . Ці рівності застосовуються для перевірки правильності визначення оцінок шуканих величин після розв’язання системи рівнянь.

Визначення оцінок шуканих величин пов’язано з великим обсягом обчислень, який швидко збільшується із збільшенням числа умовних рівнянь. Останнє необхідно для підвищення точності одержаних оцінок. У сучасні дні обробка результатів сумісних і сукупних вимірювань виконується за допомогою ЕОМ за стандартними програмами. Тому точність оцінок істинних значень вимірюваних величин може бути значно підвищена при збільшенні числа умовних рівнянь до кількох десятків і навіть сотень, а в деяких випадках і більше.

Для оцінки точності одержаного розв’язання системи рівнянь звичайно припускають, що точність визначення коефіцієнтів значно вища від точності визначення коефіцієнтів . Це припущення, як правило, виправдане в багатьох практичних випадках. При його виконанні похибки оцінок шуканих величин визначаються тільки дисперсіями результатів вимірювання останніх. А враховуючи, що згідно з рівняннями оцінки є лінійними комбінаціями величин , маємо

де- оцінка дисперсії шуканих величин

- оцінка дисперсії коефіцієнтів .

Якщо припустити, що всі результати спостережень є рівноточними, а отже, всі дисперсії у виразі однакові

то оцінка СКВ

Для обчислення рекомендується досить простий вираз

в якому залишкові похибки визначають із рівнянь після визначення оцінок згідно з системою рівнянь.

Якщо точність визначення усіх коефіцієнтів системи рівнянь (4.45) приблизно однакова, то оцінку СКВ результату вимірювань величин визначають за формулою

де- алгебраїчні доповнення головного визначника D, які одержують виключенням з нього j-го рядка та j-го стовпця.

З рівнянь випливає, що точність сукупних і сумісних вимірювань залежить від співвідношення числа шуканих величин m і числа умовних рівнянь n. Чим значніша умова , тим точніше результати обробки. Якщо m і n близькі, то результати обробки визначаються з грубими похибками.

Довірчі інтервали для істинних значень усіх вимірюваних величин одержують за розподілом Стьюдента при числі степенів вільності .

Якщо при сукупних і сумісних вимірюваннях умовні рівняння нелінійні, то застосовують їх лінеаризацію.

Таким чином, методика обробки результатів сукупних і сумісних вимірювань така:

1. Записують систему умовних рівнянь при підстановкою експериментальних даних у рівняння початкової залежності.

2. Систему умовних рівнянь приводять до нормального вигляду. Для обчислення коефіцієнтів нормальних рівнянь складають допоміжну табл. 2, яка дозволяє також перевірити правильність визначення шуканих величин.

Таблиця 2.

q			...			...		...		...				...
1			...			...		...		...				...
2			...			...		...		...				...
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
n			...			...		...		...				...
	...			...		...		...		…		...