Реферат: Усилители на биполярных транзисторах

РЕФЕРАТ

по дисциплине: «Электроника»

на тему:

«Усилители на биполярных транзисторах»

Ростов-на-Дону, 2010 г.

Содержание

1. Виды транзисторных усилителей

2. Основные задачи проектирования транзисторных усилителей

3 Применяемые при анализе схем обозначения и соглашения

4. Статистические характеристики

5. Статические и дифференциальные параметры транзисторов

6. Основные параметры усилителей

7. Обратные связи в усилителях

Список литературы

1. Виды транзисторных усилителей

Усилитель осуществляет увеличение энергии управляющего сигнала за счет энергии вспомогательного источника. Входной сигнал является как бы шаблоном, в соответствии с которым регулируется поступление энергии от источника к потребителю усиленного сигнала.

Электронными называют усилители электрических сигналов с регулирующими элементами на полупроводниковых или электровакуумных приборах.

Прежде чем описывать специфику работы конкретных усилительных каскадов на транзисторах, следует получить четкое представление о том, каково основное предназначение данных каскадов. Ведь усиливаться могут различные показатели электрических сигналов и при различных ограничениях и условиях. Да и само понятие "усиление" иногда требует пояснения.

В общем, возможна классификация усилителей по очень большому количеству признаков, относящихся как к виду выполняемых ими функций, так и к качеству или способу выполнения этих функций. В дальнейшем мы будем придерживаться следующего разделения усилителей на группы.

По виду сигналов, для усиления которых предназначен усилитель:

· усилители гармонических сигналов(при построении усилителей гармонических сигналов важнейшим является обеспечение минимального уровня вносимых в сигнал искажений);

· усилители импульсных сигналов(усилители импульсных сигналов обычно используют различные ключевые режимы работы транзисторов, здесь важнейшим фактором является минимизация задержек фронтов и спадов усиливаемых сигналов, а также устранение паразитных выбросов токов и напряжений, неизбежно возникающих при прохождении таких сигналов через каскады усиления).

По способности усиливать постоянные и переменные сигналы:

· усилители постоянного тока(усилители, обладающие способностью усиливать весьма медленные колебания, в том числе и нулевой частоты, даже в том случае, если они в первую очередь предназначены для усиления мощности или напряжения переменных сигналов);

· усилители переменного тока(прочие — не обладающие способностью усиливать сигналы нулевой частоты — усилители).

По диапазону частот, на которые рассчитан усилитель:

· усилители низкой частоты(УНЧ); предназначены для усиления частот звукового диапазона (0,01...20 кГц);

· усилители высокой частоты(УВЧ); предназначены для усиления сигналов в радиочастотном диапазоне;

По соответствию вида амплитудно-частотной характеристики полосе частот рабочего сигнала:

· узкополосные усилители; на практике принято называть усилитель узкополосным, если полоса пропускаемых частот уже, чем это минимально необходимо для качественного воспроизведения спектра усиливаемого сигнала (узкополосные УНЧ имеют полосу пропускания менее 2,5...3 кГц; узкополосные УВЧ, например, для применения в телевидении, обладают полосой пропускаемых частот4,5...5 МГц, что меньше минимально необходимого для качественного воспроизведения телевизионного сигнала);

· широкополосные усилители(часто для уменьшения нелинейных искажений и повышения устойчивости усилителя выгодно реализовывать в нем максимально широкую полосу пропускания, гораздо шире, чем это реально необходимо для всех возможных частот рабочего сигнала);

По форме амплитудно-частотной характеристики:

· избирательные или резонансные усилители(имеют частотную характеристику полосового фильтра или резонансного колебательного контура);

· апериодические усилители(имеют частотную характеристику, по форме напоминающую характеристику LС-цепи, т.е. плавно убывающую по мере роста частоты).

По усиливаемому электрическому показателю (данный признак классификации имеет в виду предназначение усилителя):

· усилители напряжения(определяющим свойством усилителя является усиление напряжения);

· усилители тока(определяющим свойством усилителя является усиление тока);

· усилители мощности(под усилителем мощностиобычно понимается усилитель или его оконечная выходная часть, рассчитанная на отдачу в цепь внешней нагрузки определенной мощности при заданной величине входного сигнала).

2. Основные задачи проектирования транзисторных усилителей

Любой электронный усилитель требует наличия внешнего источника питания с определенными характеристикам (обусловлены характеристиками самого усилителя). В применении к транзисторным усилительным каскадам это означает, что для всех транзисторов каскада должен обеспечиваться соответствующий режим по постоянному току (поданы внешние напряжения от источников питания) обеспечивающих все практически возможные токи). Задание такого режима, по сути, является заданием рабочей точки транзисторного каскада. Правильное задание рабочей точки пo постоянному току имеет большое значение, поскольку оказывает влияние на многие свойства усилителя (коэффициент усиления, уровень шумов, уровень линейных и нелинейных искажений и т.п.). Вопросу выбора и стабилизации положения рабочей точки транзисторного каскада целиком посвящена глава 3. Но из сказанного здесь читатель должен понять, что существует два существенно различающихся аспекта проектирования транзисторных схем. Первый — это организация питания и установка правильного режима по постоянному току, а второй — обеспечение усиления проходящего через усилитель переменного сигнала. Конечно, между этими двумя задачами существуют определенные пересечения, и в целом невозможно сосредотачиваться на решении одной из них, абсолютно забыв о другой, но они все равно остаются разными задачами, требующими различных подходов к своему решению.

Ясно, что при расчете цепей по постоянному току необходимо оперировать абсолютными значениями токов и напряжений, действующими в цепях, и опираться на соответствующие модели, отражающие работу транзисторов и таких режимах. А вот для анализа поведения схем при подаче на них переменных сигналов указанный метод оказывается неудобным. Действительно, зачем проводить расчеты при полных напряжений и токов в цепях, да еще и изменяющихся во времени, если нас интересует только поведение небольшой переменной составляющей, отражающей уровень полезного сигнала.

Для решения указанной задачи проводится так называемый малосигнальный анализ цепей. При этом используют малосигнальные эквивалентные схемы и группы малосигналъных параметров. Основным допущением, используемым в такой модели, является требование об относительно небольшой величине переменной составляющей посравнению с действующими в цепях постоянными токами и напряжениями. Если это требование нарушается, то большинство результатов, полученных с помощью мало сигнального, анализ не отвечают действительным процессам в цепях — требуется расчет полных токов и напряжений.

3. Применяемые при анализе схем обозначения и соглашения

Прежде всего сделаем ряд пояснений, касающихся таких фундаментальных понятий, как ток и напряжение. Мы не будем здесь подробно описывать физический смысл данных величин, поскольку предполагаем, что хотя бы с этиv читатель уже знаком. Напомним лишь стандартные правила имеющие отношение к представлению токов и напряжений в различных формулах, а также к их изображению на принципиальных схемах. В международной системе единиц напряжение выражают в вольтах (В), а ток в амперах (А).

Как известно, электрический ток — это упорядоченное движение носителей заряда. В любой электрической цепи упорядоченное движение зарядов происходит в одном из двух возможных направлений. Поэтому и электрический ток принято рассматривать как скалярную величину, имеющую одно из возможных направлений. За направление тока, независимо от природы носителей электрического заряда и их типа принимают направление, в котором перемещаются (или мог ли бы перемещаться) носители положительного заряда. Таким образом, направление электрического тока в наиболее распространенных проводниковых материалах — металлах — противоположно фактическому направлению перемещения носителей заряда — электронов. О направлении тока судят по его знаку, который зависит от того, совпадает или нет направление тока с направлением, условно принятым за положительное. Если в результате расчетов, выполненных учетом выбранного направления, ток получится со знаком плюс, то его направление, т.е. направление перемещения положительных зарядов, совпадает с направлением, выбранный за положительное. Если ток будет иметь знак минус, то его направление противоположно условно-положительном). Само условно-положительное направление тока при расчетах электрических цепей может выбираться совершение произвольно (обычно пользуются соображениями удобства расчетов).

Напряжение также представляет собой скалярную величину, которой всегда приписывают определенное направление. Обычно под направлением напряжения понимают направление, в котором под действием электрического поля перемещаются (или могли бы перемещаться) свободные носители положительного заряда. Очевидно, что на участках цепи, в которых не содержатся источники энергии, и перемещение носителей заряда осуществляется за счет энергии электрического поля, направления напряжения и тока совпадают.

При расчетах электрических цепей направление напряжениясравнивается с направлением, условно выбранным за положительное. Если в результате расчетов напряжение на рассматриваемом участке цепи получится со знаком плюс, то Направление напряжения совпадает с направлением, условно принятым за положительное; если напряжение получится со знаком минус, то его направление противоположно условно-положительному.

На принципиальных схемах направления токов и напряжений, принимаемые за условно-положительные, могут показываться стрелками.

Для обзначения токов и напряжений в формулах общепринятым является использование латинских букв I (для токов) и U (для напряжений).

При анализе цепей, находящихся под гармоническими воздействиями, широкое распространение получил символический метод комплексных амплитуд (комплексный метод, или, иногда просто — символический метод). Он основан на представлении гармонических функций с помощью комплексных чисел или, точнее, на преобразовании исходных гармонических функций из временной области (области вещественного переменного t) в частотную область (область мнимою аргумента jw).. Выглядит это так.

Каждой гармонической функции времени a(t)=А_т cos(t +ψ) можно поставить в соответствие копмплекснозначную зависимость

=А_т [cos(t + ψ) + j sin (t + ψ)] = .

Причем модуль комплексной величины a(t) равен амплитуде гармонической функции = А_т , а аргумент — ее фазе =t + ψ. Сама исходная действительная гармоническая функция равна действительной части введенной таким образом комплекснозначной функции:

Величина 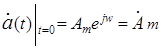называется комплексной амплитудой гармонической функции времени

a(t)=А_т cos(t +ψ).

Известно, что в установившемся режиме работы токи и напряжения всех ветвей линейной электрической цепи, находящейся под гармоническим воздействием, являются функциями времени одной частоты, т.е. токи и напряжения отдельных ветвей в этом случае отличаются только амплитудами и начальными фазами, поэтому полная информация о них при известной частоте содержится в соответствующих комплексных амплитудах. Зная амплитуды и начальные фазы токов или напряжений любой ветви, всегда можно однозначно найти их комплексные амплитуды. И обратно, по известной комплексной амплитуде можно однозначно установить амплитуду и начальную фазу исходного гармонического колебания.

Таким образом, каждой гармонической функции времени a(t) можно единственным образом поставить в соответствие комплексное число (комплексную амплитуду), которое можно рассматривать как изображение этой гармонической функции на комплексной плоскости. Причем оказывается, что линейным операциям над гармоническими функциями времени соответствуют линейные операции над их комплексными амплитудами (операции дифференцирования и интегрирования заменяются при этом операциями умножения и деления). Это позволяет существенно упростить анализ линейных цепей, находящихся под гармоническим воздействием, заменив систему интегродифференциальных уравнений, составляемую для мгновенных значений токов и напряжений в ветвях цепи, системой алгебраических уравнений для комплексных амплитуд соответствующих токов и напряжений. Отметим также, что при рассмотрении чисто активных безынерционных линейных цепей (т.е. цепей без фазовых расхождений между сигналами в различных точках) все комплексные амплитуды становятся действительнозначными и анализ сводится к оперированию с простыми действительными амплитудами гармонических функций времени.

Наряду с комплексными амплитудами в качестве изображений гармонических функций на комплексной плоскости широко используются другие комплексные величины — комплексные действующие значения:

Все правила, устанавливающие соответствие между операциями над гармоническими функциями времени и операциями над их комплексными амплитудами, справедливы и для операций над комплексными действующими значениями гармонических функций.

В большинстве реальных усилии тельных схем на транзисторах.допущение о гармоническом характере входных воздействий оказывается вполне работоспособным. Если далее предположить, что цепь линейна (это выполняется, если амплитуда входных воздействий невелика, а транзистор усилителя находится в режиме линейного усиления), то становится вполне возможным применить метод комплексных амплитуд для мало сигнального анализа транзисторных усилительных схем. Более того, мы можем даже избавиться от комнлекснозначности амплитуд, если добавим требование об отсутствии фазовых сдвигов между сигналами, что близко к истине при рассмотрении достаточно низких частот.

Анализируя схемы методом комплексных амплитуд, мы будем говорить о комплексных токах и напряжениях () строго говоря, так обычно называют комплексные действующие значения гармонических токов и напряжений, но для удобства мы часто будем подразумевать именно комплексные амплитудные значения (переход от амплитудных к действующим значениям, как было показано ранее, вообще не оказывает влияния на расчетные формулы).

В схемах при установлении направлений переменных токов и напряжений, заданных комплексными значениями, действуют все те же правила, что были описаны для постоянных токов и напряжений (т.е. знак "плюс" означает совпадение с направлением, условно принятым за положительное, а знак "минус" — несовпадение). Для условно-положительных направлений, когда это возможно, выбираются направления, совпадающие с направлениями реальных токов и напряжений, действующих в анализируемых цепях.

В различной литературе могут использоваться разные способы обозначения амплитуд, действующих значений и других параметров сигналов и схем; мы будем придерживаться следующей системы.

Зависящие от времени (как правило, гармонические) переменные электрические показатели (например, токи и напряжения) в цепях будем обозначать малыми латинскими буквами: i(t), u(t) и т.д. При этом, если нет необходимости делать особый акцент на временной зависимости мгновенных значений этих показателей, если характер данных зависимостей не определен, не имеет значения для рассматриваемого вопроса или если в зависимостях присутствует не только гармоническая, но и постоянная составляющая (показатели вообще могут быть константами), то будем использовать традиционные обозначения большими латинскими буквами: I, U и т.д.

Как правило, нам придется отдельно рассматривать переменные и постоянные составляющие токов и напряжений, в цепях. При этом для обозначения постоянных составляющих мы будем пользоваться дополнительным индексом "0", а для обозначения переменных составляющих — дополнительным индексом "-". Т.е. для полных токов и напряжений в цепях действуют формулы: U=U_о +, I ⁼ I_о +. Заметим, что в большинстве случаев анализ по переменным составляющим проводится методом комплексных амплитуд. Так что вместо зависящих от времени переменных составляющих в получаемые нами формулы можно подставлять комплексные или при определенных условиях даже действительные амплитуды этих составляющих. Обозначение с индексом "-" применяется именно там, где существует возможность вариации подставляемых в формулы значений в зависимости от некоторых условий расчетов (например, проводим ли мы расчеты для низких или для высоких частот, а также используем ли мы действительные, комплекснозначные или определенные во временной области параметры элементов).

Анализируя электрические цепи методом комплексных амплитуд, мы приходим к комплексным значениям некоторых реальных параметров этих схем (комплексные сопротивления, проводимости, коэффициенты усиления и т.п.). Все такие величины обычно не принято обозначать так, как мы это делаем для комплексных амплитуд и действующих значений, — точкой вверху. Для каждого случая, как правило, есть свое устоявшееся обозначение. Объединяет их использование прописных латинских букв (G, Y, Н и т.д.). Соответствующие же малые латинские буквы (g, у,h и т.д.) применяются для обозначения действительной составляющей таких параметров (обычно комплекснозначные параметры становятся действительными при соблюдении определенных условий, применение в формулах малых латинских букв означает, что данные условия предполагаются выполненными).

Заметим также, что иногда параметры элементов схем могут зависеть от того, рассматриваем ли мы поведение данного элемента под действием постоянных токов и напряжений или делаем то же самое для их переменных составляющих. В общем случае нет какой-то универсальной методики различения таких параметров — следует внимательно читать текстовые комментарии и понимать суть физических процессов в цепях. Однако часто речь идет о так называемых статических и дифференциальных параметрах. Мы будем придерживаться системы, когда буквенный индекс, сопровождающий статические параметры, пишется с прописной буквы ( и т.п.), а буквенный индекс, сопровождающий дифференциальные параметры, — с малой буквы и т.п.). В случаях, когда разница между статическими и дифференциальными параметрами отсутствует, чаще применяется написание с прописными буквами. Если у параметра нет буквенного индекса или для него по каким-либо причинам неудобно менять размер используемых букв в индексе, то возможен переход к малой букве в обозначении самого дифференциального параметра ( и т.п.).

4. Статистические характеристики

При анализе усилительных схем на транзисторах широко используются т.н. статические характеристики: Статическими характеристиками транзисторов называют графики, выражающие функциональную связь между постоянными токами и напряжениями на электродах транзистора.

В зависимости от того, какие токи и напряжения принимаются за независимые переменные, возможны различные" системы функциональной связи и соответствующие им семейства статических характеристик. В общем случае связь между токами и напряжениями на трех электродах транзистора можно выразить шестью различными системами (по четыре семейства характеристик в каждой системе).

Мы не будем здесь рассматривать все эти случаи, а обратимся сразу к системе, получившей наибольшее распространение. Это т.н. система статических параметров (или гибридная система), которая соответствует наиболее распространенной группе малосигнальных параметров и имеет ряд преимуществ перед другими системами.

В данной системе в качестве независимых переменных приняты входной ток и выходное напряжение:

В статическом режиме эти зависимости выражаются четырьмя семействами характеристик:

входными

выходными

обратной связи

прямой передачи

Заметим, что для разных схем включения транзистора в качестве входных и выходных выступают токи и напряжения на его различных электродах. Поэтому вид статических характеристик зависит от схемы включения транзистора.

Для однозначного установления зависимости между токами и напряжениями транзистора достаточно иметь два семейства характеристик из четырех названных. Другие два могут быть найдены с помощью перестроений. На практике наибольшее распространение получили входные и выходные характеристики. Характеристики прямой передачи и обратной связи обычно выступают в роли второстепенных.

Статические характеристики имеют большое значение при анализе работы самых разнообразных усилительных схем. По статическим характеристикам выбираете оптимальное положение рабочей точки транзистора по постоянному току, вычисляются допустимые амплитуды колебаний переменного напряжения и тока на входе усилителя, анализируется линейность усиления и многие другие показатели схемы. По выходным характеристикам можно определить, правильно ли согласован усилительный каскад с нагрузкой, и предсказать поведение этого каскада при изменениях характера нагрузки.

В реальных схемах транзисторных усилителей в качестве входных токов и напряжений выступают напряжения и токи на конкретных электродах. Например, для схемы с ОЭ входным напряжением будет напряжение на участке эмиттер—база(), а выходным током — ток коллектора (I_К ). Часто статические характеристики транзисторных схем называют по имени электрода, ток которого эти характеристики отражают. Так, в приведенном выше случае мы будем говорить о выходных коллекторных характеристиках.

5. Статические и дифференциальные параметры транзисторов

Выше мы уже упоминали о наличии у транзисторов гак называемых малосигнальных параметров. Теперь поговорим об этом подробнее. Такие параметры характеризуют работу транзистора в режиме усиления малых переменных токов и напряжений. Многие из них имеют четкую физическую интерпретацию и непосредственно присутствуют в физических эквивалентных схемах. Некоторые же допускают только чисто математическое толкование. Смысл большинства из этих параметров сохраняется и при переходе к анализу больших сигналов, но их значения изменяются и становятся зависимыми от множества не проявлявшихся при малых сигналах факторов.

Поскольку малосигнальные параметры — это параметры, отражающие работу транзистора для переменных составляющих токов и напряжений, то в большинстве случаев они являются дифференциальными эквивалентами некоторых интегральных (статических) величин, характеризующих работу на постоянном токе. Отсюда возникает второе, употребляемое иногда даже чаще, название малосигнальных параметров — дифференциальные параметры. Между двумя этими терминами не существует однозначной эквивалентности, но почти всегда речь идет об одном и том же.

В качестве примера можем рассмотреть такой важный параметр биполярного транзистора, как коэффициент передачи тока базы в схеме с ОЭ (). У этого параметра есть еще одно часто встречающееся обозначение, идущее от его роли в системе так называемых h-параметров проходного линейного четырехполюсника — или

Интегральный (статический) коэффициент передачи находится как отношение токов (рис. 1):

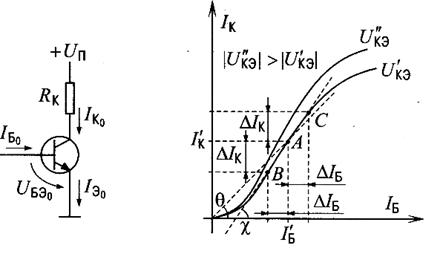Рис.1. К вычислению интегрального и дифференциального коэффициента передачи тока базы

Если рассмотреть характеристику передачи транзистора, включенного по схеме с ОЭ (рис. 2.1), то можно видеть, что в точке А, соответствующей напряжениям и токам,, , статический коэффициент передачи равен:

Предположим теперь, что на вход транзистора подан малый по амплитуде переменный сигнал. В этом случае значения токов базы и коллектора начинают колебаться в пределах (рис. 1): и . Причем и, переходя к дифференциалам:

— дифференциальный коэффициент передачи тока базы в схеме с ОЭ в точке А передаточной характеристики (рис. 1);

— угол, образованный касательной к линии передаточной характеристики в точке А и осью абсцисс (tg =).

Из рис.1. видно, что дифференциальный коэффициент передачи несколько отличается от интегрального (статического). Но на характеристике передачи можно выделить участок (В,С), где их значения близки. Т.е., если мы рассматриваем работу транзистора при некоторых ограничениях на напряжения и токи в нем (корректно заданная рабочая точка по постоянному току и малая амплитуда переменных сигналов), то мы можем не различать его статические и дифференциальные коэффициенты передачи. Заметим также, что в общем случае эти коэффициенты зависят от частоты переменного сигнала, его формы и амплитуды, температуры окружающей среды и некоторых других факторов. Так что любые вычисления с ними являются весьма приблизительными и отражают реальные процессы в транзисторах лишь в общих чертах. То же самое можно сказать и обо всех других малосигнальных (дифференциальных) и статических параметрах транзисторов.

В зависимости от конкретной ситуации (анализируемой схемы, целей анализа, ограничений на сигналы в цепях, требуемой точности и т.п.) на практике могут использоваться различные группы параметров, характеризующих транзистор в определенном режиме работы при определенных условиях. Как правило, для каждого такого случая строится соответствующая эквивалентная схема, значения элементов которой и составляют указанную группу параметров (одна и та же эквивалентная схема может использоваться и с разными группами параметров, например, при переходе от малосигнального анализа к анализу работы на постоянном токе все дифференциальные параметры заменяются на соответствующие им интегральные эквиваленты, и наоборот).

Наиболее употребимы следующие группы параметров транзисторов: Y-параметры, Z-параметры, H-параметры, S-параметры, физические параметры (часто их различают и для различных схем включения транзистора, т.е. существует группа параметров для схемы с ОБ и группа параметров для схемы с ОЭ и т.п.). Между указанными группами параметров существует довольно много пересечений (один из таких примеров нами рассмотрен выше) и взаимосвязей (когда параметры одной группы могут быть однозначно выражены через параметры другой группы).

Здесь опять следует сделать замечание, что подробное рассмотрение параметров, характеристик и физических моделей транзисторов не входит в задачу настоящей книги. Ниже вы найдете только краткое (справочное) описание этих вопросов. Для их более глубокого изучения и понимания следует обращаться к другой специализированной литературе (см. список литературы в конце книги).

6. Основные параметры усилителей

До сих пор мы рассматривали параметры и характеристики, описывающие разнообразные свойства транзисторов как основных усилительных элементов в составе электронных усилителей. Однако существуют показатели, по которым оценивается работа всего такого усилителя (или функционально законченных отдельных его каскадов) в целом. Данные параметры зависят не только от свойств применяемых в усилителе транзисторов, но и от качества самой принципиальной схемы и точности ее настройки.

К числу основных электрических показателей, характеризующих работу усилителя, относятся следующие:

– коэффициент передачи или коэффициент усиления;

– динамическая и амплитудная характеристики;

– динамический диапазон;

– предельная чувствительность;

– амплитудно-частотная характеристика;

– фазочастотная характеристика;

– амплитудно-фазовая характеристика;

– линейные искажения: оцениваются соответствующими коэффициентами линейных (частотных и фазовых) искажений; нелинейные искажения: оцениваются разнообразными коэффициентами (коэффициент нелинейных искажений коэффициент интермодуляцйи и т.п.).

Коэффициент передачи

Коэффициент передачи — это функция, определяемая как отношение выходного сигнала усилителя к его входному сигналу. В зависимости от формы математического представления самих сигналов различаются и формы представления коэффициента передачи (наиболее распространены операторные формы по Фурье или Лапласу, а соответствующие коэффициенты передачи иногда называют операторными коэффициентами передачи). При рассмотрении высоколинейных схем, которые не вносят в усиливаемый сигнал амплитудных искажений и фазовых сдвигов, вместо комплексной функции операторного коэффициента передачи оперируют более понятными, имеющими достаточно простую интерпретацию коэффициентами усиления. Различают:

коэффициент усиления по напряжению

— где и

амплитудные или действующие значения выходного и входного сигналов;

коэффициент усиления по току

—где и

амплитудные или действующие значения выходного и входного токов.

коэффициент усиления по мощности

Довольно часто коэффициенты усиления выражают в логарифмических единицах — децибелах, [дБ]:

Логарифмические единицы удобны тем, что если известны коэффициенты усиления отдельных каскадов или узлов усилителя, то его общий логарифмический коэффициент усиления находится как алгебраическая сумма логарифмических коэффициентов усиления отдельных каскадов:

=К₁ К₂ К₃ ...;

Более того, логарифмические единицы оказались настолько удобны при проектировании схем, что появился даже ряд производных от них величин. Например, мощность сигнала в схеме часто оценивается по отношению к уровню мощности в 1 мВт. При этом со знаком "+" или "-" пишется разность в децибелах текущего уровня мощности от уровня 1 мВт, который принимается за точку отсчета. Такие единицы принято обозначать дБм (децибел милливатт), т.е., например, сигнал мощностью 1 мВт в таких единицах равен 0 дБм, сигнал 10 мВт — +10 дБм, 0,01 мВ т — -20 дБм и т.п. Точно так же можно выражать и напряжение сигнала, при этом только необходимо зафиксировать сопротивление нагрузки, на котором обеспечивается данное напряжение. В высокочастотной технике используются единицы дБмкВ (децибел микровольт). Здесь за нулевую принимается точка в 1 мкВ, а сопротивление нагрузки всегда считается равным 50 Ом.

Динамическая и амплитудная характеристики

Динамическая характеристика представляет собой зависимость мгновенного значения выходного напряжения от мгновенного значения входного напряжения U_BX (t) при гармоническом входном воздействии. Зависимость амплитудного значения первой гармоники выходного напряжения от амплитуды синусоидального входного напряжения

называется амплитудной характеристикой. Точка окончания линейного участка динамической характеристики носит название точки компрессии.

Динамический диапазон

Отношение (в децибелах) наибольшего допустимого значения амплитуды входного напряжения к ее наименьшему допустимому значению называется динамическим диапазоном амплитуд (или просто динамическим диапазоном). Максимально допустимая амплитуда входного напряжения усилителя ограничена искажениями сигнала, вызванными выходом рабочих точек усилительных каскадов за пределы линейного участка характеристики управления (точка компрессии). В то же время минимальная амплитуда обычно ограничена по величине (снизу) уровнем собственных шумов усилителя, на фоне которых полезный сигнал не удается выделить с надлежащим качеством.

Амплитудно-частотная характеристика

Амплитудно-частотная характеристика (АЧХ) — зависимость модуля коэффициента передачи от частоты входного сигнала.

Фазочастотная характеристика

Фазочастотная характеристика (ФЧХ)— зависимость сдвига фазы между входным и выходным напряжением от частоты или фаза коэффициента передачи.

Рабочий диапазон частот

Рабочий диапазон частот(диапазон пропускаемых частот или полоса пропускания) представляет собой некоторый интервал значений частоты от f_H до f_B , внутри которого коэффициент усиления изменяется по определенному закону с известной степенью точности. Например, высококачественный усилитель низкой частоты должен характеризоваться законом К = const в диапазоне частот сигнала от f_min = 10 Гц до f_max = 20 кГц. Если к усилителю не предъявляются какие-либо специальные требования, то рабочий диапазон частот определяют на уровне 3 дБ, т.е. границами полосы пропускания являются частоты, на которых коэффициент усиления уменьшается не более чем в раза.

Амплитудно-фазовая характеристика

Амплитудно-фазовая характеристика (АФХ) — зависимость коэффициента усиления и фазового сдвига усилителя от частоты, построенная в полярной системе координат. Она объединяет в себе амплитудно-частотную и фазочастотную характеристики усилителя и представляет собой годограф комплексного коэффициента передачи.

Понятия об АЧХ, ФЧХ и АФХ становятся определенными лишь по отношению к линейным усилителям.

Переходная характеристика

Переходная характеристика — зависимость от времени выходного напряжения усилителя, на вход которого подан мгновенный скачок напряжения. Эта характеристика дает возможность определить переходные искажения, которые в области малых времен характеризуются фронтом выходного напряжения и оцениваются временем установления и выбросом фронта. В области больших времен искажается вершина импульса. Эти искажения оценивают относительным (в %) значением спада плоской вершины к моменту окончания импульса.

Линейные искажения

Отклонения частотных характерастик от идеальных в рабочем диапазоне частот называются частотными искажениями. Мерой частотных искажений является нормированное (относительное) усиление на границах рабочего диапазона частот, которое определяется как отношение коэффициента усиления на границе рабочего диапазона (К_Н , К_В )к коэффициенту усиления на средней рабочей частоте (К₀ ):

;

;

Часто используют величину, обратную нормированному усилению. Она носит название коэффициента частотных искажений.

M_H =1/G_H ; M_B =1/G_B .

Вследствие отклонения реальной фазочастотной характеристики усилителя от идеальной в нем имеют место фазовые искажения. Они вызваны неодинаковым сдвигом по фазе отдельных гармонических составляющих спектра сигнала сложной формы, что обусловлено наличием в цепях усилителя реактивных компонентов и инерционными свойствами полупроводниковых приборов. В результате такого неодинакового сдвига по фазе отдельных гармоник форма сигнала на выходе усилителя может стать существенно отличной от формы входного сигнала. Если вносимый усилителем фазовый сдвиг на частоте п-й гармоники пропорционален частоте , то сигнал на выходе усилителя окажется смещенным во времени на величину . Ее называют временем задержки или временем фазового пробега. Таким образом, если — вносимый усилителем фазовый сдвиг на частоте п-й гармоники — пропорционален частоте (), то взаимное расположение гармоник, а следовательно, и форма сигнала не подвергаются изменению.

На практике можно лишь с той или иной точностью приблизиться к идеальным частотной и фазовой характеристикам в полосе пропускания f=f_B —f_H , в пределах которой находится спектр усиливаемого сигнала.

Нелинейные искажения

Искажения, возникающие в усилителях вследствие нелинейности передаточных характеристик электронных приборов и характеристик намагничивания сердечников трансформаторов, называются нелинейными искажениями. При наличии нелинейных искажений в усилителе (в реальных усилителях они есть всегда) на его выходе возникают новые частоты (гармоники), отсутствующие во входном сигнале.

Общий уровень нелинейных искажений количественно оценивается коэффициентом нелинейных искажений (коэффициентом гармоник):

,

где , — амплитуды 1-й, 2-й, 3-й и т.д. гармоник выходного сигнала.

Практически имеют значение только вторая и третья гармоники. Обычно коэффициент нелинейных искажений выражается в процентах. Например, для усилителей низкой частоты простейшей бытовой радиоаппаратуры максимальным приемлемым уровнем можно считать 15...20%, а для высококачественных усилителей современной стереоаппаратуры коэффициент нелинейных искажений составляет десятые или даже сотые доли процента.

Еще один вид нелинейных искажений обусловлен появлением в выходном сигнале т.н. комбинационных частот, т.е. частот, получающихся как сумма или разность между любыми (в т.ч. и первыми) гармониками различных сигналов, присутствующих на входе усилителя. Такие искажения принято называть интермодуляционными искажениями. На практике имеют значение интермодуляционные искажения второго и третьего порядков (если и f₂ — частоты, присутствующие на входе, то интермодуляционные искажения второго порядка обусловлены наличием на выходе усилителя сигналов с частотами f₁ ±f₂ , а интермодуляционные искажения третьего порядка — с частотами 2 ±f₂ и 2f₂ ±). Коэффициентом интермодуляции называется отношение мощности интермодуляционных составляющих на выходе усилителя к минимально возможной выходной мощности полезного сигнала, превышающей уровень собственных шумов усилителя.

Абсолютный уровень интермодуляционных искажений принято оценивать по положению т.н. интермодуляционных точек. Если линейный участок динамической характеристики условно продлить в области высокой входной мощности (когда эта характеристика на самом деле уже не линейна) и одновременно наложить на этот график линию, отражающую суммарную мощность интермодуляционных составляющих второго (третьего) порядка, то точка пересечения этой линии с продленным графиком называется, соответственно, точкой интермодуляции второго (третьего) порядка.

В реальных схемах интермодуляционные искажения второго порядка часто растут медленнее интермодуляционных искажений третьего прядка. Так что интермодуляционная точка третьего порядка лежит ниже (соответствует меньшему уровню входной мощности) интермодуляционной точки второго порядка и имеет большее значение.

Помимо интермодуляционных точек часто говорят о соответствующих им динамических диапазонах по интермодуляции. Выше мы уже дали определение амплитудного динамического диапазона как отношения амплитуд сигнала в точке компрессии и в точке его возможного минимума (определяется собственными шумами). Аналогично вводится и понятие динамического диапазона по интермодуляции, т.е. диапазона уровней мощности входного сигнала, в котором обеспечивается его "безынтермодуляционная" обработка. Снизу такой диапазон также ограничен уровнем собственных шумов усилителя. А вот его верхняя граница определяется как точка, в которой уровень соответствующих интермодуляционных помех становится выше уровня собственных шумов, т.е. эти помехи начинают оказывать на выходной сигнал влияние большее, чем собственные шумы.

Коэффициент шума

Коэффициент шума характеризует уровень шумов (искажений случайного характера, обусловленных различными механическими, тепловыми, молекулярными, электронными и т.п. процессами в радиокомпонентах и соединительных проводниках), привносимых в сигнал при его прохождении через усилитель. В реальных условиях сигнал уже содержит шумы, когда поступает на вход усилителя. Поэтому коэффициент шума определяется следующим образом:

— мощность шумов на входе усилителя;

— мощность шумов на выходе усилителя;

— мощность полезного сигнала на входе усилителя;

— мощность полезного сигнала на выходе усилителя;

— собственная мощность шумов (мощность добавляемых в сигнал шумов).

Коэффициент полезного действия

Коэффициент полезного действия (КПД) отражает эффективность усилителя. Он равен отношению полезной выходной мощности (мощности полезного сигнала) к мощности, затрачиваемой источником питания на функционирование усилителя:

Выходная мощность

Номинальная выходная мощность — мощность полезного сигнала на выходе усилителя при работе на расчетную нагрузку и заданном коэффициенте гармоник или нелинейных искажений, т.е.максимальная мощность, при которой не превышается заданный уровень искажений.

Входные и выходные параметры усилителя

Помимо параметров, описывающих работу усилителя в целом, не менее важными являются характеристики его входной и выходной цепей. К ним относят в первую очередь входное и выходное сопротивления усилителя:

где

— номинальные амплитудные значения напряжения и тока первой гармоники на выходе усилителя.

В высокочастотных усилителях значительными становятся реактивные составляющие, поэтому здесь должны рассматриваться комплексные амплитуды:

Комплексные величины, называют, соответственно, входным и выходным импедансом усилителя. В диапазоне СВЧ, где анализ цепей производится в терминах их волновых свойств, для оценки параметров входных и выходных цепей усилителя могут применяться соответствующие коэффициенты отражения по входу/выходу

7. Обратные связи в усилителях

Одной из особенностей электронных усилителей является то, что они обладают преимущественно однонаправленной передачей сигналов, т.е. такой, при которой прохождение сигнала со входа на выход существенно лучше, чем обратное прохождение с выхода на вход. Однако иногда такое прохождение (с выхода на вход) может оказаться полезным (в какой-то мере это всегда и неизбежно ввиду наличия внутренних паразитных связей в транзисторах усилительного каскада). В этом случае говорят о введении в усилительный каскад цепей обратной связи (ОС).

Цепи ОС позволяют существенно влиять на многие параметры усилительных каскадов. В первую очередь к ним относятся: коэффициент усиления, амплитудно-частотная характеристика, входное сопротивление и т.п. Различают положительную (ПОС) и отрицательную (ООС) обратные связи. Возникающие помимо желания разработчика обратные связи принято называть паразитными.

Для реализации обратных связей могут использоваться самые разнообразные схемотехнические решения. В общем случае в транзисторных усилительных каскадах имеет смысл различать обратную связь по току и обратную связь по напряжению.

Вообще, изучение видов, способов реализации и характера влияния различных ОС на усилительные каскады не относится к задаче этой книги. Для подробного изучения теории обратной связи следует обратиться к специальной литературе (см. список литературы в конце книги). Однако в дальнейшем при описании конкретных схем будут приводиться и варианты включения в них различных цепей ОС, оказывающих положительное влияние на характеристики и параметры.

Список литературы

1) Манаев Е.И. Основы радиоэлектроники. — М.: Радио и связь, 2005

2) Булычев А.Л. и др. Электронные приборы: Учебник. — М.: Лайт Лтд., 2008

3) Опадчий Ю.Ф. и др. Аналоговая и цифровая электроника: Учебник для вузов. — М.: Горячая Линия — Телеком, 2009

4) Прянишников В.А. Электроника: Курс лекций. — СПб.: Корона-принт, 2008

5) Степаненко И.П. Основы теории транзисторов и транзисторных схем.— М.: 2007

6) Хоровиц П., Хилл У. Искусство схемотехники. — М.: Мир, 2003.