Главная / Рефераты / Коммуникации и связь

Реферат: Циклические коды. Коды БЧХ

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

кафедра РЭС

реферат на тему:

«Циклические коды. Коды БЧХ»

МИНСК, 2009

Циклические коды

Циклическим кодом называется линейный блоковый (n,k)-код, который характеризуется свойством цикличности, т.е. сдвиг влево на один шаг любого разрешенного кодового слова дает также разрешенное кодовое слово, принадлежащее этому же коду и у которого, множество кодовых слов представляется совокупностью многочленов степени (n-1) и менее, делящихся на некоторый многочлен g(x) степени r = n-k, являющийся сомножителем двучлена xⁿ +1.

Многочлен g(x) называется порождающим.

Как следует из определения, в циклическом коде кодовые слова представляются в виде многочленов
где n - длина кода;

- коэффициенты из поля GF(q).

Если код построен над полем GF(2), то коэффициенты принимают значения 0 или 1 и код называется двоичным.
Пример. Если кодовое слово циклического кода
то соответствующий ему многочлен

Например, если код построен над полем GF(q)=GF(2³ ), которое является расширением GF(2) по модулю неприводимого многочлена f(z)=z³ +z+1, а элементы этого поля имеют вид, представленный в таблице 1,

Таблица 1
0	000	0	a³	011	Z+1
a⁰	001	1	a⁴	110	Z² +Z
a¹	010	Z	a⁵	111	Z² +Z+1
a²	100	Z²	a⁶	101	Z² +1

то коэффициенты принимают значения элементов этого поля и поэтому они сами отображаются в виде многочленов следующего вида
где m - степень многочлена, по которому получено расширение поля GF(2);\ a_i - коэффициенты, принимающие значение элементов GF(2), т.е. 0 и 1. Такой код называется q-ным.

Длина циклического кода называется примитивной и сам код называется примитивным, если его длина n=q^m -1 на GF(q).

Если длина кода меньше длины примитивного кода, то код называется укороченным или непримитивным.

Как следует из определения общее свойство кодовых слов циклического кода - это их делимость без остатка на некоторый многочлен g(x), называемый порождающим.

Результатом деления двучлена xⁿ +1 на многочлен g(x) является проверочный многочлен h(x).

При декодировании циклических кодов используются многочлен ошибок e(x) и синдромный многочлен S(x).

Многочлен ошибок степени не более (n-1) определяется из выражения где - многочлены, отображающие соответственно принятое (с ошибкой) и переданное кодовые слова.

Ненулевые коэффициенты в е(x) занимают позиции, которые соответствуют ошибкам.

Пример.

Синдромный многочлен, используемый при декодировании циклического кода, определяется как остаток от деления принятого кодового слова на порождающий многочлен, т.е.

или

Следовательно, синдромный многочлен зависит непосредственно от многочлена ошибок е(х).Это положение используется при построении таблицы синдромов, применяемой в процессе декодирования. Эта таблица содержит список многочленов ошибок и список соответствующих синдромов, определяемых из выражения (см. таблицу 2).

Таблица 2
(x)	S(x)
1	R_g(x) [1]
X	R_g(x) [x]
X²	R_g(x) [x2]
·	·
·	·
·	·
X+1	R_g(x) [x+1]
X² +1	R_g(x) [x2+1]
·	·
·	·
·	·

В процессе декодирования по принятому кодовому слову вычисляется синдром, затем в таблице находится соответствующий многочлен е(х), суммирование которого с принятым кодовым словом дает исправленное кодовое слово, т.е. Перечисленные многочлены можно складывать, умножать и делить, используя известные правила алгебры, но с приведением результата по mod 2, а затем по mod xⁿ +1, если степень результата превышает степень (n-1).

Примеры.

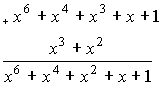Допустим, что длина кода n=7, то результат приводим по mod x⁷ +1.

При построении и декодировании циклических кодов в результате деления многочленов обычно необходимо иметь не частное, а остаток от деления.
Поэтому рекомендуется более простой способ деления, используя не многочлены, а только его коэффициенты (вариант 2 в примере).

Пример.

Матричное задание кодов

Циклический код может быть задан порождающей и проверочной матрицами. Для их построения достаточно знать порождающий g(x) и проверочный h(x) многочлены. Для несистематического циклического кода матрицы строятся циклическим сдвигом порождающего и проверочного многочленов, т.е. путем их умножения на x и

При построении матрицы H_(n,k) старший коэффициент многочлена h(x) располагается справа.

Пример. Для циклического (7,4)-кода с порождающим многочленом g(x)=x³ +x+1 матрицы G_(n,k) и H_(n,k) имеют вид: где

Для систематического циклического кода матрица G_(n,k) определяется из выражения где I_k - единичная матрица; R_k,r - прямоугольная матрица. Строки матрицы R_k,r определяются из выражений или где a_i (x) - значение i-той строки матрицы I_k ; i - номер строки матрицы R_k,r .

Пример. Матрица G_(n,k) для (7,4)-кода на основе порождающего многочлена g(x)=x³ +x+1, строится в следующей последовательности
или

Определяется R_4,3 , используя так как

Аналогичным способом определяется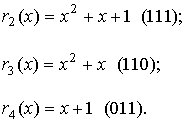

В результате получаем или

Используя выражение получим тот же результат.
Строки матрицы G_(n,k) можно определить непосредственно из выражения
где

Проверочная матрица в систематическом виде строится на основе матрицы G_(n,k) , а именно: где I_r - единичная матрица; - матрица из G_(n,k) в транспонированном виде.

Пример. Для (7,4)-кода матрица H_(n,k) будет иметь вид:

Одна из основных задач, стоящих перед разработчиками устройств защиты от ошибок при передаче дискретных сообщений по каналам связи является выбор порождающего многочлена g(x) для построения циклического кода, обеспечивающего требуемое минимальное кодовое расстояние для гарантийного обнаружения и исправления t-кратных ошибок.

Существуют специальные таблицы по выбору g(x) в зависимости от предъявляемых требований к корректирующим возможностям кода. Однако у каждого циклического кода имеются свои особенности формирования g(x). Поэтому при изучении конкретных циклических кодов будут рассматриваться соответствующие способы построения g(x).

Коды БЧХ

Одним из классов циклических кодов, способных исправлять многократные ошибки, являются коды БЧХ.

Примитивным кодом БЧХ, исправляющим t_u ошибок, называется код длиной n=q^m -1 над GF(q), для которого элементы являются корнями порождающего многочлена.

Здесь a - примитивный элемент GF(q^m ).

Порождающий многочлен определяется из выражения
где f₁ (x),f₂ (x)...- минимальные многочлены корней g(x).

Число проверочных элементов кода БЧХ удовлетворяет соотношению

Пример. Определить значение порождающего многочлена для построения примитивного кода БЧХ над GF(2) длины 31, исправляющего двух кратные ошибки (t_u =2).

Исходя из определения кода БЧХ корнями многочлена g(x) являются: , где a - примитивный элемент GF(q^m )=GF(2⁵ ).

Порождающий многочлен определяется из выражения где f₁ (x), f₂ (x), f₃ (x), f₄ (x) - минимальные многочлены корней соответственно .

Примечание.

Минимальный многочлен элемента b поля GF(q^m ) определяется из выражения , где - наименьшее целое число, при котором .

Значения минимальных многочленов будут следующими:

Так как f1(x)= f2(x)= f4(x), то

На практике при определении значений порождающего многочлена пользуются специальной таблицей минимальных многочленов (см. таблицу 8 приложения), и выражением для порождающего многочлена При этом работа осуществляется в следующей последовательности.

По заданной длине кода n и кратности исправляемых ошибок t_u определяют:
- из выражения n=2^m -1 значение параметра m, который является максимальной степенью сомножителей g(x); - из выражения j=2t_u -1 максимальный порядок минимального многочлена, входящего в число сомножителей g(x).

- пользуясь таблицей минимальных многочленов, определяется выражение для g(x) в зависимости от m и j. Для этого из колонки, соответствующей параметру m, выбираются многочлены с порядками от 1 до j, которые в результате перемножения дают значение g(x).

В выражении для g(x) содержаться минимальные многочлены только для нечетных степеней a, так как обычно соответствующие им минимальные многочлены четных степеней a имеют аналогичные выражения.

Например, минимальные многочлены элементов соответствуют минимальному многочлену элемента a¹ , минимальные многочлены элементов соответствуют минимальному многочлену a³ и т.п.

Пример. Определить значение порождающего многочлена для построения примитивного кода БЧХ над GF(2) длины 31, обеспечивающего t_u =3.

Определяем значения m и j.

Из таблицы минимальных многочленов в соответствии с m=5 и j=5 получаем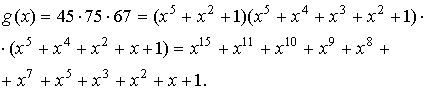

Заданные исходные данные: n и t_u или k и t_u для построения циклического кода часто приводят к выбору завышенного значения m и как следствие этого к неоправданному увеличению длины кода. Такое положение снижает эффективность полученного кода, так как часть информационных разрядов вообще не используется.

Пример. Требуется построить циклический код, исправляющий двух кратные ошибки, если длина информационной части кода k=40.

Согласно выражению для примитивного кода n=2^m -1, ближайшая длина кода равна 63, для которой m=6, а r=mt_u =12. Следовательно, код будет иметь n=63, k=51. Неиспользованных информационных разрядов будет 11(51-40).

Подобное несоответствие в ряде случаев можно устранить, применяя непримитивный код БЧХ.

Непримитивным кодом БЧХ, исправляющим t_u ошибок, называется код длины n над GF(q), для которого элементы являются корнями порождающего многочлена.

Здесь bⁱ -непримитивный элемент GF(q^m ), а длина кода n равна порядку элемента bⁱ .

Примечание.

Порядком элемента bⁱ является наименьшее n, для которого .

Пример. Порядок элемента b³ поля GF(2⁶ ) равен 21, так как .

Порождающий многочлен непримитивного кода БЧХ, по аналогии с примитивным кодом, определяется из выражения - минимальные многочлены элементов поля GF(q^m ), которые являются корнями g(x); i - степень непримитивного элемента b.

Пример. Определить значение g(x) для построения непримитивного кода БЧХ над GF(2) длины n=20, исправляющего двух кратные ошибки.

Из таблицы непримитивных элементов GF(2^m ) (см. таблицу 7 приложения) выбираем поле, элемент b которого имеет порядок больший, но близкий к заданному n.

Приложение

Таблица 1

Разложение бинома хⁿ +1 на неприводимые сомножители

Степень бинома	Последовательности степеней корней неприводимых сомножителей	Неприводимые сомножители
7	1 2 4 3 6 5	13 15
15	01 02 04 08 03 06 12 09 05 10 07 14 13 11	023 037 007 031
31	01 02 04 08 16 03 06 12 24 17 05 10 20 09 18 07 14 28 25 19 11 22 13 26 21 15 30 29 27 23	045 075 067 057 073 051
63	01 02 04 08 16 32 03 06 12 24 48 33 05 10 20 40 17 34 07 14 28 56 49 35 09 18 36 11 22 44 25 50 37 13 26 52 41 19 38 15 30 60 57 51 39 21 42 23 46 29 58 53 43 27 54 45 31 62 61 59 55 47	103 127 147 111 015 155 133 165 007 163 013 141

Примечание. В разложение всех биномов входит сомножитель 03 с корнем 00. Все сомножители представлены в восьмеричной форме.

Таблица 2

Элементы поля GF(16) как расширение GF(2) по примитивному многочлену a(z)=z⁴ +z+1

В двоичном виде	В виде многочлена	В виде степени
0000	0	0
0001	1	a⁰
0010	z	a¹
0100	z²	a²
1000	z³	a³
0011	z+1	a⁴
0110	z² +z	a⁵
1100	z³ +z²	a⁶
1011	z³ +z+1	a⁷
0101	z² +1	a⁸
1010	z³ +z	a⁹
0111	z² +z+1	a¹⁰
1110	z³ +z² +z	a¹¹
1111	z³ +z² +z+1	a¹²
1101	z³ +z² +1	a¹³
1001	z³ +1	a¹⁴

Таблица 3

Элементы поля GF(16) как расширение GF(4) по примитивному многочлену f(z)=z² +z+2

В четвертичном виде	В десятичном виде	В виде многочлена	В виде степени
00	0	0	0
01	1	1	a⁰
10	4	z	a¹
12	6	z+2	a²
32	14	3z+2	a³
11	5	z+1	a⁴
02	2	2	a⁵
20	8	2z	a⁶
23	11	2z+3	a⁷
13	7	z+3	a⁸
22	10	2z+2	a⁹
03	3	3	a¹⁰
30	12	3z	a¹¹
31	13	3z+1	a¹²
21	9	2z+1	a¹³
33	15	3z+3	a¹⁴

Таблица 4

Элементы поля GF(4) как расширение GF(2) по примитивному многочлену f(z)=z² +z+1

В двоичном виде	В виде многочлена	В виде степени	В десятичном виде
00	0	0	0
01	1	a⁰	1
10	z	a¹	2
11	z+1	a²	3

Таблица 6

Элементы поля GF(8) как расширение GF(2) по примитивному многочлену f(z)=z³ +z+1

В двоичном виде	В виде многочлена	В виде степени
000	0	0
001	1	a⁰
010	z	a¹
100	z²	a²
011	z+1	a³
110	z² +z	a⁴
111	z² +z+1	a⁵
101	z² +1	a⁶

Таблица 7

Непримитивные элементы поля GF(2^m )

¹	m	GF(2^m )	b	n
1	4	GF(2⁴ )	b³	5
b⁵	3
2	6	GF(2⁶ )	b³	21
b⁷	9
b⁹	7
3	8	GF(2⁷ )	b³	85
b⁵	51
b¹⁵	17
b¹⁷	15
4	9	GF(2⁹ )	b⁷	73
5	10	GF(2¹⁰ )	b³	341
b¹¹	93
b³¹	33
b³³	31
6	12	GF(2¹² )	b³	1365
b⁵	819
b⁷	585
b⁹	455
b¹³	315
b¹⁵	273
b²¹	195
b⁴⁵	91
b⁶³	65
b⁶⁵	63

Таблица 8

Минимальные неприводимые многочлены в поле GF(2^m )

2t_u -1	m
2	3	4	5	6	7	8	9	10
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35	7	13 15	31 37 07 31	45 75 67 57 73	103 127 147 111 015 155	211 217 235 367 277 325 203	435 567 763 551 675 747 453 727 023 545 613 543 433 477 615 435 537 771	1021 1131 1461 1231 1423 1055 1167 1541 1333 1605 1027 1751 1743 1617 1401	2011 2017 2415 3771 2257 2065 2157 2653 3515 2773 3753 2033 2443 3573 2461 3041 75 3023

Такими являются GF(2⁶ ) и b³ , порядок которого n=21.

Так как j=2t_u -1=2(2-1=3, то выражение для g(x) будет иметь вид
где f₃ (x) и f₉ (x) - минимальные многочлены элементов b³ и b⁹ поля GF(2⁶ ).

Значения этих многочленов следующие:

Выражения для f₃ (x) и f₉ (x) можно определить из таблицы минимальных многочленов, используя для этого параметр m выбранного поля GF(2^m ) и порядковые номера сомножителей g(x).

Для рассмотренного примера m=6, а порядковые номера равны 3 и 9. Поэтому
.

ЛИТЕРАТУРА

1. Лидовский В.И. Теория информации. - М., «Высшая школа», 2002г. – 120с.

2. Метрология и радиоизмерения в телекоммуникационных системах. Учебник для ВУЗов. / В.И.Нефедов, В.И.Халкин, Е.В.Федоров и др. – М.: Высшая школа, 2001 г. – 383с.

3. Цапенко М.П. Измерительные информационные системы. - . – М.: Энергоатом издат, 2005. - 440с.

4. Зюко А.Г. , Кловский Д.Д., Назаров М.В., Финк Л.М. Теория передачи сигналов. М: Радио и связь, 2001 г. –368 с.

5. Б. Скляр. Цифровая связь. Теоретические основы и практическое применение. Изд. 2-е, испр.: Пер. с англ. – М.: Издательский дом «Вильямс», 2003 г. – 1104 с.