| Скачать .docx | Скачать .pdf |
Реферат: Организация и функционирование электронных вычислительных машин
Белорусский Государственный Университет
Информатики и Радиоэлектроники
Контрольная работа
по дисциплине
Организация и функционирование ЭВМ
Выполнил: Проверил:
Cмоленский П.О. Пешков А.Т.
Зачетная книжка №510701
(Ликвидация академической разницы)
Минск, 2009
Задание 1.1
Задание предполагает нахождения значений С1, С2, С3, С4, определяемые выражениями:
С1 = А+В, С1 = А-В, С1 = В- А+, С1 =- А –В
При выполнении задания операнды А и В необходимо представить в двоично-десятичной системе, сформировать для них прямые коды и, используя заданный код в варианте по правилам двоично-десятичной арифметики, описанной в разделе «Арифметика с алгебраическими двоично-десятичными числами», найти значения С1, С2, С3, С4.
Результат должен быть представлен в прямом коде.
Условие:
Операнд А ![]()
Операнд В ![]()
Код, используемый при выполнении задания: дополнительный.
Решение:
С1 = А+В
С2 = А − В = A + (−B)
С3 = В − А = B + (−A)
С4 = − А – В = - (A+B)
| A = 5182 | = | 0101 0001 1000 0010 |
| [A]пк | = | 00.0101 0001 1000 0010 |
| [A]дк | = | 00.0101 0001 1000 0010 |
| [-A]дк | = | 11.1010 1110 0111 1110 |
| B=5493 | = | 0101 0100 1001 0011 |
| [B]пк | = | 00.0101 0100 1001 0011 |
| [B]дк | = | 00.0101 0100 1001 0011 |
| [-B]дк | = | 11.1010 1011 0110 1101 |
| C1=A+B | ||
| C1= | 00.0101 0001 1000 0010 | [A]дк |
| + | 00. 0101 0100 1001 0011 | [B]дк |
| 00. 1010 0110 0001 0101 | ||
| 0110 0110 ____ | коррекция | |
| 00.0001 0000 0110 0111 0101 | ||
| + 1 0 6 7 5 | ||
| С2=A+(-B) | ||
| C2= | 00.0101 0001 1000 0010 | [A]дк |
| + | 11.1010 1011 0110 1101 | [-B]ДК инверсный код |
| 11.1111 1100 1110 1111 | ||
| 11.0000 0011 0001 0000 | ||
| +1 | ||
| 11.0000 011 0001 0001 | ||
| - 3 1 1 | ||
| C3=B+(-A) | ||
| C3= | 00.0101 0100 1001 0011 | [B]дк |
| + | 11.1010 1110 0111 1110 | [-A]дк |
| 00.0000 0011 0001 0001 | ||
| + 3 1 1 | ||
| С4=-(A+B) | ||
| -C4= | 00.0101 0001 1000 0010 | [A]дк |
| + | 00. 0101 0100 1001 0011 | [B]дк |
| 00. 1010 0110 0001 0101 | ||
| 0110 0110 ____ | коррекция | |
| 00.0001 0000 0110 0111 0101 | [-C4] | |
| C4= | 11.0001 0000 0110 0111 0101 - 1 0 6 7 5 |
|
Дополнительный код нужно заменить инверсным и учесть это при коррекции.
(см. аналогичные примеры по операциям с 2 10-ыми числами в методических материалах).
Задание 1.2
Задание предполагает выполнение заданной операции над числами А и В, представленными с плавающей точкой.
При выполнении задания порядки и мантиссы операндов А и В, заданные в таблице, необходимо представить в двоичной системе счисления и сформировать для них прямые коды. Разрядность модуля порядка должна быть равна 3, разрядность модуля мантиссы - 6 .
Результат (порядок и мантисса) должен быть представлен в прямом коде в нормализованной форме.
Условие:
| A | B | код |
опер. |
||||||
| порядок | мантисса | порядок | мантисса | ||||||
| знак | абс.знач. | знак | абс.знач. | знак | абс.знач. | знак | абс.знач. | ||
| + | 4 | - | 0.54 | + | 2 | − | 0.80 | обр. | + |
| 0 | 100 | 1 | .100 010 | 0 | 010 | 1 | .110 011 | ||
Решение:
| [Aп]пк= | 0.100 |
| [Ам]пк= | 1.100 010 |
| [Bп]пк= | 0.010 |
| [Bм]пк= | 1.110 011 |
| [Aп]ок= | 0.100 |
| [Aм]ок= | 1.011 101 |
| [Bп]ок= | 0.010 |
| [Bм]ок= | 1.001 100 |
Выравнивание порядков:
| 00.100 [Aп] | |
| + | 11.101 [-Bп ] |
| 1 | 00.001 |
| 00.010 | Прямойкод |
Значит, сдвигаем мантиссу числа B на 2 вправо:
[Bм] = 1.001 100
Сумма мантисс:
| 11.011 101 | A |
| +11.001 100 | B |
| 11.101 001 | обр |
| 11.010 110 | прямой |
С1 - {![]() = 0.100,
= 0.100, ![]() = 11.010 110}
= 11.010 110}
Задание 1.2 принято.
Задание 2.1
Задание относится к разделу “Схемотехнические основы ЗВМ” и состоит из двух частей:
- построить блок управления аппаратного принципа, реализующий заданную ГСА ( ГСА - граф- схема алгоритма).
- построить блок управления микропрограммного принципа, реализующий заданную ГСА.
Задание 2.1
Построить цифровой автомат заданного типа (Мили или Мура) для заданной ГСА, используя заданный тип триггера (RS-, D-, T-триггер). Тип автомата, номер ГСА (соответствует номеру рисунка, на котором она находится) и тип триггера выбирается из табл.2.
Тип триггера (ТТ), тип цифрового автомата (ТЦА), номер ГСА (ГСА) задается колонками, соответственно, 1,2 и 3.
Номер варианта определяется последними двумя цифрами зачетной книжки (равен 30).
| № | Задание 2.1 | ||
| вар | ТТ | ТЦА | ГСА |
| 1 | RS | Мура | Рис.1 |
Исходная схема (рис. 1)
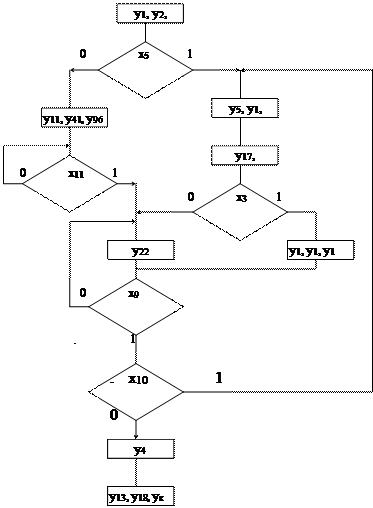 |
Решение:
Обозначим в данной ГСА операционные вершины как Ai вершины (состояние) графа автомата Мура.
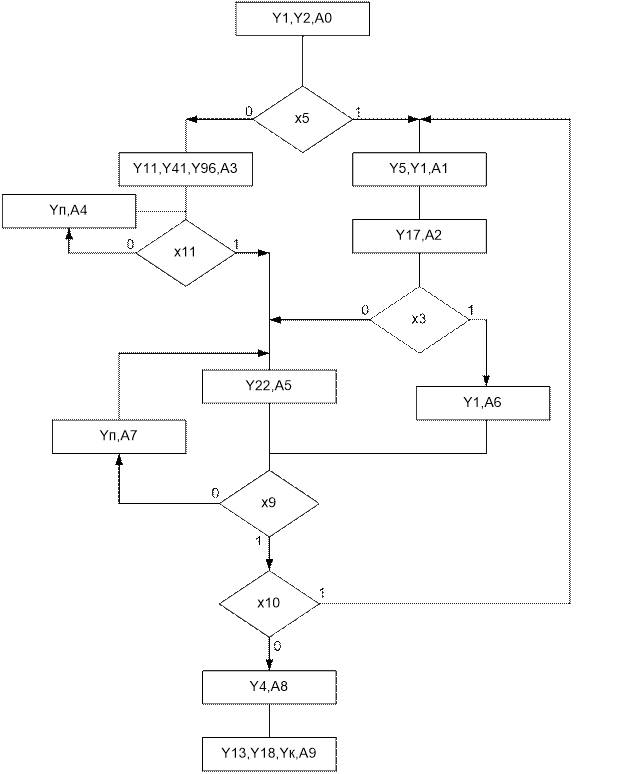
Имея граф автомата Мура, объединенная кодированная таблица переходов и выходов цифрового автомата строится за счет нахождения всех существующих путей из каждой вершины графа в ближайшую другую вершину с указанием условий, при которых имеет место данный путь, и вырабатываемых выходных сигналов, которые в автомате Мура однозначно определяются конечным состоянием (конечной вершиной):
Аi {xs s s , xp s p ...xf s f ,уn (А J ),... уm (А J )} А J ,
где:
- Аi , АJ - соответственно, начальная и конечная вершина пути;
- xs s s , xp s p ...xf s f - условия, через которые проходит рассматриваемый путь из Аi в АJ ;
- уn (А J ),... уm (А J ) - выходные сигналы автомата, однозначно зависящий от конечного состояния АJ. .
Объединенной кодированной таблицы переходов и выходов цифрового автомата составляется на основе всех возможных путей из всех вершин графа
автомата. В таблице приведена объединенной кодированной таблицы переходов и выходов для графа автомата Мура.
| Начало | Конец | |||||||||
| N | An | Q1Q2Q3Q4 | An | Q1Q2Q3Q4 | Условие | Выход | qs1 qr1 qs2 qr2 qs3 qr3 qs4 qr4 | |||
| 1 | A0 | 0 0 0 0 | A1 | 0 0 0 1 | x5 | y5y1 | 0 1 0 1 0 1 1 0 | |||
| 2 | A3 | 0 0 1 1 | ~x5 | y11y41y96 | 0 1 0 1 1 0 1 0 | |||||
| 3 | A1 | 0 0 0 1 | A2 | 0 0 1 0 | 1 | y17 | 0 1 0 1 1 0 0 1 | |||
| 4 | A2 | 0 0 1 0 | A6 | 0 1 1 0 | x3 | y1 | 0 1 1 0 1 0 0 1 | |||
| 5 | A5 | 0 1 0 1 | ~x3 | y22 | 0 1 1 0 0 1 1 0 | |||||
| 6 | A3 | 0 0 1 1 | A5 | 0 1 0 1 | x11 | y22 | 0 1 1 0 0 1 1 0 | |||
| 7 | A4 | 0 1 0 0 | ~x11 | yn | 0 1 1 0 0 1 0 1 | |||||
| 8 | A4 | 0 1 0 0 | A5 | 0 1 0 1 | x4 | y22 | 0 1 1 0 0 1 1 0 | |||
| 9 | A5 | 0 1 0 1 | A7 | 0 1 1 1 | ~x9 | yn | 0 1 1 0 1 0 1 0 | |||
| 10 | 0 1 0 1 | A1 | 0 0 0 1 | X9 x10 | Y5 y1 | 0 1 0 1 0 1 1 0 | ||||
| 11 | A8 | 1 0 0 0 | X9 ~x10 | Y4 | 1 0 0 1 0 1 0 1 | |||||
| 12 | A6 | 0 1 1 0 | A7 | 0 1 1 1 | ~x9 | yn | 0 1 1 0 1 0 1 0 | |||
| 13 | A8 | 1 0 0 0 | X9 ~x10 | Y4 | 1 0 0 1 0 1 0 1 | |||||
| 14 | A7 | 0 1 1 1 | A5 | 0 1 0 1 | 1 | Y22 | 0 1 1 0 0 1 1 0 | |||
| 15 | A8 | 1 0 0 0 | A9 | 1 0 0 1 | 1 | Y13 y18 yk | 1 0 0 1 0 1 1 0 | |||
| __ __ __ | ||||||||||
| y5= | Q1Q2Q3Q4 | |||||||||
| __ __ __ | __ __ | |||||||||
| Y1= | Q1Q2Q3Q4 | +Q1Q2Q3Q4 | ||||||||
| __ __ | ||||||||||
| y11= | Q1Q2Q3Q4 | |||||||||
| __ __ | ||||||||||
| y41= | Q1Q2Q3Q4 | |||||||||
__ __ |
||||||||||
| y96= | Q1Q2Q3Q4 | |||||||||
| __ __ __ | ||||||||||
| y17= | Q1Q2Q3Q4 | |||||||||
| __ __ | ||||||||||
| y22= | Q1Q2Q3Q4 | |||||||||
| __ ____ | ||||||||||
| y4= | Q1Q2Q3Q4 | |||||||||
| __ __ | ||||||||||
| y13= | Q1Q2Q3Q4 | |||||||||
| __ __ | ||||||||||
| y18= | Q1Q2Q3Q4 | |||||||||
| __ __ | ||||||||||
| yk= | Q1Q2Q3Q4 | |||||||||
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
qr1= Q1Q2Q3Q4x5+ Q1Q2Q3Q4x5+ Q1Q2Q3Q4+ Q1Q2Q3Q4x3+ Q1Q2Q3Q4x3+ Q1Q2Q3Q4x11+
_ _ _ _ _ _ _ _ _ _ _
Q1Q2Q3Q4x11+ Q1Q2Q3Q4x9+ Q1Q2Q3Q4x9x10+ Q1Q2Q3Q4x9+ Q1Q2Q3Q4(1,2,3,4,5,6,7,8,9,10,12,14)
_ _ _ _ _ _
qs1= Q1Q2Q3Q4x9x10+ Q1Q2Q3Q4(11,13,15)
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _
qs2 = Q1Q2Q3Q4x3+ Q1Q2Q3Q4x3+ Q1Q2Q3Q4x11+ Q1Q2Q3Q4x11+ Q1Q2Q3Q4x9+ Q1Q2Q3Q4 (4,5,6,7,8,9,12,14)
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
qr2 = Q1Q2Q3Q4x5+ Q1Q2Q3Q4x5+ Q1Q2Q3Q4+ Q1Q2Q3Q4x9x10+ Q1Q2Q3Q4x9x10+ Q1Q2Q3Q4 (1,2,3,10,11,13,15)
_ _ _ _ _ _ _ _ _ _
qs3 = Q1Q2Q3Q4x5+ Q1Q2Q3Q4+ Q1Q2Q3Q4x3+ Q1Q2Q3Q4x9(2,3,5,9,12)
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
qr3= Q1Q2Q3Q4x5+ Q1Q2Q3Q4x3+ Q1Q2Q3Q4x11+ Q1Q2Q3Q4x11+ Q1Q2Q3Q4x9x10+ Q1Q2Q3Q4x9x10+
_ _ _ _
Q1Q2Q3Q4+ Q1Q2Q3Q4(1,4,6,7,8,10,11,13,14,15)
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
qs4= Q1Q2Q3Q4x5+ Q1Q2Q3Q4x5+ Q1Q2Q3Q4x3+ Q1Q2Q3Q4x11+ Q1Q2Q3Q4x9+ Q1Q2Q3Q4x9x10+
_ _ _ _
Q1Q2Q3Q4+ Q1Q2Q3Q4(1,2,4,7,8,9,10,12,14,15)
_ _ _ _ _ _ _ _ _ _ _ _ _
qr4= Q1Q2Q3Q4+ Q1Q2Q3Q4x3+ Q1Q2Q3Q4x11+ Q1Q2Q3Q4x9x10(3,5,6,11,13)
Схемаавтомата:
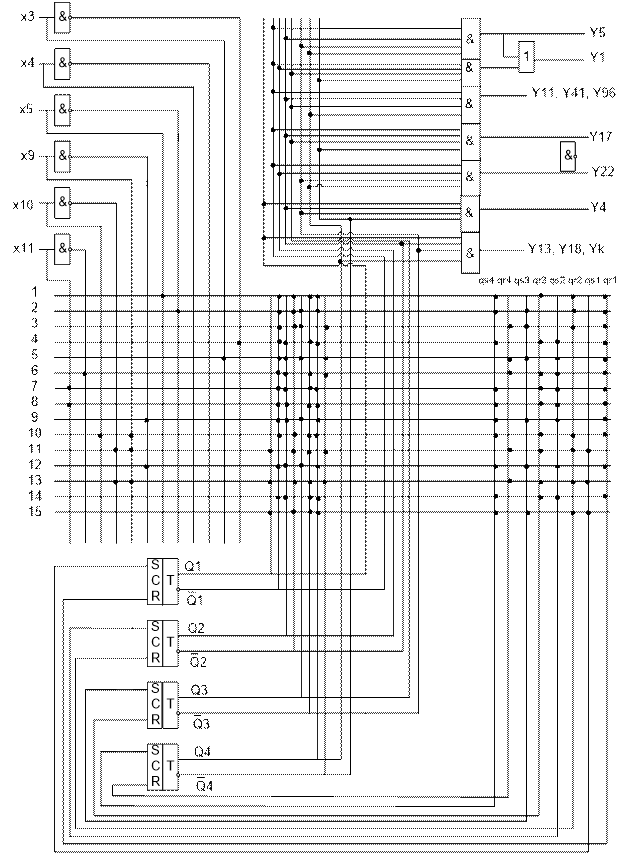
В Вашей схеме выходные сигналы зависят от входных, что не соответствует Вашему типу цифрового автомата
Задание 2.2
Написать микропрограмму, соответствующую заданной ГСА, с учетом заданных множества микроопераций (Y), множества проверяемых условий (Х), ёмкости запоминающего устройства (ЗУ) и начального адреса размещения микропрограммы (МП) в ЗУ. В каждом адресе запоминающего устройства может храниться 16 бит информации. Обозначение ук соответствует микрооперации, обозначающей последнюю микрокоманду в микропрограмме.
Если это допускает длина микрокоманды, использовать модификатор дисциплины перехода.
| Задание 2.2 | ||||
| Y | X | ёмкость ЗУ | нач. адрес МП | ГСА |
| 1. | 2. | 3. | 4. | 5. |
| 120 | 15 | 1000 | 421 | Рис.4 |
Решение:
Исходная схема (рис. 4)
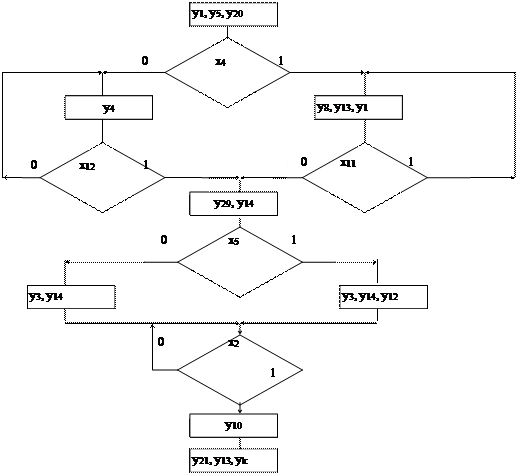 |
Микропрограмма должна реализовать алгоритм, заданный ГСА на рисунке:
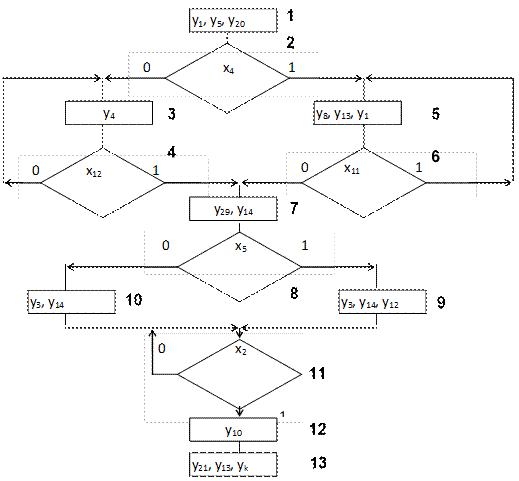
Управления объект, характеризуется следующими параметрами:
- множество проверяемых условий
- X ={x1 ,x1 , .. x15 .};
- множество выполняемых микроопераций
- Y ={y1 ,y2 , .. y120 , yк } (yк - микрооперация , означающая последнюю микрокоманду микропрограммы);
- ёмкость памяти для записи микропрограмм
- Vзу = 1кбайт = 2*29 байт;
- длина ячейки памяти
- L = 16 бит;
- начальный адрес размещения составляемой микропрограммы в памяти
- Ан =421;
Исходя из характеристик управляемого объекта, следует:
- длина поля для кодирования микроопераций равна к=7
- длина поля для кодирования условий равна р=4
- длина кода адреса равна р=9
 МКО
МКО
 МКП
МКП
Не указано, какое соответствие у Вас между дисциплинами перехода и значением модификатора М.
| Nпп | Nвер | Адрес микрокоманды | Код микрокоманды | Примечание |
| 1 | 1 | 0110100101 | 1.0000001.0000101.0 | |
| 2 | 1' | 0110100110 | 1.0010100.0000000.0 | |
| 3 | 2 | 0110100111 | 0.0100.011011010 .1 | 3 |
| 4 | 5 | 0110101000 | 1.0001000.0001101.0 | |
| 5 | 5' | 0110101001 | 1.0000001.0000000.0 | |
| 6 | 6 | 0110101010 | 0.1011.0110101000 .0 | 5 |
| 7 | 7 | 0110101011 | 1.0011101.0001110.0 | |
| 8 | 8 | 0110101100 | 0.0101. 0110110100 .1 | 10 |
| 9 | 9 | 0110101101 | 1.0000011.0001110.0 | |
| 10 | 9' | 0110101110 | 1.0001100.0000000.0 | |
| 11 | 11 | 0110101111 | 0.0010.0110101111 .1 | 11 |
| 12 | 12 | 0110110000 | 1.0001010.0000000.0 | |
| 13 | 13 | 0110110001 | 1.0010101.0001101.1 | |
| 14 | 3 | 0110110010 | 1.0000100.0000000.1 | |
| 15 | 4 | 0110110011 | 0.1100.0110110010 .1 | 3 |
| 16 | 10 | 0110110100 | 0.0000011.0001110.0 | |
| 17 | 0110110101 | 0.0000.0110101111 .1 | 11 |
Задание 2.2 принято.