| Скачать .docx | Скачать .pdf |
Реферат: по Статистике 19
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ
ТОРГОВО-ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ
Финансово-экономический факультет
КОНТРОЛЬНАЯ РАБОТА ПО ДИСЦИПЛИНЕ
«СТАТИСТИКА»
Вариант №1
Выполнила студентка:
2 курса, группы 22, з/о, (сокр.пр.)
Камилова Анна Алексеевна
Проверила:
Агентова Галина Владимировна
Москва, 2010
Содержание
ПРИЛОЖЕНИЕ К РЕШЕНИЮ ЗАДАЧ ПО СТАТИСТИКЕ. 27
Задача № 1
Произведите группировку магазинов №№ 1 ... 18 (см. Приложение 1) по признаку размер товарооборота, образовав четыре группы с равными интервалами.
Сказуемое групповой таблицы должно содержать следующие показатели:
1. число магазинов;
2. товарооборот в сумме и в среднем на один магазин;
3. издержки обращения в сумме и в среднем на один магазин;
4. относительный уровень издержек обращения (в процентах к товарообороту);
5. стоимость основных фондов;
6. численность продавцов;
7. торговая площадь.
Полученные результаты оформите в виде статистической таблицы. Сделайте выводы.
| Номер магазина | Товарооборот (млн. руб.) | Издержки обращения (млн. руб.) | Стоимость основных фондов (средне-годовая) (млн. руб.) | Численность продавцов (чел.) | Торговая площадь (м2 ) |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 148 | 20,4 | 5,3 | 64 | 1070 |
| 2 | 180 | 19,2 | 4,2 | 85 | 1360 |
| 3 | 132 | 18,9 | 4,7 | 92 | 1140 |
| 4 | 314 | 28,6 | 7,3 | 130 | 1848 |
| 5 | 235 | 24,8 | 7,8 | 132 | 1335 |
| 6 | 80 | 9,2 | 2,2 | 41 | 946 |
| 7 | 113 | 10,9 | 3,2 | 40 | 1435 |
| 8 | 300 | 30,1 | 6,8 | 184 | 1820 |
| 9 | 142 | 16,7 | 5,7 | 50 | 1256 |
| 10 | 280 | 46,8 | 6,3 | 105 | 1353 |
| 11 | 156 | 30,4 | 5,7 | 57 | 1138 |
| 12 | 213 | 28,1 | 5,0 | 100 | 1216 |
| 13 | 298 | 38,5 | 6,7 | 112 | 1352 |
| 14 | 242 | 34,2 | 6,5 | 106 | 1445 |
| 15 | 130 | 20,1 | 4,8 | 62 | 1246 |
| 16 | 184 | 22,3 | 6,8 | 60 | 1332 |
| 17 | 96 | 9,8 | 3,0 | 34 | 680 |
| 18 | 304 | 38,7 | 6,9 | 109 | 1435 |
При группировке применим формулу шага (величина интервала): i = R / n , где:
![]() – (размах вариации),
– (размах вариации),
![]() и
и ![]() – соответственно максимальное и минимальное значения группировочного признака,
– соответственно максимальное и минимальное значения группировочного признака,
![]() – число групп.
– число групп.
Тогда i =(314-80)/4=58,5
Вспомогательная таблица:
Таблица 1.
| Группы по признаку размер товаро-оборота | Номер магазина | Товаро-оборот, (млн. руб.) | Издержки обращения, (млн. руб.) | Стоимость основных фондов (средне-годовая), (млн. руб.) | Числен- ность продавцов, (чел.) |
Торговая площадь, (м2 ) |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 80 - 138,5 | 3 | 132 | 18,9 | 4,7 | 92 | 1140 |
| 6 | 80 | 9,2 | 2,2 | 41 | 946 | |
| 7 | 113 | 10,9 | 3,2 | 40 | 1435 | |
| 15 | 130 | 20,1 | 4,8 | 62 | 1246 | |
| 17 | 96 | 9,8 | 3 | 34 | 680 | |
| Всего: | 5 | 551 | 68,9 | 17,9 | 269 | 5447 |
| 138,5 - 197 | 1 | 148 | 20,4 | 5,3 | 64 | 1070 |
| 2 | 180 | 19,2 | 4,2 | 85 | 1360 | |
| 9 | 142 | 16,7 | 5,7 | 50 | 1256 | |
| 11 | 156 | 30,4 | 5,7 | 57 | 1138 | |
| 16 | 184 | 22,3 | 6,8 | 60 | 1332 | |
| Всего: | 5 | 810 | 109 | 27,7 | 316 | 6156 |
| 197 - 255,5 | 5 | 235 | 24,8 | 7,8 | 132 | 1335 |
| 12 | 213 | 28,1 | 5 | 100 | 1216 | |
| 14 | 242 | 34,2 | 6,5 | 106 | 1445 | |
| Всего: | 3 | 690 | 87,1 | 19,3 | 338 | 3996 |
| 255,5 - 314 | 4 | 314 | 28,6 | 7,3 | 130 | 1848 |
| 8 | 300 | 30,1 | 6,8 | 184 | 1820 | |
| 10 | 280 | 46,8 | 6,3 | 105 | 1353 | |
| 13 | 298 | 38,5 | 6,7 | 112 | 1352 | |
| 18 | 304 | 38,7 | 6,9 | 109 | 1435 | |
| Всего: | 5 | 1496 | 182,7 | 34 | 640 | 7808 |
Группы по признаку размер товарооборота
Таблица 2.
Группы по признаку размер товарооборота, (млн. руб.) |
Количество магазинов | Товарооборот, (млн. руб.) | Издержки обращения, (млрд. руб.) |
Относительный уровень издержек обращения, (в процентах к товарообороту) | Стоимость основных фондов (среднегодовая), (млн. руб.) | Численность продавцов, (чел.) | Торговая площадь, (м2 ) | ||
| Сумма | В среднем на один магазин | ||||||||
| Сумма | В среднем на один магазин | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 80 - 138,5 | 5 | 551 | 110,2 | 68,9 | 13,78 | 12,505 | 17,9 | 269 | 5447 |
| 138,5 - 197 | 5 | 810 | 162 | 109 | 21,80 | 13,457 | 27,7 | 316 | 6156 |
| 197 - 255,5 | 3 | 690 | 230 | 87,1 | 29,03 | 12,623 | 19,3 | 338 | 3996 |
| 255,5 - 314 | 5 | 1496 | 299,2 | 182,7 | 36,54 | 12,213 | 34 | 640 | 7808 |
| Всего: | 18 | 3547 | 447,7 | 98,9 | 1563 | 23407 | |||
Средние значения (в среднем на один магазин) вычислялись через отношение сумм к числу магазинов – как среднее арифметическое (столбцы 4,6). (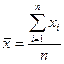 - где:
- где: ![]() – значения изучаемого признака (варианты);
– значения изучаемого признака (варианты); ![]() – количество магазинов;
– количество магазинов; ![]() – средняя арифметическая величина).
– средняя арифметическая величина).
Относительный уровень издержек обращения (в процентах к товарообороту) находился через отношение издержек к товарообороту.
Вывод:
1. Сравнительный анализ 4 групп:
- наибольшее число магазинов равно пяти и содержится в 1-ой, 2-ой и 4-ой группах, наименьшее число магазинов равно трем и содержится в 3-ей группе;
- наибольший товарооборот в 4-ой группе, наименьший – в 3-ей;
- наибольшие издержки обращения в 4-ой группе, наименьшие – в 1-ой;
- наибольший относительный уровень издержек обращения во 2-ой группе, наименьший – в 4-ой;
- наибольшая стоимость основных фондов в 4-ой группе, наименьшая – в 1-ой;
- наибольшая численность продавцов в 4-ой группе, наименьшая – в 1-ой;
- наибольшая торговая площадь в 1-ой группе, наименьшая – в 3-ей.
2. Анализируя показатели по 1 группе магазинов можно сказать, что в ней содержится наибольшее число магазинов равное пяти, как и во 2-ой и 4-ой группах; товарооборот – наименьший из всех групп; издержки обращения – наименьшие из всех групп; относительный уровень издержек обращения больше, чем в 4-ой группе, но меньше чем во 2-ой и 3-ей группах; стоимость основных фондов – наименьшая из всех групп; численность продавцов – наименьшая из всех групп; торговая площадь – больше, чем в 3-ей группе, но меньше чем во 2-ой и 4-ой группах.
Анализируя показатели по 2 группе магазинов можно сказать, что в ней содержится наибольшее число магазинов равное пяти, как и в 1-ой и 4-ой группах, товарооборот – больше, чем в 1-ой и 3-ей группах, но меньше, чем в 4-ой группе; издержки обращения – больше, чем в 1-ой и 3-ей группах, но меньше, чем в 4-ой группе; относительный уровень издержек обращения – наибольший из всех групп; стоимость основных фондов – больше, чем в 1-ой и 3-ей группах, но меньше, чем в 4-ой группе; численность продавцов – больше, чем в 1-ой группе, но меньше, чем в 3-ей и 4-ой группах; торговая площадь – больше, чем в 1-ой и 3-ей группах, но меньше, чем в 4-ой группе.
Анализируя показатели по 3 группе магазинов можно сказать, что у нее наименьшее число магазинов из всех групп; товарооборот – больше, чем в 1-ой группе, но меньше, чем во 2-ой и 4-ой группах; издержки обращения – больше, чем в 1-ой группе, но меньше, чем во 2-ой и 4-ой группах; относительный уровень издержек обращения – больше, чем в 1-ой и 4-ой группах, но меньше, чем в 3-ей группе; стоимость основных фондов – больше, чем в 1-ой группе, но меньше чем во 2-ой и 4-ой группах; численность продавцов – больше, чем в 1-ой и 2-ой группах, но меньше, чем в 4-ой группе; торговая площадь – наименьшая из всех групп.
Анализируя показатели по 4 группе магазинов можно сказать, что в ней содержится наибольшее число магазинов равное пяти, как и в 1-ой и 2-ой группах; товарооборот – наибольший из всех групп; издержки обращения – наибольшие из всех групп; относительный уровень издержек обращения – наименьший из всех групп; стоимость основных фондов – наибольшая из всех групп; численность продавцов – наибольшая из всех групп; торговая площадь – наибольшая из всех групп.
Задача № 2
Используя построенный в задаче № 1 интервальный ряд распределения магазинов по размеру товарооборота, определите:
1. среднее квадратическое отклонение;
2. коэффициент вариации;
3. модальную величину;
4. медиану.
Постройте гистограмму распределения и сделайте выводы.
Таблица 3.
Группы по признаку размер товарооборота, (млн. руб.) |
Число магазинов,
|
Середина интервала, |
||||
| 1 | 3 | 2 | 4 | 5 | 6 | 7 |
| 80 - 138,5 | 5 | 109 | 546 | -85 | 7 140 | 35 701 |
| 138,5 - 197 | 5 | 168 | 839 | -26 | 676 | 3 380 |
| 197 - 255,5 | 3 | 226 | 679 | 33 | 1 056 | 3 169 |
| 255,5 - 314 | 5 | 285 | 1 424 | 91 | 8 281 | 41 405 |
| Всего | 18 | 3 488 | 83 655 |
Средняя взвешенная вычисляется, если имеются многократные повторения значения признака и совокупность разбита на группы:
![]() , где
, где
![]() - середина интервала в i
-ой группе,
- середина интервала в i
-ой группе,
f i - число повторов (частоты) в i -ой группе.
![]() млн. руб.
млн. руб.
Дисперсию вычислим по формуле:
![]() млн. руб.
млн. руб.
Среднее квадратическое отклонение вычислим по формуле:
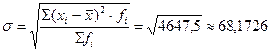 . млн. руб.
. млн. руб.
Коэффициент вариации вычислим по формуле:
![]() .
.
Вывод: Величина коэффициента вариации говорит об однородности изучаемой совокупности, так, если вариация больше 33%, то это говорит о большой колеблемости признака в изучаемой совокупности.
![]() - большая колеблемость товарооборота (совокупность не однородна).
- большая колеблемость товарооборота (совокупность не однородна).
Мода Мо для дискретного ряда – это значение признака, наиболее часто встречающееся у единиц исследуемой совокупности.
В имеющемся условии задачи нет признака, наиболее часто встречающегося у единиц исследуемой совокупности (три группы по 5 магазинов).
Предположим, что в 1-ой группе 6 магазинов и исходя из этого найдем моду.
В интервальном вариационном ряду модой приближенно считается центральное значение модального интервала (имеющего наибольшую частоту).
 , где
, где
![]() -частота модального интервала,
-частота модального интервала,
![]() -частота интервала, предшествующего модальному,
-частота интервала, предшествующего модальному,
![]() - частота интервала, следующего за модальным,
- частота интервала, следующего за модальным,
![]() -длина модального интервала,
-длина модального интервала,
![]() -начало модального интервала.
-начало модального интервала.
![]() млн. руб.
млн. руб.
Медиана Ме – это значение признака, приходящееся на середину ранжированного ряда. По обе стороны от медианы находится одинаковое количество единиц совокупности.
 , где
, где
SMe -1 - кумулятивная частота интервала, предшествующего медианному,
![]() - начало медианного интервала,
- начало медианного интервала,
![]() - частота медианного интервала,
- частота медианного интервала,
![]() - длина медианного интервала.
- длина медианного интервала.
 млн. руб.
млн. руб.
Вывод: если предположить, что в первой группе 6 магазинов, то наиболее часто встречающийся товарооборот равен 130,14 млн. руб.
Серединное (центральное) значение товарооборота равно 177,5 млн. руб.
Гистограмма распределения:

Рис. 1
Задача № 3
Проведено 5-процентное обследование качества поступившей партии товара. В выборку попало 800 единиц (на основе механического способа отбора), из которых 80 единиц оказались нестандартными. Средний вес одного изделия в выборе составил 18,6 кг, а дисперсия – 0,016.
Определите:
1. С вероятностью 0,997 пределы, в которых находится генеральная доля нестандартной продукции.
2. С вероятностью 0,954 пределы, в которых находится средний вес одного изделия во всей партии товара.
По полученным результатам сделайте выводы.
1. Вычислим с вероятностью 0,997 пределы, в которых находится генеральная доля нестандартной продукции:
Доля нестандартной продукции в выборке вычисляется по формуле
![]() , где m
– численность единиц выборочной совокупности, обладающих исследуемым признаком, а n
– количество единиц в выборке.
, где m
– численность единиц выборочной совокупности, обладающих исследуемым признаком, а n
– количество единиц в выборке.
w =80/800=0,1 то есть 10%
Предельная ошибка выборочной доли вычисляется по формуле
![]() ,
,
где  , а t – коэффициент доверия.
, а t – коэффициент доверия.
Учитывая, что ![]() ;
; ![]() ; n
/
N
=
5/100=0,05; тогда
; n
/
N
=
5/100=0,05; тогда

Найдем пределы, в которых находится генеральная доля нестандартной продукции:
![]()
10%-3,1%=6,9; 10%+3,1%=13,1%; следовательно 6,9%<P<13,1%
Вывод: с вероятностью 0,997 можно утверждать, что генеральная доля нестандартной продукции находится в пределах от 6,9% до 13,1%.
2. Вычислим с вероятностью 0,954 пределы, в которых находится средний вес одного изделия во всей партии товара:
Средний вес изделия в выборке равен 18,6 кг.
Предельная ошибка выборочной средней доли вычисляется по формуле: 
Учитывая, что ![]() ; t
=2; n
/
N
=
5/100=0,05;
; t
=2; n
/
N
=
5/100=0,05; ![]() =0,016; тогда
=0,016; тогда
 =
=![]() 0,001
0,001
Найдем пределы, в которых находится средний вес одного изделия во всей партии товара:
![]()
18,6-0,001=18,599 кг; 18,6+0,001=18,601 кг, следовательно,
18,599 кг<![]() <18,601 кг
<18,601 кг
Вывод: с вероятностью 0,954 можно утверждать, что средний вес одного изделия во всей партии товара находится в пределах от 18,599 кг до 18,601 кг.
Задача № 4
Имеется следующая информация о товарообороте торгового предприятия за 2001–2005 годы:
| Годы | 2001 | 2002 | 2003 | 2004 | 2005 |
| Товарооборот, (млн. руб.) | 40,2 | 48,3 | 54,4 | 60,2 | 64,8 |
1. Для анализа динамики товарооборота торгового предприятия в 2001–2005 гг. определите основные показатели динамики:
1.1. абсолютные приросты, темпы роста и темпы прироста (на цепной и базисной основе);
1.2. средние показатели динамики;
1.3. возможный размер товарооборота в 2008 году (используя средний абсолютный прирост);
Постройте график, характеризующий интенсивность динамики товарооборота. Полученные результаты оформите в виде статистической таблицы.
2. Произведите анализ общей тенденции развития товарооборота:
1. Расчет показателей динамики от года к году (цепные)
Таблица 4.
Наименование показателя |
Формула | 2001 | 2002 | 2003 | 2004 | 2005 |
| Абсолютный прирост, млн. руб. | - | 8,1 | 6,1 | 5,8 | 4,6 | |
| Коэффициент роста | - | 1,2015 | 1,1263 | 1,1066 | 1,0764 | |
| Темп роста, % | - | 120,15 | 112,63 | 110,66 | 107,64 | |
| Темп прироста, % | - | 20,15 | 12,63 | 10,66 | 7,64 |
Расчет показателей динамики от года к году (базисные)
Таблица 5.
| Наименование показателя | Формула | 2001 | 2002 | 2003 | 2004 | 2005 |
| Абсолютный прирост, млн. руб. | 0 | 8,1 | 14,2 | 20 | 24,6 | |
| Коэффициент роста | 1,00 | 1,2015 | 1,3532 | 1,4975 | 1,6119 | |
| Темп роста, % | 100 | 120,15 | 135,32 | 149,75 | 161,19 | |
| Темп прироста, % | - | 20,15 | 35,32 | 49,75 | 61,19 |
Расчет средних показателей динамики
Таблица 6.
| Наименование показателя | Формула | Расчет |
| Средний абсолютный прирост, млн. руб. | ||
| Средний коэффициент роста | 
|
|
| Средний темп роста | ||
| Средний темп прироста, % |
|
Найдем возможный размер товарооборота в 2008 году (используя средний абсолютный прирост):
![]() =
=![]() млн.руб.
млн.руб.
Построим график, характеризующий интенсивность динамики:

2001 2002 2003 2004 2005
Время, годы
Рис. 2.
Таблица 7.
| Годы | Товарооборот, (млн. руб.) | Абсолютный прирост, млн. руб. | Коэффициент роста | Темп роста, % | Темп прироста, % |
||||
| Базисный | Цепной | Базисный | Цепной | Базисный | Цепной | Базисный | Цепной | ||
| 1 | 2 | 2 | 3 | 5 | 6 | 7 | 8 | 9 | |
| 2001 | 40,2 | 0 | - | 1 | - | 100 | - | - | - |
| 2002 | 48,3 | 8,1 | 8,1 | 1,2015 | 1,2015 | 120,15 | 120,15 | 20,15 | 20,15 |
| 2003 | 54,4 | 14,2 | 6,1 | 1,3532 | 1,1263 | 135,32 | 112,63 | 35,32 | 12,63 |
| 2004 | 60,2 | 20 | 5,8 | 1,4975 | 1,1066 | 149,75 | 110,66 | 49,75 | 10,66 |
| 2005 | 64,8 | 24,6 | 4,6 | 1,6119 | 1,0764 | 161,19 | 107,64 | 61,19 | 7,64 |
| Всего | 267,9 | ||||||||
Вывод: Наблюдается рост товарооборота с 2001 по 2005 годы.
2. Произведем анализ общей тенденции развития товарооборота. Для этого составим таблицу:
Таблица 8.
| Год | Товарооборот (млн. руб.), у | t | yt | Теоретический уровень, |
|
| 1 | 2 | 3 | 4 | 5 | 6 |
| 2001 | 40,2 | -2 | 4 | -80,4 | 41,36 |
| 2002 | 48,3 | -1 | 1 | -48,3 | 47,47 |
| 2003 | 54,4 | 0 | 0 | 0 | 53,58 |
| 2004 | 60,2 | 1 | 1 | 60,2 | 59,69 |
| 2005 | 64,8 | 2 | 4 | 129,6 | 65,8 |
| 267,9 | 0 | 10 | 61,1 | 267,9 |
Предположим, что общая тенденция физического объема товарооборота имеет линейную зависимость.
![]() , вычислим коэффициенты а и b методом наименьших квадратов.
, вычислим коэффициенты а и b методом наименьших квадратов.
Вычислим систему уравнений:

Пусть t = 0, тогда
 ,
,
![]() ;
; ![]() .
.
![]() .
.
Фактические и теоретические уровни ряда динамики нанесем на график:

2001 2002 2003 2004 2005
Время, годы
Рис. 3
Вычислим прогнозное значение товарооборота в 2008 г:
![]() млн. руб.
млн. руб.
Вывод: Из графика видно, что данная зависимость достаточно точно показывает общую тенденцию товарооборота.
Задача № 5
Имеются следующие данные о реализации продуктов на рынке города за два периода:
| Продукты | Продано (т) | Модальная цена, (руб. за 1 кг) | ||
| сентябрь | январь | сентябрь | январь | |
| 1 | 2 | 3 | 4 | 5 |
| А | 180 | 142 | 64,40 | 73,87 |
| Б | 375 | 390 | 87,18 | 88,20 |
| В | 245 | 308 | 38,28 | 40,15 |
Определите:
1. Индивидуальные индексы цен и физического объема товарооборота.
2. Общий индекс цен.
3. Общие индексы товарооборота: в фактических и неизменных ценах.
4. Как повлияло изменение цен в январе по сравнению с сентябрем на общий объем выручки от реализации данных продуктов.
5. Покажите взаимосвязь исчисленных индивидуальных и общих индексов.
Сделайте выводы по полученным результатам.
Таблица 9.
| Продукты | Продано (т) | Модальная цена, (руб. за 1 кг). | p0 q0 |
p1 q1 |
р0 q1 |
р1 q0 |
||
сентябрь, q0 |
январь, q1 |
сентябрь, p0 |
январь, р1 |
|||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| А | 180 | 142 | 64,40 | 73,87 | 11592 | 10489,54 | 9144,8 | 13296,6 |
| Б | 375 | 390 | 87,18 | 88,20 | 32692,5 | 34398 | 34000,2 | 33075 |
| В | 245 | 308 | 38,28 | 40,15 | 9378,6 | 12366,2 | 11790,24 | 9836,75 |
| Всего: | 53663,1 | 57253,74 | 54935,24 | 56208,4 | ||||
1. Индивидуальные и общие агрегатные индексы цен.
Для характеристики изменения цен каждого вида продукции исчисляются индивидуальные индексы цен:
![]() .
.
Товар А: ![]() или 114,7 %, т.е. цена увеличилась на 14,7 %.
или 114,7 %, т.е. цена увеличилась на 14,7 %.
Товар Б: ![]() или 101,2 %, т.е. цена увеличилась на 1,2 %.
или 101,2 %, т.е. цена увеличилась на 1,2 %.
Товар В: ![]() или 104,9 %, т.е. цена увеличилась на 4,9 %.
или 104,9 %, т.е. цена увеличилась на 4,9 %.
Среднее изменение цен по всему ассортименту определяется по формуле агрегатного индекса цен:
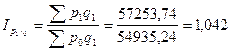 или 104,2 %, т.е. в целом цены на продукцию увеличились на 4,2 %.
или 104,2 %, т.е. в целом цены на продукцию увеличились на 4,2 %.
2. Индивидуальные и общий агрегатный индексы проданного объема продукции.
Вычислим индивидуальные индексы проданного объема продукции:
![]() .
.
Товар А: ![]() или 78,9 %, т.е. объем проданной продукции уменьшился на 21,1 %.
или 78,9 %, т.е. объем проданной продукции уменьшился на 21,1 %.
Товар Б: ![]() или 104 %, т.е. объем проданной продукции увеличился на 4 %.
или 104 %, т.е. объем проданной продукции увеличился на 4 %.
Товар В: ![]() или 125,7 %, т.е. объем проданной продукции увеличился на 25,7 %.
или 125,7 %, т.е. объем проданной продукции увеличился на 25,7 %.
Общий агрегатный индекс проданного объема продукции:
 или 102,4 %, т.е. в целом объем проданной продукции увеличился на 2,4%.
или 102,4 %, т.е. в целом объем проданной продукции увеличился на 2,4%.
3. Индивидуальные и общие агрегатные индексы розничных продаж.
Вычислим индивидуальные индексы розничных продаж:
![]() .
.
Товар А: ![]() или 90,5 %, т.е. товарооборот уменьшился на 9,5 %.
или 90,5 %, т.е. товарооборот уменьшился на 9,5 %.
Товар Б: ![]() или 105,2 %, т.е. товарооборот увеличился на 5,2 %.
или 105,2 %, т.е. товарооборот увеличился на 5,2 %.
Товар В: ![]() или 131,9 %, т.е. товарооборот увеличился на 31,9 %.
или 131,9 %, т.е. товарооборот увеличился на 31,9 %.
Для характеристики розничных продаж в целом исчисляется агрегатный индекс розничных продаж:
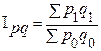 ;
;
![]() или 106,7 %, т.е. в целом объем розничных продаж увеличился на 6,7%.
или 106,7 %, т.е. в целом объем розничных продаж увеличился на 6,7%.
Взаимосвязь индексов розничных продаж, индекса физического объема и индекса цен:
![]()
Вывод: У товара А цена увеличилась на 14,7 %, у товара Б цена увеличилась на 1,2 %, у товара В цена увеличилась на 4,9 %. В целом цены на продукцию увеличились на 4,2 %.
У товара А объем проданной продукции уменьшился на 21,1 %, у товара Б объем проданной продукции увеличился на 4 %, у товара В объем проданной продукции увеличился на 25,7 %. В целом объем проданной продукции увеличился на 2,4%.
У товара А товарооборот уменьшился на 9,5 %, у товара Б товарооборот увеличился на 5,2 %, у товара В товарооборот увеличился на 31,9 %. В целом объем розничных продаж увеличился на 6,7%.
Задача № 6
Имеются следующие данные о продаже товаров торговым предприятием за два периода:
| Товарные группы | Товарооборот в фактических ценах (млн. руб.) | Изменение цен (%) | |
| 1-й период | 2-й период | ||
| 1 | 2 | 3 | 4 |
| А | 17,6 | 32,4 | +160 |
| Б | 12,1 | 18,4 | +180 |
| В | 20,2 | 44,8 | +140 |
| Г | 20,6 | 60,5 | +200 |
На основе приведенных данных определите:
1. Индивидуальные и общие индексы: цен, физического объема товарооборота и товарооборота в фактических ценах.
2. Прирост товарооборота во втором периоде по сравнению с первым периодом (общий и за счет действия отдельных факторов).
Таблица 10.
| Товарныегруппы | Товарооборот в фактических ценах (млн. руб.) | Изменение цен (%) | |||||
| 1-й период, p0 q0 | 2-й период, p1 q1 |
||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| А | 17,6 | 32,4 | +160 | 2,6 | 1,841 | 0,708 | 12,462 |
| Б | 12,1 | 18,4 | +180 | 2,8 | 1,521 | 0,543 | 6,571 |
| В | 20,2 | 44,8 | +140 | 2,4 | 2,218 | 0,924 | 18,667 |
| Г | 20,6 | 60,5 | +200 | 3 | 2,937 | 0,979 | 20,167 |
| Всего: | 70,5 | 156,1 | 57,866 | ||||
Вычислим индивидуальные индексы цен по товарным группам:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Вычислим индивидуальные индексы товарооборота в текущих ценах:
![]() .
.
Товарная группа А: ![]() или 184,1 %, т.е. объем товарооборота в текущих ценах увеличился на 84,1 %.
или 184,1 %, т.е. объем товарооборота в текущих ценах увеличился на 84,1 %.
Товарная группа Б: ![]() или 152,1 %, т.е. объем товарооборота в текущих ценах увеличился на 52,1 %.
или 152,1 %, т.е. объем товарооборота в текущих ценах увеличился на 52,1 %.
Товарная группа В: ![]() или 221,8 %, т.е. объем товарооборота в текущих ценах увеличился на 121,8 %.
или 221,8 %, т.е. объем товарооборота в текущих ценах увеличился на 121,8 %.
Товарная группа Г: ![]() или 293,7 %, т.е. объем товарооборота в текущих ценах увеличился на 193,7 %.
или 293,7 %, т.е. объем товарооборота в текущих ценах увеличился на 193,7 %.
Вычислим индивидуальные индексы физического объема реализации товара:
![]()
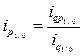
Товарная группа А: ![]() или 70,8 %, т.е. физический объем реализации товара уменьшился на 29,2 %.
или 70,8 %, т.е. физический объем реализации товара уменьшился на 29,2 %.
Товарная группа Б: ![]() или 54,3 %, т.е. физический объем реализации товара уменьшился на 45,7 %.
или 54,3 %, т.е. физический объем реализации товара уменьшился на 45,7 %.
Товарная группа В: ![]() или 92,4 %, т.е. физический объем реализации товара уменьшился на 7,6 %.
или 92,4 %, т.е. физический объем реализации товара уменьшился на 7,6 %.
Товарная группа Г: ![]() или 97,9 %, т.е. физический объем реализации товара уменьшился на 2,1 %.
или 97,9 %, т.е. физический объем реализации товара уменьшился на 2,1 %.
Общий агрегатный индекс проданного объема продукции:
 или 82,1 %, т.е. в целом объем проданной продукции уменьшился на 17,9 %.
или 82,1 %, т.е. в целом объем проданной продукции уменьшился на 17,9 %.
Среднее изменение цен по всему ассортименту определяется по формуле агрегатного индекса цен:
 или 269,8 %, т.е. в целом цены на продукцию увеличились на 169,8 %.
или 269,8 %, т.е. в целом цены на продукцию увеличились на 169,8 %.
2. Для характеристики розничных продаж в целом исчисляется агрегатный индекс розничных продаж:

![]() или 221,4 %, т.е. в целом товарооборот в текущих ценах увеличился на 212,4 %.
или 221,4 %, т.е. в целом товарооборот в текущих ценах увеличился на 212,4 %.
Вывод: У товарной группы А физический объем реализации товара уменьшился на 29,2 %, у товарной группы Б физический объем реализации товара уменьшился на 45,7 %, у товарной группы В физический объем реализации товара уменьшился на 7,6 %, у товарной группы Г физический объем реализации товара уменьшился на 2,1 %.
В целом объем проданной продукции уменьшился на 17,9 %, а цены на продукцию увеличились на 169,8 %.
У товарной группы А объем товарооборота в текущих ценах увеличился на 84,1 %. У товарной группы Б объем товарооборота в текущих ценах увеличился на 52,1 %. У товарной группы В объем товарооборота в текущих ценах увеличился на 121,8 %. У товарной группы Г объем товарооборота в текущих ценах увеличился на 193,7 %.
В текущем периоде товарооборот в фактических ценах возрос по данному ассортименту товаров по сравнению с предыдущим периодом в среднем на 212,4 %.
Задача № 7
Темпы роста выпуска продукции на предприятии в 2001 – 2005 годах составили (в процентах к предыдущим годам):
| Годы | 2001 | 2002 | 2003 | 2004 | 2005 |
| Темп роста (%) | 101,2 | 102,8 | 110,4 | 116,5 | 117,4 |
Известно, что в 2004 году было выпущено продукции на 40,1 млн. рублей.
Определите:
1. Общий прирост выпуска продукции за 2001 – 2005 гг. (%).
2. Среднегодовой темп роста и прироста выпуска продукции.
3. Методом экстраполяции возможный объем выпуска продукции на предприятии в 2007 г.
Составим таблицу:
Таблица 11.
| Годы | Темп роста выпуска продукции, % Yi/Yi-1 |
Выпуск продукции, млн.руб. Yi |
t | yt | Теоретический уровень, |
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2000 | 29,97 | -5 | 25 | -149,85 | 27,07 | |
| 2001 | 101,2 | 30,33 | -3 | 9 | -90,99 | 30,45 |
| 2002 | 102,8 | 31,18 | -1 | 1 | -31,18 | 33,83 |
| 2003 | 110,4 | 34,42 | 1 | 1 | 34,42 | 37,21 |
| 2004 | 116,5 | 40,1 | 3 | 9 | 120,3 | 40,59 |
| 2005 | 117,5 | 47,12 | 5 | 25 | 235,6 | 43,97 |
| Итоги | 213,12 | 0 | 70 | 118,3 | 213,12 |
Yi /Yi-1 = Ti =>Yi-1 = Yi /Ti
Y2003 = Y2004 /T2004 = 40,1/1,165 = 34,42
Y2002 = Y2003 /T2003 = 34,42/1,104 = 31,18
Y2001 = Y2002 /T2002 = 31,18/1,028 = 30,33
Y2000 = Y2001 /T2001 = 30,33/1,012 = 29,97
Y2005 = Y2004 *T2005 = 40,1*1,175 = 47,12
Общий прирост выпуска продукции за 2001-2005 годы:
Общий прирост = Y2005 – Y2000 = 47,12 – 29,97 = 17,15 млн. руб.
В процентах по отношению к выпуску продукции в 2000 году:
Общий прирост, в процентах = 100*17,15/29,97 = 57,22%
| Средний коэффициент роста | 
|
| Средний темп роста | |
| Средний темп прироста, % |
|
Средний коэффициент роста

Средний темп роста = 100*1,095 = 109,5 %
Средний темп прироста = 109,5 – 100 = 9,5%
Предположим, что общая тенденция физического объема товарооборота имеет линейную зависимость.
![]() , вычислим коэффициенты а и b методом наименьших квадратов.
, вычислим коэффициенты а и b методом наименьших квадратов.
Вычислим систему уравнений:

Пусть t = 0, тогда
 ,
,
![]() ;
; ![]() .
.
![]() .
.
Вычислим прогнозное значение выпуска продукции в 2007 г:
![]() млн. руб.
млн. руб.
Вывод: Общий прирост выпуска продукции за 2001 – 2005 гг. составил 57,22%. Среднегодовой темп роста составил 109,5 %, а среднегодовой темп прироста равен 9,5 %. Возможный объем выпуска продукции на предприятии в 2007 г. составил 50,73 млн.руб.
Задача № 8
По исходным данным задачи № 1 постройте уравнение регрессии между объемом товарооборота и размером издержек обращения магазинов №№ 1 ... 18.
Фактические и теоретические уровни нанесите на график корреляционного поля. Сделайте выводы.
Для удобства вычислений составим таблицу:
Таблица 12.
| Номер магазина | Товарооборот (млн. руб.), х | Издержки обращения (млн. руб.), у | |||
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 148 | 20,4 | 21904 | 416,16 | 3019,2 |
| 2 | 180 | 19,2 | 32400 | 368,64 | 3456 |
| 3 | 132 | 18,9 | 17424 | 357,21 | 2494,8 |
| 4 | 314 | 28,6 | 98596 | 817,96 | 8980,4 |
| 5 | 235 | 24,8 | 55225 | 615,04 | 5828 |
| 6 | 80 | 9,2 | 6400 | 84,64 | 736 |
| 7 | 113 | 10,9 | 12769 | 118,81 | 1231,7 |
| 8 | 300 | 30,1 | 90000 | 906,01 | 9030 |
| 9 | 142 | 16,7 | 20164 | 278,89 | 2371,4 |
| 10 | 280 | 46,8 | 78400 | 2190,24 | 13104 |
| 11 | 156 | 30,4 | 24336 | 924,16 | 4742,4 |
| 12 | 213 | 28,1 | 45369 | 789,61 | 5985,3 |
| 13 | 298 | 38,5 | 88804 | 1482,25 | 11473 |
| 14 | 242 | 34,2 | 58564 | 1169,64 | 8276,4 |
| 15 | 130 | 20,1 | 16900 | 404,01 | 2613 |
| 16 | 184 | 22,3 | 33856 | 497,29 | 4103,2 |
| 17 | 96 | 9,8 | 9216 | 96,04 | 940,8 |
| 18 | 304 | 38,7 | 92416 | 1497,69 | 11764,8 |
| Всего: | 3547 | 447,7 | 802743 | 13014,3 | 100150 |
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]()
Итак, уравнение регрессии: ![]() ;
;
![]() ;
; ![]() - уравнение регрессии между товарооборотом и стоимостью основных фондов.
- уравнение регрессии между товарооборотом и стоимостью основных фондов.
Фактические и теоретические уровни перенесем на график корреляционного поля:

Рис. 4.
Вывод: Уравнение регрессии достаточно хорошо отображает взаимосвязь между товарооборотом и стоимостью основных фондов.
ПРИЛОЖЕНИЕ К РЕШЕНИЮ ЗАДАЧ ПО СТАТИСТИКЕ
ДЛЯ ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ
| Номер магазина | Товарооборот (млн. руб.) | Издержки обращения (млн. руб.) | Стоимость основных фондов (средне-годовая) (млн. руб.) | Численность продавцов (чел.) | Торговая площадь (м2 ) |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 148 | 20,4 | 5,3 | 64 | 1070 |
| 2 | 180 | 19,2 | 4,2 | 85 | 1360 |
| 3 | 132 | 18,9 | 4,7 | 92 | 1140 |
| 4 | 314 | 28,6 | 7,3 | 130 | 1848 |
| 5 | 235 | 24,8 | 7,8 | 132 | 1335 |
| 6 | 80 | 9,2 | 2,2 | 41 | 946 |
| 7 | 113 | 10,9 | 3,2 | 40 | 1435 |
| 8 | 300 | 30,1 | 6,8 | 184 | 1820 |
| 9 | 142 | 16,7 | 5,7 | 50 | 1256 |
| 10 | 280 | 46,8 | 6,3 | 105 | 1353 |
| 11 | 156 | 30,4 | 5,7 | 57 | 1138 |
| 12 | 213 | 28,1 | 5,0 | 100 | 1216 |
| 13 | 298 | 38,5 | 6,7 | 112 | 1352 |
| 14 | 242 | 34,2 | 6,5 | 106 | 1445 |
| 15 | 130 | 20,1 | 4,8 | 62 | 1246 |
| 16 | 184 | 22,3 | 6,8 | 60 | 1332 |
| 17 | 96 | 9,8 | 3,0 | 34 | 680 |
| 18 | 304 | 38,7 | 6,9 | 109 | 1435 |
| 19 | 95 | 11,7 | 2,8 | 38 | 582 |
| 20 | 352 | 40,1 | 8,3 | 115 | 1677 |
| 21 | 101 | 13,6 | 3,0 | 40 | 990 |
| 22 | 148 | 21,6 | 4,1 | 50 | 1354 |
| 23 | 74 | 9,2 | 2,2 | 30 | 678 |
| 24 | 135 | 20,2 | 4,6 | 52 | 1380 |
| 25 | 320 | 40,0 | 7,1 | 140 | 1840 |
| 26 | 155 | 22,4 | 5,6 | 50 | 1442 |
| 27 | 262 | 29,1 | 6,0 | 102 | 1720 |
| 28 | 138 | 20,6 | 4,8 | 46 | 1520 |
| 29 | 216 | 28,4 | 8,1 | 96 | 1673 |
Список литературы
1. Галина В.А. Материалы лекций по курсу «Статистика».
2. Общая теория статистики: Статистическая методология в изучении коммерческой деятельности: Учебник / Под ред. О.Э. Башиной, А.А. Спирина. – 5-е изд., доп. и перераб. – М.: Финансы и статистика, 2007;
3. Практикум по теории статистики: Учеб. пособие / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 1999.