| Скачать .docx | Скачать .pdf |
Реферат: Группировка 30 коммерческих банков по величине прибыли
ЗАДАНИЕ 1
1. По данным таблицы произведите группировку 30 коммерческих банков по величине прибыли, образовав 6 групп с заданными интервалами:
а) до 100; б) 100-200; в) 300-500; д) 500-700; е) 700 и более
Список крупнейших банков России по размеру капитала
на 01.01.97г., млрд. руб.
Таблица 1
| ранг |
название банка |
город |
кредит-ные вложе-ния |
объем вложе-ний в ценные бумаги |
при-быль |
| 1 |
национальный резервный банк |
Москва |
2439 |
4994 |
645 |
| 2 |
ОНЭКСИМбанк |
Москва |
15581 |
1547 |
266 |
| 3 |
Международная финансовая компания |
Москва |
7612 |
510 |
512 |
| 4 |
Инкомбанк |
Москва |
9432 |
2975 |
744 |
| 5 |
ТОКОбанк |
Москва |
4318 |
852 |
282 |
| 6 |
Империал |
Москва |
5398 |
654 |
429 |
| 7 |
Автобанк |
Москва |
3900 |
1684 |
913 |
| 8 |
Международный московский банк |
Москва |
5077 |
1173 |
290 |
| 9 |
СБС |
Москва |
3256 |
4556 |
175 |
| 10 |
Международный промышленный банк |
Москва |
3419 |
597 |
18 |
| 11 |
Башкредитбанк |
Уфа |
778 |
551 |
417 |
| 12 |
Российский кредит |
Москва |
6019 |
1429 |
367 |
| 13 |
Мосбизнесбанк |
Москва |
4899 |
1837 |
481 |
| 14 |
МЕНАТЕП |
Москва |
9035 |
786 |
146 |
| 15 |
Московский индустриальный банк |
Москва |
1742 |
469 |
365 |
| 16 |
Промстройбанк России |
Москва |
2890 |
1115 |
239 |
| 17 |
Промышленно-строительный банк |
С-Петербург |
1600 |
991 |
306 |
| 18 |
Уникомбанк |
Москва |
1605 |
439 |
57 |
| 19 |
Газпромбанк |
Москва |
1764 |
673 |
265 |
| 20 |
Возрождение |
Москва |
2236 |
532 |
158 |
| 21 |
Мост-банк |
Москва |
4423 |
2020 |
129 |
| 22 |
Московский деловой мир |
Москва |
981 |
543 |
340 |
| 23 |
Межкомбанк |
Москва |
2004 |
1040 |
167 |
| 24 |
Нефтехимбанк |
Москва |
1216 |
838 |
41 |
| 25 |
Ситибанк Т/О |
Москва |
1490 |
1041 |
258 |
| 26 |
Ланта-банк |
Москва |
545 |
44 |
35 |
| 27 |
Альба-альянс |
Москва |
147 |
426 |
298 |
| 28 |
ИнтерТЭКбанк |
Москва |
1039 |
167 |
57 |
| 29 |
Мосстройэкономбанк |
Москва |
1091 |
27 |
221 |
| 30 |
Росэстбанк |
Тольятти |
511 |
195 |
243 |
По каждой группе рассчитайте:
- средний размер прибыли;
- средний размер кредитных вложений;
- средний объем вложений в ценные бумаги.
Результаты оформите в аналитической таблице. Сделайте выводы.
2. По данным таблицы определите модальное и медианное значение прибыли.
3. По показателю размер кредитных вложений рассчитайте:
- общую дисперсию по правилу сложения дисперсии;
- общую дисперсию любым другим способом;
- эмпирическое корреляционное отношение.
Сделайте выводы.
1. Определим границы интервалов и внесем в промежуточную группировочную таблицу (таблица 2)
Предварительная группировка банков по величине прибыли.
Таблица 2
| Группа банков по величине прибыли |
название банка |
Номер банка |
кредит-ные вложе-ния |
объем вложе-ний в ценные бумаги |
при-быль |
| До 100 |
Международный промышленный банк |
10 |
3419 |
597 |
18 |
| Ланта-банк |
26 |
545 |
44 |
35 |
|
| Нефтехимбанк |
24 |
1216 |
838 |
41 |
|
| Уникомбанк |
18 |
1605 |
439 |
57 |
|
| ИнтерТЭКбанк |
28 |
1039 |
167 |
57 |
|
| 100-200 |
Мост-банк |
21 |
4423 |
2020 |
129 |
| МЕНАТЕП |
14 |
9035 |
786 |
146 |
|
| Возрождение |
20 |
2236 |
532 |
158 |
|
| Межкомбанк |
23 |
2004 |
1040 |
167 |
|
| СБС |
9 |
3256 |
4556 |
175 |
|
| 200-300 |
Мосстройэкономбанк |
29 |
1091 |
27 |
221 |
| Промстройбанк России |
16 |
2890 |
1115 |
239 |
|
| Росэстбанк |
30 |
511 |
195 |
243 |
|
| Ситибанк Т/О |
25 |
1490 |
1041 |
258 |
|
| Газпромбанк |
19 |
1764 |
673 |
265 |
|
| ОНЭКСИМбанк |
2 |
15581 |
1547 |
266 |
|
| ТОКОбанк |
5 |
4318 |
852 |
282 |
|
| Международный московский банк |
8 |
5077 |
1173 |
290 |
|
| Альба-альянс |
27 |
147 |
426 |
298 |
|
| 300-500 |
Промышленно-строительный банк |
17 |
1600 |
991 |
306 |
| Московский деловой мир |
22 |
981 |
543 |
340 |
|
| Московский индустриальный банк |
15 |
1742 |
469 |
365 |
|
| Российский кредит |
12 |
6019 |
1429 |
367 |
|
| Башкредитбанк |
11 |
778 |
551 |
417 |
|
| Империал |
6 |
5398 |
654 |
429 |
|
| Мосбизнесбанк |
13 |
4899 |
1837 |
481 |
|
| 500-700 |
Международная финансовая компания |
3 |
7612 |
510 |
512 |
| национальный резервный банк |
1 |
2439 |
4994 |
645 |
|
| 700 и более |
Инкомбанк |
4 |
9432 |
2975 |
744 |
| Автобанк |
7 |
3900 |
1684 |
913 |
По данным предварительной группировки рассчитаем средние по группе значения показателей, определим численность групп и результаты занесем в итоговую таблицу (таблица 3).
Аналитическая группировка банков
Таблица 3
| Группа банков по величине прибыли |
Число банков в группе |
Средний размер кредитных вложений, млрд.руб. |
Средний размер вложений в ценные бумаги, млрд.руб. |
Средний размер прибыли, млрд.руб. |
| До 100 |
5 |
1564,8 |
417 |
41,6 |
| 100-200 |
5 |
4190,8 |
1786,8 |
155 |
| 200-300 |
9 |
3652,1 |
783,2 |
262,4 |
| 300-500 |
7 |
3059,6 |
924,8 |
386,4 |
| 500-700 |
2 |
5025,5 |
2752 |
578,5 |
| 700 и более |
2 |
6666 |
2729,5 |
828,5 |
| Итого |
30 |
3548,2 |
1498,9 |
375,4 |
По итогам группировки можно сделать вывод о том, что связь между прибылью и вложениями в кредиты и ценные бумаги есть. Сравнивая колонки 3,4 и 5: с увеличением объема вложений в ценные бумаги и кредиты средний размер прибыли увеличивается.
2. Определим модальное и медианное значение прибыли.
Рассчитаем моду по интервальному ряду распределения (таблица 4)
Ряд распределения по величине прибыли
Таблица 4
| Группа банков по величине прибыли |
Число банков, fi |
Накопленные частоты, si |
| До 100 |
5 |
5 |
| 100-200 |
5 |
10 |
| 200-300 |
9 |
19 |
| 300-500 |
7 |
26 |
| 500-700 |
2 |
28 |
| 700 и более |
2 |
30 |
| Итого |
30 |
x |
По данным таблицы 4 видно, что наиболее часто встречаются банки со средним размером прибыли от 200 до 300 млрд. руб., т.е. наибольшему числу банков (9) соответствует интервал 200-300. Данный интервал и будет модальным. Расчет моды проведем по формуле:
![]() ,
,
Где x мо – мода;
х о -верхняя граница модального интервала;
h – величина итервала;
f мо , f мо-1, f мо+1 - частоты модального, предмодального, послемодального итервала.
![]()
![]()
x мо = 200+100*0,67≈267 (млрд.руб.)
В данной совокупности наиболее часто встречаются банки со средним размером прибыли 267 млрд. руб.
Медиана определяется по формуле:
 ,
,
где Ме -медиана;
Х о - верхняя граница медианного интервала;
h - величина интервала;
N = ∑ f i - общая численность;
S ме-1 – накопленные частоты предмедианного интервала;
f ме - частота медианного интервала.
Последняя накопленная частота – 30. Медианный интервал должен содержать единицу совокупности, которая делит всю совокупность из 30 банков пополам (30/2=15). Значит, в качестве медианного в расчете берем интервал 200-300, так как средний размер прибыли до 267 млрд.руб. имеют 9 банков из данной совокупности. Интервалу 200-300 соответствует накопленная частота 19 – именно в данном интервале находится значение признака, которое разделит совокупность пополам: 15 банков будут иметь средний размер прибыли ниже медианного и 15 банков - выше медианного.
Произведем вычисление медианы:
![]()
В данной совокупности половина банков имеют прибыль ниже 256 млрд. руб.
3. По показателю размер кредитных вложений рассчитаем:
- общую дисперсию по правилу сложения дисперсии
Правило сложения дисперсии заключается в том, что общая дисперсия равна сумме межгрупповой и средней из внутригрупповых дисперсий:
![]() ,
,
Где δ² -межгрупповая дисперсия;
![]() - средняя из внутригрупповых дисперсий.
- средняя из внутригрупповых дисперсий.
Определим межгрупповую дисперсию
 ,
,
Где ![]() - средняя арифметическая:
- средняя арифметическая:
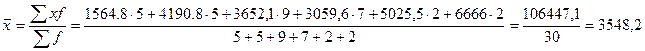
![]() +
+
+![]()
Средняя из внутригрупповых дисперсий определяется в два этапа по формуле:
 ,
,
Где ni – количество i -й группы
На втором этапе:

![]() =
=
= 975558,5
![]()
= 6610258,9
![]() +
+
+![]() =
=
= 20256031,2
![]() +
+
+ ![]() = 4426276,7
= 4426276,7
![]() = 6689982,3
= 6689982,3
![]() = 7650756
= 7650756
![]() =
=
= 9329959,4
![]()
Рассчитаем общую дисперсию другим способом:
![]()
![]() +
+
+ ![]() +
+
+![]() +
+
+![]() +
+
+![]() +
+
+![]() =
=
= 10905119,5
Эмпирическое корреляционное отношение определяется по формуле:
![]()
![]()
Это значит, что 14,5% вариации кредитных вложений объясняется признаком, положенным в основу группировки, а 85,5% вариации результативного признака – прочими факторами, которые не учтены в группировке.
![]()
Значение эмпирического корреляционного отношения 0,38 – значит связь умеренная.
ЗАДАНИЕ 2.
Имеются следующие данные по району за 1999 год (условные):
1. На начало года численность трудоспособного населения рабочего возраста составила 320 тыс. чел., работающих лиц пенсионного возраста – 15 тыс. чел., работающих подростков до 16 лет – 5тыс. чел.
2. В течение года вступило в рабочий возраст 20 тыс. чел., 0,5 тыс. чел. из них нетрудоспособны; прибыло из других районов трудоспособных лиц 2,5 тыс. чел. Выбыло по естественным причинам 15 тыс. чел.; в другие районы – 10 тыс. чел. трудоспособного населения.
Определите:
1. Численность трудовых ресурсов на начало и конец года.
2. Абсолютные и относительные показатели воспроизводства трудовых ресурсов.
1. Определим численность трудовых ресурсов на начало и конец года:
На начало года:
S н.г. = 320+15+5=340 (тыс.чел.)
S кон . г . = 340+20-0,5+2,5-15-10=337 (тыс.чел.)
2. Абсолютные и относительные показатели воспроизводства трудовых ресурсов:
Рассмотрим абсолютные показатели. К ним относятся естественное пополнение, естественное выбытие
Естественное пополнение N:
- работающие пенсионеры = 15 (тыс. чел.)
- вступившие в рабочий возраст = 20 (тыс. чел.)
- работающие подростки = 5 (тыс. чел.)
N=15+20+5=40 (тыс.чел.)
Естественное выбытие М:
- нетрудоспособные = 0,5 (тыс. чел.)
- естественные причины = 15 (тыс. чел.)
М=0,5+15=15,5 (тыс. чел.)
Расчет относительных показателей – это отношения абсолютных размеров воспроизводства к средней численности трудовых ресурсов за данный период в расчете на 1000 чел.
Средняя численность трудовых ресурсов ![]() = 337 чел. на 1000 чел.
= 337 чел. на 1000 чел.
Коэффициент естественного прироста (относительный показатель):
![]()
ЗАДАНИЕ 3.
Имеются следующие данные по предприятию:
Таблица 5
| Номер цеха |
Затраты на производство продукции, тыс.руб. |
Изменение себестоимости единицы продукции в отчетном периоде по сравнению с базисным, % |
| 1 |
1200 |
+5,0 |
| 2 |
1800 |
-3,5 |
| 3 |
2800 |
-3,0 |
| 4 |
2500 |
- |
Определите в целом по предприятию:
1. Изменение себестоимости единицы продукции.
2. Изменение общих затрат на производство продукции, если физический объем производства увеличился на 8%.
3. Сумму экономии в связи с изменением себестоимости единицы продукции.
1). Рассчитаем изменение себестоимости единицы продукции по формуле:
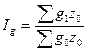
![]()
(1-0,9895)х100%=1,05%
Себестоимость единицы продукции в целом по предприятию уменьшается на 1,05%
2). 8%=8/100=0,08
Физический объем производства увеличился на 8% => 1+0,08=1,08
Изменение общих затрат:
(1200+1800+2800+2500)х1,08=8964 (тыс. руб.)
При увеличении физического объема производства на 8%, объем затрат составляет 8964 (тыс. руб.)
3). Затраты при уменьшении себестоимости = 8300х0,9895= 8212,82 (тыс. руб.)
В связи с изменениями себестоимости, сумма экономии равна
8300 – 8212,85 = 87,15 (тыс. руб.)
ЗАДАНИЕ 4.
Имеются следующие данные по 3 рынкам города о продаже яблок:
Таблица 6
| Номер рынка |
Продано яблок, тыс.р. |
Цена 1 кг. яблок, р. |
||
| Июнь |
Август |
Июнь |
Август |
|
| 1 |
2500 |
3000 |
35 |
30 |
| 2 |
1000 |
1200 |
32 |
25 |
| 3 |
1600 |
2000 |
34 |
30 |
Определите изменение средней цены на яблоки по 3 рынкам города всего и в т.ч. за счет:
- изменения цены на каждом рынке города;
- изменения структуры продаж.
Средние затраты рассчитаем при помощи арифметической взвешенной, затем найдем индекс переменного состава:
![]()
![]()
![]()
![]()
Таким образом, средняя цена на яблоки по трем рынкам города в целом изменилась на 15%
Определим изменение цены на каждом рынке города :
1 рынок: ![]() на 1-м рынке цена уменьшилась на 14%
на 1-м рынке цена уменьшилась на 14%
2 рынок: ![]() на 2-м рынке цена уменьшилась на 22%
на 2-м рынке цена уменьшилась на 22%
3 рынок: ![]() на 3-м рынке цена уменьшилась на 12%
на 3-м рынке цена уменьшилась на 12%
Изменение структуры продаж определим по формуле ()

![]() 0,99≈1
0,99≈1
За изучаемый период структура продаж практически не изменилась, поэтому изменение средней цены произошло целиком за счет изменения цены на яблоки на каждом рынке.
ЗАДАНИЕ 5.
Имеются следующие данные об изменении физического объема ВВП за период с 1990 г. (1990=100%):
Таблица 7
| Показатели |
1991 |
1992 |
1993 |
1994 |
1995 |
| Индекс физического объема |
95,0 |
81,2 |
74,2 |
64,7 |
62,2 |
Определите, как в среднем ежегодно изменяется физический объем ВВП в указанном периоде. Исчислите цепные темпы изменения ВВП (в сопоставимых ценах).
Изменение физического объема ВВП за указанный период
Таблица 8
| Показатели |
Изменение физического ВВП |
| 1991 |
|
| 1992 |
|
| 1993 |
|
| 1994 |
|
| 1995 |
|
Для характеристики изменения физического объема ВВП в указанном периоде используются следующие цепные показатели:
- абсолютный прирост; ![]()
- темпы роста; ![]()
- темпы прироста; ![]()
- абсолютное значение 1% прироста. ![]()
На основании имеющихся данных рассчитаем показатели, оформив результаты расчетов в таблицу (таблица 9)
Динамика изменения физического объема ВВП
Таблица 9
| Год |
Индекс физического объема |
Абс.прирост ∆ |
Темп роста % |
Темп прироста % |
Абс. знач А |
| 1990 |
100 |
- |
- |
- |
- |
| 1991 |
95,0 |
-5 |
95 |
5 |
10 |
| 1992 |
81,2 |
-13,7 |
85,5 |
-14,4 |
9,5 |
| 1993 |
74,2 |
-7 |
91,4 |
-8,6 |
8,1 |
| 1994 |
64,7 |
-9,5 |
87,2 |
-12,8 |
7,4 |
| 1995 |
62,2 |
-2,5 |
96,1 |
-3,9 |
6,5 |
Средний уровень ряда рассчитывается по формуле средней арифметической простой:
![]()
![]()
![]()
![]() 0,796
0,796
![]() или (20,4%)
или (20,4%)
На основании рассчитанных показателей можно сделать вывод, что наблюдается общая тенденция к снижению физического объема ВВП.
ЗАДАНИЕ 6.
Имеются следующие данные о грузообороте предприятий транспорта и перевозке грузов предприятиями транспорта за 1986-1997 гг. в одном из регионов:
Таблица 10
| Годы |
Грузооборот предприятий транспорта, млрд. ткм |
Перевозка грузов предприятиями транспорта, млн.т |
| 1986 |
280 |
285 |
| 1987 |
304 |
283 |
| 1988 |
270 |
321 |
| 1989 |
305 |
302 |
| 1990 |
301 |
316 |
| 1991 |
307 |
359 |
| 1992 |
296 |
334 |
| 1993 |
299 |
348 |
| 1994 |
296 |
333 |
| 1995 |
269 |
358 |
| 1996 |
310 |
305 |
| 1997 |
286 |
297 |
Для изучения связи между этими рядами произведите:
1. выравнивание рядов динамики по уравнению прямой;
2. вычислите коэффициент корреляции;
3. рассчитайте прогнозные значения грузооборота на 3 года вперед.
Сделайте выводы.
Расчет параметров
Таблица 11
| Годы |
Грузооборот предприятий транспорта, млрд. ткм x |
Перевозка грузов предприятиями транспорта, млн.т y |
|
|
|
|
| 1986 |
280 |
285 |
78400 |
81225 |
79800 |
322,42 |
| 1987 |
304 |
283 |
92416 |
80089 |
86032 |
317,62 |
| 1988 |
270 |
321 |
72900 |
103041 |
86670 |
324,42 |
| 1989 |
305 |
302 |
93025 |
91204 |
92110 |
317,42 |
| 1990 |
301 |
316 |
90601 |
99856 |
95116 |
318,22 |
| 1991 |
307 |
359 |
94249 |
128881 |
110213 |
317,02 |
| 1992 |
296 |
334 |
87616 |
111556 |
98864 |
319,22 |
| 1993 |
299 |
348 |
89401 |
121104 |
104052 |
318,62 |
| 1994 |
296 |
333 |
87616 |
110889 |
98568 |
319,22 |
| 1995 |
269 |
358 |
72361 |
128164 |
96302 |
324,62 |
| 1996 |
310 |
305 |
96100 |
93025 |
94550 |
316,42 |
| 1997 |
286 |
297 |
81796 |
88209 |
84942 |
321,22 |
| итого |
3523 |
3841 |
1036481 |
1237243 |
1127219 |
- |
1). Выравнивание рядов динамики по уравнению прямой.
Определим параметры уравнения по приведенным формулам:


![]()
![]() ≈-0,2
≈-0,2
Запишем уравнение прямой:
![]()
На основании полученного уравнения рассчитаем теоретические уровни признака y . Результаты расчетов занесем в таблицу (таблица 11). Проанализируем параметры: чаще всего параметр a не имеет экономической интерпретации; параметр b –сила связи, т.е. увеличение грузооборота за год в среднем приводит к уменьшению перевозки грузов на 0,2 млн.т.
2). Коэффициент корреляции рассчитаем по формуле К. Пирсона:

![]()
Так как r=-0,105, тогда можно утверждать, что связь между рядами практически отсутствует.
3). Прогнозные значения грузооборота на 3 года вперед
b =0,2 – сила связи =>грузооборот на 3 года вперед приведет в среднем к изменениям на 0,6 млрд.ткм.
0,2х3=0,6
ЗАДАНИЕ 7.
Имеются следующие данные по группе предприятий района:
Таблица 12
| Предприятие |
Стоимость основных производственных фондов, млн.руб. |
Фондоотдача (выпуск продукции на 1 руб. основных производственных фондов), руб. |
Производительность труда рабочих, тыс. руб. |
Фондовооруженность труда рабочих, тыс. руб. |
| 1 |
21,0 |
1,2 |
11,0 |
9,5 |
| 2 |
12,5 |
1,0 |
7,1 |
7,3 |
| 3 |
17,4 |
0,9 |
6,8 |
8,4 |
Определите по предприятиям района среднее значение:
1. стоимости основных производственных фондов на одно предприятие;
2. фондоотдачи;
3. производительности труда;
4. фондовооруженности труда.
1). Определим среднее значение стоимости основных производсвенных фондов на одно предприятие
![]() ( млн. руб.)
( млн. руб.)
2). Среднее значение фондоотдачи
![]() (руб.)
(руб.)
3). Среднее значение производительности труда
![]() (тыс. руб.)
(тыс. руб.)
4). Среднее значение фондовооруженности труда
![]() (тыс. руб.)
(тыс. руб.)
ЗАДАНИЕ 8
С целью определения средних затрат времени при поездках на работу населением города планируется выборочное наблюдение на основе случайного повторного отбора. Сколько людей должно быть обследовано, чтобы с вероятностью 0,954 ошибка выборочной средней не превышала 1 мин. При среднем квадратическом отклонении 15 мин.
Определяем необходимую численность выборки
![]()
По условию задачи
P=0.954 => t=2
σ =15
M=1
∆ = tM => ∆ = 2 x 1= 2
![]() (чел.)
(чел.)
Значит, 225 человек должно быть обследовано.
ЗАДАНИЕ 9
Имеются следующие данные о среднедушевых доходах и расходах на продукты питания по совокупности семей в базисном и отчетном периодах:
Таблица 13
| Показатель |
Базисный период |
Отчетный период |
| Среднедушевой доход за год, т.руб. Расходы на продукты питания, т.руб. |
40 28 |
45 33,5 |
Определите коэффициент эластичности расходов на питание в зависимости от роста дохода.
![]()
Где у0 , у1 – расходы на продукты питания соответственно в базисном и отчетном периоде;
х 0 , х 1 – среднедушевой доход соответственно за базисный и отчетный период.
![]()
![]()
![]()
ЗАДАНИЕ 10
Номинальные среднедушевые доходы населения одного из регионов составили в текущем периоде 2500 руб., за предыдущий период – 2100 руб.; доля налоговых платежей увеличилась с 20 до 22% соответственно. Цены выросли на 25%.
Как изменились реальные доходы населения.
Согласно условию:
![]()
![]()
![]()
![]()
![]()
![]()
Тогда,
![]()
подставляя значения, получим
![]()
![]()
![]()
![]()
![]()
Реальные доходы населения снизились на 13%
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Статистика: учеб. пособие для дистанционного обучения и самостоятельной работы / С.В. Чесных.- Новосибирск: СибАГС, 2005.-328с.