| Скачать .docx | Скачать .pdf |
Курсовая работа: Роль моделирования при работе над задачей в 5 классе
ГОУ СПО «Кунгурское педагогическое училище»
Роль моделирования при работе над задачей в 5 классе
Курсовая работа по методике математики
специальность: 050201 математика
группа: М – 41 отделение: очное
преподаватель методики математики
Оглавление
Введение.......................................................................................................... 3
Теоретические основы моделирования.......................................................... 5
Понятие модели и моделирования.............................................................. 5
Моделирование в решении текстовых задач............................................... 10
Задачи на встречное движение двух тел................................................... 17
Задачи на движение двух тел в одном направлении................................ 17
Задачи на движение двух тел в противоположных направлениях.......... 18
Использование моделирования при работе над задачами на движение в 5 классе........................................................................................................................ 21
Заключение.................................................................................................... 39
Список литературы....................................................................................... 40
Приложение 1................................................................................................ 42
Введение
Решению текстовых задач отводится достаточно много времени в курсе математики. В ходе работы над задачами педагог раскрывает связи между данными и искомыми величинами, отношения, заданные в условии.
Учебная деятельность при решении задач складывается из умственных действий и осуществляется эффективно, если первоначально она происходит на основе внешних материальных действий с предметами, а затем превращается во внутренние процессы.
Таким образом, действия первоначально целенаправленно отрабатываются в плане внешних операций с вещами, а затем эти действия только представляются и проговариваются и, наконец, действия сворачиваются и уходят во внутренний план.
Как правило, в процессе анализа задачи учитель, а, следовательно, и ученики используют лишь различные виды краткой записи задачи или готовые схемы. Создание модели на глазах у детей или самими учащимися в процессе решения задачи считается очень важным.
«Рисунки, схемы, чертежи не только помогают учащимся в сознательном выявлении скрытых зависимостей между величинами, но и побуждают активно мыслить, искать наиболее рациональные пути решения задач, помогают не только усваивать знания, но и овладевать умением применять их. Эти условия необходимы для того, чтобы обучение носило развивающий характер.»[10, 7]
Графические изображения, используемые для постановки познавательных задач, наглядно представляя соотношения между данными и искомыми величинами, помогают ученикам схватить смысл проблемной ситуации, а затем и найти возможный путь решения.
Главное для каждого ученика на этом этапе – понять задачу, то есть уяснить, о чем эта задача, что в ней известно, что нужно узнать, как связаны между собой данные, каковы отношения между данными и искомыми параметрами. Для этого следует применять моделирование и учить этому детей.
Целью данной курсовой работы является разработка системы приемов моделирования.
Задачи:
1) познакомиться с понятиями «модель» и «моделирование»;
2) рассмотреть разные виды моделей, включить их в практическую работу с детьми;
3) изучить теоретические, методические источники по данному вопросу;
4) систематизировать приемы моделирования;
5) разработать конспекты уроков математики, провести и проанализировать их.
Объект исследования: учебная деятельность пятиклассников на уроках математики.
Предмет: процесс формирования у пятиклассников умений решать текстовые задачи, используя модели.
Контингент: учащиеся 5 классов лицея № 1 города Кунгура.
Гипотеза данной курсовой работы: использование моделирования влияет на формирование умения решать задачи.
Обучение математике требует развития у детей самостоятельности в решении текстовых задач. Каждый ученик должен уметь кратко записывать условие задачи, иллюстрируя ее с помощью рисунка, схемы, чертежа и других видов моделей, обосновывать каждый шаг в анализе задачи и ее решении, проверять правильность решения.
Таким образом, моделирование – это один из ведущих методов обучения решению задач и важное средство познания действительности.
Теоретические основы моделирования
Понятие модели и моделирования
В науке широко используется метод моделирования. Он заключается в том, что для исследования какого-либо объекта или явления выбирают или строят другой объект, в каком-то отношении, подобный исследуемому. Построенный или выбранный объект изучают и с его помощью решают исследование задачи, а затем результаты решения этих задач переносят на первоначальные явления или объект.
Под моделью (от лат. modulus – мера, образец, норма) понимают такой материальный или мысленно представляемый объект, который в процессе познания (изучения) замещает объект – оригинал, сохраняя некоторые важные для данного исследования типичные черты. Процесс построения и использования модели, называется моделированием.
Во всех науках модели выступают, как мощное орудие познания.
Например:
1. Люди издавна интересуются, как устроена наша Вселенная. Этот интерес не только познавательный, но и сугубо практический, так как люди хотели научиться предсказывать периодические явления, связанные с устройством Вселенной, такие, как: затмение солнца и луны, наступление времен года.
Для решения этих задач, ученые строили свои представления о Вселенной в виде схемы картины мира, в которой объекты планеты солнце и звезды, планеты, земля и луна изображались точками, движущимся по каким-то кривым – траекториям их движения. Таковы, например, схемы, построенные Птолемеем, в которых центральное место занимала наша Земля, или схема Коперника, в которой центральное место занимало Солнце.
С помощью этих схем ученые решали задачи предсказания отдельных астрономических явлений. Эти схемы или картины мира – суть модели Вселенной, а метод исследования Вселенной, нахождение законов и решения задач, связанных с помощью этих моделей, является методом моделирования.
2. Люди издавна интересуются, как устроены они сами, как функционирует человеческий организм. Но исследовать эти вопросы на живом человеческом организме очень трудно. Ибо такое изучение до появления особых приборов было связано с гибелью этого организма. Тогда ученые стали исследовать устройство человеческого организма на подобных его организму животных. Изучение организма животных, их функционирование помогло установить многие важнейшие закономерности функционирования человеческого организма.
В этих исследованиях организмы животных выступали в качестве модели человеческого организма, а при этом метод есть моделирования.
В математике широко используется метод моделирования при решении задач.
Математической моделью можно назвать специальное описание (часто приближенное) некоторой проблемы, ситуации, которое дает возможность в процессе ее анализа применять формально – логический аппарат математики. При математическом моделировании имеем дело с теоретической копией, которая в математической форме выражает основные закономерности, свойства изучаемого объекта.
В процессе математического моделирования выделяют три этапа:
1. Формализация – перевод предложенной задачи (ситуации) на язык математической теории (построение математической модели задачи).
2. Решение задачи в рамках математической теории (говорят: решение внутри модели).
3.Перевод результата математического решения задачи на тот язык, на котором была сформулирована исходная задача (интерпретация решения).
Чаще всего математическая модель представляет собой несколько упрощенную схему (описание) оригинала, а значит, обладает определенным уровнем погрешности.
Одна и та же модель может описывать различные процессы, объекты, поэтому результаты внутримодельного исследования одного явления зачастую могут быть перенесены на другое. В этом состоит одно из основных достоинств математического моделирования.
Математика не только создала разнообразные внутренние модели алгебры, геометрии, функции комплексного переменного, дифференциальных уравнений и т.д., но и помогла естествознанию построить математические модели механики, электродинамики, термодинамики, химической кинетики, микромира, пространства – времени и тяготения, вероятностей передачи сообщений, управления, логического вывода.
Созданием моделей математика часто опережала потребности естествознания и техники.
Реализация универсального математического метода познания есть основная цель и задача современной математики. Она включает, в первую очередь, построение новых, неведомых математических моделей, в частности в биологии, для познания жизни и деятельности мозга, микромира, новых, фантастических технологий и техники, а также познание экономических и социальных явлений также с помощью математических моделей различными математическими методами. [Приложение 1]
Любая математическая задача состоит из условия (утверждения), вопроса или требования. Причем, в задаче обычно не одно, а несколько элементарных условий. Они представляют собой количественные или качественные характеристики объектов задачи и отношения между ними.
Требований в заданиях тоже может быть несколько. Они могут быть сформулированы, как в вопросительной, так и в утвердительной форме. Условия и требования взаимосвязаны. Систему взаимосвязанных условий и требований называют высказывательной моделью (словесной).
Глубина и значимость открытий, которые делает школьник, решая задачи, определяется характером осуществляемой им деятельности и мерой ее усвоения, тем, какими средствами этой деятельности он овладеет. Для того чтобы ученик мог выделить и освоить способ решения широкого класса задач, а не ограничивался нахождением ответа в данной, конкретной задаче, он должен овладеть некоторыми теоретическими знаниями о задаче, прежде всего, о ее структуре.
Чтобы структура задачи стала предметом анализа и изучения, необходимо отделить ее от всего несущественного и представить в таком виде, который обеспечивал бы необходимые действия. Сделать это можно путем особых знаково-символических средств – моделей, однозначно отображающих структуру задачи и достаточно простых для восприятия школьниками.
В структуре любой задачи выделяют:
1. Предметную область, то есть объекты, о которых идет речь в задаче.
2. Отношения, которые связывают объекты предметной области.
3. Требования задачи.
Структуру задачи принято делить на схематизированные и знаковые модели.
В свою очередь, схематизированные модели бывают вещественными (они обеспечивают физическое действие с предметами) и графическими (они обеспечивают графическое действие).
Графические модели используются для обобщенного, схематического воссоздания задачи. К ним относят:
· рисунки;
· схематический рисунок;
· чертеж;
· схематический чертеж.
Знаковые модели могут быть выполнены как на естественном (т.е. имеет словесную форму), так и на математическом (т.е. используются символы) языке.
На естественном языке можно отнести:
- краткую запись;
- таблицы.
На математическом языке:
- выражение;
- уравнение;
- по действиям;
- система уравнений.
Схематизированные, графические и знаковые модели, выполненные на естественном языке – вспомогательные модели, а знаковые модели, выполненные на математическом языке – решающие.
Уровень овладения моделированием определяет успех решающего. Поэтому обучение моделированию занимает особое и главное место в формировании умения решать задачи.
Полезно применять чертежи и схематические рисунки, блок – схемы, моделирование с помощью отрезков и таблиц.
Графические модели и таблицы позволяют сравнивать пары понятий: левая – правая, верхняя – нижняя, увязывать пространственную информацию с информацией меры, тем самым, формируя умение решать задачи.
Итак, модель нужна для того, чтобы понять, как устроен конкретный объект, какова его структура, основные свойства, законы развития; научиться управлять объектом или процессом, определять наилучшие способы управления при заданных целях и критериях.
Моделирование в решении текстовых задач
Обучение с применением моделирования повышает активность мыслительной деятельности учащихся, помогает понять задачу, самостоятельно найти рациональный путь решения, установить нужный способ проверки, определить условия, при которых задача имеет или не имеет решение. Модель дает возможность более полно увидеть зависимость между данными и искомыми в задаче, представить задачу в целом, помогает обобщить теоретические знания. Постановка учебной задачи составляет мотивационно–ориентировочное звено – первое звено учебной деятельности. Вторым (центральным) звеном учебной деятельности является исполнительское, то есть следующие учебные действия для решения учебной задачи:
1)преобразование условий предметной задачи с целью выявления в ней основного отношения;
2)моделирование выделенного в ней отношения в предметной, графической или буквенной форме;
3)преобразование модели отношения для изучения его свойств;
4)построение системы частных задач, решаемых общим способом.
Чтобы научить школьников самостоятельно и творчески учиться, нужно включать их в специально организованную деятельность, сделать хозяевами этой деятельности. Одним из способов включения учащихся в активную деятельность в процессе решения задач и является моделирование.
Умение решать задачи – один из основных показателей уровня математического развития, глубины усвоения учебного материала.
Действующая программа обучения математике требует развития самостоятельности у учащихся в решении текстовых задач. Еще в начальной школе каждый должен уметь кратко записывать условие задачи, иллюстрируя ее с помощью рисунка, схемы или чертежа, обосновывать каждый шаг в анализе задачи и в ее решении, проверить правильность ее решения. Однако на практике требования программы выполняются далеко не полностью, что приводит к серьезным проблемам в знаниях и навыках учащихся.
Одна из основных причин допускаемых ошибок решении текстовых задач – неправильная организация первичного восприятия учащимися условия задачи и ее анализа, которые проводятся без должной опоры на жизненную ситуацию, отраженную в задаче, без ее графического моделирования.
В 5 классе, как правило, в процессе анализа используются разные виды краткой записи или готовые схемы, а создание модели задачи на глазах учеников или самими учащимися в процессе решения задач используется крайне редко. Учителя при фронтальном анализе и решении задачи нередко ограничиваются правильными ответами двух-трех учеников, а остальные записывают за ними готовые решения без глубокого их понимания.
Для устранения отмеченных недостатков следует, прежде всего, решительно улучшить методику организации первичного восприятия и анализа задачи, чтобы обеспечить осознанный и доказательный выбор арифметического действия всеми учащимися.
Главное для каждого ученика на этом этапе – понять задачу, то есть уяснить, о чем эта задача, что в ней известно, что нужно узнать, как связаны между собой данные, каковы отношения между данными и искомыми и т.п. Для этого, где возможно, следует применять метод моделирования ситуации, отраженной в задаче.
Используемый в науке метод моделирования заключается в том, что для исследования какого-либо явления или объекта выбирают или строят другой объект, в каком-то отношении подобный исследуемому; построенный или выбранный объект изучают и с его помощью решают исследовательские задачи, а затем результат решения этих задач переносят на первоначальное явление или объект.
В 5 классе, анализируя задачу № 1:
«В школьном математическом кружке занимаются 18 учеников. В танцевальном кружке на 12 человек больше, чем в математическом, а в спортивном на 5 учеников меньше, чем в танцевальном. Сколько учеников в спортивном кружке», обычно записывают ее кратко примерно так:
в математическом кружке – 18 учеников;
в танцевальном кружке - ?, на 12 учеников больше, чем в математическом;
в спортивном кружке - ?, на 5 учеников меньше, чем в танцевальном.
Такая запись при первичном анализе задачи нерациональная, так как не раскрывает наглядно взаимодействия между данными и искомыми, не помогает в выборе действия.
Учащимся предлагается смоделировать условие задачи следующим образом:
![]() в математическом кружке –
в математическом кружке –

в танцевальном кружке –

![]() в спортивном кружке –
в спортивном кружке –
Эта модель дает наглядное представление об отношениях между данными и искомыми в задачах.
Анализируя задачу, учащиеся выясняют, что в танцевальном кружке учеников на 12 больше, чем в математическом, то есть их столько же плюс еще 12; поэтому отрезок на схеме, изображающий число учеников в танцевальном кружке, они начертят большей длины, чем отрезок, изображающий число учеников в математическом кружке. А так как число учеников в спортивном кружке на 5 меньше, чем в танцевальном, то есть их столько же, но без пяти, то и отрезок, показывающий число учеников в спортивном кружке должен быть меньше отрезка, показывающего число учеников в танцевальном кружке.
Анализируя эту схему, учащиеся самостоятельно записывают правильное решение.
Внимательно рассматривая модель, можно предложить ученикам найти другой способ решения задачи. Исходя из графической схемы задачи, учащиеся выясняют, что в спортивном кружке учеников больше, чем в математическом; определяют, на сколько больше (12-5=7(уч.)), а затем отвечают на поставленный вопрос (18+7=25(уч.)). Этот способ может служить проверкой ранее рассмотренного способа решения.
Рассмотрим, как можно смоделировать задачу № 2:
«В три магазина привезли 3840 кг масла. После того, как первый магазин продал 568 кг, второй – 642 кг и третий – 401 кг, масла осталось во всех магазинах поровну. Сколько кг масла получил каждый магазин?»
В процессе разбора этой задачи с учащимися, получаем примерно такие вспомогательные модели:
|
|
|
Осталось? Осталось? Осталось?
![]()
![]() 3840 кг
3840 кг
Получил: Осталось: Продали:
?
![]()
![]()
![]() 1-й магазин?
1-й магазин?
|
![]() ?
?
![]()
![]() 2-й магазин?
2-й магазин?
|
![]()
![]() 3-й магазин?
3-й магазин?
|
Такая модель помогает уяснить одно из важных условий задачи, которое вызвало наибольшее затруднение в решении, а именно: после того, как в каждом магазине продали часть завезенного масла, в каждом из них осталось поровну.
Модель создает предпосылки активной мыслительной деятельности в поисках разных способов решения одной и той же задачи.
Посмотрим еще одну задачу и модель к ней.
Задача 3:
«Три группы учащихся очищали каток от снега. Первая группа очистила 7/12, а вторая 2/3 того, что осталось, а третья оставшиеся 250 м2 . Вычислите площадь катка».
По предложению учеников каток изобразим в виде прямоугольника. Рассуждаем, какие размеры прямоугольника лучше взять для изображения катка. Сделаем вывод, что длину удобнее взять равной, например 12 см (число, кратное 12), а его ширину, например 6 см (число, кратное 3), на схематическом чертеже отметим данные и установим, что будем определять. Получится такая схема:
1-я группа 2-я группа
7/12 |
2/3 3-я группа |
| 250 м2 |
Схема помогает ученикам самостоятельно найти правильные решения данной задачи.
«Иногда в 5 классе задачу не проверяют или понимают под проверкой, например, прочтение решения задачи для всего класса или сверку на доске. Модель не только поможет найти рациональный способ решения задачи, но и поможет проверить его правильность.»[4, 83]
Условие задачи с пропорциональными величинами обычно кратко записывают в таблицу. Например, следующим образом.
Задача 4: «В трех одинаковых ящиках 21 кг апельсинов. Сколько килограммов апельсинов в 8 таких ящиках?»
Масса апельсинов в одном (каждом) ящике. одинаковая |
Количество ящиков. 3 8 |
Общая масса. 21 кг ? кг |
Таблица – это тоже модель задачи, но более абстрактная, чем схематический рисунок или чертеж. Она предполагает уже хорошее знание учащимися взаимозависимостей пропорциональных величин, так как сама таблица этих взаимозависимостей не показывает. Поэтому при первичном знакомстве с такой задачей таблица мало помогает представить математическую ситуацию и выбрать нужное действие.
При первичном знакомстве с таким видом задач целесообразно смоделировать условие в виде схематического рисунка или чертежа.
|
||||||
![]()
![]()
![]()
![]() 21 кг
21 кг
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
? ?
По такой модели решение задачи становится более понятным для всех учащихся.
Рассмотрим задачу 5:
«С первой яблони собрали 3 одинаковые корзины яблок, а со второй – 5 таких же корзин, причем со второй яблони собрали на 40 кг яблок больше, чем с первой. Сколько килограммов яблок собрали с каждой яблони?»
![]() 1 ябл.
1 ябл.
?
![]() 2 ябл.
2 ябл.
?
Схематический рисунок этой задачи позволяет наглядно убедиться, что разница в 40 кг возникла потому, что число корзин с яблоками, собранными со второй яблони, на две больше, чем с первой. Главное при решении – понять, что в этих двух корзинах и было 40 кг. Поняв это, дети сами записывают решение.
Модели помогают найти разные способы решения одной и той же задачи.
«Движение является темой для самых разнообразных задач. Существует самостоятельный тип задач на движение. Он объединяет такие задачи, которые решаются на основании зависимости между тремя величинами, характеризующими движение: скоростью, временем и расстоянием. Во всех случаях речь идет о равномерном прямолинейном движении» [22, 31]
Основные объекты задач на движение: пройденный путь (s), скорость (v), время (t); основное отношение (зависимость): s = vt.
Рассмотрим особенности решения основных видов задач на движение
Задачи на встречное движение двух тел
Пусть движение первого тела характеризуется величинами s1 ,v1 ,t1 ; движение второго – s2 ,v2 ,t2 . Такое движение можно представить на схематическом чертеже:
v1 v2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() t1
t2
t1
t2
 |
А s1 tвстр. s2 В
Если два тела начинают движение одновременно навстречу друг другу, то каждое из них с момента выхода и до встречи затрачивает одинаковое время, т.е. t1 = t2 = tвстр. .
Расстояние, на которое сближаются движущиеся объекты за единицу времени, называется скоростью сближения, т.е. vсбл. = v1 + v2 .
Все расстояние, пройденное движущимися телами при встречном движении, может быть подсчитано по формуле: S= vсбл * tсбл. .
Задачи на движение двух тел в одном направлении
«Среди них следует различать два типа задач:
1) движение начинается одновременно из разных пунктов;
2) движение начинается в разное время из одного пункта.
Рассмотрим случай, когда движение двух тел начинается одновременно в одном направлении из разных пунктов, лежащих на одной прямой. Пусть движение первого тела характеризуется величинами s1 ,v1 ,t1 , а движение второго - s2 ,v2 ,t2 .
Такое движение можно представить на схематическом чертеже:
v1 v2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() t1
t2
t1
t2
 |
А ss2 В
S1
Если при движении в одном направлении первое тело догоняет второе, то v1 >v2 . Кроме того, за единицу времени первый объект приближается к другому на расстоянии v1 - v2 . Это расстояние называют скоростью сближения: vсбл. = v1 - v2 .
Расстояние S, представляющее длину отрезка АВ, находят по формулам:
S = s1 - s2 и S = v сбл * tвстр .»[1, 141]
Задачи на движение двух тел в противоположных направлениях
В таких задачах два тела могут начинать движение в противоположных направлениях из одной точки: а) одновременно; б) в разное время. А могут начинать свое движение из двух разных точек, находящихся на заданном расстоянии, и в разное время.
Общим теоретическим положением для них будет следующее:
vудал. = v1 + v2 , где v1 и v2 соответственно скорости первого и второго тел, а vудал – это скорость удаления, т.е. расстояние, на которое удаляются друг от друга движущиеся тела за единицу времени.
Четкие условные обозначения помогают детям строить сложные схемы, видеть в них нужные формулы, отношения для решения задачи. Иногда четкое соблюдение условных обозначений в схеме позволяет не запутаться в числовых значениях задачи и предотвращает многие ошибки. Анализируя модель, можно увидеть несколько способов решения задачи.
Использование графических изображений способствует сознательному и прочному усвоению многих понятий. Благодаря им, математические связи и зависимости приобретают для учеников наглядный смысл, а в процессе их использования происходит углубление и развитие математического мышления учащихся.
Соблюдение точности и аккуратности при выполнении рисунков, схем, чертежей, помимо учебного, имеет важнейшее воспитательное значение. Аккуратно выполненные графические изображения в значительной степени способствуют эстетическому воспитанию детей: заставляют любоваться неожиданным, остроумным графическим решением задачи, стимулируют поиски рациональных путей решения, снижают утомляемость, повышают активность, воспитывают внимание. И наоборот, грубый чертеж мешает увидеть скрытые в условии задачи закономерности, на которых основано решение.
Графические изображения служат хорошим и удобным средством для организации коллективной и индивидуальной (дифференцированной) самостоятельной работы учащихся, быстродействующим средством для проверки знаний учащихся.
Правильно построенные графические модели условий задач позволяют ученикам во многих случаях сделать прикидку ожидаемого ответа, графическую проверку правильности решения задачи, выполненной аналитическим способом.
Также графические модели помогают организовать соответствующую работу, так как наглядно иллюстрируют то, что известно и что нужно определить; на моделях легче увидеть, каких именно данных не достает (или какие данные являются лишними) для того, чтобы, используя нужную зависимость, решить ту или иную задачу.
Умение строить учебные модели и работать с ними является одним из компонентов общего приема решения задач. С помощью модели словесно заданный текст можно перевести на математический язык и увидеть структуру математических отношений, скрытую в тексте. Использование одних и тех же знаково – символических средств при построении модели для математических задач с разными сюжетами и разных типов способствует формированию обобщенного способа анализа задачи, выделению составляющих ее компонентов и нахождению путей решения.
Таким образом, использование графической модели при решении задач обеспечит качественный анализ задач, осознанный поиск их решения, обоснованный выбор арифметического действия, рациональный способ решения и предупредит многие ошибки в решении задач учащимися. Модель задачи может быть использована и для составления и решения обратных задач для проведения исследования задачи. Модель помогает поставить условия, при которых задача имеет решение или не имеет решения; как изменяется значение искомой величины в зависимости от изменения данных величин; помогает сделать обобщения теоретических знаний; развивает самостоятельность и вариативность мышления.
Использование моделирования при работе над задачами на движение в 5 классе
Задача 1: (№ 1142)
«Из двух пунктов, расстояние между которыми 7 км 500 м, одновременно в одном направлении вышел пешеход со скоростью 6 км/ч и выехал автобус. Определите скорость автобуса, если он догнал пешехода через 15 мин?»
? км/ч 6 км/ч
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
А 7км 500 м В tвстр =15 мин
15 мин = 0,25 ч
1) 6 * 0,25 = 1,5 (км) – прошел поезд за 15 мин.
2) 7,5 + 1,5 = 9 (км) – прошел автобус до того, как догнал пешехода.
3) 9: 0,25 = 36 (км/ч) – скорость автобуса.
Ответ: 36 км/ч.
Задача 2: (№ 1169)
«а) Теплоход идет вниз по реке. Какова скорость движения теплохода, если скорость течения реки 4 км/ч, а собственная скорость теплохода (скорость в стоячей воде) равна 21 км/ч?
б) Моторная лодка идет вверх по реке. Какова скорость движения лодки, если скорость течения 3 км/ч, а собственная скорость лодки 14 км/ч?»
| Собств. v | V течения | V по течению реки | V против течения |
| 21 | 4 | ? | - |
| 14 | 3 | - | ? |
а) 21 + 4 = 25 (км/ч) – скорость теплохода.
б) 14 – 3 = 11 (км/ч) – скорость движения лодки.
Ответ: а) 25 км/ч;
б) 11 км/ч.
Задача 3: (№ 1172)
«Со станции вышел товарный поезд со скоростью 50 км/ч. Через 3 ч. с той же станции вслед за ним вышел электропоезд со скоростью 80 км/ч. Через сколько часов после своего выхода электропоезд догонит товарный поезд?
![]()
![]()
![]()
![]()
![]()
![]() 80 км/ч
50 км/ч
80 км/ч
50 км/ч
![]()
![]()
![]()
3 ч. tвстр - ?
1) 50 ∙ 3 = 150 (км) – прошел товарный поезд.
2) 80 – 50 = 30 (км/ч) – скорость сближения.
3) 150 : 30 = 5 (ч) – через это время электропоезд догонит товарный поезд.
Ответ: через 5 часов.
Задача 4: (№ 1179)
«Два поезда вышли в разное время навстречу друг другу из двух городов, расстояние между которыми 782 км. Скорость первого поезда 52 км/ч, а второго 61 км/ч. Пройдя 416 км, первый поезд встретился со вторым. На сколько один из поездов вышел раньше другого?»
![]()
![]()
![]()
![]() 52 км/ч 61 км/ч
52 км/ч 61 км/ч
 |
416 км
782 км
1) 416: 52 = 8 (ч) – шел первый поезд.
2) 782 – 416 = 366 (км) – прошел второй поезд.
3) 366: 6 = 6 (ч) – шел второй поезд.
4) 8 – 6 = 2 (ч) – на это время первый поезд вышел раньше второго.
Ответ: на 2 часа.
Задача 5: (№ 1193)
«Собственная скорость катера (скорость в стоячей воде) равна 21,6 км/ч, а скорость течения реки 4,7 км/ч. Найдите скорость катера по течению и против течения реки.»
| Собств. v | V течения | V по течению реки | V против течения |
| 21,6 | 4,7 | ? | ? |
1) 21,6 + 4,7 = 26,3 (км/ч) – скорость катера по течению.
2) 21,6 – 4,7 = 16,9 (км/ч) – скорость катера против течения.
Ответ: 26,3 км/ч; 16,9 км/ч.
Задача 6: (№ 1194)
«Скорость теплохода по течению реки равна 37,6 км/ч. Найдите собственную скорость теплохода и его скорость против течения, если скорость течения реки 3,9 км/ч.»
| Собств. v | V течения | V по течению реки | V против течения |
| ? | 3,9 | 37,6 | ? |
1) 37,6 – 3,9 = 33,7 (км/ч) – собственная скорость теплохода.
2) 33,7 – 3,9 = 29,8 (км/ч) – скорость против течения.
Ответ: 33, 7 км/ч; 29,8 км/ч.
Задача 7: (№ 1196)
« Расстояние между городами156 км. Из них одновременно навстречу друг другу выехали два велосипедиста. Один проезжает в час 13,6 км, а другой 10,4 км. Через сколько часов они встретятся?»
![]()
![]()
![]()
![]()
![]() 13,6 км/ч
10,4 км/ч
13,6 км/ч
10,4 км/ч
![]()
![]()
![]()

![]()
1 ч. tвстр -?. 1 ч.
156 км
1) 13,6 + 10,4 = 24 (км/ч) – скорость сближения.
2) 156: 24 = 6,5 (ч) – через это время они встретятся.
Ответ: через 6,5 часа.
Задача 8: (№ 1233)
«Автомашина в первый час прошла 48,3 км, во второй час она прошла на 15,8 км меньше, чем в первый, а в третий час – на 24,3 км меньше, чем за первые два часа вместе. Какой путь прошла автомашина за эти три часа?»
![]()
![]() 1 ч.
1 ч.
![]()
![]()
![]()
![]()
![]() 2 ч. ?
2 ч. ?
? 15,8 км
![]()
![]()
![]()
![]()
![]() 3 ч.
3 ч.
? 24,3 км
1) 48,3 – 15,8 = 32,5 (км) – прошла машина за 2-ой час.
2) 48,3 + 32,5 = 80,8 (км) – прошла машина за 1 и 2 час.
3) 80,8 – 24,3 = 56,5 (км) – прошла машина за 3-ий час.
4) 56,5 + 80,8 = 137,3 (км) – прошла машина за 3 часа.
Ответ: 137,3 км.
Задача 9: (№ 1268)
«Собственная скорость лодки 4,5 км/ч, скорость течения 2,5 км/ч. Найдите скорость лодки при движении по течению и против течения. Какой путь пройдет лодка по течению за 4 часа, и какой путь она пройдет против течения за 3 часа?»
| Собств. v | V течения | t (ч) | S (км) | |
| по течению реки | 4,5 | 2,5 | 4 | ? |
| против течения | 4,5 | 2,5 | 3 | ? |
1) 4,5 + 2,5 = 7 (км/ч) – скорость по течению.
2) 4,5 – 2,5 = 2 (км/ч) – скорость против течения.
3) 7 ∙ 4 = 28 (км) – путь по течению реки.
4) 2 ∙ 3 = 6 (км) – путь против течения реки.
Ответ: 28 км; 6км.
Задача 10: (№ 1285)
« Автомашина прошла 3 ч со скоростью 48,4 км/ч и 5 ч со скоростью 56,6 км/ч. Какой путь прошла автомашина за все это время?»
![]()
![]()
![]()
![]() 48,4 км/ч
56,6 км/ч
48,4 км/ч
56,6 км/ч

![]()
![]()
![]()
3 ч. 5 ч.
S - ?
1) 48,4 ∙ 3 = 145,2 (км) – автомашина прошла за 3 часа.
2) 56,6 ∙ 5 = 283 (км) – автомашина прошла за 5 часов.
3) 145,2 + 283 = 428,2 (км) прошла машина за все это время.
Ответ: 428,2 км.
Задача 11: (№ 1300)
«С одной станции в противоположных направлениях вышли два поезда в одно и то же время. Скорость одного поезда 65 км/ч, а скорость другого на а км/ч больше. Какое расстояние будет между поездами через 3 часа? Составьте выражение для решения и найдите его значение при а = 10;25.»
![]()
|
S - ?
При а = 10:
1) 65 + 10 = 75 (км/ч) - скорость второго поезда.
2) 65 + 75 = 140 (км/ч) – скорость удаления поездов.
3) 140 ∙ 3 = 420 (км) – расстояние между поездами через 3 часа.
Ответ: 420 км.
При а = 25:
1) 65 + 25 = 90 (км/ч) – скорость второго поезда.
2) 90 + 65 = 155 (км/ч) – скорость удаления поездов.
3) 155 ∙ 3 = 465 (км) – расстояние между поездами через 3 часа.
Ответ: 465 км.
Задача 12: (№ 1301)
«Скорость дельфина в 2 раза больше скорости акулы. Скорость акулы на 25 км/ч меньше скорости дельфина. Какова скорость каждого животного?»
25 км/ч
![]()
![]()
![]()
![]()
![]() Дельфин
Дельфин
х км/ч – скорость акулы
2х (км/ч) – скорость дельфина
Уравнение: 2х = х + 25
2х – х = 25
х =25
25 км/ч – скорость акулы.
25 ∙ 2 = 50 (км/ч) – скорость дельфина.
Ответ: 25 км/ч; 50 км/ч.
Задача 13: (№ 1316)
«Турист должен был пройти за два дня 25,2 км. В первый день он прошел 3/7 пути. Сколько км турист прошел во второй день?»
![]()
![]() 3/7 ?
3/7 ?
25,2 км
I способ:
1) 25,2 ∙ 3/7 = 10,8 (км) – турист прошел за 1 день.
2) 25,2 – 10,8 = 14,4 (км) – турист прошел во 2 день.
Ответ: 14,4 км.
II способ:
1) 1 – 3/7 = 4/7 (части) – всего пути прошел турист в 1 день.
2) 25,2 ∙ 4/7 = 14,4 (км) – прошел турист во 2 день.
Ответ: 14,4 км.
Задача 14: (№ 1349)
«Автомашина шла по шоссе 3 ч со скоростью 65,8 км/ч, а затем 5 ч она шла по грунтовой дороге. С какой скоростью она шла по грунтовой дороге, если весь ее путь равен 324,9 км?»
![]()
![]()
![]()
![]() 65,8 км/ч
? км/ч
65,8 км/ч
? км/ч

![]()
![]()
![]()
3 ч. 5 ч.
324,9 км
1) 65,8 ∙ 3 = 197,4 (км) – прошла машина по шоссе.
2) 324,9 – 197,4 = 127,5 (км) – прошла машина по грунтовой дороге.
3) 127,5 : 5 = 25,5 (км/ч) – скорость машины по грунтовой дороге.
Ответ: 25,5 км/ч.
Задача 15: (№ 1383)
«Скорость движения Земли вокруг Солнца 29,8 км/с, а скорость Марса на 5,7 км/с меньше. Какой путь пройдет каждая из планет за 3 секунды?»
![]() V
Земли
V
Земли
29,8 км/с
![]()
![]()
![]()
![]()
![]()
![]() V
Марса
V
Марса
? 5,7 км/с
1) 29,8 – 5,7 = 24,1 (км/с) – скорость Марса.
2) 29,8 ∙ 3 = 89,4 (км) – путь, который пройдет Земля за 3 секунды.
3) 24,1 ∙ 3 = 72,3 (км) – путь, который пройдет Марс за 3 секунды.
Ответ: 89,4 км; 72,3 км.
Задача 16: (№ 1385)
« Два пешехода вышли одновременно навстречу друг другу и встретились через 2,5 часа. Скорость первого пешехода равна 4,2 км/ч, а скорость второго 5,2 км/ч. Какое расстояние было между ними в начале движения?»
| V | t | S | |
| I | 4,2 км/ч | 2,5 ч | ? |
| II | 5,2 км/ч | 2,5 ч | ? |
1) 4,2 + 5,2 = 9,4 (км/ч) – скорость сближения.
2) 9,4 ∙ 2,5 = 23,5 (км) – расстояние между пешеходами в начале движения.
Ответ: 23,5 км.
Задача 17: (№ 1396)
«Катер, собственная скорость которого 14,8 км/ч, шел 3 ч по течению реки и 4 ч против течения. Какой путь проделал катер за все это время, если скорость течения 2,3 км/ч?»
| Собств. v | V течения | t (ч) | S (км) | |
| по течению реки | 14,8 | 2,3 | 3 | ? |
| против течения | 14,8 | 2,3 | 4 | ? |
1) (14,8 + 2,3) ∙ 3 = 51,3 (км) – путь по течению реки.
2) (14,8 – 2,3) ∙ 4 = 50 (км) – путь против течения реки.
Ответ: 51,3 км; 50 км.
Задача 18: (№ 1436)
«Два пешехода находились на расстоянии 4,6 км друг от друга. Они пошли навстречу друг другу и встретились через 0,8 ч. Найти скорость каждого пешехода, если скорость одного из них в 1,3 раза больше скорости другого.»
![]()
![]()
![]()
![]()
![]() ? км/ч
?, в 1,3 больше
? км/ч
?, в 1,3 больше
![]()
![]()
![]()
![]()

0,8 ч. 0,8 ч.
4,6 км
I способ:
1) 4,6: 0,8 = 5,75 (км/ч) – скорость сближения.
х км/ч – скорость первого пешехода.
1,3 х (км/ч) – скорость второго пешехода.
2) Уравнение: х + 1,3 х = 5,75
2,3 х = 5,75
х = 2,5
2,5 км/ч – скорость первого пешехода.
3) 2,5 ∙ 1,3 = 3,25 (км/ч) – скорость второго пешехода.
Ответ: 2,5 км/ч; 3,25 км/ч.
II способ:
1) 4,6: 0,8 = 5,75 (км/ч) – скорость сближения.
Введем дополнительную схему:
|
![]()
![]()
![]() 0,3 км/ч
0,3 км/ч
2) 1 + 1,3 = 2,3 (части) – составляет 5,75 км/ч.
3) 5,75: 2,3 = 2,5 (км/ч) – скорость первого пешехода.
4) 2,5 ∙ 1,3 = 3,25 (км/ч) – скорость второго пешехода.
Ответ: 2,5 км/ч; 3,25 км/ч.
Задача 19: (№ 1476)
«Автомобиль двигался 3,2 ч по шоссе со скоростью 90 км/ч, затем 1,5 ч по грунтовой дороге со скоростью 45 км/ч, наконец, 0,3 ч по проселочной дороге со скоростью 30 км/ч. Найдите среднюю скорость движения автомобиля на всем пути.»
|
|
|
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3,2 ч 1,5 ч 0,3 ч
(90 +45 + 30) : 3 = 55 (км/ч) – средняя скорость автомобиля.
Ответ: 55 км/ч.
При решении задач на движение широко используется метод моделирования, что способствует сознательному и прочному усвоению материала.
Благодаря моделированию математические связи и зависимости приобретают для учеников смысл, а в процессе его использования происходит углубление и развитие математического мышления учащихся.
Модели помогают ученикам в сознательном выявлении скрытых зависимостей между величинами, побуждают активно мыслить, искать наиболее рациональные пути решения задач. Моделирование наглядно представляет соотношения между данными и искомыми величинами.
При решении задач на движение используются разные виды моделей, например: схематический чертеж, схема, таблица. Использование таблицы предполагает уже хорошее знание учениками взаимозависимостей, так как сама таблица этих зависимостей не показывает.
Опираясь на чертеж, учащиеся находят возможный путь решения задачи. Используя визуальную информацию, учатся анализировать задачу и составлять полный план ее решения. Чертеж дает возможность учащимся найти не один, а несколько способов решения.
Метод моделирования позволяет активизировать познавательную деятельность учащихся на уроке.
Исследование предпочтений детей при выборе методов обучения
Пробный урок в 5 классе.
Тема: Решение задач на движение.
Цель урока: закрепление умений и навыков решать текстовые задачи на движение, используя метод моделирования.
Задачи урока:
- научить составлять схемы и таблицы при решении текстовых задач;
- развивать способность учащихся находить рациональные способы решения текстовых задач с помощью моделирования, вычислительные навыки, память;
- воспитывать аккуратность при построении чертежей, интерес к математике, внимание.
Оборудование: портрет С. Стевина; карточки с буквами и ответами; жетоны разных цветов; таблица, схематический чертеж.
Ход урока:
1. Сообщение темы и цели урока:
Тема урока: Решение задач на движение. Сегодня на уроке мы с вами будем решать задачи на движение методом моделирования. Достигать поставленной цели будем под девизом «Спорьте, ошибайтесь, заблуждайтесь, но размышляйте, и хотя криво, да сами…» Лесает.
2. Домашнее задание: повторить билеты № 11, 12, 14, 16.
3. Устные упражнения:
А) Может ли произведение десятичной дроби на натуральное число быть натуральным числом?
Б) Может ли произведение десятичных дробей быть натуральным числом?
В) Может ли при умножении натуральных чисел получиться десятичная дробь?
Г) Что нужно сделать, чтобы умножить десятичную дробь на натуральное число?
Д) Как умножить десятичную дробь на 10, 100, 1000 и т.д.?
Е) Как разделить десятичную дробь на 10, 100, 1000?
Ж) Что нужно сделать, чтобы разделить десятичную дробь на 0,1; 0,01?
З) Что называют средним арифметическим?
3.2. Решение зашифрованных примеров:
| 0,64 | С |
| 0,87 | Т |
| 2,3 | Е |
| 0,127 | В |
| 4,85 | И |
| 0,82 | Н |
1) 0,29 + 0, 35
2) 0,57 + 0,3
3) 20,7 : 9
4) 1, 016 : 8
5) 48,5 ∙ 0,1
6) 82 ∙ 0,01
Историческая справка
Знаете ли вы, что именно Симоном Стевином в 80-х годах XVI века были заново «открыты» в Европе десятичные дроби.
Стевин Симон родился в 1548 году в г. Брюгге. Он был нидерландским ученым и инженером. В 1600 г. организовал инженерскую школу, где читал лекции по математике.
Работа Стевина, которая называется «Десятина», посвящена десятичной системе мер и десятичным дробям, которые Симон ввел в употребление в Европе. Умер Стевин в 1620 году, в Гааге.
Решение задач с использованием моделирования
Переходим к главному этапу урока – решению задач на движение методом моделирования.
4.1. Работа над задачей 1: (№ 1457)
«Путь от дома до школы равен 1,1 км. Девочка проходит этот путь за 0,25 ч. С какой скоростью идет девочка?»
- Внимательно читаем условия задачи.
- Что нам уже известно в задаче?
(Путь и время)
- Что нам надо найти в задаче?
(Скорость с которой шла девочка)
- Можем мы сразу ответить на вопрос задачи?
(Да)
- Как мы найдем скорость?
(V = S/t)
- Записываем в тетради решение: (при этом: сильные помогают слабым оформить решение задачи) 1,1 : 0,25 = 4,4 (км/ч) – скорость, с которой шла девочка.
- Записываем ответ.
Работа над задачей 2: (№ 1464)
«Два пешехода вышли одновременно из одного места в противоположных направлениях. Через 0,8 часа расстояние между ними стало равным 6,8 км. Скорость одного пешехода была в 1,5 раза больше скорости другого. Найдите скорость каждого пешехода».
- Внимательно читаем задачу.
1. Чтение задачи и запись условия.
- Давайте мы к этой задаче составим чертеж.
- Что нам уже известно в задаче?
(Два пешехода вышли одновременно из одного места, в противоположных направлениях)
 |
- Что еще нам известно?
(Через 0,8 ч расстояние между ними равно 6,8 км.)
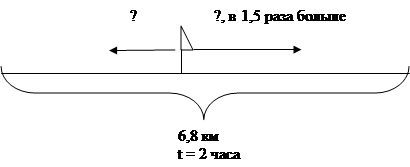 |
- Что известно про скорость пешеходов?
(Скорость одного в 1,5 раза больше другого)
2. Анализ задачи и составление плана решения.
- Посмотрите внимательно на чертеж.
- Какой главный вопрос задачи?
(Найти V каждого пешехода)
- Можно сразу ответить на вопрос задачи?
(Нет)
- Почему?
(Так как неизвестно какое расстояние прошел каждый пешеход за один час, т.е. скорость удаления)
- А можно это узнать?
(Да)
- Как мы это сделаем?
(6,8: 0,8 = 8,5 (км/ч))
Что мы знаем про скорость каждого пешехода?
(Скорость одного в 1,5 раза больше другого)
- Каким способом будем решать дальше задачу?
1 способ: (можно с помощью уравнения)
- Какое уравнение составим, зная, что скорость удаления равна 8,5 км/ч?
- Можно составить уравнение: х + 1,5х = 8,5
Что мы найдем из этого уравнения?
(Скорость первого пешехода)
- Если мы найдем скорость первого пешехода, сможем ли найти скорость второго пешехода?
(Да)
3. План решения.
- Еще раз посмотрим, как мы решили задачу. Что мы делали?
3.1. Нашли скорость удаления.
3.2. Составили уравнение.
3.3. Нашли скорость первого пешехода.
3.4. Нашли скорость второго пешехода.
4. Осуществление плана решения.
1) 6,8: 0,8 = 8,5 (км/ч) – скорость удаления.
2) х – скорость первого пешехода
1,5х – скорость второго пешехода
х + 1,5х = 8,5
2,5х = 8,5
х = 3,4
3,4 (км/ч) – скорость первого пешехода.
3) 3,4 * 1,5 = 5,1 (км/ч) – скорость второго пешехода.
Ответ: 3,4 км/ч; 5,1 км/ч.
2 способ:
- Давайте посмотрим, как еще можно решить эту задачу, не составляя уравнения.
- Введем дополнительную схему:
|
![]()
![]() II
II
1) 6,8: 0,8 = 8,5 (км/ч) – скорость удаления.
2) 1 + 1,5 = 2,5 (части) – составляет 8,5 км/ч
3) 8,5: 2,5 = 3,4 (км/ч) – скорость первого пешехода.
4) 3,4 * 1,5 = 5,1 (км/ч) – скорость второго пешехода.
Ответ: 3,4 км/ч; 5,1 км/ч.
Итог:
- Итак, эту задачу решили двумя разными способами. Ответ получили один и тот же. Это доказывает, что задачу решили правильно. Что помогло нам решить эту задачу?
(Схематический чертеж)
Работа над задачей 3: (№ 1449)
«Собственная скорость лодки 8,5 км/ч, а скорость течения 1,3 км/ч. Какое расстояние пройдет лодка по течению за 3,5 часа? Какое расстояние пройдет лодка против течения за 5,6 часа?»
- Читаем задачу.
- О каких величинах идет речь в задаче?
- Для решения этой задачи составим таблицу.
- Что известно? Запишем.
| Собств. v (км/ч) | V течения (км/ч) | t (ч) | S (км) | |
| по течению реки | 8,5 | 1,3 | 3,5 | ? |
| против течения | 8,5 | 1,3 | 5,6 | ? |
- Как найдем скорость лодки по течению реки? (8,5 + 1,3)
- Как найти скорость против течения? (8,5 - 1,3)
- Что нам известно про время?
(3,5 ч – по течению; 5,6 – против течения)
- Что нам нужно найти? (Расстояние)
- Как его найдем?
(8,5 + 1,3) * 3,5 = 34,3 (км) – путь по течению.
(8,5 – 1,3) * 5,6 = 40,32 (км) – путь против течения.
- Запишите самостоятельно решение задачи.
- Итак, что помогло нам решить эту задачу? (Таблица)
5. Итог урока:
- Чему сегодня учились на уроке?
(Решать задачи на движение)
- Кому было легко решать задачи?
- Кто испытывал трудности? Что было трудно?
6. Рефлексия.
В конце урока была проведена рефлексия, которая показала предпочтения детей при выборе методов обучения.
Всем учащимся предлагалось по три жетона разного цвета. Кто считал, что при решении задач на движение не надо никакой таблицы и чертежа, сдавал белые жетоны.
Если считали, что нужна таблица, то сдавали красные жетоны. Все данные занесены в таблицу [ Таблица 1].
Из таблицы «Предпочтения детей при выборе методов обучения» можно сделать вывод, что:
34,5 % всех учеников 5 класса считают, что для решения задач на движение не требуется наглядность. Вероятно, это связано с тем, что задачи иногда предлагаются не сложные и решаются очень быстро;
82,8 % учеников считают, что необходимо строить чертеж, так как именно чертеж помогает найти правильный путь решения задачи, а также позволяет сделать проверку данной задачи.
69 % учащихся считают, что при решении задач на движение помогает таблица. Процент ниже, т.к. таблица не всегда показывает все взаимосвязи между величинами.
Самоанализ:
При проведении данного урока поставлена следующая цель: «Закрепление умений решать задачи на движение методом моделирования», поскольку именно этот метод позволяет в полной мере усвоить изучаемую тему.
Поскольку класс отличается высоким уровнем интеллекта, то им на уроке предлагались задачи разных уровней сложности.
В ходе урока были использованы следующие методы:
- метод коллективной мыслительной деятельности (при поиске способов решения задач);
- метод диалогового обучения (при составлении таблиц соответствующих задачам);
- метод дифференцированного обучения (дополнительные задачи для сильных учеников);
Именно эти методы способствовали активизации, инициативе и творческому выражению самих учащихся. Успешному усвоению знаний также помогали такие формы работы как групповая (парная) работа, при оформлении решения задач, самостоятельная работа, устная работа, в ходе которой проведен небольшой исторический экскурс.
Для достижения поставленной цели на уроке была использована наглядность: портрет С. Стевина; карточки с буквами и ответами; таблица, схематический чертеж; жетоны разных цветов, используемые для проведения рефлексии.
Урок прошел в обстановке сотрудничества, уважения и взаимопонимания, где каждый учащийся имел возможность высказать свое мнение. Комфортности способствовала и физкультминутка.
Благодаря используемым методам, формам и средствам ведения урока, в обстановке полной комфортности, достигнута цель урока.
Заключение
Изучив более подробно и глубоко вопросы, связанные с использованием моделей, поставленные автором задачи решены.
В ходе исследования проблемы использования моделирования в процессе обучения математике выявлено следующее:
· моделирование помогает формировать умение решать текстовые задачи;
· данный метод обучения повышает интерес учащихся к изучению математики.
Главным недостатком использования моделирования является отсутствие должного внимания на систематическое использование моделирования на уроках.
Целенаправленная работа по формированию приемов умственной деятельности должна начинаться с первых уроков математики. Действуя с различными предметами, пытаясь заменить один предмет другим, подходящим по заданному признаку, дети должны научиться выделять параметры вещей, являющиеся величинами, т.е. свойства, для которых можно установить отношения равно, неравно, больше, меньше. Полученные отношения моделируются сначала с помощью предметов, графически (отрезками), а затем – буквенными формулами.
Итак, использование моделирования имеет:
образовательное значение: моделирование помогает усвоить многие вопросы теории;
воспитательное значение: способствует развитию памяти, внимания, наблюдательности;
практическое значение: быстрота и правильность вычислений.
Данная работа может стать методическим пособием для студентов КПУ, как при подготовке докладов, сообщений на эту тему, так и при проведении пробных уроков математики.
Список литературы
1) Бантова М.А., Бельтюкова Г.В. Методика преподавания математики в начальных классах./Под ред. Бантовой М.А. – 3-е изд., - М.: Просвещение, 1984. – 335 с., ил.
2) Бондаренко С. М. Учите детей сравнивать. – М.: Знание, 1981 – 96 с.
3) Виленкин Н. Я. Математика: учеб. для 5 кл. 6-е изд. – М.: Мнемозина, 1998. – 384с.: ил.
4) Володарская И., Салмина Н. Моделирование и его роль в решении задач//Математика. – 2006. - № 18. – с. 2 – 7.
5) Воспитание учащихся при обучении математике: Книга для учителя. Из опыта работы./Сост. Пичугин Л. Ф. – М.: Просвещение, 1987. – 175 с.
6) Грес П. В. Математика для гуманитариев. Уч. пособие. – М.: Логос, 2004. – 160 с.
7) Жохов В. И. Преподавание математики в 5 – 6 классах: Мет. рекомендации для учителей к учебнику Н. Я. Виленкина, В. И. Жохова, А. С. Чеснокова. – М.: Вербум-М, 2000. – 176 с.
8) Зайцева С. А. Решение составных задач на уроках математики./А. С. Зайцева, И. И. Целищева. – М.: Чистые пруды, 2006. – 32 с.
9) Кузнецов В. И. К вопросу о решении математических задач.//Начальная школа. – 1999. - № 5. – с. 27 – 33.
10) Левенберг Л. Ш. Рисунки, схемы и чертежи в начальном курсе математики. Из опыта работы./Под ред. М. И. Моро. – М.: Просвещение, 1978. – 126 с.
11) Лотарева Л. Рисуем, чертим, решаем.//Математика. – 2004. - № 41. – с. 2 – 5.
12) Математика: Интеллектуальные марафоны, турниры, бои: 5 – 11 классы: Книга для учителя. – М., 2003. – 256 с.
13) Махрова В. Н. Рисунок помогает решать задачи.//Начальная школа. – 1998. - № 7. – с. 69 – 72.
14) Методика и технология обучению математике. Курс лекций: пособие для вузов./Под ред. Н. Л. Стефановой. – М.: Дрофа, 2005. – 416 с., ил.
15) Салмина Н. П. Знак и символ в обучении. – М., 1998. – 305 с.
16) Селевко Г. К. Современные образовательные технологии: Уч. пособие. – М.: Народное образование, 1998. – 256 с.
17) Смирнова С. И. Использование чертежа при решении простых задач.//Начальная школа. – 1998. - № 5. – с. 53 – 58.
18) Стойлова Л. П. Математика: Учебник для студентов отделений и факультетов нач. классов. – М.: Издательский центр «Академия», 1997. – 464 с.
19) Сурикова С. В. Использование графовых моделей при решении задач.//Начальная школа. – 2002. - № 4. – с. 56- 63.
20) Фридман Л. М. Психолого-педагогические основы обучения математике в школе. – М.: Просвещение, 1983. – 160 с., ил.
21) Хабибуллин К. Я. Обучение методам решения задач.//Школьные технологии. – 2004. - № 3. – с. 127 – 131.
22) Шикова Р. Н. Методика обучения решению задач, связанных с движением тел.//Начальная школа. – 2000. - № 5. – с. 30 – 37.
|
![]()
|
5 класс Учитель: Пластинина Мария Игнатьевна
| № | ФИО | Не нужна наглядность | Нужен чертеж | Нужна таблица |
| 1 | Бессонов А. | + | ||
| 2 | Гичев А. | + | + | |
| 3 | Гребенкин С. | + | + | |
| 4 | Дашев А. | + | ||
| 5 | Елохин А. | + | + | + |
| 6 | Захарова В. | + | ||
| 7 | Ковтанюк И. | + | + | |
| 8 | Косова Д. | + | ||
| 9 | Кошкина А. | + | + | |
| 10 | Красненкова М. | + | + | |
| 11 | Кузьмина Ю. | + | + | |
| 12 | Купин А. | + | + | + |
| 13 | Мичкова А. | + | + | |
| 14 | Овечкина К. | + | + | |
| 15 | Омененко Д. | + | + | |
| 16 | Орлова Н. | + | + | |
| 17 | Приданова К. | + | + | |
| 18 | Романов С. | + | + | |
| 19 | Рыльский С. | + | ||
| 20 | Смирнов Д. | + | + | |
| 21 | Тарачева К. | + | ||
| 22 | Телепова К. | + | + | + |
| 23 | Уфимева А. | + | ||
| 24 | Фаяршин Д. | + | + | + |
| 25 | Хлыбова А. | + | ||
| 26 | Хон О. | + | + | + |
| 27 | Хохлявина В. | + | ||
| 28 | Шабалина Л. | + | + | |
| 29 | Шаравьев С. | + | + | |
| Всего: | 10 | 24 | 20 | |