Реферат: Гиперболическая геометрия

В 4 веке до н. э. древнегреческий ученый Эвклид свёл накопленные к тому времени математические знания в своём труде «Начала», проанализировав труды своих предшественников, возвысился до создания невиданной по тем временам точно обоснованной теории. Она опирается на ряд определений и аксиом. Исходной точкой его логической системы является положение о том, что выдвигаемые им постулаты очевидны, их справедливость признается всеми несомненной.

Имеется пять постулатов:

1. Через две точки проходит единственная прямая.

2. Ограниченную прямую линию можно непрерывно продолжить.

3. Из любой точки как из центра можно описать окружность любого радиуса.

4. Все прямые углы равны между собой.

5. Всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними внутренние односторонние углы, сумма которых меньше суммы двух прямых углов, эти прямые пересекаются и притом с той стороны, с которой эта сумма меньше суммы двух прямых углов.

Пятый постулат (так называемый постулат «о параллельных») вследствие его сравнительной сложности и малой наглядности вызвал большое число попыток доказать его как теорему, вывести его из остальных аксиом. С первого века до н.э. до 1820 математики пытались доказать справедливость пятого постулата, используя первые четыре, но преуспели лишь в замене его различными эквивалентными допущениями, такими, как «две параллельные линии всюду равно удалены друг от друга» или «любые три точки, не расположенные на одной прямой, принадлежат окружности».

Ближе всех подошел к цели иезуит, логик и математик Джироламо Саккери (1667–1733) в своей работе «Эвклид, очищенный от пятен, или Геометрическая попытка установить самые первые начала всей геометрии». Он начал свои исследования с так называемого четырехугольника Саккери (рис. 1), т.е. с четырехугольника BCED , у которого BC = DE , а углы при вершинах C и E прямые.

Рисунок 1

Заметив, что углы при вершинах B и D обязательно равны, Саккери рассмотрел поочередно три гипотезы: верхние углы четырехугольника тупые, прямые и острые. Он доказал, что любая из этих гипотез, если ее принять для какого-нибудь одного такого четырехугольника, остается в силе для всех таких четырехугольников. Саккери намеревался обосновать гипотезу о том, что верхние углы прямые, доказав, что любая другая гипотеза приводит к противоречию. Вскоре он отверг гипотезу о тупом угле (и тем самым лишил себя возможности открыть эллиптическую геометрию), поскольку, как и все геометры до 1854, рассматривал второй постулат как утверждение о том, что прямая имеет бесконечную длину, и отказываться от этого постулата он не хотел. Точно также Саккери в конце концов отверг и гипотезу об остром угле, но прежде, чем принять это ошибочное решение, он, сам того не ведая, открыл многие теоремы геометрии, получившей впоследствии название гиперболической.

А.Кэли (1821–1895) и Ф.Клейн (1849–1925) прояснили связь между двумя упомянутыми вариантами, разработав в аналитической форме то, что ими было названо «эллиптической» и «гиперболической» геометриями. Евклидова геометрия является предельным случаем каждой из них, и это верно в отношении любой из аналитических формул таких геометрий. Большие круги (геодезические) на сфере, являющейся поверхностью постоянной положительной кривизны (т.е. сумма углов криволинейного треугольника больше суммы двух прямых.), играют роль прямых и порождают эллиптическую геометрию; аналогичным образом, на поверхности постоянной отрицательной кривизны (сумма углов криволинейного треугольника меньше суммы двух прямых) геодезические круги порождают гиперболическую геометрию.

Примером поверхности положительной кривизны является поверхность шара. Условимся считать «прямой» на сфере любую окружность большого круга, т.е. окружность, получаемую при пересечении сферы плоскостью, проходящей через центр шара. Оказывается, что все прямые здесь пересекаются. Следовательно, в такой геометрии не существует параллельных прямых. Можно построить и другие наглядные и поучительные модели эллиптической и гиперболической геометрий, но важно сознавать, что все эти модели содержатся в более общем подходе Римана.

В 1854 Б.Риман (1826–1866) заметил, что из неограниченности пространства еще не следует его бесконечная протяженность. Смысл этого утверждения станет яснее, если представить, что в неограниченной, но конечной вселенной астроном в принципе мог бы увидеть в телескоп, обладающий достаточно высокой разрешающей способностью, свой собственный затылок (если отвлечься от небольшой детали, связанной с тем, что свет, отраженный от затылка, достиг бы глаза астронома через тысячи миллионов лет). В своем доказательстве того, что внешний угол при любой вершине треугольника больше внутреннего угла при любой из двух остальных вершин, Евклид неявно использовал бесконечную длину прямой. Из этой теоремы тотчас же следует теорема о том, что сумма любых двух углов треугольника меньше суммы двух прямых углов. Если отказаться от бесконечной длины прямой, то гипотеза Саккери о тупом угле становиться верной и из нее следует, что сумма углов треугольника больше суммы двух прямых. Такое положение дел было давно известно в сферической тригонометрии, где стороны треугольника являются дугами больших кругов. Риман внес эпохальный вклад, распространив представление о конечном, но неограниченном пространстве с двух на три и большее число измерений.

Ф.Клейн (1849–1925) первым увидел, как избавить сферическую геометрию от одного из ее недостатков – того, что две лежащие в одной плоскости «прямые» (два больших круга на сфере) имеют не одну общую точку, а две (рис. 2).

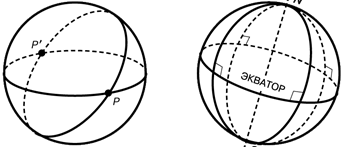
Рисунок 2

Так как для каждой точки существует одна-единственная точка-антипод (диаметрально противоположная точка), а для любой фигуры существует ее дубликат из точек-антиподов, мы можем, ничем не жертвуя, но многое приобретая, абстрактно отождествить обе точки такой пары, объединив их в одну. Таким образом можно изменить смысл термина «точка», условившись впредь называть «одной точкой» пару диаметрально противоположных точек. Иначе говоря, точки так называемой «эллиптической» плоскости представлены на единичной сфере парами точек-антиподов или диаметрами, соединяющими точки-антиподы. Вся эллиптическая прямая замкнута, как окружность, но, поскольку каждая из ее точек представлена двумя точками-антиподами на единичной сфере, полная длина эллиптической прямой равна половине длины окружности большого круга, т.е. ее полная длина равна.

Карл Гаусс первым подошел к проблеме с современной точки зрения, согласно которой геометрию, отрицающую пятый постулат, надлежит развивать ради нее самой, не ожидая, что при этом возникнет какое-то противоречие. Письма Гаусса к друзьям говорят о том, что к 1816 он преодолел традиционный предрассудок относительно неизбежности противоречия и развил «антиевклидову» геометрию, удовлетворяющую гипотезе Саккери об остром угле. В этом же направлении работали и два других выдающихся ученых того времени – Янош Бойяи и Н.И.Лобачевский. В 1833 году Бойяи опубликовал свои исследования как приложение (по-латыни «»Appendix») к курсу математики, написанному его отцом Фаркашем Бойяи. В «Аппендиксе» Янош Бойяи в чрезвычайно сжатой форме изложил основы неэвклидовой геометрии. Его отец послал экземпляр «Аппендикса» Карлу Гауссу. В ответном письме Гаусс писал, что не может хвалить работу Яноша, так как это значило бы хвалить самого себя, потому что результаты этой работы почти сплошь совпадали с теми результатами, которые были давно получены им самим. Ответ Гаусса произвел на Яноша Бойяи столь тягостное впечатление, что он даже не поверил ему. Он не знал в это время, что приоритет открытия новой геометрии уже принадлежал русскому математику Лобачевскому. Именно поэтому по сегодняшний день эту геометрию называют геометрией Лобачевского.

Один из подходов к построению гиперболической геометрии исходит из некоторых фундаментальных аксиом порядка, справедливых и в евклидовой, но не в эллиптической геометрии. Если считать «точки» исходными понятиями, то запись [ABC ] означает, что точка B лежит «между» точками A и C (это первичное отношение мы принимаем, не пытаясь его определить). Первые четыре аксиомы порядка утверждают, что 1) существует по крайней мере две точки; 2) если A и B – две различные точки, то существует по крайней мере одна точка C , для которой [ABC ]; 3) эта точка C отлична от точки A и 4) порядок [ABC] влечет за собой [CBA], но не [BCA]. «Отрезок» AB , по определению, состоит из точек P , для которых [APB], а «луч» A/B («исходящий из A в другую сторону, чем B ») – из точек Q , для которых [QAB ]. «Прямая» AB состоит из отрезка AB , точек A , B и двух лучей A/B , B/A . Пятая аксиома утверждает, что если C и D – различные точки на прямой AB , то A лежит на прямой CD (из этой же аксиомы следует, что прямые AB и CD совпадают). Шестая аксиома дает нам точку вне данной прямой, а седьмая, сформулированная М.Пашем (1843–1931), позволяет определить плоскость как множество всех точек, коллинеарных с парами точек на одной или двух сторонах данного треугольника.

Большая часть вклада Бойяи связана с теми разделами гиперболической геометрии, которые принадлежат и евклидовой геометрии. Его «абсолютная геометрия» может быть выведена из геометрии порядка, если к последней добавить еще одно фундаментальное отношение, а именно «конгруэнтность». Это отношение определяется пятью аксиомами типа «Если ABC и A B C  – два треугольника, таких, что BC  B C , CA  C A , AB  A B , а D и D  – еще две точки, такие, что [BCD ] и [B C D ] и BD  B D , то AD  A D ». Эти аксиомы служат основой теории длины и позволяют распространить отношение конгруэнтности с пар точек на углы. Определив обычным образом окружность, можно рассматривать первые четыре постулата Евклида как теоремы и доказать его первые двадцать восемь предложений, заменив слово «параллельные» на «не пересекающиеся». Однако необходимо тщательно избегать любого обращения к обычному представлению о сумме углов треугольника; например, нельзя более утверждать, что углы, опирающиеся на один и тот же сегмент окружности, равны, так как доказательство этого предложения зависело бы от суммы углов треугольника. С другой стороны, можно доказать, что три высоты остроугольного треугольника пересекаются в одной точке, построить теорию правильных многоугольников и правильных многогранников (с небольшими оговорками). Уточнив понятие параллельности (определив как параллельные лучи, которые просто не пересекаются), можно показать, что параллельность – отношение симметричное и транзитивное (т.е. если прямая r параллельна прямой s , то s параллельна r ; если r параллельна s , а s параллельна t , то r параллельна t ).

Множество прямых, параллельных данному лучу, называется «пучком параллельных»; он содержит единственную прямую, проходящую через любую заданную точку. Следуя аналогии с обычным пучком (состоящим из всех прямых, проходящих через точку), можно считать, что пучок параллельных определяет «бесконечно удаленную точку», или, по терминологии Д.Гильберта (1862–1943), «конец». Вместо того, чтобы говорить, что два луча (или две прямые) параллельны или что они принадлежат некоторому пучку параллельных M , говорят, что два луча имеют общий конец M . Луч, проходящий через точку C и принадлежащий данному пучку параллельных, принято обозначать CM , как если бы это был отрезок; тот же символ CM можно использовать и для обозначения всей прямой. Если BM и CM – параллельные лучи, то фигура MCB называется «асимптотическим треугольником», поскольку она во многом ведет себя, как обычный треугольник. В частности, два асимптотических треугольника конгруэнтны, если у них имеется по конгруэнтной стороне и конгруэнтному углу.

Рассмотрим содержание гиперболической геометрии.

Из абсолютной геометрии Бойяи можно вывести евклидову геометрию, добавив евклидову (или аффинную) аксиому: через точку B , не лежащую на данной прямой r , можно провести не более одной прямой, параллельной данной. Гиперболическую геометрию можно вывести из абсолютной геометрии, добавив гиперболическую аксиому. Система аксиом гиперболической геометрии отличается от эвклидовой аксиоматики в одном: в качестве аксиомы о параллельных берется положение о том, что «через точку, находящуюся вне прямой, можно провести две прямые линии, параллельны ей». Из этой аксиомы шаг за шагом геометрически выводятся другие свойства этой геометрии. Таким образом, лучи BM и BN на рис. 2 могут быть оба параллельны r , а если M и N их концы, то r называется «прямой MN ». Любая прямая, например t , являющаяся продолжением стороны угла NBM , образует с r пару «гиперпараллельных», т.е. пару прямых, которые не пересекаются и не параллельны. Две такие прямые имеют единственный общий перпендикуляр. Множество прямых, перпендикулярных данной прямой a , называются «пучком гиперпараллельных» с «осью» a .

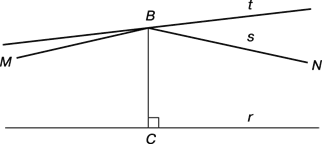
Рисунок 3

Отражение относительно BC показывает, что CBM и NBC – равные острые углы. Лобачевский назвал каждый из них «углом параллельности» П(a ), где a – длина BC . Он показал, что функция П(a ) монотонно убывает от    до 0, когда a возрастает от 0 до . Треугольник BMN естественно назвать «дважды асимптотическим треугольником». Два дважды асимптотических треугольника конгруэнтны, если имеют конгруэнтные углы. Если отрезок CB возрастает до тех пор, пока не превратится в луч CL , то BMN превращается в «трижды асимптотический треугольник» LMN , все три вершины которого являются концами (все три стороны такого треугольника бесконечны, а все три угла равны нулю). Все трижды асимптотические треугольники конгруэнтны.

Помимо геометрии римановых пространств, Риман был создателем ещё одной важнейшей геометрической дисциплины, значительно расширившей наши представления о пространстве, - топологии. Это раздел математики, занимающийся изучением свойств фигур (или пространств), которые сохраняются при непрерывных деформациях, таких, например, как растяжение, сжатие или изгибание. Непрерывная деформация – это деформация фигуры, при которой не происходит разрывов (т.е. нарушения целостности фигуры) или склеиваний (т.е. отождествления ее точек). Такие геометрические свойства связаны с положением, а не с формой или величиной фигуры. В отличие от евклидовой и римановой геометрий, геометрии Лобачевского и других геометрий, занимающихся измерением длин и углов, топология имеет неметрический и качественный характер. Раньше она носила названия «анализ ситус» (анализ положения), а также «теория точечных множеств». В научно-популярной литературе топологию часто называют «геометрией на резиновом листе», поскольку ее наглядно можно представлять себе как геометрию фигур, нарисованных на идеально упругих резиновых листах, которые подвергаются растяжению, сжатию или изгибанию.

Поясним суть ее проблем на одном примере. Возьмем некоторую поверхность и будем ее рассматривать как резиновую пленку, которую можно сжимать и растягивать, но не рвать. Тогда никакие из разрешенных операций не могут преобразовать сферу в тор (бублик); число дыр в поверхности называется ее «родом» и является «топологическим инвариантом». Аналогичный инвариант существует и для односторонних поверхностей, таких как лист Мёбиуса.

В последние десятилетия наши представления о пространстве сильно изменились под воздействием повсеместного принятия в физике концепции «пространства-времени». Связывание воедино двух фундаментальных понятий вынуждает перенести все внимание с «положения» на «событие». Выбирая из многообразия римановых метрик некоторую, в чем-то более предпочтительную, можно более удовлетворительным образом скоординировать результаты современной науки.

Литература

1. Мацуо Комацу, Многообразие геометрии, «Знание», 1981 год.

2. А.В.Силин, Н.А.Шмакова, Открываем неэвклидовую геометрию, «Просвещение», 1988 г.

3. Б.А.Розенфельд, История неэвклидовой геометрии, «Наука», 1976 г.

4. П.А.Широков, «Краткий очерк основ геометрии Лобачевского», «Наука», 1983г.

5. Н.А.Лицис, Философское и научное значение идей Н.И.Лобачевского, «Зинатне», 1976 г.

6. Энциклопедия «Мир вокруг нас».