Курсовая работа: Геометричні місця точок на площині та їх застосування

КУРСОВА РОБОТА

на тему:

«Геометричні місця точок на площині та їх застосування»

Вступ

Актуальність дослідження. Поняття геометричного місця точок у просторі (ГМТ) має велике методичне і загальноосвітнє значення. Неможливо переоцінити його роль у розвитку просторової уяви.

Розв'язування задач, в яких застосовуються геометричні місця точок як на площині, так і в просторі, активізують творчу думку і фантазію, розвивають логічне мислення, кмітливість, змушують перебирати в пам'яті всі відомі теореми з метою відбору і застосування найбільш придатної з них.

Таким чином, тема Геометричні місця точок на площині та їх застосування, на сучасному етапі є досить актуальною.

Зв ’ язок роботи з науковими планами, програмами, темами. Дана курсова робота пов’язана з дисципліною Геометрія та загальним навчальним планом Миколаївського державного університету імені В.О. Сухомлинського.

Об ’ єкт дослідження. Розділ геометрії – аналітична геометрії та його застосування на практиці.

Предметом дослідження є геометричні місця точок на площині та їх застосування.

Метою дослідження є теоретичне та практичне застосування поняття геометрії – геометричні місця точок на площині.

Відповідно до поставленої мети нам необхідно вирішити наступні завдання:

1. Дослідити наукову та методичну літературу з обраної теми курсової роботи.

2. Здійснити загальну характеристику визначення ГМТ в межах курсового дослідження.

3. Проаналізувати основні ГМТ на площині.

4. Привести приклади задач на відшукання ГМТ

5. Висвітлити процес застосування ГМТ до розв’язання задач на побудову.

Теоретичне та практичне значення . Матеріали даної курсової роботи можна використовувати при викладанні відповідної теми з курсу Геометрія, а також для участі у наукових семінарах та конференціях, викладання на уроках геометрії.

1. Визначення ГМТ

Геометричне місце точок є одним з найважливіших понять геометрії. Але воно широко використовується не лише в геометрії, ай в математичному аналізі, механіці і в багатьох технічних дисциплінах. Тому поняття геометричного місця точок має велике загальноосвітнє значення.

Означення. Геометричним місцем точок називаємо фігуру, всі точки якої мають певну властивість, яка належить обов'язково і виключно точкам цієї фігури.

Коли розглядати геометричне місце точок на площині, то можна одержати, наприклад: пряму, промінь, коло і інші плоскі криві, точку, сукупність ізольованих точок, сукупність прямих, відрізок, сукупність відрізків, дугу, сукупність дуг, деяку частину площини тощо.

На понятті про геометричне місце точок ґрунтується особливий спосіб розв'язування задач на побудову, що має назву методу геометричних місць. Суть його така: зводять всю задачу на побудову до відшукання положення на площині однієї або декількох точок, які визначаються двома умовами, що випливають з вимог задачі. Якщо відкинути одну з цих умов задачі, то вона стане невизначеною і решту умов буде задовольняти, не одна точка, а нескінченна множина точок, що утворюють якесь геометричне місце. Якщо потім відновити відкинуту умову, а відкинути другу, то решту умов, знов буде задовольняти нескінченна множина точок, що утворюють нове геометричне місце. Кожна точка перетину цих двох геометричних місць задовольняє вимогам задачі і, отже, буде шуканою. Задача матиме стільки розв'язків, скільки спільних точок мають знайдені геометричні місця.

Подана характеристика методу геометричних місць показує, що його застосовують при розв'язуванні таких задач, умову яких можна розчленувати на дві незалежні вимоги, кожна з яких окремо визначає відповідне геометричне місце точок. Правда, інколи одно з геометричних місць буває заданим самою умовою задачі.

Позитивними рисами методу є такі: а) при розв'язуванні задач методом гeoметричних місць спрощується відшукання плану розв'язування задачі і способу її побудови; б) відкидаючи одну умову задачі і змінюючи іншу, можна об'єднати декілька задач на побудову в одну групу і розглядати їх як різні варіанти деякої загальної конструктивної проблеми.

Пояснимо сказане про особливості методу геометричних місць точок на такому прикладі:

Задача. Дано трикутник ABC. Побудувати в площині три кутника точку М, яка була б на однаковій віддалі від вершин А та В і на віддалі d від третьої вершини С (рис. 202).

Аналіз. Шукана точка М повинна задовольняти дві умови: а) вона повинна знаходитись на однаковій віддалі від двох точок А і В і б) вона повинна знаходитись на віддалі d від третьої точки.

Відкинемо другу умову. Тоді одну першу умову буде задовольняти нескінченна множина точок, що утворюють геометричне місце – перпендикуляр, проведений через середину D відрізка АВ. Збережемо тепер другу умову і відкинемо першу. Тоді одну другу умову буде задовольняти нескінченна множина точок, що утворюють геометричне місце – коло з центром в точці С і радіусом, рівним d. Точки М і М₁ перетину першого геометричного місця з другим будуть Шуканими.

Побудов а. Для розв'язування задачі потрібно побудувати перше і друге геометричні місця.

Будуємо перпендикуляр ND до відрізка АВ в його середині D (основна побудова див. § 2) і коло радіусом, рівним а, з цент ром в С; точка перетину кола з перпендикуляром ND визначить шукану точку M.

Дослідження. Оскільки коло може перетинати пряму не більш ніж в двох точках, то залежно від даних (∆ ABC і d) задача може не мати жодного розв'язку або мати до двох роз в'язків. На рис. 202 показано випадок двох розв'язків.

При розв'язуванні задачі ми користувались першим і другим геометричним місцем, як даними. Ця обставина приводить до необхідності знання хоча б основних геометричних місць на площині, якщо ми бажаємо навчитись розв'язувати задачі на побудову методом геометричних місць.

2. Основні ГМТ на площині

І. Геометричним місцем точок, рівновіддалених від даної точки, є коло з центром у цій точці і з радіусом, який дорівнює даній відстані.
ІІ. Геометричним місцем точок, рівновіддалених від двох даних точок, є серединний перпендикуляр до відрізка, який з'єднує ці точки.
ІІІ. Геометричне місце точок, віддалених від даної прямої на відстань А, складається з двох прямих, паралельних даній і віддалених від неї на відстань h:
Геометричним місцем точок, рівновіддалених від двох паралельних прямих, є пряма, паралельна даним прямим і однаково віддалена від них.
Геометричне місце точок, рівновіддалених від двох прямих, що перетинаються, складається з двох прямих, які містять бісектриси кутів, отриманих в результаті перетину даних прямих.

Щоб знайти геометричне місце точок (фігуру), потрібно скласти за даною їх властивістю рівняння і назвати фігуру, яка визначається цим рівнянням.

Складаючи рівняння, спочатку позначаємо координати довільної точки шуканого геометричного місця трочок черех х, у. Потім, застосовуючи відомі рівняння (відстані між точками, середини відрізка, кола і прямої), складаємо нове рівняння, яке аналітично виражає зв’язок між координатами шуканої і даних точок. Цим самим обгрунтуємо пряме твердження: якщо М – довільна точка шуканого геометричного місця точок, то її координати задовольняють знайдене рівняння. Після цього доводимо обернене твердження: якщо координати довільної точки М задовольняють знайдене рівняння, то вона належить шуканому геометричному місцю точок.

Розглянемо приклади.

Задача 1. Дано коло радіуса R і точку А на ньому. Знайти геометричне місце точок, які ділять хорди, проведені через точку А кола, пополам.

Розв’язання. За початок координат візьмемо центр кола так, щоб точка А мала координати – R; 0 (мал. 134). Нехай АВ – довільна хорда, що проходить через точку А, а М – одна з точок шуканого геометричного місця точок, тобто така, що АМ = ВМ. Позначивши координати точок В і М відповідно через х₁ , у₁ і х, у, матимемо: Звідси

(1)

Точка В(х₁ ; у₁ ) лежить га колі, тому її координати задовольняють рівняння кола. Маємо: або, враховуючи рівності (1),

(2)

Звідси

(3)

Ми показали, що коли точка М – довільна точка шуканого геометричного місця точок, то її координати задовольняють рівняння (3).

Тепер потрібно довести, що довільна точка М (х; у), координати якої задовольняють рівняння (3), належить шуканому геометричному місцю точок. Розглянемо на координатній площині точку В з координатами х₁ =2х+R, у₁ =2у. З рівності (2) випливає, що точка В лежить на даному колі.

З другого боку, з рівності х₁ =2х+R, у₁ =2у дістанемо: Отже, точка М поділяє хорду АВ пополам.

Таким чином, рівняння є рівнянням шуканого геометричного місця точок. Цим рівнянням визначається коло радіуса з центром у точці (мал. 135).

Задача 2. Знайти геометричне місце точок, рівновіддалених від даної точки F і даної прямої d, яка не проходить через цю точку.

Розв’язання. Нехай відстань від даної точки F до даної прямої d дорівнює р. Візьмемо систему координат так, щоб вісь Ох проходила через точку F і була перпендикулярною до прямої d (мал. 136), а вісь Оу поділяла навпіл відрізок осі Ох між прямою d і точкою F.

Нехай М (х; у) – довільна точка шуканого геометричного місця точок. Опустимо з точки М на пряму d перпендикуляр МК. Координати точки К: ; координати точки F:

За умовою МК=MF. Запишемо цю рівність у координатах: Піднесемо до квадрата обидві частини цієї рівності і спростимо:

або

звідси

(1)

Ми показали, що координати х; у довільної точки М шуканого геометричного місця точок задовольняють рівняння (1). Справедливе й обернене твердження: точка, координати х, у якої задовольняють рівняння (1), належить шуканому геометричному місцю точок. Справедливі, рівність

Звідси, беручи до уваги, що х > 0 і ; маємо

З останньої рівності випливає, що точка М (х; у) рівновіддалена від прямої d і від точки F, тобто М належить шуканому геометричному місцю точок.

Знайдене рівняння у² =2 рх визначає лінію, яка називається параболою (мал. 137). Точка F називається фокусом параболи, а пряма d – директрисою.

Параболу можна побудувати так. Проведемо директрису параболи d і позначимо фокус F(мал. 138). Середина О відрізка DF належить параболі і є її вершиною. Через довільну точку К променя OF проведемо пряму, перпендикулярну до осі параболи. Знайдемо дві точки М і М₁ перетину цієї прямої з колом, центром якого є фокус F, а радіус дорівнює відстані від цієї прямої до директорії d. Точки М і М₁ належать параболі. Якщо проведемо кілька прямих, перпендикулярних до осі параболи, і побудуємо точки перетину їх з колами, центрами яких є фокус F, а радіуси дорівнюють відстаням від директриси до відповідної прямої, то дістанемо пари точок параболи. Знайдемо точки сполучимо плавною лінією за допомогою лекала.

Задача 3. Знайти геометричне місце точок, сума відстаней яких до двох даних точок є величина стала.

Розв’язання. Нехай відстань між даними точками F₁ iF₂ дорівнює 2 с. Візьмемо за початок координат середину О відрізка F₁ F₂ (мал. 139), а промінь OF₂ – за додатну піввісь Ох. Тоді точка F₁ матиме координати – с; 0, а точка F₂ – координати с; 0.

Нехай М (х; у) – довільна точка шуканого геометричного місця точок. За умовою сума F₁ M+F₂ M стала. Позначимо її через 2а. Запишемо цю рівність у координатах. За формулою відстані між двома точками дістанемо:

або

Піднесемо до квадрата обидві частини цієї рівності і спростимо:

Тепер знову піднесемо обидві частини рівності до квадрата. Дістанемо:

або після спрощення:

Оскільки F₁ M+F₂ M>F₁ F₂ , тобто 2а>2с, то а² – с² >0. Позначимо а² -с² =b² . Тоді останню рівність запишемо так: b² x² +a² y² =a² b² . Поділивши обидві частини рівності на a² b² , дістанемо:

(1)

Ми показали, що координати х; у довільної точки М шуканого геометричного місця точок задовольняють рівняння (1). Справедливе і обернене твердження: якщо координати довільної точки М задовольняють рівняння (1), то вона належить шуканому геометричному місцю точок. Таким чином, рівняння (1) є рівнянням шуканого геометричного місця точок.

Рівнянням визначається опукла замкнена лінія, яка називається еліпсом. Точки F₁ і F₂ називаються фокусами еліпса. Форму еліпса має лінія похилого розрізу циліндричних і конічних тіл: дерева, ковбаса, морквини тощо.

Еліпс можна побудувати так. Візьмемо нитку певної довжини (наприклад, 20 см) і закріпимо її кінці в точка F₁ та F₂ (мал. 140). (Довжина нитки має бути більшою за довжину відрізка F₁ F₂ ). Натягуємо нитку вістрям олівця і переміщаємо на площині. Вістря олівця опише еліпс. Для кожної точки еліпса сума її відстаней від двох нерухомих точок F₁ і F₂ є стала величина (у нашому прикладі ця сума дорівнює довжині нитки). Якщо довжину нитки залишити ту саму, а відстань між фокусами змінити і знову побудувати еліпс, то його форм а зміниться (еліпс витягнеться або округлиться).

Розглянутий спосіб побудови еліпса використовує садівник, щоб надати клумбі еліптичну форму, маляр, який будує еліптичний контур для розпису стелі, стоялр, виготовляючи дерев’яні деталі еліптичної форми.

3. Задачі на відшукання ГМТ

І. Геометричне місце точок, які перебувають на рівних віддалях від трьох даних точок А, В, С, що не лежать на одній прямій, є точка – центр кола, яке проходить через ці точки.

ІІ. Геометричне місце крайніх точок рівних відрізків, дотичних до даного кола, є коло, концентричне з даним.

ІІІ. Геометричне місце точок, які мають ту властивість, що кут між кожною парою дотичних, роведених з них до даного кола, має дану величину, є коло, концетричне з даним.

IV. Геометричне місце середин рівних хорд, проведених у даному колі К, є коло, концентричне з даним і дотичне до кожної з цих хорд.

V. Геометричне місце точок, що ділять в даному відношенні відрізки

C₁ D₁ , C₂ D₂ , C₃ D₃ і т.д. паралельних прямих, які перетинають сторони даного кута АОВ (рис. 203), є пряма, що сполучає вершину О кута з точкою, наприклад Е₃ , яка ділить один з даних відрізків C₃ D₃ в даному відношенні.

Зауваження. Якщо відношення, в якому поділені відрізки, дорівнює одиниці, то геометричним місцем точок є продовжена медіана трикутника, який одержуємо від перетину даного кута однією із згаданих паралельних прямих, проведених з вершини О.

VI. Геометричне місце точок, що їх віддалі від двох прямих АВ і CD відносяться, як m: n, є сукупність двох прямих LK і MN (рис. 204), що проходять через точку Е перетину прямих АВ і CD і через точки К і L, M і N перетину прямих, паралельних АВ і віддалених від неї на ь, з прямими, паралельними CD і віддаленими від неї на n.

VII. Геометричне місце точок, з яких відрізок АВ видно під даним кутом α, є дуга кола , стягувана хордою АВ, з центром О або О₁ (рис. 205).

Дуги АМВ і ANB, а також ентри О і О₁ симетричні відносно відрізка АВ.

Щоб побудувати центри О і О₁ , в цінцях відрізка АВ, з обох боків від нього, проводимо прямі під кутом α до прямої АВ і будуємо з точок А і В перпендикуляри до проведених прямих. На перетині цих перпендикулярів з перпендикуляром до відрізка АВ через його середину і лежать центри О і О₁ .

Зауваження. Точки А і В треба виключити, бо вони не мають властивості, яку мають всі інші точки .

VIII. Геометричне місце точок, що їх віддалі від двох даних точок А і В відносяться, як m: n, є коло, побудоване на відрізку CD, як на діаметрі, притому точки C і D на прямій АВ ділять відрізок АВ відповідно у внутрішньому і зовнішньому відношенні, рівному m: n. Інакше кажучи, точки А, С, В і D – гармонічно спряжені точки.

Доведемо теорему відносно поданого геометричного місця, або так званого кола Аполлонія.

Теорема 242. Довільна точка М така, що відношення її віддалей від двох даних точок А і В дорівн.є m: n, лежить на колі з діаметром CD, причому точки С і D ділять відрізок АВ відповідно зсередина і зовні у відношенні m: n.

Дані точки А і В і така точка М (поза прямою АВ), що МА: МВ =m: n (рис. 206).

Будуємо на прямій АВ такі дві точки С і D, що:

СА: СВ = DA: DB = m: n.

Сполучаємо точку М з точкою А, С, В і D. Через те що

, то

Тобто МС і MD – бісектриси відповідно внутрішнього і зовнішнього кутів трикутника АВМ, або кут CMD =

Отже, де не лежала б точка М, при умовы нашоъ теореми, завжди буде так, що Отже, точка М лежить на колі з діаметром CD.

Теорема 243. Довільна точка М кола з діаметром CD при умові, що точки C і D ділять відрізок АВ (точки А і В дані) відповідно зсередини і зовні у відношенні m: n, має ту властивість, що МА: МВ = m: n. Дані точки А, С, В і D так, що СА: СВ = m: n, і коло з діаметром CD (рис. 207).

Треба довести, що для довільної точки М кола існує відношення МА: МВ = m: n.

Через точку В проводимо пряму KL || MA.

З подібності трикутників АСМ, ВСК і ADM, BDL маємо:

тобто

Звідки одержуємо:

BK=BL.

Тому що то медіана прямокутного трикутника KLM, проведена на гіпотенузу, дорівнює її половині, тобто BM = BK = BL.

Таким чином, маємо що й треба було довести.

ХІХ. Геометричне місце точок, з яких два даних кола видно під одним і тим же кутом, є коло.

Доведемо теорему про дане місце точок.

Теорема 244. Будь-яка точка М, що має відносно двох даних кіл (рис. 208) К і К₁ таку властивість, що , де МЕ і MF джотичні, проведені з точки М до кола К, а MGі MH – до кола К₁ лежить на колі Аполлонія.

Нехай О і О₁ є центри кіл К і К₁ , а R і r – їх радіуси, проведені відповідно до точок F і G. Прямокутні трикутники OFM і O₁ GM подібні, бо мають по рівному гострому кутові α. Звідки маємо:

Отже, всі точки М шуканого геометричного місця лежать на колі Аполлонія, коли R≠r, і на прямій, якщо R=r.

Теорема 245. Якщо точка М лежить на колі з діаметром CD, причому точки C і D ділять лінію центрів ОО₁ даних кіл К і К₁ у відношенні R:r – радіусів цих кіл, то з точки М кола К і К₁ видно під одним і тим же кутом α.

Із точки М можна провести дотичні до кіл К і К₁ (рис. 208), якщо М зовнішня по відношенню до обох кіл. Провівши дотичну MF до кола К і дотичну MG до кола К₁ , знайдемо за властивістю кола Аполлонія, що в прямокутних трикутниках MOF і MGO₁

Якщо ж в двох прямокутних трикутниках гіпотенузи відносяться так, як два їх катети, то такі трикутники подібні. Отже, що й треба було довести.

Зауваження. Якщо дані кола К і К₁ перетинаються, то геометричне місце – коло – проходить через точки перетину; якщо кола К і К₁ внутрішньо дотикаються, то шукане геометричне місце буде точкою; якщо одне з кіл К і К₁ лежить всередині другого, то шукане геометричне місце точок не існує.

Х. геометрипчне місце точок таких, що сума квадратів їх віддалей від двох даних точок А і В дорівнює квадратові довжини даного відрізка, тобто а² (а – даний відрізок), є коло, що його центр є точка О – середина відрізка АВ, а радіус є відрізок де b дорівнює довжині відрізка АВ.

Доведемо теорему про дане місце точок.

Теорема 246. Будь-яка точка М, що має відносно двох даних точок А і В таку властивість, що МА² + МВ² = а² , де а – даний відрізок, лежить на колі з центром в точці О – середині відрізка АВ = b і радіусом

Нехай довільна точка М задовольняє рівність МА² +МВ² =а² (рис. 209).

Побудуємо паралелограм MANB; маємо:

AB² +MN² =2MA² +2MB² .

Але за умовою: АВ=b, МА² +МВ² =а² і діагональ MN=2OM, отже, з вищенаписаної рівності маємо:

4OM² =2a² -b² ,

звідки

Таким чином, доведено, що будь-яка точка М, що задовольняє умову теореми, лежить на колі, описаному з центра О радіусом

Зауваження 1. Коли дано відрізок АВ=b і відрізок, рівний а, то для того, щоб визначити точку М, що має властивість МА² +МВ² =а² , будуємо на гіпотенузі а будь-який прямокутний трикутник. Точка М перетину дуг, описаних з центрів А і В радіусами, відповідно рівними катетами побудованого прямокутного трикутника, якраз відповідає нашій умові.

Зауваження 2. а) Якщо b>a, то 2а² – b² >a² , тобто r=OM>Отже, коло, описане з центра О радіусом ОМ, охоплює відрізок АВ.

б) Якщо b=a, то 2а² -b² =a² =b² , тобто ; тим самим коло, описане з центра О радіусом ОМ, проходить через точки А і В, і, отже, АВ є діаметром цього кола.

в) Якщо b>a, але b<a √2, то OM<2a² -b² <a² , тобто OM< і, тим більше, отже, коло, описане з центра О радіусом ОМ, перетинає відрізок АВ.

г) Якщо b=a√2, то 2а² -b² =0, тобто ОМ=0, і геометричне місце точок перетворюється в точку О.

д) Якщо b>a√2, то 2а² -b² <0 і задача не має розв’язку.

Обернена теорема. Будь-яка точка М кола, описаного зсередини О даного відразка АВ, як з центра, радіусом де а – даний відрізок, задовольняє умову МА² +МВ² =а² .

Дані точки А і В, де АВ=b, відрізок а і коло, описане з середини О відрізка АВ, як з центрра, радіусом (рис. 210).

Треба довести, що будь-яка точка М побудованого кола відповідає умові: МА² + МВ² = а² .

Проводимо діаметр MN і будуємо паралелограмм MANB, з якого маємо: 2MA² + 2MB² = AB² + MN² , тобто MA² + MB² = a² , бо MN² = 2a² – b² , aAB² = b² .

ХІ. Геометричне місце точок таких, що різниця квадратів їх віддалей від двох даних точок А і В дорівнює квадратові даного відрізка а (тобто а² ), є пряма, перпендикулярна до прямої АВ в такій внутрішній або зовнішній точці С відрізка АВ, що СА² -СВ² =а² .

Доведемо теорему про дане геометричне місце точок.

Теорема 247. Будь-яка точка М, що має відносно даних точок А і В властивість: МА² – МВ² = а² , де а – даний відрізок, лежить на прямій, перпендикулярній до прямої АВ, і перетинає відрізок АВ в такій точці С, що СА² – СВ² = а² .

Дані точки А і В і відрізок а: приймемо, що точка М задовольняє умову: МА² – МВ² = а² (рис. 211 і 212).

Опустимо з точки М перпендикуляр на пряму АВ і доведемо, що точка С перетину проведеного перпендикуляра з прямою АВ задовольняє умову: СА² – СВ² = а² .

З прямокутних трикутників МАС і МСВ маємо: МА² = СА² + МС² і МВ² = СВ² + МС² , тобто МА² – МВ² = СА² – СВ² , або СА² – СВ² = а² , що й треба було довести.

Зауваження 1. Коли дані точки А та В і відрізок а, то для того, щоб побудувати точку М, яка мала б властивість МА² + МВ² = а² , на даному відрізку KLP = a, як на катеті, будуємо будь-який прямокутний трикутник KLP (рис. 213), але такий, щоб КР + LP було більше за відрізок АВ.

Коли з точки А, як з центра, опишемо дугу радіусом LP, а з точки В-дугу радіусом КР, то знайдемо точку М, що задовольняє умову МА² – МВ² = а² .

Перпендикуляр МС до прямої АВ і буде шуканим геометричним місцем (рис. 214).

Зауваження 2. а) Якщо МА² < MB² + AB² , тобто, якщо АВ² >МА² – МВ² , або АВ² > a² і АВ² > a, то – гострий і точка С лежить на відрізку АВ (рис. 211).

б) Якщо МА² = МВ² + АВ² , тобто, якщо АВ² = а² , або АВ = а, то - прямий і точка С зливається з точкою В.

в) Якщо МА² > MB² + AB² , тобто, якщо AB² < MA² – MB² , або AB² < a² і АВ < а, то - тупий і точка С лежить поза відрізком АВ (рис. 212).

Теорема 248. Будь-яка точка М прямої МС, перпендикулярної до даної прямої АВ і такої, що проходить через таку внутрішню або зовнішню точку С відрізка АВ, що СА² – СВ² = а² , де а – даний відрізок, задовольняє умову МА² – МВ² = а² .

Дані точки А і В, відрізок а і пряма МС, перпендикулярна до прямої АВ і така, що перетинає її в точці С всередині відрізка АВ (рис. 211) або поза відрізком АВ (рис. 212), причому СА² – СВ² = а² .

Доведемо, що будь-яка точка М, яка лежить на перпендикулярні МС, задовольняє умову МА² – МВ² = а² . З прямокутних трикутників МАС і МВС (рис. 211 і 212) маємо:

СА² = МА² – МС² і СВ² = МВ² – МС² .

тобто:

МА² – МВ² = СА² – СВ² , або МА² – МВ² = а² .

що й треба було довести

4. Застосування ГМТ до розв’язання задач на побудову

геометричний площина точка місце

Розв’язування задач на побудову методом геометричних місць. Задачі на побудову, що розв’язуються методом геометричних місць, можуть бути досить різноманітними. Вони часто відрізняються одна від одної як кількістю, так і особливостями тих геометричних місць, за допомогою яких визначається положення шуканої точки. Розв’язування задачі спрощукється або ускладнюється в залежності від того, в якій мірі в тексті задачі містяться прямі вказівки на ті геометричні місця, з допомогою яких дана задача може бути розв’язана.

Так, якщо задача подана у формі теореми, то відповідь на поставлене питання повністю або частково розв’язана і вимагається лише виконати відповідні побудови й обґрунтувати їх. Проілюструємо це на такому прикладі.

Відрізок прямої даної довжини ковзається по сторонах даного прямого кута. Довести, що геометричним місцем точок, що описуєються серединою цього відрізка, є чверть кола з центром у вершині прямого кута.

Тут відповідь частково відказана: шуканим геометричним місцем точок є чверть кола з центром у вершині прямго кута, і залишається побудувати радіус кола та обґрунтувати розв’язування.

Якщо ж в задачі за деякими даними вимагається побудувати певне геометричне місце точок без будь-яких вказівок до відповіді, то в такому випадку розв’язування задачі ускладнюється необхідністю спочатку знайти фігуру, утворену геометричним місцем точок, і потім відповідно обґрунтувати знайдений розв’язок. Попередній приклад задачі тепер виглядав би так.

Відрізок прямої даної довжини ковзається по сторонах даного прямого кута. Визначити геометричне місце точок, що їх описує середина цього відрізка.

Невідомість шуканої фігури в багатьох задачах на геометричні місця приводить до необхідності побудови лише ряду окремих точок її, дослідження того, чи всі ці точки належить шуканому геометричному місцю, і, нарешті, визначення положення шуканої фігури на площині відповідно до розміщення на площині даних в умові задачі елементів.

Виходячи з сказаного, розглянутий нами загальний план розв’язування задачі на побудову, на випадок розв’язування її методом геометричних місць, слід конкретизувати так:

1. В аналізі умови задачі встановлюємо способи побудови ряду окремих точок шуканого геометричного місця і будуємо робочий рисунок, зручний для обґрунтування задачі.

2. Побудова шуканої фігури внаслідок уточнення виду фігури, знайденої при аналізі.

3. Доведення установленої закономірності в розміщенні точок шуканого геометричного місця, тобто обґрунтування знайденого розв’язування задачі, причому для деяких задач доведення входить складовою частиною аналізу.

4. Дослідження розв’язку задачі в залежності від зміни даних умови і відсування найпростішого способу побудови знайденого геометричного місця точок.

Задача 1. Побудувати трикутник за основою, кутом при вершині і радіусу високого кола.

Аналіз. Нехай АВС – шуканий трикутник, А – даний його кут, r – заданий радіус вписаного кола, ВС = а – задана основа.

Розглянемо центр 0 вписаного кола. Точка О віддалена від точки ВС на відстань r (перша властивість центра). Крім цього (мал. 54), , так що (друга властивість центра).

ГМТ, яке має першу властивість, представляє пару прямих паралельних ВС. ГМТ, яке володіє другою властивістю (відрізок ВС видно із О під кутом ), представляє пару дуг сегментів, які містять кут . Кожна точка перетину цих двох геометричних місць може служити центром вписаного кола.

Побудова: 1) На довільній прямій відкладаємо відрізок ВС=а (мал. 55).

Дані будуємо поступово: 2) пару прямих р₁ і р₂ паралельних ВС і віддалених від ВС на даній відстані r; 3) пару сегментів, які містять кут ; 4) точку О як одну із точок перетину згаданих геометричних місць; 5) круг ω (О, r); 6) із точок В і С проводимо промені В і С, які дотикаються до круга, ω; 7) відмічаємо точку А перетину цих променів. Трикутник АВС – шуканий.

Дослідження: Щоб ікнули точки, перетину згадуваних вище двох геометричних місць, необхідно достатньо, щоб стріла сегмента була не менше відрізка r, тобто щоб виконувалось відношення:

(1)

Кроки 5, 6 і 7 завжди виконуються. Останнє слідує з того, що

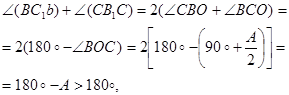
тому що промені в і с перетинаються. Не роблячи розмір між чотирма можливими однаковими розв’язками (в залежності від вибору точки О), приходимо до висновку, що при умові (1) задача має єдиний розв’язок, а якщо ця умова не виконується, то розв’язків немає.

Задача. Побудувати трикутник за його гострим кутом, при вершині, радіусом вписаного круга і сумі квадратів бокових сторін.

Аналіз. Нехай АВС – шуканий трикутник, ω(О₁ К) – описаний круг навколо нього, А=α – заданий кут, АВ² +АС² =d² ,де d – даний відрізок (мал. 56).

Величина хорди ВС визначається без умови, що її видно з деякої точки круга ω під даним кутом α, а отже, із центра О – під кутом 2α (рівним центральним кутом відповідають рівні хорди). Що стосується точки А, що вона визначається двома умовами.

1) Вона лежить на крузі ω; 2) вона належить ГМТ, для яких сума квадратів відстаней від точок В і С рівна d² (це також круг).

Побудова. Будуємо поступово: 1) круг ω (О; R) з центром в довільній точці О; 2) два радіуси ОВ і ОС цього круга під кутом 2α один до другого; 3) відрізок ВС і його середину М; 4) круг Г, який є геометричним місцем точок Р, для яких ВР² +СР² =d² ; 5) точку А перетин кругів ω і Г; 6) відрізки АВ і АС. Трикутник АВС відомий. Доведення зрозуміло з аналізу.

Дослідження. Коли круг Г існує і має спільну точку з дугою ВДС круга ω (мал. 56), то задача має єдиний розв’язок. В іншому разі розв’язку немає.

Зауваження: Так як радіус r круга Г дорівнює

МВ = Rsinα, BC = 2Rsinα, MD = R (1+cosα), то аналітично умову розв’язку можна записати так:

МВ<r≤MD

або після відповідних перетворень:

Висновок

Отже, в ході проведення дослідження ми дійшли наступних висновків.

Геометричним місцем точок називається фігура, що складається з усіх точок площини, які мають певну властивість.

Також, було досягнуто поставленої мети та вирішено визначені, відповідно до мети, завдання.

Література

1. І.Ф. Тесленко «Елементарна математика, геометрія», Київ, 1968 р.

2. Б.И. Аргунов и М.Б. Балк «Геометрические построения на плоскости», Москва, 1957 г.

3. М.І. Бурда, Л.М. Савченко «Геометрія» 8–9 кл., Київ «Освіта», 1966 р.

4. Чекова А.М. «Геометрія» 7–11 класи, 2007 р.

5. Тесленко І.Ф., Геометричні побудови, «Радянська школа», 1956 р.

Курсовая работа: Геометричні місця точок на площині та їх застосування

Вступ

2. Основні ГМТ на площині

4. Застосування ГМТ до розв’язання задач на побудову

Похожие рефераты: