| Скачать .docx | Скачать .pdf |
Реферат: Математическое выражение музыки
Настоящая наука и настоящая музыка требуют однородного мыслительного процесса. А. Эйнштейн
Нам известен пифагоров строй, т.е. математическое выражение интервальных коэффициентов, лидийской гаммы, или, в современной терминологии, строй натурального мажора:
1 9 81 4 3 27 243 2
8 64 3 2 16 128
до ре ми фа соль ля си до
9 9 256 9 9 9 256
8 8 243 8 8 8 243
Здесь цифры внизу обозначают интервальные коэффициенты соседних ступеней гаммы; напомним, что 9/8 есть тон, а 256/243- полутон. Основные консонансные (консонанс - согласованное сочетание двух звуков ) интервалы в пределах октавы - квинта и кварта - являются соответственно средним арифметическим и средним гармоническим частот основного тона и октавы. Кроме того, октава, квинта, кварта и тон образуют геометрическую пропорцию:
октава / квинта = кварта / тон.
Таким образом, музыкальная гамма разделена на пропорциональные части: она буквально пронизана пропорциями, а пропорциональность, как мы знаем, является одним из объективных критериев красоты. Однако на этом математика музыкальной гаммы не кончается, а, скорее, только начинается.
Прежде всего, из соотношения видно, что расстояния между соседними ступенями пифагорова строя неодинаковы. Поэтому, во-первых, от ноты до можно было играть только в лидийском ладу, а чтобы сыграть от этой ноты, скажем, в дорийском ладу, необходимо было перестраивать почти все струны лиры. Во-вторых, от ноты ре получался уже не лидийский, а фригийский лад и, вообще, от каждой новой ноты начинался новый лад ( 7 ладов - по одному на каждую из 7 нот октавы). Поэтому, чтобы сыграть мелодию в лидийском ладу от другой ноты (чего, безусловно, требовали ограниченные возможности человеческого голоса: один поет выше, другой - ниже), лиру, также следовало перестраивать. (Конечно, если всю жизнь играть в одном ладу и одной тональности, то семи нот в октаве будет вполне достаточно. До сих пор прекрасно обходятся семью звуками некоторые гармошки и другие инструменты).
Итак, для того, чтобы иметь возможность переходить из лада в лад и из тональности в тональность, строй должен быть равномерным, т.е. иметь одинаково высотные расстояния (интервальные коэффициенты) между звуками. Казалось бы, что проще: нужно разделить каждый тон - интервал пополам на два полутона, т.е. получить еще пять дополнительных звуков, и шкала пифагорова ![]() строя станет равномерной. Но вот тут то и таилась основная трудность.
строя станет равномерной. Но вот тут то и таилась основная трудность.
Дело в том, что половина тона (V9/8~1,0607) в точности не равна полутону (256/243~1,0545). Поэтому если в качестве единого масштаба строя взять полутон V9/8, т.е. заменить на него имеющиеся два полутона 256/243, то эти 12 новых полутонов приведут нас не точно в октаву, а чуточку выше: (V9/8) 12=(9/8)6=2,0273. Интервал между октавой, полученной шагами по 12-равномерным полутонам V9/8, и чистой октавой равен и называется пифагоровой коммой (коммой в музыкальной акустике называется интервал, не превышающий 1/9 целого тона. Пифагорова комма приблизительно равна 1/9 тона).
Представляя пифагорову комму в виде
![]()
![]()
![]()
мы получим ещё один важный результат: 12 квинт с точностью до пифагоровой коммы равны 7 октавам.
Но ![]()
![]() , т.е. новый полутон содержал иррациональное число V2,
которого пифагорейцы боялись, как огня. Взять столь “некрасивое” число в качестве единицы измерения музыкальной гаммы было немыслимым для пифагорейцев: это противоречило всей философии целочисленных отношений. Поэтому пифагорейцы пошли другим путём: в качестве основы музыкальной гаммы они взяли квинту, красивое число 3/2.
, т.е. новый полутон содержал иррациональное число V2,
которого пифагорейцы боялись, как огня. Взять столь “некрасивое” число в качестве единицы измерения музыкальной гаммы было немыслимым для пифагорейцев: это противоречило всей философии целочисленных отношений. Поэтому пифагорейцы пошли другим путём: в качестве основы музыкальной гаммы они взяли квинту, красивое число 3/2.
Рассмотрим ряд, составленный из степеней числа 3/2:
...![]()
![]()
![]() ...
...
Оказывается, с помощью этого красивого симметричного ряда можно получить все интервальные коэффициенты пифагорова строя. Начнем с середины ряда и все получаемые звуки будем сводить в одну октаву, умножая или деля их интервальные коэффициенты на нужные степени числа 2 (интервальный коэффициент октавы)ю Новые звуки будем обозначать либо ближайшим снизу основным звуком с добавлением слова “диез ” () при движении по квинтам вверх, либо ближайшим сверху основным звуком с добавлением слова “бемоль ” () при движении по квинтам вниз. Это означает соответственно повышение или понижение основного звука. Итак,
![]() соль
соль
![]()
![]()
![]()
![]() ре
ре
![]()
![]()
![]()
![]() ля
ля
![]()
![]()
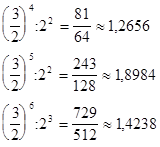
![]()
![]()
![]()
Как видим, двигаясь по квинтам вверх и вниз от основного тона, мы получили все ступени пифагорова строя, каждая из которых в свою очередь может быть повышена, понижена, дважды повышена или понижена и т.д. Процесс этот, к сожалению, бесконечен. Точного октавного повторения основного тона (до) мы так и не получим. (Легко видеть, что си-диез и ре-бемоль-бемоль совпадают с основным тоном (до) опять же с точностью до пифагоровой коммы.) Следовательно, и точно разделить октаву на целое число частей этим методом мы не сможем.
Таким образом, желая разделить пять ![]() тонов на полутона, мы получили, по крайней мере, 10 промежуточных звуков.
тонов на полутона, мы получили, по крайней мере, 10 промежуточных звуков.
Какие из этих дополнительных звуков взять: с бемолями или с диезами”? Для музыкантов, играющих на инструментах с нефиксированной высотой звуков (скрипачей, например), эта проблема не стоит. Они берут и те, и другие. В результате звучание скрипки становится более выразительным и контрастным, так как в ладе обостряются тяготения неустойчивых звуков к устойчивым. Этим во многом объясняется то “волшебное пение” скрипки, которое доступно ей одной.
Что касается инструментов с фиксированной высотой звуков, то введение 10 дополнительных звуков на 7 основных слишком бы усложнило и инструменты, и игру на них. Тем более, что и это не решщало окончательно проблему и более тонкие построения требовали всё новых и новых звуков. На сегодня в теории музыки известна масса строев с числом ступеней от 17 до 84! Но все они так и остались в кабинетах теоретиков. Практика же , руководствуясь мудрым критерием простоты (и красоты ), оставила только пять дополнительных звуков: по одному в каждом из целых тонов. Они и стали чёрными клавишами (дополнительными) фортепиано.
Так в октаве стало 12 звуков. Поскольку каждая пара дополнительных звуков отличалась лишь на пифагорову комму (это легко проверить), то их попросту приравнивали между собой (до-диез стал равен ре-бемолю и т.д.). Такое приравнивание звуков с одинаковой высотой, но разными названиями в теории музыки называется энгармонизмом . Тонкости ладового звучания были принесены в жертву простоте. Инструменты же с числом звуков в октаве, превышающим 12, можно увидеть только в музеях. В московском Музее музыкальной культуры имени М. И. Глинки хранится рояль русского писателя, музыканта и музыковеда В. Ф. Одоевского (1804-1869), в каждой октаве которого 17 клавиш.
Квинтовая цепь пифагорова строя дала простой способ настройки инструментов с фиксированной высотой звуков: органов, клавесинов, фортепиано. От основного тона (сегодня по общему признанию им является звук ля первой октавы) откладывалось ? октав - скелет музыкальной шкалы. Эти октавы заполнялись 12 звуками вверх и вниз. Какие из звуков взять за дополнительные - повышенные или пониженные, - особого значения не имело. Важно было другое: пифагорова комма оставалась внутри октавы. Её можно было переместить в любое место октавы, но нельзя было сделать только одного: нельзя было от неё избавиться! И она продолжала портить кровь музыкантам на протяжении столетий. Почему?
Если взять пифагоров строй с пониженными дополнительными звуками:
си до ре ми фа соль ля си до1
.243 1 256 9 32 81 4 1024 3 128 27 16 243 2 512
256 243 8 27 64 3 729 2 81 16 9 128 243...
то в таком строе все квинты будут звучать чисто (иметь интервальный коэффициент 3/2), кроме одной. Квинта си - соль-бемоль будет иметь интервальный коэффициент 1024 / 729 : 243 / 256 ~ 1,4798, а не 1,5! От чистой квинты она отличается на пифагорову комму: 1,5 / 1,4798 ~ 10136. Такая квинта на органе издавала пронзительный, неприятный звук, похожий на завывание волка, за что и была прозвана “волчьей квинтой” или просто “волком”. Обращением “волчьей квинты ” является “волчья кварта” соль-бемоль - си , которая тоже отличается от чистой кварты (4/3 = 1,333...) на пифагорову комму: 243 / 127 : 1024 / 729 ~ 1,3515;
1,3515 / 1,3333 ~ 1,0136. Можно сказать, что вся история развития музыкальных строев была историей борьбы с “волками”. Но об этом - чуть позже.
А сейчас обратим внимание на второй существенный недостаток пифагорова строя. Его заметил ещё во II веке древнегреческий ученый пифагореец Дидим. Дело в том, что пифагорова терция (81 / 64) при гармоническом, т.е. одновременном, исполнении обоих тонов, образующих терцию, звучит слишком напряжённо. Дидим предложил заменить пифагорову терцию (81 / 64) так называемой “чистой терцией” (5 /4 = 80 / 64), которая гармонически звучит значительно приятнее, хотя, как видим, лишь чуть - чуть отличается от пифагоровой терции. Разность пифагоровой и чистой терций (81 / 64 : 80 / 64 = 81 / 80 ~ 1,0125) называется дидимовой коммой и приблизительно равна1 / 10 целого тона.
Однако идеи Дидима, как это не раз случалось сучёными Древней Греции, опередили историю почти на полторы тысячи лет. Они не нашли подходящей почвы для развития, увяли, умерли и были воскрешены только в конце XV века...
...В XIV веке в Европе получает широкое распространение орган, ставший официальным инструментом католической церкви. С развитием органа развивается и многоголосие, которого не знала ни Древняя Греция, ни раннее средневековье. В течение столетий орган настраивался в пифагоровом строе. Никакого другого строя средневековье не знало. Но пифагоровы терции звучали на органе особенно жёстко и не давали покоя музыкантам.
В XVI веке выдающийся итальянский композитор и музыкальный теоретик Джозеффе Царлино (1517-1590) воскресил идеи Дидима. Так родился новый квинтово - терцовый строй, названный чистым строем. Новое всегда с трудом пробивает себе дорогу. Учение Царлино подверглось резким нападкам. Любопытно, что среди тех, кто не признавал учения Царлино и вёл с ним непримиримую борьбу, был Винченцо Галилей - выдающийся итальянский лютнист и отец великого революционера Галилео Галилея.
Чистая терция (5 /4), ставшая наравне с квинтой полноправной хозяйкой нового строя, звучит приятнее пифагоровой. Отметим одну поразительную закономерность: интервальный коэффициент чистой терции (её называют также большой терцией) есть среднее арифметическое интервальных коэффициентов основного тона (1) и квинты (3 /2):
![]()
![]()
А дополнение большой терции (5 /4) до квинты (3 /2) - малая терция (3 /2 : 5 /4 = 6 /5) - является средним гармоническим основного тона и квинты:
![]()
![]()
Оба этих интервала дают приятное звучание; таким образом, закон целочисленных отношений Пифагора расширяется, а внутри музыкальной гаммы появляются ещё две пропорции!
Предполагают, что ещё Архит умел выражать большую и малую терции как среднее арифметическое и гармоническое тона и квинты. Однако письменное свидетельство этому мы находим лишь в объёмном труде “Универсальная гармония” Марена Мерсенна (1588-1648) - монаха францисканского ордена, французского математика, теоретика музыки и философа, учившегося в иезуитском колледже Ла Флеш вместе с Рене Декартом. Труд Мерсенна - нескончаемое исследование об интервалах, полное всеобъемлющих умозрений. На десяти страницах огромного формата автор глубокомысленно обсуждает, например, “является ли унисон консонансом”, и попутно решает вопрос, “как бы человек мог поднять землю”, и т.д. Однако, несмотря на чрезвычайную напыщенность, которая, впрочем, была неотъемлемой чертой всех сочинений того времени, работа Мерсенна содержала интересные идеи и прозрения. В частности, это касалось консонантности и пропорций большой и малой терций. Сегодня большую и малую терции относят к группе несовершенных консонансов.
Но вернёмся к работам Царлино. Выдающейся заслугой его было не только выявление консонантности большой терции (5 /4), но и построение “совершенной гармонии” - объединение большой терции и квинты в гармоническое трезвучие. Это был первый в истории музыки аккорд, а само трезвучие
![]()
ныне именуется мажорным и является основой всего гармонического языка музыки. Кроме того, Царлино обнаружил, что если отложить те же большую терцию и квинту вниз от основного тона, то окраска звучания аккорда существенно изменится. Светлые тона мажора подёргиваются пасмурной дымкой иного звучания - минора. Приводя аккорд 2/3 : 4/5 : 1 к основному тону (умножая на 3/2, т.е. сдвигая вверх на квинту), получаем минорное трезвучие
![]()
![]()
Так был открыт закон, известный сегодня каждому юному музыканту: смена большой терции на малую переводит мажорное трезвучие в минорное.
Мажорное трезвучие было взято за основу чистого строя. Обрамляя мажорное трезвучие 1 : 5/4 : 3/2 такими же трезвучиями сверху и снизу и сводя умножением и делением на 2 построенные звуки в одну октаву, получаем чистый строй лидийской гаммы (натурального мажора)
до ре ми фа соль ля си до1
1 9 5 4 3 5 15 2
8 4 3 2 3 8
9 10 16 9 10 9 16
8 9 15 8 9 8 15
Отмечены тоны, изменившиеся по сравнению с пифагоровым строем, цифры внизу обозначают интервалы между ступенями.
Как видим, числовые характеристики чистого строя более простые. Однако сам строй стал менее равномерным: в нём, кроме полутона 15 /16, появились две разновидности целых тонов 9/8 и 10/9. Знакомые с музыкальной грамотой, конечно, увидели, что мажорные трезвучия (4:5:6) чистого строя построены на тонике (до ), субдоминанте (фа), и доминанте (соль ).
С помощью целых тонов 9/8 и 10/9 и полутона 16/15 легко построить чистый строй фригийской гаммы:
9 6 4 3 5 16
1 8 5 3 2 3 9 2
Теперь стало два деления целых тонов чистого строя. Чистый строй в истории музыки сыграл короткую, но заметную роль. Его звучание стало намного ярче и богаче по сравнению с пифагоровым строем. Чистый строй способствовал формированию мажорного и минорного ладов, развитию музыкальной гармонии. Но...
Вместе с достоинствами пришли и недостатки. Всё те же ненавистные музыкантам “волки” поселились теперь уже не на дополнительных, а на основных ступенях чистого строя! Легко проверить, что квинта между II и VI ступенями (ре - ля) является самым настоящим “волком”: 5/3:9/8 = 27/20 = 1,35:
до ре ми фа соль ля си до1 ре1
..1 9 5 4 3 5 15 2 9 ...
![]() 8 4 3 2 3 8 4
8 4 3 2 3 8 4
|
|
Следовательно, настроив орган в чистом строе ноты до , например, органист не мог уже перейти в тональности ре мажор и ре минор , т.е. в те тональности, где “волчья квинта” входит в тоническое трезвучие и встречается наиболее часто. Разумеется, приходилось исключать и те тональности, где эта квинта входила в доминанту и субдоминанту, которые также являются основными ступенями лада. Таким образом, органист оказывался что называется связанным по рукам: модуляции, т.е. переходы, в другие тональности были крайне ограничены и опасны, и это лишало музыку значительной части её выразительных средств.
“Волки” продолжали донимать органистов. На фоне “совершенной гармонии” чистого строя это было особенно невыносимо. Забавный случай рассказывают о французском композиторе и теоретике музыки, страстном приверженце чистого строя, Жане Рамо (1683-1764). Однажды Рамо, желая отказаться от предлагаемой ему должности церковного органиста, выпустил из органа столько “волков”, что привёл в ужас святых отцов и убедил их в своей “бесталанности”. Святые отцы поспешили удалиться вместе со своими лестными предложениями.
Однако проблема оставалась. Выгнать “волков” из органа, т.е. найти закон построения нового музыкального строя, а значит, и рецепт новой настройки органа, наряду с музыкантами безрезультатно пытались и математики: Кеплер, Декарт, Лейбниц, Эйлер. О теории гармонии Эйлера шутливо говорили, что она слишком музыкальна для математиков и слишком математична для музыкантов.
Но то, что не смог сделать изощрённый ум математика, сделала обыкновенная смекалка простого органиста...