| Похожие рефераты | Скачать .docx | Скачать .pdf |
Дипломная работа: Элективный курс по теме: "Сюжетные задачи"
Департамент образования города Москвы
Государственное образовательное учреждение высшего профессионального образования города Москвы
«МОСКОВСКИЙ ГОРОДСКОЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ»
Математический факультет
Кафедра теории и методики обучения математике в школе.
Дипломная работа
По теме: «Элективный курс по теме: «Сюжетные задачи»
По специальности 050201.65 «Математика» с дополнительной специальностью «Информатика»
Студента
5 курса очной формы обучения
Турилова Я.В.
Научный руководитель:
Доцент кафедры ТиМОМвШ, к. п. н.
Зубарева И.И.
Москва, 2010г.
Оглавление
Введение
Глава 1 Научно-методические и теоретические основы организации элективных курсов
§1. Психо-физиологические особенности старшеклассников
§2. История возникновения и развития элективных курсов
§3. Элективные курсы в системе образования профильной школы
Глава 2. Элективный курс по теме: «Сюжетные задачи»
§1. Роль задач в обучении математике
§2. Сюжетные задачи
§3. Программа элективного курса
§4. Разработка занятий элективного курса
Заключение
Библиография
Введение
Наилучшим путем в обучении я считаю тот, который дает материал для мышления и творческих повторений, дает материал для создания идей, а сами идеи возникают уже непосредственно в душе ребенка путем естественной деятельности его психического аппарата.
Д.Д. Галанин
Сегодня новая концепция профильного обучения на старшей ступени общего образования предоставила учащимся широкие возможности самостоятельного выбора не только уровня, но и направления математической подготовки, поставив одновременно перед теорией и практикой обучения математике проблему создания системы курсов по выбору (элективных курсов), позволяющих выстраивать индивидуальные образовательные траектории, облегчающие переход от общего к профессиональному математическому образованию.
Организация школьного математического образования строится по принципам дифференцированного обучения, т.е. у учащихся имеется возможность выбора интересующего его профиля, в том числе и математического. Поэтому разработка новых учебных пособий, методических рекомендаций, учебных программ является важной задачей педагогической науки. Элективные курсы – это обязательные для посещения курсы по выбору учащихся, которые представляют широкие возможности для реализации принципов дифференцированного обучения, так как позволяют учитывать интересы учащихся, которые хотели бы получить углубленные знания по интересующему их направлению. Разработка программ таких курсов является важной и новой задачей современного школьного математического образования. Это обусловливает актуальность темы исследования. В качестве темы элективного курса, мы выбрали «Сюжетные задачи»
Целью написания дипломной работы является разработка и анализ методического обеспечения элективного курса на тему «Сюжетные задачи».
В ходе исследования решались следующие задачи:
· анализ психолого-педагогической литературы с целью выяснения психологических и социальных особенностей контингента учащихся старших классов и выявление организационно-педагогических аспектов дифференцированного обучения;
· анализ методического обеспечения элективных курсов и курсов по выбору в профильном обучении;
· разработка методического обеспечения элективного курса «Сюжетные задачи», включающую программу, составление системы задач, методику обучения решению задач различного сюжетного содержания и разработку отдельных занятий курса.
Данная работа состоит из введения, двух глав, заключения и библиографии.
В первой главе раскрывается психолого-педагогические особенности учащихся подросткового возраста, на которых ориентирован данный элективный курс, и специфика их обучения. Здесь, исследуются социальные и психологические особенности старших школьников. На основе анализа особенностей контингента делаются выводы о психолого-педагогических особенностях обучения математики в старших классах
Во второй главе рассматривается понятие сюжетной задачи; роль и место сюжетных задач в курсе алгебры; типология текстовых задач, обзор текстовых задач, входивших в задания ГИА-9, программа курса, теоретическое обоснование курса, методические рекомендации по решению сюжетных задач и методика проведения занятий. Практическая ценность работы определяется тем, что в ней разработаны учебные материалы для проведения элективного курса по выбранной теме, в частности, подобраны и систематизированы сюжетные задачи, разработана методика обучения решению сюжетных задач и часть из этих задач решена.
Глава 1: Научно-методические и теоретические основы организации элективных курсов
§1. Психо-физиологические особенности старшеклассников
В настоящее время школа испытывает значительные трудности, одна из причин которых видится в том, что обучение и воспитание в недостаточной степени опираются на комплекс имеющихся психолого-педагогических знаний о формировании и развитии личности ученика. Формирование личности происходит прежде всего в школьные годы, поэтому педагогам надо изучать индивидуальные особенности учащихся, создавать условия для реализации их творческих устремлений. Эффективность работы педагогов и психологов проверяется тем, насколько психологически и морально готовыми к взрослой жизни оказываются старшеклассники, насколько правильный выбор пути они сделали.
В старших классах школы развитие познавательных процессов детей достигает такого уровня, что они оказываются практически готовыми к выполнению всех видов умственной работы взрослого человека, включая самые сложные. Девушки и юноши уже могут мыслить логически, заниматься теоретическими рассуждениями и самоанализом. Они относительно свободно размышляют на нравственные, политические и другие темы, практические не доступные интеллекту младшего школьника. У старшеклассников отмечается способность делать общие выводы на основании частных посылок и, напротив, переходить к частным умозаключениям на базе общих посылок, т.е. способность к индукции и дедукции. Важнейшее интеллектуальное приобретение подросткового возраста – это умение оперировать гипотезами.
К старшему школьному возрасту дети усваивают многие научные понятия, обучаются пользоваться ими в процессе решения различных задач. Это означает сформированность у них теоретического или словесно-логического мышления. Одновременно наблюдается интеллектуализация всех остальных познавательных процессов. Долгое время развитием таких сторон интеллекта, как здравый смысл, смекалка, интуиция школа пренебрегала или сводила их главным образом к приобретению учащимися трудовых умений и навыков. В структуру практического интеллекта, на совершенствование которого следует обращать особое внимание в старших классах, входят такие качества ума, как предприимчивость, экономность, расчетливость, умение быстро и оперативно решать возникающие задачи. Предприимчивость проявляется в том, что в сложной жизненной ситуации человек способен находить несколько решений возникшей проблемы, а главное, в том, что какая бы проблема перед ним не возникала, он всегда готов и в состоянии отыскать ее оптимальное решение в практическом плане. Предприимчивый человек из любой ситуации сможет найти выход. Экономность как качество практического ума состоит в том, что обладающий этим качеством человек в состоянии найти такой способ действия, который в сложившейся ситуации с наименьшими затратами и издержками приведет к нужному результату. Расчетливость проявляется в умении заглядывать далеко вперед, предвидя последствия тех или иных решений и действий, точно определять их результат и оценивать, чего он может стоить.
Умение оперативно решать поставленные задачи – динамическая характеристика практического интеллекта, проявляющаяся в количестве времени, которое проходит с момента возникновения задачи до ее практического решения. Подростковый возраст отличается повышенной интеллектуальной активностью, которая стимулируется не только естественной возрастной любознательностью подростков, но и желанием развить, продемонстрировать окружающим свои способности, получить высокую оценку с их стороны. Подростки могут формулировать гипотезы, рассуждать предположительно, исследовать и сравнивать между собой альтернативы при решении одних и тех же задач. Сфера познавательных, в том числе учебных, интересов подростков выходит за пределы школы и приобретает форму познавательной самодеятельности - стремления к поиску и приобретению знаний, к формированию полезных умений и навыков. Подростки находят занятия и книги, соответствующие их интересам, способные дать интеллектуальное удовлетворение. Стремление к самообразованию – характерная особенность и подросткового, и юношеского возраста. Развитие самосознания старшеклассников выражается в применении мотивации основных видов деятельности: учения, общения и труда, в проявлении ощущения взрослости. Все это приводит к переосмыслению содержания целей и задач деятельности. Характерной особенностью подросткового возраста является готовность и способность ко многим различным видам обучения, причем как в практическом плане (трудовые умения и навыки), так и в теоретическом (умение мыслить, рассуждать, пользоваться понятиями). На этом этапе развитии подросток способен самостоятельно выбирать нужную ему ту, или иную информацию. Мышление подростка характеризуется стремлением к широким обобщениям. Одновременно с этим складывается новое отношение к учению, особенно в последних классах школы. Ее выпускников привлекают предметы и виды знаний, где они могут лучше узнать себя, проявить самостоятельность, и к таким знаниям у них вырабатывается особенно благоприятное отношение. Специфика юности заключается в том, что именно в эти годы идет активный процесс становления мировоззрения, и к окончанию школы мы имеем дело с человеком, более или менее определившимся, со взглядами хотя и не всегда правильными, но стабильными.
Как отмечал Р.С.Немов, интеллектуальная зрелость, в том числе нравственно-мировоззренческая, готовность старших школьников ставить и решать, различные жизненные задачи в этом возрасте очевидна, хотя здесь говорить о ней пока что приходится в общем виде, имея в виду сравнительно невысокий уровень интеллектуального развития немалого числа современных юношей и девушек.
Речь идет о возможностях, которые имеются у всех старшеклассников, и многими из них практически реализуются. Значительны и индивидуальные различия, существующие между старшеклассниками, причем в настоящее время даже наблюдается тенденция к их увеличению в связи с дифференциацией учебных программ, учебных заведений, относительной свободой выбора в них учебных предметов. Большинство старших школьников к окончанию школы самоопределяются в будущей профессии. У них складываются профессиональные предпочтения, которые, однако, не всегда являются достаточно продуманными и окончательными.
Будущие профессиональные успехи детей в немалой степени определяются трудовыми умениями и навыками, которые активно формируются в школьные годы. Без достаточно высокого уровня общего интеллектуального развития немыслимы сколько-нибудь значительные успехи в любом виде деятельности. Не менее важны и специальные способности, проявляющиеся в трудовых умениях и навыках, являющихся базой для многих различных видов профессиональной деятельности. Подростковый и ранний юношеский возраст – это время профессионального самоопределения. Очень важно именно в эти годы окончательно выявить и по мере возможности развить те способности, на основе которых юноше можно было бы разумно и правильно осуществлять выбор профессии. Начиная со средних классов школы наряду с общеобразовательным должно быть организовано и специальное обучение детей, профессионально ориентирующее их в соответствии с имеющимися задатками и способностями на выбор вида и рода занятий, причем на добровольной основе. Т.е. профессионализация обучения с одновременной его дифференциацией по способностям должна вводиться параллельно и в дополнение к общеобразовательной программе, т.к. основной направленностью личности старшеклассника является, ни что иное, как, выбор своего жизненного пути, который в свою очередь неразрывно связан с выбором профессии.
§2. История возникновения и развития элективных курсов
Факультативные занятия являются одной из форм дифференцированного обучения. 10 ноября 1966 года было опубликовано правительственное постановление «О мерах дальнейшего улучшения работы средней общеобразовательной школы». В нем, в частности, отмечалось отставание уровня учебно-воспитательной работы школы от потребностей практики, и в связи с этим была намечена система мер по ликвидации этого отставания, среди которых нашли отражение новые, принципиально важные для школы формы обучения. Одной из них явились факультативы. В постановлении было сказано, что они создаются «для углубления знаний по физико-математическим, естественным и гуманитарным наукам, а также для развития разносторонних интересов и способностей учащихся». Таким образом, факультативные занятия явились формой дифференциации обучения, учитывающей индивидуальные склонности и способности учащихся.
Однако термин «факультативные предметы» был известен еще в XIX веке. П.Ф. Каптерев в своей книге «О разнообразии и единстве общеобразовательных курсов» в 1893 году употребил его для названия углубленных курсов в старших классах. По мнению Каптерева, весь общеобразовательный курс, в частности математики, должен занимать восемь лет и распадаться на восемь классов, тогда «общая часть курса должна занимать никак не менее четырех лет, причем общеобразовательные предметы не должны, конечно, прекращаться с пятого года учения, но продолжаться и в остальные годы, постепенно сокращаясь и уступая свое место факультативным, которые в последние годы учения являются преобладающими, сосредоточивающими на себе если не исключительное, то преимущественное внимание учащихся. Начавшись общими предметами, курс оканчивается факультативными».
К 1966 году, к моменту появления факультативных курсов, отечественной школой уже был накоплен значительный опыт по организации и проведению таких форм дифференцированного обучения, как классы с углубленным изучением ряда предметов и специализированные школы. Факультативные занятия не только не противоречили названным формам, но и прекрасно дополняли их, так как, являясь самой подвижной, доступной и массовой формой обучения, могли вводиться практически в каждой школе. Учитель со своими учениками, пожелавшими посещать факультатив, опираясь на примерные программы факультативных курсов, мог создать свой собственный курс, отвечающий интересам конкретных учеников, что очень важно специально подчеркнуть.
В практику работы школы факультативные занятия вошли, начиная с 1967/1968 учебного года. Начался первый этап введения факультативов по математике в школу.
Первые курсы назывались «Дополнительные главы и вопросы математики» и «Специальные курсы». В журнале «Математика в школе» были опубликованы программы этих курсов (1967. – № 1; № 2; № 3). В это время факультативные курсы были ориентированы на новую программу (с конца 60-х годов прошлого века в нашей стране началось движение за реформу математического образования) по математике и являлись местом апробации новых тем. После широкой экспериментальной проверки на факультативных занятиях некоторые темы были включены в основной курс по математике. Например, «Метод координат», «Множества и операции с ними», «Бесконечные множества», «Геометрические преобразования», «Производная» и др.
Уже в конце учебного года (10-12 июня 1968 года) в Москве состоялось совещание по обмену опытом углубленного изучения отдельных школьных предметов по выбору учащихся. Делегаты обсудили итоги первого года внедрения факультативных занятий в школу, рассмотрели широкий круг вопросов, связанных с их организацией, содержанием, методами и формами проведения, оценкой знаний учащихся, местом факультативных занятий в учебно-воспитательном процессе, связи с другими занятиями по математике, в том числе внеклассных и т.п.
По мере внедрения в жизнь новых программ обязательного курса математики, программа факультативного курса «Дополнительные главы и вопросы математики» претерпела ряд изменений. Так, в 1973/1974 учебном году, в связи с переходом 7 класса (современный 8 класс) на новые программы, а 9 класса (современный 10 класс) - на переходные программы по математике, была принята усовершенствованная программа факультативных курсов, которая, как было отмечено выше, не включила ряд тем, переведенных в основной курс.
Например, дополнительные главы по курсу математики для 7-8 классов включили следующие темы:
1. Делимость чисел и простые числа.
2. Системы счисления и арифметические основы работы электронных вычислительных машин.
3. Элементы теории множеств.
4. Метод координат.
5. Функции и графики.
6. Номограммы.
Заметим, что, практически, нет геометрических тем, из шести – только одна, связанная с координатами, которая, на самом деле, не является чисто геометрической темой.
К 1980 году был завершен переход средней школы на новую программу по математике. Факультативный курс «Дополнительные главы и вопросы математики» с успехом выполнил свои функции и был заменен на новый факультативный курс. Начался второй этап введения факультативных занятий в школе.
Новый факультативный курс включил в себя три следующие раздела:
1. Избранные вопросы математики 7-10 (8-11) классы.
2. Математика в приложениях 9, 10 (10, 11) классы.
3. Алгоритмы и программирование 8-10 (9-11) классы.
Последний раздел заменил специальные курсы по математике. Программа данных факультативных курсов была опубликована в журнале «Математика в школе» (1980. - № 4. - С. 35). Для раздела «Математика в приложениях» журнал поместил примерное тематическое планирование с указанием рекомендуемых форм проведения занятий и списком литературы Для проведения занятий по первому разделу «Избранные вопросы математики издательство «Просвещение» выпустило соответствующую литературу (7-8 класс, 1978; 9 класс, 1979; 10 класс, 1980). Приведем основные темы этого курса.
7 – 8 (в настоящее время 8-9) классы:
1. Системы счисления и арифметические основы работы электронных вычислительных машин.
2. Симметрия.
3. Элементы математической логики.
4. Множества на координатной плоскости.
5. Бесконечные множества.
В теме «Симметрия» представлен содержательный материал. Рассмотрены перемещения (движения) плоскости: осевая симметрия, параллельный перенос, поворот, переносная, или скользящая, симметрия (последовательное выполнение осевой симметрии и параллельного переноса); симметрии различных фигур, в том числе правильных многоугольников, звездчатых правильных многоугольников; красивые розетки, линейные орнаменты (бордюры), симметрии решеток.
9 (сейчас 10) класс:
1. Метод математической индукции.
2. Элементы комбинаторики.
3. Элементы теории вероятностей.
4. Языки программирования.
5. Бинарные отношения и соответствия.
10 (сейчас 11) класс:
1. Дифференциальные уравнения.
2. Комплексные числа и многочлены.
3. Элементы сферической геометрии.
Как видим, геометрических тем в девятом (десятом) классе вообще не предусмотрено. В десятом (одиннадцатом) классе в числе элементов сферической геометрии рассмотрены следующие: начальные понятия сферической геометрии; соответствие между сферической геометрией и планиметрией; сферическая тригонометрия; перемещение сферы; площади сферических многоугольников; применение сферической геометрии в навигации; картографические проекции.
В помощь учителю, ведущему факультативные занятия по этому курсу, были изданы соответствующие методические пособия (Методика факультативных занятий в 7-8 классах. – М.: Просвещение, 1981; в 9-10 классах. – М.: Просвещение, 1983).
Как мы уже отмечали, началом новой реформы можно считать съезд работников народного образования, который проходил в Москве в декабре 1988 года. На нем была принята Концепция общего среднего образования, основным направлением которой была провозглашена широкая дифференциация обучения. Реформой предусматривалось дальнейшее развитие всех форм дифференциации, в том числе и факультативной, основной целью которой является возможность углубленного изучения отдельных предметом, в том числе и математики. Таким образом, начался третий этап введения факультативных занятий по математике.
В 1990 году была опубликована новая программа факультативных курсов (Программы средней общеобразовательной школы. Факультативные курсы. Сборник № 2. – Часть 1 (математика, биология, химия). – М.: Просвещение). В ней сказано, что на факультативных занятиях учащиеся углубляют знания по основному курсу, получаемые на уроках, приобретают умения решать более трудные и разнообразные задачи. Факультативные занятия предусматриваются с 7 класса. В старших (10-11) классах углубление основного курса носит систематический характер и выполняет функции подготовки к продолжению образования и к сдаче вступительных экзаменов в вузы.
Наряду с углублением основного курса, на факультативе целесообразно и определенное расширение содержание учебного материала, в основном за счет линии современных приложений математики. Характер прикладных факультативов на разных ступенях обучения также должен быть различным. Если в 7-9 классах это преимущественно «чистый» практикум, то в старших классах учащиеся должны познакомиться и с теоретическими основами приложений. В выпускных старших классах необходимы также факультативные курсы обзорного характера, освещающие роль и место математики в современном мире.
В предложенном факультативе предусмотрены такие факультативные курсы:
1. За страницами учебников математики (не следует путать с известной серией книг по математике с одноименным названием).
2. Математическая мозаика.
3. Подготовительный факультатив.
Первые два предназначены для учащихся основной школы, а последний – для старшеклассников. Для проведения первого факультатива была выпущена следующая книга: Факультативный курс по математике: Учебное пособие для 7-9 классов средней школы /Сост. И.Л. Никольская. – М.: Просвещение, 1991. В нее вошли следующие темы:
7 класс
· системы счисления;
· простые и составные числа;
· геометрические построения;
· замечательные точки в треугольнике.
8 класс
· числовые множества;
· метод координат;
· элементы математической логики;
· геометрические преобразования плоскости.
9 класс
· функции и графики;
· уравнения, неравенства, их системы;
· замечательные теоремы и факты геометрии;
· логическое строение геометрии.
Факультативный курс «Математическая мозаика» включает в себя такие вопросы:
7 класс
· магические квадраты;
· великаны и карлики в мире чисел;
· математические ребусы и шифровки;
· лист Мебиуса;
· математические игры.
8 класс
· принцип Дирихле;
· комбинаторные задачи;
· математические парадоксы и софизмы;
· логические задачи;
· разрезание фигур.
9 класс
· контрпримеры в математике;
· эвристики, аналогия, поиск закономерностей, выдвижение гипотез и обоснование гипотез, математическая индукция;
· занимательные задачи вероятностного характера.
Подготовительный факультатив для 10-11 классов имеет более узкую и конкретную направленность. Его целью является подготовка учащихся к продолжению образования, повышение уровня их математической подготовки. Преподавание на факультативе строится как углубленное изучение вопросов, предусмотренных программой основного курса математики. В программу факультатива вошли следующие вопросы:
· алгебраические уравнения;
· неравенства, системы;
· текстовые задачи;
· функции и графики;
· начала анализа
· квадратный трехчлен
· доказательства неравенств;
· тригонометрические функции;
· показательная и логарифмическая функции;
· числа и числовые последовательности
· нестандартные уравнения и неравенства
· задачи с параметрами;
· методы решения планиметрических задач;
· стереометрические задачи и методы их решения
Для проведения данного факультатива была выпущена соответствующая литература:
· Атанасян Л.С., Болибрух А.А. и др. Факультативные курсы по математике для 10-11 классов. – М.: НИИ школ Министерства образования РФ, 1989.
· Шарыгин И.Ф. Факультативный курс по математике. Решение задач. 10 класс. – М.: Просвещение, 1989.
· Шарыгин И.Ф., Голубев В.И. Факультативный курс по математике. Решение задач. 11 класс. – М.: Просвещение, 1991.
Отличительной чертой современного этапа развития факультативной формы обучения является то, что учителям предоставляется право работать по любой из опубликованных программ, в том числе и по авторским. Это решение было принято из-за того, что обучение на факультативных занятиях по единой программе, обязательной для всех, оказалось несостоятельным. Учителя вели, как правило, факультативные занятия или спецкурсы по собственной программе, учитывая специфику своего конкретного класса, интересы и запросы ребят. Кроме этого, в современных условиях необходимо учитывать также особенности уровневой дифференциации обучения в основной школе и профильную направленность в старших классах.
В 2002 году была принята новая Концепция профильного обучения на старшей ступени общего образования (приказ № 2783 от 18 июля 2002 года), в которой, наряду с базовыми и профильными курсами, выделяются специальные элективные курсы – курсы по выбору. Их с полным правом можно считать преемниками факультативных курсов. Действительно, и те, и другие, прежде всего, направлены на удовлетворение индивидуальных склонностей, потребностей учащихся, развитие их способностей. Но есть и большая разница. Например, факультативные курсы не были обязательными для всех учащихся. Существовала специальная программа факультативов по математике, которой должен был руководствоваться каждый учитель, ведущий факультативные занятия, были изданы учебные пособия.
Элективные курсы обязательны для всех учащихся, но какими им быть в конкретной школе во многом зависит от самих школьников, их интересов, запросов. В идеале предполагается с помощью курсов по выбору для каждого ученика построить индивидуальную образовательную программу, или траекторию. Элективные курсы будут начинаться в 9 классе основной школы в рамках предпрофильной подготовки, что должно оказывать существенное влияние на выбор основного профильного направления обучения в старшей школе.
§3. Элективные курсы в системе образования профильной школы
Принципиальным положением организации школьного математического образования в настоящее время является дифференциация обучения математике – уровневая дифференциация и профильная дифференциация в старших классах средней школы.
Программа по математике для средней общеобразовательной школы, работающей по базисному учебному плану, предполагает формирование у школьников представлений о математике как части общечеловеческой культуры, как определённом методе познания мира. Но на данный момент содержание школьного курса математики не соответствует требованиям, возникшим в современных условиях. Объём знаний, необходимый человеку, резко возрастает, в то время как количество отводимых часов для занятий сокращается. Математика как школьная дисциплина оставляет учащихся на рубеже прошлых веков и чрезвычайно мало знакомит с современными научными достижениями.
Одним из средств реализации требований программы и разрешения имеющихся проблем является переход школы на профильное обучение и введение элективных курсов по математике.
На данный момент в школе можно наблюдать разновидности курсов трех типов: базовые, профильные, элективные. Каждый из курсов этих трех типов вносит свой вклад в решение задач профильного обучения.
Профильные курсы обеспечивают углубленное изучение отдельных предметов и ориентированы, в первую очередь, на подготовку выпускников школы к последующему профессиональному образованию.
Одной из важнейших составных частей системы предпрофильной подготовки учащихся основной школы являются курсы по выбору.
Основные цели, стоящие перед курсами по выбору: создать условия, способствующие осознанному выбору профиля обучения в старшей школе, способствовать формированию личной ответственности учащихся за сделанный выбор профиля обучения в старшей школе.
Элективные курсы – обязательные для посещения курсы по выбору учащихся, входящие в состав профиля обучения на старшей ступени школы. Реализуются за счет школьного компонента учебного плана.
Они играют важную роль в системе профильного обучения на старшей ступени школы. Элективные курсы связаны, прежде всего, с удовлетворением индивидуальных образовательных интересов, потребностей и склонностей каждого школьника. Именно они по существу и являются важнейшим средством построения индивидуальных образовательных программ, т.к. в наибольшей степени связаны с выбором каждым школьником содержания образования в зависимости от его интересов, способностей, последующих жизненных планов. Элективные курсы как бы «компенсируют» во многом достаточно ограниченные возможности базовых и профильных курсов в удовлетворении разнообразных образовательных потребностей старшеклассников.
По назначению можно выделить несколько типов элективных курсов. Одни из них могут являться как бы «надстройкой» профильных курсов и обеспечить для наиболее способных школьников повышенный уровень изучения того или иного учебного предмета.
Другие элективные курсы должны обеспечить межпредметные связи и дать возможность изучать смежные учебные предметы на профильном уровне. Примером таких элективных курсов могут служить курсы: «Математическая статистика» для школьников, выбравших экономический профиль, «Компьютерная графика» для индустриально-технологического профиля.
Третий тип элективных курсов поможет школьнику, обучающемуся в профильном классе, где один из учебных предметов изучается на базовом уровне, подготовится к сдаче ЕГЭ по этому предмету на повышенном уровне. Познавательные интересы многих старшеклассников часто могут выходить за рамки традиционных школьных предметов, распространяться на области деятельности человека вне круга выбранного ими профиля обучения. Это определяет появление в 10 и 11 классах элективных курсов, носящих «внепредметный» или «надпредметный» характер.
Оценивая возможность и педагогическую целесообразность введения тех или иных элективных курсов, следует, помнить и о таких важных их задачах, как формирование при их изучении умений и способов деятельности для решения практически важных задач, продолжение профориентационной работы, осознание возможностей и способов реализации выбранного жизненного пути и т.д.
Элективные курсы могут реализоваться в школе за счет времени, отводимого на компонент образовательного учреждения.
Применение в обучении элективных курсов возможно при воплощении идеи профильного обучения. Ведь профильное обучение – это не только дифференцирование содержания образования, но, как правило, и по-другому построенный учебный процесс. Именно поэтому в примерных учебных планах отдельных профилей в рамках времени, отводимого на элективные курсы, предусмотрены часы в 10-11 классах на организацию учебных практик, проектов, исследовательской деятельности.
Особую роль в успешном внедрении элективных курсов сыграет подготовка учебной литературы по этим курсам. Подчеркнем, что в качестве учебной литературы по элективным курсам могут быть использованы также учебные пособия по факультативным курсам, для кружковой работы, а также научно-популярная литература, справочные издания. Также возможны личные разработки преподавателей, построенные на тех или иных разделах различных школьных предметов и наук. Создание элективных курсов – важнейшая часть обеспечения введения профильного обучения. Поэтому их разработка и внедрение должны стать частью программ перехода к профильному обучению. Набор профильных и элективных курсов на основе базовых общеобразовательных предметов составит индивидуальную образовательную траекторию для каждого школьника. Важно отметить, что в любом случае по элективным курсам единый государственный экзамен не проводится.
Можно условно выделить следующие типы элективных курсов.
I. Предметные курсы, задача которых - углубление и расширение знаний по предметам, входящим в базисный учебный план школы.
В свою очередь, предметные элективные курсы можно разделить на несколько групп:
1) Элективные курсы повышенного уровня, направленные на углубление того или иного учебного предмета, имеющие как тематическое, так и временное согласование с этим учебным предметом. Выбор такого элективного курса позволит изучить выбранный предмет не на профильном, а на углубленном уровне. В этом случае все разделы курса углубляются более или менее равномерно.
2) Элективные спецкурсы, в которых углубленно изучаются отдельные разделы основного курса, входящие в обязательную программу данного предмета.
Ясно, что в элективных курсах этого типа выбранная тема изучается более глубоко, чем это возможно при выборе элективного курса типа « курс повышенного уровня».
3) Элективные спецкурсы, в которых углубленно изучаются отдельные разделы основного курса, не входящие в обязательную программу данного предмета. Примерами из области математики могут служить: «Комбинаторика», «Элементы теории вероятностей», «Элементы математической логики», «Элементы теории множеств», «Элементы теории полей» и др.
4) Прикладные элективные курсы, цель которых - знакомство учащихся с важнейшими путями и методами применения знаний на практике, развитие интереса учащихся к современной технике и производству. В качестве примеров таких курсов служат курсы «Геометрия и компьютер», «Прикладные задачи».
5) Элективные курсы, посвященные изучению методов познания природы. Примерами таких курсов могут быть: «Учимся проектировать на компьютере», «Компьютерное моделирование», «Компьютерная графика», «Дифференциальные уравнения как математические модели реальных процессов», «Математические модели и методы в естествознании и технике» и др.
6) Элективные курсы, посвященные истории предмета, входящего в учебный план школы (история математики).
7) Элективные курсы, посвященные изучению методов решения задач (математических, физических, химических, биологических и т.д.).
II. Межпредметные элективные курсы, цель которых - интеграция знаний учащихся о природе и обществе. Примерами таких курсов естественнонаучного профиля могут быть: «Основы космонавтики», «Алгебра Космоса», «Естествознание» и др.
III. Элективные курсы по предметам, не входящим в базисный учебный план.
Это курсы, посвященные психологическим, социальным, культурологическим, искусствоведческим проблемам.
Элективные курсы, хотя и различаются целями и содержанием, но во всех случаях они должны соответствовать запросам учащихся, которые их выбирают.
В связи с этим появляется возможность на примере учебных пособий по элективным курсам отработать условия реализации мотивационной функции учебника.
Поиски путей оптимизации содержания учебных предметов, обеспечения его соответствия меняющимся целям образования могут привести к новым подходам к структурированию содержания учебных предметов. Традиционный подход основывается на логике базовой науки. Другой подход может заключаться в отборе проблем, явлений, процессов, ситуаций, изучение которых соответствовало бы познавательным запросам учащихся. Такой подход может способствовать формированию учащихся как субъектов познавательной деятельности. С другой стороны, нельзя забывать о главной задаче российской образовательной политики – обеспечения современного качества образования на основе сохранения его фундаментальности и соответствия актуальным и перспективным потребностям личности, общества и государства. Таким образом, современная школа не должна отказываться от формирования знаний умений и навыков. При воплощении идеи элективных курсов полезно опираться на 30-летний опыт существования системы факультативных занятий в СССР. За этот период было создано более 100 программ разных факультативных курсов и, хотя не все из них получили широкое распространение в школах страны, среди них было много достойных курсов, обеспеченных учебными пособиями для учащихся и методическими пособиями для учителей. При изучении элективных курсов наиболее наглядно проявляется тенденция развития современного образования, заключающаяся в том, что усвоение предметного материала обучения из цели становится средством такого эмоционального, социального и интеллектуального развития ребенка, которое обеспечивает переход от обучения к самообразованию.
Глава 2. Элективный курс по теме: «Сюжетные задачи»
§1. Роль задач в обучении математике
Задача — проблемная ситуация с явно заданной целью, которую необходимо достичь; в более узком смысле задачей также называют саму эту цель, данную в рамках проблемной ситуации, то есть то, что требуется сделать. В первом значении задачей можно назвать, например, ситуацию, когда нужно достать предмет, находящийся очень высоко; второе значение слышно в указании: «Ваша задача — достать этот предмет». Несколько более жёсткое понимание «задачи» предполагает явными и определёнными не только цель, но и условия задачи, которая в этом случае определяется как осознанная проблемная ситуация с выделенными условиями (данным) и требованием (целью)
В связи с развернувшейся в настоящее время во многих странах мира реформой математического образования проблема постановки задач в школьном курсе математики стала одной из самых важных и животрепещущих проблем в развитии преподавания.
Если понятие математической задачи тактируется достаточно широко (в частности, если всякую теорему считать задачей), то решение задач является единственной возможностью для математической деятельности учащихся. Умения решать математические задачи является наиболее яркой характеристикой состояния математического образования.
Как же обстоит дело с обучением учащихся математической деятельности? И, прежде всего, как понимает учащийся цель постановки задач в школьном курсе математики?
Почти все учащиеся средней школы считают, что если предложенная им математическая задача решена верно, если полученный ответ совпадает с ответом, данным в учебнике, или одобрен учителем, то работа их окончена, о решенной задаче можно и нужно забыть.
Таким образом, учащиеся (а также многие учителя) забывают об обучающем характере каждой задачи, решаемой в процессе обучения, о том, что всякая решаемая ими задача должна учить их умению ориентироваться в различных проблемных ситуациях, обогащать их знания и опыт, учить их математической деятельности.
В процессе обучения математике задачи выполняют разнообразные функции. Учебные математические задачи являются очень эффективным и часто незаменимым средством усвоения учащимися понятий и методов школьного курса математики, вообще математических теорий. Велика роль задач в развитии мышления и в математическом воспитании учащихся, в формировании у них умений и навыков в практических применениях математики. Решение задач хорошо служит достижению всех тех целей, которые ставятся перед обучением математике. Именно поэтому для решения задач используется половина учебного времени уроков математики (700-800 академических часов в IV-Х классах). Правильная методика обучения решению математических задач играет существенную роль в формировании высокого уровня математических знаний, умений и навыков учащихся.
§2. Сюжетные задачи
Под сюжетными понимаются задачи, в которых описан некоторый жизненный сюжет (явление, событие, процесс), с целью нахождения определённых количественных характеристик или значений. Эти задачи имеют и другие названия: текстовые, практические, аналитические (задачи на составление уравнений или систем уравнений), арифметические и т.д.
Сюжетные задачи – это наиболее древний вид школьных задач. Они всегда широко использовались и будут использоваться в обучении математике. Ещё задолго до нашей эры в Древнем Египте, Вавилоне, Китае, Индии были известны и многие методы их решения. Однако со временем цели и функции решения сюжетных задач существенно изменялись и меняются до сих пор.
Если например до 19-ого века цели решения этих задач были чисто практические: научить решать задачи, которые часто встречаются в жизненной практике, то затем эти цели значительно расширились и, кроме практических целей, они начинают использоваться как важное общеобразовательное и методическое средство. Известный русский методист В.А. Евтушевский (1836-1888) так охарактеризовал функции сюжетных задач в обучении начальной математике: «Задачи, предлагаемые в классе, заключают в себе живой материал для упражнения мышления ученика, для вывода математических правил и для упражнения приложения этих правил в решении частных практических вопросов».
Эти три функции решения сюжетных задач сохранились и до наших дней, но их характер и значимость стали иными. Если раньше решение сюжетных задач рассматривалось чуть ли не единственным средством для осуществления каждой из указанных трёх функции, то теперь положение коренным образом изменились. Так, в настоящее время считается, что развитие мышления учащихся должно осуществляется не только в процессе решения сюжетных задач, но и в процессе всего обучения математике.Что касается третьей функции (приложение математики к решению частных практических вопросов), то современная жизненная практика наших детей и взрослых совсем иная, чем во времена В.А. Евтушевского. Те непосредственные применения, которые раньше имели различные задачи по покупку и продажу, на совместную работу, на движение и пр., теперь играют не очень существенную роль в жизни людей, особенно если учесть, что подавляющее большинство таких задач, применяемых в школьном обучении, носит искусственный характер.
Главное состоит в том, чтобы сформировать у учащихся общий подход к решению любых задач. Это подход состоит в том, что задача рассматривается как модель некоторой проблемной ситуации, как объект для тщательного изучения, а её решение – как процесс применения общих теоретических положений математики и общелогических правил вывода к условиям задачи, с целью последовательного её преобразования и перемоделирования до тех пор, пока не будет удовлетворено требование задачи – не будет найден ответ на вопрос задачи.
Следует отметить, что такой подход к решению сюжетных задач, как это показали проведенные многолетние эксперименты, обеспечивает высокий уровень развития у учащихся творческой инициативы, способностей и умений решения не только сюжетных, но и любых задач, А это важно потому, что вся творческая жизнедеятельность человека связана с решением задач: каждое самостоятельное его действие – это решение некоторой задачи, которая возникает перед ним в силу сложившихся условий и обстоятельств или которую он сам в силу своих внутренних потребностей ставит перед собой. Вооружить наших учащихся такой культурой жизнедеятельности – вот главная цель решения сюжетных и других задач в школьном обучении.
§3. Программа элективного курса
Пояснительная записка
Сюжетные задачи – это наиболее древний вид школьных задач. Они всегда широко использовались, и будут использоваться в обучении математике. Они помогают учащимся понять сущность и методику применения математического моделирования, сформировать общий подход к решению любых задач, однако в школьном курсе математики отводится недостаточно времени решению сюжетных (текстовых) задач. Это и определило необходимость в составлении данного курса.
Статистические данные анализа результатов проведения ЕГЭ с момента его существования говорят о том, что решаемость задания, содержащего текстовую задачу, составляет год от года чуть больше или меньше 30%. Такая ситуация позволяет сделать вывод, что большинство учащихся не в полной мере владеет техникой решения текстовых задач и не умеет за их часто нетрадиционной формулировкой увидеть типовые задания, которые были достаточно хорошо отработаны на уроках в рамках школьной программы. По этой причине возникла необходимость более глубокого изучения этого традиционного раздела элементарной математики.
Полный минимум знаний, необходимый для решения всех типов текстовых задач, формируется в течение первых девяти лет обучения учащихся в школе, поэтому представленный элективный курс «Текстовые задачи» рекомендуется вводить с 9-го класса. Хотя при творческом подходе учителя к его проведению, исключив пока ещё не изученные на уроках темы, можно ввести этот курс и раньше. Подобный подход возможен, так как каждая тема, за исключением первой, является вполне самостоятельной и не связана с другими. За счёт высвободившихся часов можно увеличить количество практических занятий по другим темам.
Данный элективный курс представляет возможность реализации интереса к выбранному профилю, создает условия для осознанного выбора профиля.
Цель курса:
Создание условий для:
· формирования у школьников общих подходов к решению сюжетных задач;
· овладения навыками моделирования, как одного из методов познания и решения сюжетных задач;
· формирование умений и навыков решения задач сюжетного содержания.
Задачи курса:
· обобщить виды задач, изученных ранее, и конкретизировать понятие сюжетных задач;
· определить методы моделирования учебной задачи;
· ознакомить учащихся с всевозможными подходами к решению сюжетных задач различного уровня сложности;
· помочь школьникам овладеть приемами исследовательской работы и методами решения задач.
Учебный процесс элективного курса предусматривает следующие методы и формы работы:
· изложение нового материала учителем в форме лекции;
· дифференцированный подход на практических занятиях: для всех тем курса подобраны задания различного уровня сложности, которые в зависимости от уровня усвоения материала учащимися будут им предложены;
· самостоятельная работа с учебной литературой;
· индивидуальные консультации.
Данный курс рассчитан на полгода, 14 учебных часов, по 2 часа в неделю, в течении одной четверти.
Содержание курса
В программу элективного курса включены следующие темы и ориентировочное время для их изучения
№ п/п |
Тема | Количество часов |
| 1 | Вводное занятие | 1 |
| 2 | Методы решения сюжетных задач | 3 |
| 3 | Задачи на физические процессы | 2 |
| 4 | Задачи на химические процессы | 3 |
| 5 | Задачи с экономическим содержанием | 3 |
| 6 | Итоговое занятие | 1 |
| Итого: | 12 |
Методические рекомендации элективного курса «Сюжетные задачи»
Тема 1. Вводное занятие.
На вводном занятии рекомендуется:
· объяснить учащимся цели данного элективного курса;
· поставить необходимые задачи;
· рассказать кратко о том, что будет изучаться, выяснить всевозможное применение задач в жизнедеятельности человека (с помощью учащихся);
· объяснить, каким образом будут подводиться итоги изучения курса и оцениваться работа учащихся.
Тема 2. Методы решения сюжетных задач.
Сюжетные задачи многими людьми, окончившими школу, вспоминаются как самые трудные. Для того чтобы понять, в чем состоит сложность решения этих задач, необходимо проанализировать собственный опыт их решения.
В каждой сюжетной задаче можно выделить:
· числовые значения величин, которые называются данными, или известными (их должно быть не меньше двух);
· некоторую систему функциональных зависимостей в неявной форме, взаимно связывающих искомое с данными и данные между собой (словесный материал, указывающий на характер связей между данными и искомыми);
· требование или вопрос, на который надо найти ответ.
Существуют различные методы решения данного класса задач:
· арифметический метод;
Решить задачу арифметическим методом – значит найти ответ на требование задачи посредством выполнения арифметических действий над числами. Одну и ту же задачу можно решить различными арифметическими способами. Они отличаются друг от друга логикой рассуждений, выполняемых в процессе решения задачи. Выделяют два основных подвида арифметического метода решения:
- составление пропорций по условию задачи и нахождение четвертого пропорционального;
- получение числового выражения или последовательности числовых выражений и нахождение из значений.
· алгебраический метод;
Алгебраический метод обеспечивает общий подход, общий принцип в анализе и решении. Его отличие от арифметического метода прежде всего состоит в введении неизвестной величины и её специального обозначения.
Итак, при алгебраическом методе ответ на вопрос задачи находится в результате составления и решения уравнения. В зависимости от выбора неизвестного (неизвестных), для обозначения буквой (буквами), от хода рассуждений можно составить различные уравнения по одной и той же задаче. В этом случае можно говорить о различных алгебраических способах решения этой задачи.
Составление уравнения отличается от арифметического метода не только введением буквенных обозначений неизвестной величины, но и установление зависимостей между величинами задачи. Эти зависимости представлены здесь не в виде цепочки формул, каждое звено которой связано с выполнением предшествующих действий и все звенья которой объединяются лишь в конце, а сразу в виде уравнения, в котором фиксируются все существенные связи между известными и чаще неизвестными величинами. Это возможно благодаря особой функции «х», позволяющей замещать неизвестную величину особым символом и оперировать с ним.
При алгебраическом методе решения задачи важно не вычисление конкретных значений величин, а выявление и выражение основных зависимостей между явными и неявными значениями величин, входящих в условие задачи.
При алгебраическом методе решения текстовой задачи выполняются следующие этапы:
- разработка математической модели;
- поиск алгоритма решения;
- вычисление и исследование.
· функционально-графический метод решения текстовых задач;
Функционально-графический метод решения сюжетных задач состоит в переводе условия задачи на язык функций и использовании свойств этих функций и свойств их графиков для решения задачи.
· геометрический метод;
Геометрический метод решения сюжетных задач основан на переводе условия задачи на язык геометрических величин и использовании метрических свойств геометрических фигур для ее решения.
В решении задач наиболее часто используются две разновидности этого метода:
- метод одномерных диаграмм (изображение процесса изменения одной величины отрезками);
- метод двумерных диаграмм (изображение связи нескольких величин с помощью планиметрических фигур).
Геометрический метод очень часто используется в комбинации с другими методами решения сюжетных задач как средство получения образа задачной ситуации или как средство получения дополнительных законов связи величин.
Тема 3. Задачи на физические процессы
Учащиеся должны быть знакомы со способами решения задач, а так же должны уметь применять данные методы на практике.
Основное содержание:
В рамках изучения данной темы с учащимися следует рассмотреть задачи:
· на работу;
· на равномерное движение;
· движение по и против течения;
· физические задачи (тело брошенное под углом к горизонту…).
Тема 4. Задачи на химические процессы
Задачи на химические процессы, или как их по-другому называют на сплавы, растворы и смеси , в школьных учебниках и задачниках представлены в недостаточном количестве, поэтому включение этой темы в элективный курс даёт возможность, в некоторой мере, ликвидировать этот недостаток.
В процессе анализа текстовых задач этого блока учащиеся приобретают некоторые навыки исследования и знакомятся с новыми для них методами решения задач.
Поэтому им предлагается достаточное время для индивидуальной работы. Итоговый контроль по этому блоку можно провести в виде фронтальной беседы
Основное содержание:
На основе определения процентной концентрации вещества в смеси и опорных задач на проценты рассматриваем задачи:
1) По данной общей массе смеси (раствора, сплава) и процентного содержания одного из компонентов найти новое количество компонента с изменённым процентным содержанием компонента;
2) Нахождение первоначальной массы смеси, содержащей изменение массы одного из компонентов и изменения процентного его содержания.
Тема 5. Задачи с экономическим содержанием
Экономика и математика связаны между собой уже тысячелетия. Само появление чисел, их названия и обозначения, создание систем счисления и всего того, что ныне составляет основу математики, было вызвано к жизни задачами практики, производства, обмена и торговли.
И по мере возникновения, становления и развития математики укреплялись и ее связи с экономикой - наукой об изучении закономерностей поведения людей в процессе деятельности, направленной на создание необходимых им благ, поэтому не удивительно, что и современная экономика широко использует математические методы.
Эти методы позволяют планировать экономические процессы, делать прогнозы, давать рекомендации по повышению их эффективности.
Разбирая с учащимися задачи с экономическим содержанием необходимо выделить время, для того что бы объяснить им основные экономические процессы, к которым относятся:
· купля-продажа;
· инфляция;
· кредитование;
· рост вкладов.
§4. Разработка занятий элективного курса
При изучении курса математики в школе, часто приходится встречаться с задачами, которые учителя физики называют физическими, учителя химии - химическими, а учителя экономики - экономическими. Это сюжетные (или текстовые) задачи.
В зависимости от того, какие процессы описаны сюжетом, можно относить эти задачи к разным областям наук, однако общим для всех подобных задач является то, что при их решении не обойтись без использования математики.
Приведем некоторые конспекты занятий элективного курса: «Сюжетные задачи».
Занятие №6.
Тема. ЗАДАЧИ НА ФИЗИЧЕСКИЕ ПРОЦЕССЫ
Цели:
Обучающие:формирование умений решения задач на движение нескольких объектов, задач на совместную работу, проверить усвоение методов и приемов решения задач на движение нескольких объектов, задач на совместную работу;
Развивающие :формировать способность фиксирования собственных затруднений, развитие кругозора, мышления, внимания, культуры математической речи; привитие интереса к изучению математики;
Воспитательные: воспитание ответственности, аккуратности и самостоятельности.
Этапы урока:
1 Организационный момент.
2. Актуализация знаний
3. Введение нового материала.
Занятие № 10
Тема. ЗАДАЧИ НА ХИМИЧЕСКИЕ ПРОЦЕССЫ
Цели:
Образовательные:
1) Введение понятия «задачи на химические процессы».
2) Введение понятий “концентрация”, “процентное содержание”.
3) Формирование умений решеня задач на смеси и сплавы арифметическим и алгебраическим методами.
Развивающие: через поиск решения задачи развивать творческую и мыслительную деятельность учащихся, их интеллектуальные качества: способность к «видению» проблемы, оценочным действиям, обобщению, быстрому переключению, самостоятельность, гибкость, учить учащихся корректировать свою деятельность в ходе урока; формировать умения чётко и ясно излагать свои мысли, задавать вопросы.
Воспитательные: формирование элементов социально-личностной компетентности на основе умения проектировать и осуществлять алгоритмическую и эвристическую деятельность, проверять и оценивать результаты деятельности.
Этапы урока:
1 Организационный момент.
2. Введение нового материала.
3. Первичное закрепление.
4. Домашнее задание и итоги урока.
Время |
Деятельность учителя | Деятельность учащихся |
| 1 мин | Сегодня мы с Вами познакомимся с тем, как решать задачи других видов – это задачи на химические процессы, или как их называют по другому задачи на сплавы и смеси. | Слушают учителя |
| 5 мин | Кто знает, что такое раствор? - раствор – смесь, образованная не менее чем двумя компонентами. Прежде чем приступать к решению задач, рассмотрим понятие концентрации вещества в смеси (растворе). Если смесь (раствор), имеет массу m и состоит из веществ А и В, массы которых соответственно равны mA , mB , то величину mA /m называют концентрацией вещества А (mB /m соответственно В) в смеси (растворе), а величину
процентным содержанием вещества А (соответственно В) в смеси (сплаве, растворе). При этом выполняется равенство:
Давайте использование данного понятия рассмотрим на примере следующей задачи: |
|
| 10 мин | В сосуд, содержащий 180 г 70%-го водного раствора уксуса добавили 320 г воды. Найдите концентрацию уксусной кислоты в получившемся растворе. Что требуется найти? - концентрацию уксусной кислоты. Что известно из условия задачи? Изначально было 180 г 70%-го водного раствора. Далее в этот раствор долили 320 г воды. - Каким образом вычисляется концентрация раствора? - Концентрация раствора равна отношению массы растворённого вещества к общей массе раствора. Какова масса уксусной кислоты в сосуде? - m1 =180·0,7=126 (г). А какова общая масса получившегося раствора? - Получившийся раствор имеет массу 180 г + 320 г = 500 г Итак, концентрация получившегося раствора уксусной кислоты равна k = Ответ. 0,252. |
Записывают решение. Решение. 1) m1 =180·0,7=126 (г) – масса уксусной кислоты; 2) 180 г + 320 г = 500 г – масса получившегося раствора; 3) k= Ответ. 0,252 |
| 13 мин | Имеются два сплава, состоящие из золота и меди. В первом сплаве отношение масс золота и меди равно 8:3, а во втором - 12:5. Сколько килограммов золота и меди содержится в сплаве, приготовленном из 121 кг первого сплава и 255 кг второго сплава? О каких величинах говорится в задаче? Что требуется найти? Что известно из условия задачи? Для того, чтобы решить данную задачу, мы составим и заполним следующую таблицу: |
Об отношениях масс золота и меди в двух различных сплавах и о массах этих сплавов, из которых приготовили третий сплав. - Массы золота и меди, содержащиеся в сплаве, приготовленном из первого и второго сплава. - Даны отношения веществ в сплавах. |
1 этап
О каких величинах говорится в задаче?
Какие известны?
| Число долей | Масса сплава кг | ||
| 1 сплав | Золото 8 | Медь 3 | 121 |
| 2 сплав | 12 | 5 | 255 |
| 3 сплав | - | - | |
2 этап
Что можно сразу найти , основываясь на этих данных?
- массу третьего сплава.
| 1 сплав | Число долей | Масса сплава кг | ||
| Золото 8 | Медь 3 | 121 | ||
| 2 сплав | 12 | 5 | 255 | |
| 3 сплав | - | - | 376 | |
3 этап
Какие величины требуется найти? Добавляем столбцы
| 1 сплав | Число долей | Масса сплава кг | Масса вещества | |||
| Золото 8 | Медь 3 | 121 | Золото |
Медь |
||
| 2 сплав | 12 | 5 | 255 | |||
| 3 сплав | - | - | 376 | |||
4 этап
Сколько долей золота в первом сплаве?
- масса золота составляет 8 долей
Чтобы найти массу золота которая приходится на 8 долей надо знать сколько всего равных долей в сплаве. Добавим еще один столбец.
| 1 сплав | Число долей | Масса сплава кг | Масса вещества | |||
| Золото 8 | Медь 3 | Общее кол-во долей11 | 121 | Золото |
Медь |
|
| 2 сплав | 12 | 5 | 17 | 255 | ||
| 3 сплав | - | - | - | 376 | ||
5 этап
Выполним вычисления. Поиск решения закончен.
| 1 сплав | Число долей | Масса сплава кг | Масса вещества | |||||
| Золото 8 | Медь 3 | Всего 11 | 121 | Золото
|
Медь
Можно |
|||
| 2 сплав | 12 | 5 | 17 | 255 |
Можно не вычислять |
|||
| 3 сплав | - | - | - | 376 | ||||
Запишите решение самостоятельно. 6 этап. Уащимся демонстрируется готовое решение, и они сверяют его со своим решением Решение.
121+255=376 (кг) масса III сплава, 88+180=268 (кг) масса золота в III сплаве, 376-268=108 (кг) масса меди в III сплаве. Ответ. 268 кг золота и 108 кг меди. |
||||||||
| 10 мин | Смешали 10%-й раствор серной кислоты с 30%-м раствором той же кислоты. В результате получили 600 г 15%-го раствора серной кислоты. Сколько взяли того и другого раствора? Сравните эту задачу с предыдущей. Что в них общего? Чем они отличаются? С точки зрения математики это одно и тоже. Подумайте как решить задачу алгебраическим способом. Задагние классу: первый вариант решает составляя уравнение, а второй составляя систему уравнений. Существуют еще не менее 3-х способов решения данной задачи. Их постарайтесь найти дома. |
- даны доли вещества - в предыдущей задаче были даны массы сплавов, надо было найти массы компонентов этих сплавов, а здесь надо найти массы растворов. К доске выходят два ученика первого и второго вариантов и демонстрируют свое решение. I вариант Пусть нужно взять x г 10%-го раствора, тогда придётся взять (600-x) г 30%-го раствора. Так как в результате смешивания получается 15%-ный раствор, составляем уравнение: 0,1x+0,3(600-x)=0,15·600. Решив это уравнение, получаем ответ: масса 10%-го раствора - 450 г, масса 30%-го раствора – 150 г. II вариант Решение: Пусть требуется взять x г 10%-го раствора, y г 30%-го раствора. На основании условий задачи приходим к простой системе Решая её любым способом мы найдем те же 450 г и 150 г. |
||||||
| 5 мин | Подведение итогов урока, постановка домашнего задания. Итоги: Сегодня мы с вами познакомились с новыми понятиями и новыми типами задач: на смеси и сплавы. Что вы узнали нового на сегодняшнем уроке? Чему научились? Что необычного и интересного было на занятиях? В каких задачах вы столкнулись с трудностями? Домашнее задание на раздаточном материале: Задача1. Из колбы, содержащей раствор соли, отлили в пробирку Задача 2. Смешав 40% и 15% растворы кислоты, добавили 3 кг чистой воды и получили 20% раствор кислоты. Если бы вместо 3 кг воды добавили 3 кг 80% раствора той же кислоты, то получили бы 50%-ый раствор кислоты. Сколько килограммов 40% -го и 15% растворов кислоты было смешано? Задача 3. Сколько нужно добавить воды в сосуд, содержащий 150 г 70% -го раствора уксусной кислоты, чтобы получить 6 % раствор уксусной кислоты? |
|||||||
Занятие № 14
Тема. ЗАДАЧИ С ЭКОНОМИЧЕСКИМ СОДЕРЖАНИЕМ
Цели:
Образовательные: научить решать задач на проценты с экономическим содержанием с помощью формул “сложных процентов”, формирование умений решать задачи повышенной сложности.
Развивающие: через решение задачи развивать творческую и мыслительную деятельность учащихся, их интеллектуальные качества: способность к «видению» проблемы, оценочным действиям, обобщению, быстрому переключению, самостоятельность, гибкость, учить учащихся корректировать свою деятельность в ходе урока; формировать умения чётко и ясно излагать свои мысли, задавать вопросы
Воспитательные: формирование элементов социально-личностной компетентности на основе умения проектировать и осуществлять алгоритмическую и эвристическую деятельность, проверять и оценивать результаты деятельности.
Этапы урока:
1 Организационный момент.
2. Введение нового материала.
3. Первичное закрепление.
4. Домашнее задание и итоги урока.
| Время | Деятельность учителя | Деятельность учащихся | |
| 2 мин | Организационный момент. | ||
| 12 мин | Объяснение нового материала Говорят, что имеем дело со «сложными процентами» в том случае, когда некоторая величина подвержена поэтапному изменению. При этом каждый раз ее изменение составляет определенное число процентов от значения, которое эта величина имела на предыдущем этапе. Рассмотрим 2 случая. Случай 1. В конце каждого этапа величина изменяется на одно и то же постоянное количество процентов – р%. Тогда в конце п-го этапа значение некоторой величины А, исходное значение которой равнялось А0 , определяется формулой:
Задача. Сберкасса выплачивает 3 % годовых. Через сколько лет внесенная сумма удвоится? Поиск решения. Как мы обозначим первоначальная величину вклада? Если А0 – сумма первоначального вклада, как тогда мы запишем выражение для удвоенного вклада? Какова процентная ставка банка? Запишите формулу для вычисления размера этого вклада через n лет: Итак, через n лет размер вклада удвоится. Можно ли составить уравнение на основе этих данных? Запишите решение самостоятельно. Случай 2. Прирост величины А на каждом этапе различный. Пусть величина А в конце 1-го этапа испытывает изменение на р
Средний процент прироста q% можно найти из равенства:
Обратите внимание средний процент прироста не равен среднему арифметическому процентов прироста. |
Принято первоначальную величину вклада обозначать через А0 - Удвоенный вклад будет равен: 2·А0 - три процента
Решение. Пусть первоначальная величина вклада составляет А0
рублей. Тогда через п лет эта величина равняется 2А0
р. или Составим уравнение:
Решаем его.
Ответ: вклад удвоится через 23 года. |
|
| 25 мин | Рассмотрим задачу: Акционерное общество «МММ-лимитед» объявило котировку своих акций на ближайшие 3 месяца с приростом в процентах последовательно по месяцам на 243 %, 412 % и 629 % по отношению к каждому предыдущему месяцу. Каков средний ежемесячный рост котировок акций за указанный период? Поиск решения. Как вы думаете, на какой из трех случаев данная задача? Какой формулой мы будем пользоваться? На какой срок объявлена котировка акций? Каковы значения приростов котировок акций за эти 3 месяца? Подставим эти данные в формулу. Запишите решение самостоятельно. |
-На третий случай.
- Сроком на 3 месяца, причем каждый месяц процентная ставка меняется - p1 =243%, p2 =412% и p1 =629%.
Решение.
Ответ: 404 % – средний ежемесячный рост котировок акций. |
|
| 15 мин | Решите следующую задачу самостоятельно. Задача. Себестоимость изделия понизилась за 1 полугодие на 10 %, а за второе – на 20 %. Определить первоначальную себестоимость изделия, если новая себестоимость стала 576 руб. Проверка решения. |
Решение: А0 – исходная себестоимость товара
Ответ: исходная себестоимость 800 руб. |
|
| 5 мин | Самостоятельная работа Решите любые три задачи на выбор: 1. Пусть вкладчик положил на счет в банке 25000р. и в течение 3-х лет не будет снимать деньги со счета. Подсчитаем, сколько денег будет на счете вкладчика через 3 года, если банк выплачивает 30% в год, и проценты после каждого начисления присоединяются к начальной сумме 25000р., т.е. капитализируются. 2. Зарплата служащему составляла 20000р. Затем зарплату повысили на 20%, а вскоре понизили на 20%. Сколько стал получать служащий? 3. На товар снизили цену сначала на 20%, а затем еще на 15%. При этом он стал стоить 23,8 тыс.р. Какова была первоначальная цена товара? 4. Завод увеличивал объем выпускаемой продукции ежегодно на одно и то же число процентов. Найти это число, если известно, что за 2 года объем выпускаемой продукции увеличивался на 21%. 5. Цену товара первоначально понизили на 20%, затем новую цену снизили еще на 30% и, наконец, после пересчета произвели снижение на 50%. На сколько процентов всего снизили первоначальную цену товара? |
||
| 3 мин | Подведение итогов занятия. Постановка домашнего задания. Итоги: Что узнали нового? Чему научились? Что необычного и интересного было на занятиях? В каких задачах вы столкнулись с трудностями? Домашнее задание: Задачи с экономическим содержанием: №1 Завод выпускал 12000 наручных часов в месяц. После повышения цен на отдельные детали завод стал выпускать 9000 часов в месяц. Как изменилась при этом производительность труда, если вместе с сокращением выпуска часов на заводе сократили 20% рабочих? №2 Некоторая фирма начинает выпускать кофемолки, которые предполагает реализовать по 10$ за штуку. При этом фирма должна уплатить 6$ за приобретенные детали для каждой кофемолки. Кроме этого, за аренду помещения и рекламу фирма должна уплачивать 10000$ ежегодно. Считая, что других статей расхода у фирмы не будет, определите, какое минимальное количество кофемолок должна реализовывать фирма ежегодно, чтобы не нести убытков. №3 В банк внесли сумму 50 000 руб. Банк начисляет сложные проценты по ставке 15% годовых. Какая сумма будет на счете вкладчика через 8 лет? |
||
СИСТЕМА ЗАДАЧ ПО ТЕМАМ
Задачи на химический процессы
Задача 1. Сколько нужно добавить воды в сосуд, содержащий 150 г 70% -го раствора уксусной кислоты, чтобы получить 6 % раствор уксусной кислоты?
Решение. Количество воды необходимое для доливания в сосуд обозначим через x.
| процентное содержание уксусной кислоты в растворе | Масса раствора г | Масса уксусной кислоты г | |
| Исходный раствор | 70% | 150 | 0,7·150=105 |
| Новый раствор | 6% | 150 + x | 0,06(150 + x) |
Так как масса уксусной кислоты осталась прежней, составляем и решаем уравнение
0,06(150 + x) = 105,
9 + 0,06x = 105,
0,06x = 96,
x = 1600.
Ответ. 1,6 кг воды.
Задача 2. Смешали некоторое количество 12% раствора соляной кислоты с таким же количеством 20% раствора этой же кислоты. Найти концентрацию соляной кислоты в получившейся смеси.
Решение. Обозначим: x – концентрация кислоты в смеси, y кг – масса каждого раствора.
| Концентрация соляной кислоты в растворе | Масса раствора кг | Масса соляной кислотыкг | |
| I раствор | 0,12 | у | 0,12у |
| II раствор | 0,2 | у | 0,2у |
| Смесь | x | 2у | x·2у |
По закону сохранения массы для отдельных компонентов масса соляной кислоты в смеси равна сумме масс этого вещества, входящих в первый и второй растворы
2xy=0,12y+0,2y.
Из y≠0 следует:
2x=0,12+0,2=0,32
x=0,16.
Выражаем в процентах: 16%.
Ответ. 16%
Задача 3. Смешали 8кг 18% раствора некоторого вещества с 12 кг 8% раствора этого же вещества. Найдите концентрацию получившегося раствора.
Решение. Пусть x – концентрация смеси из двух растворов.
| Концентрация вещества | Масса раствора | ||
| кг | Масса вещества кг | ||
| I раствор | 0,18 | 8 | 0,18·8=1,44 |
| II раствор | 0,08 | 12 | 0,08·12=0,96 |
| Смесь | x | 20 | x·20 |
По закону сохранения массы для отдельного вещества получаем уравнение
20x=1,44+0,96
20x=2,4
x=0,12
или в процентах:12%.
Ответ. 12%
Задача 4. Смешав 40% и 15% растворы кислоты, добавили 3 кг чистой воды и получили 20% раствор кислоты. Если бы вместо 3 кг воды добавили 3 кг 80% раствора той же кислоты, то получили бы 50%-ый раствор кислоты. Сколько килограммов 40% -го и 15% растворов кислоты было смешано?
| Концентрация вещества | Масса раствора кг | Масса кислоты кг | |
| I раствор | 0,4 | x | 0,4x |
| II раствор | 0,15 | y | 0,15y |
| Вода | - | 3 | - |
| III раствор | 0,8 | 3 | 0,8·3=2,4 |
| 1 смесь (I раствор + II раствор + вода) | 0,2 | x + y +3 | 0,2(x + y +3) |
| 2 смесь (I раствор + II раствор + III раствор) | 0,5 | x + y +3 | 0,5(x + y +3) |
Решение. Вводим обозначения: x кг было 40% раствора кислоты, y кг было 15% раствора.
Для каждой смеси составляем уравнение.
Для первой:
0,4x + 0,15y = 0,2(x + y +3).
Для второй:
0,4x + 0,15y + 2,4 = 0,5(x + y +3).
Остаётся решить следующую систему уравнений
![]()
![]()
![]()
![]()
Ответ. 3,4 кг и 1,6 кг.
Задача 5. Имеется три сосуда. В первый сосуд налили 4 кг 70% сахарного сиропа, а во второй – 6 кг 40% сахарного сиропа. Если содержимое первого сосуда смешать с содержимым третьего сосуда, то получим в смеси 55% содержание сахара, а если содержимое второго сосуда смешать с третьим, то получим 35% содержание сахара. Найдите массу сахарного сиропа в третьем сосуде и концентрацию сахара в нём.
Решение. Обозначения: x кг - масса сахарного сиропа в третьем сосуде, y – концентрация сахара в нём.
| Концентрация сахара | Масса раствора | ||
| кг | Масса сахара кг | ||
| Раствор I сосуда | 0,7 | 4 | 0,7·4=2,8 |
| Раствор II сосуда | 0,4 | 6 | 0,4·6 = 2,4 |
| Раствор III сосуда | y | x | xy |
| 1 смесь (содержимое I + III сосуда) | 0,55 | 4+x | 0,55(4+x) |
| 2 смесь (содержимое II +III сосуда) | 0,35 | 6+x | 0,35(6+x) |
По условию задачи составляем уравнения:
для 1 смеси
0,55(4+x)=2,8+ xy,
для 2 смеси
0,35(6+x)=2,4+ xy.
Итак, получаем систему уравнений:
![]()
![]()
![]()
![]()
![]()
![]()
Масса сахарного сиропа в третьем сосуде равна 1,5 кг, а массовое процентное содержание равно 15%.
Ответ. 1,5 кг, 15%.
Задача6. Из колбы, содержащей раствор соли, отлили в пробирку ![]() раствора. Затем из пробирки часть воды испарили, в результате чего процентное содержание соли в пробирке увеличилось в 3 раза. Каково было первоначальное процентное содержание соли в колбе, если известно, что после переливания в неё содержимого пробирки процент соли в колбе увеличился на 5%?
раствора. Затем из пробирки часть воды испарили, в результате чего процентное содержание соли в пробирке увеличилось в 3 раза. Каково было первоначальное процентное содержание соли в колбе, если известно, что после переливания в неё содержимого пробирки процент соли в колбе увеличился на 5%?
Решение. Обозначения: m – масса раствора в колбе, x – первоначальное содержание соли в колбе. Необходимо найти ![]() 100%.
100%.
![]() - концентрация соли в колбе.
- концентрация соли в колбе.
0,9m – осталось раствора в колбе после переливания 0,1m раствора в пробирку.
0,1x – соли в пробирке.
![]() - концентрация соли в пробирке после испарения.
- концентрация соли в пробирке после испарения.
![]() - масса раствора в пробирке после выпаривания.
- масса раствора в пробирке после выпаривания.
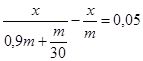
![]()
![]()
![]()
Ответ. 70%.
Задачи для самостоятельного решения учащимися:
1. В сосуд налито 4 литра 70%-го раствора кислоты. Во второй такой же сосуд налито 3 литра 90%-го раствора кислоты. Сколько литров раствора нужно перелить из второго сосуда в первый, чтобы в нём получился 75%-ый раствор кислоты?
2. После смешивания растворов, содержащих 25% и 60% кислоты, получился раствор, содержащий 39% кислоты. Определить в какой пропорции были смешаны растворы.
3. Из молока, жирность которого 5%, делают творог жирностью 15,5%, при этом остается сыворотка жирностью 0,5%. Сколько творога получится из 1 т молока?
4. Добытая руда содержит 21% меди, обогащенная - 45%. Известно, что в процессе обогащения 60% добытой руды идёт в отходы. Определить процентное содержание меди в отходах.
5. Сколько килограммов воды нужно выпарить из 0,5 т целлюлозной массы, содержащей 85% воды, чтобы получить массу с содержанием 75% воды?
6. Морская вода содержит 5% соли по массе. Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составляла 1,5%?
7. В ящик, содержащий чёрные и белые шары, среди которых было 25% белых, добавили 10 черных, после чего белых стало 20%. Сколько было сначала чёрных шаров?
8. Одна смесь содержит вещества A и B в отношении 4:5, а другая смесь содержит те же вещества, но в отношении 6:7. Сколько частей каждой смеси надо взять, чтобы получить третью смесь, содержащую те же вещества в отношении 5:6.?
9. В совхоз поступило 2 типа минеральных удобрений. В первом фосфора в 4 раза больше, чем азота, а во втором фосфора в 5 раз меньше, чем азота. В каком соотношении надо взять I и II типы удобрений, чтобы получить из них новый тип, в котором фосфора было бы в 3 раза меньше, чем азота?
10. К 12 кг сплава меди и олова добавили 8 кг другого сплава, содержащего те же металлы в обратной пропорции, получив в итоге сплав, содержащий 55% меди. Сколько процентов меди было в каждом из исходных сплавов?
11. Раствор соли массой 40 кг разлили в два сосуда так, что во 2-ом сосуде чистой соли оказалось на 2 кг больше, чем в 1-ом. Если бы во 2-ой сосуд добавили ещё 1 кг соли, то количество соли в нём стало бы вдвое больше, чем в 1-ом сосуде. Сколько раствора было в 1-ом сосуде?
12. Имеется два слитка золота с серебром. Процентное содержание золота в первом слитке 2,5 раза больше, чем процентное содержание золота во втором слитке. Если сплавить оба слитка вместе, то получится слиток, в котором будет 40% золота. Определить, во сколько раз первый слиток тяжелее второго, если известно, что при сплавке равных по весу частей первого и второго слитков получается слиток, в котором содержится 35% золота.
13. Имеется два раствора серной кислоты в воде: первый 40% и второй 60%. Эти растворы смешали, после чего добавили 5 кг чистой воды и получили 20%-ый раствор. Если бы вместо 5 кг чистой воды добавили 5 кг 80%-го раствора, то получили бы 70%-ый раствор. Сколько было 40%-го и 60%-го растворов?
14. Имеется два слитка сплавов золота и меди. В первом слитке отношение золота и меди равно 1:2, а во втором 2:3. Если сплавить ![]() первого слитка с
первого слитка с ![]() второго, то в полученном слитке окажется столько золота, сколько меди было в первом слитке. А если
второго, то в полученном слитке окажется столько золота, сколько меди было в первом слитке. А если ![]() первого слитка сплавить с половиной второго, то в получившемся слитке окажется меди на 1 кг больше, чем было золота во втором слитке. Сколько золота в каждом слитке?
первого слитка сплавить с половиной второго, то в получившемся слитке окажется меди на 1 кг больше, чем было золота во втором слитке. Сколько золота в каждом слитке?
Задачи на физический процессы
1. От двух пристаней, расстояние между которыми 660 км, отправились одновременно навстречу друг другу два парохода. Скорость первого 15 км/ч. Найдите скорость второго, если через 8 ч после начала движения между пароходами осталось 396 км.
2. От двух пристаней, расстояние между которыми 660 км, отправились одновременно навстречу друг другу два парохода. Первый пароход, начавший движение с ускорением 30 км/ч, перешел на равномерный режим движения при скорости 15 км/ч. Определите, какую скорость набрал второй пароход, начавший движение с ускорением 36 км/ч, если известно, что через 8 ч после начала движения между пароходами осталось 396 км.
3. Одновременно из пункта A выходит пешеход, а из пункта В ему навстречу выезжает велосипедист. Они встречаются через 12 мин и продолжают движение. Велосипедист приезжает в пункт А на 18 мин раньше, чем пешеход приходит в пункт В. Сколько времени затратит на дорогу каждый из них?
4. Два теплохода, скорости которых в стоячей воде одинаковы, выходят навстречу друг другу из пунктов А и В. Дойдя до пунктов А и В соответственно, они поворачивают и идут обратно. Известно, что время до второй встречи в 3,5 раза больше, чем время до первой встречи. Во сколько раз скорость течения реки меньше скорости теплоходов в стоячей воде?
5. Из города A со скоростью 60 км/ч выехал первый автомобиль, а через час вслед за ним отправился второй автомобиль со скоростью 50 км/ч. Сколько километров будет между автомобилями через 10 ч после выхода первого?
6. Бассейн наполняется водой из труб за 3 ч 45 мин. Если бассейн заполнить наполовину, открыв только первую трубу, а оставшуюся часть заполнять, открыв только вторую трубу, то на это потребуется 8 ч. За какое время наполнит бассейн каждая из труб по отдельности?
7. Сосуд наполняется шлангом за 12 мин, а полный сосуд опорожняется при открытии крана за 20 мин. За какое время наполнится пустой сосуд, если одновременно открыть кран и вливать в сосуд воду через шланг?
8. Десять работников должны были выполнить работу за 8 дней. Когда они проработали 2 дня, то оказалось, что закончить работу необходимо уже через 3 дня. Сколько еще нужно взять работников, если известно, что
производительность труда у работников одинаковая?
9. Два поезда отправились из пунктов А и В навстречу друг другу. Они встретятся на половине пути, если поезд из А выйдет на 2 ч раньше, чем поезд из В. Если же оба поезда выйдут одновременно, то через два часа расстояние между ними составит 0,25 расстояния между пунктами А и В. За сколько часов каждый поезд проходит весь путь?
10. Только что добытый каменный уголь содержит 2% воды, а после двухнедельного пребывания на воздухе он содержит 12% воды. На сколько увеличилась масса добытой тонны угля после того, как уголь две недели был на воздухе?
11. Студенческая бригада подрядилась выложить плиткой пол площадью 210 м2 . Приобретая опыт, студенты в каждый последующий день, начиная со второго, выкладывали на 1,5 м2 больше, чем в предыдущий, и запасов плитки им хватило ровно на 9 дней работы. Планируя, что производительность труда будет увеличиваться таким образом, бригадир определил, что для завершения работы понадобится еще 6 дней. Сколько коробок с плитками ему надо заказать, если одной коробки хватает на 1,3 м2 , а для замены некачественных плиток понадобится 2 коробки?
12. Пароход прошел 4 км против течения реки, а затем прошел еще 33 км по течению, затратив на весь путь один час. Найдите собственную скорость парохода, если скорость течения реки равна 6,5 км/ч.
13. Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 15 км/ч, а вторую половину пути — со скоростью 90 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом.
Задачи с экономическим содержанием
1. Завод выпускал 12000 наручных часов в месяц. После повышения цен на отдельные детали завод стал выпускать 9000 часов в месяц. Как изменилась при этом производительность труда, если вместе с сокращением выпуска часов на заводе сократили 20% рабочих?
2. Цена входного билета на стадион была 1 руб 80 коп. На сколько нужно снизить входную плату, чтобы число зрителей увеличилось на 50%, а выручка выросла на 25%?
3. Некоторая фирма начинает выпускать кофемолки, которые предполагает реализовать по 10$ за штуку. При этом фирма должна уплатить 6$ за приобретенные детали для каждой кофемолки. Кроме этого, за аренду помещения и рекламу фирма должна уплачивать 10000$ ежегодно. Считая, что других статей расхода у фирмы не будет, определите, какое минимальное количество кофемолок должна реализовывать фирма ежегодно, чтобы не нести убытков.
4. При отправке посылок наложенным платежом отправитель перекладывает все расходы на получателя. Последний при получении посылки возвращает обозначенную на ней сумму наложенного платежа переводом. Обозначим сумму наложенного платежа через Н. В нее войдет стоимость пересылаемого (С), оплата почтовых расходов за пересылку (Я), оплата страхового сбора (10% от объявленной цены Ц) и оплата за пересылку перевода обратно (10% от Н).
5. Почтатребует, чтобы объявленная ценность была не менее наложенного платежа. Сосчитайте, какими должны быть объявленная ценность и наложенный платеж (при известных С, П), чтобы общие расходы были минимальны.
6. Купец ежегодно расходует 100 фунтов стерлингов на содержание семьи и приумножает остальной капитал на одну треть. Через три года он стал вдвое богаче. Как велик стал его капитал?
7. Купец имел шестипроцентные облигации, с которых получал ежегодно по 1500 руб. процентных денег. Продав облигации по курсу 120 (то есть 120% от номинальной стоимости), часть вырученных денег купец употребил на покупку дома, х /ъ остатка положил в банк под 4%, а остальные деньги - в другой банк под 5%. Из обоих банков вместе купец получает в год 980 руб. дохода. Сколько было заплачено за дом?
8. В банк внесли сумму 50 000 руб. Банк начисляет сложные проценты по ставке 15% годовых. Какая сумма будет на счете вкладчика через 8 лет?
9. В банк внесен вклад 64 000 р. на три года. Какова годовая ставка сложных процентов, если через три года на счете вкладчика оказалось 216 000 р.?
10. Вкладчик открыл счет в банке, вложив 100 000 руб по ставке сложных процентов 40 % годовых. Вкладчик желает накопить в банке 350 000 руб. Каково наименьшее количество лет, при котором вкладчик получит интересующую его сумму?
11. Какую сумму следует внести в банк, начисляющий 35 % годовых по схеме сложных процентов, чтобы за три года накопить сумму 40 000 руб?
12. В течение года завод дважды увеличивал выпуск продукции на одно и то же число процентов. Найдите это число, если известно, что в начале года завод ежемесячно выпускал 600 изделий, а в конце года стал выпускать ежемесячно 726 изделий.
13. В первый день бригада выполнила 20% всей работы. В каждый последующий день бригада увеличивала свою производительность на 5%. За сколько дней бригада выполнила всю работу?
14. За изготовление и установку первого железобетонного кольца колодца заплатили 10 у.е., а за каждое следующее кольцо платили на 2 у.е. больше, чем за предыдущее. Кроме того, по окончании работьг было уплачено еще 40 у.е. Средняя стоимость изготовления и установки одного кольца оказалась равной 22 у.е. Сколько колец было установлено?
элективный курс задача старшеклассник
Заключение
Данная дипломная работа посвящена проблеме разработки методического инструментария для реализации принципов дифференцированного обучения математике в классах математического профиля и экономического профиля.
Основная задача элективных занятий: учитывая интересы и склонности учащихся, расширить и углубить знания по предмету, обеспечить усвоение ими программного материала, ознакомить школьников с некоторыми общими идеями современной математики, раскрыть приложения математики на практике.
Основные выводы, которые мы сделали в процессе исследования следующие:
· вводить обучение по направлениям (профилям) следует после того, как школьники получат единое математическое образование;
· на старшей ступени обучения следует обеспечить возможно большее количество направлений (профилей) обучения;
· разработка элективных курсов является важной задачей современного образования, так как данный вид курсов позволяет учитывать различные интересы школьников, выбравших определенный профиль.
В предложенном элективном курсе учтены выявленные в процессе исследования требования к разработке элективных курсов. Данный элективный курс оформлен в соответствии с выявленными требованиями к оформлению элективных курсов. Он содержит:
· пояснительную записку;
· содержание;
· тематическое планирование;
· методические рекомендации.
В процессе исследования были решены все поставленные задачи:
В ходе анализа проанализирована психолого-педагогическая литература с целью:
· выяснения психологических и социальных особенностей контингента учащихся старших классов и выявления организационно-педагогических аспектов дифференцированного обучения;
· проведен анализ методического обеспечения элективных курсов и курсов по выбору в профильном обучении;
· разработаны конспекты трех занятий по темам:
1) задачи на физические процессы 1 занятие
2) задачи на химические процессы 1 занятие
3) задачи с экономическим содержанием 1 занятие
· разработана система задач элективного курса
Таким образом, можно сделать вывод о том, что задачи исследования решены, цель исследования – разработка элективного курса по теме «Сюжетные задачи», достигнута,.
Материалы дипломной работы могут быть использованы студентами - практикантами, учителями математики, для возможной доработки и внедрения данного курса в практику школ математического профиля.
Библиография
1. Алгебра и начала анализа: Сборник задач для подготовки и проведения итоговой аттестации за курс средней школы [Текст] / И.Р Высоцкий, Л. И. Звавич, Б.П. Пигарев и др.; Под ред. С.А. Шестакова. – 2-е изд., испр. – М.: Внешсигма-М, 2004. – 207.
2. Волков, Б.С. Психология ранней юности [Текст]: Учебное пособие / Б.С. Волков. – М.: Творческий центр сфера, 2001. – 93 с.
3. Демидова, Т.Е., Тонких А.П. Теория и практика решения текстовых задач [Текст] / : Учеб. пособие для студ. высш. пед. учеб. заведений. – М.: Издательский центр «Академия», 2002 – 288 с.
4. Дубровина, И.В. Формирование личности в переходный период от подросткового к юношескому возрасту [Текст] / И.В. Дубровина.- М.: Педагогика, 1987.- 184 с.: ил.
5. Каптерев, П.Ф. О разнообразии и единстве общеобразовательных курсов [Текст] / П.Ф. Каптерев // Педагогический сборник.- 1893.-
№ 1.- С. 1-18.
6. Манвелов, С.Г. Конструирование современного урока математики [Текст]: Кн. для учителя / С.Г. Манвелов. – М.: Просвещение, 2002. – 175 с.: ил. – (Б-ка учителя).
7. Мухина, В.С. Возрастная психология. Детство. Отрочество. Юность [Текст]: Хрестоматия / В.С. Мухина, А.А. Хвостов. – М.: Академия, 2003. – 624 с.
8. Успенский, В.А. Содержание факультативных занятий по математике
9. В.А. Успенский // Математика в школе.- 1967.- № 2.- С. 33 – 38.
10. Немов, Р.С. Психология развития [Текст] : учебные планы и программы курсов / Р.С. Немов.- М.: Московский психолого-социальный институт, 1998.- 72 с.
11. Факультативный курс. Избранные вопросы математики [Текст] :
7 - 8 кл. / Н.Я. Виленкин, Р.С. Гутер, А.Н. Земляков и др.; под ред. В.В. Фирсова.- М.: Просвещение, 1978.- 192 с.
12. Факультативный курс. Избранные вопросы математики [Текст] : 9 кл. / И.Н. Антипов, Н.Я Виленкин, О.С. Ивашев-Мусатов и др.- М.: Просвещение, 1979.- 191 с.
13. Факультативный курс по математике [Текст] : учебное пособие для 7-9 кл. средней шк. / сост. И.Л. Никольская.- М.: Просвещение, 1991.- 383 с.
14. Фридман, Л.М. Сюжетные задачи по математике. История, теория, методика. [Текст] / Учеб. пос. для учителей и студентов педвузов и колледжей. – М.: Школьная пресса, 2002. – 208 с. –(Библиотека журнала «Математика в школе», вып. 15)
15. Шабанова, М.В. Элективные математические курсы: Учебное пособие [Текст] / М.В. Шабанова, О.Л. Безумова, С.Н. Котова, Е.З. Минькина, И.Н.Попов; Поморский гос. Ун-т им. М.В. Ломоносова. – Архангельск: Поморский университет, 2005. – 315 с.
16. Шарыгин, И.Ф. Факультативный курс по математике. Решение задач [Текст] : 10 кл. / И.Ф. Шарыгин.- М.: Просвещение, 1989.- 352 с.
17. Шарыгин, И.Ф. Факультативный курс по математике. Решение задач [Текст] : 11 кл. / И.Ф. Шарыгин, В.И. и др.- М.: Просвещение, 1991.- 384 с.
18. Шестаков, С.А. Сборник задач для подготовки и проведения письменного экзамена по алгебре за курс основной школы : 9 кл. [Текст]
19. С.А. Шестаков, И.Р. Высоцкий, Л.И. Звавич; под ред. С.А. Шестакова. – 2-е изд., испр. – М.: АСТ: Астрель, 2008. – 255, [1]c.
Похожие рефераты:
Особенности развития одарённых детей в процессе обучения математике в 5-6 классах
Элективные курсы по математике в профильной школе
Реализация профильного обучения в средней общеобразовательной школе
Использование цифровой лаборатории "Архимед" в школьном химическом эксперименте
Элективный курс по алгебре для 9-го класса на тему "Квадратные уравнения и неравенства с параметром"
Профильное образование в обучении школьной географии
Разработка школьного элективного курса "Полимеры вокруг нас"
Методика решения задач по теоретическим основам химической технологии
Развитие мотивации школьников при изучении химии в условиях перехода к профильному обучению
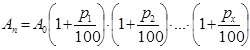 Случай 3. Иногда в задачах встречается понятие «средний процент прироста». Под этим понимают такой постоянный процент прироста, который за п этапов давал бы такое же изменение величины А, которое она получает в действительности, при неравных поэтапных процентах изменения.
Случай 3. Иногда в задачах встречается понятие «средний процент прироста». Под этим понимают такой постоянный процент прироста, который за п этапов давал бы такое же изменение величины А, которое она получает в действительности, при неравных поэтапных процентах изменения.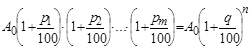
 р.
р.