| Скачать .docx | Скачать .pdf |
Дипломная работа: Дослідження нестандартних методів рішення рівнянь і нерівностей.
Дипломна робота:
Дослідження нестандартних методів рішення рівнянь і нерівностей.
ЗМІСТ
1 ІСТОРИЧНА ДОВІДКА
2 РІШЕННЯ ЗАДАЧ ІЗ ВИКОРИСТАННЯМ ВЛАСТИВОСТЕЙ ФУНКЦІЇ
2.1 Використання монотонності функції
2.2 Використання обмеженості функції
2.3 Використання періодичності функції
2.4 Використання парності функції
2.5 Використання ОПЗ функції
3 ДЕЯКІ ШТУЧНІ СПОСОБИ РІШЕННЯ РІВНЯНЬ
3.1 Множення рівняння на функцію
3.2 Угадування кореня рівняння
3.3 Використання симетричності рівняння
3.4 Дослідження рівняння на проміжках дійсної осі
ВИСНОВОК
ДОДАТОК
СПИСОК ДЖЕРЕЛ
ВВЕДЕННЯ
Не всяке рівняння або нерівність у результаті перетворень або за допомогою вдалої заміни змінної може бути зведене до рівняння (нерівності) того або іншого стандартного виду, для якого існує певний алгоритм рішення. У таких випадках іноді виявляється корисним використовувати інші методи рішення, мова про які й піде в ході даної роботи. Вище сказане визначає актуальність дипломної роботи. Об'єкт дослідження - рівняння й нерівності, що не піддаються рішенню за допомогою стандартних методів, або що відрізняються громіздкістю стандартного рішення.
Метою даної роботи є ознайомлення з нестандартними методами рішення рівнянь і нерівностей.
Для досягнення поставленої мети в даній роботі вирішувалися наступні задачі:
Зібрати відомості з історії математики про рішення рівнянь.
Розглянути й застосувати на практиці методи рішення рівнянь і нерівностей, засновані на використанні властивостей функції.
Розглянути й застосувати на практиці додаткові нестандартні методи рішення рівнянь і нерівностей
Практична значимість роботи полягає в тому, що не завжди при рішенні складних рівнянь або нерівностей варто йти по «торованій колії», намагаючись знайти рішення «у чоло»: досить лише глянути на нього й знайти зачіпку, що дозволяє уникнути складних обчислень і перетворень. Дипломна робота складається із введення, трьох глав і списку використаних джерел. У першому розділі наведені деякі відомості з історії математики про рішення рівнянь. У другому розділі розглянуті методи рішення, засновані на використанні властивостей функції. Третій розділ присвячений розгляду додаткових (штучних) методів рішення.
![]() 1 ІСТОРИЧНА
ДОВІДКА
1 ІСТОРИЧНА
ДОВІДКА
Рівняння й системи рівнянь математики вміли вирішувати дуже давно. В «Арифметиці» грецького математика з Олександрії Диофанта (III в.) ще не було систематичного викладу алгебри, однак у ній утримувався ряд задач, розв'язуваних за допомогою складання рівнянь. Є в ній така задача:
«Знайти два числа по їхній сумі 20 і добутку 96». [16]
Щоб уникнути рішення квадратного рівняння загального виду, до якого приводить позначення одного із чисел буквою і яке тоді ще не вміли вирішувати, Диофант позначав невідомі числа 10 + х і 10-х (у сучасному записі) і одержував неповне квадратне рівняння 100-х2 = 96, для якого вказував лише позитивний корінь 2.
Задачі на квадратні рівняння зустрічаються в працях індійських математиків уже з V в. н.е.
Квадратні рівняння класифікуються в трактаті «Коротка книга про вирахування алгебри й алмукабали» Мухаммеда аль-хорезми (787 - ок. 850). У ньому розглянуті й вирішені (у геометричній формі) 6 видів квадратних рівнянь, що містять в обох частинах тільки члени з позитивними коефіцієнтами. При цьому розглядалися тільки позитивні коріння рівнянь.
У роботах європейських математиків XIII – XVI ст. даються окремі методи рішення різних видів квадратних рівнянь. Злиття цих методів у загальне правило зробив німецький математик Михаель Штифель (1487 - 1567), що розглядав уже й негативні коріння.
У найвідомішому російському підручнику «Арифметика» Леонтія Пилиповича Магницького (1669-1739) було чимало задач на квадратні рівняння. От одна з них:
«Якийсь генерал хоче з 5000 чоловік баталію вчинити, і щоб та була в особі вдвічі, ніж осторонь. Кілько баталія буде мати в особі й осторонь?», тобто скільки солдатів треба поставити по фронті й скільки їм у тил, щоб число солдатів по фронту було в 2 рази більше числа солдат, розташованих їм «у тилу»?
У вавилонських текстах (3000 - 2000 років до н.е.) зустрічаються й задачі, розв'язувані тепер за допомогою систем рівнянь, що містять і рівняння другого ступеня. Приведемо один з них:
«Площі двох своїх квадратів я склав: 25![]() . Сторона другого квадрата дорівнює
. Сторона другого квадрата дорівнює ![]() сторони першого й ще 5».
сторони першого й ще 5».
Відповідна система в сучасному записі має вигляд:
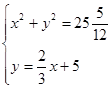
Цю задачу вавилонський автор вирішує правильно методом, що ми тепер називаємо методом підстановки, але він ще не користувався алгебраїчною символікою.
В XVI в. французький математик Франсуа Виет (1540 - 1603), що служив шифрувальником при дворі французького короля, уперше ввів літерні позначення не тільки для невідомих величин, але й для даних, тобто коефіцієнтів рівнянь. Ф. Виет для позначення нерозшифрованих букв у повідомленнях супротивника використовував рідкі букви латинського алфавіту х, у и z, що й поклало початок традиції позначати невідомі в рівняннях буквами х, у и z. Особливо цінував Виет відкриті їм формули, які тепер називаються формулами Виета. Однак сам Виет визнавав тільки позитивних корінь.
Лише в ХVII в. після робіт Декарта, Ньютона й інших математиків рішення квадратних рівнянь прийняло сучасний вид.
Повернемося в початок XVI в. Тоді професор математики болонського університету Сципион дель Ферро (1465-1526) уперше знайшов алгебраїчне рішення рівняння третього ступеня виду
x3 +px=q, (1)
де р и q - числа позитивні.
Це відкриття, по звичаях того часу, професор тримав у строгому секреті. Про нього знали лише два його учні, у тому числі якийсь Фиоре. Утаювання математичних відкриттів тоді було звичайним явищем, тому що в Італії практикувалися математичні диспути-двобої. На багатолюдних зборах супротивники пропонували один одному задачі для рішення на місці або в певний строк. Найчастіше це були задачі по алгебрі, що називали тоді великим мистецтвом. Перемагав той, хто вирішував більше задач. Переможець не тільки нагороджувався славою й призначеним грошовим призом, але й міг зайняти університетську кафедру, а потерпілий поразку часто втрачав займане місце. От чому учасникові диспуту було важливо мати невідомий інший алгоритм рішення деяких задач.
Після смерті професора дель Ферро його учень Фиоре, що сам не був глибоким математиком, викликав на публічний диспут одного з найвизначніших математиків того часу Никколо Тарталья (1499-1557). Готуючись до диспуту, Тарталья відкрив формулу для знаходження корінь кубічних рівнянь у радикалах, тому що припускав, що Фиоре вже мав цю формулу. Пізніше Тарталья писав: «Я приклав всю свою запопадливість, ретельність і уменье, щоб знайти правило для рішення кубічних рівнянь, і, завдяки благословенній долі, мені вдалося це зробити за 8 днів до строку».
Диспут відбувся 20 лютого 1535 р. Тарталья протягом двох годин вирішив 30 задач, запропонованих йому супротивником, а Фиоре не зміг вирішити ні однієї з 30 задач, запропонованих Тартальєй. Після диспуту Тарталья став знаменитим у всій Італії, але продовжував тримати відкриту формулу в секреті.
Інший італійський математик Джерол (1501 - 1576) довідався від Тартальи правило рішення кубічного рівняння (1) і дав «священну клятву», що нікому не розкриє цієї таємниці. Правда, Тарталья лише частково розкрив свою таємницю, але Кардано, познайомившись із рукописами покійного професора дель Ферро, одержав повну ясність у цьому питанні. В 1545 р. Кардано опублікував знамениту свою працю «Про велике мистецтво, або про алгебраїчні речі, в одній книзі», де вперше опублікував формулу для рішення рівняння (1), а кубічне рівняння загального виду пропонував звести до рівняння (1).
Після виходу у світло цієї книги Кардано був обвинувачений Тартальей у порушенні клятви, але формула, відкрита дель Ферро й Тартальей, і донині називається формулою Кардано.
Така повна драматизму історія відкриття формули корінь кубічного рівняння (1).
У тій же книзі Кардано привів алгебраїчне рішення рівняння четвертого ступеня. Це відкриття зробив один з його учнів Лудовико Феррари (1522 - 1565). Після цього почалися наполегливі пошуки формул, які зводили б рішення рівнянь вищих ступенів до добування корінь («рішення в радикалах»). Ці пошуки тривали біля трьох сторіч, і лише на початку XIX в. норвезький учений Нильс Хенрик Абель (1802 -1829) і французький учений Еварист Галуа (1811 -1832) довели, що рівняння ступенів вище четвертої в загальному випадку в радикалах не вирішуються.
Математик і філософ Рене Декарт (1596 -1650) уперше сформулював у своїй книзі «Геометрія» основну теорему алгебри про число корінь рівняння n-й ступеня. При цьому Декарт припускав існування не тільки щирих (позитивних) і помилкових (менших, чим нічого, тобто менших нуля - негативних) корінь, але й уявлюваних, мнимих (у Декарта - imaginaires), тобто комплексних корінь.
Ще в стародавності математики в процесі рішення задач зіштовхувалися з добуванням кореня квадратного з негативного числа; у цьому випадку задача вважалася нерозв'язною. Однак поступово з'ясовувалося, що рішення багатьох задач, що задаються в дійсних числах, одержує просте пояснення за допомогою виражень a + bi, де i2 = -1, які зрештою теж стали називати числами, але вже комплексними. Перше обґрунтування найпростіших дій над комплексними числами дав італійський математик Раффаеле Бомбелли (1530 -1572) в 1572 р., хоча ще довгий час до комплексних чисел ставилися як до чого надприродному.
Академік Петербурзької академії наук Леонард Ейлер (1707 -1783) вніс істотний вклад у питання теорії комплексних чисел. Після його робіт комплексні числа одержали остаточне визнання як предмет і засіб вивчення. Сама назва «комплексне число» було запропоновано в 1831 р. німецьким математиком Карлом Фрідріхом Гауссом (1777 - 1855).
У цей час комплексні числа широко вживаються в багатьох питаннях фізики й техніки.
Вище мова йшла про алгебраїчні рівняння, тобто рівняннях f(x) = O, де f(x) - багаточлен відносно х.
Крім алгебраїчних рівнянь, є ще й трансцендентні рівняння: показові, логарифмічні, тригонометричні й ін. Рішення трансцендентних рівнянь, а також нерівностей істотно опирається на властивості функцій, які вивчаються в математику відносно недавно.
Особливе місце серед алгебраїчних рівнянь займають так звані диофантові рівняння, тобто рівняння, у яких невідомих більше однієї.
Найбільш відомими з них є лінійні дофантові рівняння. Приклади задач, що приводять до лінійних дофантових рівнянь, знаходимо в збірнику задач ченця Алькуїна, запрошеного в 795 р. Карлом Великим викладати в першу з відомих шкіл у м. Аахен. От ця задача:
«100 шеффелей (грошових одиниць) розділили між чоловіками, жінками й дітьми (число персон 100) і дали при цьому чоловікам по 3 шеффеля, жінкам по 2 і дітям по ![]() шеффеля. Скільки було чоловіків, жінок і дітей?»
шеффеля. Скільки було чоловіків, жінок і дітей?»
Позначивши кількість чоловіків за х, кількість жінок за у, ми прийдемо до рівняння
Зх + 2y+![]() ( х-y)= 100
( х-y)= 100
Загального рішення лінійних дофантових рівнянь у ті часи ще не знали й задовольнялися лише декількома рішеннями, що задовольняють умові задачі. У самого Алькуина було наведено лише одне рішення цієї задачі: чоловіків, жінок і дітей було 11, 15 і 74, а задача має 784 рішення в натуральних числах.
Задачі, що приводять до лінійних дофантових рівнянням, були в Леонардо Пизанського (Фибоначчи) (1180 - 1240), в «Арифметиці» Л. Ф. Магницького.
Відоме рівняння Піфагора (VI в. до н.е.) х2 + в2 = z2 вирішують у натуральних числах. Його рішеннями служать трійки чисел (х; в; z):
x = (m2 -n2 )l, y = 2mnl, z = (m2 + n2 )l,
де т, п, l - будь-які натуральні числа (т> п). Ці формули допомагають знаходити прямокутні трикутники, довжини сторін яких є натуральними числами.
В 1630 р. французький математик Пьер Ферма (1601 — 1665) сформулював гіпотезу, що називають великою (або великий) теоремою Ферма: «Рівняння хп + уп = zn для натурального п ≥ 3 не має рішень у натуральних числах». Ферма не довів свою теорему в загальному випадку, але відома його запис на полях «Арифметики» Диофанта: «...неможливо куб записати у вигляді суми двох кубів, або парний ступінь у вигляді суми таких же ступенів, або взагалі будь-яке число, що є ступенем більшої, ніж друга, не можна записати у вигляді суми двох таких же ступенів. У мене є воістину дивний доказ цього твердження, але поля ці занадто вузькі, щоб його вмістити». Пізніше в паперах Ферма було знайдене доказ його теореми для п= 4. З тих пор більше 300 років математики намагалися довести велику теорему Ферма. В 1770 р. Л.Ейлер довів теорему Ферма для п = 3, в 1825 р. Адриен Лежандр (1752 1833) і Петер Дирихле (1805 - 1859) - для п = 5. Доказ великої теореми Ферма в загальному випадку не вдавався довгі роки. І тільки в 1995 р. Ендрю Вайлс довів цю теорему.
2. РІШЕННЯ ЗАДАЧ ІЗ ВИКОРИСТАННЯМ ВЛАСТИВОСТЕЙ ФУНКЦІЇ
Не всяке рівняння f(x) = g(x) або нерівність у результаті перетворень або за допомогою вдалої заміни змінної може бути зведене до рівняння або нерівності того або іншого стандартного виду, для якого існує певний алгоритм рішення. У таких випадках іноді виявляється корисним використовувати деякі властивості функцій, такі як монотонність, періодичність, обмеженість, парність і ін.
2.1 Використання монотонності функції
Функція f (x) називається зростаючої на проміжку D, якщо для будь-яких чисел x1 і x2 із проміжку D таких, що x1 < x2 , виконується нерівність f (x1 ) < f (x2 ).
Функція f (x) називається убутної на проміжку D, якщо для будь-яких чисел x1 і x2 із проміжку D таких, що x1 < x2 , виконується нерівність f (x1 ) > f (x2 ).
На показаному на малюнку 1 графіку
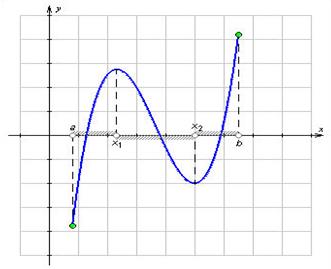
Малюнок 1
Функція y = f (x), ![]() , зростає на кожному із проміжків [a; x1
) і (x2
; b] і убуває на проміжку (x1
; x2
). Зверніть увагу, що функція зростає на кожному із проміжків [a; x1
) і (x2
; b], але не на об'єднанні проміжків
, зростає на кожному із проміжків [a; x1
) і (x2
; b] і убуває на проміжку (x1
; x2
). Зверніть увагу, що функція зростає на кожному із проміжків [a; x1
) і (x2
; b], але не на об'єднанні проміжків ![]()
Якщо функція зростає або убуває на деякому проміжку, то вона називається монотонної на цьому проміжку.
Помітимо, що якщо f – монотонна функція на проміжку D (f (x)), те рівняння f (x) = const не може мати більше одного кореня на цьому проміжку.
Дійсно, якщо x1 < x2 – корінь цього рівняння на проміжку D (f(x)), те f (x1 ) = f (x2 ) = 0, що суперечить умові монотонності.
Перелічимо властивості монотонних функцій (передбачається, що всі функції визначені на деякому проміжку D).
Сума декількох зростаючих функцій є зростаючою функцією.
Добуток ненегативних зростаючих функцій є зростаюча функція.
Якщо функція f зростає, то функції cf (c > 0) і f + c також зростають, а функція cf (c < 0) убуває. Тут c - деяка константа.
Якщо функція f зростає й зберігає знак, то функція ![]() убуває.
убуває.
Якщо функція f зростає й ненегативна, то fn
де n![]() N, також зростає.
N, також зростає.
Якщо функція f зростає й n – непарне число, то fn також зростає.
Композиція g (f (x)) зростаючих функцій f і g також зростає.
Аналогічні твердження можна сформулювати й для убутної функції.
Крапка a називається крапкою максимуму функції f, якщо існує така ε-околиця крапки a, що для будь-якого x із цієї околиці виконується нерівність f (a) ≥ f (x).
Крапка a називається крапкою мінімуму функції f, якщо існує така ε-околиця крапки a, що для будь-якого x із цієї околиці виконується нерівність f (a) ≤ f (x).
Крапки, у яких досягається максимум або мінімум функції, називаються крапками екстремуму.
У крапці екстремуму відбувається зміна характеру монотонності функції. Так, ліворуч від крапки екстремуму функція може зростати, а праворуч - убувати. Відповідно до визначення, крапка екстремуму повинна бути внутрішньою крапкою області визначення.
Якщо для кожного ![]() (x ≠ a) виконується нерівність f (x) ≤ f (a)
(x ≠ a) виконується нерівність f (x) ≤ f (a) ![]() , те крапка a називається
крапкою найбільшого значення функції на множині D:
, те крапка a називається
крапкою найбільшого значення функції на множині D:
![]()
Якщо для кожного ![]() (x ≠ b) виконується нерівність f (x) > f (b)
(x ≠ b) виконується нерівність f (x) > f (b) ![]() , те крапка b називається
крапкою найменшого значення функції на множині D.
, те крапка b називається
крапкою найменшого значення функції на множині D.
![]()
Крапка найбільшого або найменшого значення функції на множині D може бути екстремумом функції, але не обов'язково їм є.
Крапку найбільшого (найменшого) значення безперервної на відрізку функції варто шукати серед екстремумів цієї функції і її значень на кінцях відрізка.
Рішення рівнянь і нерівностей з використанням властивості монотонності ґрунтується на наступних твердженнях.
1. Нехай f(х) - безперервна й строго монотонна функція на проміжку Т , тоді рівняння f(x) = З, де З - дана константа, може мати не більше одного рішення на проміжку Т.
2. Нехай f(x) і g(х) - безперервні на проміжку T функції, f(x) строго зростає, а g(х) строго убуває на цьому проміжку, тоді рівняння f(х) = =g(х) може мати не більше одного рішення на проміжку Т. Відзначимо, що як проміжок T можуть бути нескінченний проміжок (-?;+?) , проміжки (а;+?), (-?; а), [а;+?), (-?; b], відрізки, інтервали й напівінтервали.
Приклад 2.1.1 Вирішите рівняння
![]() . [28] (1)
. [28] (1)
Рішення. Очевидно, що х ≤ 0 не може бути рішенням даного рівняння, тому що тоді ![]() . Для х > 0 функція
. Для х > 0 функція ![]() безперервна й строго зростає, як добуток двох безперервних позитивних строго зростаючих для цих х функцій f(x) = х і
безперервна й строго зростає, як добуток двох безперервних позитивних строго зростаючих для цих х функцій f(x) = х і ![]() . Виходить, в області х > 0 функція
. Виходить, в області х > 0 функція ![]() приймає кожне своє значення рівно в одній крапці. Легко бачити, що х = 1 є рішенням даного рівняння, отже, це його єдине рішення.
приймає кожне своє значення рівно в одній крапці. Легко бачити, що х = 1 є рішенням даного рівняння, отже, це його єдине рішення.
Відповідь: {1}.
Приклад 2.1.2 Вирішите нерівність
![]() . (2)
. (2)
Рішення. Кожна з функцій в = 2x
, в = 3x
, в = 4х
безперервна й строго зростаюча на всій осі. Виходить, такий же є й вихідна функція ![]() . Легко бачити, що при х = 0 функція
. Легко бачити, що при х = 0 функція ![]() приймає значення 3. У силу безперервності й строгої монотонності цієї функції при х > 0 маємо
приймає значення 3. У силу безперервності й строгої монотонності цієї функції при х > 0 маємо ![]() , при х < 0 маємо
, при х < 0 маємо ![]() . Отже, рішеннями даної нерівності є всі х < 0.
. Отже, рішеннями даної нерівності є всі х < 0.
Відповідь: (-?; 0).
Приклад 2.1.3 Вирішите рівняння
![]() . (3)
. (3)
Рішення. Область припустимих значень рівняння (3) є проміжок ![]() . На ОПЗ функції
. На ОПЗ функції ![]() й
й ![]() безперервні й строго убувають, отже, безперервна й убуває функція
безперервні й строго убувають, отже, безперервна й убуває функція ![]() . Тому кожне своє значення функція h(x) приймає тільки в одній крапці. Тому що ,
. Тому кожне своє значення функція h(x) приймає тільки в одній крапці. Тому що , ![]() те х = 2 є єдиним коренем вихідного рівняння.
те х = 2 є єдиним коренем вихідного рівняння.
Відповідь: {2}.
2.2 Використання обмеженості функції
При рішенні рівнянь і нерівностей властивість обмеженості знизу або зверху функції на деякій множині часто відіграє визначальну роль.
Якщо існує число C таке, що для кожного ![]() виконується нерівність f (x) ≤ C, те функція f називається
обмеженої зверху на множині D (малюнок 2).
виконується нерівність f (x) ≤ C, те функція f називається
обмеженої зверху на множині D (малюнок 2).
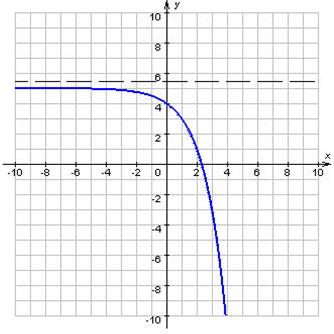
Малюнок 2
Якщо існує число c таке, що для кожного ![]() виконується нерівність f (x) ≥ c, те функція f називається
обмеженої знизу на множині D (малюнок 3).
виконується нерівність f (x) ≥ c, те функція f називається
обмеженої знизу на множині D (малюнок 3).
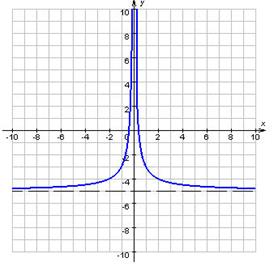
Малюнок 3
Функція, обмежена й зверху, і знизу, називається обмеженої на множині D. Геометрично обмеженість функції f на множині D означає, що графік функції y = f (x), ![]() лежить у смузі c ≤ y ≤ C (малюнок 4).
лежить у смузі c ≤ y ≤ C (малюнок 4).
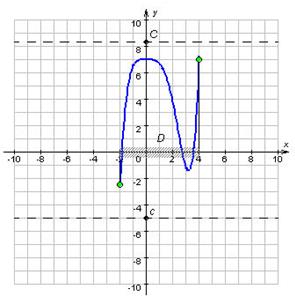
Малюнок 4
Якщо функція не є обмеженою на множині, то говорять, що вона не обмежена.
Прикладом функції, обмеженої знизу на всій числовій осі, є функція y = x2 . Прикладом функції, обмеженої зверху на множині (–∞; 0) є функція y = 1/x. Прикладом функції, обмеженої на всій числовій осі, є функція y = sin x.
Приклад 2.2.1 Вирішите рівняння
sin(x3 + 2х2 + 1) = х2 + 2х + 2. (4)
Рішення. Для будь-якого дійсного числа х маємо sin(x3
+ 2х2
+ 1) ≤ 1, х2
+ 2х + 2 = (x + 1)2
+ 1 ≥ 1. Оскільки для будь-якого значення х ліва частина рівняння не перевершує одиниці, а права частина завжди не менше одиниці, то дане рівняння може мати рішення тільки при ![]() .
.
При ![]()
![]() ,
, ![]() , тобто при
, тобто при ![]() рівняння (4) так само корінь не має .
рівняння (4) так само корінь не має .
Відповідь: O.
Приклад 2.2.2 Вирішите рівняння
![]() . (5)
. (5)
Рішення. Очевидно, що х = 0, х = 1, х = -1 є рішеннями даного рівняння. Для знаходження інших рішень у силу непарності функції f(х) = = x3 - x - sin πx досить знайти його рішення в області х > 0, х ≠ 1, оскільки якщо x0 > 0 є його рішенням, те й (-x0 ) також є його рішенням.
Розіб'ємо множину х > 0, х ? 1, на два проміжки: (0; 1) і (1; +?)
Перепишемо початкове рівняння у вигляді x3 - x = sin πx. На проміжку (0; 1) функція g(х) = x3 - x приймає тільки негативні значення, оскільки х3 < < х, а функція h(x) = sin πx тільки позитивні. Отже, на цьому проміжку рівняння не має рішень.
Нехай х належить проміжку (1; +∞). Для кожного з таких значень х функція g(х) = х3 - х приймає позитивні значення, функція h(x) = sin πx приймає значення різних знаків, причому на проміжку (1; 2] функція h(x) = sin ?x непозитивна. Отже, на проміжку (1; 2] рівняння рішень не має.
Якщо ж х > 2, то |sin πx| ≤ 1, x3 - x = x(x2 - 1) > 2∙ 3 = 6, а це означає, що й на проміжку (1; +∞) рівняння також не має рішень.
Отже, x = 0, x = 1 і x = -1 і тільки вони є рішеннями вихідного рівняння.
Відповідь: {-1; 0; 1}.
Приклад 2.2.3 Вирішите нерівність
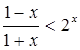 . (6)
. (6)
Рішення. ОПЗ нерівності є всі дійсні x, крім x = -1. Розіб'ємо ОПЗ нерівності на три множини: -? < x < -1, -1 < x ? 0, 0 < x < +? і розглянемо нерівність на кожному із цих проміжків.
Нехай -∞ < x < -1. Для кожного із цих x маємо g(x) =![]() < 0, а f(x) = 2x
> 0. Отже, всі ці x є рішеннями нерівності.
< 0, а f(x) = 2x
> 0. Отже, всі ці x є рішеннями нерівності.
Нехай -1 < x ≤ 0. Для кожного із цих x маємо g(x) = 1 - ![]() , а f(x) = 2x
≤ 1. Отже, жодне із цих x не є рішенням даної нерівності.
, а f(x) = 2x
≤ 1. Отже, жодне із цих x не є рішенням даної нерівності.
Нехай 0 < x < +∞. Для кожного із цих x маємо g(x) = 1 - ![]() , a
, a ![]() . Отже, всі ці x є рішеннями вихідної нерівності.
. Отже, всі ці x є рішеннями вихідної нерівності.
Відповідь: ![]() .
.
2.3 Використання періодичності функції
Функція f (x) називається періодичної з періодом T ≠ 0, якщо виконуються дві умови:
якщо ![]() , то x + T і x – T також належать області визначення D (f (x));
, то x + T і x – T також належать області визначення D (f (x));
для кожного ![]() виконана рівність
виконана рівність
f (x + T) = f (x).
Оскільки ![]() те з наведеного визначення треба, що
те з наведеного визначення треба, що
![]()
Якщо T – період функції f (x), то очевидно, що кожне число nT, де ![]() , n ≠ 0, також є періодом цієї функції.
, n ≠ 0, також є періодом цієї функції.
Найменшим позитивним періодом функції називається найменше з позитивних чисел T, що є періодом даної функції.
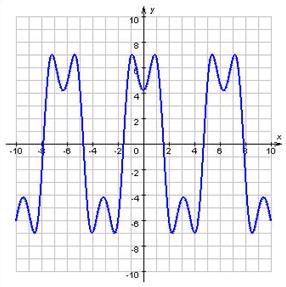
Графік періодичної функції
![]()
Графік періодичної функції звичайно будують на проміжку [x0 ; x0 + T), а потім повторюють на всю область визначення.
Гарним прикладом періодичних функцій можуть служити тригонометричні функції y = sin x, y = cos x (період цих функцій дорівнює 2π), y = tg x (період дорівнює π) і інші. Функція y = const також є періодичною. Для неї періодом є будь-яке число T ≠ 0.
На закінчення відзначимо властивості періодичних функцій. [19]
Якщо f (x) – періодична функція з періодом T, то функція
g (x) = A · f (kx + b)
де k ≠ 0 також є періодичною з періодом ![]() .
.
Нехай функції f1
(x) і f2
(x) визначені на всій числовій осі і є періодичними з періодами T1
> 0 і T2
> 0. Тоді якщо ![]() те функція
те функція ![]() періодична з періодом T, рівним найменшому загальному кратному чисел T1
і T2.
періодична з періодом T, рівним найменшому загальному кратному чисел T1
і T2.
Приклад 2.4.1 Функція ![]() періодична з періодом T = 5. Відомо, що
періодична з періодом T = 5. Відомо, що ![]() . Знайдіть
. Знайдіть
![]()
Рішення. Перетворимо окремо кожний доданок:
![]()
![]()
![]()
Тоді ![]()
Відповідь: 2.
Приклад 2.4.2 [24] Знайдіть період функції
![]()
Рішення. Перетворимо дане вираження:
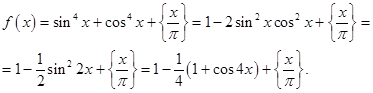
![]() має період
має період ![]() ;
;
![]() має період
має період ![]() .
.
Тоді функція ![]() має період
має період
![]()
Відповідь: ?.
Приклад 2.4.3 Нехай ![]() - періодична функція з періодом 3 така, що
- періодична функція з періодом 3 така, що
![]() ;
; ![]() .
.
Вирішите рівняння:
![]() (7)
(7)
Графік функції ![]() на множині [0;3) зображений на малюнку 3:
на множині [0;3) зображений на малюнку 3:
|
|
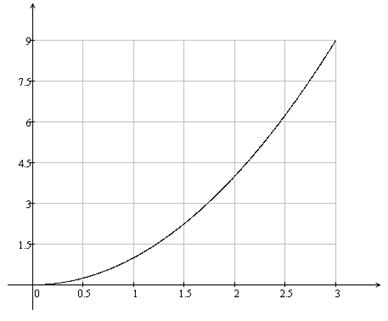
Малюнок 5
Таким чином 3 - період функції ![]() , те
, те![]() , тоді рівняння (7) прикмет вид
, тоді рівняння (7) прикмет вид ![]() , розглянемо два випадки.
, розглянемо два випадки.
1) нехай ![]() , тобто
, тобто ![]() , тоді рівняння прийме вид:
, тоді рівняння прийме вид:
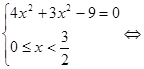
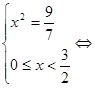
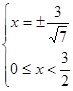 , значить
, значить ![]() і виходить
і виходить![]() ,
, ![]()
2) нехай![]() те
те![]() , тоді
, тоді ![]() рівняння прийме вид:
рівняння прийме вид:
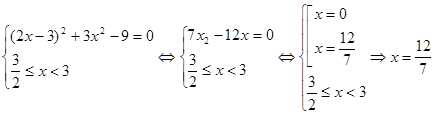 ; отже
; отже ![]() ,
, ![]()
таким чином ![]() ,
, ![]() .
.
Відповідь: ![]() .
.
2.4 Використання парності функції
Функція f (x) називається парної, якщо для кожного ![]() виконуються рівності:
виконуються рівності:
1) ![]() ,
,
2) f (–x) = f (x).
Графік парної функції на всій області визначення симетричний щодо осі OY. Прикладами парних функцій можуть служити y = cos x, y = |x|, y = x2 + |x|
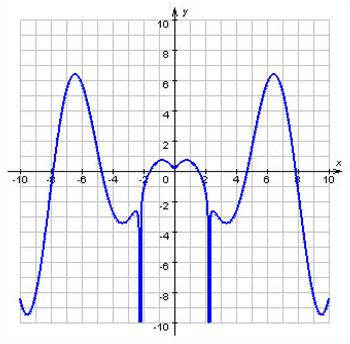
Графік парної функції 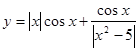
Функція f (x) називається непарної, якщо для кожного ![]() виконуються рівності:
виконуються рівності:
1) ![]() ,
,
2) f (–x) = –f (x).
Іншими словами функція називається непарної, якщо її графік на всій області визначення симетричні відносно початку координат. Прикладами непарних функцій є y = sin x, y = x3 .
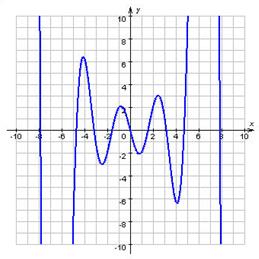
Графік непарної функції ![]()
Не слід думати, що будь-яка функція є або парної, або непарної. Так, функція![]() не є ні парної, ні непарної, тому що її область визначення
не є ні парної, ні непарної, тому що її область визначення ![]() несиметрична відносно початку координат. Область визначення функції y = x3
+ 1 охоплює всю числову вісь і тому симетрично відносно початку координат, однак f (–1) ≠ f (1). А це значить, що функція не є ні парної, ні непарної, тобто є функцією загального виду (ФЗВ).
несиметрична відносно початку координат. Область визначення функції y = x3
+ 1 охоплює всю числову вісь і тому симетрично відносно початку координат, однак f (–1) ≠ f (1). А це значить, що функція не є ні парної, ні непарної, тобто є функцією загального виду (ФЗВ).
Якщо область визначення функції симетрична відносно початки координат, то цю функцію можна представити у вигляді суми парної й непарної функцій.
Такою сумою є функція
![]()
Перший доданок є парною функцією, друге - непарної.
Порівняльна ілюстрація функцій різної парності зображена на малюнку 6
|
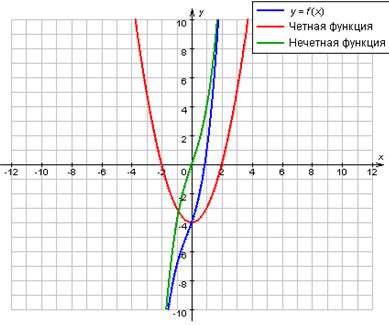
Малюнок 6
Дослідження функцій на парність полегшується наступними твердженнями.
Сума парних (непарних) функцій є парною (непарної) функцією.
Добуток двох парних або двох непарних функцій є парною функцією.
Добуток парної й непарної функції є непарною функцією.
Якщо функція f парна (непарна), то й функція 1/f парна (непарна).
Приклад 2.4.1 чи Може при якому-небудь значенні а рівняння
2x8 – 3аx6 + 4x4 – аx2 = 5
мати 5 корінь?
Рішення. Позначимо f(x) = 2х8 – 3ах6 + 4х4 – ах2 . f(x) – функція парна, тому, якщо x0 – корінь даного рівняння, те -x0 – теж. x = 0 не є коренем даного рівняння (0 ? 5). Отже, число корінь у цього рівняння при будь-якому дійсному а парне, тому 5 корінь воно мати не може.
Відповідь: не може.
2.5 Використання ОПЗ функції
Область визначення функції - це множина всіх припустимих дійсних значень аргументу x (змінної x), при яких функція ![]() визначена. Область визначення іноді ще називають областю припустимих значень функції (ОПЗ). Для знаходження ОПЗ функції потрібно проаналізувати дану відповідність і встановити заборонні операції, що зустрічаються (ділення на нуль, піднесення в раціональний ступінь негативного числа, логарифмічні операції над негативними числами й т.п.).
визначена. Область визначення іноді ще називають областю припустимих значень функції (ОПЗ). Для знаходження ОПЗ функції потрібно проаналізувати дану відповідність і встановити заборонні операції, що зустрічаються (ділення на нуль, піднесення в раціональний ступінь негативного числа, логарифмічні операції над негативними числами й т.п.).
Іноді знання ОПЗ дозволяє довести, що рівняння (або нерівність) не має рішень, а іноді дозволяє знайти рішення рівняння (або нерівності) безпосередньою підстановкою чисел з ОПЗ.
Приклад 2.5.1 Вирішите рівняння
![]() . (8)
. (8)
Рішення. ОПЗ цього рівняння складається із всіх х, одночасно задовольняючим умовам ![]() і
і ![]() , тобто ОПЗ є порожня множина. Цим рішення рівняння й завершується, тому що встановлено, що жодне число не може бути рішенням, тобто що рівняння не має корінь.
, тобто ОПЗ є порожня множина. Цим рішення рівняння й завершується, тому що встановлено, що жодне число не може бути рішенням, тобто що рівняння не має корінь.
Відповідь: O.
Приклад 2.5.2 Вирішите рівняння
![]() . (9)
. (9)
Рішення. ОПЗ цього рівняння складається із всіх x, одночасно задовольняючим умовам ![]() ,
, ![]() ,
, ![]() , тобто ОПЗ є
, тобто ОПЗ є ![]() . Підставляючи ці значення х у рівняння (9), одержуємо, що його ліва й права частини рівно 0, а це означає, що всі
. Підставляючи ці значення х у рівняння (9), одержуємо, що його ліва й права частини рівно 0, а це означає, що всі ![]() , є його рішеннями.
, є його рішеннями.
Відповідь: ![]()
Приклад 2.5.3 Вирішите нерівність
![]() . (10)
. (10)
Рішення. ОПЗ нерівності (10) є всі х, що задовольняють умові ![]() . Ясно, що х = 1 не є рішенням нерівності (10). Для х із проміжку
. Ясно, що х = 1 не є рішенням нерівності (10). Для х із проміжку ![]() маємо
маємо ![]() , а
, а ![]() . Отже, всі х із проміжку
. Отже, всі х із проміжку ![]() є рішеннями нерівності (10).
є рішеннями нерівності (10).
Відповідь: ![]() .
.
Приклад 2.5.4 [26] Вирішите нерівність
![]() . (11)
. (11)
Рішення. ОПЗ нерівності (11) є всі х із проміжку ![]() . Розіб'ємо цю множину на два проміжки
. Розіб'ємо цю множину на два проміжки ![]() й
й ![]() .
.
Для х із проміжку ![]() маємо
маємо ![]() ,
, ![]() . Отже,
. Отже, ![]() на цьому проміжку, і тому нерівність (11) не має рішень на цьому проміжку.
на цьому проміжку, і тому нерівність (11) не має рішень на цьому проміжку.
Нехай х належить проміжку ![]() , тоді
, тоді ![]() й
й ![]() . Отже,
. Отже, ![]() для таких х, і, виходить, на цьому проміжку нерівність (11) також не має рішень.
для таких х, і, виходить, на цьому проміжку нерівність (11) також не має рішень.
Отже, нерівність (11) рішень не має.
Відповідь: O.
3 ДЕЯКІ ШТУЧНІ СПОСОБИ РІШЕННЯ РІВНЯНЬ
Існують і інші нестандартні методи рішення рівнянь і нерівностей, крім використання властивостей функції. Дана глава присвячена додатковим методам рішення.
3.1 Множення рівняння на функцію
Іноді рішення алгебраїчного рівняння істотно полегшується, якщо помножити обидві його частини на деяку функцію - багаточлен від невідомої. При цьому треба пам'ятати, що можливо появу зайвих корінь - корінь багаточлена, на який множили рівняння. Тому треба або множити на багаточлен, що не має корінь, і одержувати рівносильне рівняння, або множити на багаточлен, що має корінь, і тоді кожний з таких корінь треба обов'язково підставити у вихідне рівняння й установити, чи є це число його коренем.
Приклад 3.1.1 Вирішите рівняння
![]() . (1)
. (1)
Рішення. Помноживши обидві частини рівняння на багаточлен ![]() , що не має корінь, одержимо рівняння
, що не має корінь, одержимо рівняння
![]() , (2)
, (2)
рівносильне рівнянню (1). Рівняння (2) можна записати у вигляді
![]() . (3)
. (3)
Ясно, що рівняння (3) не має дійсних корінь, тому й рівняння (1) їх не має.
Відповідь: O.
Приклад 3.1.2 [19] Вирішите рівняння
![]() . (4)
. (4)
Рішення. Помноживши обидві частини цього рівняння на багаточлен ![]() , одержимо рівняння
, одержимо рівняння
![]()
![]() , (5)
, (5)
Є наслідком рівняння (4), тому що рівняння (5) має корінь ![]() , що не є коренем рівняння (4).
, що не є коренем рівняння (4).
Рівняння (5) є симетричне рівняння четвертого ступеня. Оскільки ![]() не є коренем рівняння (5), те, розділивши обидві його частини на
не є коренем рівняння (5), те, розділивши обидві його частини на ![]() й перегрупувавши його члени, одержимо рівняння
й перегрупувавши його члени, одержимо рівняння
![]() (6)
(6)
рівносильне рівнянню (5). Позначивши ![]() , перепишемо рівняння (6) у вигляді
, перепишемо рівняння (6) у вигляді
![]() . (7)
. (7)
Рівняння (7) має два корені: ![]() і
і ![]() . Тому рівняння (6) рівносильне сукупності рівнянь
. Тому рівняння (6) рівносильне сукупності рівнянь
![]() и.
и.![]()
Вирішивши кожне із цих рівнянь, знайдемо чотири корені рівняння (6), а тим самим і рівняння (5):
![]() ,
, ![]() ,
, ![]() ,
, ![]()
Тому що корінь ![]() є стороннім для рівняння (4), те звідси одержуємо, що рівняння (4) має три корені: x1
, x2
, x3
.
є стороннім для рівняння (4), те звідси одержуємо, що рівняння (4) має три корені: x1
, x2
, x3
.
Відповідь: ![]()
3.2 Угадування кореня рівняння
Іноді зовнішній вигляд рівняння підказує, яке число є коренем рівняння.
Приклад 3.2.1 Вирішите рівняння
![]() . (8)
. (8)
Рішення. Перепишемо рівняння (8) у вигляді:
![]() . (9)
. (9)
Із зовнішнього вигляду цього рівняння очевидно, що х = 12 є його корінь. Для знаходження інших корінь перетворимо багаточлен
![]()
![]()
Тому що багаточлен ![]() не має корінь, те вихідне рівняння має єдиний корінь х = 12.
не має корінь, те вихідне рівняння має єдиний корінь х = 12.
Відповідь: {12}.
Приклад 3.2.2. Вирішите рівняння
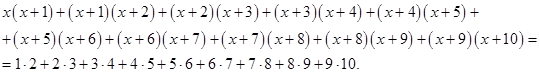 (10)
(10)
Рішення. Легко помітити, що ![]() і
і ![]() є рішеннями цього рівняння. Після розкриття дужок це рівняння перепишеться як квадратне. А це означає, що воно може мати не більше двох корінь. Тому що два корені цього рівняння знайдені, те тим самим воно й вирішено.
є рішеннями цього рівняння. Після розкриття дужок це рівняння перепишеться як квадратне. А це означає, що воно може мати не більше двох корінь. Тому що два корені цього рівняння знайдені, те тим самим воно й вирішено.
Відповідь: ![]()
3.3 Використання симетричності рівняння
Іноді зовнішній вигляд рівняння - деяка його симетричність - підказує спосіб рішення рівняння.
Приклад 3.3.1 Вирішите рівняння
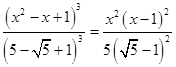 . (11)
. (11)
Рішення. Очевидно, що зовнішній вигляд рівняння підказує, що одне з корінь рівняння (11) є ![]() . Однак знайти інших корінь цього рівняння тут не так просто. Перепишемо рівняння (11) у трохи іншому виді.
. Однак знайти інших корінь цього рівняння тут не так просто. Перепишемо рівняння (11) у трохи іншому виді.
Оскільки справедливі тотожні рівності
![]()
![]() ,
,
те рівняння (11) можна переписати так:
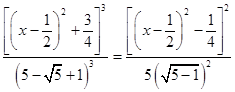 . (12)
. (12)
Тепер очевидно, що якщо ![]() ― корінь рівняння (12), те
― корінь рівняння (12), те ![]() також корінь рівняння (12), оскільки
також корінь рівняння (12), оскільки
![]() . (13)
. (13)
Покажемо, що якщо ![]() , є корінь рівняння (11), те
, є корінь рівняння (11), те ![]() також є корінь цього рівняння.
також є корінь цього рівняння.
Дійсно, тому що
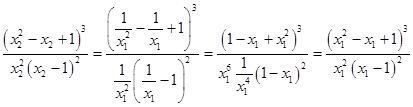
те звідси й випливає це твердження.
Отже, якщо ![]() , ― корінь рівняння (11), те воно має ще коріння
, ― корінь рівняння (11), те воно має ще коріння
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
т. е. рівняння (11) має корінь
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, 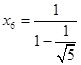 .
.
Оскільки рівняння (11) є алгебраїчне рівняння шостого ступеня, то воно має не більше шести корінь. Таким чином, ми знайшли всі коріння рівняння (11).
Відповідь: 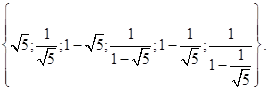
3.4 Дослідження рівняння на проміжках дійсної осі
Іноді рішення рівняння можна знайти, досліджуючи його на різних числових проміжках.
Приклад 3.4.1 Вирішите рівняння
![]() . (14)
. (14)
Рішення. Перепишемо рівняння у вигляді ![]() або, використовуючи формулу різниці
або, використовуючи формулу різниці
![]() , (15)
, (15)
у вигляді
![]() . (16)
. (16)
Звідси видно, що одне з корінь даного рівняння є ![]() . Доведемо, що рівняння
. Доведемо, що рівняння
![]() (17)
(17)
рішень не має.
Розіб'ємо числову вісь на проміжки
![]()
Для будь-якого x із проміжку ![]() маємо, що ліва частина рівняння (17) позитивна, тому на цьому проміжку рівняння рішень не має.
маємо, що ліва частина рівняння (17) позитивна, тому на цьому проміжку рівняння рішень не має.
Оскільки
![]()
![]() ,
,
те для будь-якого х із проміжку ![]() цей багаточлен позитивний. Це означає, що на проміжку
цей багаточлен позитивний. Це означає, що на проміжку ![]() рівняння (17) також не має рішень.
рівняння (17) також не має рішень.
Оскільки
![]()
![]() ,
,
те для будь-якого x із проміжку ![]() цей багаточлен позитивний. Отже, і на проміжку
цей багаточлен позитивний. Отже, і на проміжку ![]() рівняння (17) не має рішень.
рівняння (17) не має рішень.
Отже, дане рівняння (17) має єдине рішення ![]() .
.
Відповідь: {1}.
ВИСНОВОК
У процесі дослідження ціль дипломної роботи досягнута, повністю вирішені поставлені задачі й отримані наступні результати й висновки:
Наведено відомості про давнину постановки перед людиною задачі рішення рівнянь і нерівностей.
Наведено й розглянуті на прикладі методи рішення рівнянь і нерівностей, засновані на використанні властивостей функції.
Розглянуто й випробувані додаткові нестандартні методи рішення рівнянь і нерівностей.
Продовження дослідження може полягати у вивченні застосування властивостей синуса й косинуса, застосуванні похідній, використанні числових нерівностей, використанні графіків і інших нестандартних способів рішення рівнянь і нерівностей.
ДОДАТОК
Задачі для самостійного рішення:
Доведіть, що наступне рівняння не має рішень:
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]()
Вирішите рівняння:
![]()
Відповідь: {0}.
![]() .
.
Відповідь: {2}.
![]() .
.
Відповідь: {-1}.
![]() .
.
Відповідь: {2}.
![]() .
.
Відповідь: {1}.
![]() .
.
Відповідь: {1; -2}.
![]()
Відповідь: 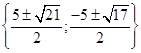 .
.
![]() .
.
Відповідь: 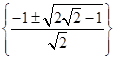
Вирішите нерівність:
![]() .
.
Відповідь: ![]() .
.
![]() .
.
Відповідь: ![]() .
.
![]() .
.
Відповідь: ![]() .
.
![]() .
.
Відповідь: ![]() .
.
![]() .
.
Відповідь: ![]()
СПИСОК ДЖЕРЕЛ
1. Абилкасимова А. Є. Алгебра 10 клас. – К., 2003
2. Алилов М. А., Колягин Ю. М. і ін. Алгебра й начало аналізу. – К., 2004
3. Болтянський В. Г., Сидоров Ю. В., Шабунин М. І. Лекції й задачі по елементарній математиці. – К., 2006
4. Газета «Математика» №20, 2008 р.
5. Голубєв В. і. Рішення складних і нестандартних задач по математиці. – К., 1995
6. Горштейн П. І. Задачі з параметрами., - К., 1999.
7. Гусєв В. А., Мордович О. Г. Математика. Довідкові матеріали. – К., 2001
8. Далингер В. А. Нестандартні рівняння й методи їхнього рішення. –К., 2005
9. Жафяров А. Ж. Профільне навчання старшокласників. К., 2001
10. Журнал «Математика в школі», 1999-2007 р.
11. Івлєв Б. М., Абрамов А. М., Дудницин Ю. П., Швардцбурд С. І. Задачі підвищених труднощів по алгебрі й початкам аналізу. – К., 2005.
12. Ковальова Г. И., Конкина Е. В. Функціональний метод рішення рівнянь і нерівностей. – К., 2006
13. Кравцов С. В. Методи рішення задач по алгебрі. – К., 2001
14. Кулагін Є. Д. 300 конкурсних задач по математиці. - К., 2003
15. Кушнір А. І. Математична енциклопедія. - К.,1995 р.
16. Литвиненко В. Н., Мордкович А. Г. Практикум по елементарній математиці. Алгебра. Тригонометрія. – К., 1991 р.