Курсовая работа: Методи розв’язування раціональних нерівностей вищих степенів

Міністерство освіти і науки України

Черкаський національний університет

імені Б. Хмельницького

Кафедра геометрії та методики навчання математики

Курсова робота

Методи розв’язування раціональних нерівностей вищих степенів

ІV курс, денна форма навчання, математичний факультет

Глушко Юлія Сергіївна

Науковий керівник:

викладач кафедри геометрії та

методики навчання математики

Воловик Оксана Петрівна

Черкаси 2010

Зміст

Вступ

§ 1. Теоретичні основи дослідження

1.1 Загальні відомості про раціональні нерівності

1.2 Теореми про рівносильність нерівностей

§ 2. Раціональні нерівності вищих степенів та методи їх розв’язування

2.1 Розв’язування раціональних нерівностей вищих степенів методом інтервалів

2.2 Розв’язування раціональних нерівностей узагальненим методом інтервалів

2.3 Розв’язування дробово-раціональних нерівностей

2.4 Розв’язування раціональних нерівностей методом заміни змінної

Висновки

Список використаних джерел

Вступ

Актуальність теми зумовлена тим, що розв’язування раціональних нерівностей вищих степенів викликає у багатьох учнів певні труднощі. Розв’язування більшості нерівностей вищих степенів вимагає знання різноманітних теоретичних відомостей, застосування різних теорем та формул. Отримати навички розв’язування раціональних нерівностей вищих степенів можна лише тоді, коли розв’язати їх достатньо велику кількість, ознайомившись з різними методами та прийомами їх розв’язання.

Все це обумовило обрання теми: «Методи розв’язування раціональних нерівностей вищих степенів»

Мета роботи полягає в тому, щоб розглянути різні методи раціональних нерівностей вищих степенів

Однією з основних функцій розв’язування раціональних нерівностей вищих степенів є формування уявлень про ідею і використання раціональних методів і прийомів.

Майстерність розв’язувати раціональних нерівностей вищих степенів ґрунтується на володінні високим рівнем знань теоретичної частини курсу та певним арсеналом методів і прийомів розв’язування раціональних нерівностей вищих степенів

Тому доцільно розглянути та ознайомитись з різноманітними методами та прийоми розв’язування раціональних нерівностей вищих степенів. Це дозволить учням розв’язувати, здавалося б, складні нерівностей просто, зрозуміло і красиво, а сформовані уміння і навички знадобляться учням при розв’язуванні ірраціональних, логарифмічних, показникових та тригонометричних. нерівностей

Для досягнення мети було поставлено наступні завдання:

-проаналізувати методичну літературу з означеної теми;

-ознайомитись з теоретичними відомостями, розглянути основні теореми та методичні факти, що стосуються даної теми;

-розглянути різноманітні методи розв’язування раціональних нерівностей вищих степенів;

-навести низку прикладів розв’язування раціональних нерівностей вищих степенів різними методами.

§ 1. Теоретичні основи дослідження

1.1 Загальні відомості про раціональні нерівності

Дві функції, що поєднані між собою знаю утворюють нерівність:

;

Розв’язком цих нерівностей називається значення , що задовольняє їх. Розв’язати нерівність – значить знайти множину всіх її розв’язків або встановити, що нерівність не має розв’язків.

Областю визначення (областю допустимих значень) нерівності називають множину всіх значень невідомого, на якій існують функції .При визначенні часто вводяться також додаткові умови, які пов’язані з характером нерівності. [2: 137]

Під множиною розв’язків системи нерівностей розуміють перетин множин розв’язків всіх нерівностей, що входять в цю систему.

Говорять, що нерівність еквівалентна системі нерівностей, якщо множина її розв’язків співпадає з множиною розв’язків цієї системи. [1: 136]

1.2 Теореми про рівносильність нерівностей

Дві нерівності з одною змінною називаються рівносильними, якщо їх розв’язки співпадають (в тому числі, якщо обидві нерівності не мають розвязків). Якщо кожен частковий розвязок нерівності являється в той же час частковим розвязком нерівності , отримані після перетворення нерівності , то нерівність називається наслідком нерівності . В наступних теоремах річ йде про перетвореннях, які ведуть до рівносильних нерівностей.[6:321]

Теорема 1. Якщо з однієї частини нерівності перенести до іншої доданок із протилежним знаком, то дістанемо нерівність, рівносильну початковій.

Теорема 2. Якщо до обох частин нерівності додати (або відняти) будь-яку функцію то дістанемо нерівність, рівносильну початковій за умовою, що області визначення отриманої і початкової нерівностей збігаються.

Теорема 3. Якщо обидві частини нерівності помножити (або поділити)на будь-яку функцію , яка зберігає сталий знак і відмінну від нуля, то при дістаємо нерівність, рівносильну початковій, а при рівносильною початковій буде нерівність протилежного змісту (передбачається, що області визначення отриманої і початкової нерівностей збігаються).

Таким чином, можемо записати:

, якщо ;

Зауваження. На практиці при застосуванні 2 і 3 теорем найчастіше замість функції береться її окремий випадок – відмінна від нуля константа. [2:143]

§ 2. Приклади розв’язування раціональних нерівностей вищих степенів різними методими

2.1 Розвязування раціональних нерівностей вищих степенів методом інтервалів

Будемо розглядати розв’язання раціональних нерівностей методом інтервалів. Існують різні схеми реалізації цього методу. Розглянемо одну з цих схем, допускаючи, що розв’язується нерівність . У випадку нерівності ця схема аналогічна.

1.Перенести всі члени нерівності вліво:

2.Ліву частину отриманої нерівності привести до спільного знаменника:

3.Багаточлени і розкласти на множники. Якщо при цьому з’являються однакові множники, то треба замінити їх відповідним степенем. Наприклад,

При скороченні треба мати на увазі, що:

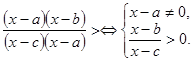
4. Виключити з розкладення нелінійні множники. Це виключення виконується таким чином.

Якщо в розкладенні є множник, , де , то його виключення залежить від знака старшого коефіцієнта і виконується за правилом:

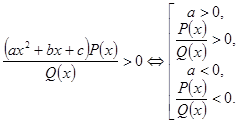
Якщо в розкладенні є множник , то його виключення здійснюється за правилами

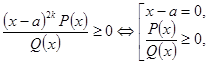
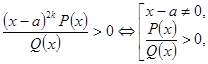
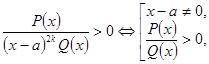
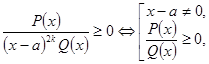
Нелінійний множник виключається за правилом:

5. На числовій осі відмітимо точки, в яких обертаються в нуль всі множники, що стоять в чисельнику і знаменнику лівої частини нерівності, отриманої в результаті виконання пунктів «1» - «4». При цьому, якщо нерівність нестрога, точки, які відповідають множникам чисельника будемо визначати зафарбованими кружками, а точки, що відповідають множникам знаменника світлими. Якщо нерівність строга, всі точки відмічаються світлими кружками.

6. Поставити знаки в кожному проміжку, на якій числова вісь розбивається відміченими точками.

Спочатку поставити знак у самому правому проміжку на числовій осі за правилом: знак «+» ставиться, якщо число множників виду парне, і знак «-», якщо це число непарне. Знаки в інших проміжках ставляться з урахуванням того, що вони чергуються в сусідніх проміжках.

7. Вибираються проміжки, в яких стоїть знак «+», якщо нерівність, отримана в пункті 4 має вигляд: , або «-», якщо ця нерівність має вигляд . Ці проміжки містять у собі крайні точки, відмічені на числовій осі зафарбованими кружками, і не містять точок, відмічених світлими кружками,. Об’єднання цих проміжків і є множиною розв’язків даної нерівності.[4:124]

Приклад 1. Розв’язати методом інтервалів нерівність

. (1)

Розв’язування:З нерівності знаходимо ОДЗ:

Далі замість нерівності (1) розв’язуємо рівняння

або звідки

Наносимо відповідні точки на числову вісь (див. рисунок).

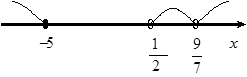
Розглядаємо кожний з утворених інтервалів окремо.

1. Підставляємо значення з інтервалу у нерівність (1). Дістаємо нерівність , яка не виконується. Тому нерівність (1) не виконується в усіх точках інтервалу .

2. Підставляючи в нерівність (1) значення з інтервалу , дістаємо правильну нерівність . Отже, нерівність (1) виконується на інтервалі .

3. Підставляючи в (3) значення з інтервалу дістаємо неправильну нерівність . Це означає, що нерівність (1) не виконується ні в одній точці інтервалу .

Остаточно маємо розв’язок нерівності (1)

Відповідь.[1:161]

Приклад 2. Розв’язати нерівність

Розв’язування: Для знаходження коренів рівняння необхідно розкласти його на множники. Отже

Отже числа,, є коренями даного рівняння. Наносимо ці числа на числову вісь і визначаємо знак лівої частини функції

на одному з інтервалів. Зокрема, взявши точку з інтервалу , дістаємо . Провівши «криву знаків», визначаємо знак в кожному з інтервалів.

+ +

1 2 3 x

Відповідь:

2.2 Розв’язування раціональних нерівностей вищих степенів узагальненним методом інтервалів

Нехай потрібно розв'язати нерівність

де цілі додатні числа;

— дійсні числа, серед яких немає рівних і такі, що . Нерівності подібного типу розв'язують із застосуванням узагальненого метода інтервалів. В основі цього метода лежить така властивість двочлена точка ділить числову вісь на дві частини, причому якщо (- парне), то вираз праворуч і ліворуч від точки зберігає додатний знак; якщо (- непарне число), то вираз праворуч від точки додатний, а ліворуч від точки від'ємний.

Для розв'язання нерівності

узагальненим методом інтервалів на числову вісь наносимо числа ; в проміжку праворуч від найбільшого з них ставимо знак «плюс», а потім, рухаючись справа наліво, при переході через чергове число змінюємо знак, якщо — непарне число, і зберігаємо знак, якщо. — парне число.

Зауваження 1. Якщо зустрічаються вирази , то праворуч від найбільшого з не обов'язково буде знак « + ». У цьому випадку найкраще визначити знак лівої частини нерівності в якомусь з інтервалів, а потім поставити знаки в кожному з інтервалів з урахуванням викладених вище міркувань.

Зауваження 2.Наведені вище міркування справедливі і для нерівностей виду

, , , де

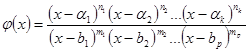Приклад 1. Розв’язати нерівність

Перепишемо нерівність у рівносильному вигляді

Числа , , , є коренями рівняння. Наносимо ці числа на числову вісь і визначаємо знак лівої частини функції

на одному з інтервалів. Зокрема, взявши точку з інтервалу , дістаємо . Проводимо через задані точки «криву знаків» з урахуванням того, що ліворуч і праворуч точки буде той самий знак «+», тому що у виразі показник степеня (число 4) є числом парним.

+ + +

-7 - 6 x

Відповідь:.

Приклад 2. Розв’язати нерівність

Числа ,, є коренями рівняння. Наносимо ці числа на числову вісь і визначаємо знак лівої частини функції на одному з інтервалів. Зокрема, взявши точку з інтервалу , дістаємо . Провівши «криву знаків» з урахуванням того, що ліворуч і праворуч точки і буде той самий знак «-», тому що у виразах і (х + 3)⁶ показник степеня (число 4 і 6 відповідно) є парні числа, визначаємо знак f(x) в кожному з інтервалів.

-3 1 5 x

Відповідь: .

Приклад 3. Розв’язати нерівність

Числа, , є коренями рівняння Наносимо дані точки на числову вісь. Оскільки дискримінант квадратного тричлена х² , то для всіх і, значить, парабола не перетинає вісь Ох. За допомогою «кривої знаків» дістаємо розв’язання.

+ +

-1 1 2 x

Відповідь: .

Приклад 4. Розв’язати нерівність

Числа , , є коренями рівняння Наносимо дані точки на числову вісь і визначаємо знак лівої частини функції на одному з інтервалів. Зокрема, взявши точку з інтервалу , дістаємо . Проводимо через задані точки «криву знаків» і дістаємо розв’язання.

+ +

-3 -1 0 x

Відповідь:..

Приклад 5. Розв’язати нерівність

Перепишемо нерівність

Числа, , є коренями рівняння Наносимо дані точки на числову вісь і визначаємо знак лівої частини функції

на одному з інтервалів. Зокрема, взявши точку з інтервалу , дістаємо . Проводимо через задані точки «криву знаків» і дістаємо розв’язання.

+ + +

- 6 x

Відповідь:.

2.3 Розв’язування дробово-раціональних нерівностей

Приклад 1. Розв’язати нерівність

Розв’язання: розкладемо чисельник і знаменник дробу, що стоїть в лівій частині нерівності, на множники:

Отриманий дріб містить два нелінійні множники: і . Перший з них додатний і його можна опустити, другий множник виключимо у відповідності з пунктом 4:

Далі, на числовій осі відмітимо точки , та інтервали, що утворюються при цьому, знаками:

+ +

-2 2 x

Виберемо інтервал відмічений знаком «-» (так як ), і нанесемо на числову вісь точку . Ця точка попадає у вибраний інтервал. «Виколюючи» точку , отримуємо інтервали і , об’єднання яких утворює множину розв’язків даної нерівності:

Відповідь: .

Приклад 2 . Розв’язати нерівність

Розв’язання: розкладемо багаточлен, що стоїть в чисельнику лівої частини нерівності, на множники. Розглянемо рівняння . Серед дільників 8 підберемо корінь рівняння . Розділимо ліву частину рівняння на двочлен :

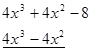
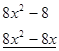
Тепер розглянемо рівняння . Серед дільників 8 підберемо рівняння і розділимо ліву частину на двочлен :

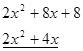
Так як квадратний тричлен не має дійсних коренів, отримаємо розкладення

Таким чином, дана нерівність перетворюється до вигляду:

Дріб в лівій частині цієї нерівності містить два нелінійних множники: квадратний тричлен , що більший нуля, і . Виключимо ці множники:

На числовій осі відмітимо точки , і інтервали, що утворюються знаками:

Виберемо інтервал зі знаком «-» і потім відмітимо на осі точку . Ця точка належить вибраному інтервалу, і тому, виключаючи цю точку, отримуємо, що - множина розв’язків даної нерівності.

Відповідь: .

Приклад 3. Розв’язати нерівність

Розв’язання: у відповідності з описаною схемою методу інтервалів

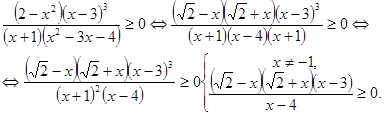
Будемо відмічати на числовій осі точки , , зафарбованими кружками (нерівність нестрога!), а точку - світлим кружком:

Розв’язок даної даної нерівності складаються з об’єднанням проміжків .

Відповідь: .

Приклад 4. Розв’язати нерівність

Розв’язування: Нанасимо на числову пряму точки , , , , . Точки , , відзначаємо темними кружками, а точки , світлими.

Провівши «кривину знаків» з урахуванням того, що в околі точок і ліва частина нерівності зберігає знак (тому що у виразах ), показники степенів є парними числами), дістанемо розв’язання Ця множина на рисунку заштрихована.

Відповідь:

Приклад 5. Розв’язати нерівність

Наносимо точки числову вісь. За допомогою «кривої знаків» дістанемо розв’язки, заштриховані на рисунку.

Зазначимо, що точка входить у множину розв’язків, тому що при дістанемо .

Відповідь: .

2.4 Розв’язування раціональних нерівностей методом заміни змінної

Приклад 1. Розв’язати нерівність

Зробивши заміну змінної , дістаємо

Коренями рівняння

є , .

Звідси

Оскільки , то дістаємо

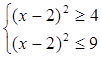
Розв’яжемо нерівність

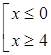
0 4 x

Розв’яжемо нерівність

-1 5 x

З малюнків бачимо, що розв’язком початкової нерівності є об’єднання множин і .

Відповідь: і

Приклад 2. Розв’язати нерівність

Зробивши заміну змінної , дістаємо

Коренями рівняння є , .

Звідси.

Оскільки , то дістаємо

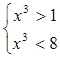
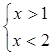
Зобразимо отриману множину за допомогою координатної прямої.

1 2 x

Відповідь: .

Висновки

Сучасна педагогічна наука стверджує, що для продуктивного засвоєння учнями знань і для їхнього інтелектуального розвитку важливо встановлювати зв’язки, як між різними розділами курсу, так і між різними дисциплінами в цілому. Для чого потрібно вміти розв’язувати раціональні нерівності? Так, щоб за їх допомогою розв’язувати задачі. Уміння розв’язувати раціональні нерівності вищих степенів дозволить учням розв’язувати, здавалося б, складні нерівності просто, також учні зможуть використовувати уміння та навички при розв’язуванні ірраціональних, логарифмічних, показникових та тригонометричних нерівності.

Тому доцільно розглянути та ознайомитись з різноманітними методами та прийоми розв’язування раціональних нерівності вищих степенів. Для досягнення мети було поставлено наступні завдання:

-проаналізувати методичну літературу з означеної теми;

-розглянути різноманітні методи розв’язування раціональних нерівностей вищих степенів;

-навести низку прикладів розв’язування раціональних нерівностей вищих степенів різними методами.

Список використаних джерел

1. Литвиненко В.Н., Мордкович А.Г.: Практикум по элементарной математике: Алгебра. Тригонометрия: Учеб. пособие для студентов физ.-мат. спец. пед. ин-тов.- 2-е изд., перераб. и доп. / В.Н.Литвиненко, А.Г. Мордкович, - М.: Просвещение, 1991.- 352 с.

2. Титаренко О.М.: Форсований курс шкільної математики: Навчальний посібник./ О.М. Титаренко – Харків: ТОРСІНГ ПЛЮС, 2005.-368 с.

3. Шарыгин И.Ф., Голубев В.И. Факультативный курс по математике: Решение задач: Учеб. пособие для 11 кл. сред. шк./ И.Ф. Шарыгин, В.И. Голубев - М.: Просвещение, 1991.-384 с.

4. Цыпкин А.Г., Пинский А.И. Справочник по методам решения задач по математике для средней школы.-2-е изд., перераб. и доп./ А.Г. Цыпкин, А.И. Пинский - М.: Наука Гл. ред. физ.-мат.лит., 1989. – 576 с.

5. Шахмейстер А.Х.: Уравнения.- 3-е издание, исправленное и дополненное / А.Х. Шахмейстер – М.: Издательство МЦНМО: СПб.: «Петроглиф»: «Виктория плюс», 2008.-264 с.

6. Ципкін О.Г.:Довідник з математики для середніх навчальних закладів / А.Г.Ципкін.- К.: Вища шк. Головне вид-во, 1988.-416 с.

7. Маслова Т.Н., Суходений А.М. Ваш домашний репетитор. — М.: ООО Изд. дом “ОНИКС 21 век”, 2003. - 672 с.

8. Математика для поступающих в экономические вузы: Уч. пос. для вузов / Под ред. проф. Н.М. Кремера. — 2-ге изд., перероб. и доп. - М.: ЮНИТИ, 1998. - 430 с.

9. Алгебра и начала аналіза: Учебн. для 10-11 кл. общ. учредж. / Под ред. А.Н. Колмогорова. - 12-е изд. - М.: Просвещение, 2002. - 384 с.

Курсовая работа: Методи розв’язування раціональних нерівностей вищих степенів

Похожие рефераты: