Реферат: Решение игры в смешанных стратегиях 2

Возникновение математических методов относят к годам Второй Мировой Войны. При генеральных штабах существовали группы математиков, военных специалистов, которые занимались планированием военных действий. Каждое действие называется операцией поэтому «математические методы» можно назвать «исследование операции». Построение модели каждой такой операции выполнялось совместным участием специалистов различного профиля.

Математические методы как наука возникла из необходимости систематизировать решения и обосновывать его, которое необходимо принимать в различных сферах (в научных и практических) деятельности человека.

Математические методы базируются на теоретических занятиях по математике, системном анализе и программировании.

Системный анализ создает методологию подхода к исследованию объектов любой природы.

Математика – это аналитический инструмент решения различных задач.

Программирование – это технический инструмент при решении задач.

Модель – это материально и мысленно представляемый объект, который в процессе познания замещает объект.

Цель курсового проекта это решить поставленную задачу.

Задачи курсового проектирования заключаются в нахождении оптимальности стратегии игры двух игроков, проверки решения расчетов на бумаге с расчетами на компьютере, поиск литературы для своей темы. Задача носит прикладной характер так как может применятся в военном деле, в спортивных мероприятиях.

ОБЩАЯ ЧАСТЬ

1.1 Математическое моделирование

ЭВМ прочно вошла в нашу жизнь, и практически нет такой области человеческой деятельности, где не применялась бы ЭВМ. ЭВМ сейчас широко используется в процессе создания и исследования новых машин, новых технологических процессов и поиске их оптимальных вариантов; при решении экономических задач, при решении задач планирования и управления производством на различных уровнях. Создание же крупных объектов в ракетотехнике, авиастроении, судостроении, а также проектирование плотин, мостов, и др. вообще невозможно без применения ЭВМ.

Для использования ЭВМ при решении прикладных задач, прежде всего прикладная задача должна быть "переведена" на формальный математический язык, т.е. для реального объекта, процесса или системы должна быть построена его математическая модель.

Слово "Модель" происходит от латинского modus (копия, образ, очертание). Моделирование - это замещение некоторого объекта А другим объектом Б. Замещаемый объект А называется оригиналом или объектом моделирования, а замещающий Б - моделью. Другими словами, модель - это объект-заменитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала.

Целью моделирования являются получение, обработка, представление и использование информации об объектах, которые взаимодействуют между собой и внешней средой; а модель здесь выступает как средство познания свойств и закономерности поведения объекта.

Математическое моделирование - это средство изучения реального объекта, процесса или системы путем их замены математической моделью, более удобной для экспериментального исследования с помощью ЭВМ.

Математическое моделирование — процесс построения и изучения математических моделей реальных процессов и явлений. Все естественные и общественные науки, использующие математический аппарат, по сути занимаются математическим моделированием: заменяют реальный объект его моделью и затем изучают последнюю. Как и в случае любого моделирования, математическая модель не описывает полностью изучаемое явление, и вопросы о применимости полученных таким образом результатов являются весьма содержательными. Математическая модель — это упрощенное описание реальности с помощью математических понятий.

Математическая модель выражает существенные черты объекта или процесса языком уравнений и других математических средств. Собственно говоря, сама математика обязана своим существованием тому, что она пытается отразить, т.е. промоделировать, на своем специфическом языке закономерности окружающего мира.

При математическом моделировании исследование объекта осуществляется посредством модели, сформулированной на языке математики с использованием тех или иных математических методов.

Путь математического моделирования в наше время гораздо более всеобъемлющ, нежели моделирования натурного. Огромный толчок развитию математического моделирования дало появление ЭВМ, хотя сам метод зародился одновременно с математикой тысячи лет назад.

Математическое моделирование как таковое отнюдь не всегда требует компьютерной поддержки. Каждый специалист, профессионально занимающийся математическим моделированием, делает все возможное для аналитического исследования модели. Аналитические решения (т.е. представленные формулами, выражающими результаты исследования через исходные данные) обычно удобнее и информативнее численных. Возможности аналитических методов решения сложных математических задач, однако, очень ограниченны и, как правило, эти методы гораздо сложнее численных.

Математическая модель является приближенным представлением реальных объектов, процессов или систем, выраженным в математических терминах и сохраняющим существенные черты оригинала. Математические модели в количественной форме, с помощью логико-математических конструкций, описывают основные свойства объекта, процесса или системы, его параметры, внутренние и внешние связи

Все модели можно разделить на два класса:

1. вещественные,

2. идеальные.

В свою очередь вещественные модели можно разделить на:

1. натурные,

2. физические,

3. математические.

Идеальные модели можно разделить на:

1. наглядные,

2. знаковые,

3. математические.

Вещественные натурные модели - это реальные объекты, процессы и системы, над которыми выполняются эксперименты научные, технические и производственные.

Вещественные физические модели - это макеты, муляжи, воспроизводящие физические свойства оригиналов (кинематические, динамические, гидравлические, тепловые, электрические, световые модели).

Вещественные математические - это аналоговые, структурные, геометрические, графические, цифровые и кибернетические модели.

Идеальные наглядные модели - это схемы, карты, чертежи, графики, графы, аналоги, структурные и геометрические модели.

Идеальные знаковые модели - это символы, алфавит, языки программирования, упорядоченная запись, топологическая запись, сетевое представление.

Идеальные математические модели - это аналитические, функциональные, имитационные, комбинированные модели.

В приведенной классификации некоторые модели имеют двойное толкование (например - аналоговые). Все модели, кроме натурных, можно объединить в один класс мысленных моделей, т.к. они являются продуктом абстрактного мышления человека.

1.2 Элементы теории игры

В общем случае решение игры представляет довольно трудную задачу, причем сложность задачи и объем необходимых для решения вычислений резко возрастает с увеличением . Однако это трудности не носят принципиального характера и связаны только сочень большим объемом расчетов, который в ряде случаев может оказаться практически невыполнимым. Принципиальная сторона метода отыскания решения остается при любом одной и той же.

Проиллюстрируем это на примере игры . Дадим ей геометрическую интерпретацию — уже пространственную. Три наши стратегии , изобразим тремя точками на плоскости ; первая лежит в начале координат (рис.1). вторая и третья — на осях Ох и Оу на расстояниях 1 от начала.

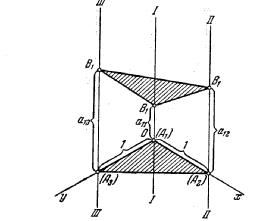
рис 1.

Через точки проводятся оси I-I, II-II и III-III, перпендикулярные к плоскости . На оси I-I откладываются выигрыши при стратегии на осях II-II и III-III — выигрыши при стратегиях . Каждая стратегия противника изобразится плоскостью, отсекающей на осях I-I, II-II и III-III, отрезки, равные выигрышам

при соответствующих стратегия и стратегия . Построив, таким образом, все стратегии противника, мы получим семейство плоскостей над треугольником (рис2) .

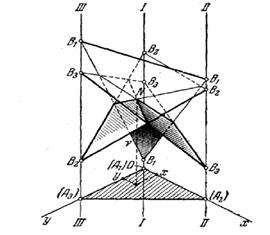
рис 2

Для этого семейства также можно построить нижнюю границу выигрыша, как мы это делали в случае, и найти на этой границе точку N с максимальной высотой нал плоскостью. Эта высота и будет ценой игры .

Частоты стратегий в оптимальной стратегии будут определяться координатами ( x , у) точки N, а именно:

Однако такое геометрическое построение даже для случая нелегко осуществимо и требует большой затраты времени и усилий воображения. В общем же случае игры оно переносится в - мерное пространство и теряет всякую наглядность, хотя употребление геометрической терминологии в ряде случаев может оказаться полезным. При решении игрна практике удобнее пользоваться не геометрическими аналогиями, а расчетными аналитическими методами, тем более, что для решения задачи на вычислительных машинах эти методы единственно пригодны.

Все эти методы по существу сводятся к решению задачи путем последовательных проб, но упорядочение последовательности проб позволяет построить алгоритм, приводящий к решению наиболее экономичным способом.

Здесь мы вкратце остановимся на одном расчетном методе решения игр — на так называемом методе «линейного программирования».

Для этого дадим сначала общую постановку задачи о нахождении решения игры . Пусть дана игра с т стратегиями игрока А иn стратегиями игрока В и задана платежная матрица

Требуется найти решение игры, т. е. две оптимальные смешанные стратегии игроков А и В

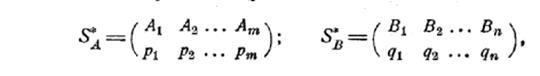
где (некоторые из чисел и могут быть равными нулю).

Наша оптимальная стратегия S * _A должна обеспечивать нам выигрыш, не меньший , при любом поведении противника, и выигрыш, равный , при его оптимальном поведении (стратегия S * _B ).Аналогично стратегия S * _B должна обеспечивать противнику проигрыш, не больший , при любом нашем поведении и равный при нашем оптимальном поведении (стратегия S * _A ).

Величина цены игры в данном случае нам неизвестна; будем считать, что она равна некоторому положительному числу. Полагая так, мы не нарушаем общности рассуждений; для того чтобы было > 0, очевидно, достаточно, чтобы все элементы матрицы были неотрицательными. Этого всегда можно добиться, прибавляя к элементам достаточно большую положительную величину L;при этом цена игры увеличится на L, а решение не изменится.

Пусть мы выбрали свою оптимальную стратегию S * _A . Тогда наш средний выигрыш при стратегии противника будет равен:

Наша оптимальная стратегия S * _A обладает тем свойством, что при любом поведении противника обеспечивает выигрыш не меньший, чем ; следовательно, любое из чисел не может быть меньше . Получаем ряд условий:

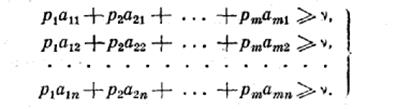(1)

Разделим неравенства (1) на положительную величину и обозначим :

Тогда условие (1) запишется виде

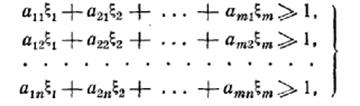(2)

где — неотрицательные числа. Так как величины удовлетворяют условию

(3)

Мы хотим сделать свой гарантированный выигрыш максимально возможным; очевидно, при этом правая часть равенства (3) принимает минимальное значение.

Таким образом, задача нахождения решения игры сводится к следующей математической задаче: определить неотрицательные величины , удовлетворяющие условиям (2), так, чтобы их сумма

была минимальной.

Обычно при решении задач, связанных с нахождением экстремальных значений (максимумов и минимумов), функцию дифференцируют и приравнивают производные нулю. Но такой прием в данном случае бесполезен, так как функция Ф, которую нужно обратить в минимум, линейна, и ее производные по всем аргументам равны единице, т. е. нигде не обращаются в нуль. Следовательно, максимум функции достигается где-то на границе области изменения аргументов, которая определяется требованием неотрицательности аргументов и условиями (2). Прием нахождения экстремальных значений при помощи дифференцирования непригоден и в тех случаях, когда для решения игры определяется максимум нижней (или минимум верхней) границы выигрыша, как мы. например, делали при решении игр .Действительно, нижняя граница составлена из участков прямых линий, и максимум достигается не в точке, где производная равна нулю (такой точки вообще нет), а на границе интервала или в точке пересечения прямолинейных участков.

Для решения подобных задач, довольно часто встречающихся на практике, в математике разработан специальный аппарат линейного программирования.

Задача линейного программирования ставится следующим образом.

Дана система линейных уравнений:

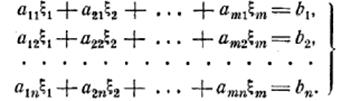(4)

Требуется найти неотрицательные значения величин удовлетворяющие условиям (4) и вместе с тем обращающие в минимум заданную однородную линейную функцию величин (линейную форму):

Легко убедиться, что поставленная выше задача теории игр является частным случаем задачи линейного программирование при

С первого взгляда может показаться, что условия (2) не эквивалентны условиям (4), так как вместо знаков равенства они содержат знаки неравенства. Однако от знаков неравенства легко избавиться, вводя новые фиктивные неотрицательные переменные и записывая условия (2) в виде:

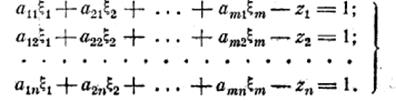(5)

Форма Ф , которую нужно обратить в минимум, равна

Аппарат линейного программирования позволяет путем сравнительно небольшого числа последовательных проб подобрать величины , удовлетворяющие поставленным требованиям. Для большей ясности мы здесь продемонстрируем применение этого аппарата прямо на материале решения конкретных игр.

1.3 Симплекс метод (минимум)

Симплекс метод - универсальный метод для решения линейной системы уравнений или неравенств и линейного функционала.

Общая идея симплексного метода (метода последовательного улучшения плана) для решения ЗЛП (задачи линейного программирования) состоит

-умение находить начальный опорный план;

-наличие признака оптимальности опорного плана;

-умение переходить к нехудшему опорному плану.

Пусть ЗЛП представлена системой ограничений в каноническом виде:

Говорят, что ограничение ЗЛП имеет предпочтительный вид, если при неотрицательной правой части левая часть ограничений содержит переменную, входящую с коэффициентом, равным единице, а в остальные ограничения равенства - с коэффициентом, равным нулю.

Пусть система ограничений имеет вид

Сведем задачу к каноническому виду. Для этого прибавим к левым частям неравенств дополнительные переменные . Получим систему, эквивалентную исходной:

которая имеет предпочтительный вид

В целевую функцию дополнительные переменные вводятся с коэффициентами, равными нулю .

Пусть далее система ограничений имеет вид

Сведём её к эквивалентной вычитанием дополнительных переменных из левых частей неравенств системы. Получим систему

Однако теперь система ограничений не имеет предпочтительного вида, так как дополнительные переменные входят в левую часть (при ) с коэффициентами, равными –1. Поэтому, вообще говоря, базисный план не является допустимым. В этом случае вводится так называемый искусственный базис. К левым частям ограничений-равенств, не имеющих предпочтительного вида, добавляют искусственные переменные . В целевую функцию переменные , вводят с коэффициентом М в случае решения задачи на минимум и с коэффициентом -М для задачи на максимум, где М - большое положительное число. Полученная задача называется М-задачей, соответствующей исходной. Она всегда имеет предпочтительный вид.

Пусть исходная ЗЛП имеет вид

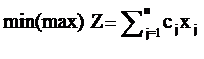(1)

(2)

(3)

причём ни одно из ограничений не имеет предпочтительной переменной. М-задача запишется так:

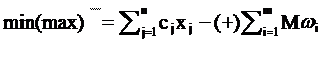(4)

(5)

, , (6)

Задача (4)-(6) имеет предпочтительный план. Её начальный опорный план имеет вид

Если некоторые из уравнений (2) имеют предпочтительный вид, то в них не следует вводить искусственные переменные.

Теорема. Если в оптимальном плане

(7)

М-задачи (4)-(6) все искусственные переменные , то план является оптимальным планом исходной задачи (1)-(3).

Для того чтобы решить задачу с ограничениями, не имеющими предпочтительного вида, вводят искусственный базис и решают расширенную М-задачу, которая имеет начальный опорный план

Решение исходной задачи симплексным методом путем введения искусственных переменных называется симплексным методом с искусственным базисом.

Если в результате применения симплексного метода к расширенной задаче получен оптимальный план, в котором все искусственные переменные , то его первые n компоненты дают оптимальный план исходной задачи.

Теорема. Если в оптимальном плане М-задачи хотя бы одна из искусственных переменных отлична от нуля, то исходная задача не имеет допустимых планов, т. е. ее условия несовместны.

Признаки оптимальности.

Теорема. Пусть исходная задача решается на максимум. Если для некоторого опорного плана все оценки неотрицательны, то такой план оптимален.

Теорема. Если исходная задача решается на минимум и для некоторого опорного плана все оценки неположительны, то такой план оптимален.

Для привидения системы ограничений неравенств к каноническому виду, необходимо в системе ограничений выделить единичный базис.

I. Ограничения вида «0»- ресурсные ограничения. Справа находится то что мы используем на производстве, слева - то что получаем. При таких ограничения вводят дополнительные переменные с коэффициентом «+1», образующие единичный базис. В целевую функцию эти переменные войдут с коэффициентом «0».

II. Ограничения вида «= ». Часто бывает, что несмотря на то что ограничения имеют вид равенства, единичный базис не выделяется или трудно выделяется. В этом случае вводятся искусственные переменные для создания единичного базиса - Yi. В систему ограничений они входят с коэффициентом «1». а в целевую функцию с коэффициентом «M», стремящимся к бесконечности (при Fmin - «+M», при Fmax - «-M»).

III. Ограничения вида «0» - Плановые ограничения. Дополнительные переменные (X), несущие определенный экономический смысл - перерасход ресурсов или перевыполнение плана, перепроизводство, добавляются с коэффициентом «-1», в целевую функцию - с коэффициентом «0». А искусственные переменные (Y) как в предыдущем случае.

1.4 Алгоритм решения задач теории игр

Обозначим некоторые определения.

Седловой точкой называется А_ij , которая является наименьшим элементом в своей строке и наибольшим элементом в столбце.

Доминирующая строка – все элементы этой строки не превосходят соответствующих элементов другой строки.

Доминирующий столбец – все элементы не меньше соответствующих элементов какого-либо другого столбца.

Доминирующие столбцы и строки можно удалить из матрицы.

Алгоритм решения

1. Проверить наличие седловой точки. Если есть седловая точка, то пишем ответ, если нет - продолжаем решение дальше

2. Удаляем доминирующие строки доминирующие столбцы. Их може6т быть несколько. На их место в оптимальной стратегии соответствующие компоненты будут равны 0

3. Решаем матричную игру (линейное программирование, графическое решение, приближенное решение)

В своей задаче я решаю матричную игру линейным программированием. (Симплекс метод)

Алгоритм решения симплекс методом (на максимум):

1. Привести задачу линейного программирования к каноническому виду.

2. Найти начальное опорное решение с базисом из единичных векторов и коэффициенты разложений векторов условий по базису опорного решения. Если опорное решение отсутствует, задача не имеет решения ввиду несовместности системы ограничений.

3. Вычислить оценки разложений векторов условий по базису опорного решения и заполнить симплексную таблицу.

4. Если выполняется признак единственности оптимального решения, то решение задачи заканчивается.

5. Если выполняется условие существования множества оптимальных решений, то путем простого перебора найти все оптимальные решения.

6. Если имеют место условия неограниченности целевой функции, то задача не имеет решения.

7. Если пункты 4—6 алгоритма не выполняются, найти новое опорное решение и перейти к пункту 3.

2 СПЕЦИАЛЬНАЯ ЧАСТЬ (РАСЧЕТНАЯ)

2.1 Исходные данные

Тема: Решение игры в смешанных стратегиях

2 -1 2 1

А = 1 3 -1 0

4 -2 2 -1

Найти оптимальную стратегию и цену игры, заданной платежной матрицей А.

2.2 Постановка задачи. Математическая модель

Математическая модель — это упрощенное описание реальности с помощью математических понятий. Математическая модель выражает существенные черты объекта или процесса языком уравнений и других математических средств.

Доминирующая строка – все элементы этой строки не превосходят соответствующих элементов другой строки.

Доминирующий столбец – все элементы не меньше соответствующих элементов какого-либо другого столбца.

Доминирующие столбцы и строки можно удалить из матрицы.

Любой задаче линейного программирования называемой исходнойили прямой,можно поставить в соответствие другую задачу,которая называется двойственной или сопряженной. Обе эти задачи образуют пару двойственных (или сопряженных) задач. Каждая из задач является двойственной к другой задаче рассматриваемой пары.

Моя задача представляет собой матрицу. Что бы ее решить сначала построим математическую модель и решим симплексным методом.

В моей матрице есть доминирующий столбец. Это последний столбец матрицы так как сказано из определения все элементы не меньше соответствующих элементов какого-либо другого столбца. Это столбец доминирует над последним столбцом.

2 -1 2 1

А = 1 3 -1 0

4 -2 2 -1

Поэтому мы его вычеркиваем и составляем симметричные задачи по новой получившейся матрице А

-1 2 0

А^* = 3 -1 0

-2 2 -1

Использовать метод линейного программирования следует тогда, когда все элементы, хотя бы одной строки матрицы строго положительны. В этом случае задача будет иметь оптимальный план из которых можно получить оптимальные стратегии, иначе в исходной задаче целевая функция может быть неограниченна, что противоречит теории Джона фон Неймана.

С = 2

Прибавляем это число к элементам матрицы А^* и получаем матрицу А^**

1 4 3

А^** = 5 1 2

0 4 1

Коэффициенты при неизвестных в целевой функции и свободные члены неравенств должны быть равны 1

Составляем систему уравнений по данной матрице и целевую функцию (математическая модель).

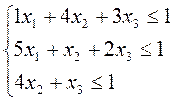
F(x) = x₁ + x₂ + x₃ → max

2.3 Анализ модели. Составление пары симметричных двойственных задач

В теории двойственности используются четыре пары двойственных задач (приведем их в матричной форме записи)

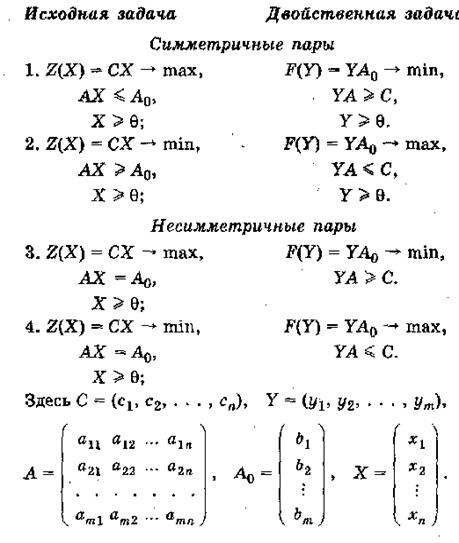
Правила составления двойственных задач:

1.Во всех ограничениях исходной задачи свободные члены должны находиться в правой части, а члены с неизвестными — в левой.

2. Ограничения-неравенства исходной задачи должны быть записаны так, чтобы знаки неравенств у них были направлены в одну сторону.

3. Если знаки неравенств в ограничениях исходной задачи «≤», то целевая функция Z(X) = с₀ + с₁ · x₁ + с₂ · x₂ + … + с_n · x_n должна максимизироваться, а если «≥», то минимизироваться.

4. Каждому ограничению исходной задачи соответствует неизвестное в двойственной задаче; при этом неизвестное, отвечающее ограничению-неравенству, должно удовлетворять условию неотрицательности, а неизвестное, отвечающее ограничению-равенству, может быть любого знака.

5. Целевая функция двойственной задачи имеет вид

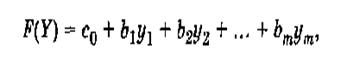
где с₀ — свободный член целевой функции Z ( X ) исходной задачи, b₁ , b₂ , …, b_m ,— свободные члены в ограничениях исходной задачи, при этом b_i — свободный член именно того ограничения исходной задачи, которому соответствует неизвестная y_i , ay₁ , y₂ , …, y_m — неизвестные в двойственной задаче.

6. Целевая функция F ( Y ) двойственной задачи должна оптимизироваться противоположным по сравнению с Z ( X ) образом, т.е. если Z ( X ) → max, то
F ( Y ) → min, и если Z ( X ) → min, то F ( Y ) → max.

7. Каждому неизвестному х _j , j = 1, 2, ..., п исходной задачи соответствует ограничение в двойственной задаче. Совокупность этих п ограничений (вместе с условиями неотрицательности неизвестных y_i , соответствующих ограничениям-неравенствам исходной задачи) образует систему ограничений двойственной задачи. Все ограничения двойственной задачи имеют вид неравенств, свободные члены которых находятся в правых частях, а члены с неизвестными y_i у₂ , ..., у_т — в левых. Все знаки неравенств имеют вид «≥», если F ( Y ) → min, и «≤», если
F ( Y ) → max.

Коэффициенты, с которыми неизвестные y_l у₂ , …, у_т входят в ограничение, соответствующее неизвестному x_j , совпадают с коэффициентами при этом неизвестном х. в ограничениях исходной задачи, а именно: коэффициент при y_i совпадает с тем коэффициентом при х _j с которым х _j входит в ограничение исходной задачи, соответствующее неизвестному y_i .

Двойственность

1) Составляем матрицу из полученной математической модели

7 6 2 1

А = 1 3 6 1

0 2 5 1

1 1 1 F

2) Транспонируем матрицу A

7 1 0 1

А^-1 = 6 3 2 1

2 6 5 1

1 1 1 Z

3) Составляем двойственную задачу

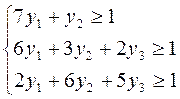
Z = y₁ + y₂ +y₃ → Min

Вот и получили пару симметричных двойственных задач. Задача на максимум и на минимум

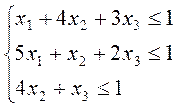
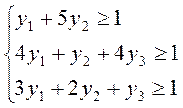
F(x) = x₁ + x₂ + x₃ → max Z(x) = y₁ + y₂ +y₃ → min

2.4 Решение симплекс методом

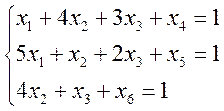
x₁ ≥ 0, x₂ ≥ 0, x₃ ≥ 0

x0	x1	x2	x3	x4	x5	x6
x4	1	1	4	3	1	0	0	1/4
x5	1	5	1	2	0	1	0	1/5
x6	1	0	4	1	0	0	1
f	0	-1	-1	-1	0	0	0

X 2

X 3

X 4

X 5

X 6

x0	x1	x2	x3	x4	x5	x6
X4	4/5	0	19/5	13/5	1	-1/5	0	4/19
X1	1/5	1	1/5	2/5	0	1/5	0
x6	1	0	4	1	0	0	1	1/4
f	1/5	0	-4/5	-3/5	0	1/5	0

Вторую таблицы рассчитаем аналогичным способом.

x0	x1	x2	x3	x4	x5	x6
x2	4/19	0	1	13/19	5/19	-1/19	0
X1	3/19	1	0	5/19	-1/19	4/19	0
x6	3/19	0	0	-23/19	-20/19	4/19	1
f	7/19	0	0	-1/19	4/19	3/19	0

Решив симплекс методом матрицу мы получим

X^* = (3/19; 4/19; 0)

Y^* = (4/19; 3/19; 0)

F(X^* ) = G(Y^* ) = 7/19

Из решения двойственных задач получим цену игры и оптимальные стратегии игроков для матрицы А^**

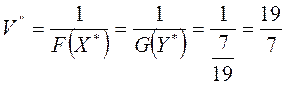
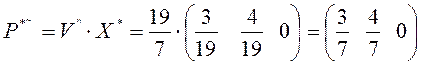
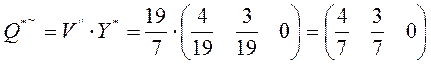
Для матрицы А^* оптимальный план остается такой же

V = V^” – С = 19/7 – 2 = 5/7

Оптимальная стратегия P^* и Q^* получаются из оптимальных стратегий P^*~ и Q^*~ приписав нули на место удаленных строк и столбцов.

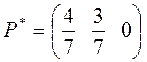
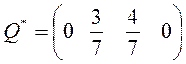
V = 5/7

Целевая функция равна 7/19

2.5 Проверка пункта 5.4 с помощью надстройки Поиск решения средствами MSExcel. Сформировать и проанализировать результаты решения.

Мною была решена задачи на тему: «Решение игры в смешанных стратегиях», в которой нужно было найти оптимальную стратегию и цену игры, заданной платежной матрицей А с помощью расчетных данных на бумаге и были произведены расчеты в компьютере с помощью надстройки Поиск решения средствами MSExcel. Ответы полученные на бумаге и в компьютере идентифицируемы (равны) друг другу. Следовательно меньше времени уходит на решение если решать на компьютере, чем на бумаге.

Сначала мы вводим данные листе Excel,а потом рассчитываем с помощью надстройки Excel. Эти данные показаны ниже.

Вводимые данные и расчет

a	b	c
1	4	3	1	1
5	1	2	1	1
0	4	1	1	16/19
1	1	1	Целевая функция
x1	x2	x3	7/19
3/19	4/19	0

Результат проверки:

Microsoft Excel 11.0 Отчет по результатам
Рабочий лист: [Дроздов.xls]Лист1
Отчет создан: 13/5/2008
Целевая ячейка (Максимум)
Ячейка	Имя	Исходное значение	Результат
$F$7	x3 Целевая функция	0	7/19
Изменяемые ячейки
Ячейка	Имя	Исходное значение	Результат
$B$8	x1	0	3/19
$C$8	x2	0	4/19
$D$8	x3	0	0
Ограничения
Ячейка	Имя	Значение	Формула
$F$4	1	$F$4<=$E$4
$F$3	1	$F$3<=$E$3
$F$5	16/19	$F$5<=$E$5
$B$8	x1	3/19	$B$8>=0
$C$8	x2	4/19	$C$8>=0
$D$8	x3	0	$D$8>=0

2.6 Проверка оптимальности найденного решения критерием оптимальности стратегии

Стратегия P^* и Q^* называется оптимальной, а число V – цена игры если справедливо неравенство M (P,Q^* ) ≤ V≤ M (P^* ,Q), где P и Q – произвольные стратегии.

Критерий оптимальности стратегий.

Для того что бы P^* и Q^* были оптимальными стратегиями соответствующих игроков, а число V было ценой игры необходимо и достаточно что б выполнялось неравенство M (P_i ,Q^* ) ≤ V≤ M (P^* ,Q_i ).

Теорема Джона фон Неймана (основная).

Любая матричная игра имеет решение т.е. существуют оптимальные стратегии и цена игры.

Если матрица имеет седловую точку, то игра имеет решение в чистых стратегиях. Если Седловых точек нет, то одна из оптимальных стратегий будет смешана.

Если одна из компонент стратегий равна 1, то остальные нулю, то стратегия называется чистой в противном смешанной.

Доминирующая строка – все элементы этой строки не превосходят соответствующих элементов другой строки.

Доминирующий столбец – все элементы не меньше соответствующих элементов какого-либо другого столбца.

Делаем проверку

P₁ = (1, 0, 0)

P₂ = (0, 1, 0)

P₃ = (0, 0, 1)

Q₁ = (1, 0, 0, 0)

Q₂ = (0, 1, 0, 0)

Q₃ = (0, 0, 1, 0)

Q₄ = (0, 0, 0, 1)

M (P^* ,Q₁ ) =

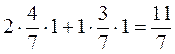
M (P₁ ,Q^* ) =

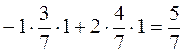
M (P1,Q^* ) ≤ V ≤ M (P^* ,Q1)

5/7 ≤ 5/7 ≤ 11/7

M (P^* ,Q₂ ) =

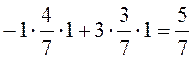
M (P₂ ,Q^* ) =

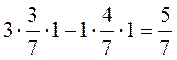
M (P2,Q^* ) ≤ V ≤ M (P^* ,Q2)

5/7 ≤ 5/7 ≤ 5/7

M (P^* ,Q₃ ) =

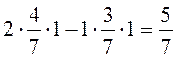
M (P₃ ,Q^* ) =

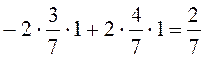
M (P3,Q^* ) ≤ V ≤ M (P^* ,Q3)

2/7 ≤ 5/7 ≤ 5/7

ЗАКЛЮЧЕНИЕ

В результате проведенной работы проанализирована литература по данной теме и решение задачи. В моем курсовом проекте нужно решить игру в смешанных стратегиях и сделать проверку. Исходные данные: платежная матрица, найти оптимальную стратегию и цену игры. Данную задачу можно решить при помощи математических методов. Что бы решить ее нужно построить математическую модель и решить эту модель симплексы методом (максимум). Я построил математическую модель. Так же решал симплекс метод при помощи компьютера (MSExcelПоиск решения) и на бумаге. Сделав анализ, что меньше времени уходит на решение, если решать на компьютере, чем на бумаге Все данные сошлись, а так же сошлась и проверка при помощи Поиск решения..

Цена игры равна 1, а оптимальный план равен P^* и Q^*

Поставленная задача была мною решена.

Библиографический список

1. А.В. Могилев, Н.И. Пак, Е.К. Хеннер, «Информатика»: Учеб. пособие для студ. пед. вузов,Под ред. Е.К. Хеннер –М.: изд. Центр «Академии »,2000

2. Н.Ш. Кример, Б.А. Путков , М.Н. Фридман, «Исследовательские операции в экономики»: Учеб. пособие для вузов, Под ред проф. Н.Ш. Кример-М.: Юнити, 2006

3. И.К Волков, Е.А Загоруйко, «Исследовательские операции»: Учеб. для вызов 2-е издание, Под ред В.С. Зарубина , А.П. Кришенко –М.: Из-во МГТУ ими Н.Э.Баумана 2002

4. Элементы теории игр. Учеб. пособие для студ. -1 изд., стер-М.: Высш. шк., 1999

5. Под ред. В.И. Ермакова, «Сборник задач по высшей математике для экономистов»: Учеб. пособие, Москва: ИНФА-М, 2002

6. Конспект по дисциплине «Математические методы»

7. Е.С. Вентцель, «Элементы теории игр», Государственное издательство физико-математической литературы, Москва, 1961