| Скачать .docx | Скачать .pdf |
Реферат: Геометрические преобразования графиков функции
| № | Функция | Преобразование | Графики |
| 1 | y = −ѓ(x) | Сначала строим график функции ѓ(x), а затем симметрично отображаем его относительно оси OX. | y = − (x2 ) y = x2 → − (x2 )
|
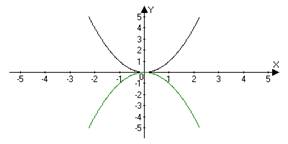
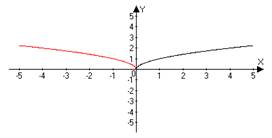
| 2 | y = ѓ(−x) | Сначала строим график функции ѓ(x), а затем симметрично отображаем его относительно оси OY. | y = √ (− x) y =√(x) → √ (− x)
|
| 3 | y = ѓ(x) +A A - const |
Сначала строим график функции ѓ(x), а затем, если А>0 поднимаем полученный график на А единиц вверх по оси OY. Если А<0, то опускаем вниз. | y = x2 → x2 +1 y = x2 → x2 –1
|
| 4 | y = ѓ(x−а) | Сначала строим график функции ѓ(x), а затем, если а>0, то график функции смещаем на а единиц вправо, а если а<0, то на а единиц влево. "−" − → "+" − ← |
y = x2 → (x+1)2 y = x2 → (x -1)2
|
| 5 | y = K ѓ(x ) k − const k>0 |
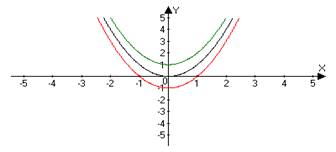
Сначала строим график функции ѓ(x), а затем, если K>0, то растягиваем полученный график в K раз вдоль оси OY. А если 0< K<1, то сжимаем полученный график в 1 ∕ Kраз вдоль оси OY. ↕ ↓ ↑ |
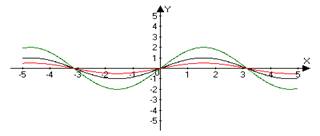
y = sin(x) → 2 sin(x) y = sin(x) → Ѕ sin(x)
|
6 7 |
y = ѓ(к x ) k − const k>0 y = A ѓ(к x+а) +В A, к, а, В − const |
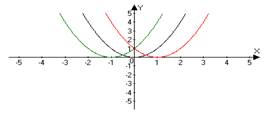
Сначала строим график функции ѓ(x), а затем, если к >1, то сжимаем полученный график в к раз вдоль оси OХ. А если 0< к <1, то растягиваем полученный график в 1∕ к раз вдоль оси OХ. к >1 − →← 0< к <1 − ←→ ѓ( x ) → ѓ(к x ) → ѓ(к( х + а ∕ к )) →A ѓ(к( х + а ∕ к )) → A ѓ(к( х + а ∕ к )) +В |
y = sin(x) → sin(2 x) y = sin(x) → sin (Ѕ x)
y = 2√(2x-2)+1 y =√x →√2x→√2(x -1) → 2√2(x -1) →2√2(x-1)+1
|
| 8 | y = │ѓ(x)│ | Сначала строим график функции ѓ(x), а затем часть графика, расположенную выше оси ОХ оставляем без изменения, а часть графика, расположенную ниже оси ОХ, заменяем симметричным отображением относительно ОХ. | y =│x3 │ y = x3 →│x3 │
|
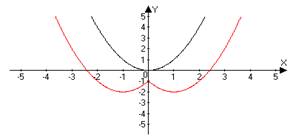
| 9 | y = ѓ(│x│) | Сначала строим график функции ѓ(x), а затем часть графика, расположенную правее оси ОУ, оставляем без изменения, а левую часть графика заменяем симметричным отображением правой относительно ОУ. | y = (│x│−1)2 −2 y = x2 →(x -1)2 → (x -1)2 − 2→(│x│−1)2 −2
|
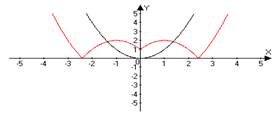
| 10 | y = │ѓ(│x│)│ | ѓ(x) → ѓ(│x│) →│ѓ(│x│)│ | y= │(│x│−1)2 - 2│ y= x2 → (x-1)2 →(x-1)2 - 2→(│x│−1)2 - 2→│(│x│−1)2 - 2│
|