| Скачать .docx | Скачать .pdf |
Реферат: Контрольная работа: Економіко-математичні методи і алгоритми
Завдання 1
У наведеній далі задачі виконати такі дії:
1.1. записати математичні моделі прямої та двоїстої задач;
1.2. симплекс-методом визначити оптимальні плани прямої та двоїстої задач, подати їх економічний аналіз;
1.3. визначити статус ресурсів, що використовуються для виробництва продукції, та рентабельність кожного виду продукції;
1.4. обчислити інтервали стійкості двоїстих оцінок стосовно зміни запасів дефіцитних ресурсів;
1.5. розрахувати інтервали можливих змін ціни одиниці рентабельної продукції.
Підприємство виготовляє чотири види продукції, використовуючи для цього три види ресурсів. Норми витрати усіх ресурсів на одиницю продукції та запаси ресурсів наведено в таблиці. Відома ціна одиниці продукції кожного виду. Визначити план виробництва продукції, що забезпечує підприємству найбільший дохід.
| Ресурс | Норма витрат на одиницю продукції за видами | Запас ресурсу | |||
| А | В | С | Д | ||
| 1 | 2 | 1 | 1 | 1 | 280 |
| 2 | 1 | 0 | 1 | 1 | 80 |
| 3 | 1 | 5 | 0 | 0 | 250 |
| Ціна одиниці продукції (ум. од.) | 4 | 3 | 6 | 7 | |
Розв'язання:
1.1. Математичні моделі прямої та двоїстої задач мають такий вигляд:
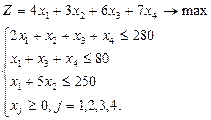
де ![]() – обсяг виробництва продукції
– обсяг виробництва продукції ![]() го виду (
го виду (![]() );
);
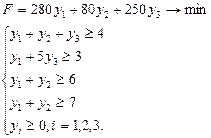
де ![]() – оцінка одиниці
– оцінка одиниці ![]() го виду ресурсу (
го виду ресурсу (![]() ).
).
Розв’яжемо пряму задачу симплекс-методом:
| Базис | Сбаз | План | 4 | 3 | 6 | 7 | 0 | 0 | 0 | |
| х1 | х2 | х3 | х4 | х5 | х6 | х7 | ||||
| х5 | 0 | 280 | 2 | 1 | 1 | 1 | 1 | 0 | 0 | 140 |
| х6 | 0 | 80 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | |
| х7 | 0 | 250 | 1 | 5 | 0 | 0 | 0 | 0 | 1 | 250 |
| 0 | -4 | -3 | -6 | -7 | 0 | 0 | 0 | |||
| х1 | 4 | 200 | 2 | 1 | 1 | 1 | 1 | 0 | 0 | |
| х6 | 0 | 80 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | |
| х7 | 0 | 250 | 0 | 1 | -4 | 0 | -3 | 0 | 1 | 250 |
| 560 | 0 | -3 | 10 | 2 | 4 | 0 | 0 | |||
Остання симплекс-таблиця, що відповідає оптимальному плану поставленої задачі, має вигляд:
| Базис | Сбаз | План | 4 | 3 | 6 | 7 | 0 | 0 | 0 |
| х1 | х2 | х3 | х4 | х5 | х6 | х7 | |||
| х2 | 3 | 50 | 1 | 0 | -1 | 1 | 0 | 1 | 1/5 |
| х5 | 0 | 150 | 0 | 0 | 2 | 1 | 1 | -1 | -1/5 |
| х4 | 7 | 80 | 0 | 1 | 3/5 | 0 | 0 | 4/7 | 0 |
| 710 | 3,6 | 0 | 1 | 0 | 0 | 7 | 0,6 | ||
З наведеної симплекс-таблиці маємо:
![]()
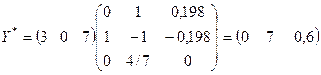 ;
;
min F = 80*7 +250*0,6 = 710 = max Z.
Оптимальний план прямої задачі передбачає виробництво лише двох видів продукції А і В у кількості відповідно 50 та 80 од. Випуск продукції А та С не передбачається (х1 = х3 = 0). Додаткові змінні х5 , х6 , х7 характеризують залишок (невикористану частину) ресурсів відповідно 1, 2 та 3. Оскільки х5 = 150, то перший ресурс використовується у процесі виробництва не повністю, а другий та третій ресурси – повністю (х6 = х7 =0). За такого оптимального виробництва продукції та використання ресурсів підприємство отримує найбільший дохід у розмірі 710 ум. од.
План двоїстої задачі дає оптимальну систему оцінок ресурсів, що використовуються у виробництві. Так, y2 = 7 та y3 = 0,6 відмінні від нуля, а ресурси 2 та 3 використовуються повністю. Двоїста оцінка y1 = 0 і відповідний вид ресурсу не повністю використовується при оптимальному плані виробництва. Така оптимальна система оцінок дає найменшу загальну вартість усіх ресурсів, що використовуються на підприємстві: min F = 710 ум. од.
Статус ресурсів прямої задачі можна визначити за допомогою додаткових змінних прямої задачі. Якщо додаткова змінна в оптимальному плані дорівнює нулю, то відповідний ресурс дефіцитний, а якщо відмінна від нуля – ресурс недефіцитний. В даному випадку другий та третій ресурси є дефіцитними, а перший ресурс не є дефіцитним.
Якщо запас другого дефіцитного ресурсу збільшити на 1 ум. од. ![]() , то цільова функція max Z збільшиться за інших однакових умов на y2
= 0,1 ум. од. і становитиме max Z = 710,1 ум. од. Елементи стовпчика «х6
» останньої симплекс-таблиці, який відповідає двоїстій оцінці y2
дають інформацію про зміни в оптимальному плані. У новому оптимальному плані значення змінної х4
збільшиться на 1, значення х5
збільшиться на 1,3, а значення х2
зменшиться на 2,3. Нові оптимальні значення змінних будуть такими:
, то цільова функція max Z збільшиться за інших однакових умов на y2
= 0,1 ум. од. і становитиме max Z = 710,1 ум. од. Елементи стовпчика «х6
» останньої симплекс-таблиці, який відповідає двоїстій оцінці y2
дають інформацію про зміни в оптимальному плані. У новому оптимальному плані значення змінної х4
збільшиться на 1, значення х5
збільшиться на 1,3, а значення х2
зменшиться на 2,3. Нові оптимальні значення змінних будуть такими: ![]() . Отже, збільшення запасу другого дефіцитного ресурсу за інших однакових умов приводить до зростання випуску продукції Д та зменшення випуску продукції В, а обсяг використання першого ресурсу збільшиться. За такого плану виробництва максимальний дохід підприємства буде max Z = 710,1, тобто зросте на y2
= 0,1.
. Отже, збільшення запасу другого дефіцитного ресурсу за інших однакових умов приводить до зростання випуску продукції Д та зменшення випуску продукції В, а обсяг використання першого ресурсу збільшиться. За такого плану виробництва максимальний дохід підприємства буде max Z = 710,1, тобто зросте на y2
= 0,1.
Проаналізуємо, як зміниться оптимальний план виробництва продукції, якщо запас дефіцитного ресурсу 3 за інших однакових умов збільшиться на одиницю ![]() . Аналогічно попереднім міркуванням, скориставшись елементами стовпчика «х7
» останньої симплекс-таблиці, можна записати новий оптимальний план:
. Аналогічно попереднім міркуванням, скориставшись елементами стовпчика «х7
» останньої симплекс-таблиці, можна записати новий оптимальний план: ![]() , max Z = 710 + 0,6 = 710,6 ум. од.
, max Z = 710 + 0,6 = 710,6 ум. од.
Отже, дохід підприємства збільшиться на 0,6 ум. од. за рахунок збільшення виробництва продукції В на 0,20 од.
Розрахуємо інтервали можливої зміни обсягів дефіцитних ресурсів, в межах яких двоїсті оцінки залишаються на рівні оптимальних значень.
Приріст (зміну) запасу ресурсу 2 позначимо ![]() . Тоді новий обсяг ресурсу становитиме
. Тоді новий обсяг ресурсу становитиме ![]() і новий оптимальний план
і новий оптимальний план
![]()
Єдина вимога, яку можна поставити до можливих нових оптимальних значень, – це умова невід’ємності, тобто
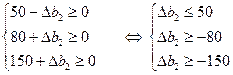
![]() .
.
Це означає, що коли запас ресурсу 2 збільшиться на 150 од. або зменшиться на 80 од., то оптимальною двоїстою оцінкою ресурсу 2 залишиться y2 = 7. Отже, запас ресурсу 2 може змінюватися у межах
![]()
![]() ,
,
![]() .
.
Згідно з цим максимально можливий дохід підприємства перебуватиме в межах
![]() ,
,
![]() .
.
Аналогічно розраховується інтервал стійкості двоїстої оцінки дефіцитного ресурсу 3:
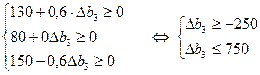
![]() .
.
Отже, якщо запас ресурсу 3 збільшиться на 750 од. або зменшиться на 250 од., то двоїста оцінка y3 = 0,6 цього ресурсу залишиться оптимальною. Згідно з цим можливий дохід підприємства та оптимальний план виробництва продукції перебуватимуть у межах
![]()
![]() ,
,
Оцінка рентабельності продукції, що виготовляється на підприємстві, виконується за допомогою двоїстих оцінок та обмежень двоїстої задачі, що характеризують кожний вид продукції.
Підставимо ![]() у систему обмежень двоїстої задачі. Якщо вартість ресурсів на одиницю продукції (ліва частина) перевищує ціну цієї продукції (права частина), то виробництво такої продукції для підприємства недоцільне. Якщо ж співвідношення виконується як рівняння, то продукція рентабельна.
у систему обмежень двоїстої задачі. Якщо вартість ресурсів на одиницю продукції (ліва частина) перевищує ціну цієї продукції (права частина), то виробництво такої продукції для підприємства недоцільне. Якщо ж співвідношення виконується як рівняння, то продукція рентабельна.
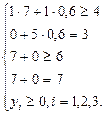
Отже, продукція В і Д рентабельна, а продукція А, С нерентабельна.
На ринку дві корпорації-конкуренти намагаються стати лідерами й контролювати всі дрібні компанії у своїй галузі. Невелика фірма внаслідок такої політики може опинитися в складі однієї з конкуруючих корпорацій, що може привести їй як зиск, так і збитки. З метою протистояння корпораціям фірма може ініціювати створення асоціації дрібних підприємств своєї галузі, що може забезпечити як великий успіх, так і цілковиту невдачу від цієї діяльності. Відповідна інформація наведена в таблиці. Який з трьох варіантів обрати фірмі?
| Варіант злиття | Успіх | Невдача | ||
| імовірність | прибуток, млн. грн. | імовірність | прибуток, млн. грн. | |
| 1 корпорація | 0,6 | 9,5 | 0,4 | -2 |
| 2 корпорація | 0,7 | 13,5 | 0,3 | -2 |
| Створення асоціації | 0,3 | 26,5 | 0,7 | -2,5 |
Розв’язання:
Визначимо очікуване значення прибутку для кожного варіанту злиття:
1 корпорація М(1) = 0,6*9,5+0,4*(-2) = 4,9 млн. грн.;
2 корпорація М(2) = 0,7*13,5+0,3*(-2) = 8,85 млн. грн.;
створення асоціації М(А) = 0,3*26,5+0,7*(-2,5) = 6,2 млн. грн.
Отже, входження до другої корпорації має найбільше очікуване значення прибутку.
Обчислимо для кожного варіанту злиття показники варіації прибутку фірми: дисперсію, середньоквадратичне відхилення та коефіцієнт варіації.
1) входження до першої корпорації:
дисперсія D(1) = 0,6*(9,5–4,9)2 +0,4*(-2–4,9)2 = 31,74;
середньоквадратичне відхилення ![]() млн. грн.;
млн. грн.;
коефіцієнт варіації ![]() .
.
2) входження до другої корпорації:
дисперсія D(2) = 0,7*(13,5–8,85)2 +0,3*(-2–8,85)2 = 50,4525;
середньоквадратичне відхилення ![]() млн. грн.;
млн. грн.;
коефіцієнт варіації ![]() .
.
3) створення асоціації:
дисперсія D(А) = 0,3*(26,5–6,2)2 +0,7*(-2,5–6,2)2 = 176,61;
середньоквадратичне відхилення ![]() млн. грн.;
млн. грн.;
коефіцієнт варіації ![]() .
.
Коефіцієнту варіації має такий зміст: це величина ризику відхилень, що припадає на одиницю очікуваного прибутку.
Отже, найменший ризик у абсолютному вимірі (середньоквадратичне відхилення) має входження у першу корпорацію. Але у відносному вимірі (коефіцієнт варіації) найменший ризик має входження до другої корпорації. Враховуючи, що крім цього входження до другої корпорації має найбільше очікуване значення прибутку, то слід обрати варіант входження до другої корпорації.
Завдання 3
Підприємство має 12 філій, розташованих в різних районах області. Керівництво має дослідити, яким чином впливають торгівельна площа, середньоденна інтенсивність потоку покупців та середньоденний дохід на річний товарообіг філії. Статистичні дані наведені в таблиці:
| № філії | Річний товарообіг, млн. грн. |
Торгівельна площа, тис. м2 |
Середньоденна інтенсивність потоку покупців, тис. чол. /день |
Середньоденний дохід, тис. грн. |
| У | Х1 | Х2 | Х3 | |
| 1 | 3,08 | 0,37 | 10,54 | 5,495 |
| 2 | 5,42 | 1,04 | 7,81 | 5,625 |
| 3 | 7 | 1,27 | 11,11 | 6,775 |
| 4 | 7,16 | 1,35 | 10,19 | 6,305 |
| 5 | 7,17 | 1,18 | 14,02 | 9,975 |
| 6 | 8,5 | 1,55 | 14,22 | 8,775 |
| 7 | 4,48 | 0,84 | 8,84 | 5,525 |
| 8 | 5,92 | 1 | 12,66 | 7,755 |
| 9 | 7,83 | 1,35 | 12,57 | 7,875 |
| 10 | 3,31 | 0,54 | 11,31 | 6,275 |
| 11 | 1,67 | 0,3 | 8,55 | 5,235 |
| 12 | 3,3 | 0,61 | 9,61 | 5,325 |
Обчислити парні коефіцієнти кореляції та дослідити модель на мультиколінеарність. Якщо є залежні фактори, виключити один з них (довести, чому саме цей фактор вилучено).
Побудувати діаграми розсіювання для припущення щодо вигляду залежності між показником та факторами, що залишилися в моделі. Обчислити оцінки параметрів множинної регресії. Дати інтерпретацію оцінок параметрів.
Визначити коефіцієнти кореляції, детермінації, оцінений коефіцієнт детермінації. Дати пояснення щодо отриманих результатів.
З надійністю 0,95 за допомогою критерію Фішера оцінити адекватність прийнятої математичної моделі статистичним даним та за допомогою критерію Стьюдента оцінити значимість параметрів регресії. Пояснити отримані результати.
Визначити частинні коефіцієнти еластичності та пояснити їх сенс.
Розв’язання:
Використаємо критерій ![]() для перевірки моделі на мультиколінеарність. Для цього нормалізуємо змінні
для перевірки моделі на мультиколінеарність. Для цього нормалізуємо змінні ![]() економетричної моделі за формулою
економетричної моделі за формулою
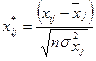 ,
,
де ![]() – кількість спостережень, (
– кількість спостережень, (![]() );
);
![]() – кількість незалежних змінних, (
– кількість незалежних змінних, (![]() );
);
![]() – середня арифметична
– середня арифметична ![]() -ї незалежної змінної;
-ї незалежної змінної;
![]() – дисперсія
– дисперсія ![]() -ї незалежної змінної.
-ї незалежної змінної.
Результати нормалізації змінних ![]() ,
, ![]() ,
, ![]() подамо в таблиці:
подамо в таблиці:
| 1 | 0,45 | 10,94 | 5,995 | -0,4207 | -0,0593 | -0,2458 |
| 2 | 1,12 | 8,21 | 6,125 | 0,0653 | -0,4515 | -0,2202 |
| 3 | 1,35 | 11,51 | 7,275 | 0,2321 | 0,0226 | 0,0059 |
| 4 | 1,43 | 10,59 | 6,805 | 0,2901 | -0,1096 | -0,0865 |
| 5 | 1,26 | 14,42 | 10,475 | 0,1668 | 0,4408 | 0,6351 |
| 6 | 1,63 | 14,62 | 9,275 | 0,4352 | 0,4695 | 0,3991 |
| 7 | 0,92 | 9,24 | 6,025 | -0,0798 | -0,3035 | -0,2399 |
| 8 | 1,08 | 13,06 | 8,255 | 0,0363 | 0,2453 | 0,1986 |
| 9 | 1,43 | 12,97 | 8,375 | 0,2901 | 0,2324 | 0,2222 |
| 10 | 0,62 | 11,71 | 6,775 | -0,2974 | 0,0514 | -0,0924 |
| 11 | 0,38 | 8,95 | 5,735 | -0,4715 | -0,3452 | -0,2969 |
| 12 | 0,69 | 10,01 | 5,825 | -0,2466 | -0,1929 | -0,2792 |
Побудуємо нову ![]() -матрицю, елементами якої є нормалізовані змінні
-матрицю, елементами якої є нормалізовані змінні ![]() , і обчислимо кореляційну матрицю:
, і обчислимо кореляційну матрицю:
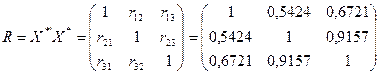 ,
,
де ![]() – матриця, транспонована до матриці
– матриця, транспонована до матриці ![]() (елементи матриці
(елементи матриці ![]() характеризують щільність зв’язку між двома незалежними змінними; (
характеризують щільність зв’язку між двома незалежними змінними; (![]() ) – парні коефіцієнти кореляції). Аналізуючи значення цих коефіцієнтів, робимо припущення, що між змінними
) – парні коефіцієнти кореляції). Аналізуючи значення цих коефіцієнтів, робимо припущення, що між змінними ![]() і
і ![]() існує сильний зв’язок.
існує сильний зв’язок.
Знайдемо визначник кореляційної матриці ![]() :
: ![]() ; потім визначимо критерій
; потім визначимо критерій ![]() :
:
![]() .
.
Для ![]() ступенів свободи і рівня значущості
ступенів свободи і рівня значущості ![]() табличне значення критерію
табличне значення критерію ![]() . Оскільки обчислене значення більше за табличне, то в моделі присутня мультиколінеарність.
. Оскільки обчислене значення більше за табличне, то в моделі присутня мультиколінеарність.
Складемо розрахункову таблицю для обчислення коефіцієнтів кореляції між факторами і показником:
| № | Y | X2 | X3 | Y2 | X2 2 | X3 2 | YX2 | YX3 |
| 1 | 3,08 | 10,54 | 5,495 | 9,4864 | 111,0916 | 30,19503 | 32,4632 | 16,9246 |
| 2 | 5,42 | 7,81 | 5,625 | 29,3764 | 60,9961 | 31,64063 | 42,3302 | 30,4875 |
| 3 | 7 | 11,11 | 6,775 | 49 | 123,4321 | 45,90063 | 77,77 | 47,425 |
| 4 | 7,16 | 10,19 | 6,305 | 51,2656 | 103,8361 | 39,75303 | 72,9604 | 45,1438 |
| 5 | 7,17 | 14,02 | 9,975 | 51,4089 | 196,5604 | 99,50063 | 100,5234 | 71,52075 |
| 6 | 8,5 | 14,22 | 8,775 | 72,25 | 202,2084 | 77,00063 | 120,87 | 74,5875 |
| 7 | 4,48 | 8,84 | 5,525 | 20,0704 | 78,1456 | 30,52563 | 39,6032 | 24,752 |
| 8 | 5,92 | 12,66 | 7,755 | 35,0464 | 160,2756 | 60,14003 | 74,9472 | 45,9096 |
| 9 | 7,83 | 12,57 | 7,875 | 61,3089 | 158,0049 | 62,01563 | 98,4231 | 61,66125 |
| 10 | 3,31 | 11,31 | 6,275 | 10,9561 | 127,9161 | 39,37563 | 37,4361 | 20,77025 |
| 11 | 1,67 | 8,55 | 5,235 | 2,7889 | 73,1025 | 27,40523 | 14,2785 | 8,74245 |
| 12 | 3,3 | 9,61 | 5,325 | 10,89 | 92,3521 | 28,35563 | 31,713 | 17,5725 |
| Сума | 64,84 | 131,43 | 80,94 | 403,848 | 1487,922 | 571,8083 | 743,3183 | 465,4972 |
| Середнє | 5,4033 | 10,9525 | 6,7450 | 33,6540 | 123,9935 | 47,6507 | 61,9432 | 38,7914 |
Обчислимо коефіцієнти кореляції:
![]() ;
;
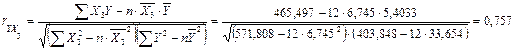
Відповідно до обчислених коефіцієнтів кореляції, показник Y має тісніший зв’язок із змінною Х3 порівняно із змінною Х2 . Тому відкинемо фактор Х2 . Будемо розглядати модель Y=Y(X1 , X3 ).
Для припущення про вигляд залежності побудуємо діаграми розсіювання між показником та факторами, що залишилися в моделі.
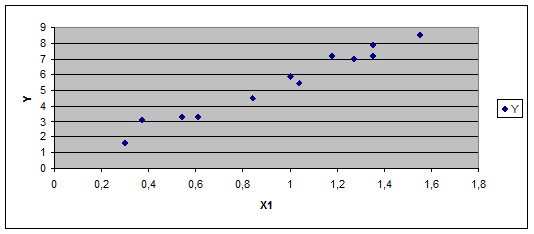
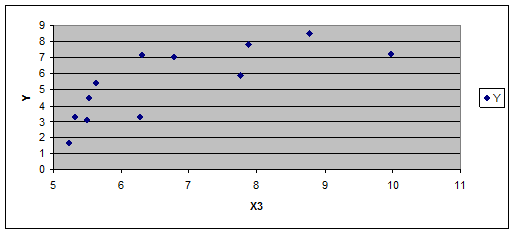
Обчислимо оцінки параметрів множинної регресії у лінійній формі:
![]() .
.
Відповідно до методу найменших квадратів (МНК) оператор оцінювання параметрів моделі має вигляд
![]() ,
,
де 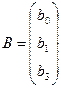 ;
; ![]() – матриця, транспонована до матриці
– матриця, транспонована до матриці ![]() . Матриця
. Матриця ![]() , крім двох векторів змінних Х1
та Х3
, містить вектор одиниць. Згідно з оператором оцінювання одержимо:
, крім двох векторів змінних Х1
та Х3
, містить вектор одиниць. Згідно з оператором оцінювання одержимо:
1) 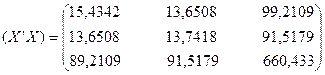 ;
;
2) 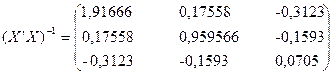 ;
;
3) 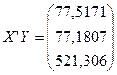 ;
;
4) 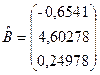 .
.
Отже, отримали таку модель лінійної множинної регресії:
![]() .
.
Оцінки параметрів моделі мають такий економічний зміст:
1) ![]() : якщо за інших рівних умов змінна Х1
збільшиться (зменшиться) на одиницю, то відповідно до цієї оцінки змінна Y збільшується (зменшується) на 4,60278. Конкретно це означає, що збільшення (зменшення) торгової площі на 1 тис. м2
приведе, за інших рівних умов, до збільшення (зменшення) річного товарообігу цієї філії на 4,60278 млн. грн.;
: якщо за інших рівних умов змінна Х1
збільшиться (зменшиться) на одиницю, то відповідно до цієї оцінки змінна Y збільшується (зменшується) на 4,60278. Конкретно це означає, що збільшення (зменшення) торгової площі на 1 тис. м2
приведе, за інших рівних умов, до збільшення (зменшення) річного товарообігу цієї філії на 4,60278 млн. грн.;
2) ![]() : якщо за інших рівних умов змінна Х3
збільшиться (зменшиться) на одиницю, то відповідно до цієї оцінки змінна Y збільшиться (зменшиться) на 0,24978. Конкретно це означає, що збільшення (зменшення) середньоденного доходу на 1 тис. грн. приведе, за інших рівних умов, до збільшення (зменшення) річного товарообігу цієї філії на 0,24978 млн. грн.
: якщо за інших рівних умов змінна Х3
збільшиться (зменшиться) на одиницю, то відповідно до цієї оцінки змінна Y збільшиться (зменшиться) на 0,24978. Конкретно це означає, що збільшення (зменшення) середньоденного доходу на 1 тис. грн. приведе, за інших рівних умов, до збільшення (зменшення) річного товарообігу цієї філії на 0,24978 млн. грн.
Обчислимо суми квадратів:
![]() .
.
Визначимо коефіцієнт детермінації
![]() ,
,
оцінений коефіцієнт детермінації
![]() ,
,
коефіцієнт множинної кореляції
![]() .
.
Оскільки отримані значення є близькими до одиниці, то можна зробити висновок про тісний зв’язок між річним товарообігом і незалежними змінними. При цьому понад 98% варіації річного товарообігу пояснюється варіацією торгівельної площі та середньоденного доходу.
Обчислимо критерій Фішера
![]() .
.
Критичне значення критерію Фішера при рівні значущості ![]() і кількості ступенів свободи
і кількості ступенів свободи ![]() та
та ![]() дорівнює
дорівнює ![]() . Порівнюючи обчислене значення критерію Фішера з критичним, робимо висновок про адекватність прийнятої математичної моделі статистичним даним.
. Порівнюючи обчислене значення критерію Фішера з критичним, робимо висновок про адекватність прийнятої математичної моделі статистичним даним.
Матриця ![]() є матрицею коваріацій оцінок параметрів моделі. Діагональні елементи
є матрицею коваріацій оцінок параметрів моделі. Діагональні елементи ![]() цієї матриці використаємо для обчислення стандартних похибок параметрів моделі.
цієї матриці використаємо для обчислення стандартних похибок параметрів моделі.
Знайдемо дисперсію залишків за формулою ![]() . Таким чином,
. Таким чином, ![]() . Визначимо стандартні похибки оцінок параметрів моделі, використовуючи дисперсію залишків:
. Визначимо стандартні похибки оцінок параметрів моделі, використовуючи дисперсію залишків:
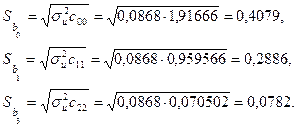
Обчислимо значення ![]() -критеріїв:
-критеріїв:
![]() ;
; ![]() ;
; 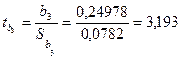 .
.
Табличне значення ![]() -критерію при
-критерію при ![]() ступенях свободи і рівні значущості α = 0,05 становить 2,262. Всі фактичні значення
ступенях свободи і рівні значущості α = 0,05 становить 2,262. Всі фактичні значення ![]() -критеріїв, окрім критерію для вільного члена, перевищують за модулем табличне значення. Отже, статистично значущими є всі параметри моделі, крім вільного члена.
-критеріїв, окрім критерію для вільного члена, перевищують за модулем табличне значення. Отже, статистично значущими є всі параметри моделі, крім вільного члена.
Визначимо коефіцієнти еластичності за формулами
![]() ,
, ![]() ,
,
де f (X ) = -0,6541 + 4,60278 X 1 + 0,24978 X 3 . – рівняння регресії, знайдене вище:
![]() ;
;
![]() .
.
Отримані коефіцієнти еластичності показують, на скільки% у середньому змінюється показник Y стосовно своєї величини при зміні відповідного фактора на 1% від свого середнього значення.
Список літератури
1. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высш. шк., 1986.
2. Машина Н.І. Економічний ризик і методи його вимірювання. Навчальний посібник. – К: ЦУЛ, 2003. –188 с.
3. Толбатов Ю.А. Економетрика: Підручник для студентів економічних спеціальностей вищих навчальних закладів. – К.: Четверта хвиля, 1997 – 320 с.