| Скачать .docx | Скачать .pdf |
Курсовая работа: Курсовая работа: Статистические методы обработки экспериментальных данных
Министерство образования Российской Федерации
Московский государственный университет печати
Факультет полиграфической технологии
Дисциплина: Математика
Курсовая работа по теме:
«Статистические методы обработки
Экспериментальных данных»
Выполнил: студент
Курс 2
Группа ЗТПМ
форма обучения заочная
Номер зачетной книжки Мз 023 н
Вариант № 13
Допущено к защите
Дата защиты
Результат защиты
Подпись преподавателя
Москва – 2010 год
| 0;3 | 3;6 | 6;9 | 9;12 | 12;15 | 15;18 | 18;21 |
| 4 | 6 | 9 | 11 | 14 | 18 | 13 |
| 21;24 | 24;27 | 27;30 | 30;33 |
| 11 | 7 | 4 | 3 |
1. Построение интервального и точечного статистических распределений результатов наблюдений. Построение полигона и гистограммы относительных частот.
i – порядковый номер;
Ii – интервал разбиения;
xi – середина интервала Ii ;
ni – частота (количество результатов наблюдений, принадлежащих данному интервалу Ii );
wi
= ![]() - относительная частота (n =
- относительная частота (n =![]() - объём выборки);
- объём выборки);
Hi
= ![]() - плотность относительной частоты (h – шаг разбиения, т.е. длина интервала Ii
).
- плотность относительной частоты (h – шаг разбиения, т.е. длина интервала Ii
).
| i | Ii | xi | ni | wi | Hi |
1 2 3 4 5 6 7 8 9 10 11 |
0;3 3;6 6;9 9;12 12;15 15;18 18;21 21;24 24;27 27;30 30;33 |
1,5 4,5 7,5 10,5 13,5 16,5 19,5 22,5 25,5 28,5 31,5 |
4 6 9 11 14 18 13 11 7 4 3 |
0,04 0,06 0,09 0,11 0,14 0,18 0,13 0,11 0,07 0,04 0,03 |
0,01 0,02 0,03 0,04 0,05 0,06 0,04 0,04 0,02 0,01 0,01 |
Объём выборки:
n =![]() =100,
=100,
wi = ni /100;
контроль: ![]() =1
=1
Длина интервала
разбиения (шаг):
h = 3 ,
Hi
= ![]()
å : 100 1,00
Статистическим распределением называется соответствие между результатами наблюдений (измерений) и их частотами и относительными частотами. Интервальное распределение – это наборы троек (Ii ; ni ; wi ) для всех номеров i, а точечное – наборы троек (xi ; ni ; wi ). Таким образом, в таблице имеются оба – и интервальное, и точечное - статистическое распределения.
Далее, строим полигон и гистограмму относительных частот.
Полигон.
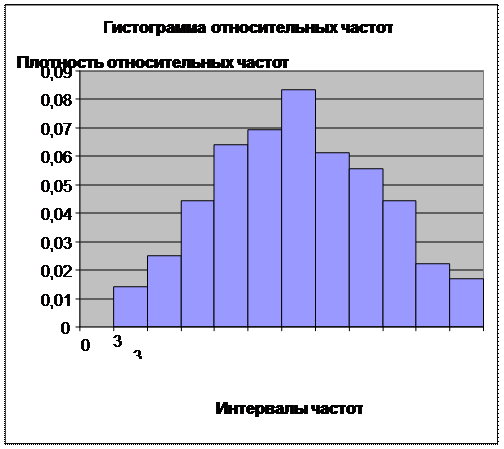
Полигон относительных частот – ломаная, отрезки которой последовательно (в порядке возрастания xi ) соединяют точки (xi ; wi ). Гистограмма относительных частот – фигура, которая строится следующим образом: на каждом интервале Ii , как на основании, строится прямоугольник, площадь которого равна относительной частоте wi ; отсюда следует, что высота этого прямоугольника равна Hi = wi /h– плотности относительной частоты. Полигон и гистограмма являются формами графического изображения статистического распределения.
2. Нахождение точечных оценок математического ожидания и
дисперсии.
В качестве точечных оценок числовых характеристик изучаемой случайной величины используются:
- для математического ожидания
![]() =
= ![]()
![]() (выборочная средняя
),
(выборочная средняя
),
- для дисперсии
s2
= ![]() (исправленная выборочная
),
(исправленная выборочная
),
где n – объём выборки, ni – частота значения xi .
Таким образом, в статистических расчетах используют приближенные равенства
MX»![]() , DX»s2
.
, DX»s2
.
Нахождение точечных оценок математического ожидания и дисперсии по данным варианта осуществим с помощью расчетной таблицы.
| i | xi | ni | xi ni | (xi
- |
1 2 3 4 5 6 7 8 9 10 11 |
1,5 4.5 7,5 10,5 13,5 16,5 19,5 22,5 25,5 28,5 31,5 |
4 6 9 11 14 18 13 11 7 4 3 |
6 27 67,5 115,5 189 297 253,5 247,5 178,5 114 94,5 |
829,44 779,76 635,04 320,76 80,64 6,48 168,48 479,16 645,12 635,04 744,12 |
![]() =
= ![]()
![]() =
=
хi ni /100 = 1590/100= 15,9
s2
= ![]() =
=
= 5324,04/99=53,78
å : 100 1590 5324,04
3.Выдвижение гипотезы о распределении случайной величины.
При выдвижении гипотезы (предположения) о законе распределения изучаемой случайной величины мы опираемся лишь на внешний вид статистического распределения. Т.е. будем руководствоваться тем, что профиль графика плотности теоретического распределения должен соответствовать профилю гистограммы: если середины верхних сторон прямоугольников, образующих гистограмму, соединить плавной кривой, то эта линия представляет в первом приближении график плотности распределения вероятностей.
Итак, изобразим график и выпишем формулу плотности нормального (или гауссовского) распределения с параметрами а и ![]() , - ¥< а <+¥,
, - ¥< а <+¥, ![]()
 |
Сравнение построенной гистограммы и графика плотности распределения приводит к следующему заключению о предполагаемом (теоретическом) законе распределения в рассматриваемом варианте исходных данных:
Вариант 13 – нормальное (или гауссовское распределение)
4.Построение графика теоретической плотности распределения.
Чтобы выписать плотность теоретического (предполагаемого) распределения, нужно определить значения параметров ![]() и а и подставить их в соответствующую формулу. Все параметры тесно связаны с числовыми характеристиками случайной величины, т.е.
и а и подставить их в соответствующую формулу. Все параметры тесно связаны с числовыми характеристиками случайной величины, т.е.
MX = а,
DX = σ2
Поскольку значения математического ожидания и дисперсии неизвестны, то их заменяют соответствующими точечными оценками, т.е. используют (уже упомянутые ранее) приближенные равенства MX»![]() , DX»s2
, что позволяет найти значения параметров распределения.
, DX»s2
, что позволяет найти значения параметров распределения.
По исходным данным была выдвинута гипотеза о нормальном распределении изучаемой случайной величины. Найдем параметры этого распределения:
_
![]()
![]()
![]() x = а, 15,9 = а, а=15,9
x = а, 15,9 = а, а=15,9
![]()
![]() s2
= σ2
53,78 = σ2
σ=7,33
s2
= σ2
53,78 = σ2
σ=7,33
Следовательно, плотность предполагаемого распределения задается формулой
F(x)= [1/(7,33*√2π)]*e[-( x-15,9)2 / 2*(7,33)2)] =0.054*e^(0,009/((x-15,9)^2))
Теперь необходимо вычислить значения f(xi )плотности f (x) при x=xi (в серединах интервалов) Для этого воспользуемся следующей схемой:
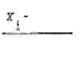
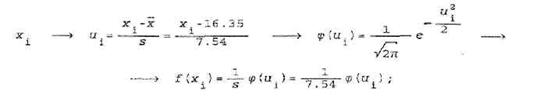 |
значения фунцкии
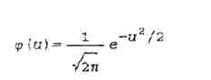 |
при u=ui находятся, например, с помощью таблицы, имеющейся в любом учебнике или задачнике по теории вероятностей и математической статистике.
![]() =15,9; s = 7,33
=15,9; s = 7,33
x i |
ui = xi - x / s | φ (u i ) | |
1,5 4,5 7,5 10,5 13,5 16,5 19,5 22,5 25,5 28,5 31,5 |
-1,96 -1,56 -1.15 -0,74 -0.33 0.08 0.49 0,90 1.31 1,72 2.13 |
0,0584 0,1182 0,2059 0,3034 0,3778 0,3977 0,3538 0,2661 0,1691 0,0909 0,0413 |
0,008 0,016 0,028 0,041 0,052 0,054 0,048 0,036 0,023 0,012 0,006 |
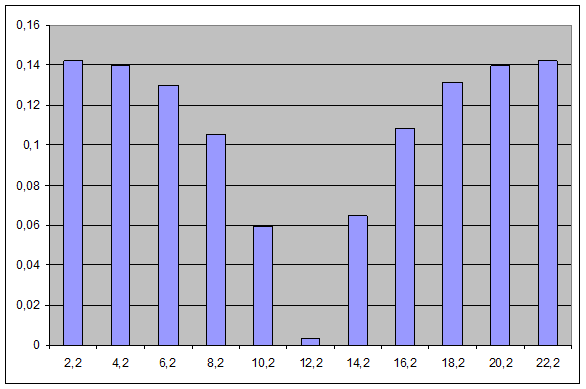
Далее, на одном чертеже строим гистограмму и график теоретической плотности распределения: гистограмма была построена ранее, а для получения графика плотности наносим точки с координатами (xi ; f(xi )) и соединяем их плавной кривой.
![]()
5.Проверка гипотезы о распределении с помощью критерия согласия Пирсона.
Ранее была выдвинута гипотеза о законе распределения рассматриваемой случайной величины. Сопоставление статистического распределения (гистограмма) и предполагаемого теоретического (графика плотности) показывает наличие некоторых расхождений между ними. Поэтому возникает естественный вопрос: чем объясняются эти несовпадения? Ответить на него можно двояко:
1) Указанные расхождения несущественны и вызваны ограниченным количеством наблюдений и случайными факторами – случайностью результата единичного наблюдения, способа группировки данных и т.п. В этом случае выдвинутая гипотеза о распределении считается правдоподобной и принимается как не противоречащая опытным данным.
2) Указанные расхождения являются существенными (неслучайными) и связаны с тем, что действительное распределение случайной величины отличается от предполагаемого. В этом случае выдвинутая гипотеза о распределении отвергается как плохо согласующаяся данными наблюдений.
Для выбора первого или второго варианта ответа и служат так называемые критерии согласия. Словари толкуют слово критерий (от греч. kriterion – средство для суждения) как признак, на основании которого производится оценка, определение и классификация чего-либо.
Существуют различные критерии согласия: К. Пирсона, А.Н. Колмогорова, Н.В. Смирнова, В.И. Романовского и другие. Мы рассмотрим лишь один из них – критерий Пирсона, называемый также критерием c2 («хи - квадрат»). (К. Пирсон (1857 - 1936) – английский математик, биолог, философ – позитивист.)
Критерий Пирсона выгодно отличается от остальных, во – первых, применимостью к любым (дискретным, непрерывным) распределениям и, во – вторых, простотой вычислительного алгоритма.
Правило проверки статистических гипотез с помощью критерия Пирсона будет объяснено на примерах.
Группировка исходных данных.
Применяется критерий Пирсона к сгруппированным данным. Предположим, что произведено n независимых опытов, в каждом из которых изучаемая случайная величина приняла определенное значение. Предположим, что вся числовая ось разбита на несколько непересекающихся промежутков (интервалов и полуинтервалов). Обозначим через nI количество результатов измерений (значений случайной величины), попавших в i-й промежуток. Очевидно, что ånI = n.
Отметим, что критерий c2 будет давать удовлетворительный для практических приложений результат, если:
1) количество n опытов достаточно велико, по крайней мере n³100;
2) в каждом промежутке окажется не менее 5…10 результатов измерений, т.е. ni ³5 при любом i; если количество полученных значений в отдельных промежутках мало (меньше 5), то такие промежутки следует объединить с соседними, суммируя соответствующие частоты.
Пусть концами построенного разбиения являются точки zi , где z1 <z2 < … <zi – 1 , т.е. само разбиение имеет вид
(- ¥ºz0 ; z1 ) , [z1 ; z2 ) , [z2 ; z3 ) , … , [zi – 1 ; zi º+¥).
После объединения соответствующих промежутков (последних двух) и замены самой левой границы разбиения на - ¥, а самой правой на + ¥ (поскольку на промежутки должна разбиваться вся числовая ось, а не только диапазон полученных в результате опыта значений), мы приходим к следующим интервальным распределениям, пригодным для непосредственного применения критерия Пирсона:
| zi –1 ; zi | - ¥; 6 | 6;9 | 9;12 | 12;15 | 15;18 | 18;21 |
| n i | 10 | 9 | 11 | 14 | 18 | 13 |
| 21;24 | 24;27 | 27;30 | 30;+∞ |
| 11 | 7 | 4 | 3 |
![]()
Вычисление теоретических частот.
Критерий Пирсона основан на сравнении эмпирических (опытных) частот с теоретическими. Эмпирические частоты nI
определяются по фактическим результатам наблюдений. Теоретические частоты, обозначаемые далее ![]() , находятся с помощью равенства
, находятся с помощью равенства
![]() = n×pi
,
= n×pi
,
где n – количество испытаний, а pi ºR(zi –1 <x<zi ) - теоретическая вероятность попадания значений случайной величины в i-й промежуток (1 £i£ 1).Теоретические вероятности вычисляются в условиях выдвинутой гипотезы о законе распределения изучаемой случайной величины.
 |
Процедура отыскания теоретических вероятностей и частот показана в расчетной таблице: _
n = 1 0 0; а=x = 15,9 ; σ = s=7,33
| i | Концы промежутков | Аргументы фунцкции Ф0 | Значения функции Ф0 | Pi = Ф0 (u i )- Ф0 (u i-1 ) | ν 1 ’ =npi | |||
| zi -1 | zi | U i- 1 = (z i-1 -x)/s |
U i = (z i -x)/s |
Ф0 (u i-1 ) | Ф0 (u i ) | |||
1 2 3 4 5 6 7 8 9 10 |
-∞ 6 9 12 15 18 21 24 27 30 |
6 9 12 15 18 21 24 27 30 +∞ |
-∞ -1,35 -0,94 -0,53 -0,12 0,29 0,70 1,11 1,51 1,92 |
-1,35 -0,94 -0,53 -0,12 0,29 0,70 1,11 1,51 1,92 +∞ |
-0,5000 -0,4115 -0,3264 -0,2019 -0,0478 0,1141 0,2580 0,3665 0,4345 0,4726 |
-0,4115 -0,3264 -0,2019 -0,0478 0,1141 0,2580 0,3665 0,4345 0,4726 0,5000 |
0,0885 0,0851 0,1245 0,1541 0,1619 0,1439 0,1085 0,0680 0,0381 0,0274 |
8,85 8,51 12,45 15,41 16,19 14,39 10,85 6,80 3,81 2,74 |
å:
1,0000
1
0
0
,00
Статистика c2 и вычисление ее значения по опытным данным.
Для того чтобы принять или отвергнуть гипотезу о законе распределения изучаемой случайной величины, в каждом из критериев согласия рассматривается некоторая (специальным образом подбираемая) величина, характеризующая степень расхождения теоретического (предполагаемого) и статистического распределения.
В критерии Пирсона в качестве такой меры расхождения используется величина
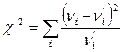 ,
,
называемая статистикой «хи - квадрат»
или статистикой Пирсона
(вообще, статистикой называют любую функцию от результатов наблюдений). Ясно, что всегда c2
³0, причем c2
= 0, тогда и только тогда, когда ![]() при каждом i , т.е. когда все соответствующие эмпирические и теоретические частоты совпадают. Во всех остальных случаях c2
¹0; при этом значение c2
тем больше, чем больше различаются эмпирические и теоретические частоты.
при каждом i , т.е. когда все соответствующие эмпирические и теоретические частоты совпадают. Во всех остальных случаях c2
¹0; при этом значение c2
тем больше, чем больше различаются эмпирические и теоретические частоты.
Прежде чем рассказать о применении статистики c2 к проверке гипотезы о закон е распределения , вычислим ее значение для данного варианта; это значение, найденное по данным наблюдений и в рамках выдвинутой гипотезы, будем обозначать через c2 набл. .
| i | n i | ||
1 2 3 4 5 6 7 8 9 10 |
10 9 11 14 18 13 11 7 4 3 |
8,85 8,51 12,45 15,41 16,19 14,39 10,85 6,8 3,81 2,74 |
0,15 0,03 0,17 0,13 0,20 0,13 0,00 0,01 0,01 0,02 |
![]() : 100 100 0,85
: 100 100 0,85
c 2 набл. = 0,85
5.4. Распределение статистики c2 .
Случайная величина имеет c2 – распределение с r степенями свободы (r = 1; 2; 3; …), если ее плотность имеет вид
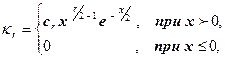
где cr
– которая положительная постоянная ( cr
определяется из равенства 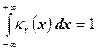 ). Случайная величина, имеющая распределение c2
с r
степенями свободы, будет обозначаться
). Случайная величина, имеющая распределение c2
с r
степенями свободы, будет обозначаться ![]() .
.
Для дальнейшего изложения важно лишь отметить, что, во – первых, распределение ![]() определяется одним параметром – числом r степеней свободы и, во – вторых, существуют таблицы, позволяющие произвольно найти вероятность попадания значений случайной величины
определяется одним параметром – числом r степеней свободы и, во – вторых, существуют таблицы, позволяющие произвольно найти вероятность попадания значений случайной величины ![]() в любой промежуток.
в любой промежуток.
Вернемся теперь к статистике ![]() . Отметим, что она является случайной величиной, поскольку зависит от результатов наблюдений и, следовательно, в различных сериях опытов принимает различные, заранее не известные значения. Понятно, кроме того, закон распределения статистики
. Отметим, что она является случайной величиной, поскольку зависит от результатов наблюдений и, следовательно, в различных сериях опытов принимает различные, заранее не известные значения. Понятно, кроме того, закон распределения статистики ![]() зависит: 1) от действительного (но неизвестного нам) закона распределения случайной величины, измерения которой осуществляются (им определяются эмпирические частоты
зависит: 1) от действительного (но неизвестного нам) закона распределения случайной величины, измерения которой осуществляются (им определяются эмпирические частоты ![]() ) ; 2) от количества произведенных наблюдений (от числа n) и от способа разбиения числовой оси на промежутки (в частности, от числа i ); 3) от теоретического (выдвинутого в качестве гипотезы) закона распределения изучаемой случайной величины (им определяются теоретические вероятности pi
и теоретические частоты
) ; 2) от количества произведенных наблюдений (от числа n) и от способа разбиения числовой оси на промежутки (в частности, от числа i ); 3) от теоретического (выдвинутого в качестве гипотезы) закона распределения изучаемой случайной величины (им определяются теоретические вероятности pi
и теоретические частоты ![]() = n×pi
)
= n×pi
)
![]()
![]() Если выдвинутая гипотеза верна, то очевидно, закон распределения статистики
Если выдвинутая гипотеза верна, то очевидно, закон распределения статистики ![]() зависти только от закона распределения изучаемой случайной величины, от числа n и от выбора промежутков разбиения. Но на самом же деле, в этом случае (благодаря мастерски подобранному Пирсоном выражению для
зависти только от закона распределения изучаемой случайной величины, от числа n и от выбора промежутков разбиения. Но на самом же деле, в этом случае (благодаря мастерски подобранному Пирсоном выражению для ![]() ) справедливо куда более серьезное утверждение. А именно, при достаточно больших n закон распределения статистики
) справедливо куда более серьезное утверждение. А именно, при достаточно больших n закон распределения статистики ![]() практически не зависит от закона распределения изучаемой случайной величины и ни от количества n произведенных опытов: при
практически не зависит от закона распределения изучаемой случайной величины и ни от количества n произведенных опытов: при ![]() распределение статистики
распределение статистики ![]() стремится к
стремится к ![]() - распределению с
r степенями свободы.
Эта теорема объясняет, почему статистика Пирсона обозначается через
- распределению с
r степенями свободы.
Эта теорема объясняет, почему статистика Пирсона обозначается через ![]() .
.
Если в качестве предполагаемого выбрано одно их трех основных непрерывных распределений (нормальное, показательное или равномерное), то r = i – 3, где i – количество промежутков, на которые разбита числовая ось (количество групп опытных данных). В общем случае
![]()
где ![]() - количество параметров предполагаемого (теоретического) распределения, которые заменены вычисленными по опытным данным оценками.
- количество параметров предполагаемого (теоретического) распределения, которые заменены вычисленными по опытным данным оценками.
Т.е. в данном варианте после группировки исходных данных получаем количество промежутков разбиения i = 10, ![]() = 2, т.к. количество параметров предполагаемого (теоретического) распределения, которые заменены вычисленными по опытным данным оценками, = 2 – это а
и s для нормального распределения.
= 2, т.к. количество параметров предполагаемого (теоретического) распределения, которые заменены вычисленными по опытным данным оценками, = 2 – это а
и s для нормального распределения.
Следовательно
R=i-Nпар -1=10-2-1=7
5.5. Правило проверки гипотезы о законе распределения случайной величины.
Ранее отмечалось (и этот факт очевиден), что статистика ![]() принимает только не отрицательные значения (всегда c2
³0), причем в нуль она обращается в одном – единственном случае – при совпадении всех соответствующих эмпирических и теоретических частот (т.е. при
принимает только не отрицательные значения (всегда c2
³0), причем в нуль она обращается в одном – единственном случае – при совпадении всех соответствующих эмпирических и теоретических частот (т.е. при ![]() для каждого i).
для каждого i).
Если выдвинутая гипотеза о законе распределения изучаемой случайной величины соответствует действительности, то эмпирические и теоретические частоты должны быть примерно одинаковы, а значит, значения статистики ![]() будут группироваться около нуля. Если же выдвинутая гипотеза ложна, то эмпирические и соответствующие теоретические частоты будут существенно разниться, что приведет к достаточно большим отклонениям от нуля значений
будут группироваться около нуля. Если же выдвинутая гипотеза ложна, то эмпирические и соответствующие теоретические частоты будут существенно разниться, что приведет к достаточно большим отклонениям от нуля значений ![]() .
.
Поэтому хотелось бы найти тот рубеж – называемый критическим значением
(или критической точкой) и обозначаемый через ![]() , который разбил бы всю область возможных значений статистики
, который разбил бы всю область возможных значений статистики ![]() на два непересекающихся подмножества: область принятия гипотезы,
характеризующаяся неравенством
на два непересекающихся подмножества: область принятия гипотезы,
характеризующаяся неравенством ![]() , и критическую область
(или область отвержения гипотезы), определяемую неравенством
, и критическую область
(или область отвержения гипотезы), определяемую неравенством ![]() .
.
Область принятия Критическая область
гипотезы
0 ![]()
![]()
Как же найти критическое значение ![]() ?
?
Если выдвинутая гипотеза о законе распределения изучаемой случайной величины верна, то вероятность попадания значений статистики ![]() в критическую область должна быть мала, так что событие {
в критическую область должна быть мала, так что событие {![]() } должно быть практически неосуществимым в единичном испытании. Эта вероятность, обозначим ее через
} должно быть практически неосуществимым в единичном испытании. Эта вероятность, обозначим ее через ![]() :
:
![]()
называется уровнем значимости.
Чтобы определить критическое значение ![]() , поступим следующим образом. Зададим какое – либо малое значение уровня значимости
, поступим следующим образом. Зададим какое – либо малое значение уровня значимости ![]() (как правило
(как правило![]() = 0,05 или
= 0,05 или![]() = 0,01) и найдем
= 0,01) и найдем ![]() как уровень уравнения
как уровень уравнения
![]()
с неизвестной x. Поскольку распределение статистики ![]() близко при
близко при ![]() к
к ![]() - распределению с r степенями свободы, то
- распределению с r степенями свободы, то
![]()
![]()
и приближенное значение![]() можно найти из уравнения
можно найти из уравнения
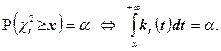
Геометрические соображения показывают, что последнее уравнение имеет единственное решение: его корень – это такое число x>0, при котором площадь под графиком функции ![]() (плотности
(плотности![]() - распределения) над участком
- распределения) над участком ![]() равна. На практике решение последнего уравнения находят с помощью специальных таблиц, имеющихся в любом руководстве по математической статистике; эти таблицы позволяют по двум входным параметрам – уровню значимости
равна. На практике решение последнего уравнения находят с помощью специальных таблиц, имеющихся в любом руководстве по математической статистике; эти таблицы позволяют по двум входным параметрам – уровню значимости ![]() и числу степеней свободы r определить критическое значение
и числу степеней свободы r определить критическое значение ![]() . (Находимое таким образом критическое значение зависит, конечно, от
. (Находимое таким образом критическое значение зависит, конечно, от ![]() и r,что при необходимости отражают и в обозначениях:
и r,что при необходимости отражают и в обозначениях: ![]() ).
).
Зададим уровень значимости как ![]() = 0,05
(условие курсовой работы) .
= 0,05
(условие курсовой работы) .
Подводя итоги, сформулируем правило проверки гипотезы
о законе распределения случайной величины с помощью ![]() - критерия Пирсона:
- критерия Пирсона:
1) Проводят n независимых наблюдений случайной величины (принято считать, что должно быть n³ 100).
2) Разбивают всю числовую ось на несколько (как правило, на 8…12) промежутков
![]()
так, чтобы количество измерений в каждом из них (называемое эмпирической
частотой ![]() ) оказалось не менее пяти (т.е.
) оказалось не менее пяти (т.е. ![]() ³ 5 при каждом i).
³ 5 при каждом i).
3) Выдвигают (например, судя по профилю гистограммы) гипотезу о законе распределения изучаемой случайной величины и находят параметры этого закона (чаще всего, заменяя математическое ожидание и дисперсию их оценками).
4) С помощью предполагаемого (теоретического) распределения находят теоретические вероятности pi
и теоретические частоты ![]() = n×pi
попадания значений случайной величины в i-й промежуток.
= n×pi
попадания значений случайной величины в i-й промежуток.
5) По эмпирическим и теоретическим частотам вычисляют значения статистики ![]() , обозначаемое через c2
набл.
.
, обозначаемое через c2
набл.
.
6) Определяют число r степеней свободы.
7) Используя заданное значение уровня значимости ![]() и найденное число степеней свободы r, по таблице находят (на пересечении строки, отвечающей r, и столбца, отвечающего
и найденное число степеней свободы r, по таблице находят (на пересечении строки, отвечающей r, и столбца, отвечающего ![]() ) критическое значение
) критическое значение ![]() .
.
8) Формулируя вывод, опираясь на основной принцип проверки статистических гипотез :
если наблюдаемое значение критерия принадлежит критической области, т.е. если ![]() , то гипотезу отвергают как плохо согласующуюся с результатами эксперимента;
, то гипотезу отвергают как плохо согласующуюся с результатами эксперимента;
если наблюдаемое значение критерия принадлежит области принятия гипотезы, т.е. ![]() , то гипотезу принимают как не противоречащую результатам эксперимента.
, то гипотезу принимают как не противоречащую результатам эксперимента.
5.6. Вывод о соответствии выдвинутой гипотезы и опытных данных в варианте.
Правило проверки выдвинутой гипотезы о законе распределения изучаемой случайной величины для данного варианта реализовано в таблице:
| Название величины | Обозначение и числовое значение величины |
| Уровень значимости (задан в условии) | |
| Количество промежутков разбиения | l =10 |
| Число степеней свободы | r=7 |
| Критическое значение (находится по таблице) | |
| Наблюдаемое значение критерия | c2 набл. = 0,85 |
| ВЫВОД | Гипотеза не принимается для данного 9 варианта, поскольку |
Замечания: 1. Заданное значение уровня значимости ![]() = 0,05 означает, что
= 0,05 означает, что
![]() ,
,
т.е. вероятность события {![]() } очень мала. Однако это событие, обладая ненулевой вероятностью, и тогда (при
} очень мала. Однако это событие, обладая ненулевой вероятностью, и тогда (при ![]() = 0,05 примерно в 5% случаев) будет отвергнута правильная гипотеза. Отвержение гипотезы, когда она верна, называется ошибкой первого рода.
Таким образом, уровень значимости
= 0,05 примерно в 5% случаев) будет отвергнута правильная гипотеза. Отвержение гипотезы, когда она верна, называется ошибкой первого рода.
Таким образом, уровень значимости ![]() - это вероятность ошибки первого рода. Отметим, что ошибкой второго рода
называется принятие гипотезы в случае, когда она неверна.
- это вероятность ошибки первого рода. Отметим, что ошибкой второго рода
называется принятие гипотезы в случае, когда она неверна.![]()
2. Иногда вместо уровня значимости ![]() задается надежность
задается надежность
![]() :
:
![]()
т.е. ![]() - это вероятность попадания значений статистики
- это вероятность попадания значений статистики ![]() в область принятия гипотезы. Поскольку события
в область принятия гипотезы. Поскольку события
{![]() } и
} и ![]()
противоположны, то
![]()
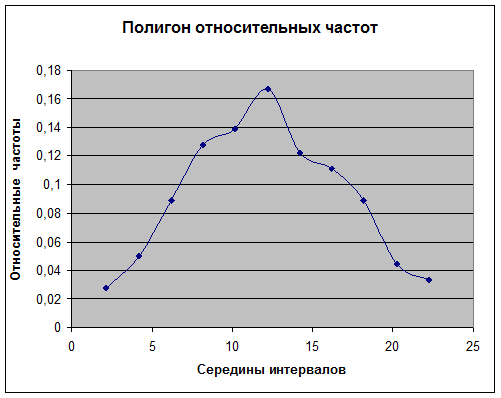 Гистограмма.
Гистограмма.