| Скачать .docx | Скачать .pdf |
Реферат: Линии второго порядка
СОДЕРЖАНИЕ
1. Линии второго порядка на евклидовой плоскости.
2. Инварианты уравнений линий второго порядка.
3. Определение вида линий второго порядка по инвариантам ее уравнения.
4. Линии второго порядка на аффинной плоскости. Теорема единственности.
5. Центры линий второго порядка.
6. Асимптоты и диаметры линий второго порядка.
7. Привидение уравнений линий второго порядка к простейшему.
8. Главные направления и диаметры линий второго порядка.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. Линии второго порядка в евклидовой плоскости.
Определение:
Евклидова плоскость
– это пространство размерности 2, ![]() (двумерное вещественное пространство).
(двумерное вещественное пространство).
Линии второго порядка представляют собой линии пересечения кругового конуса с плоскостями, не проходящими через его вершину.
Эти линии часто встречаются в различных вопросах естествознания. Например, движение материальной точки под воздействием центрального поля силы тяжести происходит по одной из этих линий.
Если секущая плоскость пересекает все прямолинейные образующие одной полости конуса, то в сечении получится линия, называемая эллипсом (рис. 1.1,а). Если секущая плоскость пересекает образующие обеих полостей конуса, то в сечении получится линия, называемая гиперболой (рис. 1.1,6). И, наконец, если секущая плоскость параллельна одной из образующих конуса (на 1.1, в — это образующая АВ), то в сечении получится линия, называемая параболой. Рис. 1.1 дает наглядное представление о форме рассматриваемых линий.
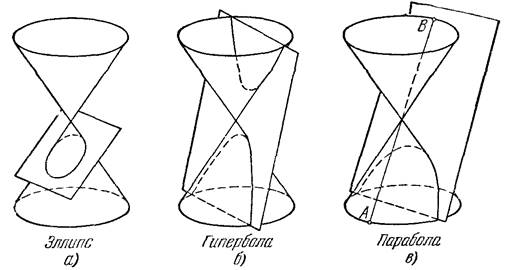
Рисунок 1.1
Общее уравнение линии второго порядка имеет следующий вид:
![]() (1)
(1)
или
![]() (1*)
(1*)
Эллипсом называется множесво точек плоскости, для которых сумма расстояний до двух фиксированных точек F 1 и F 2 этой плоскости, называемых фокусами, есть величина постоянная.
При этом не исключается совпадение фокусов эллипса. Очевидно, если фокусы совпадают, то эллипс представляет собой окружность.
Для вывода канонического уравнения эллипса выберем начало О декартовой системы координат в середине отрезка F 1 F 2 , а оси Ох и Оу направим так, как указано на рис. 1.2 (если фокусы F 1 и F 2 совпадают, то О совпадает с F 1 и F 2 , а за ось Ох можно взять любую ось, проходящую через О).
Пусть длина отрезка F 1 F 2 равна 2с. Тогда в выбранной системе координат точки F 1 и F 2 соответственно имеют координаты (-с, 0) и (с, 0). Обозначим через 2а постоянную, о которой говорится в определении эллипса. Очевидно, 2а > 2с, т. е. а > с ( Если М — точка эллипса (см. рис. 1.2), то | MF ] |+ | MF 2 | = 2 a , а так как сумма двух сторон MF 1 и MF 2 треугольника MF 1 F 2 больше третьей стороны F 1 F 2 = 2c, то 2а > 2с. Случай 2а = 2с естественно исключить, так как тогда точка М располагается на отрезке F 1 F 2 и эллипс вырождается в отрезок.).
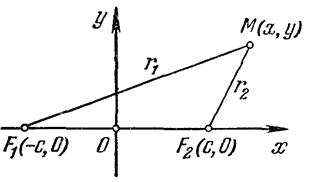 Пусть М
— точка плоскости с координатами (х, у)
(рис. 1.2). Обозначим через r1
и r2
расстояния от точки М
до точек F
1
и F
2
соответственно. Согласно определению эллипса равенство
Пусть М
— точка плоскости с координатами (х, у)
(рис. 1.2). Обозначим через r1
и r2
расстояния от точки М
до точек F
1
и F
2
соответственно. Согласно определению эллипса равенство
Рис. 1.2
r 1 + r 2 = 2а (1.1)
является необходимым и достаточным условием расположения точки М (х, у) на данном эллипсе.
Используя формулу расстояния между двумя точками, получим
![]() (1.2)
(1.2)
Из (1.1) и (1.2) вытекает, что соотношение
![]() (1.3)
(1.3)
представляет собой необходимое и достаточное условие расположения точки М с координатами х и у на данном эллипсе. Поэтому соотношение (1.3) можно рассматривать как уравнение эллипса. Путем стандартного приема «уничтожения радикалов» это уравнение приводится к виду
![]() (1.4)
(1.4)
где
![]() (1.5)
(1.5)
Так как уравнение (1.4) представляет собой алгебраическое следствие
уравнения эллипса (1.3), то координаты х и у
любой точки М
эллипса будут удовлетворять и уравнению (1.4). Поскольку при алгебраических преобразованиях, связанных с избавлением от радикалов, могли появиться «лишние корни», мы должны убедиться в том, что любая точка М,
координаты которой удовлетворяют уравнению (1.4), располагается на данном эллипсе. Для этого, очевидно, достаточно доказать, что величины r1
и r2
для каждой точки удовлетворяют соотношению (1.1). Итак, пусть координаты х
и у
точки М
удовлетворяют уравнению (1.4). Подставляя значение у2
из (1.4) в правую часть выражения (1.2) для г1
после несложных преобразований найдем, что ![]() , тогда
, тогда
![]() .
.
Совершенно аналогично найдем, что ![]() .
Таким образом, для рассматриваемой точки М
.
Таким образом, для рассматриваемой точки М
![]() ,
, ![]() (1.6)
(1.6)
т. е.r 1 + r 2 = 2а, и поэтому точка М располагается на эллипсе. Уравнение (1.4) называется каноническим уравнением эллипса. Величины а и b называются соответственно большой и малой полуосями эллипса (наименование «большая» и «малая» объясняется тем, что а>Ь).
Замечание . Если полуоси эллипса а и b равны, то эллипс представляет собой окружность, радиус которой равен R = a = b , а центр совпадает с началом координат.
Гиперболой называется множество точек плоскости, для которых абсолютная величина разности расстояний до двух фиксированных точек, F 1 и F 2 этой плоскости, называемых фокусами, есть величина постоянная ( Фокусы F 1 и F 2 гиперболы естественно считать различными, ибо если указанная в определении гиперболы постоянная не равна нулю, то нет ни одной точки плоскости при совпаденииF 1 и F 2 , которая бы удовлетворяла требованиям определения гиперболы. Если же эта постоянная равна нулю и F 1 совпадает с F 2 , то любая точка плоскости удовлетворяет требованиям определения гиперболы.).
Для вывода канонического уравнения гиперболы выберем начало координат в середине отрезка F 1 F 2 , а оси Ох и Оу направим так, как указано на рис. 1.2. Пусть длина отрезка F 1 F 2 равна 2с. Тогда в выбранной системе координат точки F 1 и F 2 соответственно имеют координаты (-с, 0) и (с, 0) Обозначим через 2а постоянную, о которой говорится в определении гиперболы. Очевидно, 2a< 2с, т. е. a < с.
Пусть М — точка плоскости с координатами (х, у) (рис. 1,2). Обозначим через r1 и r2 расстояния MF 1 и MF 2 . Согласно определению гиперболы равенство
![]() (1.7)
(1.7)
является необходимым и достаточным условием расположения точки М на данной гиперболе.
Используя выражения (1.2) для r1 и r2 и соотношение (1.7), получим следующее необходимое и достаточное условие расположения точки М с координатами х и у на данной гиперболе:
![]() .
(1.8)
.
(1.8)
Используя стандартный прием «уничтожения радикалов», приведем уравнение (1.8) к виду
![]() (1.9)
(1.9)
где
![]() (1.10)
(1.10)
Мы должны убедиться в том, что уравнение (1.9), полученное путем алгебраических преобразований уравнения (1.8), не приобрело новых корней. Для этого достаточно доказать, что для каждой точки М, координаты х и у которой удовлетворяют уравнению (1.9), величины r1 и r2 удовлетворяют соотношению (1.7). Проводя рассуждения, аналогичные тем, которые были сделаны при выводе формул (1.6), найдем для интересующих нас величин r1 и r2 следующие выражения:
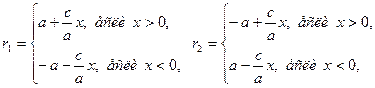 (1.11)
(1.11)
Таким образом, для рассматриваемой точки М
имеем ![]() ,
и поэтому она располагается на гиперболе.
,
и поэтому она располагается на гиперболе.
Уравнение (1.9) называется каноническим уравнением гиперболы. Величины а и b называются соответственно действительной и мнимой полуосями гиперболы.
Параболой называется множество точек плоскости, для которых расстояние до некоторой фиксированной точки F этой плоскости равно расстоянию до некоторой фиксированной прямой, также расположенной в рассматриваемой плоскости.
Указанная в определении точка F называется фокусом параболы, а фиксированная прямая — директрисой (направляющая) параболы.
Для вывода канонического уравнения параболы выберем начало О декартовой системы координат в середине отрезка FD
,
представляющего собой перпендикуляр, опущенный из фокуса F
на директрису (Естественно считать, что фокус F
не лежит на директрисе, ибо в противном случае точки плоскости, для которых были бы выполнены условия определения параболы, располагались на прямой, проходящей через F
перпендикулярно директрисе, т. е. парабола выродилась бы в прямую), а оси Ох и Оу
направим так, как указано на рис. 1.3. Пусть длина отрезка FD
равна р.
Тогда в выбранной системе координат точка F
имеет координаты (![]() ). Пусть М
— точка плоскости с координатами (х, у).
Обозначим через r
расстояние от М
до F
,
а через d
— расстояние от М
до директрисы (рис. 1.3). Согласно определении параболы равенство
r
=
d
(1.12) является необходимым и достаточным условием расположения точки М на-данной параболе.
). Пусть М
— точка плоскости с координатами (х, у).
Обозначим через r
расстояние от М
до F
,
а через d
— расстояние от М
до директрисы (рис. 1.3). Согласно определении параболы равенство
r
=
d
(1.12) является необходимым и достаточным условием расположения точки М на-данной параболе.
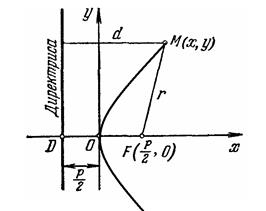 рис 1.3
рис 1.3
Так как
![]() (1.13)
(1.13)
(эта формула верна лишь для точек с неотрицательными абсциссами х. Для точек с отрицательными абсциссами, как легко видеть, выполняется соотношение г > d , и поэтому такие точки можно исключить из рассмотрения) то, согласно (1.12), соотношение
![]() (1.14)
(1.14)
представляет собой необходимое и достаточное условие расположения точки М с координатами х и у на данной параболе. Поэтому соотношение (1.14) можно рассматривать как уравнение параболы. Путем стандартного приема «уничтожения радикалов» это уравнение приводится к виду
![]() (1.15)
(1.15)
Убедимся в том, что уравнение (6.15), полученное путем алгебраических преобразований уравнения (1.14), не приобрело новых корней. Для этого достаточно доказать, что для каждой точки М, координаты х и у которой удовлетворяют уравнению (1.15), величины r и d равны (выполнено соотношение (1.12)).
Из соотношения (1.15) вытекает, что абсциссы х
рассматриваемых точек неотрицательны, т. е. ![]() . Для точек с неотрицательными абсциссами
. Для точек с неотрицательными абсциссами ![]() . Найдем теперь выражение для расстояния r
от точки М
до F
.
Подставляя у2
из выражения (1.15) в правую часть выражения для r
(1.13) и учитывая, что
. Найдем теперь выражение для расстояния r
от точки М
до F
.
Подставляя у2
из выражения (1.15) в правую часть выражения для r
(1.13) и учитывая, что ![]() ,
найдем, что
,
найдем, что ![]() .
Таким образом, для рассматриваемых точек r
=
d
,
т. е. они располагаются на параболе.
.
Таким образом, для рассматриваемых точек r
=
d
,
т. е. они располагаются на параболе.
Уравнение (1.15) называется каноническим уравнением параболы. Величина р называется параметром параболы.
Пример 1.1
. Установить вид кривой второго порядка, заданной уравнением ![]() .
.
Решение
: Предложенное уравнение определяет эллипс ![]() . Действительно, проделаем следующие преобразования:
. Действительно, проделаем следующие преобразования:
![]()
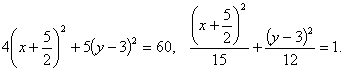
Получилось каноническое уравнение эллипса с центром в ![]() и полуосями
и полуосями ![]() и
и ![]() .
.
Пример 1.2 . Установить вид кривой второго порядка, заданной уравнением x2 + 10х - 2у + 11 = 0.
Решение : Указанное уравнение определяет параболу (С = 0). Действительно,
![]()
![]() .
.
Получилось каноническое уравнение параболы с вершиной в точке ![]() и
и ![]() .
.
2. Инварианты уравнений линий второго порядка.
Назовем инвариантом уравнения (1) линии второго порядка относительно преобразований декартовой системы координат такую функцию f ( a 11 , a 12 , ..., а33 ) от коэффициентов а in этого уравнения, значения которой не меняются при переходе к новой декартовой прямоугольной системе координат. Таким образом, если f ( a 11 , a 12 , ..., а33 ) инвариант и а’ ij - коэффициенты уравнения линии второго порядка в новой системе декартовых координат, то
f(a11 , a12 , ..., а 33 )= f(a’11 , a’12 , ..., а ’33 )
Теорема : Величины
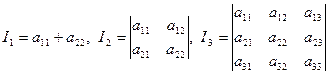 (2.1)
(2.1)
являются инвариантами уравнения (1) линии второго порядка относительно преобразований декартовой системы координат.
Доказательство .
Очевидно, инвариантность величин ![]() достаточно доказать отдельно для параллельного переноса системы координат и для поворота
достаточно доказать отдельно для параллельного переноса системы координат и для поворота
Рассмотрим сначала параллельный перенос системы координат. При этом преобразовании координат коэффициенты группы старших членов не изменяются. Поэтому не изменяются и величины ![]() .
Займемся величиной
.
Займемся величиной ![]() . В новой системе координат О'х'у'
величина
. В новой системе координат О'х'у'
величина ![]() равна
равна
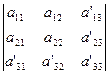 (2.2)
(2.2)
Вычитая из последней строки этого определителя первую строку, умноженную на х0 , и вторую, умноженную на у0 (х0 и у0 — координаты нового начала О'), и используя при этом выражения для а’13 и а’23 из формул параллельного переноса
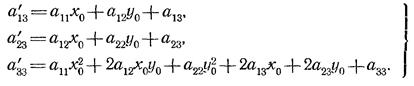 (2.3)
(2.3)
где ![]()
найдем, что этот определитель равен:
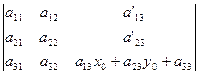
Если теперь вычесть из последнего столбца полученного определителя первый столбец, умноженный на х0
,
и второй, умноженный на y
о
, и использовать при этом выражения для а'13
и а'23
из формул (2.3), то в результате получится определитель, стоящий в правой части выражения для ![]() в формулах (2.1). Итак, инвариантность
в формулах (2.1). Итак, инвариантность ![]() при параллельном переносе системы координат доказана.
при параллельном переносе системы координат доказана.
Рассмотрим теперь поворот декартовой системы координат. При этом преобразовании коэффициенты а’ ij уравнения линии L в новой системе связаны с коэффициентами а ij уравнения этой линии в старой системе с помощью формул
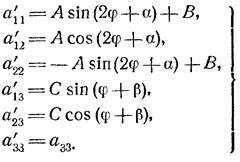 (2.4)
(2.4)
Докажем теперь инвариантность ![]() . Имеем, согласно (2.4):
. Имеем, согласно (2.4):
![]()
Таким образом, инвариантность ![]() доказана. Обратимся теперь к
доказана. Обратимся теперь к
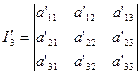
Разлагая этот определитель по элементам последнего столбца, учитывая только что доказанную инвариантность ![]() , т. е. равенство
, т. е. равенство
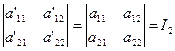
и равенство а'33 = а33 , получим
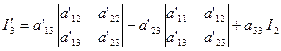 (2.5)
(2.5)
Согласно формулам (2.4) первое слагаемое в правой части (2.5) может быть преобразовано следующим образом:
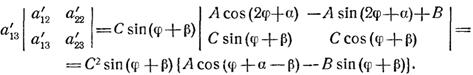 (2.6)
(2.6)
Совершенно аналогично получается равенство а'23
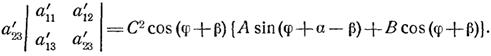 (2.7)
(2.7)
Из соотношений (2.6) — (2.7) получаем
![]() (2.8)
(2.8)
Так как величины А, В,
С
, углы ![]() не зависят от угла
не зависят от угла ![]() (эго вытекает из инвариантности
(эго вытекает из инвариантности ![]() ), то из (2.8) следует, что
), то из (2.8) следует, что ![]() так же не зависит от угла
так же не зависит от угла ![]() , т. е. при любом значении
, т. е. при любом значении ![]() имеет одно и то же значение. Но а'
ij
= а
ij
при
имеет одно и то же значение. Но а'
ij
= а
ij
при ![]() =0, и поэтому
=0, и поэтому ![]() .Таким образом, инвариантность
.Таким образом, инвариантность ![]() также установлена. Теорема доказана.
также установлена. Теорема доказана.
3. Определение вида линий второго порядка по инвариантам ее уравнения.
Введем следующие обозначения:
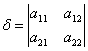

![]()
Тогда
| № | Название линии | Признаки | Наличие центра | |
| типа | класса | |||
| 1 | эллипс | точка | ||
| 2 | мнимый эллипс | |||
| 3 | точка | |||
| 4 | гипербола | |||
| 5 | 2 пересекающиеся прямые | |||
| 6 | Парабола | центра нет | ||
| 7 | 2 параллельные. прямые |
|
бесконечно много центров | |
| 8 | 2 мнимые параллельные прямые |
|
||
| 9 | 2 совпадающие прямые | |||
Пример 3.1 : Определение зависимости типа данной кривой (3.1) от параметра b с помощью инвариантов
![]() (3.1)
(3.1)
Для уравнения кривой второго порядка (3.1) имеем:
![]()
Вычислим инварианты кривой
![]() .
.
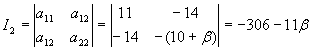 .
.
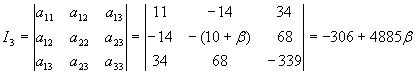 .
.
В соответствии с классификацией кривых второго порядка:
Если I 2 = 0, то уравнение (3.1) определяет кривую параболического типа.
Но I
2
= -306-11b
, следовательно, если ![]() , то уравнение (1) определяет кривую параболического типа.
, то уравнение (1) определяет кривую параболического типа.
Но при этом ![]() , следовательно, если
, следовательно, если ![]() , то уравнение (1) определяет параболу.
, то уравнение (1) определяет параболу.
Если I
2
¹ = 0, то данная кривая – центральная. Следовательно, при ![]() данная кривая – центральная.
данная кривая – центральная.
Если I
2
> 0, то уравнение (1) определяет кривую эллиптического типа. Следовательно, если ![]() , то данная кривая есть кривая эллиптического типа. Но при этом I
1
I
3
= (1-b
)(4885b
-306) < 0, и в соответствии с признаками кривых второго порядка (I
2
> 0, I
1
I
3
< 0) получим, что если
, то данная кривая есть кривая эллиптического типа. Но при этом I
1
I
3
= (1-b
)(4885b
-306) < 0, и в соответствии с признаками кривых второго порядка (I
2
> 0, I
1
I
3
< 0) получим, что если ![]() , то уравнение (1) определяет эллипс.
, то уравнение (1) определяет эллипс.
Если I
2
< 0, то уравнение (1) определяет кривую гиперболического типа. Следовательно, если ![]() , то уравнение (1) определяет кривую гиперболического типа.
, то уравнение (1) определяет кривую гиперболического типа.
Если I 2 < 0 и I 3 = 0, то уравнение (1) определяет две пересекающиеся прямые. Получим:
Следовательно, если ![]() , то уравнение (1) определяет две пересекающиеся прямые.
, то уравнение (1) определяет две пересекающиеся прямые.
Если I
2
< 0 и I
3
¹ 0, то данная кривая – гипербола. Но I
3
¹ 0 при всех ![]() за исключением точки
за исключением точки ![]() . Следовательно, если
. Следовательно, если ![]() , то уравнение (1) определяет гиперболу. Используя полученные результаты, построимтаблицу:
, то уравнение (1) определяет гиперболу. Используя полученные результаты, построимтаблицу:
| Значение парамет-ра b | |||||
| Тип кривой | Эллипс | Парабола | Гипербола | Две пересекающиеся прямые | Гипербола |
4. Линии второго порядка на аффинной плоскости. Теорема единственности.








5. Центры линий второго порядка.
Центром некоторой линии называется такая точка плоскости, по отношению к которой точки этой линии расположены симметрично парами. Линии второго порядка, обладающие единственным центром, называются центральными.
Точка S (х0 ; уа ) является центром линии, определяемой уравнением (1*) в том и только в том случае, когда её координаты удовлетворяют уравнениям:
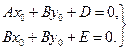 (5.1)
(5.1)
Обозначим через ![]() определитель этой системы:
определитель этой системы:
![]() .
.
Величина ![]() составляется из коэффициентов при старших членах уравнения (1*) и называется дискриминантом старших членов этого уравнения.
составляется из коэффициентов при старших членах уравнения (1*) и называется дискриминантом старших членов этого уравнения.
Если ![]() ¹ 0, то система (5.1) является совместной и определённой, т. е. имеет решение и притом единственное. В этом случае координаты центра могут быть определены по формулам:
¹ 0, то система (5.1) является совместной и определённой, т. е. имеет решение и притом единственное. В этом случае координаты центра могут быть определены по формулам:
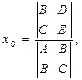
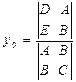
Неравенство ![]() ¹0 служит признаком центральной линии второго порядка.
¹0 служит признаком центральной линии второго порядка.
Если S (х0 , у0 ) — центр линии второго порядка, то в результате преобразования координат по формулам
![]()
![]()
(что соответствует переносу начала координат в центр линии) её уравнение примет вид
![]() ,
,
где А, В, С —
те же, что в данном уравнении (1*), а ![]() определяется формулой
определяется формулой
![]()
В случае ![]() ¹ 0 имеет место также следующая формула:
¹ 0 имеет место также следующая формула:
![]()
Где
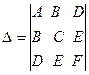 .
.
Определитель D называется дискриминантом левой части общего уравнения второй степени.
6. Асимптоты и диаметры линий второго порядка.
Асимптоты.
(от греч. слов: α, συν, πίπτω) — несовпадающая. Под асимптотой подразумевается такая линия, которая, будучи неопределенно продолжена, приближается к данной кривой линии или к некоторой ее части так, что расстояние между обеими линиями делается менее всякой данной величины; иначе говоря, А. касается данной кривой линии на бесконечном расстоянии от начала координат. Всякая другая линия, параллельная А., хотя и приближается непрестанно к кривой, однако, не может быть названа в свою очередь А., так как расстояние ее от кривой не может быть уменьшено по произволению. Таким образом, число А. для каждой кривой вполне ограничено. С тех пор как греческие геометры стали исследовать свойство кривых линий, образующихся на поверхности конуса от пересечения его плоскостью, стало известным, что ветви гиперболы, будучи неопределенно продолжены, непрестанно сближаются с двумя прямыми линиями, исходящими из центра гиперболы и одинаково наклоненными к ее оси. Эти прямые, о которых упоминает уже Архимед, были еще в древности названы А. и сохранили свое название и по настоящее время. Впоследствии Ньютон показал, что существуют криволинейные А. не только в кривых трансцендентных, но даже в алгебраических, начиная с 3 порядка последних. Действительно, ныне различают А. прямолинейные и криволинейные; но обыкновенно прямолинейной А. присваивают название Асимп., называя криволинейную — асимптотическою кривою. Основываясь на вышеприведенном определении, что прямолинейная А. есть касательная к кривой в точке, бесконечно удаленной от начала координат, легко найти уравнение А. данной кривой. В самом деле, пусть y = f(x) есть уравнение кривой линии; уравнение касательной ее в точке, определенной координатами х и у, будет, как известно, У— у = dy/dx(Х — х) или Y = (dy/dx)Х + у — x(dy/dx). Чтобы перейти от касательной к А., стоит сделать одно из следующих предположений: 1) x и y = ±∞, 2) х = ±∞, а у = конечному числу и 3) у = +∞, а х = конечному числу, так как этими предположениями мы выражаем, что точка касания находится на бесконечном расстоянии от начала координат. Так, для гиперболы, определяемой уравнением (x2 /a2 ) — (y2 /b2 ) = 1 находим Y = ±(b/a)∙[x/√(x2 — a2 )]∙X ± [ab/√(x2 — a2 )]. Полагая х = ∞, найдем ±(b/a) — [x//√(x2 — a2 )] = ±(b/a)∙[1/√(1 — a2 / x2 )] = ±(b/a), и ±[ab//√(x2 — a2 )] = 0; следовательно, уравнение А. рассматриваемой гиперболы будет У = ±(b/a)Х или, что все равно, Y = +(b/a)X и Y = -(b/a)X; последние два уравнения показывают, что гипербола имеет две А. Можно также определить А. следующим образом. Пусть будет У А. = Х + В уравнение А., не параллельной оси у. Ордината у кривой, соответствующая абсциссе x, для весьма больших величин сей абсциссы будет очень мало разниться от ординаты У а-ты, так что можно ее принять у = Ах + В ± ε, подразумевая под ε количество, уничтожающееся вместе с 1/x. Итак, полагая x = ∞, найдем пред. (Y/X) = пред.
![]()
и пред. (у — Ах) = пред. (В ± ε) = В. Следовательно, для определения постоянного количества стоит только в уравнении кривой положить Y/X = q или y = xq и сыскать предел, к которому стремится q для бесконечно больших значений х. Величина В определится, если в уравнении кривой примем у — Ах = ν, или у = Ах + ν. Изменив х на у и наоборот и рассуждая так же, как и выше, найдем А., не параллельные оси х. Так, например, уравнение рассмотренной нами гиперболы через подстановку qx вместо у дает a2 /x2 — q2 x2 /b2 = 1 или q2 = b2 /a2 — b2 /x2 ; полагая х = ∞, найдем q2 = b2 /a2 , или q = ±(b/a)A. Полагая в том же уравнении y = Ax + ν = +(b/a)x + ν, получим x2 /a2 — [(±x(b/a) + ν)2 /b2 ] = 1, или ν = ±(b/a)∙[√(x2 — a2 ) — x], где, полагая x = ∞, получим ν = 0 = B; следовательно, уравнение А. предложенной гиперболы будет, как и выше, Y = +(b/a)X, что и требовалось доказать. Бесчисленное множество кривых имеет А.; укажем, кроме упомянутой уже гиперболы, следующие кривые, имеющие А.: конхоида, логарифмическая линия, циссоида, декартов лист и др. Чертежи I, II и III представляют (см.) примеры а-ты: линии KL и MN служат (черт. I) асимптотами нормальной равносторонней гиперболы, получающейся от пересечения поверхности конуса плоскостью, — пересекающимися в точке О, начала координат, под прямыми углами;
линии AF и AG (черт. II) изображают А. частей СВ и CED так называемой пересечной гиперболы.
Змиевидная гипербола DBE (черт. III) имеет асимптотой линию АС.
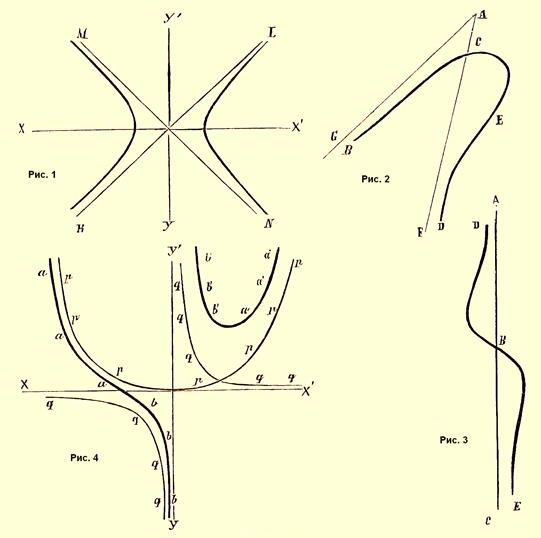
Диаметры.
В курсе аналитической геометрии доказывается, что середины параллельных хорд линии второго порядка лежат на одной прямой. Эта прямая называется диаметром линии второго порядка. Диаметр, делящий пополам какую-нибудь хорду (а значит, и все параллельные ей), называется сопряжённым этой хорде (и всем хордам, которые ей параллельны). Все диаметры эллипса и гиперболы проходят через центр.
Если эллипс задан уравнением
![]() (6.1)
(6.1)
то его диаметр, сопряжённый хордам с угловым коэффициентом k, определяется уравнением:
![]() (6.2)
(6.2)
Если гипербола задана уравнением
![]() (6.3)
(6.3)
то её диаметр, сопряжённый хордам с угловым коэффициентом k , определяется уравнением:
![]() (6.4)
(6.4)
Все диаметры параболы параллельны её оси.
Если парабола задана уравнением
y2 = 2px (6.5)
то её диаметр, сопряжённый хордам с угловым коэффициентом k , определяется уравнением
![]() (6.6)
(6.6)
Если один из двух диаметров эллипса или гиперболы делит пополам хорды, параллельные другому, то второй диаметр делит пополам хорды, параллельные первому. Такие два диаметра называются взаимно сопряжёнными.
Если k и k' — угловые коэффициенты двух взаимно сопряжённых диаметров эллипса (6.1), то
![]() (6.7)
(6.7)
Если k и k' — угловые коэффициенты двух взаимно сопряжённых диаметров гиперболы (6.3), то
![]() (6.8)
(6.8)
Соотношения (6.7) и (6.8) называются условиями сопряжённости диаметров соответственно для эллипса и для гиперболы. Диаметр линии второго порядка, перпендикулярный к сопряжённым хордам, называется главным.
7. Привидение уравнений линий второго порядка к простейшему.
Упрощение общего уравнения кривой второго порядка
Задача упрощения уравнения ![]() или
или
![]() состоит в том, чтобы в преобразованном уравнении были устранены:
состоит в том, чтобы в преобразованном уравнении были устранены:
1) член, содержащий произведение текущих координат,
2) члены, содержащие первые степени двух координат или, по крайней мере, одной из них.
В том случае, когда уравнение линии второго порядка содержит произведение текущих координат, упрощение его следует начинать с поворота осей без изменения начала координат и надлежащим выбором угла поворота добиться того, чтобы из преобразованного уравнения был устранен член, содержащий произведение текущих координат. Преобразование координат в этом случае будем вести по формулам
![]()
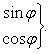 (7.1)
(7.1)
Если после устранения из преобразованного уравнения члена с произведением текущих координат в нем останутся члены с первыми степенями текущих координат, то последующим параллельным переносом осей можно, как это было показано, привести уравнение к каноническому виду.
Координатную систему, полученную в результате поворота первоначальной системы координат, будем обозначать через x1 Oy1 , а систему координат, полученную от параллельного переноса координатной системы x1 Oy1 , - через x2 O1 y2 (см. рис. 7.1)
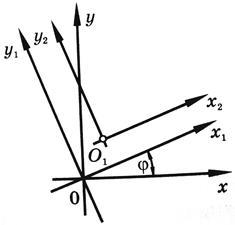
Рисунок 7.1
Упрощение уравнения центральной линии второго порядка
Дано уравнение ![]() , определяющее центральную линию второго порядка (
, определяющее центральную линию второго порядка (![]() = АС — В2
¹
0
). Перенося начало координат в центр S
(х0
;
у0
) этой линии и преобразуя уравнение
= АС — В2
¹
0
). Перенося начало координат в центр S
(х0
;
у0
) этой линии и преобразуя уравнение![]() по формулам:
по формулам:
![]()
![]()
получим;
![]() (7.2)
(7.2)
Для вычисления ![]() можно пользоваться формулой:
можно пользоваться формулой:
![]()
![]()
Или ![]()
Дальнейшее упрощение уравнения (7.2) достигается при помощи преобразования координат
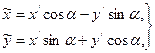 (7.3)
(7.3)
соответствующего повороту осей на угол α.
Если угол α выбран так, что:
![]() (7.4)
(7.4)
то в новых координатах уравнение линии примет вид
![]() (7.5)
(7.5)
где ![]() .
.
Замечание
. Уравнение (7.4) позволяет определить ![]() , тогда как в формулах (3) участвуют
, тогда как в формулах (3) участвуют ![]() и
и ![]() . Зная
. Зная ![]() , можно найти
, можно найти ![]() и
и ![]() по формулам тригонометрии
по формулам тригонометрии
![]()
![]()
Между коэффициентами уравнений (1*) и (7.5) существуют важные соотношения:
![]()
![]() ,
,
которые позволяют определить коэффициенты А' и С', не проводя преобразования координат.
Уравнение второй степени называется эллиптическим, если ![]() > 0, гиперболическим, если
> 0, гиперболическим, если ![]() < 0, и параболическим, если
< 0, и параболическим, если ![]() = 0.
= 0.
Уравнение центральной линии может быть только эллиптическим, или гиперболическим.
Каждое эллиптическое уравнение является уравнением либо обыкновенного эллипса, либо вырожденного эллипса (т. е. определяет единственную точку), либо мнимого эллипса (в этом случае уравнение не определяет никакого геометрического образа).
Каждое гиперболическое уравнение определяет либо обыкновенную гиперболу, либо вырожденную гиперболу (т. е. пару пересекающихся прямых).
Упрощение параболического уравнения.
Пусть уравнение ![]() является параболическим, т. е. удовлетворяет условию
является параболическим, т. е. удовлетворяет условию![]() .
.
В этом случае линия, определяемая уравнением ![]() , либо не имеет центра, либо имеет бесконечно много центров. Упрощение параболического уравнения целесообразно начать с поворота координатных осей, т. е. сначала преобразовать уравнение
, либо не имеет центра, либо имеет бесконечно много центров. Упрощение параболического уравнения целесообразно начать с поворота координатных осей, т. е. сначала преобразовать уравнение ![]() при помощи формул
при помощи формул 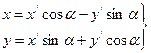 (7.6)
(7.6)
Угол ![]() следует найти из уравнения
следует найти из уравнения ![]() (7.7)тогда в новых координатах уравнение
(7.7)тогда в новых координатах уравнение ![]() приводится либо к виду
приводится либо к виду ![]() (7.8)
(7.8)
где ![]() ,
либо к виду
,
либо к виду ![]() (7.9)
(7.9)
где ![]() .
.
Дальнейшее упрощение уравнений (7.8) и (7.9) достигается путём параллельного перенесения (повёрнутых) осей.
8. Главные направления и диаметры линий второго порядка.









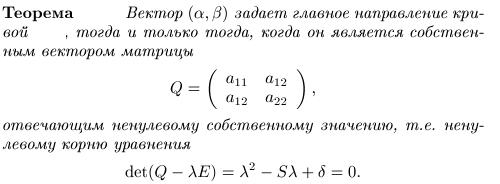



СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. А.П. Веселов, Е.В. Троицкий, Лекции по аналитической геометрии, МГУ, 2002.
2. Д.А. Клетеник, Аналитическая геометрия.
3. П.И. Кузнецов, Лекции по аналитической геометрии МГУ.
4. С.Б. Кадомцев, Аналитическая геометрия и линейная алгебра. Физматлит, 2003
5. В.А. Ильин, Э.Г. Позняк, Аналитическая геометрия.