| Скачать .docx | Скачать .pdf |
Курсовая работа: Курсовая работа: Знаходження власних значеннь лінійого оператора
Міністерство освіти і науки України
ФАКУЛЬТЕТ ІНФОРМАТИКИ
КАФЕДРА ІНФОРМАЦІЙНИХ УПРАВЛЯЮЧИХ СИСТЕМ ТА ТЕХНОЛОГІЙ
Реєстраційний №________
Дата ___________________
КУРСОВА РОБОТА
Тема:
Знаходження власних значень лінійного оператора
Рекомендована до захисту
“____” __________ 2008р.
Робота захищена
“____” __________ 2008р.
з оцінкою
_____________________
Підписи членів комісії
Зміст
Вступ
Теоретична частина
1. Означення і найпростіші властивості лінійних операторів
2. Матриця лінійного оператора
3. Власні вектори й власні значення лінійного оператора
Практична частина
1. Опис програми
2. Текст програми
3. Контрольний приклад
Висновок
Список літератури
Вступ
Власні значення грають при вивченні лінійних операторів дуже велику роль.
Нехай в дійсному лінійному просторі 
задан лінійний оператор 
. Якщо вектор 
, відмінний від нуля, переводиться оператором у вектор, пропорційний самому ,
,
де 
– деяке дійсне число, то вектор називається власним вектором оператора , а число – власним значенням цього оператора, причому, власний вектор відноситься до власного значення .
Обертання евклідової площини навколо початку координат на кут, що не являється кратним 
, є прикладом лінійного оператора, що не має власних векторів. Прикладом іншого випадку є розтягнення площини, при якому всі вектори, що виходять з початку координат, причому всі нульові вектори площини будуть для нього власними; всі вони відносяться до власного значення 5.
Теоретична частина
1. Означення і найпростіші властивості лінійних операторів
В теорії лінійних просторів та її застосування важливу роль відіграють лінійні оператори, які інакше називають лінійними перетвореннями.
Нехай 
– деякий векторний простір над полем 
.
Означення 1.
Вважають, що у векторному просторі задано оператор, якщо вказано правило (закон), за яким кожному вектору 
простору ставиться у відповідність деякий вектор 
цього ж простору. Про цьому вектор називають образом вектора , а називають прообразом вектора .
Як бачимо, оператор у векторному просторі – це функція, множиною відправлення і множиною прибуття якої є простір .
Означення 2.
Оператор 
у векторному просторі називається лінійним, якщо він задовольняє такі умови:
Лінійні оператори в просторі називають також лінійним перетворенням простору .
З означення 2 випливають безпосередньо такі властивості лінійних операторів:
1. Будь-який лінійний оператор у просторі залишає нерухомим нульовий вектор 
цього простору, тобто 
.
2. Всякий лінійний оператор у просторі протилежному вектору – будь-якого вектора , ставить у відповідність вектор, протилежний образу вектора , тобто 
.
3. Кожен лінійний оператор у просторі будь-який лінійний комбінації довільно вибраних векторів 
простору ставить у відповідність лінійну комбінацію (з тими самими коефіцієнтами) образів цих векторів, тобто 
.
2. Матриця лінійного оператора
Нехай – деякий лінійний оператор у просторі 
. Виберемо в який-небудь базис 
. Оператор відображає вектори цього базису в деякі вектори 
. Кожен вектор 
єдиним способом лінійно виражається через вектори базису . Припустимо, що
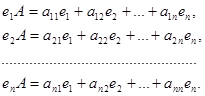
Складемо з коефіціентів 
матрицю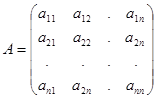 
. Рядками матриці є координатні рядки векторів 
в базисі . Оскльки координатні рядки векторів 
визначені однозначно, то й матриця визначається оператором в базисі 
.
Будемо вважати, що в базисі 
лінійний оператор задається матрицею .
Отже, при зафіксованому базисі кожному лінійному оператору простору відповідає певна квадратна матриця 
-го порядку – матриця цього оператора.
3. Власні вектори й власні значення лінійного оператора
Означення 1.
Підпростір 
лінійного простору називається інваріантним відносно оператора , якщо 
, тобто якщо образ 
будь-якого вектора 
із 
міститься в .
Нехай 
–одновимірний підпростір простору , а 
–деякий лінійний оператор цього простору. Підпростір , як відомо, породжується будь-яким своїм вектором 
, тобто є сукупністю всіх векторів виду 
, де 
– будь яке число з поля Р. Якщо підпростір інваріантний відносно оператора , то 
, тобто 
, де 
–деяке число з поля Р. Тоді й для будь-якого вектора підпростору 
, бо 
, і тому 
.
Означення 2.
Вектор , що заддовільняє співвідношення 
, де 
називається власним вектором оператора , а число 
–
власним значенням оператора , що відповідає власному вектору 
.
Отже, якщо одглвимірний підпростір простору 
інваріантний відносно лінійного оператора , то всі вектори цього підпростору є власними векторами оператора з тим самим власним значенням оператора .
Практична частина
1. Опис програми
n – вимірність матриці;
m – максимальне допустиме число ітерацій;
e – точність;
a – на вході – двовимірний масив елементів матриці А, на виході матриця А блочно-діагональна, причому блоки розміри 1х1 містять дійсні власні значення, блоки розміру 2х2 містять комплексні власні значення, записані в стовпцях (рядках) для правих (лівих) власних векторів;
t – двовимірний масив власних векторів А;
b – цілочислова змінна.
Лінійний оператор потрібно задати за допомогою матриці.
2. Текст програми
uses crt;
const dim=10;
type ar=array[1..dim,1..dim]of real;
var ff:text;
i100,j100,n100,b,m:integer;
e:real;
a,t:ar;
procedure eigen(n,m:integer;e:real;var a,t:ar;var b:integer);
var c,c1,c2,co,ch,d,e1,f,g,h,p,r,s,s1,s2,si,sh,x,y:real;
i,j,k,n1,q:integer;
u,v,w,z:boolean;
function zn(x:real):integer;
begin if x<0 then zn:=-1 else zn:=1; end;
begin
u:=false;v:=u;w:=u;n1:=n-1;e1:=sqrt(e);
if b<>0 then
begin
if b<0 then v:=true else w:=true;
for i:=1 to n do
for j:=1 to n do
if i=j then t[i,j]:=1 else t[i,j]:=0;
end;
for q:=1 to m do
begin
if u then begin b:=1-q; exit; end;
i:=1; z:=false;
repeat
j:=i+1;
repeat
if(abs(a[i,j]+a[j,i])>e1) or
(abs(a[i,j]-a[j,i])>e1) and
(abs(a[i,i]-a[j,j])>e1) then z:=true;
j:=j+1;
until (j>n) or z;
i:=i+1;
until (i>n1) or z;
if not z then begin b:=q-1; exit; end;
u:=true;
for k:=1 to n1 do
for j:=k+1 to n do
begin
h:=0; g:=0; f:=0; y:=0;
for i:=1 to n do
begin
x:=sqr(a[i,k]);d:=sqr(a[i,j]); y:=y+x-d;
if (i<>k) and (i<>j) then
begin
h:=h+a[k,i]*a[j,i]-a[i,k]*a[i,j];
p:=x+sqr(a[j,i]); r:=d+sqr(a[k,i]);
g:=g+p+r; f:=f-p+r;
end;
end;
h:=2*h; d:=a[k,k]-a[j,j];
p:=a[k,j]+a[j,k]; r:=a[k,j]-a[j,k];
if abs(p)<=e then begin c:=1; s:=0; end
else
begin
x:=d/p; c:=x+zn(x)*sqrt(1+x*x);
s:=zn(x)/sqrt(1+c*c); c:=s*c;
end;
if y<0 then begin x:=c; c:=s; s:=-x; end;
co:=c*c-s*s; si:=2*s*c; d:=d*co+p*si;
h:=h*co-f*si; x:=(r*d-h/2)/(g+2*(r*r+d*d));
if abs(x)<=e
then begin ch:=1; sh:=0; end
else begin ch:=1/sqrt(1-x*x); sh:=ch*x; end;
c1:=ch*c-sh*s; c2:=ch*c+sh*s;
s1:=ch*s+sh*c; s2:=-ch*s+sh*c;
if (abs(s1)>e)or(abs(s2)>e) then
begin
u:=false;
for i:=1 to n do
begin
p:=a[k,i];a[k,i]:=c1*p+s1*a[j,i];
a[j,i]:=s2*p+c2*a[j,i];
if v then
begin
p:=t[k,i]; t[k,i]:=c1*p+s1*t[j,i];
t[j,i]:=s2*p+c2*t[j,i];
end;
end;
for i:=1 to n do
begin
p:=a[i,k];a[i,k]:=c2*p-s2*a[i,j];
a[i,j]:=-s1*p+c1*a[i,j];
if w then
begin
p:=t[i,k];t[i,k]:=c2*p-s2*t[i,j];
t[i,j]:=-s1*p+c1*t[i,j];
end;
end;
end;
end;
end;
b:=m;
end;
begin clrscr;
write('введите максимальное количество итераций');read(m);
write('введите точность');read(e);
assign(ff,'vlasn.dat');
reset(ff);
read(ff,n100);
for i100:=1 to n100 do
for j100:=1 to n100 do
read(ff,a[i100,j100]);
b:=0;
eigen(n100,m,e,a,t,b);
for i100:=1 to n100 do begin
for j100:=1 to n100 do
write(a[i100,j100],' ');
writeln; end;
writeln;
writeln(b);
readkey;
end.
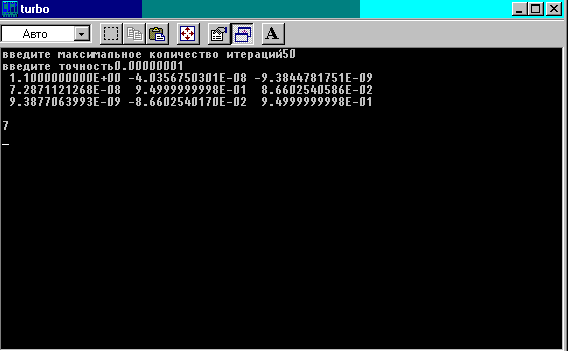
3. Контрольний приклад
При e=10-8 і m=50 для матриці
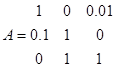
за 7 ітерацій знайдено власні значення
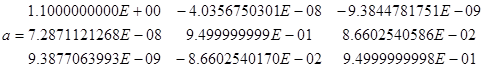
Тобо отримали такі власні значення 
, 
, 
Висновок
Таким чином, задача знаходження інваріантних відносно оператора 
одновимірних підпросторів простору 
рівнозначна задачі згаходження власних векторів оператора 
.
Список літератури
1. А. Г. Курош «Курс высшей алгебры», «Наука», Москва 1975
2. С. Т. Завало, В. М. Костарчук, Б. И. Хацет «Алгебра и теория чисел», Том 1,«Высшая школа», Киев 1974
3. С. Т. Завало, В. М. Костарчук, Б. И. Хацет «Алгебра и теория чисел», Том 2,«Высшая школа», Киев 1976