| Скачать .docx | Скачать .pdf |
Дипломная работа: Дипломная работа: Обобщ нно булевы решетки
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
Вятский государственный гуманитарный университет
Математический факультет
Кафедра алгебры и геометрии
Выпускная квалификационная работа
Обобщенно булевы решетки
Выполнил:
студент V курса математического факультета
Онучин Андрей Владимирович
Научный руководитель:
к.ф.-м.н., доцент кафедры алгебры и геометрии ВятГГУ
Чермных Василий Владимирович
Рецензент:
д.ф.-м.н., профессор, зав. кафедрой алгебры и геометрии ВятГГУ
Вечтомов Евгений Михайлович
Работа допущена к защите в государственной аттестационной комиссии
«___» __________2005 г. Зав. кафедрой Е.М. Вечтомов
«___»__________2005 г. Декан факультета В.И. Варанкина
Киров
2005
Содержание
Введение.......................................................................................................... 3
Глава 1............................................................................................................. 4
1.1. Упорядоченные множества................................................................... 4
1.2. Решётки.................................................................................................. 5
1.3. Дистрибутивные решётки..................................................................... 7
1.4. Обобщённые булевы решётки, булевы решётки................................. 8
1.5. Идеалы................................................................................................... 9
Глава 2........................................................................................................... 11
2.1. Конгруэнции....................................................................................... 11
2.2. Основная теорема............................................................................... 16
Библиографический список.......................................................................... 22
Введение
Булева решётка представляет собой классический математический объект, который начал интенсивно изучаться в работах М. Стоуна 30-е годы 20-го века, расширением этого понятия до обобщённо булевых решёток занимались Г. Гретцер и Е. Шмидт в своих трудах конца 50-х годов.
Цель данной работы: установление взаимно однозначного соответствия между конгруэнциями и идеалами в обобщённо булевых решётках. (Для булевых решёток это положение доказано в книге [2], кроме того, сформулировано в книге [3] в качестве упражнений). А также – установление связи между обобщённо булевыми решётками и булевыми кольцами.
Данная дипломная работа состоит из двух глав: в первой главе даны основные понятия, а так же содержатся базовые сведения из теории решёток. Кроме того, в первой главе рассмотрено несколько простейших теорем.
Вторая глава представляет собой основную часть данной дипломной работы. Опираясь на работы Гретцера Г., но более подробно, рассмотрены свойства конгруэнций и связь конгруэнций и идеалов в обобщённо булевых решётках (Теоремы 2.1, 2.2, 2.3.). Кроме того реализована основная цель данной дипломной работы: установлена связь между булевыми кольцами и обобщённо булевыми решётками (Основная теорема).
Глава 1
1.1. Упорядоченные множества
Упорядоченным множеством
P
называется непустое множество, на котором определено бинарное отношение ![]() , удовлетворяющее для всех
, удовлетворяющее для всех ![]() следующим условиям:
следующим условиям:
1. Рефлексивность: ![]() .
.
2. Антисимметричность. Если ![]() и
и ![]() , то
, то ![]() .
.
3. Транзитивность. Если ![]() и
и ![]() , то
, то ![]() .
.
Если ![]() и
и ![]() , то говорят, что
, то говорят, что ![]() меньше
меньше ![]() или
или ![]() больше
больше ![]() , и пишут
, и пишут ![]() или
или ![]() .
.
Примеры упорядоченных множеств:
1. Множество целых положительных чисел, а ![]() означает, что
означает, что ![]() делит
делит ![]() .
.
2. Множество всех действительных функций ![]() на отрезке
на отрезке ![]() и
и ![]() означает, что
означает, что ![]() для
для ![]() .
.
Цепью
называется упорядоченное множество, на котором для любых ![]() имеет место
имеет место ![]() или
или ![]() .
.
Используя отношение порядка, можно получить графическое представление любого конечного упорядоченного множества P
. Изобразим каждый элемент множества P
в виде небольшого кружка, располагая x
выше y
, если ![]() . Соединим x
и y
отрезком. Полученная фигура называется диаграммой
упорядоченного множества P
.
. Соединим x
и y
отрезком. Полученная фигура называется диаграммой
упорядоченного множества P
.
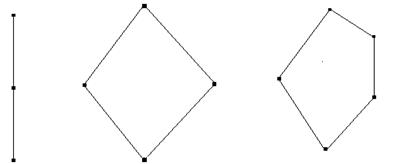 |
Примеры диаграмм упорядоченного множества:
1.2. Решётки
Верхней гранью подмножества Х в упорядоченном множестве Р называется элемент a из Р , больший или равный всех x из X .
Точная верхняя грань подмножества X упорядоченного множества P – это такая его верхняя грань, которая меньше любой другой его верхней грани. Обозначается символом sup X и читается «супремум X ».
Согласно аксиоме антисимметричности упорядоченного множества, если точная верхняя грань существует, то она единственна.
Понятия нижней грани и точной нижней грани (которая обозначается inf X и читается «инфинум ») определяются двойственно. Также, согласно аксиоме антисимметричности упорядоченного множества, если точная нижняя грань X существует, то она единственна.
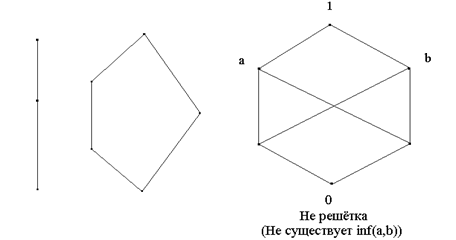 |
Решёткой
Примеры решёток:
Примечание. Любая цепь является решёткой, т.к. ![]() совпадает с меньшим, а
совпадает с меньшим, а ![]() с большим из элементов
с большим из элементов ![]() .
.
Наибольший элемент, то есть элемент, больший или равный каждого элемента упорядоченного множества, обозначают 1, а наименьший элемент, то есть меньший или равный каждого элемента упорядоченного множества, обозначают 0.
На решётке можно рассматривать две бинарные операции:
![]() - сложение и
- сложение и
![]() - произведение
- произведение
Эти операции обладают следующими свойствами:
1. ![]() ,
, ![]() идемпотентность;
идемпотентность;
2. ![]() ,
, ![]() коммутативность;
коммутативность;
3. ![]() ,
, ![]() ассоциативность;
ассоциативность;
4. ![]() ,
, ![]() законы поглощения.
законы поглощения.
ТЕОРЕМА 1.1.
Пусть L
- множество с двумя бинарными операциями ![]() , обладающими свойствами (1) – (4). Тогда отношение
, обладающими свойствами (1) – (4). Тогда отношение ![]() (или
(или ![]() ) является порядком на L
, а возникающее упорядоченное множество оказывается решёткой, причём:
) является порядком на L
, а возникающее упорядоченное множество оказывается решёткой, причём: ![]() и
и ![]() .
.
Доказательство.
Рефлексивность отношения ![]() вытекает из свойства (1). Заметим, что оно является следствием свойства (4):
вытекает из свойства (1). Заметим, что оно является следствием свойства (4):
![]()
![]()
Если ![]() и
и ![]() , то есть
, то есть ![]() и
и ![]() , то в силу свойства (2), получим
, то в силу свойства (2), получим ![]() . Это означает, что отношение
. Это означает, что отношение ![]() антисимметрично.
антисимметрично.
Если ![]() и
и ![]() , то применяя свойство (3), получим:
, то применяя свойство (3), получим: ![]() , что доказывает транзитивность отношения
, что доказывает транзитивность отношения ![]() .
.
Применяя свойства (3), (1), (2), получим:
![]() ,
,
![]() .
.
Следовательно, ![]() и
и ![]() .
.
Если ![]() и
и ![]() , то используя свойства (1) – (3), имеем:
, то используя свойства (1) – (3), имеем:
![]() , т.е.
, т.е. ![]() .
.
По определению точней верхней грани убедимся, что ![]() .
.
Из свойств (2), (4) вытекает, что ![]() и
и ![]() .
.
Если ![]() и
и ![]() , то по свойствам (3), (4) получим:
, то по свойствам (3), (4) получим:
![]() .
.
Отсюда по свойствам (2) и (4) следует, что
![]() .
.
Таким образом, ![]() .
.
Пусть L решётка, тогда её наибольший элемент 1 характеризуется одним из свойств:
1.![]()
![]() .
.
2.![]()
![]() .
.
Аналогично характеризуется наименьший элемент ![]() :
:
1.![]()
![]()
2.![]()
![]() .
.
1.3. Дистрибутивные решётки
Решётка L
называется дистрибутивной
, если для любых ![]() выполняется:
выполняется:
D1. ![]() .
.
D2. ![]() .
.
В любой решётке тождества D1 и D2 равносильны. Доказательство этого факта содержится в книге [2], стр. 24.
Примеры дистрибутивных решёток:
1. Множество целых положительных чисел, ![]() означает, что
означает, что ![]() делит
делит ![]() . Это решётка с операциями НОД и НОК.
. Это решётка с операциями НОД и НОК.
2. Любая цепь является дистрибутивной решёткой.
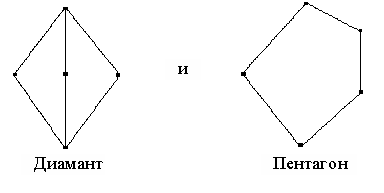 |
ТЕОРЕМА 1.2. Решётка L с 0 и 1 является дистрибутивной тогда и только тогда, когда она не содержит подрешёток вида
Доказательство этой теоремы можно найти в книге [1].
1.4. Обобщённо булевы решётки, булевы решётки
Всюду далее под словом «решётка» понимается произвольная дистрибутивная решётка с 0.
Решётка L
называется обобщённой булевой
,
если для любых элементов ![]() и d из L
,
таких что
и d из L
,
таких что ![]() существует относительное дополнение
на интервале
существует относительное дополнение
на интервале ![]() , т.е. такой элемент
, т.е. такой элемент ![]() из L
, что
из L
, что ![]() и
и ![]() .
.
(Для ![]() ,
, ![]() , интервал
, интервал
![]() |
|![]() ; для
; для ![]() ,
, ![]() можно так же определить полуоткрытый интервал
можно так же определить полуоткрытый интервал
![]() |
|![]() ).
).
ТЕОРЕМА 1.3. (О единственности относительного дополнения в обобщённо булевой решётке). Каждый элемент обобщённо булевой решётки L имеет только одно относительное дополнение на промежутке.
Доказательство.
Пусть для элемента ![]() существует два относительных дополнения
существует два относительных дополнения ![]() и
и ![]() на интервале
на интервале ![]() . Покажем, что
. Покажем, что ![]() . Так как
. Так как ![]() относительное дополнение элемента
относительное дополнение элемента ![]() на промежутке
на промежутке ![]() , то
, то ![]() и
и ![]() , так же
, так же ![]() относительное дополнение элемента
относительное дополнение элемента ![]() на промежутке
на промежутке ![]() , то
, то ![]() и
и ![]() .
.
Отсюда
![]()
![]() ,
,
таким образом ![]() , т.е. любой элемент обобщённой булевой решётки имеет на промежутке только одно относительное дополнение.
, т.е. любой элемент обобщённой булевой решётки имеет на промежутке только одно относительное дополнение.
Решётка L
называется булевой
,
если для любого элемента ![]() из L
существует дополнение
, т.е. такой элемент
из L
существует дополнение
, т.е. такой элемент ![]() из L
, что
из L
, что ![]() и
и ![]()
ТЕОРЕМА 1.4. (О единственности дополнения в булевой решётке). Каждый элемент булевой решётки L имеет только одно дополнение.
Доказательство аналогично доказательству теоремы 1.3.
ТЕОРЕМА 1.5. (О связи обобщённо булевых и булевых решёток).
Любая булева решётка является обобщённо булевой, обратное утверждение не верно.
Доказательство.
Действительно, рассмотрим произвольную булеву решётку L
.
Возьмём элементы a
и d
из L
, такие что ![]() . Заметим, что относительным дополнением элемента a
до элемента d
является элемент
. Заметим, что относительным дополнением элемента a
до элемента d
является элемент ![]() , где a
’ –
дополнение элемента a
в булевой решётке L
. Действительно,
, где a
’ –
дополнение элемента a
в булевой решётке L
. Действительно, ![]() , кроме того
, кроме того ![]() . Отсюда следует, что решётка L
является обобщённо булевой.
. Отсюда следует, что решётка L
является обобщённо булевой.
1.5. Идеалы
Подрешётка I
решётки L
называется идеалом
,
если для любых элементов ![]() и
и ![]() элемент
элемент ![]() лежит в I
. Идеал I
называется собственным,
если
лежит в I
. Идеал I
называется собственным,
если ![]() . Собственный идеал решётки L называется простым
, если из того, что
. Собственный идеал решётки L называется простым
, если из того, что ![]() и
и ![]() следует
следует ![]() или
или ![]() .
.
Так как непустое пересечение любого числа идеалов снова будет идеалом, то мы можем определить идеал, порождённый множеством H
в решётке L
, предполагая, что H
не совпадает с пустым множеством. Идеал, порождённый множеством H
будет обозначаться через (
H
]
. Если ![]() , то вместо
, то вместо ![]() будем писать
будем писать ![]() и называть
и называть ![]() главным идеалом
.
главным идеалом
.
ТЕОРЕМА 1.5.
Пусть L
– решётка, а H
и I
– непустые подмножества в L
, тогда I
является идеалом тогда и только тогда, когда если ![]() , то
, то ![]() , и если
, и если ![]() , то
, то ![]() .
.
Доказательство.
Пусть I
– идеал, тогда ![]() влечёт за собой
влечёт за собой ![]() , так как I
– подрешётка. Если
, так как I
– подрешётка. Если ![]() , то
, то ![]() и условия теоремы проверены.
и условия теоремы проверены.
Обратно, пусть I
удовлетворяет этим условиям и ![]() . Тогда
. Тогда ![]() и так как
и так как ![]() , то
, то ![]() , следовательно, I
– подрешётка. Наконец, если
, следовательно, I
– подрешётка. Наконец, если ![]() и
и ![]() , то
, то ![]() , значит,
, значит, ![]() и I
является идеалом.
и I
является идеалом.
Глава 2
2.1. Конгруэнции
Отношение эквивалентности
(т.е. рефлексивное, симметричное и транзитивное бинарное отношение) ![]() на решётке L
называется конгруэнцией на L
, если
на решётке L
называется конгруэнцией на L
, если ![]() и
и ![]() совместно влекут за собой
совместно влекут за собой ![]() и
и ![]() (свойство стабильности)
. Простейшими примерами являются ω, ι, определённые так:
(свойство стабильности)
. Простейшими примерами являются ω, ι, определённые так:
![]() (ω)
(ω)
![]()
![]() ;
; ![]() (ι)
для всех
(ι)
для всех ![]() .
.
Для ![]() обозначим через
обозначим через ![]() смежный класс
, содержащий элемент
смежный класс
, содержащий элемент ![]() , т.е.
, т.е. ![]() |
|![]()
Пусть L
– произвольная решётка и ![]() .
Наименьшую конгруэнцию
, такую, что
.
Наименьшую конгруэнцию
, такую, что ![]() для всех
для всех ![]() , обозначим через
, обозначим через ![]() и назовём конгруэнцией, порождённой множеством
и назовём конгруэнцией, порождённой множеством
![]() .
.
ЛЕММА 2.1.
Конгруэнция ![]() существует для любого
существует для любого ![]() .
.
Доказательство.
Действительно, пусть Ф
= ![]() |
|![]() для всех
для всех ![]()
![]() . Так как пересечение в решётке
. Так как пересечение в решётке ![]() совпадает с теоретико-множественным пересечением, то
совпадает с теоретико-множественным пересечением, то ![]() для всех
для всех ![]() . Следовательно, Ф
=
. Следовательно, Ф
=![]() .
.
В двух случаях мы будем использовать специальные обозначения: если ![]() или
или ![]() и
и ![]() - идеал, то вместо
- идеал, то вместо ![]() мы пишем
мы пишем ![]() или
или ![]() соответственно. Конгруэнция вида
соответственно. Конгруэнция вида ![]() называется главной; её значение объясняется следующей леммой:
называется главной; её значение объясняется следующей леммой:
ЛЕММА 2.2.
![]() =
=![]() |
|![]() .
.
Доказательство.
Пусть ![]() , тогда
, тогда ![]() , отсюда
, отсюда ![]() . С другой стороны рассмотрим
. С другой стороны рассмотрим ![]() , но тогда
, но тогда ![]() . Поэтому
. Поэтому ![]() и
и ![]() .
.
Заметим, что ![]() - наименьшая конгруэнция, относительно которой
- наименьшая конгруэнция, относительно которой ![]() , тогда как
, тогда как ![]() - наименьшая конгруэнция, такая, что
- наименьшая конгруэнция, такая, что![]() содержится в одном смежном классе. Для произвольных решёток о конгруэнции
содержится в одном смежном классе. Для произвольных решёток о конгруэнции ![]() почти ничего не известно. Для дистрибутивных решёток важным является следующее описание конгруэнции
почти ничего не известно. Для дистрибутивных решёток важным является следующее описание конгруэнции ![]() :
:
ТЕОРЕМА 2.1.
Пусть ![]() - дистрибутивная решётка,
- дистрибутивная решётка, ![]() и
и ![]() . Тогда
. Тогда ![]() и
и ![]() .
.
Доказательство.
Обозначим через Ф
бинарное отношение, определённое следующим образом: ![]() и
и ![]() .
.
Покажем, что Ф – отношение эквивалентности:
1) Ф – отношение рефлексивности: x · a = x · a ; x + b = x + b ;
2) Ф – отношение симметричности:
![]()
![]() x·a = y·a
и
x+b = y+b
x·a = y·a
и
x+b = y+b ![]() y·a = x·a
и
y+b = x+b
y·a = x·a
и
y+b = x+b
![]()
![]() ;
;
3) Ф – отношение транзитивности.
Пусть ![]()
![]() x·
a
=
y
·
a
и
x
+
b
=
y
+
b
и пусть
x·
a
=
y
·
a
и
x
+
b
=
y
+
b
и пусть ![]()
![]() y
·с =
z
·с
и y
+
d
= z
+
d
.
Умножим обе части x
·
a
=
y
·
a
на элемент с
, получим x
·
a
·
c
=
y
·
a
·
c
. А обе части y
·с =
z
·с
умножим на элемент a
, получим y
·
c
·
a
=
z
·
c
·
a
. В силу симметричности x
·
a
·
c
=
y
·
a
·
c
=
z
·
a
·
c
. Аналогично получаем x
+
b
+
d
=
y
+
b
+
d
=
z
+
b
+
d
. Таким образом
y
·с =
z
·с
и y
+
d
= z
+
d
.
Умножим обе части x
·
a
=
y
·
a
на элемент с
, получим x
·
a
·
c
=
y
·
a
·
c
. А обе части y
·с =
z
·с
умножим на элемент a
, получим y
·
c
·
a
=
z
·
c
·
a
. В силу симметричности x
·
a
·
c
=
y
·
a
·
c
=
z
·
a
·
c
. Аналогично получаем x
+
b
+
d
=
y
+
b
+
d
=
z
+
b
+
d
. Таким образом ![]() .
.
Из всего выше обозначенного следует, что Ф – отношение эквивалентности.
Покажем, что Ф
сохраняет операции. Если ![]() и z
и z![]() L
, то (
x
+
z
) ·
a
= (
x
·
a
) + (
z
·
a
) = (
y
·
a
) + (
z
·
a
) = (
y
+
z
) ·
a
и (
x
+
z
)+
b
=
z
+(
x
+
b
) =
z
+(
y
+
b
)
; следовательно,
L
, то (
x
+
z
) ·
a
= (
x
·
a
) + (
z
·
a
) = (
y
·
a
) + (
z
·
a
) = (
y
+
z
) ·
a
и (
x
+
z
)+
b
=
z
+(
x
+
b
) =
z
+(
y
+
b
)
; следовательно, ![]() . Аналогично доказывается, что
. Аналогично доказывается, что ![]() и, таким образом, Ф
– конгруэнция.
и, таким образом, Ф
– конгруэнция.
Наконец, пусть ![]() - произвольная конгруэнция, такая, что
- произвольная конгруэнция, такая, что ![]() , и пусть
, и пусть ![]() . Тогда x
·
a
=
y
·
a
,
x
+
b
=
y
+
b
,
. Тогда x
·
a
=
y
·
a
,
x
+
b
=
y
+
b
, ![]() и
и ![]() . Поэтому вычисляя по модулю
. Поэтому вычисляя по модулю ![]() , получим
, получим
![]()
![]()
![]() , т.е.
, т.е. ![]() , и таким образом,
, и таким образом, ![]() .
.
СЛЕДСТВИЕ ИЗ ТЕОРЕМЫ 2.1.
Пусть I
– произвольный идеал дистрибутивной решётки L
. Тогда ![]() в том и только том случае, когда
в том и только том случае, когда ![]() для некоторого
для некоторого ![]() . В частности, идеал I
является смежным классом по модулю
. В частности, идеал I
является смежным классом по модулю ![]() .
.
Доказательство. Если ![]() , то
, то ![]() и элементы x
·
y
·
i
,
i
принадлежат идеалу I
.
и элементы x
·
y
·
i
,
i
принадлежат идеалу I
.
Действительно ![]() .
.
Покажем, что ![]() .
.
Воспользуемся тем, что ![]() (*), заметим, что
(*), заметим, что ![]() и
и ![]() , поэтому мы можем прибавить к тождеству (*)
, поэтому мы можем прибавить к тождеству (*) ![]() или
или ![]() , и тождество при этом будет выполняться.
, и тождество при этом будет выполняться.
![]() Прибавим
Прибавим ![]() :
: ![]() , получим
, получим ![]() .
.
![]() Прибавим
Прибавим ![]() :
: ![]() , получим
, получим ![]() .
.
Отсюда ![]() . Таким образом,
. Таким образом,![]() .
.
Обратно согласно лемме 2, ![]() |
|![]()
Однако ![]() и поэтому
и поэтому ![]() |
|![]()
Если ![]() , то
, то ![]() откуда
откуда
![]() .
.
Действительно, ![]() (**).
(**).
Рассмотрим правую часть этого тождества:
Объединим первое и второе слагаемые –
![]() .
.
Объединим первое и третье слагаемые –
![]() ,
,
таким образом ![]() (***)
(***)
Заметим, что ![]() , поэтому прибавим к обеим частям выражения (***) y
:
, поэтому прибавим к обеим частям выражения (***) y
:
![]()
![]()
Но ![]() , отсюда
, отсюда ![]() .
.
Следовательно, условие следствия из теоремы 2.1. выполнено для элемента ![]() . Наконец, если
. Наконец, если ![]() и
и ![]() , то
, то ![]() , откуда
, откуда ![]() и
и ![]() , т.е.
, т.е. ![]() является смежным классом.
является смежным классом.
ТЕОРЕМА 2.2.
Пусть L
– булева решётка. Тогда отображение ![]()
![]()
![]() является взаимно однозначным соответствием между конгруэнциями и идеалами решётки L
. (Под
является взаимно однозначным соответствием между конгруэнциями и идеалами решётки L
. (Под ![]()
![]() понимаем класс нуля по конгруэнции
понимаем класс нуля по конгруэнции ![]() , под
, под ![]() понимаем решётку конгруэнций.)
понимаем решётку конгруэнций.)
 Доказательство.
В силу следствия из теоремы 2.1. это отображение на множество идеалов; таким образом мы должны только доказать, что оно взаимно однозначно, т.е. что смежный класс
Доказательство.
В силу следствия из теоремы 2.1. это отображение на множество идеалов; таким образом мы должны только доказать, что оно взаимно однозначно, т.е. что смежный класс ![]() определяет конгруэнцию
определяет конгруэнцию ![]() . Это утверждение, однако, очевидно. Действительно
. Это утверждение, однако, очевидно. Действительно ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() (*), последнее сравнение в свою очередь равносильно сравнению
(*), последнее сравнение в свою очередь равносильно сравнению ![]() , где с – относительное дополнение элемента
, где с – относительное дополнение элемента ![]() в интервале
в интервале ![]() .
.
Действительно, помножим выражение (*) на с :
![]() , но
, но![]() , а
, а ![]() , отсюда
, отсюда ![]() .
.
Таким образом, ![]() в том и только том случае, когда
в том и только том случае, когда ![]() .
.
Примечание. Приведённое доказательство не полностью использует условие, что L – дистрибутивная решётка с дополнениями. Фактически, мы пользовались только тем, что L имеет нуль и является решёткой с относительными дополнениями. Такая решётка называется обобщённой булевой решёткой.
ТЕОРЕМА 2.3
(Хасимото [1952]). Пусть L
– произвольная решётка. Для того, чтобы существовало взаимно однозначное соответствие между идеалами и конгруэнциями решётки L
, при котором идеал, соответствующий конгруэнции ![]() , являлся бы смежным классом по
, являлся бы смежным классом по ![]() , необходимо и достаточно, чтобы решётка L
была обобщённой булевой.
, необходимо и достаточно, чтобы решётка L
была обобщённой булевой.
 Доказательство.
Достаточность следует из доказательства теоремы 2.2. Перейдём к доказательству необходимости.
Доказательство.
Достаточность следует из доказательства теоремы 2.2. Перейдём к доказательству необходимости.
Идеалом, соответствующим конгруэнции ![]() , должен быть (0]
; следовательно, L
имеет нуль 0.
, должен быть (0]
; следовательно, L
имеет нуль 0.
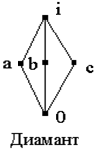
 Если L
содержит диамант
Если L
содержит диамант ![]() , то идеал (
a
]
не может быть смежным классом, потому что из
, то идеал (
a
]
не может быть смежным классом, потому что из ![]() следует
следует ![]() и
и ![]() . Но
. Но ![]() , значит, любой смежный класс, содержащий
, значит, любой смежный класс, содержащий ![]() , содержит и
, содержит и ![]() , и
, и ![]() .
.
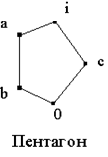
Аналогично, если L
содержит пентагон ![]() и смежный класс содержит идеал
и смежный класс содержит идеал ![]() , то
, то ![]() и
и ![]() , откуда
, откуда ![]() . Следовательно, этот смежный класс должен содержать
. Следовательно, этот смежный класс должен содержать ![]() и
и ![]() .
.
Итак, решётка L не содержит подрешёток, изоморфных ни диаманту, ни пентагону. Поэтому, по теореме 1.2., она дистрибутивна.
Пусть ![]() и
и ![]() . Согласно следствию из теоремы 2.1., для конгруэнции
. Согласно следствию из теоремы 2.1., для конгруэнции ![]() идеал
идеал ![]() так же является смежным классом, следовательно,
так же является смежным классом, следовательно, ![]() , откуда
, откуда ![]() . Опять применяя следствие из теоремы 2.1. получим,
. Опять применяя следствие из теоремы 2.1. получим, ![]() для некоторого
для некоторого ![]() . Так как
. Так как ![]() , то
, то ![]() и
и ![]() . Следовательно,
. Следовательно, ![]() о полу орого ледствие 4 получим, цииодержать , соответствующим конгруэнции образом мы должны только доказать, ______________ и
о полу орого ледствие 4 получим, цииодержать , соответствующим конгруэнции образом мы должны только доказать, ______________ и ![]() , т.е. элемент
, т.е. элемент ![]() является относительным дополнением элемента
является относительным дополнением элемента ![]() в интервале
в интервале ![]() .
.
2.2. Основная теорема
(1)  Пусть
Пусть ![]() - обобщённая булева решётка. Определим бинарные операции
- обобщённая булева решётка. Определим бинарные операции ![]() на B
, полагая
на B
, полагая ![]() и обозначая через
и обозначая через ![]() относительное дополнение элемента
относительное дополнение элемента ![]() в интервале
в интервале ![]() . Тогда
. Тогда ![]() - булево кольцо, т.е. (ассоциативное) кольцо, удовлетворяющее тождеству
- булево кольцо, т.е. (ассоциативное) кольцо, удовлетворяющее тождеству ![]() (а следовательно и тождествам
(а следовательно и тождествам ![]() ,
, ![]() ).
).
(2) Пусть ![]() - булево кольцо. Определим бинарные операции
- булево кольцо. Определим бинарные операции ![]() и
и ![]() на
на ![]() , полагая, что
, полагая, что ![]() и
и ![]() . Тогда
. Тогда ![]() - обобщённая булева решётка.
- обобщённая булева решётка.
Доказательство.
(1) Покажем, что ![]() - кольцо.
- кольцо.
Напомним определение. Кольцо ![]() - это непустое множество
- это непустое множество ![]() с заданными на нём двумя бинарными операциями
с заданными на нём двумя бинарными операциями ![]() , которые удовлетворяют следующим аксиомам:
, которые удовлетворяют следующим аксиомам:
1. Коммутативность сложения: ![]() выполняется
выполняется ![]() ;
;
2. Ассоциативность сложения: ![]() выполняется
выполняется ![]() ;
;
3. Существование нуля, т.е. ![]() ,
, ![]() ;
;
4. Существование противоположного элемента, т.е. ![]() ,
, ![]() ,
, ![]() ;
;
5. Ассоциативность умножения: ![]() ,
, ![]() ;
;
6. Закон дистрибутивности.
Проверим, выполняются ли аксиомы кольца:
1. Относительным дополнением до ![]() элемента
элемента ![]() будет элемент
будет элемент ![]() , а относительным дополнением
, а относительным дополнением ![]() элемент
элемент ![]()
![]() . В силу того, что
. В силу того, что ![]() , а так же единственности дополнения имеем
, а так же единственности дополнения имеем ![]() .
.
2. Покажем, что ![]() .
.
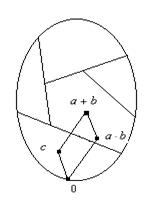
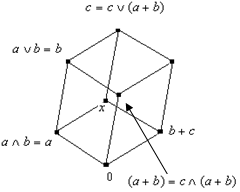 Рассмотрим все возможные группы вариантов:
Рассмотрим все возможные группы вариантов:
1) Пусть ![]() , тогда
, тогда ![]() (Далее везде под элементом x будем понимать сумму
(Далее везде под элементом x будем понимать сумму ![]() ).
).
Аналогично получаем ![]() в случаях
в случаях ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() . Заметим, что когда один из элементов равен нулю (например, c
)
, то получаем тривиальные варианты (a+
b
=
a
+
b
).
. Заметим, что когда один из элементов равен нулю (например, c
)
, то получаем тривиальные варианты (a+
b
=
a
+
b
).
2) Пусть ![]() , а элемент c
не сравним с ними. Возможны следующие варианты:
, а элемент c
не сравним с ними. Возможны следующие варианты:
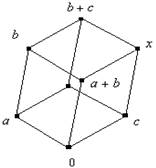
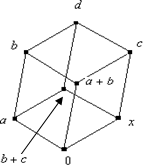
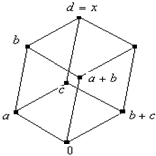
Нетрудно заметить, что во всех этих случаях ![]() , кроме того:
, кроме того:
если c=a+b , то (a+b)+c=0=a+(b+c) ;
если c =0 , то получаем тривиальный вариант.
Вариант, когда c равен наибольшему элементу решётки d , мы уже рассматривали.
Если c=b , то (a+b)+c=(a+b)+b=a и a+(b+c)=a+(b+b)=a.
Если c=a, то (a+b)+c=(a+b)+a=b и a+(b+c)=a+(b+a)=b .
 Аналогично для случаев
Аналогично для случаев ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() .
.
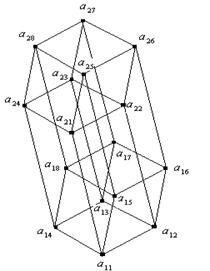
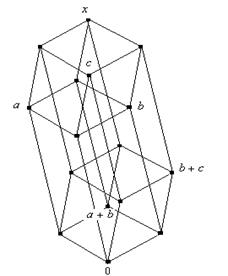
3) Под элементами нижнего уровня будем понимать элементы ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , т.е. те элементы 4-х мерного куба, которые образуют нижний трёхмерный куб.
, т.е. те элементы 4-х мерного куба, которые образуют нижний трёхмерный куб.
Под элементами верхнего уровня будем понимать элементы ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , т.е. те элементы 4-х мерного куба, которые образуют верхний трёхмерный куб.
, т.е. те элементы 4-х мерного куба, которые образуют верхний трёхмерный куб.
Под фразой «элемент верхнего уровня, полученный из элемента ![]() нижнего уровня сдвигом по соответствующему ребру» будем понимать элемент
нижнего уровня сдвигом по соответствующему ребру» будем понимать элемент ![]() верхнего уровня.
верхнего уровня.
Пусть a
,
b
,
c
несравнимы. Рассмотрим следующие варианты: ![]() и
и ![]() .
.
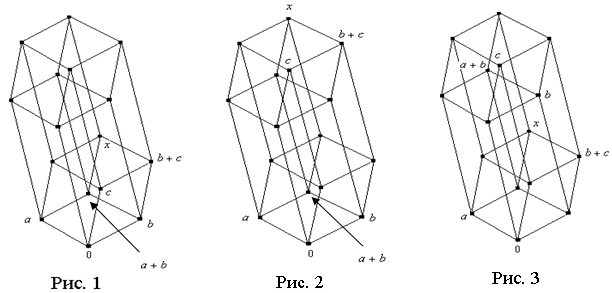 Пусть
Пусть ![]() . Заметим, что это возможно только в случаях, когда
. Заметим, что это возможно только в случаях, когда ![]() принадлежат нижнему уровню, причём лежат на позициях элементов
принадлежат нижнему уровню, причём лежат на позициях элементов ![]() (рис. 1). Либо a
,
b
остаются на своих позициях, элемент c
сдвигается на верхний уровень по соответствующему ребру (рис. 2). Либо элемент a
остаётся на своей позиции, элементы b
,
c
сдвигаются на верхний уровень по соответствующему ребру (рис 3).
(рис. 1). Либо a
,
b
остаются на своих позициях, элемент c
сдвигается на верхний уровень по соответствующему ребру (рис. 2). Либо элемент a
остаётся на своей позиции, элементы b
,
c
сдвигаются на верхний уровень по соответствующему ребру (рис 3).
 Нетрудно заметить, что во всех этих случаях
Нетрудно заметить, что во всех этих случаях ![]() .
.
Пусть ![]() , здесь так же
, здесь так же ![]() .
.
Таким образом мы рассмотрели все основные группы вариантов расположения элементов a , b , c и во всех этих случаях ассоциативность сложения выполняется.
3. Рассмотрим в решётке элемент ![]() , к нему существует относительное дополнение
, к нему существует относительное дополнение ![]() до элемента
до элемента ![]() , т.е.
, т.е. ![]() и
и ![]() . Учитывая, что в решётке
. Учитывая, что в решётке ![]() и
и ![]() , имеем следующее:
, имеем следующее: ![]() и
и ![]() . Отсюда
. Отсюда ![]() .
.
4. Рассмотрим относительное дополнение элемента ![]() до
до ![]() , это элемент
, это элемент ![]() . Таким образом:
. Таким образом: ![]() и
и ![]() . Учитывая, что в решётке выполняются тождества
. Учитывая, что в решётке выполняются тождества ![]() и
и ![]() имеем следующее:
имеем следующее: ![]() и
и ![]() . Отсюда
. Отсюда ![]() .
.
5. Так как в решётке выполняется ассоциативность ![]() , а так же имея
, а так же имея ![]() , то
, то ![]() .
.
6. Докажем дистрибутивность ![]() или что то же самое
или что то же самое
![]() (*).
(*).
Докажем, что дополнения левой и правой частей выражения (*) до верхней грани ![]() совпадают.
совпадают.
Нетрудно заметить, что дополнением правой части выражения (*) до элемента ![]() будет являться элемент
будет являться элемент ![]() .
.
Покажем это:
![]() , по определению относительного дополнения элемента
, по определению относительного дополнения элемента ![]() (
(![]() ), где за
), где за ![]() приняли элемент
приняли элемент ![]() , а элемент
, а элемент ![]() за
за ![]() .
.
![]() , по определению относительного дополнения элемента
, по определению относительного дополнения элемента ![]() (
(![]() ) , где за
) , где за ![]() приняли элемент
приняли элемент ![]() , а элемент
, а элемент ![]() за
за ![]() .
.
Покажем, что и для левой части (*) элемент ![]() будет являться относительным дополнением до верхней грани
будет являться относительным дополнением до верхней грани ![]() :
:
![]() , т.к.
, т.к. ![]() .
.
![]()
Мы показали, что дополнения элементов ![]() и
и ![]() до верхней грани
до верхней грани ![]() совпадают, следовательно, в силу единственности дополнения
совпадают, следовательно, в силу единственности дополнения ![]() . А значит и
. А значит и ![]() , т.е. дистрибутивность доказана.
, т.е. дистрибутивность доказана.
Таким образом, для ![]() все аксиомы кольца выполняются.
все аксиомы кольца выполняются.
Заметим, что ![]() выполняется в силу того, что
выполняется в силу того, что ![]() , а в решётке
, а в решётке ![]() .
.
Также выполняется ![]() , потому что
, потому что ![]() .
.
Таким образом, ![]() - булево кольцо.
- булево кольцо.
Доказательство (2). Частичную упорядоченность ![]() имеем исходя из того, что исходное булево кольцо
имеем исходя из того, что исходное булево кольцо ![]() - частично упорядоченное множество. Кроме того
- частично упорядоченное множество. Кроме того ![]() - решётка, т.к.
- решётка, т.к. ![]() существуют sup(x
,
y
) и inf(x
,
y
), заданные соответствующими правилами:
существуют sup(x
,
y
) и inf(x
,
y
), заданные соответствующими правилами: ![]() и
и ![]() .
.
Покажем, что решётка дистрибутивна, т.е. что выполняется тождество ![]() (*)
(*)
Рассмотрим левую часть выражения (*):
![]() .
.
Рассмотрим правую часть выражения (*):
![]() ,
,
т.о. тождество ![]() верно, т.е. решётка
верно, т.е. решётка ![]() является дистрибутивной.
является дистрибутивной.
Покажем, что у каждого элемента ![]() в дистрибутивной решётке
в дистрибутивной решётке ![]() есть относительное дополнение. Для этого рассмотрим произвольные элементы
есть относительное дополнение. Для этого рассмотрим произвольные элементы ![]() , но они так же должны являться элементами решётки
, но они так же должны являться элементами решётки ![]() , следовательно, в ней должны лежать и
, следовательно, в ней должны лежать и ![]() , которым в кольце соответствуют
, которым в кольце соответствуют ![]() .
.
Рассмотрим элемент булева кольца ![]() (в решётке лежит соответствующий ему элемент), заметим, что
(в решётке лежит соответствующий ему элемент), заметим, что
![]()
и ![]() .
.
Поэтому элемент ![]() будет являться в дистрибутивной решётке
будет являться в дистрибутивной решётке ![]() относительным дополнением
относительным дополнением ![]() до верхней грани
до верхней грани ![]() .
.
Таким образом, ![]() будет являться дистрибутивной решёткой с относительными дополнениями (обобщённой булевой).
будет являться дистрибутивной решёткой с относительными дополнениями (обобщённой булевой).
Библиографический список
1. Гретцер, Г. Общая теория решёток [Текст] / Г. Гретцер. – М.: Мир, 1982.
2. Биркгоф, Г. Теория решёток [Текст] / Г. Биркгоф. – М.: Наука, 1984.
3. Скорняков, Л.А. Элементы алгебры [Текст] / Л.А. Скорняков. – М.: Наука, 1989.