| Скачать .docx | Скачать .pdf |
Реферат: Контрольная работа: Статистические методы определения экономических показателей
Задача 1
По данным таблице произведите группировку 30 коммерческих банков по величине кредитных вложений. Результаты группировки изложите в сводных групповых таблицах и проанализируйте.
| Номер банка |
Кредитные вложения млн. руб. |
Капитал, млн. руб. |
Прибыль, млн. руб. |
| 1 |
50,2 |
106,3 |
2,5 |
| 2 |
0,5 |
100,1 |
0,1 |
| 3 |
89,8 |
95,7 |
2,0 |
| 4 |
88,3 |
90,9 |
5,3 |
| 5 |
21,0 |
88,1 |
22,1 |
| 6 |
59,9 |
87,9 |
0,2 |
| 7 |
0,1 |
86,9 |
0,9 |
| 8 |
156,0 |
101,7 |
5,9 |
| 9 |
145,5 |
101,0 |
0,1 |
| 10 |
93,3 |
97,8 |
0,1 |
| 11 |
136,4 |
96,3 |
3,9 |
| 12 |
150,8 |
96,3 |
0,4 |
| 13 |
135,4 |
95,0 |
13,4 |
| 14 |
99,9 |
93,2 |
17,2 |
| 15 |
111,3 |
92,6 |
5,6 |
| 16 |
167,1 |
86,8 |
12,3 |
| 17 |
98,3 |
86,7 |
1,1 |
| 18 |
171,0 |
85,3 |
4,8 |
| 19 |
148,3 |
83,9 |
3,6 |
| 20 |
117,3 |
80,9 |
13,6 |
| 21 |
180,0 |
79,7 |
2,0 |
| 22 |
198,1 |
103,4 |
2,4 |
| 23 |
215,0 |
101,8 |
49,3 |
| 24 |
211,0 |
101,1 |
2,0 |
| 25 |
250,5 |
98,0 |
6,6 |
| 26 |
199,7 |
95,8 |
16,8 |
| 27 |
256,7 |
84,7 |
19,1 |
| 28 |
366,8 |
106,4 |
9,7 |
| 29 |
298,5 |
97,7 |
34,4 |
| 30 |
302,5 |
92,9 |
5,1 |
Решение:
Определим величину интервала
h=(xmax - xmin)/n =(366,8-0,1)/4=91,7.
Обозначим границы групп: 0,1-91,7 – 1 группа; 91,8-183,4 – 2 группа; 183,5-275,1 – 3 группа; 275,2-366,8 – 4 группа.
Разнесем показатели, характеризующие состояние банков по 4 указанным выше группам и подсчитаем групповые итоги. Полученным данным занесем в таблицу.
Определим общие итоги по каждому показателю. Полученные данные занесем в таблицу.
| Величина кредитных вложений, млн. руб. |
Номера банков |
Число банков |
Кредитные вложения, млн. руб. |
Капитал, млн. руб. |
Прибыль, млн. руб. |
| 0,1-91,7 |
7, 2, 5, 1, 6, 4, 3 |
7 |
309,8 |
655,9 |
55,7 |
| 91,8-183,4 |
10, 17, 14, 15, 20, 13, 11, 9, 19, 12, 8, 16, 18, 21 |
14 |
1910,6 |
1277,2 |
84 |
| 183,5-275,1 |
22, 26, 24, 23, 25, 27 |
6 |
1331 |
584,8 |
96,2 |
| 275,2-366,8 |
29, 30, 28 |
3 |
967,8 |
297 |
49,2 |
| Итого |
30 |
4519,2 |
2814,9 |
285,1 |
Полученные в таблицы абсолютные данные пересчитываем в «проценты к итогу»
Например, 1группа:
доля банков: 7/30*100%=23,3%
структура кредитных вложений: 309,8/4519,2*100%=44,26 и т.д.
Таблица 1.
Группировка коммерческих банков региона по величине кредитных вложений в % к итогу
| Величина кредитных вложений, млн. руб. |
Число банков |
Доля банков |
Структура кредитных вложений, млн. руб. |
Структура капитала, млн. руб. |
Структура прибыли, млн. руб. |
| 0,1-91,1 |
7 |
23,3 |
6,9 |
23,3 |
19,5 |
| 91,8-183,4 |
14 |
46,7 |
42,3 |
45,4 |
29,5 |
| 183,5-275,1 |
6 |
20,0 |
29,5 |
20,8 |
33,8 |
| 275,2-366,8 |
3 |
10,0 |
21,3 |
10,5 |
17,2 |
| Итого |
30 |
100 |
100 |
100 |
100 |
Из таблицы 1 видно, что в основном преобладают банки второй группы, т.е. средне-активно работающие на рынке кредитования. Их удельный вес в общей численности коммерческих банках составляет 46,7%, на их долю приходится 45,2% всего капитала, 42,3 % кредитных вложений и только 29,5% прибыли. В то же время, следующая, более активная по сравнению с предыдущей группа коммерческих банков численностью лишь 20,0%, имеет 20,8% капитала и 29,5 % кредитных вложений. Но она наиболее выгодно размещает свои кредиты. Ее прибыль составляет 33,8 % от общей массы прибыли коммерческих банков
Таблица 2
Группировка коммерческих банков региона по величине кредитных вложений
| Величина кредитных вложений, млн. руб. |
Число банков |
Кредитные вложения, млн. руб. |
Прибыль, млн. руб. |
||
| 0,1-91,7 |
7 |
309,8 |
44,26 |
55,7 |
7,96 |
| 91,8-183,4 |
14 |
1910,6 |
136,77 |
84 |
6,00 |
| 183,5-275,1 |
6 |
1331 |
221,83 |
96,2 |
16,07 |
| 275,2-366,9 |
3 |
967,8 |
322,60 |
49,2 |
16,40 |
| Итого |
30 |
4519,2 |
- |
285,1 |
- |
| В среднем на один банк |
- |
- |
150,64 |
9,51 |
|
Чем активнее банк работает на рынке кредитования, тем выше прибыль.
Задача 2
Выполните вторичную группировку данных представленных в таблице, выделив три группы предприятий со средней численностью работающих до 500, 501-5000, 5001 и более человек.
| Группы предприятий по среднегодовой численности работающих |
Число предприятий, % |
Объем продукции, % |
| До 100 |
7 |
3 |
| 101-200 |
35 |
6 |
| 201-500 |
24 |
8 |
| 501-3000 |
12 |
15 |
| 3001-10000 |
18 |
26 |
| 10001 и более |
4 |
42 |
| Итого |
100 |
100 |
Решение:
В первую группу предприятий с численностью до 500 чел. полностью войдут 3 первые группы (до 100, 101-200, 201-500). Тогда доля предприятий этих групп составит 66% (7+35+24), а объем продукции –17% (3+6+8).
Для расчета показателей группы предприятий с численностью 501-5000 чел. необходимо взять 4 группу и добавить 2000 от интервала 3001-10000. Поскольку данный интервал составляет 7000 чел, то 2000-это 2/7 пятой группы. Тогда доля предприятий группы 501-5000 рассчитывается так:
12+(18/7)*2=17,4 ≈17%.
Аналогично рассчитываем объем продукции:
15+(26/7)*2=22,4%.
В третью группу предприятий с численностью 5001 чел. и более войдут 5/7 пятой группы:
(18/7)*5+4=16,86≈17%.
Объем продукции составит(26/7)*5+43=60,6%.
Вторичная группировка представлена в таблице:
Группировка промышленных предприятий по среднегодовой численности работающих (в % к итогу)
| Группы предприятий по среднегодовой численности работающих |
Число предприятий, % |
Объем продукции, % |
| До 500 |
66 |
17 |
| 501-5000 |
17 |
22,4 |
| 5001и более |
17 |
60,6 |
| Итого |
100 |
100 |
Задача 3
На основе данных таблицы определите средний возраст персонала.
Распределение сотрудников предприятия по возрасту:
| Возраст |
Число сотрудников (чел.) |
| До 25 |
8 |
| 25-30 |
32 |
| 30-40 |
68 |
| 40-50 |
49 |
| 50-60 |
21 |
| 60 и более |
3 |
| Итого |
181 |
Решение:
Для определения среднего возраста персонала найдем середины интервалов. При этом величины открытых интервалов (первого и последнего) условно приравниваются к величинам интервалов, примыкающих к ним (второго и предпоследнего).
С учетом этого середины интервалов будут: 22,5 27,5 35,0 45,0 55,0 65,0
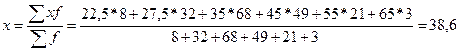
Задача 4
По данным таблицы определите моду и медиану.
| Номер студента |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| Возраст |
19 |
21 |
19 |
20 |
20 |
20 |
21 |
23 |
20 |
22 |
Решение:
Модальный возраст в данном случае – 20 лет, так как он повторяется в 4 раза, т.е. чаще, чем все другие.
Для расчета медианы по не сгруппированным данным ранжируем студентов по возрасту:
| х1 |
х2 |
х3 |
х4 |
х5 |
х6 |
х7 |
х8 |
х9 |
х10 |
| 19 |
19 |
20 |
20 |
20 |
20 |
21 |
21 |
22 |
22 |
Определим порядковый номер медианы по формуле:
![]()
![]()
Это значит, что медиана расположена между 5 и 6 значением признака. Она равна средней арифметической из суммы пятого и шестого значений:
![]()
Задача 5
По данным таблицы определите моду, медиану.
Распределение населения области по уровню среднедушевых денежных доходов
| Среднедушевой денежный доход (в среднем за месяц), руб. |
Численность населения, тыс. чел |
| До 4000 |
22,1 |
| 4000-6000 |
27,8 |
| 6000-8000 |
25,2 |
| 8000-10000 |
19,6 |
| 10000-12000 |
14,3 |
| 12000-16000 |
17,6 |
| 16000-20000 |
9,0 |
| 20000 и более |
11,1 |
| Итого: |
146,7 |
Решение:
Интервал с границами 4000-6000 в данном распределении будет модальным, так как он имеет наибольшую величину.
Формула для определения моды по интервальным рядам имеет следующий вид:
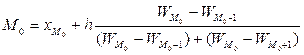 ,
,
где:
ХMo — начало модального интервала;
WMo— частота, соответствующая модальному интервалу;
WMo-1 — предмодальная частота;
WMo+1— послемодальная частота.
![]()
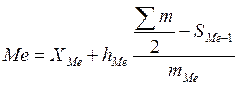
где:
ХMe— нижняя граница медианного интервала;
h — величина интервала;
SMe-1— накопленная частота интервала, предшествующего медианному;
mMe— частота медианного интервала.
Для определения медианного интервала необходимо рассчитывать накопленную частоту каждого последующего интервала до тех пор, пока она не превысит Ѕ суммы накопленных частот (в нашем случае 73,35).
Таким образом, медианным является интервал с границами 6000-8000. Тогда медиана равна:
| Интервал |
Накопленная частота, млн. чел. |
| До 4000 |
22,1 |
| 4000-6000 |
49,9 |
| 6000-800 |
75,1 |
![]()
Задача 7
По данным о вводе в действие жилых домов (млн. м2) рассчитать цепные, базисные
а) абсолютные приросты;
б) темпы роста;
в) темпы прироста.
Показатель |
2001 |
2002 |
2003 |
2004 |
2005 |
| Общая площадь, млн. м2 |
7,0 |
6,5 |
5,9 |
5,5 |
4,9 |
Решение
| Абсолютный прирост |
Темп роста, % |
Темп прироста, % |
|||||
| цепной |
базисный |
цепной |
базисный |
цепной |
базисный |
||
| 1 |
7,0 |
||||||
| 2 |
6,5 |
6,5-7,0=-0,5 |
6,5-7,0=-0,5 |
6,5/7,0*100=92,86 |
6,5/7,0*100=92,86 |
92,86-100= -7,14 |
92,86-100= -7,14 |
| 3 |
5,9 |
5,9- 6,5=-0,6 |
5,9-7,0= -1,1 |
5,9/6,5*100 =90,77 |
5,9/7,0*100=84,29 |
90,77-100= -9,23 |
84,29-100= -15,71 |
| 4 |
5,5 |
5,5-5,9=-0,4 |
5,5-7,0=-1,5 |
5,5/5,9*100=78,57 |
5,5/7,0*100=78,57 |
93,22-100= -6,78 |
78,57-100=--21,43 |
| 5 |
4,9 |
4,9-5,5=-0,4 |
4,9-7,0=-2,1 |
4,9/5,5*100=89,09 |
4,9/7,0*100=70,00 |
89,09-100= -10,91 |
70,00-100= -30,00 |
Задача 8
Имеются данные о реализации овощной продукции в области. Определите индекс товарооборота, сводный индекс цен, сводный индекс физического объема реализации.
| Наименование товара |
Август |
Сентябрь |
||
| Цена за 1 кг, руб. (p0) |
Продано, т (q0) |
Цена за 1 кг, руб. (p1) |
Продано, т (q1) |
|
| Лук |
12 |
18 |
12 |
15 |
| Картофель |
11 |
22 |
10 |
27 |
| Морковь |
9 |
20 |
7 |
24 |
| Итого |
х |
Х |
х |
х |
Решение:
Добавим в таблицу расчетные графы:
| Наименование товара |
Август |
Сентябрь |
Расчетные графы |
||||
| Цена за 1 кг, руб. (p0) |
Продано, т (q0) |
Цена за 1 кг, руб. (p1) |
Продано, т (q1) |
P0q0 |
P1q1 |
P0q1 |
|
| Лук |
12 |
18 |
12 |
15 |
216 |
180 |
180 |
| Картофель |
11 |
22 |
10 |
27 |
242 |
270 |
297 |
| Морковь |
9 |
20 |
7 |
24 |
180 |
168 |
216 |
| Итого |
х |
Х |
х |
х |
638 |
618 |
693 |
Рассчитаем индекс товарооборота:
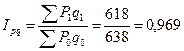 или 96, 9%
или 96, 9%
Товарооборот в целом по данной товарной группе в текущем периоде по сравнению с базисным уменьшился на 3,1 % (100% - 96,9%)
Вычислим сводный индекс цен
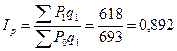 или 89,2%
или 89,2%
По данной товарной группе цены в сентябре по сравнению с августом в среднем снизились на 10,8%.
3) Рассчитаем индекс физического объема реализации:
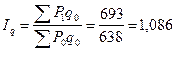 или 108,6 %
или 108,6 %
Физический объем реализации увеличился на 8,6%.
Задача 9
По данным таблицы проведите анализ цен реализации товара в 2-х регионах.
| Регион |
Август |
Сентябрь |
||
| Цена руб. (p0) |
Продано, шт. (q0) |
Цена, руб. (p1) |
Продано, шт. (q1) |
|
| 1 |
12 |
10000 |
13 |
8000 |
| 2 |
17 |
20000 |
19 |
9000 |
| Итого |
х |
30000 |
х |
27000 |
Решение:
Добавим в таблицу расчетные графы
| Регион |
Август |
сентябрь |
Расчетные графы |
||||
| Цена руб. (p0) |
Продано, т (q0) |
Цена за 1 кг., руб. (p1) |
Продано, т (q1) |
P0q0 |
P1q1 |
P0q1 |
|
| 1 |
12 |
10000 |
13 |
8000 |
120000 |
234000 |
216000 |
| 2 |
17 |
20000 |
19 |
9000 |
340000 |
171000 |
153000 |
| Итого |
Х |
30000 |
х |
27000 |
46000 |
405000 |
369000 |
Вычислим индекс переменного состава.
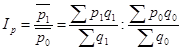 |
![]() или 97,8
или 97,8
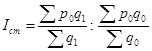 |
Рассчитаем индекс структурных сдвигов
![]() или 89,1%
или 89,1%
Из данных таблицы видно, что цена в каждом регионе в сентябре по сравнению с августом возросла. В целом же, средняя цена снизилась на 2,2%. (97,8% - 100%). Такое несоответствие объясняется влиянием изменением структуры реализации товаров регионам: в сентябре по более высокой цене продавали товара вдвое больше, в сентябре
Ситуация принципиально изменилась. В целом по полученному значению индекса структурных сдвигов можно сделать вывод, что цены за счет структурных сдвигов цены снизились на 10,9% (100%-89,1%)
Задача 10
По данным таблицы определите среднее линейное отклонение, размах вариации, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
| Группы работников по стажу, лет |
Количество рабочих, чел. |
| 6-10 |
15 |
| 10-14 |
30 |
| 14-18 |
45 |
| 18-22 |
10 |
Решение:
Расчетная таблица имеет следующий вид:
| Группы работников по стажу, лет |
Количество рабочих, чел. (f) |
Середина интервала, (х) |
хf |
½x-`x½ |
½x-`x½f |
(x-`x)2 |
(x-`x)2f |
x2 |
x2f |
| 6-10 |
15 |
8 |
120 |
6 |
90 |
36 |
540 |
64 |
960 |
| 10-14 |
30 |
12 |
360 |
2 |
60 |
4 |
120 |
144 |
4320 |
| 14-18 |
45 |
16 |
720 |
2 |
90 |
4 |
180 |
256 |
11520 |
| 18-22 |
10 |
20 |
200 |
6 |
60 |
36 |
360 |
400 |
4000 |
| Всего |
100 |
14 |
1400 |
16 |
300 |
80 |
1200 |
864 |
20800 |
1) Определим средний стаж по формуле средней арифметической
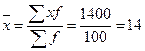 лет
лет
2) Определим среднее линейное отклонение
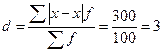 года
года
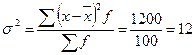
3) Рассчитаем дисперсию
4. Рассчитаем среднее квадратическое отклонение:
![]() года
года
5.Найдем размах вариации:
R=22-6=16 лет
6. Найдем коэффициент вариации:
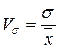
![]()
Рассчитанные показатели свидетельствуют о том, что средний стаж работы составляет 14 лет, отклонение индивидуальных значений стажа от среднего составляет в среднем 3 года; среднее квадратическое отклонение – 3,5 года - небольшое, следовательно, средняя арифметическая хорошо отражает представленную совокупность. Совокупность однородна по изучаемому признаку. Вариация признака < 33, т.е. умеренная.