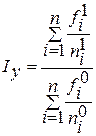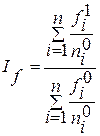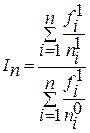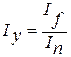| Скачать .docx | Скачать .pdf |
Курсовая работа: Курсовая работа: Статистическая оценка деятельности предприятия строительной отрасли
План
Введение
Раздел 1. Анализ результатов производственной деятельности предприятия
1.1 Общая характеристика предприятия строительной отрасли
1.2 Расчёт показателей динамики изучаемых экономических явлений
1.3 Определение тенденции динамики изучаемых показателей
1.4 Индексный факторный анализ изучаемых показателей
Раздел 2. Определение взаимосвязей и взаимозависимостей между экономическими показателями предприятия
2.1 Характеристика и экономический анализ изучаемых показателей
2.2 Установление наличия и характера взаимосвязи между изучаемыми признаками
2.3 Построение корреляционных уравнений
2.4 Оценка силы корреляционной связи
Выводы
Графическое приложение
Список используемой литературы
Введение
Цель расчетно-графической работы – провести статистический анализ производственно-хозяйственной деятельности предприятия, изучить особенности практической работы по статистике на предприятиях строительной отрасли и приобрести навыки использования статистических методов в анализе производственно-хозяйственной деятельности предприятия. Именно статистические методы позволяют разработать эффективную стратегию развития предприятия, что является одной из главных задач экономиста, на основе прогнозирования динамики основных показателей и соотношений между ними. Анализ производственно-хозяйственной деятельности направлен на оценку её эффективности и рациональности использования сырьевых, трудовых, финансовых и других ресурсов предприятия, выявление резервов производства, подготовку аналитической базы для принимаемых управленческих решений.
Анализ позволяет не только выявить отклонения анализируемых показателей от намеченного (ожидаемого, планового и т.п.) уровня, но и установить причины отклонений, качественную связь между изучаемыми характеристиками.
В каждый данный момент времени показатели работы предприятия имеют определенные количественные характеристики, между ними существуют определенные количественное соотношение. Изменяются размеры явлений, изменяются количественные соотношения как между этими явлениями, так и между признаками одного и того же явления. Вот эта количественная сторона явлений и составляет предмет статистической науки. Но статистика позволяет изучить не только количественную сторону явления, сколько количество в связи с его качественным содержанием. Данные статистики в размерах и количественных отношениях экономических явлений имеют очень большое значение. Они широко используются для решения множества практических вопросов, например, для оценки эффективности использования различных ресурсов, определения закономерностей изменения изучаемых явлений и структуры исследуемых объектов, определения причин изменения отдельных показателей работы предприятия и способов выявления причинно-следственных связей, и на основе проведенного анализа – для поиска резервов повышения эффективности производственно-финансовой деятельности предприятия и путей их использования.
Данная расчетно-графическая работа поможет закрепить все знания, полученные на лекциях, практических занятиях, а также при самостоятельной работе с литературой по курсу «Статистика». Тематика расчетно-графической работы состоит из рассмотрения двух разделов: 1. Анализ результатов производственной деятельности предприятия; 2. Определение взаимосвязей и взаимозависимостей между экономическими показателями предприятия. В конце работы будут приведены выводы из проведённых исследований и даны основные рекомендации о способах повышения эффективности и рентабельности производства. Будет графически проиллюстрирована динамика основных статистических показателей.
производственный хозяйственный статистический анализ
Раздел 1. Анализ результатов производственно-хозяйственной деятельности предприятия
1.1 Общая характеристика предприятия строительной отрасли
Строительство, как отрасль материального производства существенно отличается от других отраслей народного хозяйства. Это объясняется особым характером продукции, условиями вложения денежных средств, их основания и возврата, методами организации и управления строительным процессом, особенностями технологии строительного производства.
Строительное предприятие – это предприятие, которое действует в сфере строительства и осуществляет научные, экспериментальные, изыскательные и проектные работы, добычу сырьевых ресурсов и их переработку, изготовление материалов, изделий и конструкций, возведение всех видов зданий и сооружений, транспортное обслуживание. Деятельность строительных предприятий обеспечивается наличием в их распоряжении необходимых ресурсов: людских, денежных, материальных, энергетических, с помощью которых создаётся продукция. Одним из основных показателей производственно хозяйственной деятельности строительного предприятия является продукция строительного предприятия – это материальные ценности, созданные в результате деятельности строительного предприятия. Продукция может относиться к категории «конечной» (законченные и сданные в эксплуатацию здания и сооружения) или к «промежуточной» - изделия предприятий стройиндустрии, отдельные виды работ, части зданий и др.
Строительные организации – это строительные предприятия, осуществляющие возведение, реконструкцию, капитальный ремонт зданий и сооружений, монтаж оборудования.
Таким образом, различают такие задачи строительных организаций:
1. Новое строительство – строительство зданий, сооружений на новых площадках или на площадках после сноса старых зданий;
2. Расширение производства предприятий – это строительство вторых и последующих очередей определённых предприятий;
3. Техническое перевооружение – полное или частичное перевооружение действующих предприятий без увеличения площадей этих предприятий;
4. Реконструкция – переоборудование и переустройство действующих предприятий с увеличением производственных площадей.
5. Капитальный ремонт – это восстановление зданий и сооружений амортизировавшихся в процессе эксплуатации.
В целом строительная организация состоит из следующих компонентов:
1. Организация-заказчик планирует и финансирует строительство, осуществляет технический надзор за строительством, поставляет оборудование, эксплуатирует результаты строительства;
2. Организация-проектировщик разрабатывает проект строительства: архитектуру, технологию и т.д.; осуществляет авторский надзор над строительством, проектировщик отвечает за правильность составления сметы, за качество и уровень, принятых технических решений;
3. Генеральный подрядчик организовывает и отвечает за строительство в целом, за качество выполняемых работ, за соблюдение срока работ;
4. Субподрядчик отвечает за узкий спектр работ – только за работы, которые ему поручены организацией генподрядчик.
Основной целью строительных организаций является удовлетворение потребностей населения в строительной продукции и получение прибыли, так как за счёт прибыли предприятие может развиваться и получение прибыли является важнейшим условием конкурентоспособности предприятия.
Прибыль – это разница между суммарной выручкой, или суммарными поступлениями, которые получает предприятие от продажи своей продукции, и суммарными экономическими издержками, которые несёт предприятие для того, чтобы произвести и реализовать эту продукцию. Общие экономические издержки оценивают все использованные в процессе производства ресурсы в соответствии с принципом альтернативных издержек. Выручка напрямую зависит от цен и объёма выпускаемой продукции, а объём продукции зависит, прежде всего, от количества трудовых ресурсов и от производительности труда одного работника.
В первом разделе курсовой работы будут рассмотрены такие показатели работы строительного предприятия как численность работников, ввод в действие жилья, производительность труда 1 работника, среднемесячная заработная плата и объем СМР в ценах текущего года.
Численность работников – число работников предприятия ( среднесписочная численность работников), определяется за период более одних суток путём деления суммарной списочной численности работников за календарный день отчётного периода на число календарных дней отчётного периода.
Ввод в действие жилья (объём работ) – количественный показатель, который характеризует объём работ выполненный строительной организацией по основной деятельности (производство строительных конструкций, строительство жилых объектов).
Объем СМР в ценах текущего года – это количественный показатель, который характеризует объем строительно-монтажных работ, выполненных строительной организацией.
Заработная плата - вознаграждение, которое предприятие (фирма) обязано выплатить рабочим и служащим за их труд соразмерно его количеству и качеству по установленным в договоре (контракте) и законе нормам.
Производительность труда - показатель эффективности использования трудовых ресурсов, трудового фактора Измеряется количеством продукции в натуральном или денежном выражении, произведенным одним работником за определенное время (час, день, месяц, год).
Себестоимость продукции – текущие издержки производства и обращения, реализации продукции, исчисленные в денежном выражении. Включают материальные затраты, амортизацию основных средств, заработную плату основного и вспомогательного персонала, дополнительные (накладные) расходы, непосредственно связанные, обусловленные производством и реализацией данного вида и объёма продукции. Чем меньше себестоимость продукции, тем выше прибыль предприятия, а, следовательно, повышается рентабельность предприятия.
В системе экономических показателей себестоимости принадлежит одно из важнейших мест, т.к. она:
- отображает результаты производственно-хозяйственной деятельности;
- является одним из основных элементов, которые определяют прибыль и уровень рентабельности;
- отображает характер использования материальных ресурсов, рабочей силы, уровень хозяйственного руководства строительной организации, уровень культуры труда;
- является основой составляющей стоимости;
- является важным показателем при определении экономической эффективности инвестиций в новую технику, технологию, организацию производства и других следствий.
В первой части первого раздела будет проанализирована динамика показателей ввода в действие жилья и среднемесячной заработной платы за 5 лет, сделаны выводы и изображены графически полученные результаты анализа. Во второй части первого раздела будет проведён индексный анализ производительности труда.
1.2 Расчет показателей динамики ввода в действие жилья и среднемесячной заработной платы
Таблица 1.1 Исходные данные
| Годы |
Ввод в действие жилья, м2 |
Среднемесячная заработная плата, грн. |
| 2006 |
5958,16 |
287,59 |
| 2007 |
5841,45 |
308,43 |
| 2008 |
3090,57 |
304,26 |
| 2009 |
6640,67 |
232,37 |
| 2010 |
5189,16 |
282,38 |
Абсолютные показатели динамики характеризуют скорость изменения уровней динамического ряда и представляют собой разность между сравниваемым уровнем и уровнем более раннего периода, принятым за базу сравнения. Если база сравнения – предыдущий уровень, то показатель является цепным , если за базу сравнения взят начальный уровень, то показатель является базисным .
Абсолютный базисный прирост: ![]() (1.1)
(1.1)
Абсолютный цепной прирост: ![]() (1.2)
(1.2)
Абсолютное изменение имеет ту же единицу измерения, что и уровни ряда с добавлением единицы времени, за которую произошло изменение.
Относительные показатели динамики необходимы для сравнения развития разных объектов, особенно если их абсолютные характеристики различны. Относительные показатели дают возможность определить во сколько раз или на сколько процентов произошло изменение между данным уровнем динамического ряда и предшествующим уровнем (цепным, базисным).
Базисный темп роста:
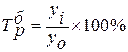 (1.3)
(1.3)
Цепной темп роста:
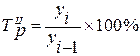 (1.4)
(1.4)
Базисный темп прироста
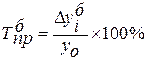 или
или ![]() (1.5 а, б)
(1.5 а, б)
Цепной темп прироста:
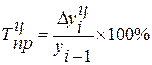 или
или ![]() (1.6 а, б)
(1.6 а, б)
Сравнение абсолютного прироста и темпа прироста за одни и те же периоды времени показывают, что замедление темпов прироста не всегда сопровождается уменьшением абсолютных приростов. Поэтому, чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста. Абсолютное значение одного процента прироста является результатом сопоставления этих величин.
![]() (1.7)
(1.7)
Таблица 1.2.
Показатели динамики ввода в действие жилья за 2006-2010 гг., м2
![]()
| годы |
Абсолютный прирост,у, м2 |
Темп роста, Тр , % |
Темп прироста, Тпр , % |
Абсолютное значение1% прироста, А, м2 |
||||
| 2006 |
5958,2 |
Б |
Ц |
Б |
Ц |
Б |
Ц |
- |
| 2007 |
5841,5 |
-116,71 |
-116,71 |
98,04117 |
98,04117 |
-1,95883 |
-1,95883 |
59,5816 |
| 2008 |
3090,6 |
-2867,59 |
-2750,88 |
51,87122 |
52,90758 |
-48,1288 |
-47,0924 |
58,4145 |
| 2009 |
6640,7 |
682,51 |
3550,1 |
111,455 |
214,8688 |
11,45505 |
114,8688 |
30,9057 |
| 2010 |
5189,2 |
-769 |
-1451,51 |
87,09333 |
78,14212 |
-12,9067 |
-21,8579 |
66,4067 |
![]() = y02
- y01
= 5841,5 – 5958,2 = -116,71
= y02
- y01
= 5841,5 – 5958,2 = -116,71
![]() = y03
- y01
= 3090,6 - 5958,2 = -2867,59
= y03
- y01
= 3090,6 - 5958,2 = -2867,59
Dyб 04 = y04 - y01 = 6640,7 - 5958,2 = 682,51
Dyб 05 = y05 – y01 = 5189,2 - 5958,2= -769
![]() =
=
![]() =
-116,71
=
-116,71
![]() = y03
- y02
= 3090,6 - 5841,5 = -2750,88
= y03
- y02
= 3090,6 - 5841,5 = -2750,88
![]() =
98,04
=
98,04
Трб 03 = (3090,6/5958,2)*100% = 51,87%
Трц 03 = (3090,6/5841,5)*100% = 52,91%
Тпрб 02 = Тпрц 02 = 98,04117-100 = -1, 96%
Тпрб 03 = 51,87 – 100 = -48,13%
Тпрц 03 = 52,90758 – 100 = -47,09% и т. д.
А02
= 5958,2 ![]() 0,01 = 59,5816 и т. д.
0,01 = 59,5816 и т. д.
Таблица 1.3. Показатели динамики среднемесячной заработной платы за 2006 - 2010 гг, грн.
| Годы |
Средне-месячная заработная плата, грн |
Абсолютный прирост,у, м2 |
Темп роста, Тр , % |
Темп прироста, Тпр , % |
Абсолютное значение1% прироста, А, м2 |
|||||
| Б |
Ц |
Б |
Ц |
Б |
Ц |
|||||
| 2006 |
287,59 |
- |
- |
- |
- |
- |
- |
- |
||
| 2007 |
308,43 |
20,84 |
20,84 |
107,25 |
107,25 |
7,25 |
7,25 |
2,87 |
||
| 2008 |
304,26 |
16,67 |
-4,17 |
105,80 |
98,65 |
5,8 |
-1,35 |
3,08 |
||
| 2009 |
232,37 |
-55,22 |
-71,89 |
80,79 |
76,37 |
-19,201 |
-23,63 |
3,04 |
||
| 2010 |
282,38 |
-5,21 |
50,01 |
98,19 |
121,53 |
-1,81 |
21,52 |
2,32 |
||
Рассмотрим соотношения между цепными и базисными показателями по данным таблиц 1.2., 1.3.:
1) Сумма цепных абсолютных приростов равна последнему базисному абсолютному приросту, т. е. приросту за весь промежуток времени.
![]() (1.8)
(1.8)
Для показателей динамики ввода в действие жилья:
-116,71 – 2750,88 + 3550,1 – 1451, 51 = -769
Для среднемесячной заработной платы:
20,84 – 4,17 – 71,89 +50,01 = -5,21
2) Произведение цепных коэффициентов роста равно базисному коэффициенту роста за весь период.
![]() (1.9)
(1.9)
Для показателей динамики ввода в действие жилья:
0,9804*0,5290*2,1486*0,7814 = 0,8707
Для показателей динамики среднемесячной заработной платы:
1,0724*0,9865*0,7637*1,2153 = 0,9819
Определим средние показатели динамики: средний абсолютный прирост, средний темп роста, средний темп прироста и средний уровень ряда.
Эти показатели необходимы при обобщении характеристик тенденции за определённый период и незаменимы при сравнении развития за неодинаковые по длительности отрезки времени, при выборе аналитического выравнивания тренда.
Средний абсолютный прирост:
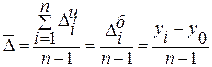 (1.10)
(1.10)
Средний темп роста:
![]() (1.11)
(1.11)
Средний темп прироста:
![]() (1.12)
(1.12)
Таблица 1.4.Средние показатели динамики
| Показатель |
Ввод в действие жилья |
Среднемесячная заработная плата |
| Средний абсолютный прирост |
-192,25 |
-1,27 |
| Средний темп роста |
96,60 |
99,94 |
| Средний темп прироста |
-0,04 |
-0,06 |
Вывод : за анализируемый период 2006- 2010гг. ввод в действие жилья в среднем снизился на 192,25м2 или на 0,04%. Среднемесячная заработная плата снизилась на 1,27 грн. или на 0,06%.
1.3 Определение тенденций динамики ввода в действие жилья и среднемесячной заработной платы
Сглаживание с помощью скользящих средних
Скользящая средняя позволяет сгладить колебания отдельных уровней динамического ряда и довольно отчётливо выявить тенденцию развития показателей. Этот метод является эмпирическим приёмом предварительного анализа.
Таблица 1.5.Расчёт скользящих средних ввода в действие жилья за 2006-2010 гг., м2
![]()
| Годы |
Ввод в действие жилья, м2 |
Скользящая сумма |
Скользящая средняя |
| 2006 |
5958,2 |
- |
- |
| 2007 |
5841,5 |
14890,18 |
4963,393 |
| 2008 |
3090,6 |
15572,69 |
5190,897 |
| 2009 |
6640,7 |
14920,4 |
4973,467 |
| 2010 |
5189,2 |
- |
- |
Вывод: анализируя предварительные данные по скользящим средним показателей ввода в действие жилья можно сделать предварительные выводы о том, что эти показатели подчиняются уравнению параболы.
Таблица 1.6. Расчёт скользящих средних среднемесячной заработной платы за 2006 - 2010 гг., грн.
| Годы |
Среднемесячная заработная плата, грн. |
Скользящая сумма |
Скользящая средняя |
| 287,59 |
- |
- |
|
| 2007 |
308,43 |
900,28 |
300,0933 |
| 2008 |
304,26 |
845,06 |
281,6867 |
| 2009 |
232,37 |
819,01 |
273,0033 |
| 2010 |
282,38 |
- |
- |
Вывод: анализируя предварительные данные по скользящим средним показателей среднемесячной заработной платы можно сделать предварительные выводы о том, что эти показатели подчиняются уравнению прямой, при чем заметна тенденция к понижению.
Метод аналитического выравнивания
Для того чтобы представить количественную модель, выражающую общую тенденцию изменений уровней динамического ряда во времени, используется аналитическое выравнивание ряда динамики. В этом случае фактические уровни заменяются уровнями, вычисленными на основе определённой кривой. Предполагается, что она отражает общую тенденцию изменения во времени изучаемого показателя. При этом выравнивании динамического ряда закономерно изменяющийся уровень изучаемого показателя оценивается как функция времени: Yt = f(t). Выбор формы кривой во многом определяет результаты экстраполяции тренда, поэтому основная задача этого метода состоит в выборе аналитического уравнения, которое наилучшим образом будет описывать тенденцию динамики изучаемых показателей.
Рассмотрим аналитическое выравнивание ряда динамики по прямой, которая описывается уравнением вида:
![]() (1.13)
(1.13)
Для вычисления параметров тренда воспользуемся методом наименьших квадратов. Оптимизация данного метода состоит в минимизации суммы квадратов отклонений фактических уровней ряда от выровненных уровней. Для каждого типа тренда МНК даёт систему нормальных уравнений, разрешив которую вычисляются параметры тренда.
Разрешающая система нормальных уравнений метода аналитического выравнивания по прямой имеет вид:
![]()
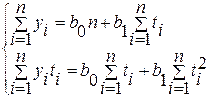 , (
, (![]() )
) 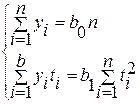
Аналитическое выравнивание ряда динамики по параболе описывается уравнением вида:
![]() (1.14)
(1.14)
Разрешающая система нормальных уравнений метода аналитического выравнивания по параболе имеет вид:
![]()
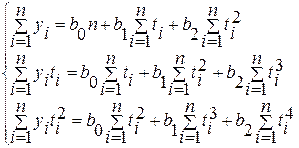 ,
(
,
(![]() )
)
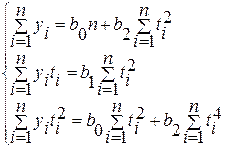 , где b0
, b1
и b2
- параметры уравнений
, где b0
, b1
и b2
- параметры уравнений
Таблица №1.7 Аналитическое выравнивание ввода в действие жилья по прямой
| годы |
Ввод в действие жилья, м2 |
ti |
Yi ti |
Ti 2 |
Yt |
yi -yt |
(yi-yt ) 2 |
| 2006 |
5958,2 |
-2 |
-11916,3 |
4 |
5491,758 |
466,442 |
217568,1 |
| 2007 |
5841,5 |
-1 |
-5841,45 |
1 |
5417,88 |
423,62 |
179453,9 |
| 2008 |
3090,6 |
0 |
0 |
0 |
5344,002 |
-2253,4 |
5077821 |
| 2009 |
6640,7 |
1 |
6640,67 |
1 |
5270,124 |
1370,576 |
1878479 |
| 2010 |
5189,2 |
2 |
10378,32 |
4 |
5196,246 |
-7,046 |
49,64612 |
| Итого |
26720,01 |
0 |
-738,78 |
10 |
26720 |
0,19 |
7353371 |
Значение параметров уравнения прямой рассчитывается следующим образом:
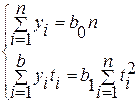 b
0
=(
S
yi
)/
n
=
26720,01/5 =
5344,002
b
0
=(
S
yi
)/
n
=
26720,01/5 =
5344,002
,
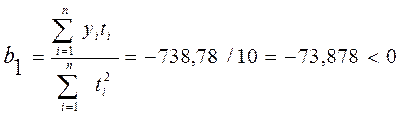
Для данного уравнения b0
– показатель среднего уровня динамического ряда, т.к. вычислительная формула этого параметра совпадает с формулой простой арифметической. b1
– линейный коэффициент регрессии, показывающий направление тренда, в данном случае b1
![]() показывает тенденцию снижения уровней динамического ряда, что видно визуально из таблицы 1.7.
показывает тенденцию снижения уровней динамического ряда, что видно визуально из таблицы 1.7.
Таким образом, уравнение прямой имеет вид:
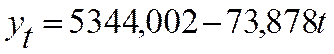
Таблица 1.8 Аналитическое выравнивание ввода в действие жилья по параболе
| годы |
Ввод в действие жилья, м2 |
ti |
Yi*ti |
Ti2 |
yi*ti2 |
Ti4 |
Yt |
Yi - Yt |
(yi-yt)2 |
| 2006 |
5958,2 |
-2 |
-11916,3 |
4 |
23832,8 |
16 |
6010,592 |
-52,392 |
2744,922 |
| 2007 |
5841,5 |
-1 |
-5841,45 |
1 |
5841,5 |
1 |
5158,473 |
683,027 |
466525,9 |
| 2008 |
3090,6 |
0 |
0 |
0 |
0 |
0 |
4825,18 |
-1734,58 |
3008768 |
| 2009 |
6640,7 |
1 |
6640,67 |
1 |
6640,7 |
1 |
5010,713 |
1629,987 |
2656858 |
| 2010 |
5189,2 |
2 |
10378,32 |
4 |
20756,8 |
16 |
5715,072 |
-525,872 |
276541,4 |
| Итого |
26720,01 |
0 |
-738,78 |
10 |
57071,8 |
34 |
26720,03 |
0 |
6411438 |
Значение параметров уравнения параболы рассчитываются следующим образом:
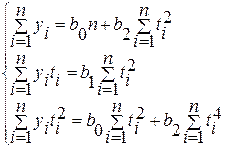 ,
, 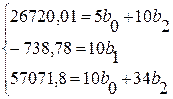 ,
,
![]()
![]() 5b0
= 26720,01– 10b
2
b
2
= 259,413
5b0
= 26720,01– 10b
2
b
2
= 259,413
57071,8 = 2(26720,01 – 10b
2
) + 34b
2
![]() ,
,
![]()
Таким образом, ![]() ,
, ![]() ,
, ![]()
Уравнение параболы имеет вид:
![]()
Так как основной целью аналитического выравнивания является экстраполяция, следовательно, требуется выяснить какое из уравнений прямой или параболы – лучше описывает тенденцию динамики среднесписочной численности работников, для этого рассчитаем среднюю квадратическую ошибку уравнения тренда и коэффициент вариации:
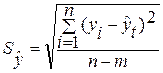 , (1.15)
, (1.15)
где n – число уровней ряда, m – число параметров в уравнении тренда ( для прямой m=2), ![]() - соответственно фактическое и расчётное значения уровней динамического ряда.
- соответственно фактическое и расчётное значения уровней динамического ряда.
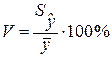
где ![]() - средний уровень динамического ряда. (1.16)
- средний уровень динамического ряда. (1.16)
Для уравнения прямой:
n = 5, m = 2
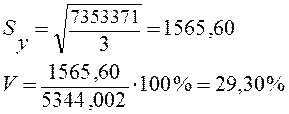
Для уравнения параболы:
n = 5, m = 3
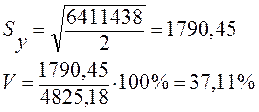
Поскольку коэффициент вариации для уравнения параболы больше, чем для уравнения прямой, то уравнение прямой более точно описывает основную тенденцию динамики ввода в действие жилья.
Аналогичные расчеты аналитического выравнивания по уравнению прямой и параболы для среднемесячной заработной платы представлены в таблицах 1.9, 1.10
Таблица 1.9 Аналитическое выравнивание среднемесячной заработной платы по прямой
| годы |
Среднемесячная заработная плата, грн |
ti |
Yi*ti |
ti^2 |
Yt |
yi-yt |
(yi-yt )^2 |
| 2006 |
287,59 |
-2 |
-575,18 |
4 |
300,302 |
-12,712 |
161,595 |
| 2007 |
308,43 |
-1 |
-308,43 |
1 |
291,654 |
16,776 |
281,434 |
| 2008 |
304,26 |
0 |
0 |
0 |
283,006 |
21,254 |
451,733 |
| 2009 |
232,37 |
1 |
232,37 |
1 |
274,358 |
-41,988 |
1762,99 |
| 2010 |
282,38 |
2 |
564,76 |
4 |
265,71 |
16,67 |
277,889 |
| Итого |
1415,03 |
0 |
-86,48 |
10 |
1415,03 |
0 |
2935,64 |
Таблица 1.10 Аналитическое выравнивание среднемесячной заработной платы по параболе
| годы |
Среднемесячная заработная плата, грн |
ti |
Yi*ti |
ti^2 |
yi*ti^2 |
Ti^4 |
Yt |
yi-yt |
(yi-yt )^2 |
| 2006 |
287,59 |
-2 |
-575,18 |
4 |
1150,36 |
16 |
289,299 |
-1,709 |
2,920681 |
| 2007 |
308,43 |
-1 |
-308,43 |
1 |
308,43 |
1 |
297,158 |
11,272 |
127,058 |
| 2008 |
304,26 |
0 |
0 |
0 |
0 |
0 |
294,011 |
10,249 |
105,042 |
| 2009 |
232,37 |
1 |
232,37 |
1 |
232,37 |
1 |
279,858 |
-47,48 |
2255,11 |
| 2010 |
282,38 |
2 |
564,76 |
4 |
1129,52 |
16 |
254,699 |
27,681 |
766,2378 |
| Итого |
1415,03 |
0 |
-86,48 |
10 |
2820,68 |
34 |
1415,03 |
0 |
3256,369 |
Значение параметров уравнения прямой для среднемесячной заработной платы рассчитываются аналогично вводу в действие жилья:
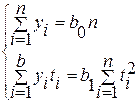
b0
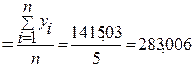
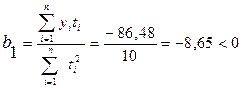
Линейный коэффициент регрессии меньше нуля, поэтому, как и для ввода в действие жилья, наблюдается тенденция снижения уровней динамического ряда среднемесячной заработной платы.
Уравнение прямой имеет вид:
![]()
Аналогичным способом найдем значения параметров уравнения параболы:
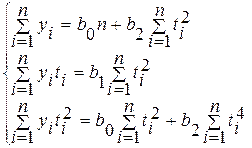
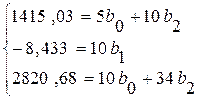
![]() <0
<0
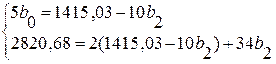 ,
, ![]() ,
,
![]()
Таким образом, b0 = 294 ,011, b1 = - 8, 65, b2 = -5,503
Уравнение параболы имеет вид:
![]()
Так как основной целью аналитического выравнивания является экстраполяция, следовательно, требуется выяснить какое из уравнений прямой или параболы лучше описывает тенденцию динамики ввода в действие жилья, для этого рассчитаем среднюю квадратическую ошибку уравнения тренда и коэффициент вариации:
Для уравнения прямой:
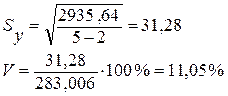
Для уравнения параболы:
![]()
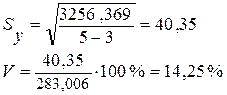
Поскольку коэффициент вариации для уравнения параболы больше, чем для уравнения прямой, то уравнение прямой более точно описывает основную тенденцию динамики среднемесячной заработной платы.
Прогноз показателей динамики на 2006 год
Если предположить, что общие условия, определяющие тенденцию развития в прошлом, не претерпевают существенных изменений и тенденция развития явления характеризуется определёнными аналитическими уравнениями в обоих случаях, то представляется возможность экстраполяции при t = 3.
Для ввода в действие жилья:
![]() = 5122,368м2
– предполагается снижение ввода в действие жилья приблизительно на 1,28% по сравнению с 2010 г.
= 5122,368м2
– предполагается снижение ввода в действие жилья приблизительно на 1,28% по сравнению с 2010 г.
Для среднемесячной заработной платы:
![]() = 257,050грн. – предполагается снижение среднемесячной заработной платы приблизительно на 8,9% по сравнению с 2010 г.
= 257,050грн. – предполагается снижение среднемесячной заработной платы приблизительно на 8,9% по сравнению с 2010 г.
1.4 Индексный факторный анализ производительности труда
Таблица 1.11
| № |
Наименование показателя |
Ед. измере-ния |
Предприятие №1 |
Предприятие №2 |
Предприятие №3 |
|||
| 2009 |
2010 |
2009 |
2010 |
2009 |
2010 |
|||
| 1 |
Объём СМР в ценах текущего года |
тыс. грн. |
4136,74 |
3568,85 |
3224,99 |
3503,20 |
3568,85 |
3977,31 |
| 2 |
Численность работников |
чел. |
291,8 |
281,3 |
283,4 |
277,17 |
281,3 |
284,5 |
| 3 |
Производительность труда 1 работника, в ценах текущего года |
тыс. грн. |
14774,52 |
13217,77 |
11856,92 |
13171,92 |
13217,77 |
14569,24 |
Производительность рассчитывается по следующей формуле:
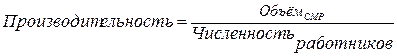 (1.17)
(1.17)
Рассчитаем индивидуальный индекс производительности труда 1-го работника по формуле:
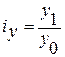 (1.18)
(1.18)
для каждого из трёх предприятий.
Для предприятия №1
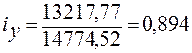 (89,4%)
(89,4%)
Для предприятия №2
![]() (111%)
(111%)
Для предприятия №3
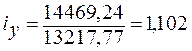 (110,2%)
(110,2%)
Выводы: за 2010г. по сравнению с 2009г. Производительность затрат на первом предприятии снизилась на 10,6%, на втором предприятии возросла на 11%, на третьем предприятии также возросла на 10,2%.
Рассчитаем сводные индексы по следующим формулам, представленным в таблице 1.12
Таблица 1.12
| Сводный индекс производительности труда |
Сводный индекс объёма СМР |
Сводный индекс численности работников |
Взаимосвязь индексов |
|
|
|
|
|
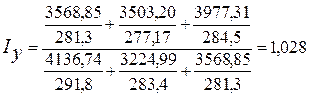 или 102,8%
или 102,8%
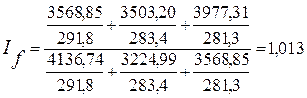 или 101,3%
или 101,3%
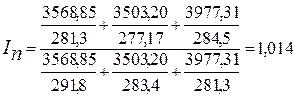 или 101,4%
или 101,4%
Проверим взаимосвязь индексов:
![]() 1,028 = 1,028
1,028 = 1,028
Вывод: в 2010 г. по сравнению с 2009 г. производительность труда 1 работника по всем предприятиям повысилась на 2,8%, объём СМР повысился на 1,3%, а численность работников повысилась до 1,4%.
Проанализируем динамику изменения производительности труда и определим влияние отдельных факторов в нашем случае объём СМР и численность работников на изменение результативного показателя – производительности труда.
Абсолютное изменение производительности труда рассчитаем по формуле:
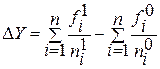 ;
; ![]() (1.19)
(1.19)
Абсолютное сокращение производительности труда, обусловленное изменением объёма СМР рассчитывается по формуле:
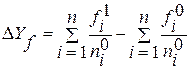 ;
; ![]() (1.20)
(1.20)
Абсолютное сокращение производительности труда, обусловленное изменением численности работников, рассчитывается по формуле:
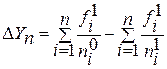 ;
; ![]() (1.21)
(1.21)
Проверка:
1,06 = 0,49 + 0,58; 1,06 = 1,06
Вывод: в 2010 г. по сравнению с 2009 г. производительность труда по всем трём предприятиям возросла на 1,06 тыс. грн, в том числе за счёт роста объёма СМР на 0,49 тыс. грн. и сокращение численности работников на 1 чел.
Рассчитаем индексы переменного, постоянного состава и индекс структурных сдвигов по следующим формулам, представленным в таблице 1.13
Таблица 1.13
| Индекс переменного состава |
Индекс постоянного состава |
Индекс структурных сдвигов |
|
|
|
|
| Характеризует изменение средней рентабельности затрат по всем предприятиям в целом |
Характеризует изменение общей рентабельности затрат за счёт изменения рентабельности затрат каждого предприятия |
Характеризует изменение средней рентабельности затрат за счёт структурных сдвигов на предприятиях |
![]() =(102,7%)
=(102,7%)
![]() =(103%)
=(103%)
![]()
= (99,7%)
Проверим взаимосвязь индексов:
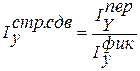 (1.22)
(1.22)
![]() , 0,997= 0,997
, 0,997= 0,997
Вывод: Средняя производительность труда по всем предприятиям в целом выросла на 2,7%, в том числе за счёт увеличения производительности труда по всем предприятия на 3% и за счёт изменения структуры предприятий средняя производительность труда снизилась на 0,3%.
Раздел 2. Определение взаимосвязей и взаимозависимостей между экономическими показателями
2.1 Характеристика и экономический анализ показателей
Современная наука исходит из взаимосвязи всех явлений в природе и обществе. Объём продукции предприятия связан с численностью работников, мощностью двигателей, стоимостью производственных фондов и ещё многими признаками.
Невозможно управлять явлениями, предсказать их развитие без изучения характера, силы и других особенностей связи. Поэтому методы исследования, измерения связей составляют чрезвычайно важную часть методологии научного исследования, в том числе и статистического.
Корреляционная связь между признаками может возникать разными путями. Важнейший путь – причинная зависимость результативного признака (его вариации) от вариации факторного признака.
В данном разделе будут рассмотрены такие показатели работы предприятий строительной отрасли как ввод в действие жилья, продуктивность работы 1чел. В ценах текущего года и себестоимость.
Экономический смысл таких категорий как численность работников, ввод в действие жилья и себестоимость были рассмотрены в первом разделе в пункте 1.1.
В данном случае себестоимость является результативным признаком. Ввод в действие жилья – первичным факторным признаком. Продуктивность работы 1 чел. в ценах текущего года - вторичным факторным признаком.
Далее будут выявлены зависимости между показателями с помощью методов сравнения параллельных рядов и аналитических группировок, а также с помощью корреляционно-регрессионного анализа. Оценка силы связи будет определена с помощью корреляционного отношения и коэффициента Пирсона. Существенность коэффициентов регрессии будет проверена с помощью коэффициентов эластичности, критериев Стьюдента и Фишера.
2.2 Установление наличия и характера взаимосвязи между признаками
Таблица 2.1. Исходные данные
| № |
Ввод в действие жилья м2 |
Продуктивность работы 1 чел. в ценах текущего года |
Себестоимость, тыс.грн. |
| Х |
V |
У |
|
| 1 |
5958,2 |
14774,52 |
4969,30 |
| 2 |
5841,5 |
14569,24 |
5063,08 |
| 3 |
3090,6 |
11856,92 |
5093,30 |
| 4 |
6640,7 |
13171,92 |
5256,89 |
| 5 |
5189,2 |
13217,77 |
5138,10 |
Наличие и характер взаимосвязи можно определить при помощи двух методов: сравнения параллельных рядов и аналитических группировок.
Сравнение параллельных рядов позволяет сделать вывод о наличии достаточно сильной обратной связи в первой паре сравниваемых признаков, в данном случае ярко прослеживается по всей совокупности, что увеличение численности работников ведёт к снижению себестоимости. В остальных парах сравниваемых признаков достаточно сложно определить направление связи, можно предположить, что в третьей паре сравниваемых признаков прослеживается прямая связь.
Воспользуемся методом аналитических группировок, который благодаря группировке и усреднению величин результативного признака позволит более чётко увидеть связь сравниваемых признаков.
Сгруппируем данные в 3 группы:
![]() (2.1)
(2.1)
![]()
![]()
Таблица 2.3Аналитические группировки
| Группы по первичному факторному признаку (Х) |
Среднее значение результативного признака в группе (у) |
|
| 3090,6 – 4273,97 |
5093,30 |
|
| 4273,97 – 5457,34 |
5138,10 |
|
| 5457,34 – 6640,71 |
5096,42 |
|
| Группы по вторичному факторному признаку (V) |
Среднее значение результативного признака в группе (у) |
|
| 11856,92 – 12829,45 |
5093,30 |
|
| 12829,45 – 13801,98 |
5197,49 |
|
| 13801,98 – 14774,52 |
5016,19 |
|
| Группы по первичному факторному признаку (Х) |
Среднее значение в группе другого факторного признака (V) |
|
| 3090,6 – 4273,97 |
11856,92 |
|
| 4273,97 – 5457,34 |
13217,77 |
|
| 5457,34 – 6640,71 |
14138,23 |
|
Вывод: Метод аналитических группировок показал, что в первых двух парах признаков существует обратная связь (с ростом факторного признака происходит уменьшение результативного признака), которая может быть выражена уравнением параболы. В последней паре признаков наблюдается прямая связь, поэтому она может быть выражена уравнением прямой.
2.3 Построение корреляционных уравнений
Уравнение параболы имеет вид:
![]() (2.2)
(2.2)
Применяя метод наименьших квадратов, получим разрешающую систему уравнений:
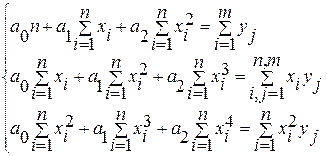
Нахождение параметров уравнения парной корреляции для связи между Х и Y для уравнения прямой
| № |
x |
y |
xy |
x^2 |
y(x) |
y-y(x) |
(y-y(x))^2 |
| 1 |
3090,6 |
5093,3 |
15741353 |
9551808,4 |
5069,46 |
23,8423 |
568,454 |
| 2 |
5189,2 |
5138,1 |
26662629 |
26927797 |
5101,75 |
36,3487 |
1321,23 |
| 3 |
5841,5 |
5063,1 |
29575982 |
34123122 |
5111,79 |
-48,689 |
2370,62 |
| 4 |
5958,2 |
4969,3 |
29608083 |
35500147 |
5113,58 |
-144,28 |
20818,1 |
| 5 |
6640,7 |
5256,9 |
34909429 |
44098896 |
5124,09 |
132,813 |
17639,2 |
| Итог |
26720,2 |
25520,67 |
136497476 |
25520,7 |
0 |
42717,6 |
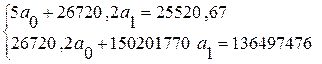
Решив систему матричным методом, находим:
![]() = 5021,8991
= 5021,8991
![]() = 0,01538815
= 0,01538815
Отсюда, уравнение прямой имеет вид: y x = 5018,47+0,02 x
Таблица 2.5. Нахождение параметров уравнения парной корреляции для связи между X и Y по параболе
| № |
x |
y |
x*y |
x^2 |
x2*y |
x^3 |
x^4 |
y(x) |
| 1 |
3090,6 |
5093,3 |
15741353 |
9551808,4 |
48650225724 |
29520818917 |
91237042946166 |
4728,821611 |
| 2 |
5189,2 |
5138,1 |
26662629 |
138355020986 |
13971756626 |
725106231885195 |
3978,723378 |
|
| 3 |
5841,5 |
5063,1 |
29575982 |
34123122 |
172765366686 |
199279038321 |
1164387472088440 |
3745,573146 |
| 4 |
5958,2 |
4969,3 |
29608083 |
35500147 |
211516975855,4 |
211495677912 |
1260260454061680 |
3703,861308 |
| 5 |
6640,7 |
5256,9 |
34909429 |
44098896 |
23182789672 |
292754944000 |
194471267135730 |
3459,916752 |
| Σ |
26720,2 |
25520,67 |
136497476 |
150201770 |
754465259799,4 |
843247226502 |
5185703872617220 |
25520,67 |
| Y-Y(x) |
(Y-Y(x))^2 |
| 364,4783888 |
132844,4959 |
| 1159,376622 |
1344154,151 |
| -1317,526854 |
1735877,011 |
| 1265,438692 |
1601335,084 |
| -1796,983248 |
3229148,792 |
| 0 |
8043359,534 |
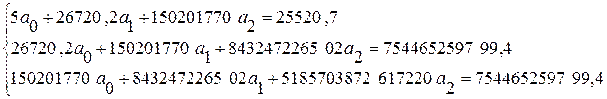
Решив систему методом обратной матрицы, находим:
![]() =
5833,488341,
=
5833,488341, ![]() =
-0,357426816
=
-0,357426816 ![]() =0
=0
Следовательно, уравнение параболы имеет вид:
![]()
Чтобы узнать, какое из уравнений – параболы или прямой – лучше описывает корреляционную связь, рассчитаем среднюю квадратическую ошибку:
Для прямой: ![]()
а также коэффициент вариации: ![]()
Для параболы:
![]() и
и ![]()
Так как коэффициент вариации для уравнения прямой меньше, чем для уравнения параболы, уравнение прямой более точно описывает корреляционную связь между поизводительностью труда 1 работника и рентабельности.
Таблица 2.6. Нахождение параметров уравнения парной корреляции для связи между V и Y для уравнения прямой
| № |
v |
y |
v^2 |
v*y |
y(v) |
y-y(v) |
(y-y(v))^2 |
| 1 |
11857 |
5093,3 |
140586552 |
60390850,6 |
5218,623 |
-125,3232 |
15705,90446 |
| 2 |
13172 |
5256,9 |
173499476 |
69243334,5 |
5166,023 |
90,8668 |
8256,775342 |
| 3 |
13218 |
5138,1 |
174709444 |
67914224 |
5164,189 |
-26,0892 |
680,6463566 |
| 4 |
14569 |
5063,1 |
212262754 |
73765227,7 |
5110,13 |
-47,0504 |
2213,74014 |
| 5 |
14775 |
4969,3 |
218286441 |
73419022,2 |
5101,919 |
-132,6192 |
17587,85221 |
| Итог о |
67590,37 |
25520,67 |
919344668 |
344732659 |
25520,67 |
0 |
44444,9 |
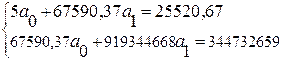
Решив систему матричным методом, находим:
![]() = 5692.89
= 5692.89
![]() = -0.04
= -0.04
Отсюда, уравнение прямой имеет вид:
![]()
Таблица 2.7. Нахождение параметров уравнения парной корреляции для связи между V и Y по параболе
| v |
y |
v*y |
v^2 |
v^2y |
v^3 |
v^4 |
y(v) |
||||
| 1 |
11857 |
5093,3 |
60390850,6 |
140586552 |
716049485302 |
1666957239793 |
19765111992225600 |
5188,935877 |
|||
| 2 |
13172 |
5256,9 |
69243334,5 |
173499476 |
912069395384 |
2285362864448 |
30102799650509100 |
5122,197135 |
|||
| 3 |
13218 |
5138,1 |
67914224 |
174709444 |
897674594216 |
2309389796232 |
30525514326594600 |
5119,862547 |
|||
| 4 |
14569 |
5063,1 |
73765227,7 |
212262754 |
1074707549777 |
3092354182009 |
45052508077689100 |
5051,296737 |
|||
| 5 |
14775 |
4969,3 |
73419022,2 |
218286441 |
1084730811261 |
3225391734375 |
47655162875390600 |
5040,841846 |
|||
| Итог |
67590,37 |
25520,67 |
344732659 |
919344668 |
4685231835941 |
12579455816857 |
173101096922409000 |
25520,67 |
|||
| y-y(v) |
(y-y(v))^2 |
||||||||||
| -95,6358768 |
9146,220948 |
||||||||||
| 134,7028654 |
18144,86194 |
||||||||||
| 18,23745257 |
332,6046763 |
||||||||||
| 11,80326308 |
139,3170193 |
||||||||||
| -71,5418465 |
5118,2358 |
||||||||||
| 0 |
32881,24039 |
||||||||||
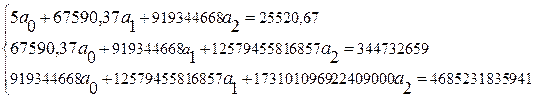
Решив систему методом обратной матрицы, находим:
![]() =5790,701099 a1
= -0,050751895 ,
=5790,701099 a1
= -0,050751895 , ![]() a2
= 0
a2
= 0
Следовательно, уравнение параболы имеет вид:
![]()
Чтобы узнать, какое из уравнений – прямой или параболы – лучше описывает корреляционную связь, рассчитаем:
Для прямой:
![]()
а также коэффициент вариации:
![]()
Для параболы:
![]() и
и ![]()
Так как коэффициент вариации для уравнения прямой меньше, чем для уравнения параболы, уравнение прямой более точно описывает корреляционную связь между выручкой и рентабельностью.
Таблица 2.8 . Нахождение параметров уравнения парной корреляции для связи между X и V по прямой
| № |
x |
v |
x*v |
x^2 |
v(x) |
v-v(x) |
(v-v(x))^2 |
| 1 |
3090,6 |
11856,92 |
36644996,95 |
9551808,36 |
12107,98058 |
-251,0605779 |
63031,4138 |
| 2 |
5189,2 |
13217,77 |
68589652,08 |
26927796,64 |
13421,18264 |
-203,4126404 |
41376,70226 |
| 3 |
5841,5 |
14569,24 |
85106215,46 |
34123122,25 |
13829,36033 |
739,8796672 |
547421,922 |
| 4 |
5958,2 |
14774,52 |
88029545,06 |
35500147,24 |
13902,38553 |
872,1344691 |
760618,5323 |
| 5 |
6640,7 |
13171,92 |
87470769,14 |
44098896,49 |
14329,46092 |
-1157,540918 |
1339900,977 |
| Итог |
26720,2 |
67590,4 |
365841179 |
150201771 |
67590,37 |
0,00 |
2752349,547 |
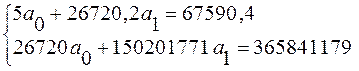
Решив систему методом обратной матрицы, находим:
![]() = 10174,03;
= 10174,03; ![]() =0,625751
=0,625751
Следовательно, уравнение прямой имеет вид:
![]()
Таблица 2.9. Нахождение параметров уравнения парной корреляции для связи между Х и V по параболе
| № |
x |
v |
x*v |
x^2 |
x^2v |
x^3 |
x^4 |
v(x) |
| 1 |
3090,6 |
11856,92 |
36644996,95 |
9551808,36 |
113255027579,9 |
29520818917,4 |
91237042946165,9 |
11688,07134 |
| 2 |
5189,2 |
13217,77 |
68589652,08 |
26927796,64 |
355925422594,3 |
139733722324,3 |
725106231885195,0 |
14080,87648 |
| 3 |
5841,5 |
14569,24 |
85106215,46 |
34123122,25 |
497147957609,6 |
199330218623,4 |
1164387472088440,0 |
14113,05705 |
| 4 |
5958,2 |
14774,52 |
88029545,06 |
35500147,24 |
524497635400,3 |
211516977285,4 |
1260260454061680,0 |
14084,71225 |
| 5 |
6640,7 |
13171,92 |
87470769,14 |
44098896,49 |
580867136654,6 |
292847541921,1 |
1944712671635730,0 |
13711,67003 |
| Σ |
26720,2 |
67590,4 |
365841179 |
150201771 |
2071693179838,6 |
872949279071,6 |
5185703872617220,0 |
67590,38714 |
| v-v(x) |
(v-v(x))^2 |
|||||||
| 168,84866 |
28509,87 |
|||||||
| -863,10648 |
744952,79 |
|||||||
| 456,18296 |
208102,89 |
|||||||
| 689,80775 |
475834,73 |
|||||||
| -539,75003 |
291330,1 |
|||||||
| 0 |
1748730,4 |
|||||||
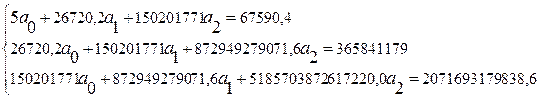
Решив систему методом обратной матрицы, находим:
![]() = 2306,042255;
= 2306,042255; ![]() = 4,24,
= 4,24, ![]() = -0,00038.
= -0,00038.
Следовательно, уравнение прямой имеет вид:
![]()
Среднее значение выручки за вычетом НДС: ![]() .
.
Чтобы узнать, какое из уравнений – прямой или параболы – лучше описывает корреляционную связь между производительностью труда 1 работника и рентабельностью, рассчитаем:
Для прямой: ![]()
а также коэффициент вариации: ![]()
Для параболы: ![]() и
и ![]()
Так как коэффициент вариации для уравнения параболы меньше, чем для уравнения прямой, уравнение параболы более точно описывает корреляционную связь.
2.4 Оценка силы корреляции
Корреляционное отношение: 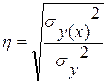 , (2.4)
, (2.4)
где 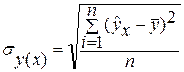 (2.5)- дисперсия результативного признака у
, величина которого объясняется связью с фактором х
(факторная дисперсия). Она вычисляется по индивидуальным данным, полученным для каждой единицы совокупности на основе уравнения регрессии;
(2.5)- дисперсия результативного признака у
, величина которого объясняется связью с фактором х
(факторная дисперсия). Она вычисляется по индивидуальным данным, полученным для каждой единицы совокупности на основе уравнения регрессии;
![]()
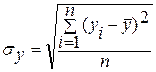 (2.6) – общая дисперсия результативного признака, выражающая влияние на него всех причин и условий.
(2.6) – общая дисперсия результативного признака, выражающая влияние на него всех причин и условий.
Чем ближе значение корреляционного отношения к 1, тем теснее связь между признаками.
![]() Таблица 2.7
Таблица 2.7![]() Вспомогательная таблица для расчёта дисперсий для связи X и Y
Вспомогательная таблица для расчёта дисперсий для связи X и Y
| № |
Y |
Y(X) |
(Y-Yср)^2 |
(Y(X)-Yср)^2 |
| 1 |
5093,3 |
5069,46 |
117,5056 |
1202,7024 |
| 2 |
5138,1 |
5101,75 |
1153,2816 |
5,7121 |
| 3 |
5063,1 |
5111,79 |
1684,2816 |
58,5225 |
| 4 |
4969,3 |
5113,58 |
18181,8256 |
89,1136 |
| 5 |
5256,9 |
5124,09 |
23335,6176 |
398,0025 |
| Итого |
25520,67 |
25520,7 |
44472,512 |
1754,0531 |
| Среднее |
5104,14 |
![]()
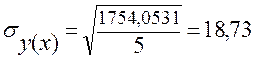
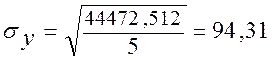
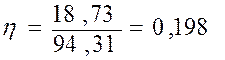
Поскольку величина корреляционного отношения находится в интервале ![]() , значит, связь между признаками X и Y - слабая. Таким образом, вариация результативного признака у
, значит, связь между признаками X и Y - слабая. Таким образом, вариация результативного признака у
![]() обусловлена не только действием фактора х
, но и другими причинами и факторами.
обусловлена не только действием фактора х
, но и другими причинами и факторами.
Таблица 2.8Вспомогательная таблица для расчёта дисперсий для связи V и Y
| № |
Y |
Y(V) |
(Y-Yср)^2 |
(Y(V)-Yср)^2 |
| 1 |
5093,3 |
5218,623 |
117,5056 |
13106,35729 |
| 2 |
5256,9 |
5166,023 |
23335,6176 |
3829,505689 |
| 3 |
5138,1 |
5164,189 |
1153,2816 |
3605,882401 |
| 4 |
5063,1 |
5110,13 |
1684,2816 |
35,8801 |
| 5 |
4969,3 |
5101,919 |
18181,8256 |
4,932841 |
| Итого |
25520,67 |
25520,67 |
44472,512 |
20582,55832 |
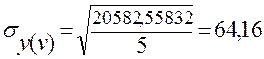
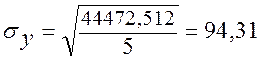
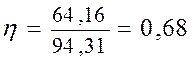
Поскольку величина корреляционного отношения близка к единице и находится в интервале ![]() , значит, связь между признаками V и Y - умеренная, но с учётом погрешностей можно сказать даже слабая. Таким образом, вариация результативного признака у
, значит, связь между признаками V и Y - умеренная, но с учётом погрешностей можно сказать даже слабая. Таким образом, вариация результативного признака у
![]() обусловлена не только действием фактора х
, но и другими причинами и факторами.
обусловлена не только действием фактора х
, но и другими причинами и факторами.
Таблица 2.9 Впомогательная таблица для расчёта дисперсий связи Х и V
| № |
V |
V(X) |
(V-Vср)^2 |
(V(X)-Vср)^2 |
| 1 |
11856,92 |
12107,98058 |
2759432,612 |
1988363,453 |
| 2 |
13217,77 |
13421,18264 |
90182,49242 |
9387,935643 |
| 3 |
14569,24 |
13829,36033 |
1104949,96 |
96899,17924 |
| 4 |
14774,52 |
13902,38553 |
1578656,551 |
147695,3521 |
| 5 |
13171,92 |
14329,46092 |
119822,5917 |
658348,7339 |
| Итого |
67590,4 |
67590,37 |
5653044,206 |
2900694,654 |
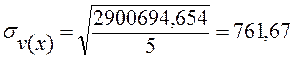
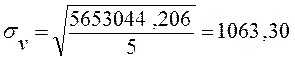
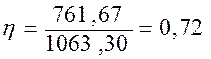
Поскольку величина корреляционного отношения близка к единице и находится в интервале ![]() , значит, практически вся вариация результативного признака у
, значит, практически вся вариация результативного признака у
![]() обусловлена действием фактора x. Таким образом, связь между признаками V и X - сильная.
обусловлена действием фактора x. Таким образом, связь между признаками V и X - сильная.
Теснота парной линейной корреляционной связи, кроме корреляционного отношения, может быть измерена коэффициентом корреляции Пирсона. Этот показатель представляет собой стандартизованный коэффициент регрессии, т.е. коэффициент, выраженный не в абсолютных единицах измерения признаков, а в долях среднего квадратического отклонения результативного признака.
Рассчитаем линейный коэффициент парной корреляции:
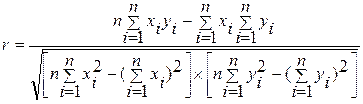 (2.7)
(2.7)
Для связи Х и V:
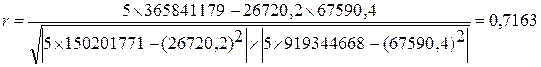
Полученное значение линейного коэффициента корреляции свидетельствует о наличии сильной обратной связи между вводом в действие жилья (Х) и продуктивностью работы 1 чел. в ценах текущего года (V).
При проверке возможности использования линейной функции в качестве формы уравнения определяют разность квадратов:
![]() (2.8)
(2.8)
(0,72)2 – (-0,7163)2 = 0 < 0,1
Данная разность доказывает правильность применения линейного уравнения корреляционной зависимости для связи Х и V.
Коэффициент корреляции достаточно точно оценивает степень тесноты связи лишь в случае наличия линейной зависимости между признаками. Однако линейный коэффициент корреляции нецелесообразно применять при наличии криволинейной зависимости, поскольку он недооценивает степень тесноты связи и даже может быть равен нулю.
Действительно значение коэффициента корреляции для связей, где предполагалась параболическая зависимость, очень мало:
r = 0,1989 – для связи X и Y
r = - 0,5138 – для связи V и Y
Следовательно, условие (2.8) выполняется, что доказывает правильность применения нелинейного уравнения (уравнения параболы) корреляционной зависимости для связи Х и V и связи X и Y.
Показатели корреляционной связи, вычисленные по ограниченной совокупности, являются лишь оценками той или иной статистической закономерности, поскольку в любом параметре сохраняется элемент не полностью погасившейся случайности, присущей индивидуальным значениям признаков. Поэтому необходима статистическая оценка степени точности и надёжности параметров корреляции. Оценка линейного коэффициента корреляции и корреляционного отношения осуществляется с помощью критерия Стьюдента, критерия Фишера, среднеквадратической ошибки уравнения регрессии, а также коэффициента эластичности.
Критерий Стьюдента рассчитывается по формуле :
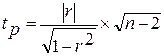 (2.9)
(2.9)
По таблице распределения Стьюдента для числа степеней свободы – 3 и уровня значимости ![]() критическое значение коэффициента Стьюдента tкр
=3,182.
критическое значение коэффициента Стьюдента tкр
=3,182.
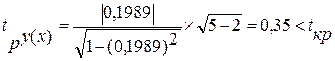
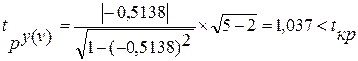
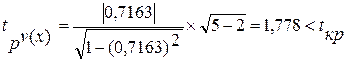
Таким образом, лишь с вероятностью меньше 5% можно утверждать, что величина tр = 0,35 могла появиться в силу случайностей выборки. Такое событие маловероятно, а поэтому можно считать с вероятностью 95%, что в генеральной совокупности действительно существует обратная связь между изучаемыми признаками, т.е. отличие выборочного коэффициента от нуля является существенным и связь установлена надёжно.
Однако следует отметить, что коэффициент корреляции для связи Х и V близок к единице, следовательно, распределение его оценок отличается от нормального или распределения Стьюдента, так как он ограничен величиной 1. В таких случаях более целесообразно использовать метод преобразования корреляции, предложенный Фишером, где для оценки надёжности коэффициента его величину преобразовывают в форму, не имеющую такого ограничения.
Критерий Фишера рассчитывается по формуле:
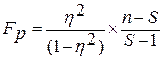 , (2.10)
, (2.10)
где S – число параметров уравнения; n – количество изучаемых уровней
Критерий Фишера для n = 5 и уровня значимости ![]() = 0,05 для линейной связи Fкр
= 10,13, а для параболической связи Fкр
= 19
= 0,05 для линейной связи Fкр
= 10,13, а для параболической связи Fкр
= 19
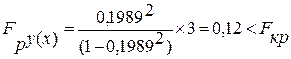
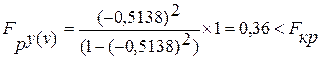
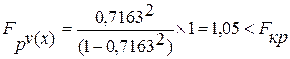
Следовательно, зависимость между признаками Х и Y, Y и V, а также Х и V не выявилась существенной.
Коэффициент регрессии применяется для определения коэффициента эластичности, который показывает, на сколько процентов изменится величина результативного признака при изменении признака-фактора на 1%.
Коэффициент эластичности рассчитывается по формуле:
![]() , (2.12)
, (2.12)
где ![]() - среднее значение факторного признака;
- среднее значение факторного признака;
![]() - среднее значение результативного признака
- среднее значение результативного признака
Для связи Х и Y: ![]()
Для связи V и Y: ![]()
Для связи Х и V: ![]()
Следовательно, с увеличением производительности труда 1 человека, в ценах текущего года и ввода в действие жилья на 1% себестоимость увеличивается на 0,16% и снижается на 0,13% соответственно. С увеличением продуктивности работы 1 чел. на 1% ввод в действие жилья увеличивается на 1,68%.
Выводы
Данное индивидуальное задание содержит следующие статистические методы: метод скользящей средней, метод аналитического выравнивания, экстраполяцию, индексный метод, метод аналитических группировок и сравнения параллельных рядов, корреляционный и регрессионный метода анализа.
- В первом разделе данной расчетно-графической работы были рассчитаны различные показатели динамики (абсолютный прирост, темп роста, темп прироста, абсолютное изменение одного процента прироста, а также средние показатели динамики) ввода в действие жилья и среднемесячной заработной платы за 5 лет, для выявления тенденций динамики были построены аналитические уравнения и результаты анализа представлены в графическом приложении.
- За анализируемый период 2006- 2010гг. ввод в действие жилья в среднем снизился на 192,25м2 или на 0,04%. Среднемесячная заработная плата снизилась на 1,27 грн. или на 0,06%.
- Аналитические уравнения, составленные в этом разделе позволили построить прогнозы ввода в действие жилья и среднемесячной заработной платы. Выявилось, что коэффициент вариации для уравнения параболы больше, чем для уравнения прямой, значит, уравнение прямой более точно описывает основную тенденцию динамики ввода в действие жилья, аналогичная ситуация наблюдается для динамики среднемесячной заработной платы.
- Прогнозы показали снижение ввода в действие жилья приблизительно на 1,28%, а также снижение среднемесячной заработной платы приблизительно на 8,9% по сравнению с уровнем 2010 г.
- Индексный факторный анализ рентабельности затрат показал, что в 2010 г. по сравнению с 2009 г. производительность труда 1 работника по всем предприятиям повысилась на 2,8%, объём СМР повысился на 1,3%, а численность работников повысилась на 1,4%.
- Оценка деятельности каждого предприятия показала, что за 2010г. по сравнению с 2009г. производительность затрат на первом предприятии снизилась на 10,6%, на втором предприятии возросла на 11%, на третьем предприятии также возросла на 10,2%.
- Индексы по методу средних отношений показали, что средняя производительность труда по всем предприятиям в целом выросла на 2,7%(что показывает индекс переменного состава), в том числе за счёт увеличения производительности труда по всем предприятия на 3% (это показывает индекс постоянного состава) и за счёт изменения структуры предприятий средняя производительность труда снизилась на 0,3%(это показывает индекс структурных сдвигов).
- Во втором разделе анализировалась взаимосвязь между себестоимостью (результативный фактор) и вводом в действие жилья и производительностью труда 1 чел. в ценах текущего года (факторные признаки), построены и проанализированы корреляционные уравнения, оценена сила корреляционной связи.
- Метод сравнения параллельных рядов, метод аналитических группировок и корреляционно-регрессионный анализ показали, что между продуктивностью работы 1 чел. и себестоимостью существует обратная связь (т.е. с ростом факторного признака происходит уменьшение результативного), которую можно выразить уравнением параболы. Связь между вводом в действие жилья и себестоимостью описывается уравнением параболы, а между численностью работников и вводом в действие жилья – уравнением прямой , как и предполагалось первоначально.
- Полученные значения корреляционного отношения свидетельствуют о наличии сильной связи между продуктивностью работы 1 чел. в ценах текущего года и себестоимостью, а также между продуктивностью работы 1 чел. в ценах текущего года и вводом в действие жилья. Между вводом в действие жилья и себестоимостью обнаружена умеренная связь, но с учётом погрешностей можно сказать даже слабая.
- По результатам расчёта критерия Фишера можно сделать вывод о том, что связь между продуктивностью работы 1 чел. и себестоимостью, вводом в действие жилья и себестоимостью, а также продуктивностью работы 1 чел. в ценах текущего года и вводом в действие жилья не выявилась существенной.
- Результаты расчёта коэффициента эластичности показали, что с увеличением продуктивности работы 1 человек, в ценах текущего года и ввода в действие жилья на 1% себестоимость увеличивается на 0,16% и снижается на 0,13% соответственно. С увеличением продуктивности работы 1 чел. на 1% ввод в действие жилья увеличивается на 1,68%.
На мой взгляд, предприятие работает не очень эффективно, поскольку наблюдается нестабильность экономических показателей исследуемого периода. Увеличение численности работников обеспечивает пропорциональное снижение себестоимости, однако это экстенсивный способ снижения себестоимости, который не всегда учитывает качество выполняемых работ и высокий уровень производительности труда.
Основные пути повышения эффективности производства строительного предприятия:
Эффективное производство достигается тогда, когда уже невозможно перераспределить наличные ресурсы, чтобы увеличить выпуск одного экономического блага без уменьшения выпуска другого.
1. Совершенствование аппарата управления, систематическое повышение уровня квалификации работников, подготовка кадровых резервов, потенциально способных к управленческой деятельности.
2. Повышения уровня технологий, задействованных в процессе строительства, для увеличения производительности труда.
3. Повышение качества и темпов ввода в действие жилья.
4. Воспользоваться принципом возрастающей экономии от масштаба, т.е. необходимо наращивать объём производства, поскольку это приводит к относительной экономии имеющихся ресурсов.
5. Активная инновационная деятельность предприятия – основа для снижения издержек производства, улучшения экологического состояния окружающей среды, а, следовательно, и получения дополнительной экономической прибыли.
6. Определение экономической целесообразности сооружения, размещения данного объекта в данной местности с учётом обеспечения предприятия сырьём, топливом, водой, а также условий реализации готовой продукции.
7. Учёт не только прямых, но и дополнительных затрат.
8. Рациональные проектные решения.
9. Исключение земляных работ в зимний период времени.
10. Автоматизация производственных процессов, применение эффективных машин и механизмов.
11. Развитие малоотходных и ресурсосберегающих технологий – создание замкнутых технологических циклов, с полным использованием поступающего сырья и не вырабатывающих отходов, выходящих за их рамки.
12. Повышение эффективности использования топливно-энергетических ресурсов за счёт совершенствования эксплуатации действующего энергетического хозяйства на предприятии и внедрение широкой гаммы энергосберегающих мероприятий – от автоматизированных систем учёта до модернизации технологических процессов.