Реферат: Теоремы Генки механика деформируемого твердого тела

Содержание.

Введение………………………………………………………………… 3

1. Основные уравнения………………………………………………. 4

1.1. Общие положения……………………………………………… 4

1.2. Основные уравнения………………………………………….. 4

1.3. Линии скольжения……………………………………………. 6

1.4. Состояние текучести…………………………………………. 7

1.5. Полуобратный метод………………………………………… 8

2. Линии скольжения, их свойства………………………………… 9

2.1. Характеристические линии………………………………… 9

2.2. Свойства линий скольжения………………………………. 13

Введение.

Первые работы по математической теории пластичности относятся к семидесяти годам XIX века и связаны с именами Сен-Венана, рассмотревшего уравнения плоской деформации, и М. Леви, составившего, следуя идеям Сен-Венана, уравнения в трехмерном случае; ему же принадлежит способ линеаризации уравнений плоской задачи.

В последующие годы развитие теории пластичности протекало вяло. Некоторое оживление наступило в начале XX века, когда были опубликованы работы Хаара и Кармана (1909 г.) и Р. Мизеса (1913 г.). В первой из них сделана попытка получить уравнения теории пластичности исходя из некоторого вариационного принципа. В работе Мизеса четко сформулировано новое условие текучести (условие постоянства интенсивности касательных напряжений).

Начиная с двадцатых годов, теория пластичности интенсивно развивается, вначале – преимущественно в Германии. В работах Г. Генки, Л. Прандтля, Р. Мизеса и других авторов были получены важные результаты как по основным уравнениям теории пластичности, так и по методам решения плоской задачи. К этому времени относятся и первые систематические экспериментальные исследования законов пластической деформации при сложном напряженном состоянии, а также первые успешные приложения теории пластичности к техническим вопросам. Уже с тридцатых годов теория пластичности привлекает внимание широкого круга ученых и инженеров; развертываются интенсивные теоретические и экспериментальные исследования во многих странах. Теория пластичности наряду с газовой динамикой становится наиболее энергично развивающимся разделом механики сплошных тел.

1. Основные уравнения.

1.1. Общие положения. При плоской деформации перемещения частиц тела параллельны плоскости и не зависят от :

. (1)

Подобное состояние возникает в длинных призматических телах при нагрузках, нормальных к боковой поверхности и не зависящих от .

Как обычно, считаем тело изотропным и однородным. В любом сечении будет одна и та же картина напряженного и деформированного состояний; компоненты напряжения зависят только от , причем равны нулю из-за отсутствия соответствующих сдвигов. Таким образом, является одним из главных напряжений.

В теории упругости приведенные условия достаточны для формулировки проблемы плоской деформации. В теории пластичности необходимы дополнительные упрощения, так как иначе невозможно получить приемлемую математическую формулировку вопроса.

В дальнейшем используется схема жесткопластического тела. Эта концепция вносит погрешность, которую трудно оценить. Однако сколько-нибудь последовательный анализ плоской задачи затруднителен, если отказаться от схемы жесткопластического тела.

Гораздо целесообразнее исходить из схемы жесткопластического тела, которая позволяет одновременно рассматривать поле напряжений и поле смещений, связывая последнее со смещениями жестких областей. Тем самым строится в известном смысле и приближенное решение упругопластических задач.

1.2. Основные уравнения. Из (1) вытекает, что . Вследствие пренебрежения упругими деформациями

, (2)

откуда . (3)

Как уже отмечалось, является одним из главных напряжений. Остальные главные напряжения являются корнями квадратного уравнения

.

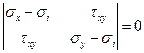Отсюда

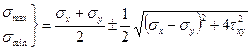. (4)

Очевидно, что - среднее главное напряжение, тогда максимальное касательное напряжение будет

.

Интенсивность касательных напряжений также равна

. (5)

Таким образом, главные напряжения равны

,

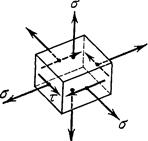
т. е. напряженное состояние в каждой точке характеризуется наложением гидростатического давления на напряжение чистого сдвига (рис. 1).

Рис. 1. Значения косинусов, определяющих первое (пусть ) главное направление, находятся из системы

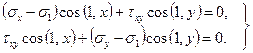
Исключая , получаем:

. (6)

Направления площадок, на которых действуют максимальные касательные напряжения, составляют угол с главным направлением.

1.3. Линии скольжения. Линия скольжения – линия, в каждой точке своей касающаяся площадки максимального касательного напряжения. Очевидно, что имеются два ортогональных семейства линий скольжения, характеризуемые уравнениями:

, ,

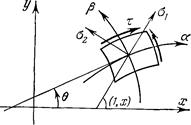где - некоторые параметры. Линии первого семейства (-линии) соответствуют фиксированным значениям параметра ; вдоль – линии постоянен параметр . Линия отклоняется вправо от первого главного направления на 45⁰ (рис. 2); линия отклоняется влево от первого главного направления на тот же угол.

Рис. 2.

Условимся фиксировать направления линий так, чтобы они образовывали правую систему координат; при этом касательное напряжение положительно (рис. 2). Угол наклона касательной к линии , отсчитываемый в положительном направлении от оси , обозначим через .

Дифференциальные уравнения семейств соответственно будут

. (7)

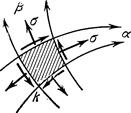Линии скольжения покрывают область ортогональной сеткой. Бесконечно малый элемент, выделенный линиями скольжения, испытывает одинаковое растяжение в направлениях линий скольжения (рис. 3).

Рис. 3.

1.4. Состояние текучести. Пусть среда находится в состоянии идеальной пластичности. Тогда должно выполняться условие текучести

или

.

Обозначая через , получаем:

. (8)

Сюда следует присоединить два дифференциальных уравнения равновесия (объемные силы отсутствуют):

(9)

Если на границе тела заданы напряжения, то мы располагаем полной системой уравнений для определения напряженного состояния (притом независимо от деформации). Задачи этого типа называются статически определимыми.

К приведенным уравнениям следует присоединить соотношения, связывающие компоненты напряжения с приращениями компонент деформации; это будут соотношения (7), в которых нужно отбросить слагаемые, относящиеся к упругой деформации, т. е. соотношения теории пластичности Сен-Венана-Мизеса (12). В случае плоской деформации остаются лишь три соотношения (для ), из которых вытекает уравнение

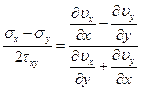, (10)

утверждающее, что направление площадки максимального касательного напряжения совпадает с направлением площадки, испытывающей максимальную скорость деформации сдвига. Кроме того, должно выполняться условие несжимаемости

(11)

Для пяти неизвестных имеем пять уравнений (8) – (11).

1.5. Полуобратный метод. Если задача статически определима, то напряжения находятся независимо от скоростей ; для нахождения скоростей имеем тогда линейную (при найденных напряжениях) систему уравнений (10), (11).

Если задача статически неопределима, то необходимо совместное решение уравнений для напряжений и скоростей, что связано с известными трудностями. В таких задачах часто используют полуобратный метод: пытаются подобрать такое поле линий скольжения, для которого распределение скоростей было бы в согласии с граничными условиями. При этом приходится в той или иной мере задавать контуры пластической зоны и дополнять граничные условия для напряжения. Подобные приемы, несмотря на их очевидную ограниченность, позволили найти много важных решений. В связи с этим, в частности, имеет большое значение анализ системы уравнений (8), (9) для напряжений. Обратимся к подробному изучению свойств решений этой системы уравнений.

2. Линии скольжения, их свойства.

2.1. Характеристические линии. Рассмотрим уравнения в напряжениях (8), (9).

Возьмем известные формулы теории напряжений:

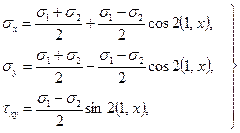
заменим в них полусумму главных напряжений через , полуразность – через (согласно условию текучести) и перейдем к углу . Тогда будет

(12)

Очевидно, что при этом условие текучести (8) удовлетворяется.

Внося эти значения в уравнения равновесия, получаем систему двух нелинейных дифференциальных уравнений в частных производных первого порядка относительно неизвестных функций , :

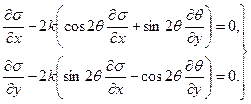(13)

Методы построения и свойства решения полученной системы дифференциальных уравнений прежде всего определяются ее типом. Покажем, что эта система гиперболического типа.

Для установления гиперболичности системы нужно показать, что существуют два различных вещественных семейства характеристических линий.

Пусть вдоль некоторой линии в плоскости , (рис. 4) известны значения искомых функций .

Рис. 4.

Будем разыскивать решение , , принимающее вдоль линии заданное значение . Задача построения такого решения называется задачей Коши . На геометрическом языке эта задача состоит в проведении интегральной поверхности через заданную кривую.

Если – характеристическая линия, решение задачи Коши невозможно, ибо тогда невозможно вдоль однозначно определить из дифференциальных уравнений первые производные от решения (на геометрическом языке – тогда невозможно однозначно определить вдоль касательную плоскость к интегральной поверхности). На линии известны и . Значит, если они дифференцируемые, то известны и производные . При этом и отсчитываются в локальной системе координат, образованной касательной и нормалью к в некоторой точке (рис. 4). Заметим, что уравнения равновесия и условие пластичности не изменяются при переходе от системы координат к системе . Дифференциальные уравнения (13) также сохраняют прежний вид:

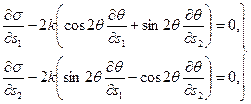(14)

причем угол , определяющий направление площадки скольжения в точке , здесь отсчитывается от оси . Если отлично от 0, , то, зная на производные , можно найти из (14) производные и решить задачу Коши.

Если же совпадает с линией скольжения, то =0, , и упомянутые производные нельзя определить из дифференциальных уравнений (14). В этом случае линия будет характеристической линией.

Таким образом, характеристические линии совпадают с линиями скольжения ; очевидно, что существуют два различных вещественных семейства характеристических линий, следовательно, исходная система – гиперболического типа.

Если координатные оси совпадают с направлениями касательных к линиям скольжения, то дифференциальные уравнения (14) принимают простую форму

(15)

где - производные вдоль линий .

Эти уравнения имеют простой механический смысл; они являются дифференциальными уравнениями равновесия бесконечно малого элемента пластической среды , образованного сеткой линий скольжения (элемента скольжения ; рис. 3), которая является как бы естественной координатной сеткой данной задачи.

Так как – произвольная точка на линии скольжения, то вдоль линий скольжения семейств имеем соответственно

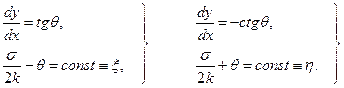(16)

Эти соотношения для плоской задачи теории пластичности впервые были выведены Г. Генки (1923 г.). Для сыпучей среды несколько более общие соотношения были получены ранее (1903 г.) Кёттером.

При переходе от одной линии скольжения семейства к другой параметр , вообще говоря, изменяется. Точно так же при переходе от одной линии семейства к другой изменяется параметр . Таким образом, зависит только от параметра , а – только от , т. е.

Если известны поле линий скольжения и на них – значения параметров , , то в каждой точке известны , т. е. известны компоненты напряжения . Заметим, что в рассматриваемой проблеме в отличие от линейной задачи (например, задачи для волнового уравнения) характеристические линии зависят от искомого решения – поля напряжений. В частности, произвольная кривая , если вдоль нее реализуется подходящее напряженное состояние (т.е. определен соответствующий угол ), может быть характеристикой.

2.2. Свойства линий скольжения. Линии скольжения обладают рядом замечательных свойств, изученных в основном Генки. Рассмотрим эти свойства.

1) Вдоль линии скольжения давление изменяется пропорционально углу линии скольжения с осью . Это свойство очевидно, так как вдоль –линии , вдоль –линии .

2) Если переходить от одной линии скольжения семейства к другой вдоль любой линии скольжения семейства , то угол и давление будут изменяться на одну и ту же величину (первая теорема Генки).

В самом деле, из соотношений

(17)

вытекает, что

. (18)

Возьмем две какие-либо линии скольжения семейства и две линии скольжения семейства (рис. 5). Вдоль этих линий соответственно имеем:

.

Внося эти значения в формулы (18) для точек пересечения , легко находим:

,

т. е. . Точно так же получаем:

.

Очевидно, что мы придем к аналогичным выводам, если будем переходить от одной линии скольжения семейства к другой вдоль любой линии .

3) Если известно значение в какой-либо точке заданной сетки скольжения, то оно может быть вычислено всюду в поле.

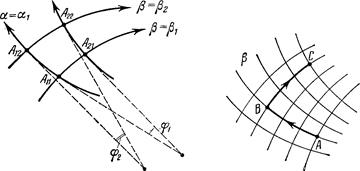
Рис. 5. Рис. 6.

Пусть в точке (рис. 6) известно ; в этой точке мы знаем , следовательно, вычисляем сразу значение параметра для – линии скольжения, проходящей через .

Далее, в точке легко находим и ; значение давления в точке получаем по формуле .

4) Если некоторый отрезок линии скольжения – прямой, то вдоль него постоянны , , параметры , и компоненты напряжения . Действительно, пусть, скажем, отрезок – линии – прямой; вдоль него и постоянен параметр . Но тогда согласно (17) и . Стало быть, и параметр вдоль рассматриваемого отрезка также постоянен.

Если в некоторой области прямолинейны оба семейства линий скольжения, то в этой области напряжения распределены равномерно, причем параметры , постоянны.

5) Если некоторый отрезок линии скольжения семейства (или ) – прямой, то все соответствующие отрезки линий (или ), отсекаемые линиями семейства (или ) (рис. 7), - прямые.

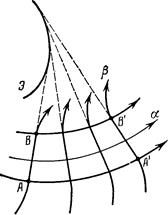Этот вывод следует из второго свойства, поскольку угол между соответствующими касательными к любым двум линиям скольжения остается постоянным при движении по избранным линиям .

Рис. 7.

В такой области напряжения постоянны вдоль каждого прямого отрезка, но при переходе от одного отрезка к другому. Будем называть подобное напряженное состояние простым .

По доказанному вдоль каждого из прямолинейных отрезков оба параметра , постоянны; так как параметр принимает постоянное значение вдоль каждой – линии, то во всей области .

6) Прямые отрезки, отсекаемые линиями скольжения другого семейства, имеют одинаковую длину. В самом деле, рассмотрим линии скольжения , . Эволюта (геометрическое место центров кривизны) какой-либо кривой является огибающей семейства нормалей к кривой. Очевидно, что линии скольжения и имеют одну и ту же эволюту . Как известно, исходная кривая может быть построена путем разматывания нити с эволюты. Но тогда при вычерчивании кривой нить будет короче на отрезок , чем при вычерчивании кривой .

7) Будем передвигаться вдоль некоторой лини скольжения; тогда радиусы кривизны линий скольжения другого семейства в точках пересечения изменяются на пройденные расстояния (вторая теорема Генки).

Радиусы кривизны , линий , определяются соотношениями

, . (19)

Радиус кривизны () положителен, если центр кривизны находится в направлении возрастания (возрастания ). Рассмотрим бесконечно близкие линии семейств , , ограничивающие элемент скольжения (рис. 8). Очевидно, что

.

Вычислим производную от вдоль линии :

.

По доказанному угол между двумя линиями постоянен, следовательно,

, . (20)

Второе соотношение выводится подобно первому.

Точки пересечения , нормалей , и , являются центрами кривизны соответственно линий , в точке .

Радиус кривизны – линии в точке равен сумме радиуса кривизны – линии в точке и длины дуги (рис. 9).

Рис. 8. Рис. 9.

Теорема Генки может быть представлена также и в другой форме (Прандтль): центры кривизны – линий в точках пересечения с линией образуют эвольвенту линии .

8) Теорема Генки показывает, что радиус кривизны линий скольжения при движении в сторону их вогнутости уменьшаетс я.

Если пластическое состояние простирается достаточно далеко, то радиус кривизны линий должен обратиться в нуль, что отвечает пересечению эвольвенты с линией скольжения . При этом линия семейства имеет в точке острие. Кроме того, из построения (рис. 9) ясно, что в точке бесконечно близкие линии скольжения , сходятся. Точка принадлежит огибающей линий скольжения семейства . Таким образом, огибающая линий скольжения одного семейства есть геометрическое место точек возврата линий скольжения второго семейства.

Имея в точку возврата, линии скольжения не могут пересечь огибающую. Другими словами, огибающая является границей аналитического решения.

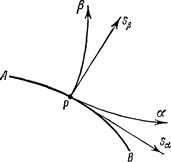Пусть – огибающая – линий. Проведем в некоторой ее точке локальную систему координат , (рис. 10). Из соотношений (19) вытекает, что в точке производная ограничена, а обращается в бесконечность, так Рис. 10.

как для линий на огибающей радиус кривизны . Но тогда из дифференциальных уравнений равновесия (15) заключаем, что ограничена, а . Итак, вдоль огибающей нормальная производная среднего давления обращается в бесконечность .

9) Если производные компонент напряжения испытывают разрывы при переходе через линию скольжения (например, через некоторую линию ), то кривизна линий скольжения второго семейства () разрывна вдоль линии .

В локальной системе , нормальные напряжения равны среднему давлению (рис. 3), а касательные напряжения постоянны.

Производная непрерывна, производная же по условию разрывна вдоль – линии.

На - линии имеем , следовательно, при переходе через линию разрывна производная

,

т. е. кривизна также изменяется скачком.

Таким образом, ортогональная сетка линий скольжения может быть скомпонована из кусков различных аналитических кривых; в местах склейки касательная непрерывно поворачивается, кривизна же испытывает, вообще говоря, разрывы.

Список литературы

1. Качанов Л. М. Основы теории пластичности. М., 1969.