| Скачать .docx | Скачать .pdf |
Курсовая работа: Курсовая работа: Регрессионный анализ. Транспортная задача
Регрессионный анализ
Задача
Некоторая фирма занимается поставками различных грузов на короткие расстояния внутри города. Необходимо оценить стоимость таких услуг, зависящую от затрачиваемого на поставку времени. В качестве наиболее важного фактора, влияющего на время доставки, выбрано пройденное расстояние. Были собраны исходные данные о десяти поставках (табл.).
| Расстояние, км |
3,5 |
2,4 |
4,9 |
4,2 |
3,0 |
1,3 |
1,0 |
3,0 |
1,5 |
4,1 |
| Время, мин |
16 |
13 |
19 |
18 |
12 |
11 |
8 |
14 |
9 |
16 |
Постройте график исходных данных, определите по нему характер зависимости между расстоянием и потраченным временем, постройте уравнение регрессии, проанализируйте силу регрессионной связи и сделайте прогноз поездки на 2 км.
Решение
Для расчёта стоимости услуг, зависящих от затрачиваемого на поставку времени, вычислим суммы (рис. 1):
| t |
y(t) |
|
||||||||||||
|
|
|
|
|
|
|
||||||||
| 1 |
3,50 |
16,00 |
12,25 |
56,00 |
256,00 |
15,22 |
2,63 |
|||||||
| 2 |
2,40 |
13,00 |
5,76 |
31,20 |
169,00 |
12,30 |
1,70 |
|||||||
| 3 |
4,90 |
19,00 |
24,01 |
93,10 |
361,00 |
18,95 |
28,58 |
|||||||
| 4 |
4,20 |
18,00 |
17,64 |
75,60 |
324,00 |
17,08 |
12,14 |
|||||||
| 5 |
3,00 |
12,00 |
9,00 |
36,00 |
144,00 |
13,89 |
0,09 |
|||||||
| 6 |
1,30 |
11,00 |
1,69 |
14,30 |
121,00 |
9,37 |
17,88 |
|||||||
| 7 |
1,00 |
8,00 |
1,00 |
8,00 |
64,00 |
8,57 |
25,27 |
|||||||
| 8 |
3,00 |
14,00 |
9,00 |
42,00 |
196,00 |
13,89 |
0,09 |
|||||||
| 9 |
1,50 |
9,00 |
2,25 |
13,50 |
81,00 |
9,90 |
13,67 |
|||||||
| 10 |
4,10 |
16,00 |
16,81 |
65,60 |
256,00 |
16,82 |
10,36 |
|||||||
| сумма |
|
|
|
|
|
|
|
|||||||
| 13,60 |
||||||||||||||
| a1 = |
2,66 |
|||||||||||||
| a0 = |
5,91 |
|||||||||||||
| r2 = |
0,92 |
91,83% |
||||||||||||
| 8,17 |
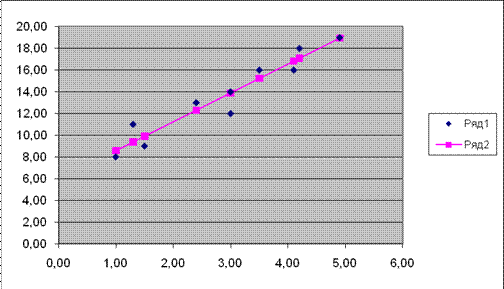
Рис .1 - График исходных данных
Вывод: существует сильная связь между исходными данными.
Задача
В таблице приведены данные по объемам собранного урожая овощей из тепличного хозяйства за последний год (по месяцам), а также данные о затраченной электроэнергии, воде и удобрениях.
| Месяц |
Объем собранного урожая |
Факторы, влияющие на урожай |
||
| Электроэнергия, кВт |
Удобрения, тонн |
Вода, литр |
||
| t |
y |
x 1 |
x 2 |
x 3 |
| январь |
140 |
165 |
138 |
134 |
| февраль |
138 |
164 |
139 |
128 |
| март |
158 |
158 |
157 |
168 |
| апрель |
144 |
159 |
142 |
147 |
| май |
142 |
148 |
144 |
146 |
| июнь |
134 |
152 |
136 |
140 |
| июль |
122 |
143 |
122,5 |
132 |
| август |
125 |
146 |
128 |
135 |
| сентябрь |
124 |
148 |
119 |
125 |
| октябрь |
138 |
150 |
142 |
126 |
| ноябрь |
157 |
156 |
159 |
143 |
| декабрь |
161 |
160 |
164 |
150 |
Необходимо определить степень влияния каждого отдельного фактора на результат (объем урожая). Для этого необходимо построить графики исходных данных, построить уравнения регрессии, проанализировать силу регрессионной связи (по коэффициенту детерминации) и сделать прогноз урожая по двум-трем значениям (в пределах прогноза исходных данных).
Решение
Строим графики исходных данных (рис. 2, 3):
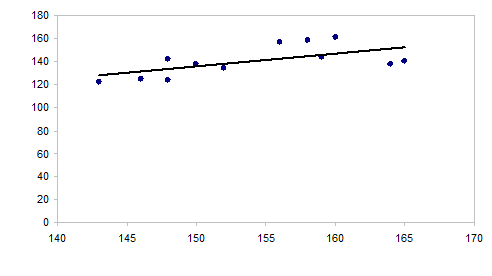
Рис. 2 - График зависимости урожая от удобрения
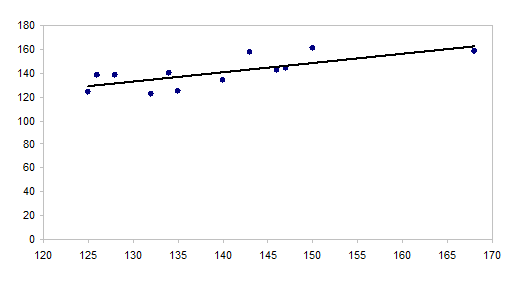
Рис. 3 - График зависимости урожая от воды
Численные коэффициенты функции регрессии для первой зависимости:
Численные коэффициенты функции регрессии
| X1 i |
Y i |
X1 i І |
X1 i Y i |
Y i І |
Y i p |
(Y i p -y)І |
(Y i -y)І |
| 165 |
140 |
27225 |
23100 |
19600 |
152,5778 |
151,9747 |
0,0625 |
| 164 |
138 |
26896 |
22632 |
19044 |
151,4485 |
125,4073 |
5,0625 |
| 158 |
158 |
24964 |
24964 |
24964 |
144,673 |
19,56251 |
315,0625 |
| 159 |
144 |
25281 |
22896 |
20736 |
145,8022 |
30,82711 |
14,0625 |
| 148 |
142 |
21904 |
21016 |
20164 |
133,3803 |
47,19267 |
3,0625 |
| 152 |
134 |
23104 |
20368 |
17956 |
137,8974 |
5,534888 |
39,0625 |
| 143 |
122 |
20449 |
17446 |
14884 |
127,734 |
156,6506 |
333,0625 |
| 146 |
125 |
21316 |
18250 |
15625 |
131,1218 |
83,32442 |
232,5625 |
| 148 |
124 |
21904 |
18352 |
15376 |
133,3803 |
47,19267 |
264,0625 |
| 150 |
138 |
22500 |
20700 |
19044 |
135,6388 |
21,26283 |
5,0625 |
| 156 |
157 |
24336 |
24492 |
24649 |
142,4144 |
4,684729 |
280,5625 |
| 160 |
161 |
25600 |
25760 |
25921 |
146,9315 |
44,64219 |
430,5625 |
| 1849 |
1683 |
285479 |
259976 |
237963 |
738,2566 |
1922,25 |
|
| Среднее значение |
140,25 |
Коэффициент детерминации r2 =0,384059.
Коэффициент детерминации низкий поэтому модель не адекватна.
Численные коэффициенты функции регрессии для первой зависимости, представляем расчеты виде таблицы:
Численные коэффициенты функции регрессии
| X2 i |
Y i |
X2 i І |
X2 i Y i |
Y i І |
Y i p |
(Y i p -y)І |
(Y i -y)І |
| 138 |
140 |
19044 |
19320 |
19600 |
137,5802 |
7,127725 |
0,0625 |
| 139 |
138 |
19321 |
19182 |
19044 |
138,5088 |
3,031641 |
5,0625 |
| 157 |
158 |
24649 |
24806 |
24964 |
155,224 |
224,2202 |
315,0625 |
| 142 |
144 |
20164 |
20448 |
20736 |
141,2947 |
1,091391 |
14,0625 |
| 144 |
142 |
20736 |
20448 |
20164 |
143,1519 |
8,421225 |
3,0625 |
| 136 |
134 |
18496 |
18224 |
17956 |
135,723 |
20,49389 |
39,0625 |
| 122,5 |
122 |
15006,25 |
14945 |
14884 |
123,1866 |
291,1588 |
333,0625 |
| 128 |
125 |
16384 |
16000 |
15625 |
128,294 |
142,9452 |
232,5625 |
| 119 |
124 |
14161 |
14756 |
15376 |
119,9365 |
412,64 |
264,0625 |
| 142 |
138 |
20164 |
19596 |
19044 |
141,2947 |
1,091391 |
5,0625 |
| 159 |
157 |
25281 |
24963 |
24649 |
157,0812 |
283,29 |
280,5625 |
| 164 |
161 |
26896 |
26404 |
25921 |
161,7243 |
461,1463 |
430,5625 |
| 1690,5 |
1683 |
240302,3 |
239092 |
237963 |
1856,658 |
1922,25 |
|
| Среднее значение |
140,25 |
Коэффициенты регрессии — сдвиг а0 и наклон а1 прямой у:
| a0= |
9,430782 |
| a1= |
0,928619 |
Коэффициент детерминации r2 =0,965877.
Коэффициент детерминации высокий, поэтому модель адекватна и можно делать прогноз.
Прогноз на три шага вперед y13=120.9, y14=154.3, y15=142.2.
Численные коэффициенты функции регрессии для первой зависимости, представляем расчеты виде таблицы:
Численные коэффициенты функции регрессии
| X 3i |
Y i |
X 3i І |
X 3i Y i |
Y i І |
Y i p |
(Y i p -y)І |
(Y i -y)І |
| 134 |
140 |
17956 |
18760 |
19600 |
135,8979 |
18,94079 |
0,0625 |
| 128 |
138 |
16384 |
17664 |
19044 |
131,1502 |
82,80727 |
5,0625 |
| 168 |
158 |
28224 |
26544 |
24964 |
162,8018 |
508,5838 |
315,0625 |
| 147 |
144 |
21609 |
21168 |
20736 |
146,1847 |
35,22048 |
14,0625 |
| 146 |
142 |
21316 |
20732 |
20164 |
145,3934 |
26,4545 |
3,0625 |
| 140 |
134 |
19600 |
18760 |
17956 |
140,6456 |
0,156535 |
39,0625 |
| 132 |
122 |
17424 |
16104 |
14884 |
134,3153 |
35,22048 |
333,0625 |
| 135 |
125 |
18225 |
16875 |
15625 |
136,6892 |
12,67937 |
232,5625 |
| 125 |
124 |
15625 |
15500 |
15376 |
128,7763 |
131,6463 |
264,0625 |
| 126 |
138 |
15876 |
17388 |
19044 |
129,5676 |
114,1144 |
5,0625 |
| 143 |
157 |
20449 |
22451 |
24649 |
143,0195 |
7,670238 |
280,5625 |
| 150 |
161 |
22500 |
24150 |
25921 |
148,5586 |
69,03215 |
430,5625 |
| 1674 |
1683 |
235188 |
236096 |
237963 |
1042,526 |
1922,25 |
|
| Среднее значение |
140,25 |
Коэффициенты регрессии — сдвиг а0 и наклон а1 прямой у:
| a0= |
29,86486 |
| a1= |
0,791291 |
Коэффициент детерминации r2 =0,542347.
Коэффициент детерминации низкий, поэтому модель не адекватна.
Задача
Санаторный комплекс ежегодно заключает с пекарней договор на выпечку хлеба сорта С1 . Чтобы полностью использовать свои производственные мощности пекарня также выпекает хлеб сорта С2 , который пускает в свободную продажу. В таблице приведены данные выпуска хлеба (тыс. шт.) пекарней за последний год
| Месяц |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| С1 |
1 |
2,3 |
1,5 |
0,5 |
4 |
5 |
2 |
3,5 |
1 |
4,5 |
2,5 |
1,5 |
| С2 |
9 |
6,5 |
8,1 |
8,7 |
4 |
0,2 |
7,6 |
5 |
8,7 |
2 |
7 |
8,4 |
Проанализируйте график исходных данных и постройте регрессионную модель функции производственных возможностей пекарни. Проверьте удовлетворительность модели и сделайте прогноз выпуска хлеба С2 , если санаторный комплекс сделает заказ хлеба С1 3 тысячи булок.
Решение
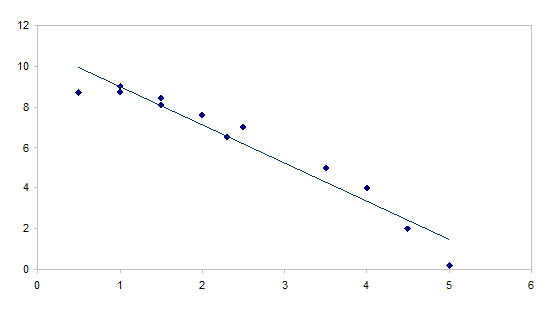
Рис. 4 - График исходных данных
Суммы, необходимые для расчета коэффициентов линейной регрессии и коэффициента детерминации вычислим с помощью таблицы, учитывая данные зависимости объема собранного урожая от количества электроэнергии.
| x |
y |
x2 |
xy |
yp |
(yp -ycp )2 |
(y-ycp )2 |
| 1 |
9 |
1 |
9 |
8.981453 |
7.370065 |
7.471111 |
| 2.3 |
6.5 |
5.29 |
14.95 |
6.533438 |
0.071167 |
0.054444 |
| 1.5 |
8.1 |
2.25 |
12.15 |
8.039909 |
3.144387 |
3.361111 |
| 0.5 |
8.7 |
0.25 |
4.35 |
9.922997 |
13.36875 |
5.921111 |
| 4 |
4 |
16 |
16 |
3.332187 |
8.611173 |
5.137778 |
| 5 |
0.2 |
25 |
1 |
1.449098 |
23.20897 |
36.80444 |
| 2 |
7.6 |
4 |
15.2 |
7.098364 |
0.691721 |
1.777778 |
| 3.5 |
5 |
12.25 |
17.5 |
4.273731 |
3.971792 |
1.604444 |
| 1 |
8.7 |
1 |
8.7 |
8.981453 |
7.370065 |
5.921111 |
| 4.5 |
2 |
20.25 |
9 |
2.390642 |
15.02356 |
18.20444 |
| 2.5 |
7 |
6.25 |
17.5 |
6.15682 |
0.012066 |
0.537778 |
| 1.5 |
8.4 |
2.25 |
12.6 |
8.039909 |
3.144387 |
4.551111 |
| å=29.3 |
å=75.2 |
å=95.79 |
å=137.95 |
å=85.98811 |
å=91.34667 |
Находим коэффициенты регрессии — сдвиг а0 и наклон а1 прямой у:
| a0= |
10,86454 |
| a1= |
-1,88309 |
Коэффициент детерминации r2 =0,941338.
Коэффициент детерминации высокий поэтому модель адекватна и можно делать прогноз.
Если санаторный комплекс сделает заказ хлеба С1 3 тысячи булок, то прогноз С2 =-1,88309*3000+10,86454=5215,7.
Транспортная задача
Задача
Заводы некоторой автомобильной фирмы расположены в городах А, В и С. Основные центры распределения продукции сосредоточены в городах D и E. Объемы производства указанных трех заводов равняются 1000, 1300 и 1200 автомобилей ежеквартально.
Величины квартального спроса в центрах распределения составляют 2300 и 1400 автомобилей соответственно.
Стоимости перевозки автомобилей по железной дороге по каждому из возможных маршрутов приведены в таблице
Стоимость перевозки автомобилей, руб./шт.
| D |
E |
|
| А |
80 |
215 |
| В |
100 |
108 |
| С |
102 |
68 |
Постройте математическую модель, позволяющую определить количество автомобилей, перевозимых из каждого завода в каждый центр распределения, таким образом, чтобы общие транспортные расходы были минимальны.
Задаем целевую функцию и ограничения с помощью «Поиска решений»:
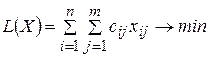 ;
;
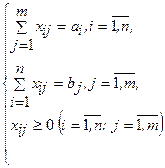
Получаем:
| Стоимость перевозки автомобилей, руб./шт |
||||
| D |
Е |
V |
Издержки |
|
| А |
80 |
215 |
1000 |
|
| В |
100 |
108 |
1300 |
|
| С |
102 |
68 |
1200 |
|
| Спрос |
2300 |
1400 |
291600 |
|
| Продукция |
||||
| D |
Е |
Сумма |
||
| А |
1000 |
0 |
1000 |
|
| В |
1300 |
0 |
1300 |
|
| С |
0 |
1200 |
1200 |
|
| Y |
0 |
200 |
200 |
|
| Сумма |
2300 |
1400 |
||
Задача
Постройте транспортную модель для исходных данных задачи 2.1 при условии, что квартальный спрос в пункте распределения D упал до 1900 автомобилей, а выпуск на заводе В увеличился до 1500 автомобилей за квартал.
Решение
Задаем целевую функцию и ограничения с помощью «Поиска решений»:
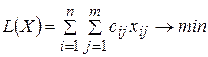 ;
;
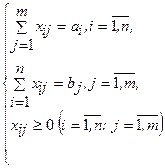
Получаем:
| Стоимость перевозки автомобилей, руб./шт |
|||||
| D |
Е |
F |
V |
Издержки |
|
| А |
80 |
215 |
0 |
1000 |
|
| В |
100 |
108 |
0 |
1500 |
|
| С |
102 |
68 |
0 |
1200 |
|
| Спрос |
1900 |
1400 |
400 |
273200 |
|
| Продукция |
|||||
| D |
Е |
F |
Сумма |
||
| А |
1000 |
0 |
0 |
1000 |
|
| В |
900 |
200 |
400 |
1500 |
|
| С |
0 |
1200 |
0 |
1200 |
|
| Сумма |
1900 |
1400 |
400 |
||
Задача
Три электрогенерирующие станции мощностью 25, 40 и 30 миллионов кВт×ч поставляют электроэнергию в три города. Максимальная потребность в электроэнергии этих городов оценивается в 30, 35 и 24 миллионов кВт×ч. Цены за миллион кВт-ч в данных городах приведены в табл. 4.4.
Стоимость за электроэнергию, руб. /млн. кВтч
| Города |
||||
| 1 |
2 |
3 |
||
| Станция |
1 |
600 |
700 |
400 |
| 2 |
320 |
300 |
350 |
|
| 3 |
500 |
480 |
450 |
|
В августе на 20% возрастает потребность в электроэнергии в каждом из трех городов. Недостаток электроэнергии могут восполнить из другой электросети по цене 1000 за 1 миллион кВт-ч. Но третий город не может подключиться к альтернативной электросети. Электрогенерирующие станции планируют разработать наиболее экономичный план распределения электроэнергии и восполнения ее недостатка в августе. Сформулируйте эту задачу в виде транспортной модели.
Решение
Задаем целевую функцию и ограничения с помощью «Поиска решений»:
![]() ;
;
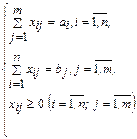
Получаем:
| Стоимость за электроэнергию, руб. /млн. кВтч |
||||||
| Города |
Издержки |
|||||
| 1 |
2 |
3 |
Мощность |
|||
| Станция |
1 |
600 |
700 |
400 |
25 |
|
| 2 |
320 |
300 |
350 |
40 |
||
| 3 |
500 |
480 |
450 |
30 |
||
| 4 |
1000 |
1000 |
10000 |
12 |
||
| Потребление |
36 |
42 |
29 |
48570 |
||
| Города |
||||||
| 1 |
2 |
3 |
Сумма |
|||
| Станция |
1 |
0 |
0 |
25 |
25 |
|
| 2 |
24 |
16 |
0 |
40 |
||
| 3 |
0 |
26 |
4 |
30 |
||
| 4 |
12 |
0 |
0 |
12 |
||
| Сумма |
36 |
42 |
29 |
|||
Задача
Найти тремя методами опорный план ТЗ, в которой запасы на трех складах равны 210, 170, 65 ед. продукции, потребности четырех магазинов равны 125, 90, 130, 100 ед. продукции, тарифы перевозки в рублях за единицу продукции следующие:

Решение
Проверка сбалансированности задачи показывает, что суммарный объем запасов равен суммарному объему потребностей, т.е. введение фиктивных столбцов или строк не потребуется
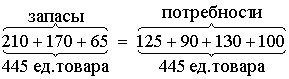
Результаты нахождения опорного плана различными методами представлены в табл.
Транспортная таблица с опорным планом северо-западного угла
| Пункты отправления, |
Пункты потребления, |
Запасы, ед. продукции |
|||
|
|
|
|
|
||
|
|
125 5 |
85 8 |
1 |
2 |
210/85/0 |
|
|
2 |
5 5 |
130 4 |
35 9 |
170/165/35/0 |
|
|
9 |
2 |
3 |
65 1 |
65/0 |
| Потребность, ед. продукции |
125/0 |
90/5/0 |
130/0 |
100/65/0 |
|
Опорный план ![]() , найденный методом северо-западного угла
, найденный методом северо-западного угла
 [ед.товара]
[ед.товара]
Соответствующая ЦФ (общие затраты на перевозку)
![]() [руб.].
[руб.].
Транспортная таблица с опорным планом минимального элемента
| Пункты отправления, |
Пункты потребления, |
Запасы, ед. продукции |
|||
|
|
|
|
|
||
|
|
5 |
45 8 |
130 1 |
35 2 |
210/80/45/0 |
|
|
125 2 |
45 5 |
4 |
9 |
170/45/0 |
|
|
9 |
2 |
3 |
65 1 |
65/0 |
| Потребность, ед. продукции |
125/0 |
90/45/0 |
130/0 |
100/35/0 |
|
Опорный план ![]() , найденный методом минимального элемента
, найденный методом минимального элемента
 [ед.товара]
[ед.товара]
![]() [руб.]
[руб.]
Транспортная таблица с опорным планом Фогеля
|
|
|
|
|
|
Штрафы строк, |
||||
|
|
5 |
8 |
110 1 |
100 2 |
210/110/0 |
1 |
1 |
1 |
7 |
|
|
125 2 |
25 5 |
20 4 |
9 |
170/45/25/0 |
2 |
1 |
1 |
1 |
|
|
9 |
65 2 |
3 |
1 |
65/0 |
1 |
1 |
– |
– |
|
|
125/0 |
90/25/0 |
130/20/0 |
100/0 |
|||||
| Штрафы столбцов, |
3 |
3 |
2 |
1 |
|||||
| – |
3 |
2 |
1 |
||||||
| – |
3 |
3 |
7 |
||||||
| – |
3 |
3 |
– |
||||||
На первом шаге нахождения опорного плана методом Фогеля возникает ситуация равенства значений максимальных штрафов транспортной матрицы
![]()
Минимальные тарифы в этих столбцах также совпадают
![]() .
.
Поэтому необходимо сравнить суммарные штрафы ![]() клеток (2,1) и (3,2)
клеток (2,1) и (3,2)
![]() ;
;
![]() .
.
Т.к. ![]() , то выбираем на первом шаге для заполнения клетку (2,1).
, то выбираем на первом шаге для заполнения клетку (2,1).
Опорный план ![]()
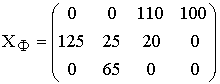 [ед.товара],
[ед.товара], ![]() [руб.]
[руб.]
Задача
Найти тремя методами опорный план ТЗ, в которой запасы на трех складах равны 160, 140, 170 ед. продукции, потребности четырех магазинов равны 120, 50, 200, 110 ед. продукции, тарифы перевозки в рублях за единицу продукции следующие:
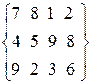
Решение
Суммарный объем запасов равен суммарному объему потребностей
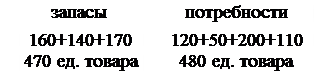 |
Транспортная таблица с опорным планом северо-западного угла
| Пункты отправления, |
Пункты потребления, |
Запасы, ед. продукции |
|||
|
|
|
|
|
||
|
|
120 7 |
40 8 |
1 |
2 |
160/40/0 |
|
|
4 |
10 5 |
130 9 |
8 |
140/130/0 |
|
|
9 |
2 |
70 3 |
100 6 |
170/100/0 |
| фиктивный склад |
0 |
0 |
0 |
10 0 |
10/0 |
| Потребность, ед. продукции |
120/0 |
50/10/0 |
200/70/0 |
110/10/0 |
|
Опорный план ![]() , найденный методом северо-западного угла [ед.товара].
, найденный методом северо-западного угла [ед.товара].

Соответствующая ЦФ (общие затраты на перевозку)
![]()
Транспортная таблица с опорным планом минимального элемента
| Пункты отправления, |
Пункты потребления, |
Запасы, ед. продукции |
|||
|
|
|
|
|
||
|
|
7 |
8 |
160 1 |
2 |
160/0 |
|
|
110 4 |
5 |
9 |
30 8 |
140/30/0 |
|
|
9 |
50 2 |
40 3 |
80 6 |
170/120/80/0 |
| фиктивный склад |
10 0 |
0 |
0 |
0 |
10/0 |
| Потребность, ед. продукции |
120/110/0 |
50/0 |
200/40/0 |
110/30/0 |
|
Опорный план ![]() , найденный методом минимального элемента
, найденный методом минимального элемента
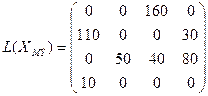
![]()
Транспортная таблица с опорным планом Фогеля
|
|
|
|
|
|
Штрафы строк, |
||||||
|
|
7 |
8 |
50 1 |
110 2 |
160/50/0 |
1 |
1 |
6 |
- |
- |
- |
|
|
110 4 |
30 5 |
9 |
8 |
140/110/0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
9 |
20 2 |
150 3 |
6 |
170/20/0 |
1 |
1 |
1 |
1 |
7 |
- |
| фикт. |
10 0 |
0 |
0 |
0 |
10/0 |
0 |
- |
- |
- |
- |
- |
|
|
120/110/0 |
50/30/0 |
200/150/0 |
110/0 |
|||||||
| Штрафы столбцов, |
4 |
2 |
1 |
2 |
|||||||
| 3 |
3 |
2 |
4 |
||||||||
| 3 |
3 |
2 |
- |
||||||||
| 5 |
3 |
6 |
– |
||||||||
| 5 |
3 |
- |
- |
||||||||
| 4 |
5 |
- |
- |
||||||||
Опорный план ![]() , найденный методом Фогеля [ед.товара],
, найденный методом Фогеля [ед.товара],
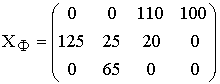
![]()
Задача
Некоторая фирма производит автомобили четырех различных марок М 1 , М 2 , М 3 , М 4 . Завод в городе А производит только автомобили марок М3 , M4 , в городе В – только автомобили марок М 1 , М 2 , M 4 , а в городе С – только автомобили марок М 1 , М 2 . Ежеквартальные объемы выпуска каждого завода и величины спроса в каждом пункте распределения приведены в таблице 1.3. Постройте соответствующую модель экономичных перевозок и определите целевую функцию по двум вариантам:
• каждому виду продукции должна соответствовать одна транспортная матрица;
• все виды продукции представлены в одной общей матрице с использованием запрещающих тарифов в клетках, связывающих разные виды продукции.
Объемы производства заводов и спроса пунктов распределения автомобилей, шт/квартал
| Марка автомобиля |
||||
| M 1 |
M 2 |
M 3 |
M 4 |
|
| Заводы |
||||
| А |
— |
— |
700 |
300 |
| В |
500 |
600 |
— |
400 |
| С |
800 |
400 |
— |
— |
| Пункты распределения |
||||
| D |
700 |
500 |
500 |
600 |
| Е |
600 |
500 |
200 |
100 |
Стоимость перевозки автомобилей, руб./шт
| D |
Е |
|
| А |
80 |
215 |
| В |
100 |
108 |
| С |
102 |
68 |
Решение:
Составляем для каждого вида продукции транспортную матрицу:
Транспортная матрица для первого вида продукции:
| D |
Е |
Объем |
|
| А |
0 |
0 |
0 |
| В |
100 |
108 |
500 |
| С |
102 |
68 |
800 |
| Спрос |
700 |
600 |
|
| издержки |
111200 |
||
| D |
Е |
Сумма |
|
| А |
0 |
0 |
0 |
| В |
500 |
0 |
500 |
| С |
200 |
600 |
800 |
| Сумма |
700 |
600 |
|
Транспортная матрица для второго вида продукции:
| D |
Е |
Объем |
|
| А |
0 |
0 |
0 |
| В |
100 |
108 |
600 |
| С |
102 |
68 |
400 |
| Спрос |
500 |
500 |
|
| издержки |
88000 |
||
| D |
Е |
Сумма |
|
| А |
0 |
0 |
0 |
| В |
500 |
100 |
600 |
| С |
0 |
400 |
400 |
| Сумма |
500 |
500 |
|
Транспортная матрица для третьего вида продукции:
| D |
Е |
Объем |
|
| А |
80 |
215 |
700 |
| В |
0 |
0 |
0 |
| С |
0 |
0 |
0 |
| Спрос |
500 |
200 |
|
| издержки |
83000 |
||
| D |
Е |
Сумма |
|
| А |
500 |
200 |
700 |
| В |
0 |
0 |
0 |
| С |
0 |
0 |
0 |
| Сумма |
500 |
200 |
|
Транспортная матрица для четвертого вида продукции:
| D |
Е |
Объем |
|
| А |
80 |
215 |
300 |
| В |
100 |
108 |
400 |
| С |
0 |
0 |
0 |
| Спрос |
600 |
100 |
|
| издержки |
64800 |
||
| D |
Е |
Сумма |
|
| А |
300 |
0 |
300 |
| В |
300 |
100 |
400 |
| С |
0 |
0 |
0 |
| Сумма |
600 |
100 |
|
Целевая функция равна сумме издержек по каждому виду продукции 347000.
Объединяем все виды продукции в одной общей матрице и с помощью «Поиска решений» находим оптимальный план и целевую функцию:
| D1 |
E1 |
D2 |
E2 |
D3 |
E3 |
D4 |
E4 |
производство |
|||||||||||
| A3 |
10000 |
10000 |
10000 |
10000 |
80 |
215 |
10000 |
10000 |
700 |
||||||||||
| A4 |
10000 |
10000 |
10000 |
10000 |
10000 |
10000 |
80 |
215 |
300 |
||||||||||
| B1 |
100 |
108 |
10000 |
10000 |
10000 |
10000 |
10000 |
10000 |
500 |
||||||||||
| B2 |
10000 |
10000 |
100 |
108 |
10000 |
10000 |
10000 |
10000 |
600 |
||||||||||
| B4 |
10000 |
10000 |
10000 |
10000 |
10000 |
10000 |
100 |
108 |
400 |
||||||||||
| C1 |
102 |
68 |
10000 |
10000 |
10000 |
10000 |
10000 |
10000 |
800 |
||||||||||
| C2 |
10000 |
10000 |
102 |
68 |
10000 |
10000 |
10000 |
10000 |
400 |
||||||||||
| спрос |
700 |
600 |
500 |
500 |
500 |
200 |
600 |
100 |
347000 |
||||||||||
| D1 |
E1 |
D2 |
E2 |
D3 |
E3 |
D4 |
E4 |
||||||||||||
| A3 |
0 |
0 |
0 |
0 |
500 |
200 |
0 |
0 |
700 |
||||||||||
| A4 |
0 |
0 |
0 |
0 |
0 |
0 |
300 |
0 |
300 |
||||||||||
| B1 |
500 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
||||||||||
| B2 |
0 |
0 |
500 |
100 |
0 |
0 |
0 |
0 |
600 |
||||||||||
| B4 |
0 |
0 |
0 |
0 |
0 |
0 |
300 |
100 |
400 |
||||||||||
| C1 |
200 |
600 |
0 |
0 |
0 |
0 |
0 |
0 |
800 |
||||||||||
| C2 |
0 |
0 |
0 |
400 |
0 |
0 |
0 |
0 |
400 |
||||||||||
| 700 |
600 |
500 |
500 |
500 |
200 |
600 |
100 |
||||||||||||
Задача о назначениях
Задача
а). Строительной компании «Спецстройкурнож» необходимо выполнить бетонные работы на 4 строящихся объектах. В фирме имеется 4 бригады бетонщиков, которые могут выполнить эту работу. Бригадиры каждой бригады побывали на объектах, оценили объемы работ и рассчитали сроки, за которые они могут выполнить работы.
| Бригада |
Объект |
|||
| 1 |
2 |
3 |
4 |
|
| №1 |
30 |
40 |
50 |
60 |
| №2 |
36 |
41 |
52 |
58 |
| №3 |
28 |
44 |
49 |
57 |
| №4 |
35 |
39 |
49 |
63 |
Перед руководством фирмы стоит задача распределения бригад по объектам таким образом, чтобы суммарный срок выполнения всех работ был минимальным. Поскольку количества бригад и объектов одинаковы, следовательно, имеем сбалансированную задачу о назначениях.
Решение
С помощью «Поиска решения» распределяем бригады по объектам таким образом, чтобы суммарный срок выполнения всех работ был минимальным.
| Бригада |
Объект |
|||
| 1 |
2 |
3 |
4 |
|
| №1 |
30 |
40 |
50 |
60 |
| №2 |
36 |
41 |
52 |
58 |
| №3 |
28 |
44 |
49 |
57 |
| №4 |
35 |
39 |
49 |
63 |
| целевая функция |
175 |
|||
| Бригада |
Объект |
|||
| 1 |
2 |
3 |
4 |
|
| №1 |
0 |
1 |
0 |
0 |
| №2 |
0 |
0 |
0 |
1 |
| №3 |
1 |
0 |
0 |
0 |
| №4 |
0 |
0 |
1 |
0 |
| ∑ |
1 |
1 |
1 |
1 |
б). Несбалансированная задача. Пока руководство фирмы «Спецстройизбкурнож» решало, какую бригаду бетонщиков послать на какой объект, освободилась от работ на предыдущем объекте еще одна бригада и выразила готовность также подключиться к работе на одном из четырех объектов. Бригадир этой бригады оценил работы на каждом объекте и подсчитал, что работы на первом объекте его бригада выполнит за 29 рабочих дней, на втором объекте за 40 дней, на третьем объекте за 48 дней и на четвертом – за 59 дней
Решение
С помощью «Поиска решений» распределяем бригады по объектам таким образом, чтобы суммарный срок выполнения всех работ был минимальным.
| Бригада |
Объект |
|||
| 1 |
2 |
3 |
4 |
|
| №1 |
30 |
40 |
50 |
60 |
| №2 |
36 |
41 |
52 |
58 |
| №3 |
28 |
44 |
49 |
57 |
| №4 |
35 |
39 |
49 |
63 |
| №5 |
29 |
40 |
48 |
59 |
| цел. функция |
173 |
|||
| Бригада |
Объект |
|||
| 1 |
2 |
3 |
4 |
|
| №1 |
0 |
0 |
0 |
0 |
| №2 |
0 |
0 |
0 |
1 |
| №3 |
1 |
0 |
0 |
0 |
| №4 |
0 |
1 |
0 |
0 |
| №5 |
0 |
0 |
1 |
0 |
| ∑ |
1 |
1 |
1 |
1 |
Общая распределительная задача линейного программирования
Задача
На фабрике эксплуатируются три типа ткацких станков, которые могут выпускать четыре вида тканей. Известны следующие данные о производственном процессе:
производительности станков по каждому виду ткани, м/ч
 ;
;
себестоимость тканей, руб./м
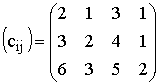 ;
;
фонды рабочего времени станков (![]() ): 90, 220, 180 ч;
): 90, 220, 180 ч;
планируемый объем выпуска тканей (![]() ): 1200, 900, 1800, 840 м.
): 1200, 900, 1800, 840 м.
Требуется распределить выпуск ткани по станкам с целью минимизации общей себестоимости производства ткани.
Решение
| 1.1 |
||||||||||||||||||||
| 1 |
1 |
1 |
1 |
|||||||||||||||||
| ai |
0,5 |
0,5 |
0,5 |
0,5 |
||||||||||||||||
| 0,33333 |
0,33333 |
0,33333 |
0,3333 |
|||||||||||||||||
| 1.2 |
||||||||||||||||||||
| 90 |
1 |
90 |
||||||||||||||||||
| 220 |
* |
0,5 |
= |
110 |
||||||||||||||||
| 180 |
0,33333 |
60 |
||||||||||||||||||
| 1.3 |
||||||||||||||||||||
| 24 |
30 |
18 |
42 |
|||||||||||||||||
| bj |
12 |
15 |
9 |
21 |
||||||||||||||||
| 8 |
10 |
6 |
14 |
|||||||||||||||||
| 1200 |
900 |
1800 |
840 |
|||||||||||||||||
| bj' |
50 |
30 |
100 |
20 |
||||||||||||||||
| b(фиктив)' |
60 |
|||||||||||||||||||
| 1.4 |
||||||||||||||||||||
| 2 |
1 |
3 |
1 |
|||||||||||||||||
| cij |
3 |
2 |
4 |
1 |
* |
24 |
30 |
18 |
42 |
|||||||||||
| 6 |
3 |
5 |
2 |
|||||||||||||||||
| 48 |
30 |
54 |
42 |
|||||||||||||||||
| = |
72 |
60 |
72 |
42 |
||||||||||||||||
| 144 |
90 |
90 |
84 |
|||||||||||||||||
| 2. |
ai |
bj |
||||||||||||||||||
| 90 |
50 |
|||||||||||||||||||
| 110 |
30 |
|||||||||||||||||||
| 60 |
100 |
|||||||||||||||||||
| 260 |
20 |
|||||||||||||||||||
| 60 |
||||||||||||||||||||
| 260 |
||||||||||||||||||||
| 3. |
||||||||||||||||||||
| 48 |
30 |
54 |
42 |
0 |
90 |
|||||||||||||||
| 72 |
60 |
72 |
42 |
0 |
110 |
|||||||||||||||
| 144 |
90 |
90 |
84 |
0 |
60 |
|||||||||||||||
| 50 |
30 |
100 |
20 |
60 |
||||||||||||||||
| 50 |
30 |
10 |
0 |
0 |
||||||||||||||||
| 0 |
0 |
90 |
20 |
0 |
Поиск оптимального решения |
|||||||||||||||
| 0 |
0 |
0 |
0 |
60 |
||||||||||||||||
| 4. |
||||||||||||||||||||
| 50 |
30 |
10 |
0 |
0 |
1 |
|||||||||||||||
| xij |
0 |
0 |
90 |
20 |
0 |
/ |
0,5 |
= |
||||||||||||
| 0 |
0 |
0 |
0 |
60 |
0,3333 |
|||||||||||||||
| 50 |
30 |
10 |
0 |
0 |
||||||||||||||||
| = |
0 |
0 |
180 |
40 |
0 |
|||||||||||||||
| 0 |
0 |
0 |
0 |
180 |
||||||||||||||||
| 5. |
||||||||||||||||||||
| 50 |
30 |
10 |
0 |
0 |
24 |
30 |
18 |
42 |
0 |
|||||||||||
| 0 |
0 |
180 |
40 |
0 |
* |
12 |
15 |
9 |
21 |
0 |
||||||||||
| 0 |
0 |
0 |
0 |
180 |
8 |
10 |
6 |
14 |
0 |
|||||||||||
| 1200 |
900 |
180 |
0 |
0 |
2 |
1 |
3 |
1 |
0 |
|||||||||||
| 0 |
0 |
1620 |
840 |
0 |
* |
3 |
2 |
4 |
1 |
0 |
||||||||||
| 0 |
0 |
0 |
0 |
0 |
6 |
3 |
5 |
2 |
0 |
|||||||||||
| 2400 |
900 |
540 |
0 |
|||||||||||||||||
| 0 |
0 |
6480 |
840 |
L(x)= |
11160 |
|||||||||||||||
| 0 |
0 |
0 |
0 |
|||||||||||||||||
Задача
Некоторая фирма содержит три магазина, которым еженедельно следует доставлять товар: первому магазину – 1050 кг сыра, второму – 600 мешков муки, третьему – 2400 упаковок сока. Товары доставляются грузовыми машинами четырех транспортных предприятий. Количество машин на этих предприятиях составляет 65, 40, 45 и 20 машин. Все машины имеют различную грузоподъемность [ед. тов. / маш.], в зависимости от типа машины и типа перевозимого груза
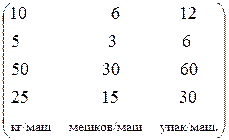
Стоимости использования машин [руб. / маш.] в зависимости от дальности перевозки и емкости машины равны
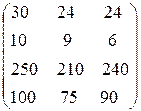 .
.
Организуйте экономичную перевозку товаров (при решении используйте метод северо-западного угла).
Решение:
| Этапы решения распределительной задачи: |
|||||||||||
| 1.1 |
|||||||||||
| 0,2 |
0,2 |
0,2 |
|||||||||
| ai |
0,1 |
0,1 |
0,1 |
||||||||
| 1 |
1 |
1 |
|||||||||
| 0,5 |
0,5 |
0,5 |
|||||||||
| 1.2 |
|||||||||||
| 65 |
0,2 |
13 |
|||||||||
| 40 |
* |
0,1 |
= |
4 |
|||||||
| 45 |
1 |
45 |
|||||||||
| 20 |
0,5 |
10 |
|||||||||
| 1.3 |
|||||||||||
| 10 |
6 |
12 |
|||||||||
| bj |
5 |
3 |
6 |
||||||||
| 50 |
30 |
60 |
|||||||||
| 25 |
15 |
30 |
|||||||||
| 1050 |
600 |
2400 |
|||||||||
| bj |
21 |
20 |
40 |
||||||||
| a фикт |
9 |
||||||||||
| 1.4 |
|||||||||||
| 30 |
24 |
24 |
1500 |
720 |
1440 |
||||||
| cij |
10 |
9 |
6 |
* |
50 |
30 |
60 |
= |
500 |
270 |
360 |
| 250 |
210 |
240 |
12500 |
6300 |
14400 |
||||||
| 100 |
75 |
90 |
5000 |
2250 |
5400 |
||||||
| 2. |
ai |
bj |
|||||||||
| 13 |
21 |
||||||||||
| 4 |
20 |
||||||||||
| 45 |
40 |
||||||||||
| 10 |
81 |
||||||||||
| 9 |
|||||||||||
| 81 |
|||||||||||
| 3. |
|||||||||||
| 1500 |
720 |
1440 |
13 |
||||||||
| 500 |
270 |
360 |
4 |
||||||||
| 12500 |
6300 |
14400 |
45 |
||||||||
| 5000 |
2250 |
5400 |
10 |
||||||||
| 0 |
0 |
0 |
9 |
||||||||
| 21 |
20 |
40 |
|||||||||
| 13 |
0 |
0 |
|||||||||
| 4 |
0 |
0 |
|||||||||
| 4 |
20 |
21 |
Поиск оптимального решения |
||||||||
| 0 |
0 |
10 |
|||||||||
| 0 |
0 |
9 |
|||||||||
| 4. |
13 |
0 |
0 |
0,2 |
65 |
0 |
0 |
||||
| 4 |
0 |
0 |
0,1 |
40 |
0 |
0 |
|||||
| xij |
4 |
20 |
21 |
/ |
1 |
= |
4 |
20 |
21 |
||
| 0 |
0 |
10 |
0,5 |
0 |
0 |
20 |
|||||
| 0 |
0 |
9 |
0 |
0 |
0 |
0 |
|||||
| 5. |
|||||||||||
| 65 |
0 |
0 |
10 |
6 |
12 |
650 |
0 |
0 |
|||
| 40 |
0 |
0 |
5 |
3 |
6 |
200 |
0 |
0 |
|||
| 4 |
20 |
21 |
* |
50 |
30 |
60 |
= |
200 |
600 |
1260 |
|
| 0 |
0 |
20 |
25 |
15 |
30 |
0 |
0 |
600 |
|||
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||
| 650 |
0 |
0 |
30 |
24 |
24 |
19500 |
0 |
0 |
|||
| 200 |
0 |
0 |
10 |
9 |
6 |
2000 |
0 |
0 |
|||
| 200 |
600 |
1260 |
* |
250 |
210 |
240 |
= |
50000 |
1E+05 |
3E+05 |
|
| 0 |
0 |
600 |
100 |
75 |
90 |
0 |
0 |
54000 |
|||
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||
| L(x)= |
553900 |
||||||||||
Модели управления запасами
Задача
Объем продажи некоторого магазина составляет в год 500 упаковок супа в пакетах. Величина спроса равномерно распределяется в течение года. Цена покупки одного пакета равна 2 руб. За доставку заказа владелец магазина должен заплатить 10 руб. Время доставки заказа от поставщика составляет 12 рабочих дней (при 6-дневной рабочей неделе). По оценкам специалистов, издержки хранения в год составляют 40 коп. за один пакет. Необходимо определить: сколько пакетов должен заказывать владелец магазина для одной поставки; частоту заказов; точку заказа. Магазин работает 300 дней в году.
Постройте график затрат Q [10; 200] с учетом затрат владельца магазина на закупку пакетов супа у поставщика. Графически определите наиболее выгодный объем заказа.
Решение
Пусть Q -
размер заказа; T
=300 -
продолжительность периода планирования; D
=500 - величина спроса за период планирования; К=
10 - издержки одного заказа (стоимость доставки); ![]() - удельные издержки хранения за период; с
=2 — цена продукта. Тогда:
- удельные издержки хранения за период; с
=2 — цена продукта. Тогда:
Издержки заказа за период планирования:![]() ;
;
Издержки хранения за период планирования : ![]() ;
;
Издержки на закупку товара: ![]() .
.
При этом совокупные издержки: 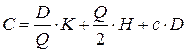 .
.
Формула совокупных издержек:
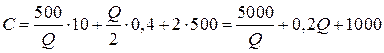 .
.
Для нахождения наименьшего значения функции С найдем ее производную и прировняем ее к нулю.
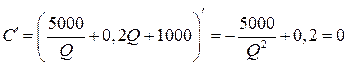
Отсюда получаем: ![]() .
.
Оптимальное число заказов:
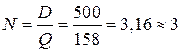 .
.
Число дней между заказами:
![]() дней.
дней.
Так как длина интервала между поставками равна 100 дней, а время доставки – 12 дней, то заказ нужно возобновить, когда уровень запаса достаточен для удовлетворения потребностей на 12 рабочих дней.
Так как ежедневная потребность равна 500/300=1,67 упаковок супа в
день, то заказы должны делаться регулярно при достижении уровня запаса ![]() пачек супа.
пачек супа.
График затрат Q [10; 200] с учетом затрат владельца магазина на закупку пакетов супа у поставщика (рис. 5):
![]()
![]()
|
|
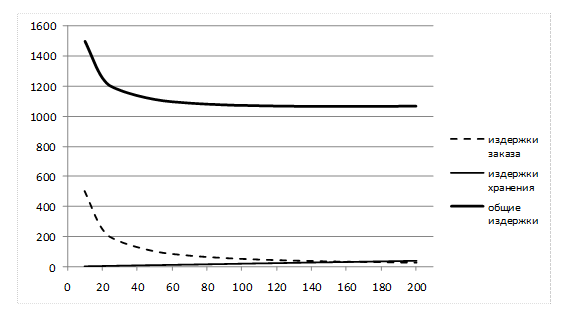
Рис. 5
Оптимальный размер заказа (точка пересечения графиков издержек заказа и издержек хранения) приблизительно равен 158 пакетов супа.
Величина общих годовых издержек составит примерно 1060 руб.
Задача
На некотором станке производятся детали в количестве 2000 штук в месяц. Эти детали используются для производства продукции на другом станке с интенсивностью 500 шт. в месяц. По оценкам специалистов компании, издержки хранения составляют 50 коп. в год за одну деталь. Стоимость производства одной детали равна 2,50 руб., а стоимость на подготовку производства составляет 1000 руб. Каким должен быть размер партии деталей, производимой на первом станке, с какой частотой следует запускать производство этих партий?
Решение
Для начала определяем сколько производит первый и второй станки за год деталей:
первый станок = 2000*12=24000;
второй станок = 500 * 12 = 6000.
Затем по формулам модели Уилсона находим, оптимальный план, частоту заказов и общие издержки.
![]()
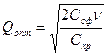
![]()
![]()
Qопт=5656,85
С=2121,32
τ месс=11,31
Задача
Фирма может производить изделие или покупать его. Если фирма сама выпускает изделие, то каждый запуск его в производство обходится в 20 руб. Интенсивность производства составляет 120 шт. в день. Если изделие закупается, то затраты на осуществление заказа равны 15 руб. Затраты на содержание изделия в запасе независимо от того, закупается оно или производится, равны 2 коп. в день. Потребление изделия фирмой оценивается в 26 000 шт. в год.
Предполагая, что фирма работает без дефицита, определите, что выгоднее: закупать или производить изделие (в месяце 22 рабочих дня).
Подтвердите свое решение графически, для этого на одном рисунке постройте графики общих затрат фирмы для случаев покупки и производства изделий.
Решение
Производство изделий:
Обозначим Q -
размер выпускаемой партии; D
=26000 шт. - величина спроса в год; ![]() шт. – величина спроса в день;
шт. – величина спроса в день; ![]() шт. - интенсивность производства; К=
20 руб. – стоимость каждого запуска изделия в производство;
шт. - интенсивность производства; К=
20 руб. – стоимость каждого запуска изделия в производство; ![]() руб. - издержки хранения за год. Тогда:
руб. - издержки хранения за год. Тогда:
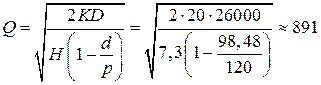 шт.
шт.
Cовокупные издержки:
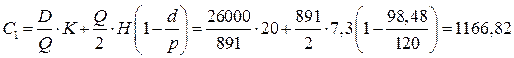 руб.
руб.
Покупка изделий
Обозначим Q -
размер приобретаемой партии; D
=26000 шт. - величина спроса в год; К=
15 руб. – стоимость каждой покупки; ![]() руб. - издержки хранения за год. Тогда:
руб. - издержки хранения за год. Тогда:
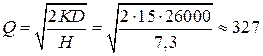 шт.
шт.
Совокупные издержки:
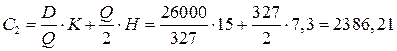 руб.
руб.
|
|
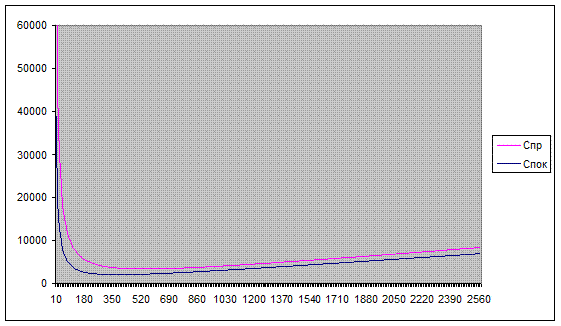
Рис. 6 - Графики общих затрат фирмы для случаев покупки и производства изделий
Вывод: выгоднее производить изделия, чем покупать их.
Задача
При строительстве участка автодороги длиной 500 м используют гравий, расход которого составляет 120 кг/м. Сроки строительства составляют 17 дней. Работа идет в одну смену. Расход гравия равномерный. Гравий доставляется грузовыми машинами, емкостью 7 т, в течение 4 часов. Затраты на один рейс грузовика равны 15 руб. Затраты на хранение гравия на месте строительства составляют 1 руб. 10 коп. в сутки за тонну.
Определить: оптимальный объем заказа, количество грузовых машин, используемых для доставки, период поставок, точку заказа, затраты за всю стройку. Постройте график двух последних циклов изменения запаса гравия на месте строительства.
Решение
Пусть Q –
оптимальный объем заказа; D
=![]() т - величина спроса за период строительства; К=
т - величина спроса за период строительства; К=
![]() руб. - издержки одного заказа (здесь 7 - грузоподъемность машины);
руб. - издержки одного заказа (здесь 7 - грузоподъемность машины); ![]() руб. - удельные издержки хранения за период; Т=17 дней –
период планирования;
руб. - удельные издержки хранения за период; Т=17 дней –
период планирования; ![]() сут. (принимаем время смены 8 часов). Тогда:
сут. (принимаем время смены 8 часов). Тогда:
Издержки заказа за период планирования :![]() ;
;
Издержки хранения за период планирования:![]() .
.
Оптимальный размер заказа составит:
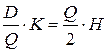 или
или 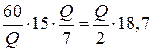 , откуда
, откуда 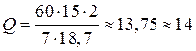 т.
т.
Количество грузовых машин равно ![]() ед.
ед.
Период поставок: 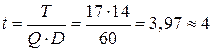 дня.
дня.
Точка заказа: ![]() т.
т.
Затраты на всю стройку составят:
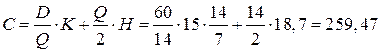 руб.
руб.
Так как период поставок равен 4 дня, а время работы равно 17 дней, получим 4 полные поставки и в 16-й день еще одну машину с гравием.
Задача
Пусть затраты на заказ равны 10 руб., затраты на хранение продукции 1 руб. в сутки, интенсивность потребления товара 5 шт. в день, цена товара – 2руб. за штуку, а при объеме закупки 15 шт. и более- 1руб.
Определите оптимальный размер заказа, цену покупки и затраты на управление запасами. Постройте график общих затрат.
Пусть Q -
размер заказа; ![]() - величина потребления за день; К=
10 - издержки одного заказа; h
=1 - удельные издержки хранения за день; сi
— цена продукта при соответствующем размере заказа.
- величина потребления за день; К=
10 - издержки одного заказа; h
=1 - удельные издержки хранения за день; сi
— цена продукта при соответствующем размере заказа.
Издержки заказа за период планирования: ![]() ;
;
Издержки хранения за период планирования: ![]() ;
;
Издержки на закупку товара:![]() .
.
Совокупные издержки:
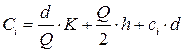 .
.
При размере заказа менее 15 шт формула совокупных издержек запишется в виде:
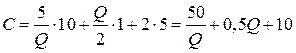 .
.
Для нахождения наименьшего значения функции С находим ее производную и прировняем ее к нулю.
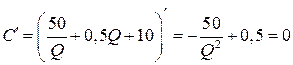
![]() .
.
Аналогично находим при заказе 15 шт. и более:
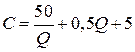 ;
; 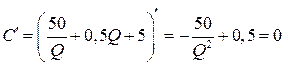 ;
; ![]() .
.
![]()
Общие издержки для каждого размера заказа и вида скидок с выбором наименьшего значения:
| Размер заказа |
Менее 15 шт. |
15 шт. и более |
| Цена 1 шт., руб. |
2 |
1 |
| Размер заказа, шт. |
10 |
15 |
| Издержки заказа, руб. |
5 |
3,33 |
| Издержки хранения, руб. |
5 |
7,5 |
| Издержки на закупку товара, руб. |
10 |
5 |
| Общие затраты, руб. |
20 |
15,83 |
Выбираем размер заказа, минимизирующий общие годовые издержки. Заказ
в размере 15 шт. будет минимизировать общие затраты, оптимальный размер
заказа ![]() шт.
шт.
При этом цена покупки составит ![]() руб., затраты на управление запасами составят
руб., затраты на управление запасами составят ![]() руб.
руб.
График общих
|
|
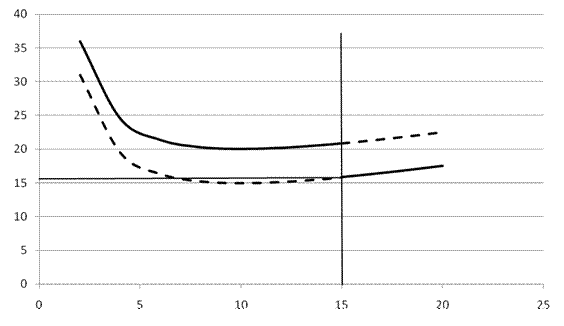
Рис.7
Задача
Рассмотрим задачу 5.1. Пусть поставщик супа в пакетах предоставляет следующие скидки
| Размер заказа |
Цена, руб./шт. |
| 1-199 |
2 |
| 200-499 |
1,96 (2% скидки) |
| 500 и более |
1,92 (4% скидки) |
Следует ли владельцу магазина воспользоваться одной из скидок, предоставляемых поставщиком? Каковы при этом будут размер заказа и общие затраты на управление запасами? Постройте график общих затрат.
Решение
Пусть Q - размер заказа; T =300 - продолжительность периода планирования; D =500 - величина спроса за период планирования; К= 10 - издержки одного заказа; Н =0,4 - удельные издержки хранения за период; сi — цена продукта при соответствующем размере заказа. Тогда:
Издержки заказа за период планирования: ![]() ;
;
Издержки хранения за период планирования : ![]() ;
;
Издержки на закупку товара : ![]() .
.
Совокупные издержки:
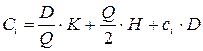 .
.
Оптимальный заказ:
 .
.
Поэтому для первого уровня цен принимаем ![]() ; для других цен -
; для других цен - ![]()
![]() . Рассчитываем общие издержки для каждого размера заказа и вида скидок, а затем выбрать наименьшее значение.
. Рассчитываем общие издержки для каждого размера заказа и вида скидок, а затем выбрать наименьшее значение.
| Размер заказа |
1-199 |
200-499 |
500 и более |
| Цена пакета, руб. |
2 |
1,96 |
1,92 |
| Размер заказа, шт. |
158 |
200 |
500 |
| Издержки заказа за год, руб. |
31,65 |
25,0 |
10 |
| Издержки хранения за год, руб. |
31,6 |
40 |
100 |
| Издержки на закупку товара за год, руб. |
1000 |
980 |
960 |
| Совокупные издержки, руб. |
1063,25 |
1045,0 |
1070,0 |
Выберем тот размер заказа, который минимизирует общие годовые
издержки. Из таблицы видно, что заказ в размере 200 пакетов супа будет
минимизировать совокупные издержки, следовательно, оптимальный размер
заказа ![]() пакетов.
пакетов.
При этом совокупные издержки за год составят ![]() руб.
руб.
![]()
![]()
![]()
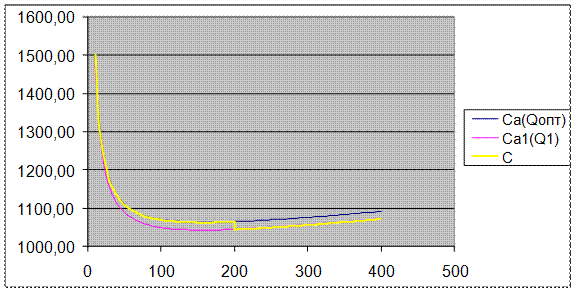
Рис. 8 - График общих затрат
Задача
Какое количество товара заказывать и по какой цене, каковы затраты при оптимальной организации управления запасами? Известно, что n =240 шт./дн.; С 0 = 30 руб.; С h = 3 руб./шт.дн.; a = 6 руб./шт.; a 1 = 5 руб./шт.; a2 =3 руб./шт.; Qp 1 = 50 шт.; QP 2 =500 шт.
Решение
Пусть Q -
размер заказа; v
=240 шт./дн. - величина спроса за период планирования; С0
=
30 руб. - издержки одного заказа; ![]() руб./шт.дн. - удельные издержки хранения за период; сi
— цена продукта при соответствующем размере заказа. Тогда:
руб./шт.дн. - удельные издержки хранения за период; сi
— цена продукта при соответствующем размере заказа. Тогда:
Издержки заказа за период планирования: ![]() ;
;
Издержки хранения за период планирования: ![]() ;
;
Издержки на закупку товара:![]() .
.
Совокупные издержки:
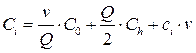 .
.
Оптимальный заказ:
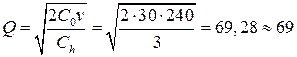 .
.
Поэтому для первого уровня цен принимаем ![]() ; для других цен -
; для других цен - ![]()
![]() . Далее рассчитаем общие издержки для каждого размера заказа и вида скидок, а затем выбрать наименьшее значение.
. Далее рассчитаем общие издержки для каждого размера заказа и вида скидок, а затем выбрать наименьшее значение.
| Размер заказа |
1-49 |
50-499 |
500 и более |
| Цена ед. товара, руб. |
6 |
5 |
3 |
| Размер заказа, шт. |
49 |
69 |
500 |
| Издержки заказа, руб. |
146,94 |
104,35 |
14,40 |
| Издержки хранения, руб. |
73,50 |
103,50 |
750,00 |
| Издержки на закупку товара, руб. |
1440,00 |
1200,00 |
720,00 |
| Совокупные издержки, руб. |
1660,44 |
1407,85 |
1484,40 |
Выберем тот размер заказа, который минимизирует общие издержки. Из
таблицы видно, что заказ в размере 69 единиц товара будет минимизировать
совокупные издержки, следовательно, оптимальный размер заказа ![]() .
.
Вывод: совокупные издержки 1407,85 руб.
Расчет и анализ сетевых моделей
1. Рассчитайте табличным методом представленный сетевой график. Определите критический путь.
![]()
Решение
Расчёты сетевого графика табличным методом приведены в таблице:
| hi |
i |
j |
РН |
tij |
РО |
ПО |
tij |
ПН |
Rij |
rij |
| - |
0 |
1 |
0 |
2 |
2 |
7 |
2 |
5 |
5 |
0 |
| - |
0 |
2 |
0 |
2 |
2 |
2 |
2 |
0 |
0 |
0 |
| - |
0 |
3 |
0 |
1 |
1 |
7 |
1 |
6 |
6 |
0 |
| 1 |
1 |
4 |
2 |
4 |
6 |
11 |
4 |
7 |
5 |
0 |
| 1 |
2 |
5 |
2 |
5 |
7 |
8 |
5 |
3 |
1 |
0 |
| 1 |
2 |
6 |
2 |
8 |
10 |
10 |
8 |
2 |
0 |
0 |
| 1 |
3 |
6 |
1 |
3 |
4 |
10 |
3 |
7 |
6 |
6 |
| 1 |
4 |
7 |
6 |
1 |
7 |
12 |
1 |
11 |
5 |
4 |
| 1 |
5 |
7 |
7 |
4 |
11 |
12 |
4 |
8 |
1 |
0 |
| 2 |
6 |
8 |
10 |
5 |
15 |
15 |
5 |
10 |
0 |
0 |
| 2 |
7 |
8 |
11 |
3 |
14 |
15 |
3 |
12 |
1 |
1 |
| 2 |
8 |
- |
15 |
- |
15 |
15 |
- |
15 |
0 |
0 |
Критический путь: 0-2-6-8
2. Рассчитайте табличным методом представленный сетевой график.. Определите критический путь.
![]()
Решение
Расчёты сетевого графика табличным методом приведены в таблице:
| hi |
i |
j |
РН |
tij |
РО |
ПО |
tij |
ПН |
Rij |
rij |
| - |
1 |
2 |
0 |
2 |
2 |
2 |
2 |
0 |
0 |
0 |
| 1 |
2 |
3 |
2 |
5 |
7 |
7 |
5 |
2 |
0 |
0 |
| 1 |
2 |
4 |
2 |
6 |
8 |
9 |
6 |
3 |
1 |
0 |
| 1 |
2 |
5 |
2 |
3 |
5 |
12 |
3 |
9 |
7 |
2 |
| 1 |
3 |
5 |
7 |
0 |
7 |
12 |
0 |
12 |
5 |
0 |
| 1 |
3 |
6 |
7 |
7 |
14 |
14 |
7 |
7 |
0 |
0 |
| 1 |
4 |
8 |
8 |
8 |
16 |
17 |
8 |
9 |
1 |
1 |
| 2 |
5 |
7 |
7 |
5 |
12 |
17 |
5 |
12 |
3 |
5 |
| 1 |
6 |
7 |
14 |
3 |
17 |
17 |
3 |
14 |
0 |
0 |
| 1 |
6 |
11 |
14 |
8 |
22 |
39 |
8 |
31 |
17 |
17 |
| 2 |
7 |
8 |
17 |
0 |
17 |
17 |
0 |
17 |
0 |
0 |
| 2 |
7 |
11 |
17 |
7 |
24 |
39 |
7 |
32 |
15 |
15 |
| 2 |
8 |
9 |
17 |
4 |
21 |
21 |
4 |
17 |
0 |
0 |
| 1 |
9 |
10 |
21 |
4 |
25 |
34 |
4 |
30 |
9 |
0 |
| 1 |
9 |
11 |
21 |
18 |
39 |
39 |
18 |
21 |
0 |
0 |
| 1 |
10 |
11 |
25 |
5 |
30 |
39 |
5 |
34 |
9 |
9 |
| 4 |
11 |
- |
39 |
- |
39 |
39 |
- |
39 |
0 |
0 |
Критический путь: 1-2-3-6-7-8-9-11
3. Рассчитайте табличным методом представленный сетевой график. Определите критический путь.
![]()
Решение
Расчеты сетевого графика табличным методом приведены в таблице:
| hi |
i |
j |
РН |
tij |
РО |
ПО |
tij |
ПН |
Rij |
rij |
| - |
0 |
1 |
0 |
18 |
18 |
48 |
18 |
30 |
30 |
0 |
| - |
0 |
2 |
0 |
15 |
15 |
26 |
15 |
11 |
11 |
0 |
| - |
0 |
4 |
0 |
30 |
30 |
30 |
30 |
0 |
0 |
0 |
| 1 |
1 |
3 |
18 |
22 |
40 |
70 |
22 |
48 |
30 |
0 |
| 1 |
1 |
9 |
18 |
12 |
30 |
100 |
12 |
88 |
70 |
52 |
| 1 |
2 |
5 |
15 |
9 |
24 |
35 |
9 |
26 |
9 |
0 |
| 1 |
2 |
6 |
15 |
15 |
40 |
62 |
15 |
40 |
25 |
0 |
| 1 |
3 |
9 |
40 |
30 |
70 |
100 |
30 |
70 |
30 |
0 |
| 1 |
4 |
7 |
30 |
25 |
55 |
55 |
25 |
30 |
0 |
0 |
| 1 |
4 |
8 |
30 |
30 |
60 |
90 |
30 |
60 |
30 |
30 |
| 1 |
5 |
7 |
24 |
20 |
44 |
55 |
20 |
35 |
11 |
11 |
| 1 |
5 |
10 |
24 |
5 |
29 |
80 |
5 |
75 |
51 |
26 |
| 1 |
6 |
10 |
40 |
15 |
55 |
80 |
15 |
65 |
25 |
0 |
| 2 |
7 |
8 |
55 |
35 |
90 |
90 |
35 |
55 |
0 |
0 |
| 2 |
8 |
11 |
90 |
32 |
122 |
122 |
32 |
90 |
0 |
0 |
| 2 |
9 |
11 |
70 |
22 |
99 |
122 |
22 |
100 |
30 |
23 |
| 2 |
10 |
11 |
55 |
42 |
97 |
122 |
42 |
80 |
25 |
25 |
| 3 |
11 |
- |
122 |
- |
122 |
122 |
- |
122 |
- |
- |
Критический путь: 0-4-7-8-11
4.Рассчитайте секторным методом представленный сетевой график. Определите критический путь.
![]()
Решение
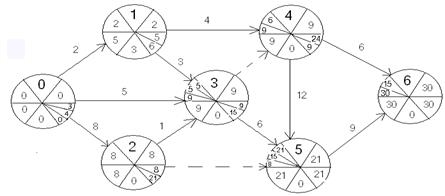
Критический путь 0-2-3-4-5-6
5. Рассчитайте представленный сетевой график методом диагональной таблицы . Определите критический путь.
Решение
Расчёты сетевого графика методом диагональной таблицы:
| Ti P |
i/j |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 0 |
0 |
2 |
|||||||||
| 2 |
1 |
3 |
8 |
6 |
4 |
7 |
|||||
| 5 |
2 |
4 |
|||||||||
| 10 |
3 |
2 |
|||||||||
| 8 |
4 |
11 |
|||||||||
| 6 |
5 |
10 |
|||||||||
| 9 |
6 |
7 |
|||||||||
| 12 |
7 |
4 |
|||||||||
| 19 |
8 |
5 |
|||||||||
| 24 |
9 |
||||||||||
| TiП |
0 |
2 |
8 |
13 |
8 |
9 |
12 |
15 |
19 |
24 |
|
| Ti P |
0 |
2 |
5 |
10 |
8 |
6 |
9 |
12 |
19 |
24 |
|
| r |
0 |
0 |
3 |
3 |
0 |
3 |
3 |
3 |
0 |
0 |
Критический путь: 0-1-4-8-9
6. Рассчитайте представленный сетевой график методом диагональной таблицы . Определите критический путь.
![]()
Решение
Расчёты методом диагональной таблицы:
| Ti P |
i/j |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
1 |
8 |
5 |
4 |
|||||
| 8 |
2 |
0 |
0 |
||||||
| 5 |
3 |
0 |
11 |
||||||
| 8 |
4 |
5 |
|||||||
| 8 |
5 |
6 |
|||||||
| 14 |
6 |
10 |
|||||||
| 24 |
7 |
4 |
|||||||
| 28 |
8 |
||||||||
| TiП |
0 |
8 |
8 |
9 |
8 |
14 |
24 |
28 |
|
| Ti P |
0 |
8 |
5 |
8 |
8 |
14 |
24 |
28 |
|
| r |
0 |
0 |
3 |
1 |
0 |
0 |
0 |
0 |
Критический путь:1-2-5-6-7-8