| Скачать .docx | Скачать .pdf |
Реферат: Решение нелинейных уравнений методом простых итераций
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ВОСТОЧНО-СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
Реферат на тему: «Решение нелинейных уравнений
методом простых итераций»
Выполнил:. Бубеев Б.М.
Проверил: Ширапов Д.Ш.
Улан-Удэ
2011 г.
Введение
Нелинейные уравнения можно разделить на 2 класса - алгебраические и трансцендентные. Алгебраическими уравнениями называют уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные). В частности, многочлен является целой алгебраической функцией. Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и другие) называются трансцендентными.
Методы решения нелинейных уравнений делятся на две группы:
1. точные методы ;
2. итерационные методы .
Точные методы позволяют записать корни в виде некоторого конечного соотношения (формулы). Из школьного курса алгебры известны такие методы для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений.
Как известно, многие уравнения и системы уравнений не имеют аналитических решений. В первую очередь это относится к большинству трансцендентных уравнений. Доказано также, что нельзя построить формулу, по которой можно было бы решить произвольное алгебраическое уравнение степени выше четвертой. Кроме того, в некоторых случаях уравнение содержит коэффициенты, известные лишь приблизительно, и, следовательно, сама задача о точном определении корней уравнения теряет смысл. Для их решения используются итерационные методы с заданной степенью точности.
Пусть дано уравнение
|
|
(1) |
где:
1. Функция f (x ) непрерывна на отрезке [a, b ] вместе со своими производными 1-го и 2-го порядка.
2. Значения f (x ) на концах отрезка имеют разные знаки (f (a ) * f (b ) < 0).
3. Первая и вторая производные f' (x ) и f'' (x ) сохраняют определенный знак на всем отрезке.
Условия 1) и 2) гарантируют, что на интервале [a, b ] находится хотя бы один корень, а из 3) следует, что f (x ) на данном интервале монотонна и поэтому корень будет единственным.
Решить уравнение (1) итерационным методом значит установить, имеет ли оно корни, сколько корней и найти значения корней с нужной точностью.
Всякое значение ![]() , обращающее функцию f
(x
) в нуль, т.е. такое, что:
, обращающее функцию f
(x
) в нуль, т.е. такое, что:
|
|
называется корнем уравнения (1) или нулем функции f (x ).
Задача нахождения корня уравнения f (x ) = 0 итерационным методом состоит из двух этапов:
1. отделение корней - отыскание приближенного значения корня или содержащего его отрезка;
2. уточнение приближенных корней - доведение их до заданной степени точности.
Процесс отделения корней начинается с установления знаков функции f (x ) в граничных x = a и x = b точках области ее существования.
Пример 1. Отделить корни уравнения:
| f (x ) º x 3 - 6х + 2 = 0. |
(2) |
Составим приблизительную схему:
| x |
-¥ |
-3 |
-1 |
0 |
1 |
3 |
+¥ |
| f(x) |
- |
- |
+ |
+ |
- |
+ |
+ |
Следовательно, уравнение (2) имеет три действительных корня, лежащих в интервалах [-3, -1], [0, 1] и [1, 3].
Приближенные значения корней (начальные приближения ) могут быть также известны из физического смысла задачи, из решения аналогичной задачи при других исходных данных, или могут быть найдены графическим способом.
В инженерной практике распространен графический способ определения приближенных корней.
Принимая во внимание, что действительные корни уравнения (1) - это точки пересечения графика функции f (x ) с осью абсцисс, достаточно построить график функции f (x ) и отметить точки пересечения f (x ) с осью Ох, или отметить на оси Ох отрезки, содержащие по одному корню. Построение графиков часто удается сильно упростить, заменив уравнение (1) равносильным ему уравнением:
|
|
(3) |
где функции f 1 (x ) и f 2 (x ) - более простые, чем функция f (x ). Тогда, построив графики функций у = f 1 (x ) и у = f 2 (x ), искомые корни получим как абсциссы точек пересечения этих графиков.
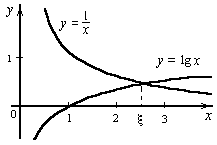
Рисунок 2.
Пример 2. Графически отделить корни уравнения (Рисунок 2):
| x lg x = 1. |
(4) |
Уравнение (4) удобно переписать в виде равенства:
lg x=![]() .
.
Отсюда ясно, что корни уравнения (4) могут быть найдены как абсциссы точек пересечения логарифмической кривой y
= lg x
и гиперболы y
= ![]() . Построив эти кривые, приближенно найдем единственный корень
. Построив эти кривые, приближенно найдем единственный корень ![]() уравнения (4) или определим его содержащий отрезок [2, 3].
уравнения (4) или определим его содержащий отрезок [2, 3].
Итерационный процесс состоит в последовательном уточнении начального приближения х 0 . Каждый такой шаг называется итерацией . В результате итераций находится последовательность приближенных значений корня х 1 , х 2 , ..., хn . Если эти значения с увеличением числа итераций n приближаются к истинному значению корня, то говорят, что итерационный процесс сходится .
Для использования метода итерации исходное нелинейное уравнение f (х ) = 0 заменяется равносильным уравнением
| x = j(x ). |
(8) |
Пусть известно начальное приближение корня х = х 0 . Подставляя это значение в правую часть уравнения (8), получим новое приближение:
| х 1 = j(х 0 ). |
Далее, подставляя каждый раз новое значение корня в (8), получаем последовательность значений:
|
|
(9) |
Геометрически метод итерации может быть пояснен следующим образом. Построим на плоскости хОу
графики функций у = х
и у =
j
(х
).
Каждый действительный корень ![]() уравнения (8) является абсциссой точки пересечения М
кривой у =
j
(х
) с прямой у = х
(Рисунок 6, а
).
уравнения (8) является абсциссой точки пересечения М
кривой у =
j
(х
) с прямой у = х
(Рисунок 6, а
).
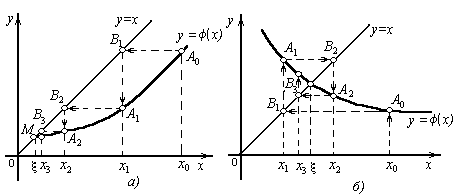
Рисунок 6.
Отправляясь от некоторой точки А
0
[x
0
, j
(x
0
)],
строим ломаную А
0
В
1
А
1
В
2
А
2
... (“лестница”), звенья которой попеременно параллельны оси Ох
и оси Оу
, вершины А
0
, А
1
, А
2
, ...
лежат на кривой у=
j
(х
),
а вершины В
1
, В2
, В
3
, …, - на прямой у = х.
Общие абсциссы точек А
1
и В
1
, А
2
и В
2
, ..., очевидно, представляют собой соответственно последовательные приближения х
1
, х
2
, ...
корня ![]() .
.
Возможен также другой вид ломаной А 0 В 1 А 1 В 2 А 2 ... - “спираль” (Рисунок 6, б ). Решение в виде “лестницы” получается, если производная j' (х ) положительна, а решение в виде “спирали”, если j' (х ) отрицательна.
На Рисунке 6, а, б
кривая у
= j (х
) в окрестности корня ![]() - пологая, то есть
- пологая, то есть ![]() <1, и процесс итерации сходится. Однако, если рассмотреть случай, где
<1, и процесс итерации сходится. Однако, если рассмотреть случай, где ![]() >1, то процесс итерации может быть расходящимся (Рисунок 7).
>1, то процесс итерации может быть расходящимся (Рисунок 7).
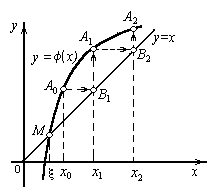
Рисунок 7.
Поэтому для практического применения метода итерации нужно выяснить достаточные условия сходимости итерационного процесса.
Теорема:
Пусть функция
j (х
) определена и дифференцируема на отрезке
[a, b
], причем все ее значения
j (х
) ![]() [a
, b
].
[a
, b
].
Тогда, если существует правильная дробь q такая, что
![]()
![]() q
< 1
q
< 1
при a < x < b, то: 1) процесс итерации
![]()
сходится независимо от начального значени я х 0 I [a , b ];
2) предельное значение
![]() является единственным корнем уравнения
х =
j
(х
) на отрезке
[a, b
].
является единственным корнем уравнения
х =
j
(х
) на отрезке
[a, b
].
Пример 5. Уравнение
| f (x ) = x 3 - x - 1 = 0 |
(10) |
имеет корень x ![]() [1, 2], так как f
(1) = - 1 < 0 и f
(2) = 5 > 0.
[1, 2], так как f
(1) = - 1 < 0 и f
(2) = 5 > 0.
Уравнение (10) можно записать в виде
| х = х 3 - 1. |
(11) |
Здесь
j (х ) = х 3 - 1 и j' (х ) = 3х 2 ;
поэтому
j' (х
) ![]() 3 при 1
3 при 1 ![]() х
х
![]() 2
2
и, следовательно, условия сходимости процесса итерации не выполнены.
Если записать уравнение (10) в виде
|
|
(12) |
то будем иметь:
![]() .
.
Отсюда ![]() при 1
при 1 ![]() х
х
![]() 2 и значит, процесс итерации для уравнения (12) быстро сойдется.
2 и значит, процесс итерации для уравнения (12) быстро сойдется.
Найдем корень x уравнения (10) с точностью до 10-2 . Вычисляем последовательные приближения хn с одним запасным знаком по формуле
![]()
Найденные значения помещены в Таблицу 1:
Таблица 1
Значения последовательных приближений xi.
| i |
0 |
1 |
2 |
3 |
4 |
| xi |
1 |
1,260 |
1,312 |
1,322 |
1,3243 |
С точностью до 10-2 можно положить x = 1,324.