| Скачать .docx | Скачать .pdf |
Книга: Книга: Вивчення диференціального числення функцій однієї та багатьох змінних в умовах модульно-рейтингової
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ДОНБАСЬКИЙ ГІРНІЧО-МЕТАЛУРГІЙНИЙ ІНСТИТУТ
Т.М. Сукач
Вивчення диференціального числення функцій однієї та багатьох змінних в умовах модульно-рейтингової системи
Навчальний посібник
Алчевськ, 2004
Передмова
Вища математика, як навчальна дисципліна, є однією з осноних при підготовці висококваліфікованих кадрів у вищих технічних та інших навчальних закладах. Диференціальне числення є основним розділом курсу вищої математики в цілому.
Без засвоєння основних положень, на яких базується диференціальне числення, не можна на належному якісному рівні застосовувати теорію та методи вищої математики при розв’язанні ряду задач з різних галузей знань (при вивченні фізики, електротехніки, інших інженерних та економічних спеціальностей).
Матеріал посібника поділено на 4 глави:
1) Функція, границя, неперервність; 2) Диференціальне чис-лення функції однієї змінної; 3) Дослідження функції за допомогою похідних; 4) Диференціальне числення функцій багатьох змінних.
Кожна глава складається з параграфів, яки містять короткі теоретичні відомості та приклади розв’язання типових вправ. Для самостійної роботи студентів наводиться комплекс типових вправ з відповідями. Наприкінці кожної глави запропоновано зразки контрольних робот з теми, питання до колоквіуму, завдання семестрової роботи студентів. Наведена інструкція що до модульно-рейтингового контролю знань студентів при вивченні даного розділу вищої математики.
Зміст посібника, а також рівень навчальних вимог до знань студентів відповідає програмі курсу “Вища математика для інженерно-технічних, економічних спеціальностей вищих навчальних закладів, студентів технічних коледжів”.
1. Функція, границя, неперервність
1.1 Функція. Область визначення функції
Нехай маємо множину Х
дійсних чисел. Якщо кожному числу ![]() за певним правилом або законом поставлено у відповідність одне дійсне число у
, з множини
за певним правилом або законом поставлено у відповідність одне дійсне число у
, з множини ![]() , то говорять, що на множені Х
визначено функцію
і записують
, то говорять, що на множені Х
визначено функцію
і записують ![]() .
.
При цьому множина Х
називається областю визначення
або областю існування
функції; х
називають аргументом
або незалежною змінною; у
називають залежною змінною або функцією
; ![]() називають значенням функції
в точці х
;
називають значенням функції
в точці х
; ![]() — множина, до якої належить значення функції.
— множина, до якої належить значення функції.
Множину всіх значень функції, яких вона набуває при ![]() , називають областю значень
функції.
, називають областю значень
функції.
Приклад 1. Знайти область визначення функції
![]() .
.
Розв’язання. Функція у існує, якщо підкореневий вираз невід’ємний. Тому область визначення знаходиться з нерівності:
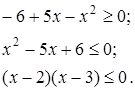
 |
Таким чином, областю визначення даної функції є відрізок ![]() .
.
Приклад 2. Знайти область визначення функції
![]() .
.
Розв’язання.
Функція визначена, якщо ![]() .
.
Таким чином, область визначення даної функції є сукупність інтервалів:
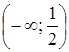 та
та 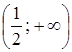 .
.
Приклад 3. Знайти область визначення функції
![]() .
.
Розв’язання. Функція визначена, якщо
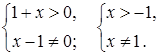
Тобто
 |
![]() .
.
1.2 Парність, непарність функцій. Періодичність функцій
Нехай функцію ![]() задано на проміжку
задано на проміжку ![]() , який є симетричним відносно початку координат. Це може бути або нескінченний інтервал
, який є симетричним відносно початку координат. Це може бути або нескінченний інтервал ![]() , або скінчений інтервал
, або скінчений інтервал ![]() , або відрізок
, або відрізок ![]() , де а
— будь-яке дійсне число.
, де а
— будь-яке дійсне число.
Функція ![]() , визначена на проміжку
, визначена на проміжку ![]() , називається парною
, якщо для будь-якого
, називається парною
, якщо для будь-якого ![]() виконується рівність
виконується рівність
![]()
Графік парної функції симетричний відносно осі ординат.
Функція ![]() , визначена на проміжку
, визначена на проміжку ![]() , називається непарною
, якщо для будь-якого
, називається непарною
, якщо для будь-якого ![]() виконується рівність
виконується рівність
![]()
Графік непарної функції симетричний відносно початку координат.
Приклад 1.
Нехай ![]() , де
, де ![]() . Згідно з відомою властивістю даної функції,
. Згідно з відомою властивістю даної функції,
![]()
Отже, ![]() є непарною функцією.
є непарною функцією.
Приклад 2.
Нехай ![]() , де
, де ![]() . Відомо, що
. Відомо, що
![]()
Отже, ![]() є парною функцією.
є парною функцією.
Приклад 3. Дослідити на парність чи непарність функцію
![]()
Знайдемо область визначення функції:
![]()
Знайдемо ![]() :
:
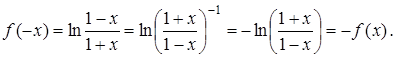
Одержали, що ![]() , тобто
, тобто ![]() — непарна.
— непарна.
Функція ![]() , визначена на всій числовій осі, називається періодичною
, якщо існує число
, визначена на всій числовій осі, називається періодичною
, якщо існує число ![]() таке, що для всіх
таке, що для всіх ![]() виконується тотожність
виконується тотожність
![]()
Число Т
при цьому називається періодом функції ![]() , а саму функцію називають Т
-переодічною
.
, а саму функцію називають Т
-переодічною
.
Якщо число Т
є періодом функції ![]() , то й число –Т
є також періодом
, то й число –Т
є також періодом ![]() :
:
![]()
Якщо ![]() — періодична функція з періодом Т, то функція
— періодична функція з періодом Т, то функція ![]() , де
, де ![]() , є періодичною з періодом
, є періодичною з періодом ![]() .
.
Зокрема, якщо розглянути функцію ![]() , де
, де ![]() — сталі, то періодом цієї функції є число
— сталі, то періодом цієї функції є число ![]() .
.
Зауважимо, що функцію ![]() у фізиці називають гармонікою
, число
у фізиці називають гармонікою
, число ![]() називають амплітудою
,
називають амплітудою
, ![]() — циклічною частотою
, а
— циклічною частотою
, а ![]() — початковою фазою гармоніки
.
— початковою фазою гармоніки
.
Приклад 4.
Знайти період функції ![]() .
.
Розв’язання.
Функція ![]() має період
має період ![]() , тому функція
, тому функція ![]() має період
має період ![]() .
.
Приклад 5.
Знайти період функції ![]() .
.
Розв’язання.
Функція ![]() має період
має період ![]() , тому
, тому ![]() має період
має період ![]() .
.
Приклад 6.
Знайти період функції ![]() .
.
Розв’язання.
Функція ![]() має період
має період ![]() .
.
Тренувальні вправи
Дослідити на парність чи непарність функції:
1. 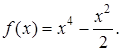 [Парна]
[Парна]
2. ![]() [Непарна]
[Непарна]
3. ![]() [Парна] 4.
[Парна] 4. ![]() [Парна]
[Парна]
5. ![]() [Ні парна, ні непарна]
[Ні парна, ні непарна]
1.3 Основні елементарні функції та їх графіки
1. Лінійна функція:
![]() .
.
Графік функції — пряма, досить знати дві точки, бажано точки перетину з осями координат:
![]() ;
; ![]() .
.
2. Степенева функція:
![]() .
.
Якщо ![]() , функція визначена на всій числовій осі, тобто
, функція визначена на всій числовій осі, тобто ![]() .
.
Якщо ![]() — функція парна, то приймає значення
— функція парна, то приймає значення ![]() . Ії графіками будуть параболи відповідно другого, четвертого і т.д. порядків.
. Ії графіками будуть параболи відповідно другого, четвертого і т.д. порядків.
Якщо ![]() — графіки параболи третього, п’ятого і т.д. порядків.
— графіки параболи третього, п’ятого і т.д. порядків.
3. Показникова функція:
![]() .
.
Область її визначення ![]() , область значень
, область значень ![]() . Якщо
. Якщо ![]() , функція , якщо
, функція , якщо ![]() , функція ¯.
, функція ¯.
Причому, для довільного ![]() , тобто графік довільної експоненти проходить через точку
, тобто графік довільної експоненти проходить через точку ![]() .
.
4. Логарифмічна функція:
|
|
5. Тригонометричні функції:
![]() .
.
Функції ![]() та
та ![]() визначені для всіх
визначені для всіх ![]() та мають множину значень
та мають множину значень ![]() .
.
Функція ![]() визначена всюди, крім
визначена всюди, крім ![]() ,
, ![]() , та монотонно зростає в кожному інтервалі області визначення.
, та монотонно зростає в кожному інтервалі області визначення.
Функція ![]() всюди визначена, крім
всюди визначена, крім ![]() , та монотонно спадає в кожному інтервалі області визначення.
, та монотонно спадає в кожному інтервалі області визначення.
Множина значень ![]() та
та ![]() — проміжок
— проміжок ![]() .
.
Функції ![]() ,
, ![]() ,
, ![]() — непарні, їх графіки симетричні відносно початку координат,
— непарні, їх графіки симетричні відносно початку координат, ![]() — парна, її графік симетричний відносно
— парна, її графік симетричний відносно ![]() .
.
Функції періодичні. Найменший період синуса та косинуса ![]() ,
, ![]() та
та ![]() —
— ![]() .
.
6. Обернені тригонометричні функції
Тригонометричні функції в інтервалі монотонності мають обернені:
![]() — обернена до
— обернена до ![]() на відрізку
на відрізку 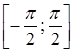 ;
;
![]() — обернена до
— обернена до ![]() на відрізку
на відрізку ![]() ;
;
![]() — обернена до
— обернена до ![]() на відрізку
на відрізку 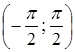 ;
;
![]() — обернена до
— обернена до ![]() на відрізку
на відрізку ![]() .
.
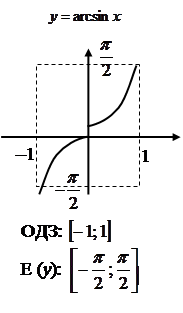 |
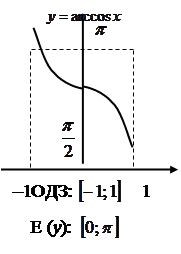 |
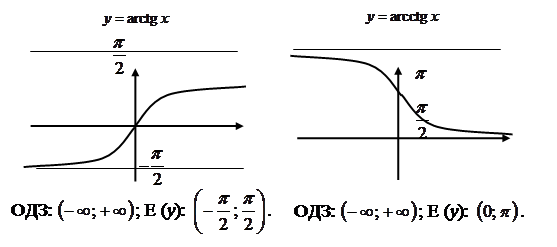
7. Перетворення графіків функцій
При побудові графіків функцій часто використовують дефор-мації та паралельне перенесення вздовж осі ![]() та
та ![]() .
.
Треба знати, що:
1) графік функції ![]() — дзеркальне відображення графіка
— дзеркальне відображення графіка ![]() відносно осі
відносно осі ![]() ;
;
2) графік функції ![]() — дзеркальне відображення графіка
— дзеркальне відображення графіка ![]() відносно осі
відносно осі ![]() ;
;
3) графік функції ![]() , де
, де ![]() — паралельне перенесення графіка
— паралельне перенесення графіка ![]()
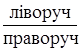 на а
одиниць масштабу вздовж осі
на а
одиниць масштабу вздовж осі ![]() ;
;
4) графік функції![]() , де
, де ![]() — паралельне перенесення графіка
— паралельне перенесення графіка ![]()
![]() на а
одиниць масштабу вздовж осі
на а
одиниць масштабу вздовж осі ![]() ;
;
5) графік функції ![]() — стиснення в
— стиснення в ![]() разів
разів ![]() , або розтягнення в
, або розтягнення в ![]() разів
разів ![]() графіка
графіка ![]() вздовж осі
вздовж осі ![]() ;
;
6) графік функції ![]() — розтягнення в
— розтягнення в ![]() разів
разів ![]() , або стиснення в
, або стиснення в ![]() разів
разів![]() , графіка
, графіка ![]() вздовж осі
вздовж осі ![]() ;
;
7) графік функції ![]() — дзеркальне відображення від осі
— дзеркальне відображення від осі ![]() від’ємної частини (під віссю
від’ємної частини (під віссю ![]() ) графіка функції
) графіка функції![]() , додатна частина графіка залишається на місці.
, додатна частина графіка залишається на місці.
8) графік функції ![]() — дзеркальне відображення від осі
— дзеркальне відображення від осі ![]() правої частини (з додатної півплощини) графіка
правої частини (з додатної півплощини) графіка ![]() в ліву півплощину, додатна частина графіка залишається на місці.
в ліву півплощину, додатна частина графіка залишається на місці.
Аналогічно визначаються нескінченно малі й нескінченно великі величини при ![]() .
.
Нескінченно великі величини знаходяться в тісному зв’язку з нескінченно малими: якщо при даному граничному переході функція ![]() є нескінченно великою, то функція
є нескінченно великою, то функція ![]() при цьому самому граничному переході буде нескінченно малою й навпаки.
при цьому самому граничному переході буде нескінченно малою й навпаки.
Властивості нескінченно малих
1.
Функцію ![]() можна подати у вигляді
можна подати у вигляді ![]() , де
, де ![]() – стале число;
– стале число; ![]() — нескінченно мала при
— нескінченно мала при ![]() , тоді і тільки тоді, коли
, тоді і тільки тоді, коли ![]() .
.
2.
Якщо ![]() , то
, то 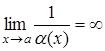 .
.
3. Алгебраїчна сума довільного скінченого числа нескінченно малих функцій є функція нескінченно мала (у самому граничному переході).
4. Добуток нескінченно малої на обмежену функцію є величина нескінченно мала.
5. Добуток скінченого числа нескінченно малих є величина нескінченно мала.
6. Добуток нескінченно малої на постійну є величина нескінченно мала.
7.
Частка ![]() від ділення нескінченно малої при
від ділення нескінченно малої при ![]() на функцію, границя якої відмінна від нуля, тобто
на функцію, границя якої відмінна від нуля, тобто ![]() , є величина нескінченно мала.
, є величина нескінченно мала.
При обчисленні границь необхідно знати такі теореми:
1.
![]()
2.
![]()
3.
Якщо ![]() і
і ![]() існують, то
існують, то
![]()
![]()
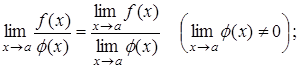
![]()
4. Для всіх основних елементарних функцій у довільній точці їх визначення справедлива рівність
![]()
5.
Якщо ![]() то
то 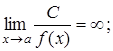
якщо ![]() то
то 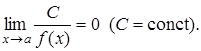
6.
Якщо ![]() то
то 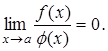
7.
Якщо ![]()
![]()
![]() то
то ![]()
8.
Якщо ![]() при
при ![]() , то
, то ![]()
9.
Якщо ![]() при
при ![]() , то
, то ![]()
10.
Якщо змінна величина ![]() зростаюча при
зростаюча при ![]() і обмежена при
і обмежена при ![]() , то вона має границю
, то вона має границю ![]() .
.
Порівняння двох нескінченно малих функцій одного й того самого аргументу х
при ![]() характеризується наступними означеннями й теоремами.
характеризується наступними означеннями й теоремами.
Нескінченно малі функції ![]() і
і ![]() називаються нескінченно малими одного порядку при
називаються нескінченно малими одного порядку при ![]() , якщо
, якщо 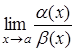 дорівнює кінцевому числу
дорівнює кінцевому числу ![]() .
.
Якщо ![]() , то
, то ![]() називається нескінченно малою більш високого порядку в порівнянні з
називається нескінченно малою більш високого порядку в порівнянні з ![]() .
.
Якщо ![]() , то
, то ![]() і
і ![]() називаються еквівалентними нескінченно малими, й пишуть
називаються еквівалентними нескінченно малими, й пишуть ![]() .
.
Якщо 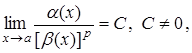 то
то ![]() називається нескін-ченно малою порядку Р
у порівнянні з нескінченно малою
називається нескін-ченно малою порядку Р
у порівнянні з нескінченно малою ![]() .
.
Теореми про еквівалентні нескінчено малі
1. Границя відношення двох нескінченно малих функцій не зміниться, якщо ці нескінченно малі замінити величинами, їм екві-валентними.
2. Щоб дві нескінченно малі функції були еквівалентними, необхідно й достатньо, щоб їх різниця була нескінченно малою більш високого порядку в порівнянні з кожною з них.
Якщо ![]() при
при ![]() , то справедливі такі еквівалентності
:
, то справедливі такі еквівалентності
:
1. ![]() 2.
2. ![]()
3. ![]() 4.
4. ![]()
5. ![]() 6.
6. ![]()
7. ![]() 8.
8. 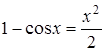
При обчисленні границь найчастіше використовують деякі важливі формули:
![]() — перша важлива границя
;
— перша важлива границя
;
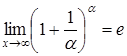 ;
; 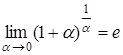 — друга важлива границя
,
— друга важлива границя
,
де е — ірраціональне число, е = 2,718281...
Наслідки з важливих границь
1. ![]() 2.
2. ![]()
3. ![]() 4.
4. ![]()
5. 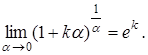 6.
6. 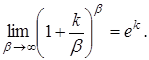
Розкриття невизначеностей
Обчислення границь зводиться до підстановки в даний вираз граничного значення аргументу. Якщо при цьому одержуємо неви-значені вирази вигляду ![]() то знаходження границь у цих випадках називається розкриттям
невизначеності
.
то знаходження границь у цих випадках називається розкриттям
невизначеності
.
Для розкриття невизначеності, перш ніж перейти до границі, необхідно перетворити даний вираз.
Невизначеність виду ![]()
Щоб розкрити невизначеність виду ![]() , треба чисельник та знаменник дробу поділити почленно на найвищий степінь змінної.
, треба чисельник та знаменник дробу поділити почленно на найвищий степінь змінної.
Приклад 1. Знайти границю:
а) 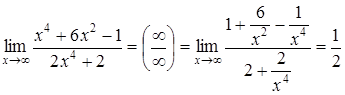 .
.
б) 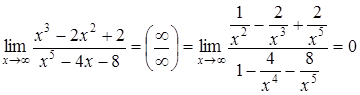 .
.
в) 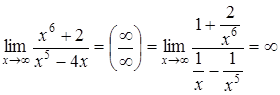 .
.
г) 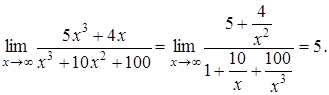
Невизначеність виду ![]()
Якщо чисельник та знаменник дробу поліном, що перетворюється в нуль при ![]() , для розкриття невизначеності чисельник та знаменник треба поділити на
, для розкриття невизначеності чисельник та знаменник треба поділити на ![]() .
.
Приклад 3. Обчислити:
а) 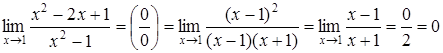 .
.
б) 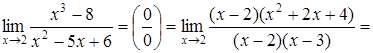
![]()
Приклад 4. Знайти границі:
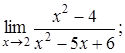
Розв’язання.
Безпосередня підстановка числа ![]() під знак границі приводить до невизначеності 0/0. Перетворимо вираз, розклавши чисельник і знаменник на множники і скоротивши на
під знак границі приводить до невизначеності 0/0. Перетворимо вираз, розклавши чисельник і знаменник на множники і скоротивши на ![]() :
:
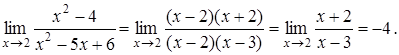
Невизначеність виду ![]()
Невизначеність виду ![]() перетвореннями приводиться до виду
перетвореннями приводиться до виду ![]() та
та ![]() .
.
Приклад 5.
а) 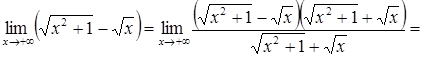
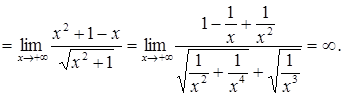
б) 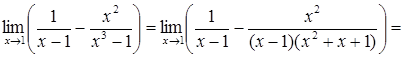
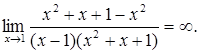
Невизначеність виду ![]()
Невизначеність виду ![]() розкривається за допомогою другої стандартної границі.
розкривається за допомогою другої стандартної границі.
Приклад 6.
а) 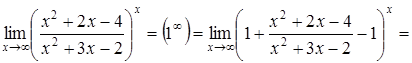
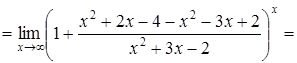
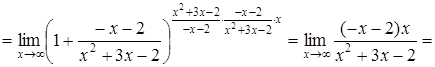
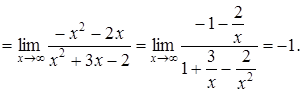
б) 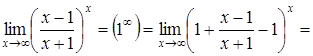
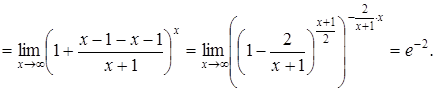
в) 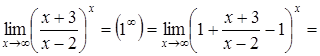
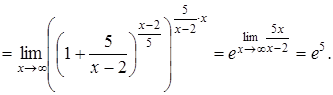
Приклади обчислення границь за допомогою еквівалентних нескінченно малих:
а) 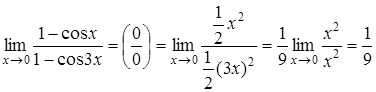 .
.
б) 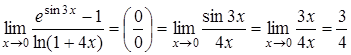 .
.
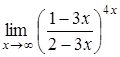 .
. ![]()
1. 5 Неперервність функції. Дослідження функції на неперервність
Функція![]() називається неперервною в точці
називається неперервною в точці
![]() , якщо існує границя функції в цій точці і вона дорівнює значенню функції в точці
, якщо існує границя функції в цій точці і вона дорівнює значенню функції в точці ![]() :
:
![]()
Функція ![]() в точці
в точці ![]() буде неперервною тоді і тільки тоді, коли виконуються умови:
буде неперервною тоді і тільки тоді, коли виконуються умови:
1.
функція ![]() визначена в околі точки
визначена в околі точки ![]() ;
;
2.
існує границя ![]() функції в точці
функції в точці ![]() ;
;
3. границя функції дорівнює значенню функції в цій точці, тобто
![]() (1)
(1)
Разом усі ці умови є необхідними й достатніми для того, щоб функція ![]() була неперервною в точці
була неперервною в точці ![]() .
.
На практиці при дослідженні функцій на неперервність користуються ознаками, які безпосередньо випливають із співвідношення (1), а саме:
для того, щоб функція ![]() була неперервною в точці
була неперервною в точці ![]() , треба щоб:
, треба щоб:
1.
![]() була визначеною в околі точки
була визначеною в околі точки ![]() ;
;
2.
існувала лівостороння границя функції в точці, тобто існувало число ![]() ;
;
3. існувала правостороння границя функції – число
![]() ;
;
4. лівостороння й правостороння границя були рівні
![]() =
=![]() ;
;
5.
правостороння й лівостороння границя в точці ![]() дорівнювали значенню функції в цій точці, тобто
дорівнювали значенню функції в цій точці, тобто
![]() =
=![]() =
=![]()
Якщо хоч одна с цих умов не виконується в точці, яка є внутрішньою точкою проміжку, в якому визначена функція, то функція в цій точці називається розривною .
Якщо функція ![]() визначена на відрізку
визначена на відрізку ![]() , то в точках а
і b
можна ставити питання тільки про односторонню неперервність, а саме, в точці а
— про неперервність справа, а в точці b
— зліва. Тому природно постає питання про введення таких понять, як неперервність функції в точці зліва і справа.
, то в точках а
і b
можна ставити питання тільки про односторонню неперервність, а саме, в точці а
— про неперервність справа, а в точці b
— зліва. Тому природно постає питання про введення таких понять, як неперервність функції в точці зліва і справа.
Функція ![]() називається неперервною в точці
називається неперервною в точці ![]() зліва
, якщо виконуються умови:
зліва
, якщо виконуються умови:
1.
![]() визначена в точці
визначена в точці ![]() (існує число
(існує число ![]() );
);
2.
в точці ![]() існує лівостороння границя функції;
існує лівостороння границя функції;
3.
лівостороння границя функції дорівнює значенню функції в точці ![]() .
.
Отже, якщо ![]() неперервна в точці
неперервна в точці ![]() зліва, то виконується співвідношення
зліва, то виконується співвідношення
![]() =
=![]() ,
,
де ![]() — лівостороння границя функції в точці
— лівостороння границя функції в точці ![]() .
.
Функція ![]() називається неперервною в точці
називається неперервною в точці ![]() справа
, якщо виконуються умови:
справа
, якщо виконуються умови:
1.
![]() визначена в точці
визначена в точці ![]() (існує число
(існує число ![]() );
);
2.
в точці ![]() існує правостороння границя функції;
існує правостороння границя функції;
3.
правостороння границя функції дорівнює значенню функції в точці ![]() .
.
Отже, для неперервної функції справа повинно виконуватися співвідношення
![]() =
=![]() ,
,
де ![]() — правостороння границя функції
— правостороння границя функції ![]() в точці
в точці ![]() .
.
Точкою розриву функції ![]() називають точку
називають точку ![]() в околі якої функція визначена, але в самій точці не задовольняє умові неперервності, що
в околі якої функція визначена, але в самій точці не задовольняє умові неперервності, що ![]() .
.
1.
Точка ![]() є точкою усувного розриву
, якщо існує
є точкою усувного розриву
, якщо існує ![]() , проте
, проте ![]() не визначена в точці
не визначена в точці ![]() , або
, або ![]() . Даний розрив можна усунути, для цього до визначають певним чином функцію в точці
. Даний розрив можна усунути, для цього до визначають певним чином функцію в точці ![]() ;
;
2.
Точка ![]() є точкою розриву першого роду
, якщо існують скінченні ліва
є точкою розриву першого роду
, якщо існують скінченні ліва ![]() та права
та права ![]() границі функції, але
границі функції, але ![]() , різницю
, різницю
![]()
називають стрибком функції ![]() в точці
в точці ![]()
3.
Точка ![]() є точкою розриву другого роду
функції
є точкою розриву другого роду
функції ![]() , якщо в точці
, якщо в точці ![]() не існує принаймні одна з односторонніх границь функції.
не існує принаймні одна з односторонніх границь функції.
Приклад 1.
Дослідити точки розриву функції 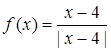 .
.
 Розв’язання.
В точці
Розв’язання.
В точці ![]() функція не визначена. Знайдемо при
функція не визначена. Знайдемо при ![]() границі даної функції зліва та справа:
границі даної функції зліва та справа:
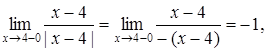
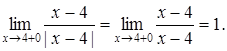
Оскільки односторонні границі скінченні, але
![]() ,
,
то ![]() є точкою розриву першого роду.
є точкою розриву першого роду.
Стрибок в даному випадку в точці ![]() дорівнює 2.
дорівнює 2.
Приклад 2.
Дослідити на неперервність функцію ![]()
 Розв’язання.
Дана функція визначена у всіх точках за винятком х
= 0. Знайдемо односторонні границі функції в цій точці:
Розв’язання.
Дана функція визначена у всіх точках за винятком х
= 0. Знайдемо односторонні границі функції в цій точці:
![]()
Рівність ![]() означає, що х
= 0 є точкою усувного розриву.
означає, що х
= 0 є точкою усувного розриву.
Приклад 3. Визначити характер розриву функції
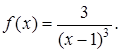
 Розв’язання.
Функція в точці
Розв’язання.
Функція в точці ![]() не визначена.
не визначена.
При ![]() маємо
маємо ![]() , при
, при ![]()
![]() . Отже,
. Отже, ![]() ,
, ![]() .
.
Тому точка ![]() є точкою розриву другого роду.
є точкою розриву другого роду.
2. Диференціальне числення функції однієї змінної
2.1 Похідна функції в точці ![]()
Похідною функції
![]() в точці
х
називається границя (як що вона існує) відношення приросту функції
в точці
х
називається границя (як що вона існує) відношення приросту функції ![]() до приросту аргументу
до приросту аргументу ![]() , коли приріст аргументу прямує до нуля, тобто:
, коли приріст аргументу прямує до нуля, тобто:
![]() . (2.1)
. (2.1)
Функція, яка має скінчену похідну в точці х , називається диференційовною в цій точці. Приріст диференційовної в точці х функції має вигляд
![]() , (2.2)
, (2.2)
де ![]() – нескінченно мала функція при
– нескінченно мала функція при ![]() , тобто диференційовна функція неперервна.
, тобто диференційовна функція неперервна.
Якщо ![]() , тоді функція
, тоді функція ![]() в точці х має нескінченну похідну.
в точці х має нескінченну похідну.
Основні правила диференціювання
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
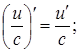 (4)
(4)
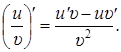 (5)
(5)
Похідні основних елементарних функцій
![]() (6)
(6)
![]() (7)
(7)
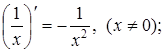 (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
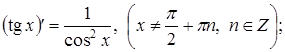 (12)
(12)
![]() (13)
(13)
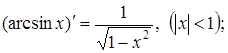 (14)
(14)
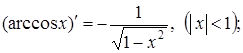 (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
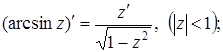 (18)
(18)
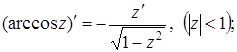 (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
Приклад 1.
Знайти похідну функції  .
.
Розв’язання. Застосовуючи основні правила диференцію-вання, маємо:
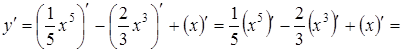
![]()
Приклад 2.
Знайти похідну функції ![]() .
.
Розв’язання.
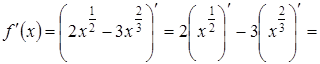
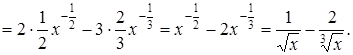
Приклад 3.
Знайти похідну функції ![]() .
.
Розв’язання. Використовуючи формули, маємо:
![]()
Приклад 4.
Знайти похідну функції ![]() .
.
Розв’язання.
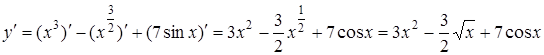 .
.
Приклад 5.
Знайти похідну функції ![]() .
.
Розв’язання.
![]() .
.
Приклад 6.
Знайти похідну функції ![]() .
.
Розв’язання.
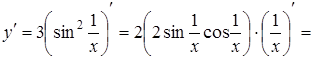
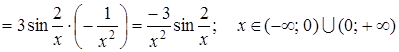 .
.
Приклад 7.
Знайти похідну функції ![]() .
.
Розв’язання.
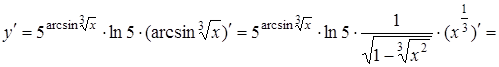
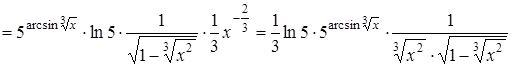 .
.
2.2 Похідна складеної та оберненої функції
Якщо функція 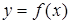 має похідну в точці х
, а функція
має похідну в точці х
, а функція 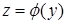 – має похідну в точці
– має похідну в точці 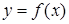 , тоді складена функція
, тоді складена функція 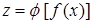 диференційовна в точці х
, причому
диференційовна в точці х
, причому
![]() або
або 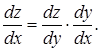
Наведене правило обчислення похідної складеної функції застосовується і для композиції довільного скінченого числа функцій.
Наприклад, для складеної функції виду ![]() , де
, де ![]() ,
, ![]() ,
, ![]() – диференційовні у відповідних точках функції, має місце рівність
– диференційовні у відповідних точках функції, має місце рівність
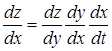 .
.
Якщо неперервна та строго монотонна в деякому околі точки х
функція 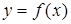 має похідну
має похідну 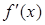 в цій точці, тоді обернена функція
в цій точці, тоді обернена функція 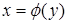 в точці у має похідну, причому
в точці у має похідну, причому
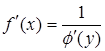 .
.
Приклад 1.
Знайти похідну функції 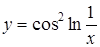 .
.
Розв’язання.
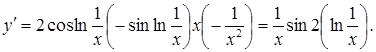
Приклад 2.
Знайти похідну функції ![]() .
.
Розв’язання. Використовуючи правило диференціювання добутку двох функцій, знаходимо:
![]()
![]()
Приклад 3.
Обчислити похідну функції ![]() .
.
Розв’язання. За правилом диференціювання частки маємо:
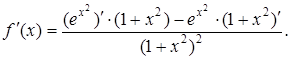
Знайдемо похідну функції ![]() , розглядаючи ії як композицію двох диференційованих функцій
, розглядаючи ії як композицію двох диференційованих функцій ![]() та
та ![]() . За правилом обчислення похідної функції дістанемо:
. За правилом обчислення похідної функції дістанемо:
![]() , тобто
, тобто ![]() .
.
Таким чином,
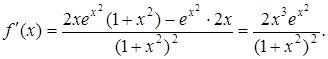
Приклад 4. Знайти похідну функції, оберненої до
![]() .
.
Розв’язання.
Дана функція скрізь неперервна та строго монотонна, її похідна ![]() , не перетворюється в нуль в жодній точці, тому за правилом диференціювання оберненої функції маємо:
, не перетворюється в нуль в жодній точці, тому за правилом диференціювання оберненої функції маємо:
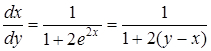 .
.
Приклад 5.
Знайти похідну функції 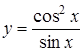 .
.
Розв’язання.
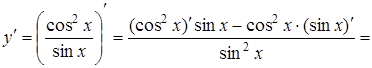
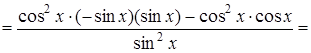
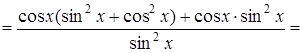
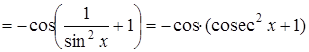
2. 3 Диференціювання показниково-степеневої функції
Похідна показниково-степеневої функції ![]() ,
, ![]() знаходиться за формулою
знаходиться за формулою
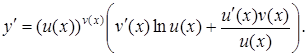
Похідні показникових та логарифмічних функцій
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
Якщо ![]() – диференційовна функція від х
, формули мають вигляд:
– диференційовна функція від х
, формули мають вигляд:
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
Приклад 1.
Знайти похідну функції ![]() .
.
Розв’язання. Застосовуючи наведені формули, маємо:
![]()
Приклад 2.
Знайти похідну функції ![]() .
.
Розв’язання. Застосовуючи формули, знаходимо:
![]()
Приклад 3.
Знайти похідну функції ![]() .
.
Розв’язання. За наведеними формулами, маємо:
![]()
2.4 Диференціювання неявної функції та функції, заданої параметрично
Щоб продиференціювати функцію, яка задається виразом ![]() , необхідно цей вираз продиференціювати по х
, вважаючи у
функцією від х
, і з одержаної рівності знайти
, необхідно цей вираз продиференціювати по х
, вважаючи у
функцією від х
, і з одержаної рівності знайти ![]() .
.
Похідна функції
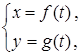
яка задана параметрично, обчислюється за формулою:
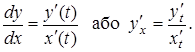
за умови, що ![]() диференційовні в точці
диференційовні в точці ![]() функції, причому
функції, причому ![]() .
.
Приклад 1.
Знайти похідну функції, яка задана неявно рівнянням ![]() .
.
Розв’язання. Диференціюючи, дістанемо:
![]()
відкіля
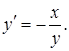
Приклад 2. Знайти похідну функції, яка задана неявно
![]() .
.
Розв’язання. Диференціюючи, маємо
![]()
![]()
З цього рівняння знаходимо ![]() :
:
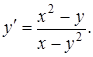
Приклад
3.
Знайти ![]() , якщо
, якщо ![]() .
.
Розв’язання.
![]()
![]()
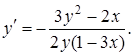
Приклад 4.
Знайти в точці ![]() похідну
похідну ![]() функції, яка задана параметрично:
функції, яка задана параметрично:
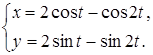
Розв’язання. Застосовуючи формулу обчислення похідної функції, яка задана параметрично, маємо:
![]()
![]()
Таким чином,
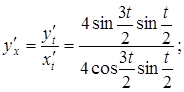
![]()
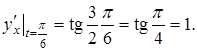
Приклад
5.
Знайти ![]() , якщо
, якщо ![]() .
.
Розв’язання.
![]()
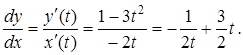
Тренувальні вправи
Знайти похідні функцій, які задані неявно:
1. ![]() .
. 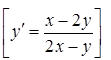
2. ![]() .
. 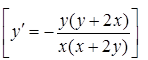
3. ![]() .
. 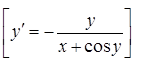
4. 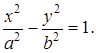 .
. 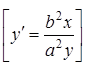
5. ![]() .
. 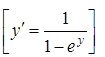
6. ![]() .
. 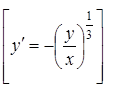
7. ![]() .
. ![]()
8. ![]() .
. 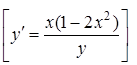
9.
Знайти ![]() в точці М
(1, 1), якщо
в точці М
(1, 1), якщо ![]() .
. ![]()
10.
Знайти![]() при
при![]() , якщо
, якщо ![]() .
. ![]()
11. ![]() .
. 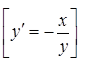
12. ![]() .
. 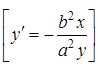
13. ![]() .
. 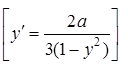
14. ![]() .
. 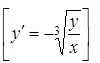
15. ![]() .
. 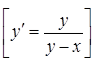
16. ![]() .
. 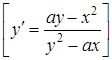
17. ![]() .
. 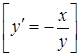
18. ![]() .
. 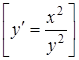
19*
. ![]() .
. 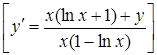
20. ![]() .
. ![]()
Знайти похідну функції, яка задана параметрично:
21. 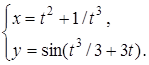
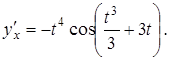
22. 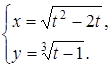
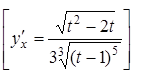
23. 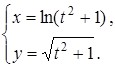
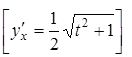
24. 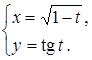
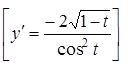
25. 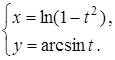
![]()
![]()
26. 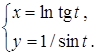
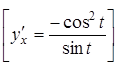
27. 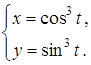
![]()
28. 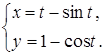
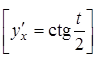
29. 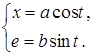
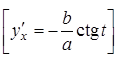
30. 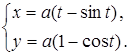
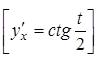
31. 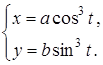
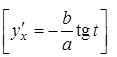
32. 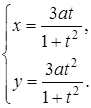
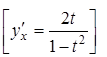
33. 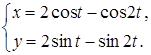
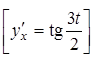
34. 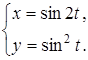
![]()
35. 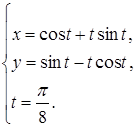
![]()
36. 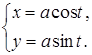
![]()
37*
. 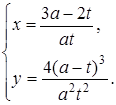
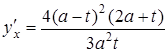
![]()
2.5 Логарифмічне диференціювання
Якщо маємо громіздкі вирази, що містять добутки, частки, степені, то перш, ніж знаходити похідну, вираз рекомендується прологарифмувати.
Приклад 1.
Знайти похідну функції 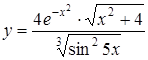 .
.
Розв’язання. Прологарифмуємо функцію:
![]()
Знайдемо похідну від лівої та правої частин:
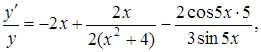
звідки
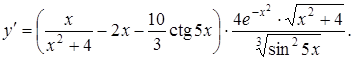
Такий же спосіб використається для знаходження похідної так званої степенево-показникової функції
![]() .
.
Приклад 2. Продиференціювати функцію:
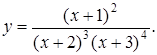
Розв’язання. Цю функцію можна диференціювати як частку двох функцій, але це приведе до складних обчислень. Тому краще спочатку прологарифмувати функцію, а потім продиференціювати.
Дійсно,
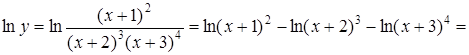
![]()
Диференціюючи (у розглядаємо як складену функцію), маємо:
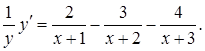
Тоді
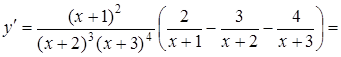
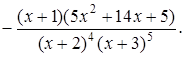
2.6 Геометричний та фізичний зміст похідної
Похідна, особливо її геометричний та фізичний зміст, широко застосовуються при розв’язанні цілого ряду задач в різних галузях діяльності.
Геометричний зміст похідної
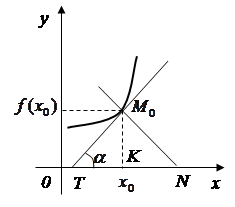 Похідна функції
Похідна функції ![]() для кожного значення х
дорівнює кутовому коефіцієнту дотичної
до графіка даної функції у відповідній точці, тобто
для кожного значення х
дорівнює кутовому коефіцієнту дотичної
до графіка даної функції у відповідній точці, тобто
![]() ,
,
де ![]() – кут, який утворює дотична до графіка функції в точці
– кут, який утворює дотична до графіка функції в точці ![]() з додатним напрямком осі
з додатним напрямком осі ![]() .
.
На основі геометричного змісту похідної рівняння дотичної до графіка функції ![]() записується таким чином:
записується таким чином:
![]()
Якщо неперервна функція в точці ![]() має нескінченну похідну, тоді дотичною до графіка функції в точці
має нескінченну похідну, тоді дотичною до графіка функції в точці ![]() буде пряма
буде пряма ![]() .
.
Для нормалі, тобто прямої, що проходить через точку дотику ![]() , перпендикулярно до дотичної (пряма
, перпендикулярно до дотичної (пряма ![]() ), рівняння має вигляд
), рівняння має вигляд 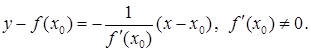
У випадку ![]() нормаллю буде пряма
нормаллю буде пряма ![]() ; якщо функція в точці
; якщо функція в точці ![]() має нескінченну похідну, тоді нормаллю до кривої буде пряма
має нескінченну похідну, тоді нормаллю до кривої буде пряма ![]() .
.
У деяких задачах потрібно знайти кут ![]() між кривими
між кривими ![]() та
та ![]() в їх точці перетинання.
в їх точці перетинання.
Кутом ![]() між кривими вважається величина кута
між кривими вважається величина кута ![]() між дотичними до даних кривих, в їх точці перетинання;
між дотичними до даних кривих, в їх точці перетинання; ![]() обчислюється за формулою:
обчислюється за формулою:
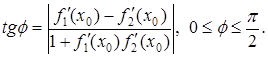
В задачах на застосування геометричного змісту похідної часто зустрічаються також такі поняття, як відрізок дотичної , відрізок нормалі , піддотична , піднормаль , довжини яких визначають за формулами:
а) відрізок дотичної ![]() :
:
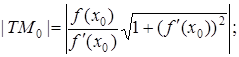
б) відрізок нормалі ![]() :
:
![]()
в) піддотична ТК:
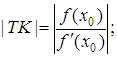
г) піднормаль ![]() :
:
![]()
Приклад 1.
Знайти, під яким кутом функція ![]() перетинає вісь абсцис.
перетинає вісь абсцис.
Розв’язання.
Косинусоїда перетинає вісь абсцис в точках ![]() . Якщо
. Якщо ![]() , тоді
, тоді
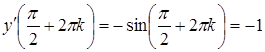 ,
,
тобто кутовий коефіцієнт дотичної до косинусоїди дорівнює –1. Це означає, що в точках ![]() графік функції
графік функції ![]() перетинає вісь абсцис під кутом
перетинає вісь абсцис під кутом ![]() .
.
Якщо ![]() , тоді
, тоді 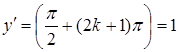 . Тому в цих точках косинусоїда перетинає вісь
. Тому в цих точках косинусоїда перетинає вісь ![]() під кутом
під кутом ![]() .
.
Приклад 2. Записати рівняння дотичної до кривої
![]() в точці
в точці ![]() .
.
Розв’язання.
Згідно з формулою рівняння дотичної до графіку функції, для того, щоб скласти рівняння дотичної, треба обчислити значення функції та похідної функції в точці ![]() :
:
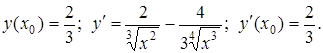
Отже, отримаємо рівняння дотичної:
![]() або
або ![]()
Приклад 3.
Знайти рівняння нормалі до кривої, яка задана параметрично: ![]() в точці
в точці ![]() .
.
Розв’язання. Рівняння нормалі має вигляд:
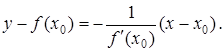
Значення ![]() та
та ![]() відповідають значенню
відповідають значенню ![]() :
:
![]()
Похідну знайдемо за формулою похідної, заданої параметрично:
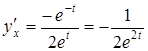 .
.
В точці ![]() маємо
маємо ![]() . Таким чином, рівняння нормалі записується у вигляді
. Таким чином, рівняння нормалі записується у вигляді
![]() , або
, або ![]() .
.
Приклад 4.
Знайти рівняння дотичної й нормалі до кривої ![]() у точці
у точці ![]() .
.
Розв’язання. Значення похідної даної функції в точці А:
![]()
Рівняння дотичної:
![]()
Рівняння нормалі:
![]()
Фізичний зміст похідної
Під фізичним змістом похідної розуміють швидкість зміни функції в даній точці. Наприклад:
1) при русі тіла швидкість ![]() в даний момент часу
в даний момент часу ![]() є похідною від шляху
є похідною від шляху ![]() :
:![]()
![]()
2) при обертовому русі твердого тіла навколо осі ![]() кутова швидкість
кутова швидкість ![]() в даний момент часу
в даний момент часу ![]() є похідною від кута повороту
є похідною від кута повороту ![]() :
:
![]()
3) при охолодженні тіла швидкість охолодження в момент часу ![]() є похідною від температури
є похідною від температури
![]()
4) теплоємність С
для даної температури ![]() є похідною від кількості тепла
є похідною від кількості тепла ![]() :
:
![]()
5) при нагріванні стержня коефіцієнт лінійного розширення ![]() при даному значенні температури
при даному значенні температури ![]() є похідною від довжини
є похідною від довжини ![]() :
:
![]()
Приклад 1.
Знайти швидкість точки, рух якої описується рівнянням ![]() , наприкінці третьої та десятої секунд.
, наприкінці третьої та десятої секунд.
Розв’язання. Швидкість визначається за формулою
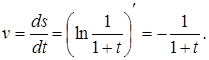
Коли ![]() , маємо
, маємо ![]() (м/с).
(м/с).
Коли ![]() , маємо
, маємо ![]() (м/с).
(м/с).
Приклад 2.
Знайти швидкість точки, яка рухається по колу радіуса ![]() , оббігаючи коло за час
, оббігаючи коло за час ![]() .
.
Розв’язання.
Нехай точка починає рухатися з положення А
проти годинникової стрілки. Нехай за час ![]() вона дійшла до положення
вона дійшла до положення ![]() .
.
Кут між її радіусом-вектором та віссю ![]() дорівнює в цей час
дорівнює в цей час ![]() , тому що точка проходить кут
, тому що точка проходить кут ![]() за час Т, кут
за час Т, кут ![]() – за одиницю часу і кут
– за одиницю часу і кут ![]() – за час
– за час ![]() .
.![]()
Отже, в будь-який момент ![]() положення точки
положення точки ![]() можна визначити через її дві координати:
можна визначити через її дві координати:
![]()
Компоненти швидкості знаходимо з таких обчислень:
![]()
Тоді швидкість точки буде:
![]()
2.7 Диференціал функції
Диференціал функції, як і похідна, застосовується при розв’язанні ряду практичних задач, зокрема в наближених обчисленнях.
Диференціалом функції
![]() в точці х
називається головна (лінійна відносно
в точці х
називається головна (лінійна відносно ![]() ) частина приросту
) частина приросту ![]() диференційовної в точці х
функції.
диференційовної в точці х
функції.
Диференціал дорівнює добутку похідної функції в точці х на приріст незалежної змінної, тобто
![]()
Зокрема, диференціалом незалежної змінної є ії приріст:
![]()
Тоді формула диференціала має вигляд
![]()
відкіля
![]()
Основні властивості диференціала
Для довільних диференційованих функцій 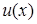 та
та 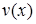 мають місце такі рівності:
мають місце такі рівності:
1. ![]() ;
;
2. ![]() — довільні сталі
— довільні сталі![]() ;
;
3. ![]() ;
;
4. 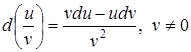 ;
;
5.
![]() .
.
П
риклад 1.
Знайти диференціал функції ![]() .
.
Розв’язання. За формулою
![]()
Приклад 2.
Знайти диференціал функції ![]() .
.
Розв’язання. За формулою
![]()
Застосування диференціала до наближених обчислень
При малих ![]() справедлива формула
справедлива формула ![]() , тобто
, тобто
![]() .
.
Приклад 1.
Обчислити наближено за допомогою диференці-ала значення функції ![]() в точці
в точці ![]() .
.
Розв’язання.
Найближча к 1,97 точка, в якої легко обчислити значення ![]() и
и ![]() , — це точка
, — це точка ![]() .
.
![]()
![]()
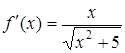 ,
, ![]() .
.
За наведеною формулою маємо
![]()
Приклад 2. Знайти, наскільки зміниться довжина ребра куба, якщо об’єм його зменшиться з 64 до 63,98 м3 .
Розв’язання. Якщо х – об’єм куба, а у – його ребро, тоді
![]() .
.
За умовою задачі ![]() ,
, ![]() . Приріст
. Приріст ![]() сторони куба обчислюємо наближено:
сторони куба обчислюємо наближено:
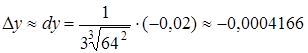 ,
,
тобто ребро куба зменшиться на 0,0004166 м.
![]()
2.8 Похідні та диференціали вищих порядків
Похідні вищих порядків
Похідною другого порядку
(другою похідною функції) 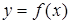 у точці х
називається похідна від її першої похідної
у точці х
називається похідна від її першої похідної 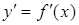 при умові, що
при умові, що 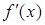 диференційовна в точці х
. Вона позначається такими символами:
диференційовна в точці х
. Вона позначається такими символами:
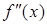 ,
, 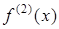 ,
, 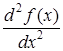 ,
, 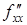 ,
, 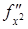 .
.
Аналогічно визначається похідна п
-го порядку функції 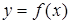 , яка має (п
-1) похідну в точці х
:
, яка має (п
-1) похідну в точці х
:
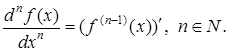
Похідну, для якої існує п -а похідна в точці х , називають п разів диференційовною в цій точці.
Основні формули обчислення похідних вищих порядків
![]()
![]()
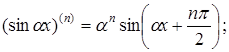
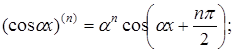
![]()
зокрема,
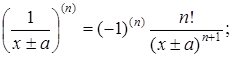
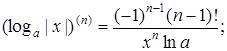
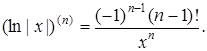
Основні правила обчислення похідних
Якщо функції ![]() та
та ![]() п разів диференційовні, тоді мають місце такі рівності:
п разів диференційовні, тоді мають місце такі рівності:
1) ![]()
2) 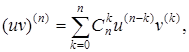 (формула Лейбніца)
(формула Лейбніца)
де 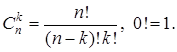
Обчислення похідних вищих порядків функцій, заданих параметрично
Якщо функція задана параметрично рівняннями ![]() ,
, ![]() , тоді похідні
, тоді похідні 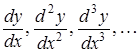 обчислюються за формулами:
обчислюються за формулами:
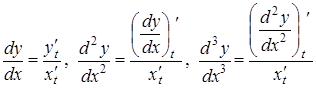 і т.д.
і т.д.
Для похідної другого порядку має місце формула:
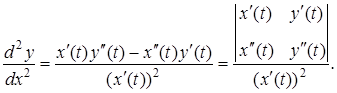
Диференціали вищих порядків
Диференціалом другого порядку двічі диференційовної функції ![]() називають диференціал від диференціала першого порядку функції
називають диференціал від диференціала першого порядку функції ![]() , тобто
, тобто ![]() . У випадку, коли х
– незалежна змінна, диференціали обчислюються за формулами:
. У випадку, коли х
– незалежна змінна, диференціали обчислюються за формулами:
![]()
![]()
![]()
Якщо ж х
— деяка функція від t
, ![]() , тоді
, тоді
![]()
![]() і т.д.
і т.д.
Якщо для функцій ![]() та
та ![]() , х
— незалежна змінна, існують диференціали
, х
— незалежна змінна, існують диференціали ![]() та
та ![]() , тоді
, тоді
![]() (
(![]() — сталі),
— сталі),
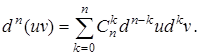
Приклад 1.
Знайти похідну другого порядку функції, заданої параметрично ![]()
Розв’язання.
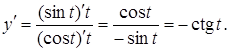
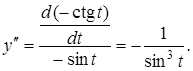
Приклад 2. Знайти похідну другого порядку функції
![]()
Розв’язання. Спочатку знаходиться перша похідна від складної функції:
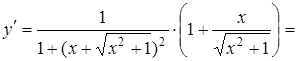
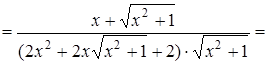
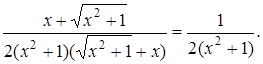
Тоді друга похідна дорівнює:
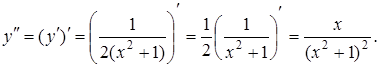
Приклад 3.
Знайти диференціал другого порядку функції ![]() в точці
в точці ![]() .
.
Розв’язання.
Згідно з формулою для обчислення диференці-алу другого порядку ![]() обчислюється
обчислюється ![]() :
:
![]()
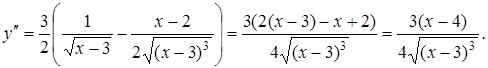
Тоді ![]()
Отже, ![]()
Приклад 4.
Знайти ![]() у випадку, коли функція задана неявно рівнянням
у випадку, коли функція задана неявно рівнянням ![]()
Розв’язання.
Диференціюємо ліву та праву частини рівняння, маючи на увазі, що у
є функція від х
: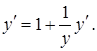
Звідси 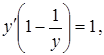 тобто
тобто 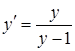 , тому
, тому
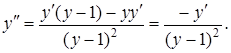
Підставляючи замість ![]() відповідне значення, знаходимо:
відповідне значення, знаходимо:
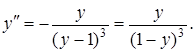
Приклад 5.
Знайти ![]() функції, яка задана параметрично рівняннями:
функції, яка задана параметрично рівняннями: ![]()
Розв’язання. За правилами диференціювання функції, заданої параметрично, маємо:
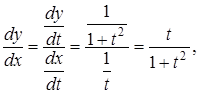
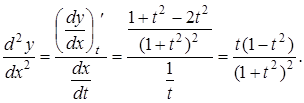
Приклад
6.
Знайти ![]() , якщо
, якщо ![]() .
.
Розв’язання.
З попереднього прикладу маємо ![]() ,
, ![]() . Тоді
. Тоді
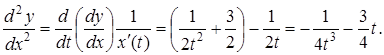
Приклад 7.
Знайти ![]() , якщо
, якщо ![]() .
.
Розв’язання.
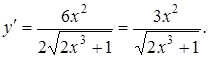
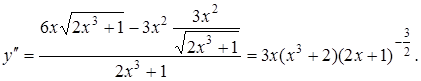
3. Дослідження функції за допомогою похідних
3.1 Монотонність функції. Екстремум функції
Припустимо, що функція ![]() визначена на деякому проміжку (а
; b
), а
визначена на деякому проміжку (а
; b
), а ![]() є внутрішньою точкою цього проміжку.
є внутрішньою точкою цього проміжку.
Функція ![]() називається зростаючою в точці
називається зростаючою в точці
![]() , якщо існує окіл
, якщо існує окіл ![]() точки
точки ![]() , який міститься в проміжку (а
; b
) і такий, що
, який міститься в проміжку (а
; b
) і такий, що ![]() , для всіх
, для всіх ![]() і
і ![]() для всіх
для всіх ![]() .
.
Якщо функція ![]() диференційовна на інтервалі
(а
; b
) і зростає (спадає) на цьому інтервалі, то її похідна на інтервалі
(а
; b
) невід’ємна, тобто
диференційовна на інтервалі
(а
; b
) і зростає (спадає) на цьому інтервалі, то її похідна на інтервалі
(а
; b
) невід’ємна, тобто ![]() .
.
Якщо функція ![]() диференційована на інтервалі
(а
; b
) і ії похідна
диференційована на інтервалі
(а
; b
) і ії похідна ![]() для
для ![]() , то ця функція зростає (спадає) на інтервалі
(а
; b
).
, то ця функція зростає (спадає) на інтервалі
(а
; b
).
Функція ![]() називається спадною в точці
називається спадною в точці
![]() , якщо існує окіл
, якщо існує окіл ![]() точки
точки ![]() , який міститься в проміжку (а
; b
) і такий, що
, який міститься в проміжку (а
; b
) і такий, що ![]() , для будь якого
, для будь якого ![]() і
і ![]() для будь якого
для будь якого ![]() .
.
Якщо існує окіл ![]() точки
точки ![]() , який міститься в проміжку (а
; b
) і такий, що
, який міститься в проміжку (а
; b
) і такий, що ![]() для всіх
для всіх ![]() , то точка
, то точка ![]() називається точкою максимуму функції
називається точкою максимуму функції ![]() , а саме число
, а саме число ![]() називається максимумом функції
називається максимумом функції ![]() в точці
в точці
![]() .
.
Якщо існує окіл ![]() точки
точки ![]() , який міститься в проміжку (а
; b
) і такий, що
, який міститься в проміжку (а
; b
) і такий, що ![]() для всіх
для всіх ![]() , то точка
, то точка ![]() називається точкою мінімуму функції
називається точкою мінімуму функції ![]() , а саме число
, а саме число ![]() називається мінімумом функції
називається мінімумом функції ![]() в точці
в точці
![]() .
.
Точки максимуму й мінімуму функції називають ще екстремальними точками , а максимум і мінімум називають екстремумом функції .
![]()
Приклад 1.
Довести, що функція ![]() є зростаючою в інтервалі
є зростаючою в інтервалі ![]() .
.
Розв’язання.
Знаходимо похідну функції ![]() :
:
![]()
У кожній точці ![]() маємо
маємо ![]()
Отже, за попередньою теоремою робимо висновок, що функція ![]() є зростаючою в кожній точці даного інтервалу.
є зростаючою в кожній точці даного інтервалу.
Приклад 2.
Довести, що показникова функція ![]() ,
, ![]() ,
, ![]() , в інтервалі
, в інтервалі ![]() при
при![]() є спадною, а при
є спадною, а при ![]() — зростаючою.
— зростаючою.
Розв’язання.
Знаходимо похідну функції ![]() :
:
![]()
Внаслідок того, що ![]() при
при ![]() , то
, то
![]()
Отже, при ![]() функція
функція ![]() є спадною.
є спадною.
Якщо ![]() , то
, то ![]() і тому
і тому ![]() . Таким чином,
. Таким чином, ![]() у цьому випадку є зростаючою.
у цьому випадку є зростаючою.
Приклад 3. Знайти інтервали зростання і спадання функції:
![]() .
.
Розв’язання. Знаходимо похідну:
![]()
При будь якому ![]() маємо
маємо ![]() .
.
Отже, функція ![]() на всій числовій осі
на всій числовій осі ![]() є зростаючою.
є зростаючою.
Приклад 4. Знайти інтервали зростання і спадання функції:
![]() .
.
Розв’язання. Знаходимо похідну:
![]() .
.
При ![]() маємо
маємо ![]() , при
, при ![]() маємо
маємо ![]() .
.
Отже, в інтервалі ![]() функція
функція ![]() спадає, а в інтервалі
спадає, а в інтервалі ![]() зростає.
зростає.
При цьому точка ![]() є точкою мінімуму заданої функції.
є точкою мінімуму заданої функції.
Приклад 5. Знайти інтервали зростання і спадання функції:
![]() .
.
Розв’язання. Знайдемо похідну:
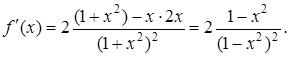
Знайдемо точки, в яких ![]() . Це є всі точки, де
. Це є всі точки, де ![]() . Розв’яжемо цю нерівність:
. Розв’яжемо цю нерівність:
![]() або
або ![]() .
.
Отже, в інтервалі ![]() функція зростає. Тоді в інтервалах
функція зростає. Тоді в інтервалах ![]() ,
, ![]() функція спадає.
функція спадає.
Робимо висновок, що точка ![]() є точкою є точкою мінімуму, а точка
є точкою є точкою мінімуму, а точка ![]() — точкою максимуму заданої функції, при цьому мінімум функції дорівнює
— точкою максимуму заданої функції, при цьому мінімум функції дорівнює ![]() , максимум
, максимум ![]() .
.
Необхідна ознака існування екстремуму
Якщо функція ![]() у внутрішній точці
у внутрішній точці ![]() проміжку
проміжку ![]() має екстремум, то в цій точці похідна
має екстремум, то в цій точці похідна ![]() , якщо вона існує, дорівнює нулю.
, якщо вона існує, дорівнює нулю.
Внутрішня точка ![]() проміжку
проміжку ![]() називається стаціонарною
точкою функції
називається стаціонарною
точкою функції ![]() , якщо в цій точці
, якщо в цій точці ![]() . Стаціонарні точки і точки, в яких похідна не існує, називаються критичними точками
функції.
. Стаціонарні точки і точки, в яких похідна не існує, називаються критичними точками
функції.
Перше правило дослідження функції на екстремум
Щоб дослідити функцію ![]() на екстремум, треба:
на екстремум, треба:
1)
знайти стаціонарні точки заданої функції, для цього слід розв’язати рівняння ![]() , з коренів цього рівняння вибрати тільки дійсні і ті, які є внутрішніми точками існування функції;
, з коренів цього рівняння вибрати тільки дійсні і ті, які є внутрішніми точками існування функції;
2)
знайти точки, в яких похідна ![]() не існує (функція
не існує (функція ![]() в ціх точках існує). Якщо критичних точок функція
в ціх точках існує). Якщо критичних точок функція ![]() не має, то вона не має й екстремальних точок. Така функція не має екстремуму. Якщо критичні точки є, то їх треба досліджувати далі, для чого:
не має, то вона не має й екстремальних точок. Така функція не має екстремуму. Якщо критичні точки є, то їх треба досліджувати далі, для чого:
3) у кожній критичній точці перевірити зміну знака похідної першого порядку.
Якщо ![]() при переході через критичну точку (зліва направо) змінює знак з + на –, то ця точка є точкою максимуму. Якщо
при переході через критичну точку (зліва направо) змінює знак з + на –, то ця точка є точкою максимуму. Якщо ![]() змінює знак з – на +, то ця критична точка є точкою мінімуму.
змінює знак з – на +, то ця критична точка є точкою мінімуму.
Якщо при переході через критичну точку знак похідної не змінюється, то розглядувана критична точка не є екстремальною точкою заданою функції.
Теорема.
Нехай точка ![]() є стаціонарною для функції
є стаціонарною для функції ![]() і нехай в цій точці існує похідна другого порядку
і нехай в цій точці існує похідна другого порядку ![]() , яка не дорівнює нулю
, яка не дорівнює нулю ![]() . Тоді, якщо
. Тоді, якщо ![]() , то
, то ![]() є точкою мінімуму, якщо
є точкою мінімуму, якщо ![]() , то
, то ![]() є точкою максимуму функції
є точкою максимуму функції ![]() .
.
Друге правило дослідження функції на екстремум.
Щоб дослідити функцію ![]() на екстремум, треба:
на екстремум, треба:
1) знайти стаціонарні точки заданої функції;
2)
знайти похідну другого порядку в стаціонарній точці. Якщо в стаціонарній точці ![]()
![]() , то
, то ![]() є екстремальною точкою для функції
є екстремальною точкою для функції ![]() , а саме, точкою мінімуму, якщо
, а саме, точкою мінімуму, якщо ![]() , і точкою максимуму, якщо
, і точкою максимуму, якщо ![]() .
.
Приклад 6. Дослідити функцію на екстремум:
![]() .
.
Розв’язання.
Знаходимо похідну:![]() . Прирівнюємо похідну
. Прирівнюємо похідну ![]() до нуля і розв’язуємо рівняння:
до нуля і розв’язуємо рівняння:
![]()
Дістаємо стаціонарні точки: ![]()
Знаходимо похідну другого порядку:
![]()
Підставляємо у вираз для ![]() значення
значення ![]() і
і ![]() :
:
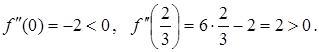
Отже, ![]() є точкою максимуму,
є точкою максимуму, ![]() — точкою мінімуму функції
— точкою мінімуму функції ![]() , причому максимум і мінімум відповідно дорівнюють
, причому максимум і мінімум відповідно дорівнюють 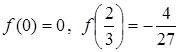 .
.
Приклад 7. Дослідити функцію на екстремум:
![]()
Розв’язання. Знаходимо похідну першого порядку:
![]() .
.
Прирівнюємо похідну ![]() до нуля і розв’язуємо утворене рівняння:
до нуля і розв’язуємо утворене рівняння:
![]() .
.
Звідси знаходимо стаціонарні точки:
![]()
Знайдемо похідну другого порядку:
![]()
Тоді ![]()
Отже, в точці ![]() функція має мінімум
функція має мінімум ![]() , а в точці
, а в точці ![]() — максимум
— максимум ![]() .
.
3. 2 Знаходження найбільшого і найменшого значень функції
Нехай на відрізку 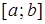 задано неперервну функцію
задано неперервну функцію 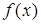 , тоді за теоремою Вейєрштрасса функція на даному відрізку досягає свого найбільшого і свого найменшого значень. Це може статися як всередині відрізка, так і на його кінцях.
, тоді за теоремою Вейєрштрасса функція на даному відрізку досягає свого найбільшого і свого найменшого значень. Це може статися як всередині відрізка, так і на його кінцях.
Якщо функція набуває найбільшого значення всередині відрізка, то це найбільше значення є одночасно і один з максимумів (локальний максимум) заданої функції.
Теж саме можна сказати про найменше значення функції. Але може бути й так, що одне із значень функція набуває всередині відрізка, а друге на одному з кінців.
Звідси випливає спосіб знаходження точок, в яких функція набуває найбільшого та найменшого значення на відрізку ![]() :
:
1) знайти критичні точки функції;
2) обчислити значення функції в критичних точках, які належать відрізку, і на кінцях відрізка;
3)
найбільше (найменше) значення серед утвореної множини і буде найбільшим (найменшим) значенням функції, заданої на відрізку ![]() .
.
Приклад 1.
Знайти найбільше і найменше значення функції ![]() на відрізку
на відрізку 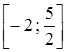 .
.
Розв’язання. Знаходимо стаціонарні точки. Для цього знайдемо похідну:
![]()
Прирівнюючи цю похідну до нуля і розв’язуючи рівняння
![]() ,
,
дістаємо стаціонарні точки: ![]() . Точок, в яких функція не існує, немає.
. Точок, в яких функція не існує, немає.
Обчислюємо значення функції в точках ![]() , а також на кінцях відрізка, тобто в точках
, а також на кінцях відрізка, тобто в точках ![]() :
:
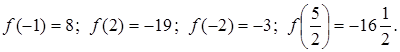
Отже, найбільше значення ![]() , найменше є
, найменше є ![]() .
.
Приклад 2.
Знайти найбільше та найменше значення функції ![]() на відрізку
на відрізку ![]() .
.
Розв’язання.
Функція є неперервною на відрізку ![]() . Знаходимо екстремуми функції. Обчислюємо першу похідну:
. Знаходимо екстремуми функції. Обчислюємо першу похідну:
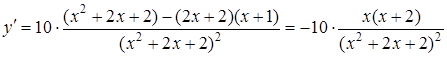 .
.
Функція має дві критичні точки: ![]() . Але
. Але ![]() не належить відрізку
не належить відрізку ![]() . В точці
. В точці ![]() функція має максимум, причому
функція має максимум, причому ![]() . Обчислюємо значення функції
. Обчислюємо значення функції ![]() на кінцях відрізка:
на кінцях відрізка: ![]() .
.
Таким чином, ![]() .
.
Приклад 3.
Знайти найбільше та найменше значення функції ![]() на відрізку
на відрізку ![]() .
.
Розв’язання.
Знаходимо критичні точки функції, розв’язавши рівняння ![]() :
:
![]() .
.
Коренями цього рівняння є числа: ![]() . Проте ці точки не належать відрізку
. Проте ці точки не належать відрізку ![]() , тому всередині цього відрізка критичних точок немає.
, тому всередині цього відрізка критичних точок немає.
Обчислюємо значення функції на кінцях відрізка:
![]() .
.
Отже, ![]() .
.
3.3 Інтервали опуклості та угнутості кривої, точки перегину
Графік функції ![]() може бути опуклим
або угнутим
.
може бути опуклим
або угнутим
.
Графік функції ![]() є опуклим
на проміжку
є опуклим
на проміжку ![]() , якщо відповідна дуга кривої лежить нижче дотичної, проведеної в довільній точці
, якщо відповідна дуга кривої лежить нижче дотичної, проведеної в довільній точці ![]() .
.
Графік функції ![]() є угнутим
на проміжку
є угнутим
на проміжку ![]() , якщо відповідна дуга кривої лежить вище дотичної, проведеної в довільній точці
, якщо відповідна дуга кривої лежить вище дотичної, проведеної в довільній точці ![]() .
.
Для дослідження графіка функції на опуклість застосовується друга похідна функції. Якщо друга похідна двічі диференційовної функції ![]() від’ємна
від’ємна ![]() в інтервалі
в інтервалі ![]() , тоді графік функції
, тоді графік функції ![]() опуклий на даному проміжку, якщо друга похідна додатна
опуклий на даному проміжку, якщо друга похідна додатна ![]() , тоді графік функції угнутий на
, тоді графік функції угнутий на ![]() .
.
Точка, при переході через яку крива змінює опуклість на угнутість або навпаки, називається точкою перегину .
Точками перегину функції ![]() можуть бути лише точки, в яких друга похідна
можуть бути лише точки, в яких друга похідна ![]() дорівнює нулю або не існує. Такі точки називають критичними точками другого роду
.
дорівнює нулю або не існує. Такі точки називають критичними точками другого роду
.