| Скачать .docx | Скачать .pdf |
Реферат: Контрольная работа: Исследование зависимости между объемом производства, капитальными вложениями и выполнением норм
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
БЕЛГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. В.Г.ШУХОВА
Кафедра Экономики и Организации производства
КОНТРОЛЬНАЯ РАБОТА
по дисциплине
«ЭКОНОМИКО-МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ»
Студентка: гр.ЭКд-21В
Н.В. Гребенникова
Руководитель: к.т.н., доц.
О.В.Доможирова
Белгород 2009
ЧАСТЬ 1
Постановка задачи
Для производства двух видов продукции А и Б используются три типа ресурсов. Нормы затрат ресурсов на производство единицы продукции каждого вида, цена единицы продукции каждого вида, а также запасы ресурсов, которые могут быть использованы предприятием, приведены в табл. 2.2.
Таблица 2.2
| Типы ресурсов |
Нормы затрат ресурсов на единицу продукции |
Запасы ресурсов |
|
| А |
Б |
||
| Электроэнергия |
1 |
7 |
24 |
| Сырье |
2 |
2 |
24 |
| Оборудование |
9 |
2 |
16 |
| Цена ед. продукции |
15 |
20 |
|
| Прибыль ед продукц |
3 |
9 |
|
Требуется:
I. Cформулировать экономико-математическую модель задачи в виде ОЗЛП.
II. Привести ОЗЛП к канонической форме.
III. Сформулировать экономико-математическую модель задачи двойственной к исходной.
IV. Построить многогранник решений (область допустимых решений) и найти оптимальную производственную программу путем перебора его вершин и геометрическим способом.
V. Решить задачу с помощью симплекс-таблиц.
Решение:
I . Оптимизационная модель задачи запишется следующим образом
а) целевая функция ![]()
б) ограничения: 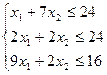
в) условия неотрицательности переменных х1 ≥0 ; х2 ≥0.
II . Приведем ОЗЛП к канонической форме. Для этого введем дополнительные переменные x 3 , x 4 и x 5.
а) целевая функция ![]()
б) ограничения: 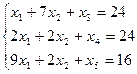
в) условия неотрицательности переменных ![]()
III . Сформулируем экономико-математическую модель задачи двойственную к исходной. Матрица В условий прямой задачи и матрица В’ – транспонированная матрица В – имеют следующий вид:
| 1 |
7 |
24 |
|
1 |
2 |
9 |
3 |
||
| B= |
2 |
2 |
24 |
|
B’= |
7 |
2 |
2 |
9 |
| 9 |
2 |
16 |
|
|
24 |
24 |
16 |
Zmin |
|
| 3 |
9 |
Fmax |
|
|
|
|
|
|
В двойственной задаче нужно найти минимум функции
Z = 24y1
+ 24y2
+16y3
, при ограничениях 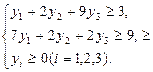
Систему ограничений-неравенств двойственной задачи обратим в систему уравнений:
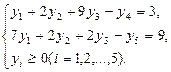
Компоненты у1 , у2 , у3 оптимального решения двойственной задачи оценивают добавочные переменные х3 , х4 , х5 прямой задачи.
1) х1+7х2≥24 (0;3,43) (24;0)
2) 2х1+2х2≥24 (0;12) (12;0)
3) 9х1+2х2≥16 (0:8) (1,78;0)
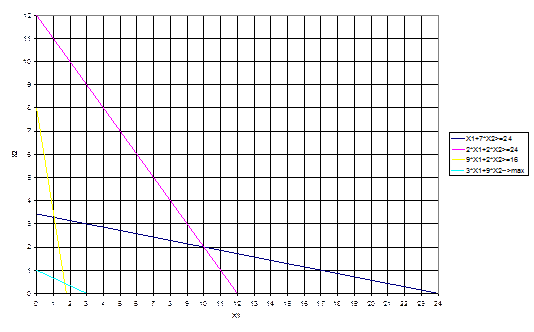
Однако нам необходимо найти такую точку, в которой достигался бы max целевой функции.
Оптимальную производственную программу можно найти двумя способами:
1) путем перебора его вершин
Находим координаты вершин многоугольника ABCDE и подставляя в целевую функцию находим ее значение.
А: А (0; 0) Z(A) =3×0+9×0=0
В: В (0; 3,43) Z(B) = 3×0+9×3,43=30,87
D: D (1,78; 0) Z(B) = 3×1,78+9×8=5,38
С: – это пересечение первого и второго уравнений
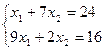 ;
;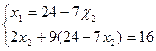 ;216 -63x
2
+2x
2
=16; x
2
=1,04.
;216 -63x
2
+2x
2
=16; x
2
=1,04.
С (1,04; 3,28) Z(C) = 3×1,04+9×3,28=32,64
Находим max значение целевой функции. Оно находится в точке
С (1,04; 3,28). Таким образом max прибыль составит 32,68у.д.е. при выпуске продукта Р в количестве 1,04 у.е. и R – 3,28 у.е.
2) геометрическим способом
Целевая функция геометрически изображается с помощью прямой уровня, т.е. прямой на которой Z=3X1 +9X2 – принимает постоянное значение.
Если С – произвольная const, то уравнение прямой имеет вид
3X1 +9X2 =С
При изменении const С получаем различные прямые, параллельные друг другу. При увеличении С прямая уровня перемещается в направлении наискорейшего возрастания функции Z, т.е. в направлении ее градиента. Вектор градиента ![]()
Точкой min Z будет точка первого касания линии уровня с допустимым многоугольником. Точкой max – точка отрыва линии уровня от допустимого многоугольника. Эти точки чаще всего совпадают с некоторыми вершинами допустимого многоугольника, хотя их может быть и бесчисленное множество, если линия уровня Z параллельна одной из сторон допустимого многоугольника. Это точка С (1,04; 3,28) Z=32,68 у.д.е.
Решим задачу с помощью симплекс-таблиц.
Пусть необходимо найти оптимальный план производства двух видов продукции P и R.
1. Построим оптимизационную модель:
F(X)=3X1
+9X2
→max 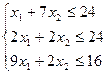
2. Преобразуем задачу в приведенную каноническую форму. Для этого введем дополнительные переменные X3 , X4 и X5 .
F(X)=3X1
+9X2
→max 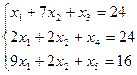
Построим исходную симплекс-таблицу и найдем начальное базисное решение.
| Баз. пер. |
Своб. член |
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
| Х3 |
24 |
1 |
7 |
1 |
0 |
0 |
| Х4 |
24 |
2 |
2 |
0 |
1 |
0 |
| Х5 |
16 |
9 |
2 |
0 |
0 |
1 |
| F |
0 |
– 3 |
– 9 |
0 |
0 |
0 |
Базисное решение (0; 0; 24;24; 16). F=0.
Находим генеральный столбец и генеральную строку
![]() . Генеральный элемент 7
. Генеральный элемент 7
Баз. пер. |
Своб. член |
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
| Х3 |
3,23 |
|
1 |
0 |
0 |
0 |
| Х2 |
17,14 |
0 |
0 |
1 |
0 |
|
| Х5 |
9,14 |
0 |
0 |
0 |
1 |
|
| F |
30,86 |
0 |
0 |
0 |
0 |
Базисное решение (0; 8; 4; 0; 10). F=40.
![]() 2,22222. Генеральный элемент 1,8.
2,22222. Генеральный элемент 1,8.
| Баз. пер. |
Своб. член |
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
| Х1 |
2,22 |
1 |
0 |
0,55 |
1,11 |
0 |
| Х2 |
7,56 |
0 |
1 |
-0,11 |
1,77 |
0 |
| Х5 |
2,74 |
0 |
0 |
1,82 |
5,63 |
1 |
| F |
46,65 |
0 |
0 |
-1,665 |
-13,3 |
0 |
Базисное решение (2,22; 7,56; 0; 0; 2,74). F=46,65.
Эта таблица является последней, по ней читаем ответ задачи. Оптимальным будет решение (2,22; 7,56; 0; 0; 2,74), при котором Fmax =46,65, т.е. для получения наибольшей прибыли, равной 46,65 денежных единиц, предприятие должно выпустить 2,22 единиц продукции вида P и 7,56 единиц продукции вида R, при этом ресурсы A и B будут использованы полностью, а 2,74 единиц ресурса С останутся неизрасходованными.
ЧАСТЬ 2
Постановка задачи
Исследовать зависимость между объемом производства, капитальными вложениями и выполнением норм выработки. Для построения модели собраны данные по исследуемым переменным на 12-ти предприятиях объединения.
Предполагая, что зависимость между переменными имеет линейный характер, анализ провести в следующей последовательности:
а) построить уравнение регрессии ![]() ;
;
б) построить уравнение регрессии ![]() ;
;
в) исследовать модели ![]() ,
, ![]() и сделать соответствующие выводы;
и сделать соответствующие выводы;
г) построить уравнение регрессии ![]() и выполнить исследование множественной модели в полном объеме (см.п.3.2).
и выполнить исследование множественной модели в полном объеме (см.п.3.2).
Решение:
А).
Строим уравнение регрессии
![]() ;
;
1. Экономическая теория и расположение точек на диаграмме рассеяния (Приложение 2) позволяют предположить линейную связь между переменными
СМ. ПРИЛОЖЕНИЕ 2. Диаграмма рассеяния, отражающая зависимость производства от капиталовложений.
По формулам (3.34) и (3.35) или (3.36) вычислим оценки параметров функции регрессии ![]() и
и ![]() .
.
![]() (3.34)
(3.34)
![]() (3.35)
(3.35)
Для упрощение расчетов и их наглядности составляют рабочую таблицу, которая содержит все исходные данные и промежуточные результаты, необходимые для вычисления оценок параметров (см. прил 1). В таблице приведены значения ![]() , которые не нужны непосредственно для вычисления
, которые не нужны непосредственно для вычисления ![]() и
и ![]() , но потребуются нам в дальнейшем.
, но потребуются нам в дальнейшем.
Итак, по формулам(3.34) и (3.36) вычисляем ![]() и
и ![]() :
:
![]()
![]() 622
622
Оцениваемое соотношение можно записать в виде
![]()
Оцениваемое соотношение можно записать в виде
![]()
Подставляя в полученное уравнение значения ![]() из таблицы в приложении 1, вычислим значения регрессии
из таблицы в приложении 1, вычислим значения регрессии ![]() . Совокупность этих значений называемых также предсказанными, образуют прямую регрессии (см. прил 2) отражающую зависимость объёма производств от капиталовложений, при условии, что остальные неучтенные факторы и случайности не оказывают влияния на производительность труда.
. Совокупность этих значений называемых также предсказанными, образуют прямую регрессии (см. прил 2) отражающую зависимость объёма производств от капиталовложений, при условии, что остальные неучтенные факторы и случайности не оказывают влияния на производительность труда.
СМ. ПРИЛОЖЕНИЕ 3. Диаграмма рассеяния, отражающая зависимость производства от среднего процента выполнения норм..
По формулам (3.34) и (3.35) или (3.36) вычислим оценки параметров функции регрессии ![]() и
и ![]() .
.
![]()
![]()
Оцениваемое соотношение можно записать в виде
![]()
Подставляя в полученное уравнение значения ![]() из таблицы в приложении 1, вычислим значения регрессии
из таблицы в приложении 1, вычислим значения регрессии ![]() . Совокупность этих значений называемых также предсказанными, образуют прямую регрессии (см. прил 3) отражающую зависимость объёма производств от среднего процента выполнения норм, при условии, что остальные неучтенные факторы и случайности не оказывают влияния на производительность труда.
. Совокупность этих значений называемых также предсказанными, образуют прямую регрессии (см. прил 3) отражающую зависимость объёма производств от среднего процента выполнения норм, при условии, что остальные неучтенные факторы и случайности не оказывают влияния на производительность труда.
В) Исследование регрессивной модели.
![]() ,
, ![]()
1. ![]()
Коэффициент регрессии b 11 показывает, что объём производства в среднем возрастает на 2,1622*10000 = 21622 руб, если капиталовложения увеличатся на 1000 рублей.
После определения значений ![]() можно вычислить остатки
можно вычислить остатки ![]() . и их квадраты, которые будут характеризовать точность оценки регрессии или степень согласованности расчетных значений и наблюдаемых значений переменной
. и их квадраты, которые будут характеризовать точность оценки регрессии или степень согласованности расчетных значений и наблюдаемых значений переменной ![]() .
.
Для оценки тесноты связи между исследуемыми явлениями вычислим коэффициент корреляции по формуле (3.15)(необходимые промежуточные результаты заимствуем из табл.приложение1)
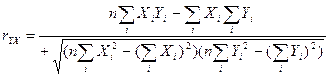 (3.15)
(3.15)
![]()
Чем больше ![]() , тем теснее связь между изучаемыми количественными признаками.
, тем теснее связь между изучаемыми количественными признаками.
Получен очень высокий коэффициент корреляции. Это свидетельствует о том, что связь между объёмом производства и уровнем капиталовложения очень тесная, хотя и не функциональная. Очевидно, что к действию объясняющей переменной примешивается влияние побочных факторов. Чем меньше это влияние и ограниченнее воздействие случайностей, тем ближе коэффициент корреляции к ±1. Отсюда видна связь между величиной ![]() и регрессией Функция линейной регрессии отражает линейное соотношение между переменными тем лучше, чем больше коэффициент корреляции приближается к ±1. В этом смысле коэффициент корреляции часто служит критерием при выборе вида регрессии. С его помощью устанавливают, действительно ли переменная
и регрессией Функция линейной регрессии отражает линейное соотношение между переменными тем лучше, чем больше коэффициент корреляции приближается к ±1. В этом смысле коэффициент корреляции часто служит критерием при выборе вида регрессии. С его помощью устанавливают, действительно ли переменная ![]() зависит от
зависит от ![]() и в какой степени.
и в какой степени.
Содержание этого этапа заключается в статистической проверке значимости (надежности): уравнения регрессии, коэффициентов регрессии и корреляции.
1. Значимость уравнения регрессии определяется возможностью надежно прогнозировать среднее отклика по заданным значениям факторной переменной. Так как ![]() – случайные величины, то полученное уравнение регрессии может существенно отличаться от того «истинного» уравнения, которое соответствует генеральной совокупности.
– случайные величины, то полученное уравнение регрессии может существенно отличаться от того «истинного» уравнения, которое соответствует генеральной совокупности.
Для оценки надёжности выборочного уравнения регрессии применяется ![]() - критерий Фишера, рассчитываемый по формуле:
- критерий Фишера, рассчитываемый по формуле:
![]() (3.37)
(3.37)
![]() (3.38)
(3.38)
где ![]() – дисперсия результативного признака, обусловленная регрессией, т.е. влиянием на
– дисперсия результативного признака, обусловленная регрессией, т.е. влиянием на ![]() факторных переменных, включенных в модель;
факторных переменных, включенных в модель; ![]() – дисперсия результативного признака, обусловленная влиянием второстепенных факторов и случайных помех;
– дисперсия результативного признака, обусловленная влиянием второстепенных факторов и случайных помех; ![]() – объём выборки;
– объём выборки; ![]() – количество факторных переменных.
– количество факторных переменных.
Для оценки надежности выборочного уравнения регрессии воспользуемся формулой (3.37)
![]()
По статистическим таблицам распределения Фишера (приложение 4) на ![]() -ном уровне значимости при числе степеней свободы
-ном уровне значимости при числе степеней свободы ![]() и
и ![]() находим критическую точку
находим критическую точку ![]()
Так как ![]() делаем вывод о значимости полученного уравнения регрессии.
делаем вывод о значимости полученного уравнения регрессии.
Для оценки надёжности парного коэффициента корреляции ![]() применим формулу (3.43)
применим формулу (3.43)
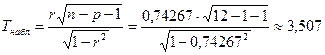
По таблице распределения Стьюдента (приложение 5) на ![]() -ном уровне значимости при числе степеней свободы
-ном уровне значимости при числе степеней свободы ![]() находим критическую точку
находим критическую точку ![]()
Так как ![]() делаем вывод о значимости
делаем вывод о значимости ![]() т. е., отклоняем гипотезу
т. е., отклоняем гипотезу ![]() об отсутствии линейной корреляционной связи в генеральной совокупности, рискуя ошибиться при этом лишь в
об отсутствии линейной корреляционной связи в генеральной совокупности, рискуя ошибиться при этом лишь в ![]() -х случаев.
-х случаев.
Вычислим теперь коэффициент детерминации (квадрат смешанной корреляции) ![]() Отсюда заключаем, что в случае простой регрессии
Отсюда заключаем, что в случае простой регрессии ![]() общей дисперсии объём производства на 55,16 % зависит от капиталовложений.
общей дисперсии объём производства на 55,16 % зависит от капиталовложений.
Дальнейшее исследование модели связано с указанием доверительных интервалов для параметров регрессии и генерального коэффициента корреляции. Для уяснения сути этих процедур необходимы предварительные пояснения.
Задача регрессионного анализа состоит в нахождении истинных значений параметров, т.е. в определении соотношения между ![]() и
и ![]() в генеральной совокупности
в генеральной совокупности ![]()
где ![]() - генеральные коэффициенты регрессии.
- генеральные коэффициенты регрессии.
Мы же находим оценки параметров регрессии ![]() наиболее хорошо согласующиеся с опытными данными. Эти реализации
наиболее хорошо согласующиеся с опытными данными. Эти реализации ![]() являются случайными величинами, которые более или менее удалены от значения параметра
являются случайными величинами, которые более или менее удалены от значения параметра ![]() .
.
Иначе говоря, возможные значения оценок ![]() рассеиваются вокруг истинного значения параметра
рассеиваются вокруг истинного значения параметра ![]() . Разность между
. Разность между ![]() и
и ![]() возникающая за счет оценивания на основе имеющихся данных, называется ошибкой оценки. Для характеристики рассеяния выборочных оценок
возникающая за счет оценивания на основе имеющихся данных, называется ошибкой оценки. Для характеристики рассеяния выборочных оценок ![]() вокруг генерального параметра
вокруг генерального параметра ![]() используются стандартные ошибки или дисперсии оценок параметров регрессии. Мера рассеяния оценки параметра регрессии определяется по формуле (3.44). Стандартная ошибка коэффициента регрессии зависит:
используются стандартные ошибки или дисперсии оценок параметров регрессии. Мера рассеяния оценки параметра регрессии определяется по формуле (3.44). Стандартная ошибка коэффициента регрессии зависит:
1) от рассеяния остатков ![]() . Чем больше доля вариации значений -
переменной
. Чем больше доля вариации значений -
переменной ![]() , необъясненной её зависимостью от
, необъясненной её зависимостью от ![]() тем больше
тем больше ![]() ;
;
2) от рассеяния значений объясняющей переменной ![]() . Чем сильнее это рассеяние, тем меньше
. Чем сильнее это рассеяние, тем меньше ![]() . Отсюда следует, что при вытянутом облаке точек на диаграмме рассеяния получаем более надежную оценку функции регрессии, чем при небольшое скоплении точек, близко расположенных друг к другу;
. Отсюда следует, что при вытянутом облаке точек на диаграмме рассеяния получаем более надежную оценку функции регрессии, чем при небольшое скоплении точек, близко расположенных друг к другу;
3) от объёма выборки. Чем больше объём выборки, тем меньше стандартная ошибка коэффициента регрессии.
Знание стандартных сшибок коэффициентов регрессии позволяет построить для параметров интервальные оценки. Надежность оценки определяется вероятностью, с которой утверждается, что построенный по результатам выборки доверительный интервал содержит неизвестный параметр генеральной совокупности. Эта вероятность называется доверительной. Её обычно выбирают близкой к единице: ![]() и т. д. Тогда можно ожидать, что при серии наблюдений параметр генеральной совокупности будет правильно оценен (т.е. доверительный интервал покроет истинное значение этого параметра) приблизительно в
и т. д. Тогда можно ожидать, что при серии наблюдений параметр генеральной совокупности будет правильно оценен (т.е. доверительный интервал покроет истинное значение этого параметра) приблизительно в ![]() случаев и лишь в (
случаев и лишь в (![]() )% случаев оценка будет ошибочной. Если
)% случаев оценка будет ошибочной. Если ![]() близка к единице, то риск ошибки ничтожен. Риск ошибки определяется уровнем значимости
близка к единице, то риск ошибки ничтожен. Риск ошибки определяется уровнем значимости ![]() . В экономических исследованиях чаще всего
. В экономических исследованиях чаще всего ![]() .
.
Тогда риск ошибки составляет ![]() (
(![]() ).
При этом также говорят о
).
При этом также говорят о ![]() -ном доверительном интервале.
-ном доверительном интервале.
Доверительный интервал для параметров регрессии ![]() записываемся в виде следующей формулы (3.45):
записываемся в виде следующей формулы (3.45):
![]() .(3.45):
.(3.45):
Определим доверительные границы для параметра регрессии ![]() , (
, (![]() обычно не рассматривается, т. к. лишен экономического смысла).
обычно не рассматривается, т. к. лишен экономического смысла).
Пользуясь табл. 3.6. по формуле (3.44) вычислим стандартную ошибку оценки параметра регрессии:
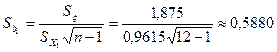
Зададимся уровнем значимости ![]() Число степеней свободы для нашего примера
Число степеней свободы для нашего примера ![]() . По приложению 5 находим, что
. По приложению 5 находим, что ![]() . В соответствии с формулой (3.45) получаем следующие доверительные границы для
. В соответствии с формулой (3.45) получаем следующие доверительные границы для ![]()
![]()
или
![]()
Итак, с вероятностью 0,588 можно утверждать, что неизвестное знамение параметра регрессии ![]() содержится в интервале
содержится в интервале
![]()
При построении доверительного интервала для коэффициента корреляции
генеральной совокупности ![]() прибегают к преобразованию Фишера по формуле (3.46):
прибегают к преобразованию Фишера по формуле (3.46):
![]()
Подставляя выборочный коэффициент корреляции ![]() получаем значение
получаем значение ![]() :
:
![]()
Стандартную ошибку ![]() вычисляем по приближенной формуле (3.47):
вычисляем по приближенной формуле (3.47):
![]() 0,333.
0,333.
Доверительные границы для величины ![]() на заданном уровне значимости
на заданном уровне значимости ![]() определяются по формуле (3.48):
определяются по формуле (3.48): ![]() .
.
При уровне значимости ![]() . Таким образом, доверительные границы для величины
. Таким образом, доверительные границы для величины ![]() при
при ![]() будут следующими:
будут следующими:
![]()
или
![]()
и доверительный интервал для ![]()
![]()
Доверительные границы для коэффициента корреляции ![]() находят путем обратного пересчета величины
находят путем обратного пересчета величины ![]() по формуле (3.49):
по формуле (3.49):
![]() =
= ![]()
![]()
Итак, с вероятностью 0,55 можно утверждать, что коэффициент корреляции в генеральной совокупности содержится в интервале
![]()
2. ![]()
![]()
Коэффициент регрессии ![]() показывает, что объём производства в среднем возрастает на 5,5514*10000 = 55514 т/ч, если средний процент выполнения норм увеличился на 1%
показывает, что объём производства в среднем возрастает на 5,5514*10000 = 55514 т/ч, если средний процент выполнения норм увеличился на 1%
Коэффициент Корреляции
![]()
Получен очень высокий коэффициент корреляции. Это свидетельствует о том, что связь между объёмом производства и средним процентом выполнения норм.
Содержание этого этапа заключается в статистической проверке значимости (надежности): уравнения регрессии, коэффициентов регрессии и корреляции.
1. Значимость уравнения регрессии определяется возможностью надежно прогнозировать среднее отклика по заданным значениям факторной переменной. Так как ![]() – случайные величины, то полученное уравнение регрессии может существенно отличаться от того «истинного» уравнения, которое соответствует генеральной совокупности.
– случайные величины, то полученное уравнение регрессии может существенно отличаться от того «истинного» уравнения, которое соответствует генеральной совокупности.
Для оценки надёжности выборочного уравнения регрессии применяется ![]() - критерий Фишера, рассчитываемый по формуле:
- критерий Фишера, рассчитываемый по формуле:
![]() (3.37)
(3.37)
![]() (3.38)
(3.38)
где ![]() – дисперсия результативного признака, обусловленная регрессией, т.е. влиянием на
– дисперсия результативного признака, обусловленная регрессией, т.е. влиянием на ![]() факторных переменных, включенных в модель;
факторных переменных, включенных в модель; ![]() – дисперсия результативного признака, обусловленная влиянием второстепенных факторов и случайных помех;
– дисперсия результативного признака, обусловленная влиянием второстепенных факторов и случайных помех; ![]() – объём выборки;
– объём выборки; ![]() – количество факторных переменных.
– количество факторных переменных.
Для оценки надежности выборочного уравнения регрессии воспользуемся формулой (3.37)
![]()
По статистическим таблицам распределения Фишера на ![]() -ном уровне значимости при числе степеней свободы
-ном уровне значимости при числе степеней свободы ![]() и
и ![]() находим критическую точку
находим критическую точку ![]()
Так как ![]() делаем вывод о значимости полученного уравнения регрессии.
делаем вывод о значимости полученного уравнения регрессии.
Для оценки надёжности парного коэффициента корреляции ![]() применим формулу (3.43)
применим формулу (3.43)
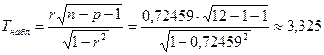
По таблице распределения Стьюдента на ![]() -ном уровне значимости при числе степеней свободы
-ном уровне значимости при числе степеней свободы ![]() находим критическую точку
находим критическую точку
![]()
Так как ![]() делаем вывод о значимости
делаем вывод о значимости ![]() т. е., отклоняем гипотезу
т. е., отклоняем гипотезу ![]() об отсутствии линейной корреляционной связи в генеральной совокупности, рискуя ошибиться при этом лишь в
об отсутствии линейной корреляционной связи в генеральной совокупности, рискуя ошибиться при этом лишь в ![]() -х случаев.
-х случаев.
Вычислим теперь коэффициент детерминации (квадрат смешанной корреляции) ![]() Отсюда заключаем, что в случае простой регрессии
Отсюда заключаем, что в случае простой регрессии ![]() общей дисперсии объём производства на 52,50 % зависит от среднего процента выполнения нормы.
общей дисперсии объём производства на 52,50 % зависит от среднего процента выполнения нормы.
Дальнейшее исследование модели связано с указанием доверительных интервалов для параметров регрессии и генерального коэффициента корреляции. Для уяснения сути этих процедур необходимы предварительные пояснения.
Задача регрессионного анализа состоит в нахождении истинных значений параметров, т.е. в определении соотношения между ![]() и
и ![]() в генеральной совокупности
в генеральной совокупности ![]()
где ![]() - генеральные коэффициенты регрессии.
- генеральные коэффициенты регрессии.
Мы же находим оценки параметров регрессии ![]() наиболее хорошо согласующиеся с опытными данными. Эти реализации
наиболее хорошо согласующиеся с опытными данными. Эти реализации ![]() являются случайными величинами, которые более или менее удалены от значения параметра
являются случайными величинами, которые более или менее удалены от значения параметра ![]() .
.
Иначе говоря, возможные значения оценок ![]() рассеиваются вокруг истинного значения параметра
рассеиваются вокруг истинного значения параметра ![]() . Разность между
. Разность между ![]() и
и ![]() возникающая за счет оценивания на основе имеющихся данных, называется ошибкой оценки. Для характеристики рассеяния выборочных оценок
возникающая за счет оценивания на основе имеющихся данных, называется ошибкой оценки. Для характеристики рассеяния выборочных оценок ![]() вокруг генерального параметра
вокруг генерального параметра ![]() используются стандартные ошибки или дисперсии оценок параметров регрессии. Мера рассеяния оценки параметра регрессии определяется по формуле (3.44). Стандартная ошибка коэффициента регрессии зависит:
используются стандартные ошибки или дисперсии оценок параметров регрессии. Мера рассеяния оценки параметра регрессии определяется по формуле (3.44). Стандартная ошибка коэффициента регрессии зависит:
1) от рассеяния остатков ![]() . Чем больше доля вариации значений -
переменной
. Чем больше доля вариации значений -
переменной ![]() , необъясненной её зависимостью от
, необъясненной её зависимостью от ![]() тем больше
тем больше ![]() ;
;
2) от рассеяния значений объясняющей переменной ![]() . Чем сильнее это рассеяние, тем меньше
. Чем сильнее это рассеяние, тем меньше ![]() . Отсюда следует, что при вытянутом облаке точек на диаграмме рассеяния получаем более надежную оценку функции регрессии, чем при небольшое скоплении точек, близко расположенных друг к другу;
. Отсюда следует, что при вытянутом облаке точек на диаграмме рассеяния получаем более надежную оценку функции регрессии, чем при небольшое скоплении точек, близко расположенных друг к другу;
3) от объёма выборки. Чем больше объём выборки, тем меньше стандартная ошибка коэффициента регрессии.
Знание стандартных сшибок коэффициентов регрессии позволяет построить для параметров интервальные оценки. Надежность оценки определяется вероятностью, с которой утверждается, что построенный по результатам выборки доверительный интервал содержит неизвестный параметр генеральной совокупности. Эта вероятность называется доверительной. Её обычно выбирают близкой к единице: ![]() и т. д. Тогда можно ожидать, что при серии наблюдений параметр генеральной совокупности будет правильно оценен (т.е. доверительный интервал покроет истинное значение этого параметра) приблизительно в
и т. д. Тогда можно ожидать, что при серии наблюдений параметр генеральной совокупности будет правильно оценен (т.е. доверительный интервал покроет истинное значение этого параметра) приблизительно в ![]() случаев и лишь в (
случаев и лишь в (![]() )% случаев оценка будет ошибочной. Если
)% случаев оценка будет ошибочной. Если ![]() близка к единице, то риск ошибки ничтожен. Риск ошибки определяется уровнем значимости
близка к единице, то риск ошибки ничтожен. Риск ошибки определяется уровнем значимости ![]() . В экономических исследованиях чаще всего
. В экономических исследованиях чаще всего ![]() .
.
Тогда риск ошибки составляет ![]() (
(![]() ).
При этом также говорят о
).
При этом также говорят о ![]() -ном доверительном интервале.
-ном доверительном интервале.
Доверительный интервал для параметров регрессии ![]() записываемся в виде следующей формулы (3.45):
записываемся в виде следующей формулы (3.45):
![]() .(3.45):
.(3.45):
Определим доверительные границы для параметра регрессии ![]() , (
, (![]() обычно не рассматривается, т. к. лишен экономического смысла).
обычно не рассматривается, т. к. лишен экономического смысла).
Пользуясь табл. 3.6. по формуле (3.44) вычислим стандартную ошибку оценки параметра регрессии:
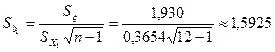
Зададимся уровнем значимости ![]() Число степеней свободы для нашего примера
Число степеней свободы для нашего примера ![]() . По приложению 5 находим, что
. По приложению 5 находим, что ![]() . В соответствии с формулой (3.45) получаем следующие доверительные границы для
. В соответствии с формулой (3.45) получаем следующие доверительные границы для ![]()
![]()
или
![]()
Итак, с вероятностью 0,52 можно утверждать, что неизвестное знамение параметра регрессии ![]() содержится в интервале
содержится в интервале
![]()
При построении доверительного интервала для коэффициента корреляции
генеральной совокупности ![]() прибегают к преобразованию Фишера по формуле (3.46):
прибегают к преобразованию Фишера по формуле (3.46): ![]()
Подставляя выборочный коэффициент корреляции ![]() получаем значение
получаем значение ![]() :
:
![]()
Стандартную ошибку ![]() вычисляем по приближенной формуле (3.47):
вычисляем по приближенной формуле (3.47):
![]() 0,333.
0,333.
Доверительные границы для величины ![]() на заданном уровне значимости
на заданном уровне значимости ![]() определяются по формуле (3.48):
определяются по формуле (3.48): ![]() .
.
При уровне значимости ![]() . Таким образом, доверительные границы для величины
. Таким образом, доверительные границы для величины ![]() при
при ![]() будут следующими:
будут следующими:
![]()
или
![]()
и доверительный интервал для ![]()
![]()
Доверительные границы для коэффициента корреляции ![]() находят путем обратного пересчета величины
находят путем обратного пересчета величины ![]() по формуле (3.49):
по формуле (3.49):
![]() =
= ![]()
![]()
Итак, с вероятностью 0,5% можно утверждать, что коэффициент корреляции в генеральной совокупности содержится в интервале
![]()
Г) Построим уравнение регрессии ![]() и выполнить исследование множественной модели в полном объеме (см.п.3.2).
и выполнить исследование множественной модели в полном объеме (см.п.3.2).
Будем искать зависимость объёма производства, капиталовложениями и выполнением норм выработки в виде линейной множественной регрессии.
![]() (3.55)
(3.55)
Объясняющие переменные Х1 и Х2 оказывают совместное одновременное влияние на зависимую переменную У.
Приведем формулы для вычисления ![]() по МНК
по МНК
![]() (3.56)
(3.56)
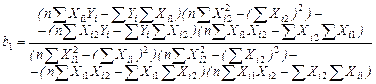 (3.57)
(3.57)
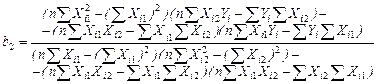 (3.58)
(3.58)
Используя промежуточные результаты из табл. 3.4 и 3.7, по формулам (3.56), (3.57) и (3.58) вычисляем коэффициенты регрессии:
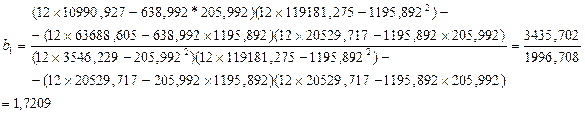
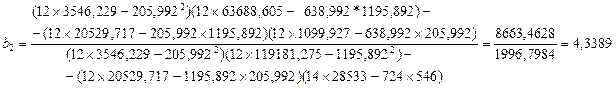
![]()
Итак, в соответствии с (3.55) уравнение регрессии запишем в виде
![]() (3.59)
(3.59)
Подставляя в это уравнение значения ![]() и
и ![]() получим
получим ![]() , а затем вычислим остатки
, а затем вычислим остатки ![]() (см. приложение 1).
(см. приложение 1).
Таким образом, если рассматривать зависимость Объёма производства от капиталовложений и от среднего процента выполнения норм, то объем производства в среднем изменится на 1,7209*10000 рублей при условии, что капиталовложения изменится на 1000 рублей при исключении влияния среднего процента выполнения норм. Если исключить влияние капиталовложений, то обьем производства в среднем изменится на 4,3389 *10000 рублей при изменении среднего процента выполнения норм на один процент.
Обратим внимание, что по сравнению с коэффициентом регрессии в уравнении с одной объясняющей переменной данный коэффициент регрессии ![]() несколько уменьшился. Это можно объяснить тем, что переменная
несколько уменьшился. Это можно объяснить тем, что переменная ![]() коррелирует с
коррелирует с ![]() , в чем мы ещё убедимся при выполнении корреляционного анализа. Поэтому переменная
, в чем мы ещё убедимся при выполнении корреляционного анализа. Поэтому переменная ![]() влияет на
влияет на ![]() через
через ![]() , что приводит к ослаблению силы зависимости
, что приводит к ослаблению силы зависимости ![]() от
от ![]() .
.
Коэффициенты регрессии отражают зависимость объёма производства от соответствующей переменной при исключении влияния на зависимую переменную двух других объясняющих переменных.
Стандартизированные коэффициенты регрессий ![]() ;
вычисляются по формуле:
;
вычисляются по формуле:
![]() (3.61)
(3.61)
где ![]() -
обычный коэффициент регрессии, а
-
обычный коэффициент регрессии, а ![]() и
и ![]() - стандартные отклонения переменных
- стандартные отклонения переменных ![]() и
и ![]() соответственно.
соответственно.
По формуле (3.61) вычислим стандартизированные коэффициенты регрессии
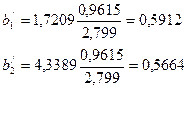
Уравнение множественной регрессии в стандартизированном масштабе примет вид
![]() (3.62)
(3.62)
где ![]()
Для вычисления множественного коэффициента корреляции можно воспользоваться и другой формулой, если вспомнить, что он непосредственно связан с коэффициентом детерминации ![]()
![]()
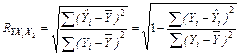 (3.65)
(3.65)
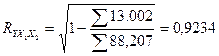
Получен очень высокий коэффициент корреляции. Это свидетельствует о том, что зависимость объема производства от капиталовложений и среднего процента выполнения норм очень высокая..
Оценим значимость уравнений регрессии
Значимость уравнения регрессии определяется возможностью надежно прогнозировать среднее отклика по заданным значениям факторной переменной. Так как ![]() – случайные величины, то полученное уравнение регрессии может существенно отличаться от того «истинного» уравнения, которое соответствует генеральной совокупности.
– случайные величины, то полученное уравнение регрессии может существенно отличаться от того «истинного» уравнения, которое соответствует генеральной совокупности.
Для оценки надёжности выборочного уравнения регрессии применяется ![]() - критерий Фишера, рассчитываемый по формуле:
- критерий Фишера, рассчитываемый по формуле:
![]() (3.37)
(3.37)
![]()
![]() (3.38)
(3.38)
![]()
Уравнение регрессии считается значимым (т.е., выделенные факторные переменные "хорошо", "надёжно" описывают исследуемую зависимость, если значение
![]() (3.40)
(3.40)
где ![]() – табличное значение F-критерия Фишера-Снедекора на уровне значимости
– табличное значение F-критерия Фишера-Снедекора на уровне значимости ![]() при числе степеней свободы
при числе степеней свободы ![]() и
и ![]() . Критическая точка находится по статистическим таблицам «Критические точки распределения Фишера на %5-ном уровне значимости».
. Критическая точка находится по статистическим таблицам «Критические точки распределения Фишера на %5-ном уровне значимости».
![]()
Вывод: Уравнение регрессии считается значимым (т.е., выделенные факторные переменные "хорошо", "надёжно" описывают исследуемую зависимость.
Для оценки надежности множественного коэффициента корреляции
также применяется ![]() - критерий Фишера, рассчитываемый по формуле:
- критерий Фишера, рассчитываемый по формуле:
![]() (3.41)
(3.41)
![]()
где ![]() - множественный коэффициент корреляции.
- множественный коэффициент корреляции.
Множественный коэффициент корреляции значим (т.е. надежно отличается от нуля), если
![]() (3.42)
(3.42)
Коэффициенты детерминации ![]() Делаем Вывод: Общий объём производства зависит на 85,27% от капиталовложений и среднего выполнения норм.
Делаем Вывод: Общий объём производства зависит на 85,27% от капиталовложений и среднего выполнения норм.
При проверке гипотезы ![]() используется статистика
используется статистика
![]() (3.68)
(3.68)
имеющая ![]() - распределение с
- распределение с ![]() степенями свободы. Если
степенями свободы. Если ![]() ,то гипотеза
,то гипотеза ![]() считается и принимается альтернативная гипотеза
считается и принимается альтернативная гипотеза ![]() .
.
Оценим значимость коэффициентов регрессии, рассматривая зависимость производительности труда от уровня механизация работ, и среднего возраста работников и среднего процента выполнения нормы. Воспользуемся для этого формулами (3.44), (3.68), и двусторонней критической областью:
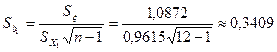

![]()
![]()
По таблице ![]() - распределения для
- распределения для ![]() и
и ![]() находим критическое значение
находим критическое значение ![]() .
.
Поскольку ![]() существенно отлично от нуля и отражает. таким образом, отметим значимое влияние капиталовложений на объём производства.,
существенно отлично от нуля и отражает. таким образом, отметим значимое влияние капиталовложений на объём производства., ![]() , отметим значимое влияние среднего процентного выполнения норм на объём производства.
, отметим значимое влияние среднего процентного выполнения норм на объём производства.
Процедуру расчета доверительных интервалов мы опускаем, поскольку она не содержит ничего нового по сравнению со схемой, изложенной в 3.2.