Реферат: Собственные интегралы, зависящие от параметра

Глава 1. Собственные интегралы, зависящие от параметра

Пункт 1. Понятие интеграла, зависящего от параметра

Для того чтобы дать определение интеграла, зависящего от параметра, введем функцию . Пусть эта функция будет определена на некотором множестве, где и , то есть в результате получится множество . Если функция непрерывна в D , то тогда имеет смысл интеграл 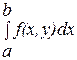, где x принадлежит некоторому конечному или бесконечному промежутку , значит, интеграл может быть несобственным.

На основании этого можно дать определение интеграла, зависящего от параметра.

Определение.

Интеграл 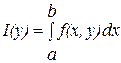называется интегралом, зависящим от параметра, если интегрируема на промежутке при любом фиксированным , где .

Следовательно, представляет собой функцию переменной (параметра) , определенную в промежутке . Возможно также существование интеграла при фиксированном , тогда он будет представлять собой функцию переменной (параметра) , определенную в промежутке . Обозначается она так , так что .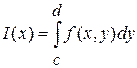

Основная задача будет состоять в том, чтобы, зная свойства функции , получить информацию о свойствах функции . Эти свойства имеют многообразные применения, особенно при вычислении несобственных интегралов.

Пример. Найти интеграл от функции ,

Функция непрерывна на отрезке при любом фиксированном , а значит, она интегрируема. Тогда

.

Пункт 2. Предельный переход под знаком интеграла. Непрерывность интеграла как функции параметра

Определение.

Пусть - это предельная точка множества .Функция называется равномерно сходящейся к функции при по переменной , если выполняются следующие условия:

1. для при существует конечная предельная функция ;

2. . (1)

Замечание 1.

В цепочки (1) зависит только от и не зависит от , а неравенство выполняется при любых одновременно.

Замечание 2.

Если , то в цепочке (1) неравенство следует заменить на ().

Теорема 1 (признак сходимости). Если функция определена на множестве , то для того, чтобы она имела предельную функцию и сходилась к ней равномерно необходимо и достаточно, чтобы выполнялась цепочка

Докажем теорема так.

Необходимость . Пусть функция равномерно сходится. Если заменим в определении на и выберем соответственно , а затем возьмем два значения и из так, чтобы выполнялись условия и . В результате получим и откуда следует последнее неравенство в цепочке .

Достаточность . Теперь пусть существует предельная функция . Нужно доказать равномерную сходимость функции к предельной функции. Для этого совершим переход к пределу в неравенстве при , получается . Что и подтверждает равномерную сходимость к функции .

Теорема 2 (о непрерывности предельной функции). Если функция при любом фиксированном непрерывна на и равномерно сходится к предельной функции по переменной при , то функция также непрерывна на .

Легко обобщается теорема Дини: если функция непрерывна для любого фиксированного на и при возрастании функция, монотонно возрастая, стремится к предельной функции , то сходится к равномерно.

Теорема 3 (предельный переход по параметру под знаком интеграла). Если функция непрерывна при постоянном значении на и сходится равномерно по переменной к предельной функции при , то тогда имеет место равенство

(2)

Доказательство.

Непрерывность следует из теоремы 2, значит, она интегрируема на отрезке . В силу равномерной сходимости к выполняется . Тогда при тех же и имеем:

откуда следует , что доказываетформулу (2).

Замечание 3.

Равенство (2) можно записать и в другом виде

. (2`)

Следствие 1.

Если функция при постоянном непрерывна по и при возрастании стремится, монотонно возрастая, к непрерывной предельной функции , то справедливы формулы (2) и (2`).

В предположении, что область представляет собой конечный промежуток , рассмотрим вопрос о непрерывности функции .

Пример (№3713 (в)). Найти .

1. функция непрерывная функция на . Функции и также непрерывны на .

2. непрерывная функция (т.4 и сл.2) в промежутке , значит

3. .

Теорема 4 (о непрерывности интеграла как функции параметра). Пусть функция определена и непрерывна в прямоугольнике 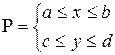, тогда интеграл будет непрерывной функцией от параметра в промежутке .

Доказательство.

Так как непрерывна на замкнутом множестве, то по теореме Кантора она равномерно непрерывна на данном прямоугольнике . Возьмем любое и зафиксируем . Тогда нашему значению будет соответствовать , такое, что для любых двух точек , принадлежащих , из неравенств и , будет следовать . Положим , , где , - любые из , и , где . Тогда получим

. Это означает, что функция равномерно стремится к . В таком случае по теореме 3 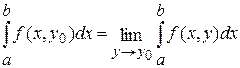, а уже отсюда следует равенство , то есть наша функция непрерывна на .

Замечание 4. Совершенно аналогично доказывается теорема для 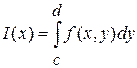, где .

Следствие 2. Если непрерывна на прямоугольнике , то .

Пример . Найти .

1. непрерывна на

2. тогда по теореме 4. и следствию 2 получаем

Пункт 3. Дифференцирование под знаком интеграла

При изучении свойств функции важное значение имеет вопрос о ее производной по параметру. Вычислить производную можно по формуле , которую вывел Лейбниц 1697. Рассмотрим теорему, устанавливающую простые достаточные условия для применимости этой формулы.

Теорема (о дифференцировании интеграла, зависящего от параметра). Пусть функция определена и непрерывна в прямоугольнике и имеет там непрерывную частную производную . Пусть 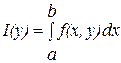, . Тогда:

1. функция имеет в промежутке производную ;

2. , то есть , .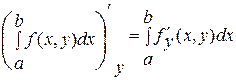

Доказательство.

Возьмем любую точку и зафиксируем ее. Придадим приращение и точка . Тогда , ,

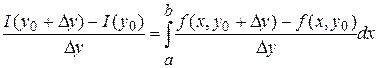(1)

По теореме Лагранжа . Следовательно,

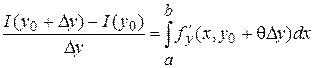. (2)

Переходя в (2) к пределу при , приняв во внимание теорему о допустимости предельного перехода под знаком интеграла, получим:

.

Из этого следует, что существует, причем 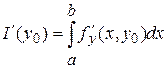. Так как - любое , то существует для любого , причем .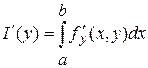

Пример. Найти производную функции .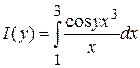

1. непрерывна на

2. 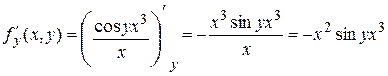. Эта функция также непрерывна на .

3.

4.

Пункт 4. Интегрирование по параметру под знаком интеграла

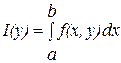Рассмотрим вопрос об интегрировании по параметру функции . Если она интегрируема, то интеграл будет иметь вид . Достаточное условие для равенства двух повторных интегралов дает следующая теорема.

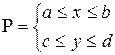Теорема. Если непрерывная по обеим переменным функция на прямоугольнике , то 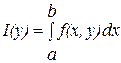интегрируемая на промежутке функция и справедливо равенство , то есть .

Также можно расписать с помощью повторных интегралов следующим образом .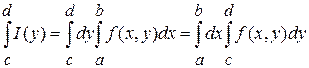

Докажем более общее равенство.

для любого . (1)

В левой и правой частях равенства (1) мы имеем две функции от параметра t . Вычислим их производные по t . Так как , то (т.4 п.2), а следовательно есть интеграл с переменным верхним пределом от непрерывной функции. Тогда по теореме Барроу:

, . (2)

В правой части стоит интеграл 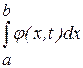, где . Действительно функция удовлетворяет условиям теоремы п.3, она также непрерывна по в силу теоремы 4 п.2.Мы можем найти производную , которая будет непрерывна как функция двух переменных.

Тогда по теореме о дифференцировании по параметру под знаком интеграла

, . (3)

Видим, что левая и правая части равенства (1) имеют в промежутке совпадающие производные (см. (2) и (3)). А значит они отличаются в этом промежутке только на постоянную величину, т. е. .

. (4)

Положив в (4) t = c , получим . Значит, будем иметь вместо (4) для любого

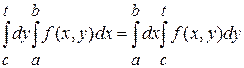. (5)

Пусть в (5) t = d , получим

.

Что и требовалось получить.

Глава 2. Несобственные интегралы, зависящие от параметра

Пункт 1. Равномерная сходимость несобственных интегралов, зависящих от параметра

При рассмотрении теории интегралов, зависящих от параметра, в случае несобственных интегралов особую роль играет понятие равномерной сходимости. Выясним это понятие сначала для несобственных интегралов первого рода (НИЗП-1), затем для интегралов второго рода (НИЗП-2).

Пусть функция определена и непрерывна на некотором прямоугольнике и при любом фиксированном существует несобственный интеграл, зависящий от параметра, этой функции на любом промежутке . Тогда интеграл сходится и равен

.

В этом случае называют несобственным интегралом первого рода (НИЗП-1).

Утверждение о том, что 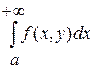сходится при каждом означает следующее: при каждом фиксированном

.

Следовательно,

или .

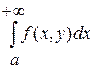Это значит, что для каждого по любому можно указать число такое, что если , то . Важно заметить, что зависит и от ,и от :. Если же для любого можно указать число , зависящее только от , такое, что при выполняется для, то в этом случае называется равномерно сходящимся относительно параметра .

Теперь сформулируем критерий Коши для равномерной сходимости для нашего случая следующим образом:

Теорема 1. (критерий Коши равномерной сходимости для НИЗП-1). Для того чтобы интеграл сходился равномерно по переменной на промежутке , необходимо и достаточно, чтобы выполнялась цепочка

, .

Рассмотрим достаточные признаки равномерной сходимости.

Теорема 2. (признак Вейерштрасса равномерной сходимости НИЗП-1). Пусть функция определена и непрерывна на прямоугольнике и удовлетворяет условиям:

1. непрерывна по переменной ,

2. существует функция , что ,

3. - сходится.

Из этого следует, что 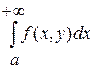сходится равномерно по .

Доказательство.

В соответствии с условием 3) критерия Коши о сходимости несобственных интегралов 1-го рода от функции одной переменной имеем:

(1)

Тогда при тех же , что и в цепочке, получаем

.

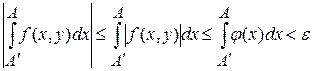А отсюда по теореме 1 следует равномерная сходимость интеграла .

Ч. т. д.

Замечание.

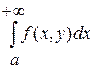При выполнении условий теоремы 2 говорят, что функция имеет интегрируемую мажоранту или что интеграл мажорируется сходящимся интегралом .

Следствие.

Пусть выполняются следующие условия:

1. функция определена и непрерывна по ;

2. функция ограничена на прямоугольнике ;

3. интеграл 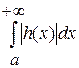сходится, тогда следует, что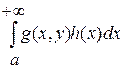

сходится равномерно по .

Обозначим через и возьмем в качестве , а в качестве функции . Тогда, исходя из теоремы 2, получим цепочку (1).

Совершенно аналогично вводится понятие равномерной сходимости несобственных интегралов второго рода (НИЗП-2).

Пусть функция определена в области 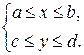(a,b,c – конечные числа). Пусть при несобственный интеграл сходится. В этом случае будет представлять собой функцию переменной (параметра) , определенную в промежутке . Утверждение, что несобственный интеграл сходится при , означает следующее. При каждом фиксированном интеграл

(здесь ). Это значит, что для каждого из по любому можно указать такое, что при условии выполняется . Важно отметить, что число выбирается по , и для каждого оно будет своим, другими словами, зависит и от , и от : . Если же можно указать такое , зависящее только от , такое, что при выполнении условия будет верно сразу для всех , несобственный интеграл называется равномерно сходящимся относительно параметра. Короче говорят, интеграл называется равномерно сходящимся по переменной на , если он сходится при и выполняется цепочка .

Для НИЗП-2 справедливы теоремы аналогичные т.1 и т. 2.

Теорема 3. (критерий Коши равномерной сходимости НИЗП-2). Для того чтобы НИЗП-2 равномерно сходился по необходимо и достаточно, чтобы:

, .

Теорема 4. Пусть функция определена в области 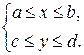и удовлетворяет следующим условиям:

1. функция непрерывна по , при ;

2. существует такая функция , что , и .

3. - сходится

НИЗП-2 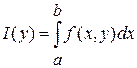сходится равномерно по на .

Доказательство проводится аналогично доказательству теоремы 2.

Пример. Исследовать на равномерную сходимость интеграл .

Для определения равномерной сходимости необходимо проверить выполнение всех условий теоремы 2.

1. определена и непрерывна в области ;

2. существует функция , , для любого ;

3. 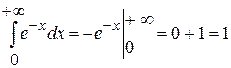, то есть сходится.

Так как все условия выполнены, то интеграл сходится равномерно относительно на любом промежутке .

Пункт 2. Непрерывность НИЗП, предельный переход под знаком интеграла.

В этом пункте мы рассмотрим предельный переход под знаком интеграла, имеющего бесконечный предел, и непрерывность интеграла как функции параметра. Условия, достаточные для допустимости предельного перехода, даются следующей теоремой:

Теорема 1. Пусть функция , определенная на прямоугольнике , удовлетворяет условиям:

1. функция по на промежутке ;

2. равномерно стремится к при по , где ;

3. интеграл сходится равномерно по на .

В результате справедливо равенство

(1)

Доказательство.

Функция будет непрерывной. По условию равномерной сходимости для любого найдется такое , что , для , но только . Переходя к пределу при под знаком интеграла, получим . Значит интегрируемая на бесконечном промежутке функция. Тогда при , имеем

.

Если взять произвольное число , зафиксировать число так, чтобы второе и третье слагаемые справа стали меньше , а затем приблизить к , чтобы первое слагаемое стало меньше . Тогда получим , что приводит к равенству (1).

Ч.т.д.

Следствие.

Пусть функция неотрицательна и непрерывна по , при , и монотонно возрастая, стремится к с возрастанием . Если функция непрерывна и интегрируема на промежутке , то справедлива формула (1).

Простым следствием из теоремы 1 является теорема о непрерывности интеграла по параметру.

Теорема 2. Пусть функция определена и непрерывна для значений и значений . Если 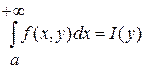сходится равномерно относительно на , тогда - непрерывная функция от параметра в этом промежутке.

Доказательство (аналогично теореме для собственных интегралов).

По теореме Кантора при и функция равномерно непрерывна, а значит если - это любое фиксированное из значение, то наша функция равномерно, относительно , стремится к при . Так как сходится равномерно, то по т.1 следует

,

значит интеграл - непрерывная функция.

Пункт 3. Интегрирование по параметру НИЗП

Чтобы выяснить интегрируема ли функция по параметру, необходимо рассмотреть следующую теорему.

Теорема 1. Пусть функция определена и непрерывна, как функция от двух переменных, в множестве Если интеграл сходится равномерно по на , то справедлива формула

. (1)

Доказательство.

При любом выполняется равенство

. (2)

Так как функция непрерывна при и , по теореме о непрерывности интеграла как функции параметра следует, что

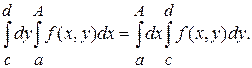(3)

Тогда из (2).

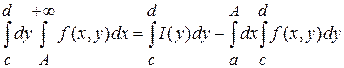Так как 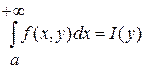сходится равномерно, то при произвольном будет . В результате этого оценим левую часть (3) по модулю:

в силу (3) 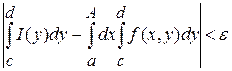. Последнее означает, что

.

Так как левая часть существует в этом равенстве, то по определению несобственных интегралов правая часть также существует, причем равная 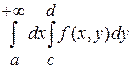. То есть справедлива формула (1).

Ч.т.д.

Следствие.

Если непрерывная функция неотрицательная при и интеграл непрерывен по на , то имеет смысл формула (1).

Таким образом, мы установили право переставлять два интеграла, из которых один распространен на бесконечный промежуток, а другой – на конечный. Очень часто приходится переставлять интегралы, взятые в бесконечных промежутках по формуле .

Чаще всего такую перестановку сложно проделать.

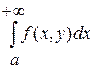Теоремы 2. Пусть функция неотрицательна и непрерывна при , , интегралы и 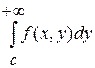(*) существуют и являются непрерывными функциями по переменным соответственно. Тогда, если существует один из интегралов, то существует и второй, причем они равны между собой.

Замечание.

Интегралы (*) будут заведомо интегрированы, если они равномерно сходятся по и соответственно.

Пример. Проинтегрируем функцию .

Имеем 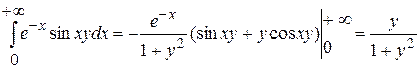. Все условия т. 2 п. 2 выполняются. Положим , где - любое конечное число. По теореме т. 1 п. 3

.

Следовательно, интегрируя обе части равенства по от 0 до , будем иметь

.

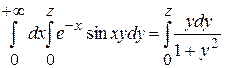Но 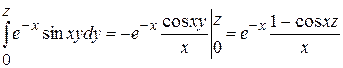(это равенство установлено для ; оно верно и при , если в этой точке понимать его в предельной). В том случае для любого конечного примет вид:

.

Пункт 4. Дифференцирование НИЗП по параметру

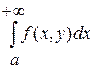Теорема 1. Пусть функция определена и непрерывна по на промежутке , . Она имеет там непрерывную частную производную , интеграл сходится при каждом на , а сходится равномерно. Тогда справедлива формула

. (*)

Доказательство.

Так как непрерывна и сходится равномерно относительно на , то для нее, в силу т. 3 п. 3, выполняется формула (1) пункта 3. Заменим в формуле (1) и получим:

Откуда 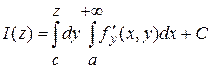. Производная правой части последнего равенства существует и равна , значит существует производная и у левой части, причем . Это равенство установлено для , что выполняется формула (*).

Ч.т.д.