| Скачать .docx | Скачать .pdf |
Реферат: Решения к Сборнику заданий по высшей математике Кузнецова Л.А. - 2. Дифференцирование. Зад.17
Задача 17
. Найти производную ![]() -го порядка.
-го порядка.
17.1. ![]()
y'= eαx +αxeαx
y''= 2αeαx +α2 xeαx
y'''= 3α2 eαx +α3 xeαx
y( n ) = nαn -1 eαx +αn xeαx
17.2. ![]()
y'= 2cos2x-sin(x+1)
y''= -4sin2x-cos(x+1)
y'''= -8cos2x+sin(x+1)
y(n) = 2n sin(π/2+2x)+cos(π/2+x+1)
17.3. ![]()
y'= 7/5*5 √e7 x -1
y''= 49/25*5 √e7 x -1
y'''= 343/125*5 √e7 x -1
y( n ) = (7/5)n *5 √e7 x -1
17.4. 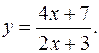
y'= -2/(2x+3)2
y''= 8/(2x+3)3
y'''= -48/(2x+3)4
y(n) = (-1)n 2n n!/(2x+3)n+1
17.5. ![]()
y'= 5lge
5x+2
y''= -25lge
(5x+2)2
y'''= 250lge
(5x+2)3
y(n) = (-1)n+1 5n (n-1)!lge , n≠1
(5x+2)n
17.6. ![]()
y'= 3lna*a3x
y''= 32 ln2 a*a3x
y'''= 33 ln3 a*a3x
y(n) = 3n lnn a*a3x
17.7. 
y'= 1/(3x+2)2
y''= -2/(3x+2)3
y'''= 54/(3x+2)4
y(n) = (-1)n+1 3n-1 n!
(3x+2)n+1
17.8. ![]()
y'= lge
x+4
y''= -lge_
(x+4)2
y'''= 2lge
(x+4)3
y(n) = (-1)n+1 (n-1)!lge , n≠1
(x+4)n
17.9. ![]()
y'= 1/(2√x)
y''= -1/(4√x)
y'''= 1/(8√x)
y(n) = 1/(2n √x)
17.10. 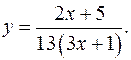
y'= 1/(3x+1)2
y''= -6/(3x+1)3
y'''= 54/(3x+1)4
y(n) = (-1)n+1 3n-1 n!/(3x+1)n+1
17.11. ![]()
y'= 3ln2*33x+5
y''= 32 ln2 2*33x+5
y'''= 33 ln3 2*33x+5
y(n) = 3n lnn 2*33x+5
17.12. ![]()
y'= cos(x+1)-2sin2x
y''= -sin(x+1)-4cos2x
y'''= -cos(x+1)+8sin2x
y(n) = sin(π/2+x+1)+2n cos(π/2+2x)
17.13. ![]()
y'= 2/3*3 √e2 x+ 1
y''= 4/9*3 √e2 x+ 1
y'''= 16/81*3 √e2 x+ 1
y(n) = (2/3)n *3 √e2 x +1
17.14. 
y'= -5/(5x+1)2
y''= 50/(5x+1)3
y'''= -750/(5x+1)4
y(n) = (-1)n+1 5n n!/(5x+1)n+1
17.15. ![]()
y'= 3lge
3x+1
y''= -9lge
(3x+1)2
y'''= 54lge
(3x+1)3
y(n) = (-1)n+1 3n (n-1)!lge , n≠1
(3x+1)n
17.16. ![]()
y'= 5ln5*75x
y''= 52 ln2 5*75x
y'''= 53 ln3 5*75x
y(n) = 5n lnn 5*75x
17.17. 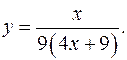
y'= 1/(4x+9)2
y''= -8/(4x+9)3
y'''= 96/(4x+9)4
y(n) = (-1)n+1 4n-1 n!/(4x+9)n+1
17.18. ![]()
y'= lge
x+1
y''= -lge_
(x+1)2
y'''= 2lge
(x+1)3
y(n) = (-1)n+1 (n-1)!lge , n≠1
(x+1)n
17.19. 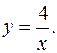
y'= -4/x2
y''= 8/x3
y'''= -24/x4
y(n) = (-1)n 4n!/xn-1
17.20. 
y'= 1/(2x+3)2
y''= -4/(2x+3)3
y'''= 24/(2x+3)4
y(n) = (-1)n+1 2n-1 n!/(2x+3)n+1
17.21. ![]()
y'= 2lna*a2x+3
y''= 22 ln2 a*a2x+3
y'''= 23 ln3 a*a2x+3
y(n) = 2n lnn a*a2x+3
17.22. ![]()
y'= 3cos(3x+1)-5sin5x
y''= -9sin(3x+1)-25cos5x
y'''= -27cos(3x+1)+125sin5x
y(n) = 3n sin(π/2+3x+1)+5n cos(π/2+5x)
17.23. ![]()
y'= 3/2*√e3x+1
y''= (3/2)2 *√e3x+1
y'''= (3/2)3 *√e3x+1
y(n) = (3/2)n *√e3x+1
17.24. 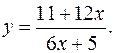
y'= -6/(6x+5)2
y''= 36/(6x+5)3
y'''= 216/(6x+5)4
y(n) = (-1)n 6n /(6x+5)n+1
17.25. ![]()
y'= 2lge
2x+7
y''= -4lge
(2x+7)2
y'''= 16lge
(2x+7)3
y(n) = (-1)n+1 2n (n-1)!lge , n≠1
(2x+7)n
17.26. ![]()
y'= kln2*2kx
y''= k2 ln2 2*2kx
y'''= k3 ln3 2*2kx
y(n) = kn lnn 2*2kx
17.27. 
y'= 1/(x+1)2
y''= -2/(x+1)3
y'''= 6/(x+1)4
y(n) = (-1)n+1 n!/(x+1)n+1
17.28. ![]()
y'= 1/((x+5)ln3)
y''= -1/(x+5)2
y'''= 2/(x+5)3
y(n) = (-1)n+1 (n-1)!/(x+5)n
17.29. 
y'= 2/(1-x)2
y''= -4/(1-x)3
y'''= 12/(1-x)4
y(n) = (-1)n+1 2!/(1-x)n+1
17.30. 
y'= 1/(4x+3)2
y''= -2/(4x+3)3
y'''= 6/(4x+3)4
y(n) = (-1)n+1 n!/(4x+3)n+1
17.31. ![]()
y'= 2ln3*32x+5
y''= 22 ln2 3*32x+5
y'''= 23 ln3 3*32x+5
y(n) = 2n lnn 3*32x+5