| Скачать .docx | Скачать .pdf |
Реферат: Исследование экономико-математических моделей
Задание 1
Значения цены, спроса и предложения на определенный вид товара приведены в таблице:
Цена Х |
Спрос У1 |
Предложение У2 |
| 8,6 | 2220 | 1101,93 |
| 9,6 | 1825 | 1102,93 |
| 10,6 | 1869 | 1252,93 |
| 11,6 | 1625 | 1286,93 |
| 12,6 | 1375 | 1328,93 |
| 13,6 | 1377 | 1411,93 |
| 14,6 | 1145 | 1573,93 |
| 15,6 | 1045 | 1620,93 |
| 16,6 | 1005 | 1748,93 |
| 17,6 | 1025 | 1838,93 |
| 18,6 | 795 | 1906,93 |
На основе статистических данных оценить параметры регрессии спроса и предложения на цену, если допустит, что стохастическая зависимость между спросом и ценой можно описать квадратичной функцией, а предложением и ценой – линейной функцией.
Оценить адекватность эконометрических моделей статистическим данным с надежностью Р=0.95 и найти:
– точку равновесной цены: 1) графически, 2) аналитически, развязав уравнение У1=У2, 3) с помощью «паутинообразной» модели с точностью 0,01, предварительно проверив сходимость этого итерационного метода; 4) с помощью процедуры «Подбор параметра». Сравнить результаты, полученные всеми способами;
– значение коэффициента эластичности спроса и предложения в точке равновесия.
Построить доверительные зоны регрессий спроса и предложения.
Сделать выводы.
Супермаркет |
Х |
Y |
X? |
Y? |
XY |
| 20 | 340 | 3 | 115600 | 9 | 1020 |
? |
5084 | 38 | 1349608 | 77,3 | 9899,9 |
?/n |
254,2 | 1,9 | 67460,4 | 3,865 | 495 |
Начнем с того, что найдем уравнение регрессии. Для этого найдем:
Значение дисперсии.
Для этого нам понадобится средняя арифметическая простая, которая находится по формуле: Хср=?Х/n Хср= 149,6/11=13,6?2ср=??2/n?ср= 16175,27/11=1470,5
Теперь найдем значение дисперсии по формуле Dх?=?Х?/n – (х)? Dy?=?y?/n – (y)
Dх?= 194,96–13,6?=10 D?y=2236173,39–1470,48?=73865,5
S=vD Sx=v10=3,2 Sy=v73865,5=271,8
Теперь найдем коэффициент корреляции (вон показывает степень тесноты связи Х и?). Численное значение коэффициента корреляции количественно измеряет тесноту корреляционной связи. Чем больше коэффициент корреляции тем плотнее точки корреляционного поля прилегают к линии регрессии. Знак коэффициента корреляции отражает характер влияния Х и?.
r=?X?/n-?ср*Xср/Sx*Sy r=0,99
В нашем случае очень сильная теснота корреляционной связи между ценой и предложением. Это значит, что 99% изменения предложения объясняется изменением цены.
Теперь вычислим коэффициент регрессии.
Вон определяется по формуле: b1= r*(Sy/Sx) b1=0,99* (271,8/3,2)=85,182
B0=?ср-b*Xср b0=1470,5–85,182*13,6=312,01
Уравнение регрессии будет иметь следующий вид:
У=b1х+b0=85,182x + 312,01
Строим точечную диаграмму по выходным данным Y( ). С помощью функции «Добавит линию тренда» строим линейный тип линии тренда (рис. 3.1). При этом включаем опцию вывода уравнения линии тренда и коэффициента детерминации R2.
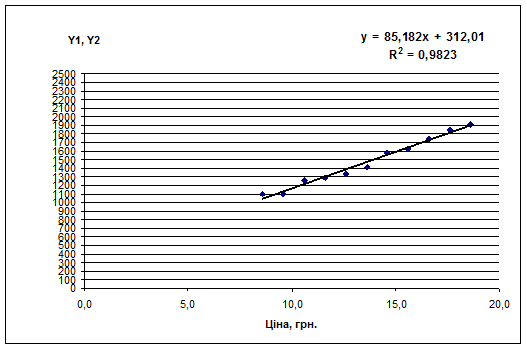
Рис. 1.1.
Получили линейное уравнение регрессии
У=b1х+b0=85,182x + 312,01.
Уравнение линейной регрессии появилось на графике таким способом:
- После построения в MS Excel обычной точечной диаграммы за диапазонами Х и В с помощью мастера диаграмм (вкладка Стандартные / Точечная), выделяем ряд построенных точек правой кнопкой мыши, и в появившемся контекстном меню изберем команду (Добавит линию тренда).
- Тип линии тренда выберем Линейная, а на вкладке Параметры ставим галочке напротив полей Показывать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации R2 (то есть коэффициент детерминации R2). Таким образом, построен точечный график функции В(Х) в виде корреляционного поля и к нему прибавлена линия линейного тренда. Дальше в работе избирал соответствующий тип линии тренда аналогично выстраиваются нелинейные тренды.
Выборочный коэффициент детерминации равняется R2 = 0,99813, а коэффициент корреляции составляет r = v0,9813 = 0,9911.
С помощью функции СРЗНАЧ определим средние значения величин: Xcp = 13,6, Y2cp = 1470,5. Тогда определим средний коэффициент эластичности для этой модели:
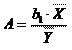 , A = 85,182*13,6/1470,5 = 0,78
, A = 85,182*13,6/1470,5 = 0,78
то есть при росте показателя на 1% показатель Y растет на 0,78%.
Вычислим теоретические значения зависимой переменной. Средняя погрешность аппроксимации MAPE, которая характеризует точность аппроксимации выборки построенным уравнениям регрессии находится по формуле
MAPE =.
Объясним, как рассчитывается средняя погрешность аппроксимации MAPE при построении уравнения линейной регрессии (таблица 3.1).
Таблица 3.1
B |
C |
D |
E |
F |
| 1 | Y2 |
X |
Y^ |
100*|Y-Y^|/Y |
| 2 | 1101,93 | 8,6 | 1044,570 | 5,21 |
| 3 | 1102,93 | 9,6 | 1129,752 | 2,43 |
| 4 | 1252,93 | 10,6 | 1214,933 | 3,03 |
| 5 | 1286,93 | 11,6 | 1300,115 | 1,02 |
| 6 | 1328,93 | 12,6 | 1385,297 | 4,24 |
| 7 | 1411,93 | 13,6 | 1470,479 | 4,15 |
| 8 | 1573,93 | 14,6 | 1555,661 | 1,16 |
| 9 | 1620,93 | 15,6 | 1640,842 | 1,23 |
| 10 | 1748,93 | 16,6 | 1726,024 | 1,31 |
| 11 | 1838,93 | 17,6 | 1811,206 | 1,51 |
| 12 | 1906,93 | 18,6 | 1896,388 | 0,55 |
| 13 | 1470,479 | 13,6 | MAPE= |
2,35 |
Столбец Е (Y^) рассчитывается путем подставления соответствующего Хt из диапазона С2:С13 то есть (0,65:0,89) в формулу линейной регрессии У=b1х+b0=85,182x + 312,01. То есть Y^ – это точки, что принадлежат линии тренда (точки на прямой, которая является линией тренда). Диапазон F2:F13 рассчитывается соответственно за формулой 100*|Y-Y^|/Y – это значения, которые стоят под знаком?, а следу значения MAPE – это среднее значение столбца диапазона F2:F13. Для выразительности наведем таблицу 3.1 в режиме формул (таблица 3.2).
Таблица 3.2
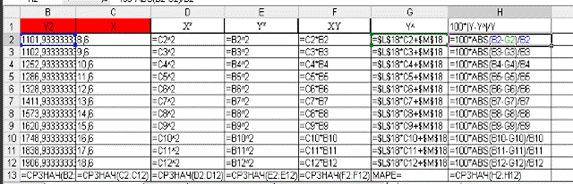
Таким образом, используя функции Excel, получим, что для этой регрессии MAPE = 2,35% – значение в амбарчике H13. Дальше, при расчете MAPE нелинейной функции регрессии будем использовать данный алгоритм.
Проверим линейную модель на адекватность с помощью критерия Фишера. Определим наблюдаемое значение критерия
![]() .
.
Табличное значение критерия при надежности Р=0,95 и степенях свободы k1 = 1, k2 = n – 2 = 9 равняется 5,12, поскольку наблюдаемое значение больше критического, то эта линейная модель является адекватной.
Используя t-статистику, с надежностью Р=0,95 оценим значимость коэффициента корреляции. Вычислим наблюдаемое значение t-статистики
![]() .
.
Табличное значение -критерия при и количества степеней свободы n – 2 = 10, tтабл = 2,26. Поскольку расчетное значение -критерію больше табличного, то линейный коэффициент корреляции является статистически значимым.
С помощью функции ЛИНЕЙН найдем стандартные погрешности параметров (вторая строка результатов): S(b0)= 53,2; S(b1)= 3,8. (Таблица 1.3)
Таблица 1.3
| ЛИНИЙ | ||
| b1, b0 | 85,18181818 | 312,006061 |
S1, S0 |
3,809489866 | 53,1911746 |
| 0,982317878 | 39,9542668 | |
| 499,9886736 | 9 | |
| 798153,6364 | 14367,0909 | |
Вычислим t-статистики:
![]() ;
; 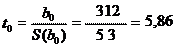 .
.
Поскольку первое и второе значение больше табличного, то параметры уравнения регрессии есть значимыми с надежностью Р=0,95.
Построим квадратичную линию регрессии (квадратичный тренд), возведем расчеты к вспомогательной таблице 1.4.
Таблица 1.4
| Цена | Спрос | ||||||
| N | Х | У1 | t^2 | t^3 | t^4 | yt | Y*t^2 |
| 1 | 8,6 | 2220 | 74,0 | 636,1 | 5470,08 | 19092,00 | 164191,20 |
| 2 | 9,6 | 1825 | 92,2 | 884,7 | 8493,47 | 17520,00 | 168192,00 |
| 3 | 10,6 | 1869 | 112,4 | 1191,0 | 12624,77 | 19811,40 | 210000,84 |
| 4 | 11,6 | 1625 | 134,6 | 1560,9 | 18106,39 | 18850,00 | 218660,00 |
| 5 | 12,6 | 1375 | 158,8 | 2000,4 | 25204,74 | 17325,00 | 218295,00 |
| 6 | 13,6 | 1377 | 185,0 | 2515,5 | 34210,20 | 18727,20 | 254689,92 |
| 7 | 14,6 | 1145 | 213,2 | 3112,1 | 45437,19 | 16717,00 | 244068,20 |
| 8 | 15,6 | 1045 | 243,4 | 3796,4 | 59224,09 | 16302,00 | 254311,20 |
| 9 | 16,6 | 1005 | 275,6 | 4574,3 | 75933,31 | 16683,00 | 276937,80 |
| 10 | 17,6 | 1025 | 309,8 | 5451,8 | 95951,26 | 18040,00 | 317504,00 |
| 11 | 18,6 | 795 | 346,0 | 6434,9 | 119688,32 | 14787,00 | 275038,20 |
| ? | 149,6 | 15306,0 | 2144,6 | 32158,0 | 500343,8 | 193854,6 | 2601888,4 |
По данным таблицы система имеет вид:
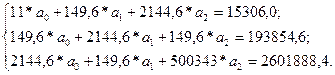
Развязав эту систему методом Гауса, одержимо такие значения коэффициентов кривой тренда: a0 = 103,167; a1 = 0,919; a2 = 0,0045.
Таким образом, уравнение параболы, которая является моделью тренда, имеет вид:
Y1x = 4583,9 – 351,37*x + 4583,9*x2
Построим оба ряду на одном корреляционном поле (рис. 1.2)
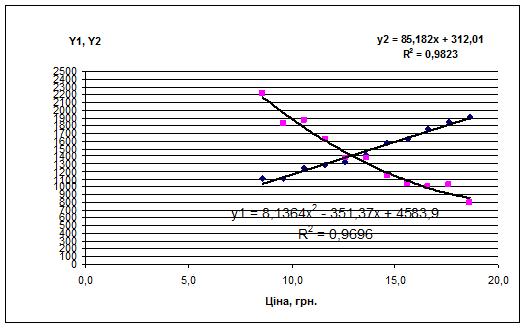
Рис. 1.2.
Коэффициент детерминации очень большой 0,9696 – связь очень сильная. Коэффициент кореляции также очень большой 0,9847 – модель адекватная.
Найдем точку равновесной цены.
Графически – Х = 12,9; В = 1409.
Паутинообразным методом: Х = 12,871; В = 1408,40. (рис. 1.3):
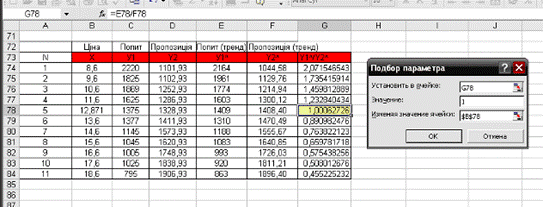
Рис. 1.3.
Методом Поиска решения (рис. 1.4, рис. 1.5):
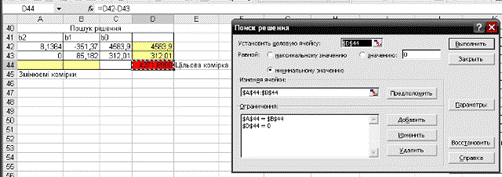
Рис. 1.4.
| Поиск решения | |||
| b | b1 | b0 | |
| 8,1364 | -351,37 | 4583,9 | 1408,73517 |
| 0 | 85,182 | 312,01 | 1408,73517 |
| 12,87508118 | 12,87508 | 0,0000000 | Целевой амбарчик |
| Зминюеми амбарчика | |||
Рис. 1.5.
Методом Поиска решения: Х = 12,875; В = 1408,735.
За 3-я методами видим, что 3-й метод – метод Поиска решения точнее всего, то есть точка равновесия имеет координаты Х = 12,875; В = 1408,735.
Построим точечную графику статистических данных, линии регрессии и ее доверительной зоны.
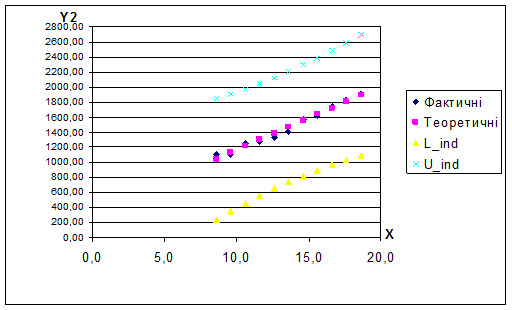
Рис. 1.6.
Выводы
1. В результате расчетов получены модели Y1 = 8,1364X2 – 351,37Х +4583,9 и Y2 = 85,182X + 312,01. Анализируя параметры моделей возможно сделать следующие выводы, что поскольку коэффициент регрессии положительный b1, то это свидетельствует о том, что направление связи между X и Y прямой, то есть при росте Х значения Y тоже будут увеличиваться, и наоборот поскольку коэффициент регрессии відємний b1, то это свидетельствует о том, что направление связи между X и Y обратной, то есть при росте Х значения Y будут понижаться.
2. Линейный коэффициент корреляции 0,9911 и коэффициент детерминации R2=0,9823. Значение коэффициенту корреляции свидетельствует о том, что между факторами существует очень сильная прямая связь. Значение коэффициенту детерминации показывает, что на 98,23% вариация Y2 зависит от X и на 1,77% от факторов, которые не вошли в модель.
3. Расчеты за критерием Фишера F=499 и Fкр.=5,11 подтвердили адекватность модели данным задачи.
4. По критерию Стьюдента, была проведенная проверка значимости параметров модели с надежностью 95%. Поскольку первое значение t – статистики больше, чем критическое значение, то можно сделать вывод, что полученные параметры являются значимыми и для генеральной совокупности параметры уравнения линии регрессии отличаются от 0.
6. По критерию Стьюдента была проведенная проверка значимости линейного коэффициента корреляции с надежностью 95%. Поскольку значение tr – статистики больше, чем критическое значение, то можно сделать вывод, что в генеральной совокупности между факторами существует связь, то есть и коэффициент регрессии статистически значим и модель является адекватной.
Задание №2
Производственная фирма выпускает продукцию с применением труда рабочих и основных средств производства.
Х1 (основные средства предприятия) |
Х2 | В (объем выпущенной продукции) |
| 50+N | 90+K | 152+10*N/K |
| 60+N | 100+K | 172+10*N/K |
| 70+N | 110+K | 192+10*N/K |
| 80+N | 120+K | 213+10*N/K |
| 90+N | 130+K | 232+10*N/K |
| 100+N | 140+K | 253+10*N/K |
| 110+N | 150+K | 275+10*N/K |
| 120+N | 160+K | 293+10*N/K |
| 130+N | 170+K | 314+10*N/K |
| 140+N | 180+K | 334+10*N/K |
| 150+N | 190+K | 354+10*N/K |
Построить производственную мультипликативную регрессию, оценив ее параметры.
Проверить адекватность построенной модели выходным данным.
Сделать экономический анализ параметров производственной функции.
Определить прогнозное значение выпуска при.
Построить интервал доверия прогноза с надежностью 0,95.
Оценить эффективность и масштаб производства.
На основе построенной регрессии развязать задачу оптимального выпуска продукции: определить, какая комбинация факторов производства является оптимальной, а также найти максимальный объем выпуска, если на расходы производства существует ограничение в 160 тыс. грн., стоимость аренды единицы фондов составляет (4+K) тыс. грн., стоимость труда одного человека – (1+K) тыс. грн.
Построить изокванту максимального выпуска и изокосту. Найти графическое решение задачи о комбинации ресурсов и сравнить с аналитическим.
Определить предельную норму замены единицы фондов трудом.
Производственная фирма выпускает продукцию согласно варианта 14 с применением труда рабочих и основных средств производства (табл. 2.1).
Таблица 2.1
В |
Х1 |
Х2 |
| 292 | 64 | 91 |
| 312 | 74 | 101 |
| 332 | 84 | 111 |
| 353 | 94 | 121 |
| 372 | 104 | 131 |
| 393 | 114 | 141 |
| 415 | 124 | 151 |
| 433 | 134 | 161 |
| 454 | 144 | 171 |
| 474 | 154 | 181 |
| 494 | 164 | 191 |
Найдем точечные оценки параметров множественной линейной регрессии с помощью функции Excel ЛИНЕЙН.
Но согласно этого задания связь в модели полный функциональный R2 = 1, R = 1, коэффициенты детерминации и корреляции равняются 1 (также и в модели множественной линейной регрессии) – нет смысла бедствовать множественную линейную регрессию (рис. 2.1)
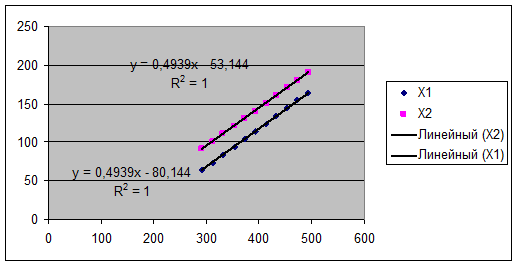
Рис. 2.1.
Задание №3 (оценивается в 10 баллов)
Значения объемов производства некоторой фирмы и соответствующих расходов производства приведены в таблице:
| Объем производства Y | Расходы производства C | Цена p. |
| 20+N/5 | 190+N-K | 16 |
| 30+N/5 | 210+N-K | 16 |
| 25+N/5 | 100+N-K | 14 |
| 35+N/5 | 230+N-K | 14 |
| 40+N/5 | 240+N-K | 13 |
| 50+N/5 | 400+N-K | 12 |
| 60+N/5 | 375+N-K | 15 |
| 55+N/5 | 330+N-K | 12 |
| 55+N/5 | 280+N-K | 12 |
| 70+N/5 | 470+N-K | 13 |
| 65+N/5 | 400+N-K | 13 |
| 75+N/5 | 550+N-K | 12 |
| 70+N/5 | 600+N-K | 12 |
Построить квадратичную зависимость расходов производства от объемов производства и оценить статистическое качество модели, что построено.
1. Для условий совершенной рыночной конкуренции (если значение цены на продукцию фирмы) необходимо сделать следующее:
Построить функции маржинальных расходов и дохода и построить их графику. Графически определить оптимальный объем производства.
Аналитически определить оптимальный объем производства фирмы, за которого прибыль фирмы будет максимальной, и определить соответствующий данному объему производства прибыль. Определить объем производства, за которого прибыль фирмы будет неотъемлемой.
2. Для условий монополии фирмы на рынке (значение цены на продукцию фирмы для этого случая приведено в таблице) необходимо сделать следующее:
Построить линейную зависимость цены от объемов производства и оценить статистическое качество модели, что построено.
Построить функции маржинальных расходов и дохода и построить их графику. Графически определить оптимальный объем производства.
Аналитически определить оптимальный объем производства фирмы, за которого прибыль фирмы будет максимальной, и определить соответствующий данному объему производства прибыль. Определить объем производства, за которого прибыль фирмы будет неотъемлемой.
Проанализировать и описать полученные результаты.
Расчетная таблица для варианта 14 выглядит следующим образом:
| Объем производства Y | Расходы производства C | Цена, р |
| 22,8 | 203 | 16 |
| 32,8 | 223 | 16 |
| 27,8 | 113 | 14 |
| 37,8 | 243 | 14 |
| 42,8 | 253 | 13 |
| 52,8 | 413 | 12 |
| 62,8 | 388 | 15 |
| 57,8 | 343 | 12 |
| 57,8 | 293 | 12 |
| 72,8 | 483 | 13 |
| 67,8 | 413 | 13 |
| 77,8 | 563 | 12 |
| 72,8 | 613 | 12 |
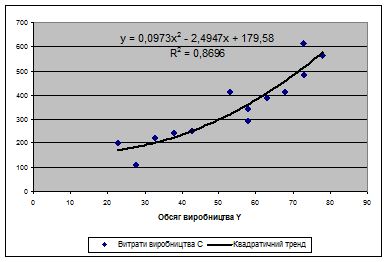
Корреляционное поле с линией квадратичного тренда (рис. 3.1):
Рис. 3.1.
Уравнение квадратичного тренда: в = 0,0973х2 – 2,4947х + 179,58.
R = vR2 = v0,8696 = 0,932523 – сильная корреляция.
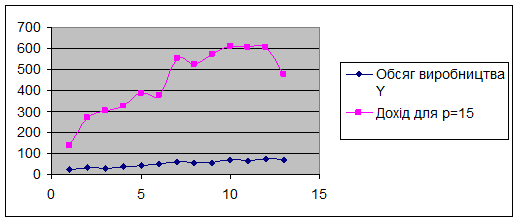
График объемов производства и доходов (рис. 3.2):
Рис. 3.2.
Следу, оптимальный объем производства №1 = 22,8 – минимальная расходная маржа.
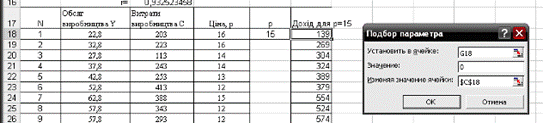
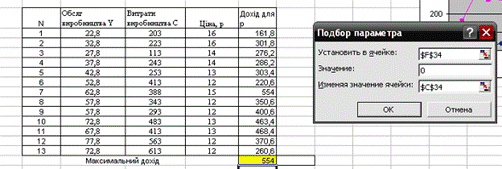
Определим доход (рис. 3.3)
Рис. 3.3.
| N | Объем производства Y | Расходы производства C | Цена, р |
р |
Доход для р=15 |
| 1 | 13,53333333 | 203 | 16 | 15 | 0 |
Доход (прибыль) будет при объеме производства В = 13,5333.
N |
Объем производства Y | Расходы производства C | Цена, р |
р |
Доход для р=15 |
| 1 | 13,53333333 | 203 | 16 | 15 | 0 |
| 2 | 32,8 | 223 | 16 | 269 | |
| 3 | 27,8 | 113 | 14 | 304 | |
| 4 | 37,8 | 243 | 14 | 324 | |
| 5 | 42,8 | 253 | 13 | 389 | |
| 6 | 52,8 | 413 | 12 | 379 | |
| 7 | 62,8 | 388 | 15 | 554 | |
| 8 | 57,8 | 343 | 12 | 524 | |
| 9 | 57,8 | 293 | 12 | 574 | |
| 10 | 72,8 | 483 | 13 | 609 | |
| 11 | 67,8 | 413 | 13 | 604 | |
| 12 | 77,8 | 563 | 12 | 604 | |
| 13 | 72,8 | 613 | 12 | 479 | |
| Максимальный доход | 609 | ||||
Максимальный доход будет при объеме производства 72,8.
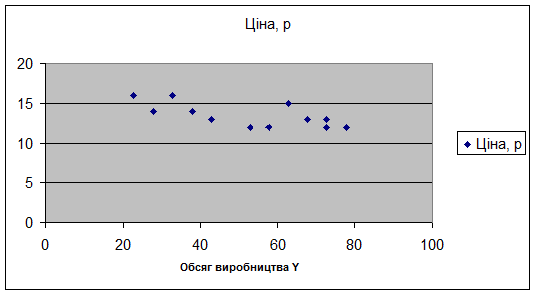
Зависимость цен от объема производства (рис. 3.4.)
Рис. 3.4.
Графика объемов производства и доходов для цен р (рис. 3.5).
Рис. 3.5.
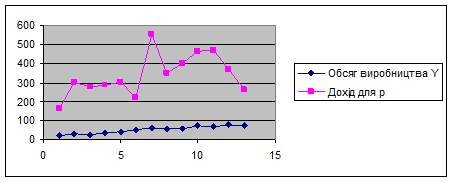
Максимальный доход 554 при объему производства 62,8 (рис. 3.6).
N |
Объем производства Y | Расходы производства C | Цена, р |
Доход для р=15 |
Доход для р |
| 1 | 13,53333333 | 203 | 16 | 0 | 161,8 |
| 2 | 32,8 | 223 | 16 | 269 | 301,8 |
| 3 | 27,8 | 113 | 14 | 304 | 276,2 |
| 4 | 37,8 | 243 | 14 | 324 | 286,2 |
| 5 | 42,8 | 253 | 13 | 389 | 303,4 |
| 6 | 52,8 | 413 | 12 | 379 | 220,6 |
| 7 | 62,8 | 388 | 15 | 554 | 554 |
| 8 | 57,8 | 343 | 12 | 524 | 350,6 |
| 9 | 57,8 | 293 | 12 | 574 | 400,6 |
| 10 | 72,8 | 483 | 13 | 609 | 463,4 |
| 11 | 67,8 | 413 | 13 | 604 | 468,4 |
| 12 | 77,8 | 563 | 12 | 604 | 370,6 |
| 13 | 72,8 | 613 | 12 | 479 | 260,6 |
Максимальный доход |
609 | 554 | |||
Рис. 3.6.
Неотъемлемый доход для второго варианта при объеме производства Y=12, 68 (рис. 3.7 и 3.8).
Рис. 3.7.
N |
Объем производства Y | Расходы производства C | Цена, р |
Доход для р |
| 1 | 12,6875 | 203 | 16 | 0 |
Рис. 3.8.
Список использованной литературы
1. Кулинич О.И. Економетрия: Практикум. – Хм.: Издательство «Подилля», 1998 – 157 с.
2. Лук’яненко И.Г., Красникова Л.И. Економетрика: Учебник. – К.: Общество «Знания», КОО, 1998 – 494 с.
3. Наконечный С.И., Терещенко Т.О., Романюк Т.п. Економетрия: Учебник. – Вид. 2-ге, допов. но перероб. – К.: КНЕУ, 2000 – 296 с.
4. Толбатов Ю.А. Економетрика: Учебник для студентов экономических специальностей высших учебных заведений. – К.: Четвертая волна, 1997 – 320 с.
5. Гливенко С.В., Соколов М.О., Телиженко О.М. Экономическое прогнозирование: Навч. пособие. – Сумы, ВТД «Университетская книга», 2004. – 207 с.
6. Грабовецкий Б.Е. Экономическое прогнозирование и планирование: Навч. пособие. – К.: Центр учебной литературы, 2003. – 188 с.
7. Ерина А.М., Кальян З.О. Теория статистики: Практикум. – К.: КНЕУ, 1997. – с. 187–190.
8. Гусаров В.М. Теория статистики: Учебн. пособие для вузов. – М., 1998. – с. 143–155.
9. Статистика: Учебник / С.С. Герасименко но др. – К., 1998. – с. 138–144.