| Скачать .docx | Скачать .pdf |
Дипломная работа: Топологическая определяемость верхних полурешёток
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Вятский государственный гуманитарный университет
Математический факультет
Кафедра алгебры и геометрии
Выпускная квалификационная работа
Топологическая определяемость верхних полурешёток.
Выполнил:
студент V курса математического факультета
Малых Константин Леонидович
Научный руководитель:
кандидат физико-математических наук, доцент кафедры алгебры и геометрии В.В. Чермных
Рецензент:
доктор физико-математических наук, профессор, заведующий кафедрой алгебры и геометрии Е.М. Вечтомов
Допущена к защите в государственной аттестационной комиссии
«___» __________2005 г. Зав. Кафедрой Е.М. Вечтомов
«___»___________2005 г. Декан факультета В.И. Варанкина
Киров 2005
Оглавление.
Введение …………………………………………………………………стр. 3
Глава 1 ……………………………………………………………………стр. 4
1. Упорядоченные множества ………………………………………стр. 4
2. Решётки.……………………………………………………………стр. 5
3. Дистрибутивные решётки ………………………………………..стр. 8
4. Топологические пространства……………………………………стр.10
Глава 2…………………………………………………………………….стр.11
1. Верхние полурешётки…………………………………………….стр.11
2. Стоуново пространство …………………………………………..стр.15
Список литературы……………………………………………………….стр.21
Введение.
Дистрибутивная решётка является одним из основных алгебраических объектов. В данной работе рассматривается частично упорядоченное множество P ( L ) простых идеалов. Оно даёт нам много информации о дистрибутивной решётке L , но оно не может её полностью охарактеризовать. Поэтому, для того, чтобы множество P ( L ) характеризовало решётку L , необходимо наделить его более сложной структурой. Стоун [1937] задал на множестве P ( L ) топологию.
В этой работе рассматривается этот метод в несколько более общем виде.
Работа состоит из двух глав. В первой главе вводятся начальные понятия, необходимые для изучения данной темы. Во второй главе рассматриваются верхние полурешётки, а также множество простых идеалов с введенной на нём топологией.
Глава 1.
1. Упорядоченные множества.
Определение
:
Упорядоченным множеством
![]() называется непустое множество, на котором определено бинарное отношение
называется непустое множество, на котором определено бинарное отношение ![]() , удовлетворяющее для всех
, удовлетворяющее для всех ![]() следующим условиям:
следующим условиям:
1.Рефлексивность: ![]() .
.
2.Антисимметричность: если ![]() и
и ![]() , то
, то ![]() .
.
3.Транзитивность: если ![]() и
и ![]() , то
, то ![]() .
.
Если ![]() и
и ![]() , то говорят, что
, то говорят, что ![]() меньше
меньше ![]() или
или ![]() больше
больше ![]() , и пишут
, и пишут ![]() или
или ![]() .
.
Примеры упорядоченных множеств:
1. Множество целых положительных чисел, а ![]() означает, что
означает, что ![]() делит
делит ![]() .
.
2. Множество всех действительных функций ![]() на отрезке
на отрезке ![]() и
и
![]() означает, что
означает, что ![]() для
для ![]() .
.
Определение:
Цепью
называется упорядоченное множество, на котором для ![]() имеет место
имеет место ![]() или
или ![]() .
.
Используя отношение порядка, можно получить графическое представление любого конечного упорядоченного множества ![]() . Изобразим каждый элемент множества
. Изобразим каждый элемент множества ![]() в виде небольшого кружка, располагая
в виде небольшого кружка, располагая ![]() выше
выше ![]() , если
, если ![]() . Соединим
. Соединим ![]() и
и ![]() отрезком. Полученная фигура называется диаграммой
упорядоченного множества
отрезком. Полученная фигура называется диаграммой
упорядоченного множества ![]() .
.
Примеры диаграмм упорядоченных множеств:
2. Решётки
Определение:
Верхней гранью
подмножества ![]() в упорядоченном множестве
в упорядоченном множестве ![]() называется элемент
называется элемент ![]() из
из ![]() , больший или равный всех
, больший или равный всех ![]() из
из ![]() .
.
Определение:
Точная верхняя грань
подмножества ![]() упорядоченного множества
упорядоченного множества ![]() – это такая его верхняя грань, которая меньше любой другой его верхней грани. Обозначается символом
– это такая его верхняя грань, которая меньше любой другой его верхней грани. Обозначается символом ![]() и читается «супремум X».
и читается «супремум X».
Согласно аксиоме антисимметричности упорядоченного множества, если точная верхняя грань существует, то она единственна.
Понятия нижней грани и точной нижней грани (которая обозначается ![]() и читается «инфинум») определяются двойственно. Также, согласно аксиоме антисимметричности упорядоченного множества, если точная нижняя грань
и читается «инфинум») определяются двойственно. Также, согласно аксиоме антисимметричности упорядоченного множества, если точная нижняя грань ![]() существует, то она единственна.
существует, то она единственна.
Определение:
Решёткой
![]() называется упорядоченное множество
называется упорядоченное множество ![]() , в котором любые два элемента
, в котором любые два элемента ![]() и
и ![]() имеют точную нижнюю грань, обозначаемую
имеют точную нижнюю грань, обозначаемую ![]() , и точную верхнюю грань, обозначаемую
, и точную верхнюю грань, обозначаемую ![]() .
.
Примеры решёток:
1. Любая цепь является решёткой, т.к. ![]() совпадает с меньшим, а
совпадает с меньшим, а ![]() с большим из элементов
с большим из элементов ![]() .
.
2.
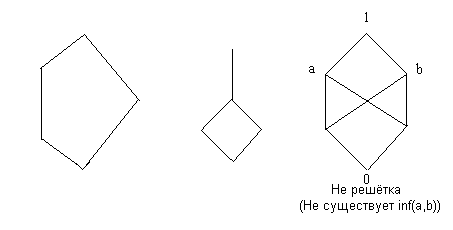
Наибольший элемент, то есть элемент, больший или равный каждого элемента упорядоченного множества, обозначают ![]() , а наименьший элемент, то есть меньший или равный каждого элемента упорядоченного множества, обозначают
, а наименьший элемент, то есть меньший или равный каждого элемента упорядоченного множества, обозначают ![]() .
.
На решётке можно рассматривать две бинарные операции:
![]() - сложение и
- сложение и
![]() - произведение
- произведение
Эти операции обладают следующими свойствами:
1. ![]() ,
, ![]() идемпотентность
идемпотентность
2. ![]() ,
, ![]() коммутативность
коммутативность
3. ![]() ,
,
![]() ассоциативность
ассоциативность
4. ![]() ,
,
![]() законы поглощения
законы поглощения
Теорема
. Пусть
![]() - множество с двумя бинарными операциями
- множество с двумя бинарными операциями ![]() , обладающими свойствами (1) – (4). Тогда отношение
, обладающими свойствами (1) – (4). Тогда отношение ![]() (или
(или ![]() ) является порядком на
) является порядком на
![]() , а возникающее упорядоченное множество оказывается решёткой, причём:
, а возникающее упорядоченное множество оказывается решёткой, причём:
![]()
![]()
Доказательство.
Рефлексивность отношения ![]() вытекает из свойства (1). Заметим, что оно является следствием свойства (4):
вытекает из свойства (1). Заметим, что оно является следствием свойства (4):
![]()
![]()
Если ![]() и
и ![]() , то есть
, то есть ![]() и
и ![]() , то в силу свойства (2), получим
, то в силу свойства (2), получим ![]() . Это означает, что отношение
. Это означает, что отношение ![]() антисимметрично.
антисимметрично.
Если ![]() и
и ![]() , то применяя свойство (3), получим:
, то применяя свойство (3), получим: ![]() , что доказывает транзитивность отношения
, что доказывает транзитивность отношения ![]() .
.
Применяя свойства (3), (1), (2), получим:
![]() ,
,
![]() .
.
Следовательно, ![]() и
и ![]()
Если ![]() и
и ![]() , то используя свойства (1) – (3), имеем:
, то используя свойства (1) – (3), имеем:
![]() , т.е.
, т.е. ![]()
По определению точней верхней грани убедимся, что
![]()
Из свойств (2), (4) вытекает, что ![]() и
и ![]()
Если ![]() и
и ![]() , то по свойствам (3), (4) получим:
, то по свойствам (3), (4) получим:
![]()
Отсюда по свойствам (2) и (4) следует, что
![]() , т.е.
, т.е.
Таким образом, ![]() . ■
. ■
Пусть ![]() решётка, тогда её наибольший элемент
решётка, тогда её наибольший элемент ![]() характеризуется одним из свойств:
характеризуется одним из свойств:
1.![]()
![]()
2.![]()
![]() .
.
Аналогично характеризуется наименьший элемент ![]() :
:
1.![]()
![]()
2.![]()
![]() .
.
3. Дистрибутивные решётки.
Определение:
Решётка ![]() называется дистрибутивной
, если для
называется дистрибутивной
, если для ![]() выполняется:
выполняется:
1. ![]()
2. ![]()
В любой решётке тождества (1) и (2) равносильны. Доказательство этого факта содержится в книге [1], стр. 24.
Теорема:
Решётка ![]() с 0 и 1 является дистрибутивной тогда и только тогда, когда она не содержит подрешёток вида
с 0 и 1 является дистрибутивной тогда и только тогда, когда она не содержит подрешёток вида
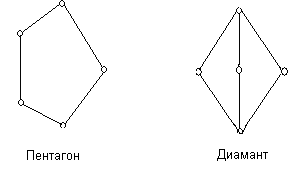
Доказательство этого факта можно найти в книге [2].
Далее под словом “решётка” понимается произвольная дистрибутивная решётка с 0 и 1 (причём ![]() ).
).
Определение:
Непустое множество ![]() называется идеалом
в решётке
называется идеалом
в решётке ![]() , если выполняются условия:
, если выполняются условия:
1. ![]()
2. ![]()
Определение:
Идеал ![]() в решётке
в решётке ![]() называется простым
, если
называется простым
, если
![]() или
или ![]() .
.
Идеал, порождённый множеством Н (т.е. наименьший идеал, содержащий H ), будет обозначаться (Н]. Если Н = { a } , то вместо ({ a }] будем писать ( a ] и называть ( a ] главным идеалом.
Обозначим через I ( L ) множество всех идеалов решётки L. I ( L ) будем называть решёткой идеалов.
Определение:
Решётки ![]()
![]() и
и ![]()
![]() называются изоморфными
(обозначение:
называются изоморфными
(обозначение: ![]() ), если существует взаимно однозначное отображение
), если существует взаимно однозначное отображение ![]() , называемое изоморфизмом,
множества
, называемое изоморфизмом,
множества ![]() на множество
на множество ![]() , такое, что
, такое, что
![]() ,
,
![]() .
.
4. Топологические пространства.
Определение:
Топологическое пространство
– это непустое множество ![]() с некоторой системой
с некоторой системой ![]() выделенных его подмножеств, которая удовлетворяет аксиомам:
выделенных его подмножеств, которая удовлетворяет аксиомам:
1. Пустое множество и само пространство ![]() принадлежит системе
принадлежит системе ![]() :
: ![]() .
.
2. Пересечение любого конечного числа множеств из ![]() принадлежит
принадлежит ![]() , т.е.
, т.е. ![]() .
.
3. Объединение любого семейства множеств из ![]() принадлежит
принадлежит ![]() , т.е.
, т.е. ![]() .
.
Таким образом, топологическое пространство – это пара <![]() ,
, ![]() >, где
>, где ![]() - такое множество подмножеств в
- такое множество подмножеств в ![]() , что
, что ![]() и
и ![]() замкнуто относительно конечных пересечений и произвольных объединений. Множества из
замкнуто относительно конечных пересечений и произвольных объединений. Множества из ![]() называют открытыми, а их дополнения в
называют открытыми, а их дополнения в ![]() замкнутыми.
замкнутыми.
Определение: Пространство называется компактным , если в любом его открытом покрытии можно выбрать конечное подпокрытие.
Определение: Подмножество пространства называется компактным , если в любом его открытом покрытии можно выбрать конечное подпокрытие.
Определение:
Топологическое пространство называется ![]() - пространством
, если для любых двух различных его точек существует открытое множество, содержащее ровно одну из этих точек.
- пространством
, если для любых двух различных его точек существует открытое множество, содержащее ровно одну из этих точек.
Глава 2.
1. Верхние полурешётки.
Определение: Ч.у. множество называется верхней полурешёткой , если sup { a , b } существует для любых элементов a и b .
Определение:
Непустое множество I
верхней полурешётки L
называется идеалом
, если для любых ![]() включение
включение ![]() имеет место тогда и только тогда, когда
имеет место тогда и только тогда, когда ![]() .
.
Определение
: Верхняя полурешётка ![]() называется дистрибутивной
, если неравенство
называется дистрибутивной
, если неравенство ![]() ≤
≤ ![]()
![]() (
(![]() ,
, ![]() ,
, ![]() L) влечёт за собой существование элементов
L) влечёт за собой существование элементов ![]() , таких, что
, таких, что ![]() ,
, ![]() , и
, и ![]() =
= ![]() .(рис.1). Заметим, что элементы
.(рис.1). Заметим, что элементы ![]() и
и ![]() не обязательно единственны.
не обязательно единственны.
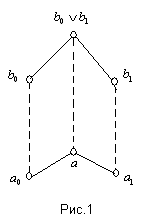
Некоторые простейшие свойства дистрибутивной верхней полурешётки даёт:
Лемма 1 :
(*). Если <![]() ,
,![]() > - произвольная полурешётка, то верхняя полурешётка
> - произвольная полурешётка, то верхняя полурешётка ![]() дистрибутивна тогда и только тогда, когда решётка
дистрибутивна тогда и только тогда, когда решётка ![]() дистрибутивна.
дистрибутивна.
(**). Если верхняя полурешётка ![]() дистрибутивна, то для любых
дистрибутивна, то для любых ![]() существует элемент
существует элемент ![]() , такой, что
, такой, что ![]() и
и ![]() . Следовательно, множество
. Следовательно, множество ![]() является решёткой.
является решёткой.
(***). Верхняя полурешётка ![]() дистрибутивна тогда и только тогда, когда множество
дистрибутивна тогда и только тогда, когда множество ![]() является дистрибутивной решёткой.
является дистрибутивной решёткой.
Доказательство.
(*). ![]() <
<![]() ,
,![]() > - дистрибутивна и
> - дистрибутивна и ![]() , то для элементов
, то для элементов ![]() ,
, ![]() , справедливо равенство
, справедливо равенство ![]() :
:
![]()
значит, полурешётка <![]() ,
,![]() > - дистрибутивна.
> - дистрибутивна.
![]()
![]() <
<![]() ,
,![]() > - дистрибутивна. Пусть решётка
> - дистрибутивна. Пусть решётка ![]() содержит диамант или пентагон (рис.2).
содержит диамант или пентагон (рис.2).
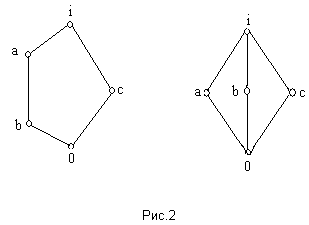
1) Пусть решётка ![]() содержит пентагон,
содержит пентагон, ![]() . Нужно найти такие элементы
. Нужно найти такие элементы ![]() и
и ![]() , чтобы выполнялось равенство
, чтобы выполнялось равенство ![]() . Но множество элементов меньших b
или c
состоит из элементов {0,
b
,
c
}
и их нижняя граница не даст a
.
Получили противоречие с тем, что <
. Но множество элементов меньших b
или c
состоит из элементов {0,
b
,
c
}
и их нижняя граница не даст a
.
Получили противоречие с тем, что <![]() ,
,![]() > - дистрибутивна. Значит, наше предположение неверно и решётка
> - дистрибутивна. Значит, наше предположение неверно и решётка ![]() не содержит пентагона.
не содержит пентагона.
2) Пусть решётка ![]() содержит диамант,
содержит диамант, ![]() . Аналогично, множество элементов меньших b
или c
состоит из элементов {0,
b
,
c
},
их нижняя граница не даст a
.
Значит, решётка
. Аналогично, множество элементов меньших b
или c
состоит из элементов {0,
b
,
c
},
их нижняя граница не даст a
.
Значит, решётка ![]() не содержит диаманта.
не содержит диаманта.
Можно сделать вывод, что решётка ![]() дистрибутивна.
дистрибутивна.
(**). Имеем ![]() , поэтому
, поэтому ![]() , где
, где ![]() (по определению дистрибутивной полурешётки). Кроме того,
(по определению дистрибутивной полурешётки). Кроме того, ![]() является нижней границей элементов
является нижней границей элементов ![]() и
и ![]() .
.
Рассмотрим идеалы, содержащие элемент ![]() и
и ![]() -
- ![]() и
и ![]() . Тогда
. Тогда ![]() Ø ,т.к.
Ø ,т.к. ![]() , нижняя граница элементов a
и b
, содержится там.
, нижняя граница элементов a
и b
, содержится там.
Покажем, что I ( L ) – решётка, т.е. существуют точные нижняя и верхняя грани для любых A и B .
Покажем, что ![]() совпадает с пересечением идеалов A
и B
.
Во-первых,
совпадает с пересечением идеалов A
и B
.
Во-первых, ![]() - идеал. Действительно,
- идеал. Действительно, ![]() и
и ![]() и
и ![]() Во-вторых, пусть идеал
Во-вторых, пусть идеал ![]() и
и ![]() . Тогда
. Тогда ![]() , т.е.
, т.е. ![]() - точная нижняя грань идеалов A
и B
,
т.е.
- точная нижняя грань идеалов A
и B
,
т.е. ![]() .
.
Теперь покажем, что ![]() совпадает с пересечением всех идеалов
совпадает с пересечением всех идеалов ![]() , содержащих A
и B
.
Обозначим
, содержащих A
и B
.
Обозначим ![]() . Поскольку
. Поскольку ![]() для
для ![]()
![]() для
для ![]()
![]() ,
то C
идеал. По определению C
он будет наименьшим идеалом, содержащим A
и B
.
,
то C
идеал. По определению C
он будет наименьшим идеалом, содержащим A
и B
.
(***). ![]() Пусть
Пусть ![]() – верхняя дистрибутивная полурешётка. Покажем, что
– верхняя дистрибутивная полурешётка. Покажем, что
![]() .
.
Пусть ![]() , т.е.
, т.е. ![]() (рис.3), для некоторых
(рис.3), для некоторых ![]()
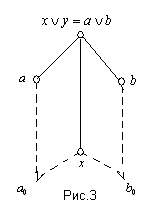
Понятно, что ![]() . По дистрибутивности, существуют
. По дистрибутивности, существуют ![]() такие, что
такие, что ![]() . Т.к. A
– идеал, то
. Т.к. A
– идеал, то ![]() , потому что
, потому что ![]() . Аналогично,
. Аналогично, ![]() . Т.е.
. Т.е. ![]() . Точно также,
. Точно также, ![]() . Если
. Если ![]() , то легко показать, что
, то легко показать, что ![]() .
.
Доказали, что ![]() - идеал. Очевидно, он является верхней гранью идеалов A
и B
.
Если C
содержит A
и B
, то C
будет содержать элементы
- идеал. Очевидно, он является верхней гранью идеалов A
и B
.
Если C
содержит A
и B
, то C
будет содержать элементы ![]() для любых
для любых ![]() , т.е.
, т.е. ![]() Поэтому
Поэтому ![]() , поскольку
, поскольку ![]() является верхней гранью идеалов A
и B
и содержится в любой верхней грани.
является верхней гранью идеалов A
и B
и содержится в любой верхней грани.
Теперь покажем, что выполняется равенство:
![]() .
.
![]() . Пусть
. Пусть ![]() , где
, где ![]() ,
,![]() . Т.к.
. Т.к. ![]() , то
, то ![]() , откуда
, откуда ![]() и следовательно
и следовательно ![]() . Аналогично,
. Аналогично, ![]() , значит,
, значит, ![]()
![]() . Пусть
. Пусть ![]() ,где
,где ![]()
![]()
![]()
![]()
![]() .
.
Отсюда следует дистрибутивность решётки ![]() .
.
![]()
![]() – дистрибутивная решётка,
– дистрибутивная решётка, ![]() . Теперь рассмотрим идеалы, образованные этими элементами:
. Теперь рассмотрим идеалы, образованные этими элементами:
![]()
(![]() ,будет нижней границей для
,будет нижней границей для ![]() ). Поэтому
). Поэтому ![]() , что и доказывает дистрибутивность полурешётки
, что и доказывает дистрибутивность полурешётки ![]() . ■
. ■
2. Стоуново пространство.
Определение
: Подмножество ![]() верхней полурешётки
верхней полурешётки ![]() называется коидеалом
, если
называется коидеалом
, если ![]() из неравенства
из неравенства ![]() следует
следует ![]() и
и ![]() существует нижняя граница
существует нижняя граница ![]() множества
множества ![]() , такая, что
, такая, что ![]() .
.
Определение:
Идеал ![]() полурешётки
полурешётки ![]() называется простым
, если
называется простым
, если ![]() и множество
и множество ![]() является коидеалом.
является коидеалом.
В дальнейшем нам потребуется лемма Цорна, являющаяся эквивалентным утверждением аксиоме выбора.
Лемма Цорна.
Пусть
A
– множество и
X
– непустое подмножество множества
P
(
A
). Предположим, что
X
обладает следующим свойством: если
C
– цепь в <![]() >, то
>, то ![]() . Тогда
X
обладает максимальным элементом.
. Тогда
X
обладает максимальным элементом.
Лемма 2
: Пусть ![]() – произвольный идеал и
– произвольный идеал и ![]() – непустой коидеал дистрибутивной верхней полурешётки
– непустой коидеал дистрибутивной верхней полурешётки ![]() . Если
. Если ![]() , то в полурешётке
, то в полурешётке ![]() существует простой идеал
существует простой идеал ![]() такой, что
такой, что ![]() и
и ![]() .
.
Доказательство.
Пусть X – множество всех идеалов в L , содержащих I и не пересекающихся с D . Покажем, что X удовлетворяет лемме Цорна.
Пусть C
–
произвольная цепь в X
и ![]() Если
Если ![]() , то
, то ![]() для некоторых
для некоторых ![]() Пусть для определённости
Пусть для определённости ![]() . Тогда
. Тогда ![]() и
и ![]() , т.к.
, т.к. ![]() - идеал. Поэтому
- идеал. Поэтому ![]() . Обратно, пусть
. Обратно, пусть ![]() , тогда
, тогда ![]() , для некоторого
, для некоторого ![]() Получаем
Получаем ![]() , откуда
, откуда ![]() .
.
Доказали, что M –
идеал, очевидно, содержащий I
и не пересекающийся с D
, т.е. ![]() . По лемме Цорна X
обладает максимальным элементом, т.е. максимальным идеалом P
среди содержащих I
и не пересекающихся с D
.
. По лемме Цорна X
обладает максимальным элементом, т.е. максимальным идеалом P
среди содержащих I
и не пересекающихся с D
.
Покажем, что P
– простой. Для этого достаточно доказать, что L
\
P
является коидеалом. Пусть ![]() L
\
P
и
L
\
P
и ![]() . Поскольку
. Поскольку ![]() , то
, то ![]() , иначе в противном случае
, иначе в противном случае ![]() по определению идеала. Следовательно,
по определению идеала. Следовательно, ![]() . Если
. Если ![]() , то
, то ![]() и
и ![]() пересекающихся с D
в силу максимальности P
.
Получаем
пересекающихся с D
в силу максимальности P
.
Получаем ![]() и
и ![]() для некоторых элементов
для некоторых элементов ![]() . Существует элемент
. Существует элемент ![]() такой, что
такой, что ![]() и
и ![]() , по определению коидеала, следовательно
, по определению коидеала, следовательно ![]() и
и ![]() для некоторых
для некоторых ![]() Заметим, что
Заметим, что ![]() и
и ![]() не лежат в P
,
т.к. в противном случае
не лежат в P
,
т.к. в противном случае ![]() .
.
Далее, ![]() , поэтому
, поэтому ![]() для некоторых
для некоторых ![]() и
и ![]() . Как и прежде
. Как и прежде ![]() . Кроме того
. Кроме того ![]() , поэтому
, поэтому ![]() - нижняя грань элементов a
и b
,
не лежащая в P
. ■
- нижняя грань элементов a
и b
,
не лежащая в P
. ■
В дальнейшем, через ![]() будем обозначать дистрибутивную верхнюю полурешётку с нулём, через
будем обозначать дистрибутивную верхнюю полурешётку с нулём, через ![]() множество всех простых идеалов полурешётки
множество всех простых идеалов полурешётки ![]() .
.
Множества вида ![]() представляют элементы полурешётки
представляют элементы полурешётки ![]() в ч.у. множестве
в ч.у. множестве ![]() (т.е.
(т.е. ![]() ). Сделаем все такие множества открытыми в некоторой топологии.
). Сделаем все такие множества открытыми в некоторой топологии.
Обозначим через ![]() топологическое пространство, определённое на множестве
топологическое пространство, определённое на множестве ![]() . Пространство SpecL
будем называть стоуновым пространством
полурешётки L
.
. Пространство SpecL
будем называть стоуновым пространством
полурешётки L
.
Лемма 3 : Для любого идеала I полурешётки L положим:
![]()
Тогда множества вида ![]() исчерпывают все открытые множества в стоуновом пространстве
SpecL
.
исчерпывают все открытые множества в стоуновом пространстве
SpecL
.
Доказательство.
Нужно проверить выполнение аксиом топологического пространства.
1) Рассмотрим идеал, образованный 0. Тогда
![]() ,
,
но 0 лежит в любом идеале, а значит ![]() .
.
2) Возьмём произвольные идеалы ![]() и
и ![]() полурешётки
полурешётки ![]() и рассмотрим
и рассмотрим
![]()
![]()
Пусть ![]() . Тогда существуют элементы a
. Тогда существуют элементы a![]() и
и ![]() Отсюда следует, что
Отсюда следует, что ![]() , где L
\
P
– коидеал. По определению коидеала существует элемент d
, где L
\
P
– коидеал. По определению коидеала существует элемент d![]() такой, что
такой, что ![]() и
и ![]() , значит,
, значит,![]() . Т.к.
. Т.к. ![]() , следовательно,
, следовательно, ![]() . Получаем, что
. Получаем, что ![]() .
.
Обратное включение очевидно.
2) Пусть ![]() - произвольное семейство идеалов. Через
- произвольное семейство идеалов. Через ![]() обозначим множество всех точных верхних граней конечного числа элементов, являющихся представителями семейства
обозначим множество всех точных верхних граней конечного числа элементов, являющихся представителями семейства ![]() . Покажем, что
. Покажем, что ![]() - идеал. Пусть
- идеал. Пусть ![]() , тогда
, тогда ![]() , где
, где ![]() для некоторого идеала
для некоторого идеала ![]() . Тогда
. Тогда ![]() лежит в идеале
лежит в идеале ![]() , следовательно,
, следовательно, ![]() и
и ![]() , т.е.
, т.е. ![]() . Обратно очевидно.
. Обратно очевидно.
Доказали, что ![]() - идеал. Теперь рассмотрим произвольное объединение.
- идеал. Теперь рассмотрим произвольное объединение.
![]() ■
■
Лемма 4
: Подмножества вида ![]() пространства
пространства ![]() можно охарактеризовать как компактные открытые множества.
можно охарактеризовать как компактные открытые множества.
Доказательство.
![]() Действительно, если семейство
Действительно, если семейство ![]() открытых множеств покрывает множество
открытых множеств покрывает множество ![]() , т.е.
, т.е. ![]()
![]() , то
, то ![]() Отсюда следует, что
Отсюда следует, что ![]() для некоторого конечного подмножества
для некоторого конечного подмножества ![]() , поэтому
, поэтому ![]()
![]() . Таким образом, множество
. Таким образом, множество ![]() компактно.
компактно.
![]() Пусть открытое множество r
(
I
)
компактно, тогда
Пусть открытое множество r
(
I
)
компактно, тогда ![]() и можно выделить конечное подпокрытие
и можно выделить конечное подпокрытие ![]() для некоторых
для некоторых ![]() .
.
Покажем, что I
порождается элементом ![]() .
.
Предположим, что это не так, и в идеале I
найдётся элемент b
не лежащий в ![]() . Тогда [
b
)
– коидеал, не пересекающийся с
. Тогда [
b
)
– коидеал, не пересекающийся с ![]() . По лемме 2 найдётся простой идеал P
содержащий
. По лемме 2 найдётся простой идеал P
содержащий ![]() и не пересекающийся с [
b
).
Получаем,
и не пересекающийся с [
b
).
Получаем, ![]() , т.к.
, т.к. ![]() (т.е.
(т.е. ![]() ), но
), но ![]() , т.к.
, т.к. ![]()
![]() , противоречие. Следовательно, компактным открытым множеством r
(
I
)
будет только в случае, если
, противоречие. Следовательно, компактным открытым множеством r
(
I
)
будет только в случае, если ![]() - главный идеал.■
- главный идеал.■
Предложение 5:
Пространство ![]() является
является ![]() - пространством.
- пространством.
Доказательство.
Рассмотрим два различных простых идеала ![]() и Q
. Хотя бы один не содержится в другом. Допустим для определённости, что
и Q
. Хотя бы один не содержится в другом. Допустим для определённости, что ![]() . Тогда r
(
P
)
содержит Q
, но не содержит P
,
т.е. SpecL
является
. Тогда r
(
P
)
содержит Q
, но не содержит P
,
т.е. SpecL
является ![]() - пространством. ■
- пространством. ■
Теорема 6
: Стоуново пространство ![]() определяет полурешётку
определяет полурешётку ![]() с точностью до изоморфизма.
с точностью до изоморфизма.
Доказательство.
Нужно показать, что две полурешётки ![]() и
и ![]() изоморфны тогда и только тогда, когда пространства
изоморфны тогда и только тогда, когда пространства ![]() и
и ![]() гомеоморфны.
гомеоморфны.
![]() Очевидно, если решётки изоморфны, то пространства, образованные этими полурешётками будут совпадать.
Очевидно, если решётки изоморфны, то пространства, образованные этими полурешётками будут совпадать.
![]() Пусть
Пусть ![]() и
и ![]() гомеоморфны (
гомеоморфны (![]() ) и
) и ![]() . Тогда a
определяет компактное открытое множество r
(
a
)
. Тогда a
определяет компактное открытое множество r
(
a
)![]() .
Множеству r
(
a
)
соответствует компактное открытое множество
.
Множеству r
(
a
)
соответствует компактное открытое множество ![]() , с однозначно определённым элементом
, с однозначно определённым элементом ![]() по лемме 4. Таким образом получаем отображение
по лемме 4. Таким образом получаем отображение ![]() :
: ![]() , при котором
, при котором ![]() . Покажем, что
. Покажем, что ![]() - изоморфизм решёток. Если a
,
b
–
различные элементы из
- изоморфизм решёток. Если a
,
b
–
различные элементы из ![]() , то
, то ![]() , следовательно,
, следовательно, ![]() , поэтому
, поэтому ![]() и
и ![]() - инъекция.
- инъекция.
Для произвольного ![]() открытому множеству
открытому множеству ![]() соответствует
соответствует ![]() и очевидно
и очевидно ![]() , что показывает сюръективность
, что показывает сюръективность ![]() .
.
Пусть a
,
b
–
произвольные элементы из ![]() . Заметим, что
. Заметим, что ![]() . Открытому множеству
. Открытому множеству ![]() при гомеоморфизме
при гомеоморфизме ![]() соответствует открытое множество
соответствует открытое множество ![]() , а
, а ![]() соответствует
соответствует ![]() . Следовательно,
. Следовательно, ![]() =
=![]() . Поскольку
. Поскольку ![]() =
=![]() , то
, то ![]() , т.е.
, т.е. ![]() ■
■
Литература.
1. Биргкоф Г. Теория решёток. – М.:Наука, 1984.
2. Гретцер Г. Общая теория решёток. – М.: Мир, 1982.
3. Чермных В.В. Полукольца. – Киров.: ВГПУ, 1997.