Реферат: Числовая последовательность понятие и виды

Содержание:

Введение………………………………………………………………………………3

1.Теоретическая часть……………………………………………………………….4

Основные понятия и термины…………………………………………………....4

1.1 Виды последовательностей…………………………………………………...6

1.1.1.Ограниченные и неограниченные числовые последовательности…..6

1.1.2.Монотонность последовательностей…………………………………6

1.1.3.Бесконечно большие и бесконечно малые последовательности…….7

1.1.4.Свойства бесконечно малых последовательностей…………………8

1.1.5.Сходящиеся и расходящиеся последовательности и их свойства..…9

1.2Предел последовательности………………………………………………….11

1.2.1.Теоремы о пределах последовательностей……………………………15

1.3.Арифметическая прогрессия…………………………………………………17

1.3.1. Свойства арифметической прогрессии…………………………………..17

1.4Геометрическая прогрессия…………………………………………………..19

1.4.1. Свойства геометрической прогрессии…………………………………….19

1.5. Числа Фибоначчи……………………………………………………………..21

1.5.1 Связь чисел Фибоначчи с другими областями знаний…………………….22

1.5.2. Использование ряда чисел Фибоначчи для описания живой и неживой природы…………………………………………………………………………….23

2. Собственные исследования…………………………………………………….28

Заключение……………………………………………………………………….30

Список использованной литературы…………………………………………....31

Введение.

Числовые последовательности это очень интересная и познавательная тема. Эта тема встречается в заданиях повышенной сложности, которые предлагают учащимся авторы дидактических материалов, в задачах математических олимпиад, вступительных экзаменов в Высшие Учебные Заведения и на ЕГЭ. Мне интересно узнать связь математических последовательностей с другими областями знаний.

Цель исследовательской работы: Расширить знания о числовой последовательности.

Задачи:

1. Рассмотреть последовательность;

2. Рассмотреть ее свойства;

3. Рассмотреть аналитическое задание последовательности;

4. Продемонстрировать ее роль в развитии других областей знаний.

5. Продемонстрировать использование ряда чисел Фибоначчи для описания живой и неживой природы.

1. Теоретическая часть.

Основные понятия и термины.

Определение. Числовая последовательность– функция вида y = f(x), x О N, где N – множество натуральных чисел (или функция натурального аргумента), обозначается y = f(n) или y1, y2,…, yn,…. Значения y1, y2, y3,… называют соответственно первым, вторым, третьим, … членами последовательности.

Число a называется пределом последовательности x = {x_n }, если для произвольного заранее заданного сколь угодно малого положительного числа ε найдется такое натуральное число N, что при всех n>N выполняется неравенство |x_n - a| < ε.

Если число a есть предел последовательности x = {x_n }, то говорят, что x_n стремится к a, и пишут .

Последовательность {yn} называют возрастающей, если каждый ее член (кроме первого) больше предыдущего:

y1 < y2 < y3 < … < yn < yn+1 < ….

Последовательность {yn} называют убывающей, если каждый ее член (кроме первого) меньше предыдущего:

y1 > y2 > y3 > … > yn > yn+1 > … .

Возрастающие и убывающие последовательности объединяют общим термином – монотонные последовательности.

Последовательность называется периодической, если существует такое натуральное число T, что начиная с некоторого n, выполняется равенство yn = yn+T . Число T называется длиной периода.

Арифметическая прогрессия- это последовательность {an}, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называют арифметической прогрессией, а число d – разностью арифметической прогрессии.

Таким образом, арифметическая прогрессия – это числовая последовательность {an}, заданная рекуррентно соотношениями

a1 = a, an = an–1 + d (n = 2, 3, 4, …)

Геометрическая прогрессия- это последовательность, все члены которой отличны от нуля и каждый член которой, начиная со второго, получается из предыдущего члена умножением на одно и то же число q.

Таким образом, геометрическая прогрессия – это числовая последовательность {bn}, заданная рекуррентно соотношениями

b1 = b, bn = bn–1 q (n = 2, 3, 4…).

1.1 Виды последовательностей.

1.1.1 Ограниченные и неограниченные последовательности.

Последовательность {bn} называют ограниченной сверху, если существует такое число М, что для любого номера n выполняется неравенство bn≤ M;

Последовательность {bn} называют ограниченной снизу, если существует такое число М, что для любого номера n выполняется неравенство bn≥ М;

Последовательности, ограниченные одновременно сверху и снизу, называются ограниченными.

Например:

1.1.2 Монотонность последовательностей.

Последовательность {bn} называют невозрастающие (неубывающей), если для любого номера n справедливо неравенство bn≥ bn+1 (bn ≤bn+1);

Последовательность {bn} называют убывающей (возрастающей), если для любого номера n справедливо неравенство bn> bn+1 (bn <bn+1);

Убывающие и возрастающие последовательности называют строго монотонными, невозрастающие- монотонными в широком смысле.

Последовательности, ограниченные одновременно сверху и снизу, называются ограниченными.

Последовательность всех этих типов носят общее название- монотонные.

1.1.3 Бесконечно большие и малые последовательности.

Бесконечно малая последовательность- это числовая функция или последовательность, которая стремится к нулю.

Последовательность an называется бесконечно малой, если

ℓimn→0 an=0. Например, последовательность чисел an=1/n — бесконечно малая.

Функция называется бесконечно малой в окрестности точки x0, если ℓimx→x0 f(x)=0.

Функция называется бесконечно малой на бесконечности, если ℓimx→.+∞ f(x)=0 либо ℓimx→-∞ f(x)=0

Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если ℓimx→.+∞ f(x)=а , то f(x) − a = α(x), ℓimx→.+∞ f((x)-a)=0.

Бесконечно большая последовательность- числовая функция или последовательность, которая стремится к бесконечности.

Последовательность an называется бесконечно большой, если

ℓimn→0 an=∞.

Функция называется бесконечно большой в окрестности точки x0, если ℓimx→x0 f(x)= ∞.

Функция называется бесконечно большой на бесконечности, если

ℓimx→.+∞ f(x)= ∞ либо ℓimx→-∞ f(x)= ∞ .

1.1.4 Свойства бесконечно малых последовательностей.

Сумма двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.

Разность двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.

Алгебраическая сумма любого конечного числа бесконечно малых последовательностей сама также является бесконечно малой последовательностью.

Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.

Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

Любая бесконечно малая последовательность ограничена.

Если стационарная последовательность является бесконечно малой, то все её элементы, начиная с некоторого, равны нулю.

Если вся бесконечно малая последовательность состоит из одинаковых элементов, то эти элементы — нули.

Если {xn} — бесконечно большая последовательность, не содержащая нулевых членов, то существует последовательность {1/xn} , которая является бесконечно малой. Если же всё же {xn} содержит нулевые элементы, то последовательность {1/xn} всё равно может быть определена, начиная с некоторого номера n, и всё равно будет бесконечно малой.

Если {an} — бесконечно малая последовательность, не содержащая нулевых членов, то существует последовательность {1/an}, которая является бесконечно большой. Если же всё же {an}содержит нулевые элементы, то последовательность {1/an} всё равно может быть определена, начиная с некоторого номера n, и всё равно будет бесконечно большой.

1.1.5 Сходящиеся и расходящиеся последовательности и их свойства.

Сходящаяся последовательность- это последовательность элементов множества Х, имеющая предел в этом множестве.

Расходящаяся последовательность- это последовательность, не являющаяся сходящейся.

Всякая бесконечно малая последовательность является сходящейся. Её предел равен нулю.

Удаление любого конечного числа элементов из бесконечной последовательности не влияет ни на сходимость, ни на предел этой последовательности.

Любая сходящаяся последовательность ограничена. Однако не любая ограниченная последовательность сходится.

Если последовательность {xn} сходится, но не является бесконечно малой, то, начиная с некоторого номера, определена последовательность {1/xn}, которая является ограниченной.

Сумма сходящихся последовательностей также является сходящейся последовательностью.

Разность сходящихся последовательностей также является сходящейся последовательностью.

Произведение сходящихся последовательностей также является сходящейся последовательностью.

Частное двух сходящихся последовательностей определено, начиная с некоторого элемента, если только вторая последовательность не является бесконечно малой. Если частное двух сходящихся последовательностей определено, то оно представляет собой сходящуюся последовательность.

Если сходящаяся последовательность ограничена снизу, то никакая из её нижних граней не превышает её предела.

Если сходящаяся последовательность ограничена сверху, то её предел не превышает ни одной из её верхних граней.

Если для любого номера члены одной сходящейся последовательности не превышают членов другой сходящейся последовательности, то и предел первой последовательности также не превышает предела второй.

Если все элементы некоторой последовательности, начиная с некоторого номера, лежат на отрезке между соответствующими элементами двух других сходящихся к одному и тому же пределу последовательностей, то и эта последовательность также сходится к такому же пределу.

Пример. Доказать, что последовательность (xn)=((2n+1)/n) сходится к числу 2.

Решение.

Имеем |xn-2|=|((2n+1)/n)-2|= 1/n. для любого α>0, m принадлежит N такое, что 1/m<α. Тогда n>m справедливо неравенство 1/m<α и, следовательно, |xn-1|<α; т.е. ℓimn→∞ xn=2.

1.2 Предел последовательности.

Если число a есть предел последовательности x = {x_n }, то говорят, что x_n стремится к a, и пишут .

Чтобы сформулировать это определение в геометрических терминах введем следующее понятие.

Окрестностью точки x₀ называется произвольный интервал (a, b), содержащий эту точку внутри себя. Часто рассматривается окрестность точки x₀ , для которой x₀ является серединой, тогда x₀ называется центром окрестности, а величина (b–a)/2 – радиусом окрестности.

Итак, выясним, что же означает геометрически понятие предела числовой последовательности. Для этого запишем последнее неравенство из определения в виде

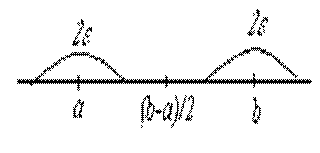
Это неравенство означает, что все элементы последовательности с номерами n>N должны лежать в интервале (a – ε; a + ε).

Следовательно, постоянное число a есть предел числовой последовательности {x_n }, если для любой малой окрестности с центром в точке a радиуса ε (ε – окрестности точки a) найдется такой элемент последовательности с номером N, что все последующие элементыс номерами n>N будут находиться внутри этой окрестности.

Пример 1.

1. Пусть переменная величина x последовательно принимает значения

Докажем, что предел этой числовой последовательности равен 1. Возьмем произвольное положительное число ε. Нам нужно найти такое натуральное число N, что при всех n>N выполняется неравенство |x_n - 1| < ε. Действительно, т.к.

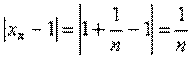то для выполнения соотношения |x_n - a| < ε достаточно, чтобы

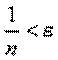или .

Поэтому, взяв в качестве N любое натуральное число, удовлетворяющее неравенству , получим что нужно. Так если взять, например,

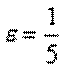то, положив N=6, для всех n>6 будем иметь

2. Используя определение предела числовой последовательности, доказать что

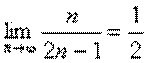Возьмем произвольное ε > 0. Рассмотрим

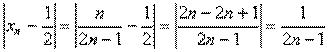Тогда , если или , т.е. .

Поэтому выберем любое натуральное число, удовлетворяющее неравенству

Замечание 1. Очевидно, что если все элементы числовой последовательности принимают одно и то же постоянное значение x_n = c, то предел этой последовательности будет равен самой постоянной. Действительно, при любом ε всегда выполняется неравенство

|x_n - c| = |c - c| = 0 < ε.

Замечание 2. Из определения предела следует, что последовательность не может иметь двух пределов. Действительно, предположим, что x_n → a и одновременно x_n → b. Возьмем любое и отметим окрестности точек a и b радиуса ε. Тогда по определению предела, все элементы последовательности, начиная с некоторого, должны находиться как в окрестности точки а, так и в окрестности точки b, что невозможно.

Замечание 3. Не следует думать, что каждая числовая последовательность имеет предел. Пусть, например, переменная величина принимает значения

Несложно заметить, что эта последовательность не стремится ни к какому пределу.

Пример 2.

Доказать, что ℓimn→∞qⁿ=0 при |q| < 1.

Доказательство:

1). Если q=0, то равенство очевидно. Пусть α> 0- произвольно и 0<|q|<1. тогда пользуясь неравенством Бернулли, получим

1/|q|= (1+(1/|q|-1))ⁿ > 1+n(1/|q|-1)> n(1/|q|-1)

Отсюда

|q|ⁿ=|q|ⁿ< |q| / (n(1-|q|) <αn>|q| / (n(1-|q|)

1.2.1.Теоремы о пределах последовательностей.

1. Последовательность, имеющая предел, ограничена;

2. Последовательность может иметь только один предел;

3. Любая неубывающая (невозрастающая) и не ограниченная сверху (снизу) последовательность имеет предел;

4. Предел постоянной равен этой постоянной:

ℓimn→∞ C=C

5.Предел суммы равен сумме пределов: ℓimn→∞(an+bn)= ℓimn→∞ an+ ℓimn→∞ bn;

6. Постоянный множитель можно выносить за знак предела:

ℓim n→∞ (Сan)= Cℓim n→∞ an;

7. Предел произведения равен произведению пределов:

ℓimn→∞ (an∙bn)= ℓimn→∞ an ∙ ℓimn→∞ bn;

8. Предел частного равен частному пределов, если предел делителя отличен от нуля:

ℓimn→∞ (an/bn)= ℓimn→∞ an / ℓimn→∞ bn, если

ℓimn→∞bn≠0;

9. Если bn ≤ an ≤ cn и обе последовательности {bn}и {cn} имеют один и тот же предел α, то ℓimn→∞ an=α.

Пример.

Найдем предел ℓimn→∞ ((3n-1)/(4n+5)).

Имеем

ℓimn→∞ ((3n-1)/(4n+5))= ℓimn→∞(n(3-1/n))/ (n(4+5/n)= (ℓimn→∞ 3-1/n)/ (ℓimn→∞ 4+5/n)= (ℓimn→∞ 3- ℓimn→∞ 1/n)/ (ℓimn→∞ 4+ 5 ℓimn→∞ 1/n)= (3-0)/(4+5∙0)=3/4.

1.3 Арифметическая прогрессия.

Арифметическая прогрессия- это последовательность {an}, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом d, называемым разностью прогрессии:

an+1= an+ d, n=1, 2, 3… .

Любой член последовательности может быть вычислен по формуле

an= a1+ (n – 1)d, n≥1

1.3.1. Свойства арифметической прогрессии

1. Если d> 0, то прогрессия является возрастающей; если d< 0- убывающая;

2. Любой член арифметической прогрессии, начиная со второго, является средним арифметическим предыдущего и следующего члена прогрессии:

an= (an-1 + an+1)/2, n≥2

3. Сумма n первых членов арифметической прогрессии может быть выражена формулами:

Sn= ((2a1+ d(n-1))/2)∙n

4. Сумма n последовательных членов арифметической прогрессии начиная с члена k:

Sn= ((ak+ak+n-1)/2)∙n

5. Пример суммы арифметической прогрессии является сумма ряда натуральных чисел до n включительно:

Sn=(n(n+1))/2

Пример 1.

Известно, что при любом n сумма Sn членов некоторой арифметической прогрессии выражается формулой Sn=4n²-3n. Найти три первых члена этой прогрессии.

Решение:

Sn=4n²-3n ( по условию).

Пустьn=1, тоS1=4-3=1=a1 => a1=1;

Пустьn=2, тоS2=4∙2²-3∙2=10=a1+a2; a2=10-1=9;

Таккакa2=a1+d, то d= a2-a1=9-1=8;

a3= a2+d=17

Ответ: 1; 9; 17.

Пример 2.

При делении девятого члена арифметической прогрессии на второй член в частном получается 5, а при делении тринадцатого члена на шестой член в частном получается 2 и в остатке 5. Найти первый член и разность прогрессии.

Решение:

a1, a2, a3…, an- арифметическая прогрессия

a9/a2=S;

a13/a6=2 ( остатокS)

a9= S∙a2;

a13=2a6+S.

Используя формулу для n-ого члена прогрессии получим систему уравнений

{a1+8d= S(a1+d); a1+12d = 2(a1+S∙d)+S

{ 4a1=3d; a1=2d-S

Откуда 4(2d-S)=3d => Sd= 20 => d=4.

Ответ: a1=3; d=4.

1.4.Геометрическая прогрессия.

Геометрическая прогрессия- это последовательность {bn}, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же отличное от нуля число q, называемое знаменателем прогрессии:

bn+1= bnq, n= 1, 2, 3… .

Любой член геометрической прогрессии может быть вычислен по формуле:

bn= b1qⁿ‾¹

1.4.1. Свойства геометрической прогрессии.

1. Логарифмы членов геометрической прогрессии образуют арифметическую прогрессию.

2. b²n= bn-i bn+i, i< n

3. Произведение первых n членов геометрической прогрессии можно рассчитать по формуле:

Pn= (b1∙bn)ⁿ َ ²

4. Произведение членов геометрической прогрессии начиная с k-ого члена, и заканчивая n-ым членом, можно рассчитать по формуле:

Pk,n= (Pn)/(Pk-1);

5. Сумма n первых членов геометрической прогрессии:

Sn= b1((1-qⁿ)/(1-q)), q≠ 1

Sn= qbn, q=1;

6. Если |q|< 1, то bn→0 при n→+∞, и Sn→(b1)/(1-q), при n→+∞

Примре1.

Пусть а1, а2, а3, … , аn, … – последовательные члены геометрической прогрессии, Sn – сумма ее первых n членов.

Решение:

Sn= a1+a2+a3+…an-2+an-1+ an= a1an (1/an+a2/a1an+a3/a1an+…+an-2/a1an+an-1/a1an+1/a1)= a1an (1/an+ a2/a2an-1+…+ an-2/an-2a3+an-1/an-1a2+1/a1)=

a1a2 (1/an+ 1/an-1+ 1/an-2+…+ 1/a3+1/a2+ 1/a1).

Ч.т.д.

1.5.Числа Фибоначчи.

В 1202 году появилась книга итальянского математика Леонардо из г. Пиза, в которой содержались сведения по математике, приводились решения всевозможных задач. Среди них была простая, не лишенная практической ценности, задача о кроликах: "Сколько пар кроликов в один год от одной пары рождается?"

В результате решения этой задачи получился ряд чисел 1, 2, 3, 5,8, 13, 21, 34, 55, 89, 144 и т.д. Этот ряд чисел позже был назван именем Фибоначчи, так называли Леонардо.

Чем же примечательны числа, полученные Фибоначчи?

(В этом ряду каждое последующее число является суммой двух предыдущих чисел). Математически ряд Фибоначчи записывается следующим образом:

И₁ , И₂ , : И_n, где И_n = И _{n - 1} + И_{n - 2}

Такие последовательности, в которых каждый член является функцией предыдущих, называют рекуррентными, или возрастными последовательностями.

Рекуррентным является и ряд чисел Фибоначчи, а члены этого ряда называют числами Фибоначчи.

Оказалось, что они обладают рядом интересных и важных свойств.

Спустя четыре столетия после открытия Фибоначчи ряда чисел немецкий математик и астроном Иоганн Кеплер установил, что отношение рядом стоящих чисел в пределе стремится к золотой пропорции.

Ф - обозначение золотой пропорции от имени Фидий - греческий скульптор, применявший золотую пропорцию при создании своих творений.

[Если при делении целого на две части отношение большей части к меньшей равно отношению целого к большей части, то такая пропорция называется "золотой" и равно примерно 1,618].

1.5.1.Связь чисел Фибоначчи сдругими областями знаний

Свойства ряда чисел Фибоначчи неразрывно связаны с золотой пропорцией и выражают порой магическую и даже мистическую сущность закономерностей и явлений.

Фундаментальную роль числа в природе определил еще Пифагор своим утверждением "Все есть число". Поэтому математика являлась одной из основ религии последователей Пифагора (пифагорейского союза). Пифагорейцы считали, что бог Дионис положил число в основу мировой организации, в основу порядка; оно отражало единство мира, его начало, а мир представлял собой множество, состоящее из противоположностей. То, что приводит противоположности к единству, и есть гармония. Гармония является божественной и заключается в числовых соотношениях.

Числа Фибоначчи обладают многими интересными свойствами. Так, сумма всех чисел ряда от 1-го до И_n равна следующему через одно число (И_n+2 ) без 2-х единиц.

Отношение расположенных через одно чисел Фибоначчи в пределе стремится к квадрату золотой пропорции, равному приблизительно 2,618: Удивительное свойство! Получается, что Ф + 1 = Ф^2.

Золотая пропорция является иррациональной величиной, она отражает иррациональность в пропорциях природы. Числа Фибоначчи отражают целочисленность природы. Совокупность этих закономерностей отражают диалектическое единство двух начал: непрерывного и дискретного.

В математике известны фундаментальные числа и е, к ним возможно добавить Ф.

Оказывается все эти универсальные иррациональные числа, широко распространенные в различных закономерностях, связаны между собой.

е i + 1 = 0 - эта формула открыта Эйлером и позже де Муавром и названа в честь последнего.

Ф = 2 Cos

Не свидетельствуют ли эти формулы об органическом единстве чисел е, , Ф?

Об их фундаментальности?

1.5.2. Использование ряда чисел Фибоначчи для описания живой и неживой природы

Мир живой и неживой природы, казалось бы между ними дистанция огромного размера, это скорее антиподы, чем родственники. Но не следует забывать, что живая природа в конечном итоге возникла из неживой (если не на нашей планете, то в космосе) и должна была по законам наследственности сохранить какие-то черты своей прародительницы.

Мир неживой природы - это прежде всего мир симметрии, придающий его творениям устойчивость и красоту. Симметрия сохранилась и в живой природе. Симметрия растений унаследована от симметрии кристаллов, симметрия которых унаследована от симметрии молекул и атомов, а симметрия атомов - от симметрии элементарных частиц.

Характерной чертой строения растений и их развития является спиральность. Спирально закручиваются усики растений, по спирали происходит рост тканей в стволах деревьев, по спирали расположены семечки в подсолнечнике. Движение протоплазмы в клетке часто спиральное, носители информации - молекулы ДНК - также скручены в спираль. Установлены и винтовое расположение атомов в некоторых кристаллах (винтовые дислокации). Кстати, кристаллы с винтовой структурой обладают сверхпрочностью. Не потому ли живая природа и предпочла этот вид структурной организации, унаследовав его от неорганических веществ?

Чем же может быть выражена данная закономерность, сходство живой и неживой природы?

Чешуйки сосновой шишки располагаются по спирали, их число равно 8 и 13 или 13 и 21. В корзинках подсолнечника семена также располагаются по спиралям, их число обычно составляет 34 и 55 или 55 и 89.

Присмотритесь к ракушкам. Когда-то они служили домиками для маленьких моллюсков, которые они выстроили сами. Моллюски давно погибли, а их домики будут существовать тысячелетия. Выступы-ребра на поверхности ракушки инженеры называют ребрами жесткости - они резко повышают прочность конструкции. Эти ребра расположены по спирали и в любой ракушке их 21.

Возьмите любую черепаху - от болотной до гигантской морской - и вы убедитесь, что рисунок на панцире у них аналогичный: на овальном поле расположено 13 сросшихся пластин - 5 пластин в центре и 8 - по краям, а на периферийной кайме около 21 пластины.

На лапах у черепах 5 пальцев, а позвоночный столб состоит из 34 позвонков. Все указанные величины отвечают числам Фибоначчи.

У ближайшего родственника черепахи - крокодила туловище покрыто 55 роговыми пластинами. На теле кавказской гадюки расположено 55 темных пятен. В ее скелете насчитывается 144 позвонка.

Следовательно, развитие черепахи, крокодила, гадюки, формирование их тел, осуществлялось по закону ряда чисел Фибоначчи.

У комара: 3 пары ног, на голове 5 усиков - антенны, брюшко делится на 8 сегментов.

У стрекозы: массивный корпус и длинный тонкий хвост. В корпусе выделяется три части: голова, грудь, брюшко.

Брюшко разделено на 5 сегментов, хвост состоит из 8 частей.

Нетрудно видеть в этих числах развертывание ряда чисел Фибоначчи. Длина хвоста, корпуса и общая длина стрекозы связаны между собой золотой пропорцией: L хвоста = L стрекозы = Ф

L корпуса
L хвоста

Высшим типом животных на планете являются млекопитающие. Число позвонков у многих домашних животных равно или близко 55, число пар ребер примерно 13, грудная кость содержит 7 + 1 элемент.

У собаки, свиньи, лошади - 21 + 1 пара зубов, у гиены - 34, у одного из видов дельфинов - 233.

Ряд чисел Фибоначчи определяет общий план развития организма, эволюции видов. Но развитие живого осуществляется не только скачками, но и непрерывно. Организм любого животного находится в постоянном изменении, постоянном приспособлении к среде своего обитания. Мутации наследственности нарушают план развития. И неудивительно, что при общем преобладающем проявлении чисел Фибоначчи в развитии организмов часто наблюдаются отклонения от дискретных величин. Это не ошибка природы, а проявление подвижности организации всего живого, его непрерывного изменения.

Числа Фибоначчи отражают основную закономерность роста организмов, следовательно, и в строении человеческого тела они должны каким-то образом проявиться.

У человека:

1 - туловище, голова, сердце и т.д.

2 - руки, ноги, глаза, почки

Из 3 частей состоят ноги, руки, пальцы рук

5 пальцев на руках и ногах

8 - состав руки вместе с пальцами

12 пар ребер (одна пара атрофирована и присутствует в виде рудимента)

20 - число молочных зубов у ребенка

32- число зубов у взрослого человека

34 - число позвонков

Общее число костей скелета человека близко к 233.

Этот список частей тела человека можно продолжить. В их перечне очень часто встречаются числа Фибоначчи или близкие к ним величины. Отношение рядом стоящих чисел Фибоначчи приближается к золотой пропорции, значит, и соотношение чисел различных органов часто отвечает золотой пропорции.

Человек, как и другие живые творения природы, подчиняется всеобщим законам развития. Корни этих законов нужно искать глубоко - в строении клеток, хромосом и генов, и далеко - в возникновении самой жизни на Земле.

2. Собственные исследования.

Задача № 1.

Какое число должно стоять вместо вопросительного знака 5; 11; 23; ?; 95; 191? Как вы его нашли?

Решение:

Нужно умножить предыдущее число на 2 и прибавить единицу. Так получаем:

(5∙2)+1=11;

(11∙2)+1=23;

(23∙2)+1=47 => 47- число вместо знака вопроса.

Ответ: 47.

Задача № 2.

Найти сумму Sn=1/(1∙2)+1/(2∙3)+1/(3∙4)+…+1/n(n+1)

Решение:

Запишем что 1/n(n+1)= 1/n - 1/(n+1). Тогда перепишем сумму в виде разности =>

Sn= (1-1/2)+(1/2-1/3)+(1/3-1/4)+…+(1/(n-1) – 1/n)+ (1/n - 1/(n+1))= 1-1/(n+1)= =n/(n+1n).

Ответ: n/(n+1n).

Задача № 3.

Пользуясь определение предела последовательности, докажите что:

ℓim n→∞an=a, еслиan= (3n-1)/(5n+1); a= 3/5

Решение:

Покажем, что для любого ε>0 существует такой номер N(ε), что |an-a|< ε, для

n> N(ε)

|an-a|<|(3n-1)/(5n+1) - 3/5| = |(5(3n-1)-3(5n+1))/5(5n+1)|= |-8/5(5n+1)|= 8/5(5n+1)

8/5(5n+1) < ε => 5n+1> 8/5ε => n> (8/25ε)- 1/5

Из последнего неравенства следует что можно выбрать N(ε)= [(8/25ε)- 1/5] и при любых n> N(ε) будет выполняться неравенство |an-a|< ε. Значит, по определению предела последовательности ℓimn→∞ (3n-1)/(5n+1)=3/5

Задача № 4.

Вычислите пределы числовых последовательностей

ℓimn→∞ (3-4n)²/(n-3)³-(n+3)²=

ℓimn→∞ (9-24n+16n²)/( n³-9n²+27n-27)- (n³+9n²+27n+27)=

ℓimn→∞(16n²-24n+9)/(-18n²-54)=

ℓimn→∞ (16-24|n+9|n²)/((-18-54)/n²)= 16/-18= -8/9.

Задача № 5.

Найти ℓimn→∞ (tgx)/ x

Решение:

Имеем ℓimn→∞ (tgx)/ x= ℓimn→∞ (sinx)/ x ∙ 1/ (cosx)= ℓimn→∞ (sinx)/x ∙ ℓimn→∞ 1/(cosx)= 1∙1/1=1

Ответ : 1.

Заключение.

В заключении я бы хотела сказать, что мне было очень интересно работать по данной теме. Так как эта тема очень интересная и познавательная. Я познакомилась с определением последовательности, с её видами и свойствами, с числами Фибоначчи. Познакомилась с пределом последовательности, с прогрессиями. Рассмотрела аналитические задания, содержащие последовательность. Узнала методы решения заданий с последовательностью, связь математических последовательностей с другими областями знаний.

Список использованной литературы.

1. Математика. Большой справочник для школьников и поступающих в вузы./

Д.И. Аверьянов, П.И. Алтынов, И.И. Баврин и др.- 2-е изд.- Москва: Дрофа, 1999.

2. Ресурсы Интернета :

· ru.wikipedia.org

· www.pm298.ru

· www.krugosvet.ru

· www.uztest.ru