Реферат: Описанная сфера на олимпиадах и ЕГЭ

Данная работа выполняется в рамках проекта по созданию математической странички для школьников на сайте лицея-интерната и будет размещена в разделе «Математические методы».

Цель работы – создание справочника, посвященного методу решения геометрических задач с описанной сферой на олимпиадах и ЕГЭ.

Для достижения данной цели нам необходимо было решить следующие задачи :

1) ознакомиться с понятием описанной сферы;

2) изучить особенности комбинаций описанной сферы с пирамидой, призмой, цилиндром и конусом;

3) среди геометрических задач выбрать те, которые содержат условие наличия описанной сферы;

4) проанализировать, систематизировать и проклассифицировать собранный материал;

5) сделать подборку задач для самостоятельного решения;

6) оформить результат исследования в виде реферата.

Практическая значимость – подготовленные нами материалы могут быть использованы при подготовке школьников к олимпиадам, ЕГЭ и последующему обучению в вузе.

1 Сфера и шар

1.1 Сфера и шар: основные понятия и определения

Сферой называется поверхность, состоящая всех точек пространства, расположенных на данном расстоянии от данной точки.

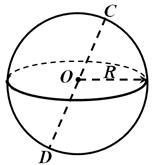
Рис. 1

Данная точка называется центром сферы (точка О на рис. 1), а данное расстояние радиусом сферы . Любой отрезок, соединяющий центр и какую-нибудь точку сферы, так же называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы (отрезок DC на рис. 1). Отметим, что сфера может быть получена вращением полуокружности вокруг её диаметра.

Шаром называется тело, ограниченное сферой. Центр, радиус и диаметр сферы называются также центром , радиусом и диаметром шара . Очевидно, шар радиуса R с центром в О содержит все точки пространства, которые расположены от точки О на расстоянии, не превышающем R (включая точку О ), и не содержит других точек. Шаром также называют фигуру вращения полукруга вокруг его диаметра. Шаровой сегмент – часть шара, отсекаемая от него какой-нибудь плоскостью. Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость. Плоскость, проходящая через центра шара, называется диаметральной плоскостью. Сечение шара диаметральной плоскостью называется большим кругом , а сечение сферы – большой окружностью. Шаровой сектор – геометрическое тело, которое получается при вращении кругового сектора с углом, меньшим 90^о , вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов. Шаровой сектор состоит из шарового сегмента и конуса с общим основанием.

Площадь поверхности сферы:

S = 4πR ² ,

где R – радиус шара, S - площадь сферы.

Объем сферы

V =

где V – объём шара

Объем шарового сектора

V = ,

V – объём шарового сегмента.

Площадь сегментальной поверхности

где - высота сегмента, площадь сегментальной поверхности

Радиус основания сегмента

где - радиус основания сегмента, - высота сегмента, 0<H < 2R .

Площадь сферической поверхности шарового сегмента

где - площадь сферической поверхности шарового сегмента.

В пространстве для шара и плоскости возможны три случая:

1) Если расстояние от центра шара до плоскости больше радиуса шара, то шар и плоскость не имеют общих точек.

2) Если расстояние от центра шара до плоскости равно радиусу шара, то плоскость имеет с шаром и ограничивающей его сферой только одну общую точку.

3) Если расстояние от центра шара до плоскости меньше радиуса шара, то пересечение шара с плоскостью представляет собой круг. Центр этого круга является проекцией центра шара на данную плоскость. Пересечение плоскости со сферой является окружностью указанного круга.

1.2 Описанная сфера

1.2.1 Определения и свойства

Сфера называется описанной около многогранника (а многогранник — вписанным в сферу ), если все вершины многогранника лежат на сфере.

Из определения описанной сферы следуют два факта:

1) все вершины вписанного в сферу многогранника равноудалены от некоторой точки (от центра описанной сферы);

2) каждая грань вписанного в сферу многогранника является вписанным в некоторую окружность многоугольником, именно в ту окружность, которая получается в сечении сферы плоскостью грани; при этом основание перпендикуляров, опущенных из центра описанной сферы на плоскости граней, являются центрами описанных около граней окружностей.

Теорема 1. Около многогранника можно описать сферу, если и только если выполняется любое из условий:

а) около всякой грани многогранника можно описать окружность, и оси окружностей, описанных около граней многогранника, пересекаются в одной точке;

б) плоскости, перпендикулярные к ребрам многогранника и проходящие через их середины, пересекаются в одной точке;

в) существует единственная точка, равноудаленная от всех вершин многогранника.

Доказательство.

Необходимость. Пусть около многогранника описана сфера. Докажем, что выполняется условие а). Действительно, поскольку плоскость данной грани многогранника пересекает сферу по окружности, то вершины грани, принадлежащие сфере и плоскости грани, принадлежат линии их пересечения — окружности. Поскольку центр сферы равноудален от всех вершин данной грани, то он лежит на перпендикуляре к этой грани, проведенном через центр описанной около грани окружности.

Достаточность. Пусть выполняется условие а). Докажем, что около многогранника можно описать сферу. В самом деле, поскольку общая точка перпендикуляров к граням, проведенных через центры описанных около граней окружностей, равноудалена от всех вершин многогранника, то около многогранника описывается сфера с центром в этой точке.

Условие а) в данном случае равносильно условиям б) и в).

Если сфера описана около многогранника, то: а) основание перпендикуляра, опущенного из центра сферы на любую грань, является центром окружности, описанной около этой грани (как основание высоты пирамиды с равными боковыми ребрами — радиусами сферы, проведенными из ее центра в вершины данной грани); б) центр сферы, описанной около многогранника, может находиться внутри многогранника, на его поверхности (в центре описанной около грани окружности, в частности — в середине некоторого ребра), вне многогранника.

1.2.2 Описанная сфера и пирамида

Рис.2

Теорема 2 . Около пирамиды можно описать сферу, если и только если около ее основания можно описать окружность.

Доказательство. Пусть около основания пирамиды описывается окружность. Тогда эта окружность и точка вне плоскости этой окружности — вершина пирамиды — определяют единственную сферу, которая и будет описанной около пирамиды. И обратно. Если около пирамиды описана сфера, то сечение сферы плоскостью основания пирамиды есть окружность, описанная около основания.

Следствие 1. Около всякого тетраэдра можно описать сферу.

Следствие 2. Около всякой правильной пирамиды можно описать сферу, центр которой лежит на высоте пирамиды или ее продолжении.

Центр сферы, описанной около пирамиды, может находиться:

· с вершиной пирамиды по одну сторону от плоскости ее основания — внутри пирамиды, в плоскости боковой грани (в центре описанной около этой грани окружности), вне пирамиды;

· в плоскости основания — в центре описанной около основания окружности;

· с вершиной пирамиды по разные стороны от плоскости ее основания.

Теорема 3 . Если боковые рёбра пирамиды равнонаклонены к плоскости её основания, то около пирамиды можно описать сферу.

Доказательство. Поскольку боковые ребра равнонаклонены к плоскости основания пирамиды, то около основания пирамиды можно описать окружность, а тогда около пирамиды можно описать сферу.

Эту теорему можно сформулировать иначе: если пирамида имеет равные боковые ребра, то около пирамиды можно описать сферу.

Обратная теорема не верна

Теорема 4. Если около пирамиды описан шар, то его центр является точкой пересечений всех плоскостей, проведенных через середины ребер пирамиды перпендикулярно к этим ребрам.

Доказательство. В самом деле, любая точка, равноудаленная от двух вершин пирамиды, прилежащих к одному ребру, лежит в плоскости, проведенной перпендикулярно к этому ребру пирамиды через его середину. Поэтому центр описанного шара, будучи равноудаленным от всех вершин пирамиды, должен находиться в каждой из таких плоскостей, т.е. он является точкой пересечения всех этих плоскостей. При выполнении чертежа школьники часто помещают центр описанного шара наугад, не представив себе достаточно хорошо данной пространственной конфигурации и тем более не проводя никаких рассуждений о положении этого центра. При этом, как правило, центр ставится внутри пирамиды. Между тем центр описанного шара может лежать и внутри, и вне, и на поверхности пирамиды (в зависимости от конкретного вида пирамиды).

Теорема 5. Около усеченной пирамиды можно описать сферу, если и только если выполняется любое из условий:

a) около оснований пирамиды описываются окружности, линия центров которых перпендикулярна их плоскостям;

b) все боковые ребра пирамиды равнонаклонены к плоскости одного из оснований;

c) все боковые ребра пирамиды равны между собой;

d) все боковые грани пирамиды — равнобочные трапеции.

Доказательство. Пусть около оснований данной усеченной пирамиды можно описать окружности, и плоскости этих окружностей перпендикулярны линии их центров. Тогда, как известно, такие две окружности определяют единственную сферу, которая и будет описанной около данной пирамиды.

Пусть, наоборот, около данной усеченной пирамиды описана сфера. Тогда сечения сферы плоскостями оснований пирамиды будут окружности, описанные около оснований. Далее. Прямая, перпендикулярная плоскостям оснований пирамиды и проходящая через центр сферы, пройдет через центры окружностей, описанных около оснований.

Условие a ) равносильно условиям b ), c ), d ).

Следствие. Около всякой правильной усеченной пирамиды можно описать сферу.

1.2.3 Описанная сфера и призма

Рис.3

Теорема 6. Около призмы можно описать сферу, если и только если призма прямая и около ее основания можно описать окружность.

Доказательство.

Необходимость. Если призма вписана в сферу, то каждая ее грань вписана в окружность — сечение сферы плоскостью этой грани. Значит, около основания призмы можно описать окружность, и все боковые грани призмы как параллелограммы, вписанные в окружности, — прямоугольники и поэтому призма прямая.

Достаточность. Пусть призма прямая и около ее основания описывается окружность. Тогда окружности, описанные около оснований призмы, плоскости которых перпендикулярны линии их центров, определяют единственную сферу, которая и будет описанной около призмы.

Следствия:

а) около всякой правильной призмы можно описать сферу;

б) около всякой прямой треугольной призмы можно описать сферу;

в) около всякого прямоугольного параллелепипеда можно описать сферу;

Центр описанной около призмы сферы равноудален от плоскостей оснований призмы и может находиться внутри призмы, на ее боковой грани (в центре описанной около грани окружности), вне призмы.

1.2.4 Описанная сфера и цилиндр

Рис.4

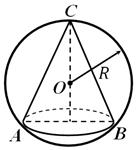
Рис.5

Сфера называется описанной около цилиндра , если на ней лежат окружности оснований цилиндра (рис. 4). Около цилиндра всегда можно описать сферу.

1.2.5 Описанная сфера и конус

Сфера называется описанной около конуса , если на ней лежат вершина и окружность основания конуса (рис. 5). Около конуса всегда можно описать сферу; её радиус равен радиусу окружности, описанной около осевого сечения конуса. Усечённый конус называется вписанным в шар, если его основания являются сечениями поверхности шара.

2 Примеры олимпиадных заданий

2.1 Примеры олимпиадных заданий с пирамидой

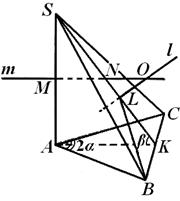
Рис.6

Пример 1. В треугольной пирамиде S АВС ребро ВС равно а, АВ=АС, ребро S А перпендикулярно к основанию АВС пирамиды, двугранный угол при ребре S А равен 2α , а при ребре ВС равен β (рис. 6) . Найти радиус описанного шара.

Решение. Рассмотрим пирамиду S АВС, о которой идет речь в условии задачи. Поскольку ребро SA перпендикулярно к плоскости основания, то ВА S = CAS = 90°, а потому угол ВАС какраз и является линейным углом двугранного угла при ребре SA . Таким образом, в основании пирамиды лежит равнобедренный треугольник с углом 2α при вершине, а высота пирамиды совпадает с ребром S А.

Так как проекции боковых ребер SB и S С на плоскость основания равны, то и сами эти ребра равны. Поэтому грань В S С — равнобедренный треугольник, и его высота, опущенная из вершины S , попадает в середину К ребра ВС. По теореме о трех перпендикулярах АК — высота треугольника ВАС. Отсюда ясно, что угол S КА — линейный угол двугранного угла при ребре ВС, т. е. S КА = β .

Центр описанного шара лежит на пересечении прямой l , перпендикулярной к плоскости В S С и проходящей через центр окружности, описанной около треугольника В S С, с плоскостью, проходящей через середину ребра А S перпендикулярно к нему. Прямая l лежит в плоскости А S К: в самом деле, плоскость В S С проходит через прямую ВС, перпендикулярную к плоскости А S К , т. е. плоскости В S С и А S К перпендикулярны; в то же время прямая l перпендикулярна к плоскости В S С и проходит через линию пересечения этих плоскостей, так что она лежит в плоскости А S К .

Итак, центр шара лежит в плоскости А S К . Вынесем эту плоскость на специальный чертеж. Центр шара О будет тогда лежать на пересечении прямой l и прямой m , перпендикулярной к А S и проходящей через его середину. Но, вообще говоря, могут представиться три возможности: прямые l и т пересекаются внутри, или вне треугольника А S К или на его стороне, и нам придется рассмотреть все эти возможности (см. рис. 7, 8, 9). Ниже, в ходе выкладок, мы покажем, что две из них на самом деле не осуществляются. Нас интересует радиус R описанного шара, т.е. расстояние от точки О — точки пересечения перпендикуляров т иl ксторонам угла К S А — до точки S , вершины этого угла. Прежде всего отыщем SL — проекцию искомого расстояния на сторону SK треугольника KAS . Так как в треугольнике АК B (рис. 6) нам известен катет ВК= а и угол КАВ = α, то АК= а ctg α .

Рис. 7

Рис.8

Далее, из треугольника КА S имеем

SK = .

Так как L — центр описанной около треугольника В S С окружности, то LS = L В, aпотому из треугольника ВК L находим, что ( S К- SL ) ² +КВ ² =В L ² , т. е.

SL =.

Отметив, что проведенные вычисления отрезка SL никак не зависели от местоположения центра О описанного шара, вернемся к рис. 7, 8, 9. Обозначим через N точку пересечения прямой m со стороной S К. Ясно, что прямые l и т пересекаются вне треугольника КА S , если SN <SL (рис. 8); если же S N > SL , то точка О лежит внутри этого треугольника (рис. 7); наконец, если SN = SL , то точка О лежит на стороне S К этого треугольника (рис. 9). Выясним, какое из этих положений имеет место на самом деле.

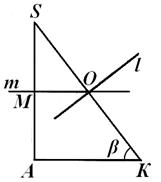
Рис.9

Так как МN — средняя линия треугольника КА S , то SN = S К . Сравнивая длины отрезков SN и SL , без труда докажем, что при любых а, α и

(из геометрических соображений следует, что а > 0, 0° < < 90° и 0° < β < 90°). Следовательно, каковы бы ни были размеры а , α и β пирамиды S АВС, центр О описанного шара всегда лежит вне пирамиды. Это в свою очередь означает, что вынесенная нами плоская конфигурация в плоскости КА S может иметь лишь вид, указанный на рис 8; расположения, изображенные на рис. 7 и 9, в действительности иметь места не могут. Рассматривая рис. 8, легко покажем, что = β , а потому LO = NL tgβ = (SL —S N) tgβ. Подставляя сюда полученные выше выражения для SL и S N , получаем после очевидных вычислений:

L О = а tgα sinβ .

Наконец, из прямоугольного треугольника О LS находим

R = = .

Как видим, выкладки в задаче оказались простыми — главная трудность решения лежит в рассуждениях, устанавливающих положение центра описанного шара.

Ответ: R = .

Пример 2. В шар радиуса R вписана правильная треугольная пирамида с плоским углом  при вершине. Найти объем пирамиды, а также боковую поверхность конуса, описанного около указанной пирамиды .

Рис.10

Решение. Пусть сторона основания пирамиды равна a , радиус основания конуса, описанного около этой пирамиды равен r , тогда (рис. 10). Грани пирамиды – равнобедренные треугольники. Тогда DK – высота, медиана и биссектриса ABD . Из прямоугольного треугольника ADK имеем . Высоту пирамиды найдем из прямоугольного треугольника AOD :

, .

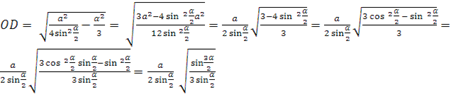DM – диаметр шара. Тогда в сечении шара, проходящем через диаметр DM и точку А , получим прямоугольный треугольник AMD . Из метрических соотношений в прямоугольном треугольнике имеем ,

откуда

Тогда площадь основания найдем по формуле:

И из формулы находим объем пирамиды:

Ребро AD по определению описанного конуса является его образующей. Тогда найдем боковую поверхность описанного конуса по формуле S _бок = r l :

Ответ: ; .

Пример 3. В основании пирамиды лежит квадрат со стороной а. Высота пирамиды проходит через середину одного из ребер основания и равна . Найти радиус сферы, описанной около пирамиды.

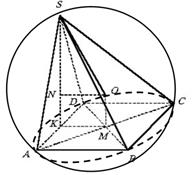
Рис.11

Решение. Типичной ошибкой при решении этой задачи является утверждение о том, что центр описанной сферы находится на грани SBC (рис. 11). В действительности положение точки О не связано с гранью SBC.

В силу равноудаленности точки О от вершин S, A, B, C, D следует, что OABCD – правильная четырехугольная пирамида. Следовательно, на грань ABCD точка О проектируется в точку М – точку пересечения диагоналей. Треугольник ASD равнобедренный, тогда высота пирамиды SK является медианой треугольника ASD , . Из прямоугольного треугольника SAK найдем SA :

Следовательно, треугольник SAD – равносторонний и OASD – правильная треугольная пирамида. Тогда точка О проектируется на грань SAD в центр треугольника SAD . Отсюда

, .

Из треугольника SON находим искомый радиус SO,

, .

Ответ: .

Пример 4. В шар радиуса R вписана правильная шестиугольная усечённая пирамида, у которой плоскость нижнего основания проходит через центр шара, а боковое ребро составляет с плоскостью основания угол 60 . Определить объём пирамиды.

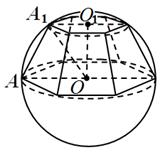
Рис.12

Решение. По условию, OAA ₁ = 60 (рис. 12); значит,

О ₁ ОА ₁ =30 и А ₁ О ₁ = А ₁ О = ,OO ₁ = .

Находим

S _{нижн.осн.} = 6, S _{верхн. осн.} =_{нижн. осн.} .

Окончательно получим

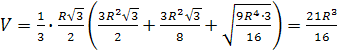Ответ:

2.2 Примеры олимпиадных заданий с призмой

Пример 1. В шар, объем которого равен V , вписана прямая треугольная призма. Основанием призмы служит прямоугольный треугольник с острым углом , а наибольшая ее боковая грань есть квадрат. Найти объем призмы.

Рис.13

Решение. Сначала определим положение центра шара относительно призмы. Сечения шара плоскостями оснований призмы - круги, в которые вписаны эти основания (рис. 13), а так как основания призмы равны, то равны и одинаково удалены от центра шара круги сечений. Каждый из центров О ₁ и О ₂ совпадает с серединой соответствующей гипотенузы.

Рис.14

Рис.15

Из свойств сечений шара плоскостью известно, что перпендикуляр, проведенный из центра шара О кплоскости круга сечения, проходит через центр этого круга. Следовательно, О ₁ О плоскости АВС. Прямая О ₁ О проходит также через O ₂ и перпендикулярна плоскости Таким образом, центр шара лежит на грани в середине отрезка O ₁ O . Все боковые грани призмы — прямоугольники, причем грань — наибольшая из них (так как АВ — гипотенуза треугольника A ВС ). Эта грань по условию — квадрат. Сечение шара плоскостью грани — большой круг шара, поэтому радиус круга, изображенного на рис. 14, равен радиусу шара R . Заметим, что высота призмы АА ₁ = a ₄ = . Теперь остается найти площадь основания:

S _А _B _С = . Из (рис. 15)

имеем АС = АВ , значит,

S _А _B _С = .

Теперь получаем:

V _приз. .

По условию,

R ³ = V ,

откуда R ³ = ,следовательно,

V _приз.

Ответ: V _приз.

Рис.17

Пример 2. Найти отношение поверхности и объёма шара соответственно к поверхности и объёму вписанного куба

Решение. Пусть радиус шара равен R , ребро куба равно а;

тогда R ² - , откуда а= .

Обозначим объемы и поверхности шара и куба соответственно через V ₁ , V ₂ , и S ₁ , S ₂ .

Имеем

V ₁ =, V ₂ = = , S ₁ =4, S ₂ = 6а ² =8R ² ,

откуда

V ₁ V ₂ = , S ₁ S ₂ = .

Ответ: V ₁ V ₂ = , S ₁ S ₂ = .

2.3 Примеры олимпиадных заданий с цилиндром

Рис.18

Пример. Найдите отношение объёма шара к объёму прямого кругового цилиндра, вписанного в этот шар, если известно, что меньший угол между диагоналями осевого сечения цилиндра равен и диаметр основания больше высоты цилиндра (рис. 18).

Решение. Объём шара нам известен , а объём цилиндра найдём по формуле , но , поэтому

Пусть ABCD - осевое сечение цилиндра (см. рис. 18). Так как диаметр основания, больше высоты цилиндра, то – угол АОВ. Из треугольника АВО следует, что высота цилиндра

Радиус основания цилиндра

Угол .

Получается, что

Подставим найденные данные в формулу объёма цилиндра:

;

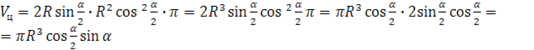Таким образом,

Найдём отношение

Ответ: .

2.4 Примеры олимпиадных заданий с конусом

Рис.19

Пример 1. В шар радиуса R вписан круговой конус; угол между образующими конуса в осевом сечении равен α. Найти высоту, образующую и радиус основания конуса.

Решение. Сечение шара, проходящее через ось конуса,— это большой круг шара, в который вписан АВ S (рис. 19), где A В — диаметр основания конуса. Продолжим высоту (ось) конуса SO до пересечения с окружностью большого круга в точке Е и рассмотрим Е S А:

в этом треугольнике

SE = 2R , S АЕ = 90° и А S Е= .

Поэтому

А S = 2R .

Теперь из А OS находим

A О = r = 2R , SO = h= 2R

Ответ : SO= 2R А S = 2R , A О =.

Пример 2. Отношению высоты конуса к радиусуописанного вокруг него шара равно k . Найти отношение объёмов этих тел. Выяснить при каких k задача имеет смысл.

Рис.20

Решение. Рассмотрим осевое сечение конуса (рис. 20). Пусть h — высота конуса, R — радиус шара, описанного около конуса. Тогда, по условию, =k , т. е. h = kR .

Выразим радиус r основания конуса через R ; рассмотрев хорды АС и ВЕ, получим:

В D D Е = А D D С (т. к. AD=DC ,

– прямоугольный, AD – высота, опущенного из вершины прямого угла).

T. е.

(следовательно, k < 2).

V _ш =; V _к == .

Таким образом,

, (при 0 < k < 2).

Ответ: , (при 0 < k < 2).

Пример 3. В усеченном конусе радиусы нижнего и верхнего оснований равны соответственно r ₁ и r ₂ , а образующая конуса наклонена к плоскости нижнего основания под углом α (рис. 21). Найти радиус шара, в который вписан данный усеченный конус.

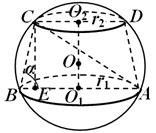
Рис.21

Решение. В сечении шара, проходящем через ось усеченного конуса, получается большой круг шара, в который вписана трапеция АВС D . Рассмотрим A ВС, который также вписан в большой круг шара. В этом треугольнике известен угол С BA = α . В силу теоремы синусов, АС = 2R . Таким образом, для определения R достаточно найти АС. Опустим из точки С перпендикуляр СЕ на АВ. Очевидно,

АЕ= r ₁ + r ₂ , ВЕ = r ₁ - r ₂ ,а СЕ = ( r ₁ - r ₂ ) .

Поэтому по теореме Пифагора

АС = = =

==, откуда R = .

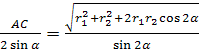Ответ: R .

3 Примеры заданий ЕГЭ

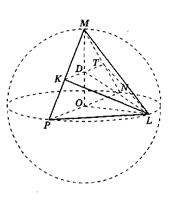
Рис. 22

3.1 Примеры заданий ЕГЭ с пирамидой

Пример 1. Отрезок Р N , равный 8, — диаметр сферы. Точки М, L лежат на сфере так, что объем пирамиды Р N М L наибольший (рис. 22). Найдите площадь треугольника К L Т, где К и Т — середины ребер РМ и N М соответственно.

Решение. Пусть О — центр сферы, а R — ее радиус. Поскольку Р N = 2R = 8 и точки М и L лежат на сфере, то ОР = О L = О N = ОМ = R = 4. Сечения сферы плоскостями Р LN и РМ N — окружности радиуса R = 4,описанные около треугольников Р LN и РМ N , причем РМ N = Р LN = 90°, как вписанные углы, опирающиеся на диаметр Р N .

Пусть Н — высота пирамиды, опущенная из вершины М , аh — высота треугольника Р LN , проведенная к стороне Р N . Поскольку точка М лежит на сфере, а плоскость Р LN содержит центр сферы, то Н R , причем Н = R , если МО Р NL . Аналогично, так как точка L лежит на сфере, то h R , причем h = R , если L О Р N .

Отсюда для объема пирамиды Р N М L имеем

При этом

если .

Таким образом, пирамида Р N М L имеет наибольший объем, если треугольники Р LN и РМ N прямоугольные, равнобедренные с общей гипотенузой Р N , лежащие во взаимно перпендикулярных плоскостях. Так как треугольники L О N , L ОР, L ОМ, РОМ, N ОМ равны по двум катетам, то треугольники L М N и L МР правильные со стороной

NL =Р L = ON =4

Отсюда следует, что медианы L К и L Т этих треугольников равны, причем

L К = = 2.

Треугольник К L Т равнобедренный, и его высота LD является медианой прямоугольного равнобедренного треугольника L ОМ. Отсюда

LD = = 2.

КТ — средняя линия треугольника РМ N и поэтому КТ = 0,5Р N =R . Следовательно, площадь S _К _L _Т = КТ LD = 4.

Ответ: 4.

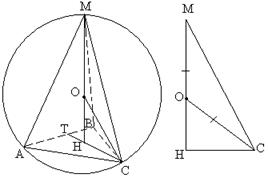
Рис.23

Пример 2. В правильной треугольной пирамиде сторона основания равна 5, а боковые рёбра наклонены к основанию под углом 60 ^о . Найдите радиус, описанной вокруг пирамиды сферы.

Решение. Пусть АВСМ указанная пирамида (см. рис. 23) Центр описанной сферы лежит на высоте пирамиды, т. к. пирамида правильная.

Основание высоты пирамиды – центр треугольника АВС , т. е. точка пересечения медиан. Тогда:

СН= СТ = СН= = = .

Теперь рассмотрим треугольник МНС. Здесь угол МСН равен 60^о , как угол между боковым ребром МС и основанием АВС . Угол НМС равен30. МО=ОС как радиусы. Значит, треугольник МОС равнобедренный. Как известно, в равнобедренном треугольнике углы при основании равны. Следовательно,

ОСМ = ОМС = 30, ОСН = МСН - МСО = 60 - 30= 30.

Из прямоугольного треугольника ОСН определим гипотенузу ОС , используя связь тригонометрических функций в прямоугольном треугольнике:

ОС = = .

Ответ: OC = .

3.2 Примеры заданий ЕГЭ с призмой

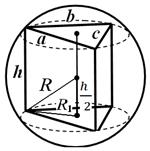
Рис.25

Пример 1. Основанием призмы служит треугольник со сторонами a , b , c . Высота призмы h (рис 25). Найти радиус описанной сферы.

Решение. Поскольку около призмы описана сфера, то призма прямая и её боковое ребро равно высоте. Радиус окружности, описанной около основания призмы, вычисляется по формуле

Тогда

Ответ:

Рис.26

Пример 2. Радиус шара R . В шар вписана правильная п-угольная призма, высота которой 2 h (рис 26). Найти сторону основания призмы.

Решение. Пусть К – центр описанного шара. Имеем: KB = R , OK = h . Пусть ОМ АВ , тогда

OB =

(из треугольника OKB ).

Из треугольника OMB находим

a = 2MB = 2OB .

Итак, a = .

Ответ: a = .

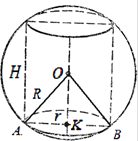
Рис.27

3.3 Примеры заданий ЕГЭ с цилиндром

Пример 1. Высота кругового цилиндра на 10 больше радиуса основания, а площадь полной поверхности равна 144 . Найдите радиус описанной сферы.

Решение. Радиус описанной сферы

(рис. 27).

Площадь поверхности цилиндра

, 144

144,

упростим данное выражение:

36.

Получим квадратное уравнение

Найдём корни этого уравнения

Корень не подходит, так как он отрицательный. Высота

Найдём радиус описанной сферы:

Ответ: .

Пример 2. В шар вписан прямой круговой цилиндр (рис. 28). Во сколько раз объём шара больше объёма цилиндра, если известно, что отношение радиуса шара к радиусу основания цилиндра вдвое меньше, чем отношение поверхности шара к боковой поверхности цилиндра.

Рис. 28

Решение. Отношение объёма шара к объёму вписанного цилиндра

По условию известно, что

; –

равносторонний

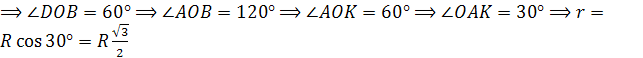
Найдём отношение объёмов шара и вписанного цилиндра

Ответ: 16:9.

3.4 Примеры заданий ЕГЭ с конусом

Рис. 29

Пример 1. Диаметр основания конуса равен 6 м, образующая наклонена к плоскости основания под углом 60° (рис. 29). Найдите площадь описанной около конуса сферы.

Решение. Пусть С - вершина конуса, О — центр его основания, АСВ - осевое сечение конуса. Поскольку образующая конуса наклонена к плоскости основания под углом 60° и СО — высота конуса, то прямая АВ - проекция прямой СА на плоскость основания конуса. Следовательно, САВ равен углу между образующей конуса и площадью его основания. Поэтому САВ= 60° и равнобедренный треугольник АВС — правильный. Отсюда следует, что

СА = АВ = ВС = 6м.

Найдем положение центра сферы, описанной около конуса. По определению такой сферы, окружность основания конуса — сечение описанной сферы и вершина конуса лежит на этой сфере. По свойству диаметра сферы, проходящего через центр любого ее сечения, прямая СО перпендикулярна плоскости основания конуса и поэтому центр О ₁ описанной сферы лежит на прямой СО. Отсюда следует, что центр О ₁ сферы, описанной около конуса, есть центр окружности, описанной около его осевого сечения.

В правильном треугольнике

АВС R = O ₁ C = (м)

Найдем площадь сферы:

(м² ).

Ответ: 48 м² .

Рис. 30

Пример 2. В шар радиуса R = 6 см вписан конус высотой h (рис. 30). Выразить объем и боковую поверхность конуса как функции аргумента h .

Решение. Имеем:

где r — радиус основания, L — образующая конуса.

Из учитывая, что r = ВА – высота, опущенная из вершины прямого угла на гипотенузу, имеем:

r ² = и . Или r ² и , .

Теперь получаем:

или .

Ответ:

Рис. 31

Пример 3. В шар вписан конус, образующая которого равна диаметру основания (рис 31). Найти отношение поверхности конуса к поверхности шара.

Решение. Изобразим осевое сечение конуса, которое пройдет через центр шара. Так как диаметр основания конуса равен образующей, то в сечении получим правильный треугольник, вписанный в окружность (рис. 31). Пустьрадиус шара равен R : тогда

АВ =R , А D =

Обозначим полную поверхность конуса через S ₁ , а поверхность шара через S ₂ . Имеем

откуда S ₁ : S ₂ = 9:16.

Ответ: S ₁ : S ₂ = 9:16.

Заключение

В процессе исследования мы выяснили, что задачи с описанной сферой достаточно часто предлагаются школьникам на ЕГЭ, поэтому умение решать задачи данного типа играет немало важную роль в успешной сдаче экзаменов. Так же задачи с описанной сферой часто встречаются на олимпиадах по математике различного уровня. Соответствующие примеры приведены в нашей работе. На данном этапе мы ограничились рассмотрением задач на комбинацию описанной сферы с пирамидой, призмой, цилиндром, конусом. Подобраны задачи для самостоятельной работы. В процессе выполнения работы нами были использованы следующие методы: работа с научной и научно-популярной литературой, сбор информации в сети Internet, анализ, систематизация, классификация и обработка на компьютере. В настоящий момент результаты представлены в виде реферата. В дальнейшем планируется дополнить работу новыми задачами.

Список литературы

1. Абрамович М.И., Стародубцев М.Т. Математика (геометрия и тригонометрические функции). Учебное пособие для подготовительных отделений вузов – М: Высшая школа, 1976. – 304 с.

2. Войтович Ф.С. Комбинации геометрических тел: (вписанные и описанные шары): Книга для учащихся. – Минск: Народная асвета, 1992. – 160 с.

3. Говоров В.М., Дыбов П.Т., Мирошин Н.В. И др. Список конкурсных задач по математике (с методическими указаниями и решениями): учебное пособие. – второе издание – М: Наука, 1986. – 384 с.

4. Денищева Л.О., Безрукова Г.К., Бойченко Е.М. и др. Единый государственный экзамен, математика, контрольные измерительные материалы – М: Просвещение 2005. – 80 с.

5. Денищева Л.О., Глазков Ю.А., Краснянская К.А. и др. Единый государственный экзамен. Математика. Учебно-тренировочные материалы для подготовки учащихся / ФИПИ – М: Интелект-Центр, 2008. – 240 с.

6. Дорофеев Г.В., Потапов К.М., Розов Н.Х. Пособие по математике для поступающих в вузы – М: Наука 1972. – 528 с.

7. Егерев В.К., Зайцев В.В., Кордемский Б.А. и др. 2500 задач по математике с решениями для поступающих в вузы: – М: ООО «Издательский дом «ОНИКС 21 век»: ООО «Издательство «Мир и Образование», 2002. – 912 с.

8. Звавич Л.И., Рязановский А.Р. Геометрия в таблицах – М: Дрофа 2007. – 128 с.

9. Климин С.В., Стрункина Т.В., Пантелеева Е.И. и др. Единый государственный экзамен, тестовые задания – М: Просвещение 2002. – 24 с.

10. Моденов В.П., Дорофеев Г.В., Новоселов С.И. и др. Пособие по математике – М: Издательство Московского университета, 1972. – 404 с.

11. Шувалова Э.З., Каплун В.И. Геометрия: учебное пособие для подготовительных отделений вузов – М: Высшая школа, 1980. – 265 с.

12. http://kvant.mirror1.mccme.ru/pdf/2000/06/kv0600solut.pdf

13. http://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D1%80%D1%82%D0%B0%D0%BB:%D0%9D%D0%B0%D1%83%D0%BA%D0%B0

14. http://rgp.nm.ru/geometriia/praktika11/zadatcha119.html

Приложение. Задания для самостоятельного решения

1. В пирамиде FABC грани ABF и ABC перпендикулярны, BF :FA = 15:11. Тангенс угла между прямой BC и плоскостью ABF равен 5. Точка М выбрана на ребре BC так, чтоB М :М C = 4:11. Точка Т лежит на прямой FA и равноудалена от точек М и В. Центр сферы, описанной около пирамиды FABC , лежит на ребре AB , площадь этой сферы равна 36. Найдите объём пирамиды АСМТ. (Ответ: 6)

2. Основанием пирамиды FABCD является прямоугольник ABCD . Плоскость AFC перпендикулярно плоскости ABC , тангенс угла FAC равен , тангенс угла между прямой BC и плоскостью AFC равен . Точка М лежит на ребре BC , ВМ =BC . Точка L лежит на прямой FA и равноудалена от точек М и C . Объём пирамиды L В D М равен 72. Центр сферы, описанной около пирамиды FABCD , лежит на плоскости её основания. Найдите радиус этой сферы. (Ответ: 5)

3. Около правильной пирамиды FABC описана сфера, центр которой лежит в плоскости основания ABC пирамиды. Точка М лежит на ребре AB так, что A М : М B =1:3. Точка Т лежит на прямой FA и равноудалена от точки М и В . Объём пирамиды ТВСМ равен . Найдите радиус сферы, описанной около пирамидыFABC . (Ответ: )

4. Отрезок AB – диаметр сферы. Точки С, D лежат на сфере так, что объём пирамиды ABCD наибольший. Найдите косинус угла между прямыми СМ и АВ, если М – середина ребра BD . (Ответ: )

5. Отрезок Р N , равный 8, - диаметр сферы. Точка М, L лежат на сфере так, что объём пирамиды Р N М L наибольший. Найдите площадь треугольника KLT , где K иT – середины рёбер РМ и N М соответственно. (Ответ: 4)

6. Дана сфера радиуса 6. Сечением сферы плоскостью является окружность с диаметром КТ . Плоскость сечения удалена от центра сферы на расстояние 5. Точка Р выбрана на сфере, а точкаL – на окружности сечения так, что объём пирамиды РК L Т наибольший. Найдите угол между прямой LM и плоскостьюPTK , если М середина ребра РК. (Ответ: 30)

7. Через центр О данной сферы проведено сечение. Точка F выбрана на сфере, а точки A , B , C , D – последовательно на окружности сечения так, что объём пирамиды FABCD наибольший. Точки М, Т, L – середины рёбер FB , CD иAD соответственно. Площадь треугольника MLT равна 64. Найдите радиус сферы. (Ответ: 2)

8. Через центр О данной сферы проведено сечение. Точка F выбрана на сфере, а точки A , B , C , D – последовательно на окружности сечения так, что объём пирамиды FABCD наибольший. Найдите синус угла между прямой АМ и плоскостью BFD . (Ответ: )

9. Дана сфера радиусом 10. Сечением этой сферы плоскостью является окружность с диаметром АВ. Плоскость сечения удалена от центра сферы на расстояние 8. Точка D выбрана на сфере, а точка С – на окружности сечения так, что объём пирамиды АВС D наибольший. Найдите площадь грани ACD .(Ответ: 27)

10. Основанием пирамиды является прямоугольник. Плоскость перпендикулярна плоскости АВС , тангенс угла между прямой ВС и плоскостью FAC равен 2. Точка М лежит на ребре ВС и МВ = Точка L лежит на прямой FA и равноудалена от точек М и С . Центр сферы, описанной около пирамиды FA В CD , лежит в плоскости основания пирамиды, радиус этой сферы равен 4. Найдите объём пирамиды LA МС. (Ответ: 48)

11. В шар, радиусом 2 вписана правильная треугольная призма АВСА ₁ В ₁ С ₁ . Прямая АС ₁ Образует с плоскостью АВВ ₁ угол 45. Найдите объём призмы. (Ответ: 288)

12. В шар вписана правильная треугольная призма АВСА ₁ В ₁ С ₁ , объём которой равен 4,5. Прямая ВА ₁ образует с плоскостью ВСС ₁ угол45. Найдите площадь поверхности шара. (Ответ: 11)

13. В шар радиусом вписана правильная треугольная призма АВСА ₁ В ₁ С ₁ . Прямая АВ ₁ образует с плоскостью АСС ₁ угол 45. Найдите объём призмы. (Ответ: 36)

14. Вычислить ребра правильной треугольной призмы, зная радиус R описанного шара и угол наклона α радиуса этого шара, проведенного в вершину призмы, к боковой грани, содержащей эту вершину. (Ответ: 2)

15. В шар радиуса R вписан прямой круговой конус. Найти боковую поверхность конуса, если его высота равна h . (Ответ: )

16. В шар вписан конус. Площадь осевого сечения конуса равна S . Угол между его высотой и образующей равен α . Найдите объём шара. (Ответ: )

17. Определите боковую поверхность конуса, зная длину радиуса R описанного вокруг него шара и угол α, под которым из центра шара видна образующая конуса. (Ответ: )

18. Найдите отношение площади полной поверхности прямого конуса, вписанного в шар, к площади поверхности этого шара, если что угол при вершине осевого сечения конуса равен α и . (Ответ: )

19. В шар вписан конус так, что его высота делится центром шара в среднем и крайнем отношении. Найти угол при вершине осевого сечения конуса. Определить, во сколько раз объем шара больше объема конуса. (Ответ: ; в 4 раза)