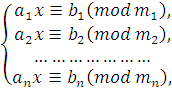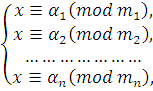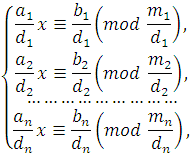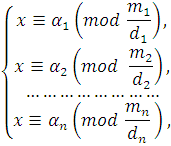Курсовая работа: Теория сравнений

Введение

Методы теории сравнений широко применяются в различных областях науки, техники, экономики. Этот раздел алгебры занимает важное место в вузовском образовании математиков, физиков и других специалистов, однако очень часто изучается недостаточно глубоко. Задача данной курсовой работы – изучить теоретический материал и рассмотреть ряд основополагающих задач по одному из основных разделов теории чисел: сравнения первой степени с одной и несколькими переменными, сравнения высших степеней и т.д.

Основная часть курсовой работы состоит из трех глав. В первой главе раскрываются основные понятия теории сравнений, такие как сравнения в кольце целых чисел, основные теоремы и свойства сравнений. Во второй главе рассматриваются сравнения первой степени с одной переменной. Далее рассматриваются сравнения высших степеней и системы сравнений первой степени. В приложении приводятся примеры решения текстовых задач, которые сводятся к неопределенным уравнениям первого порядка и решаются с помощью сравнений.

Изложение теоретического материала иллюстрируется большим количеством примеров с подробными решениями.

В работе приводится список литературы по теме.

1. Теория сравнений

1.1 Сравнения в кольце целых чисел

Понятие сравнения было введено впервые Гауссом. Несмотря на свою кажущуюся простоту, это понятие очень важно и имеет много приложений.

Возьмем произвольное фиксированное натуральное число и будем рассматривать остатки при делении на m различных целых чисел. При рассмотрении свойств этих остатков и произведении операций над ними удобно ввести понятие так называемого сравнения по модулю.

Определение . Целые числа и называются сравнимыми по модулю , если разность делится на , т.е. если .

Таким образом, сравнение представляет собой соотношение между тремя числами и , причем , играющее роль своего рода эталона сравнения, мы называем «модулем». Для краткости будем это соотношение между и записывать:

и будем называть соответственно левой и правой частями сравнения. Число , стоящее под знаком модуля, будем всегда считать положительным, т.е. запись будет означать, что .

Если разность не делится на , то мы будем записывать:

.

Согласно определению, означает, что делится на .

Примеры .

1. так как и делится на .

2. , так как и делится на .

3. , так как и делится на .

1.2 Основные теоремы о сравнениях

Теорема 1 (признак сравнимости двух чисел по модулю ). Два целых числа и сравнимы по модулю тогда и только тогда, когда и имеют одинаковые остатки при делении на .

Доказательство . Пусть остатки при делении и на равны, т.е.

где

Вычтем (1.2) из (1.1); получим т.е. или

Обратно, пусть это означает, что или

Разделим на ; получим Подставив в (1.3), будем иметь т.е. при делении на получается тот же остаток, что и при делении на .

Пример 1 . Определим, сравнимы ли числа и по модулю .

Решение. При делении и на получаются одинаковые остатки Следовательно,

Определение . Два или несколько чисел, дающие при делении на одинаковые остатки, называются равноостаточными или сравнимыми по модулю .

Теорема 2 . Отношение сравнимости рефлексивно: .

Доказательство . и имеют одинаковые остатки при делении на .

Теорема 3 . Отношение сравнимости симметрично: если , то .

Доказательство . Если и имеют одинаковые остатки при делении на , то остатки от деления и на также равны.

Теорема 4 . Отношение сравнимости транзитивно: если

то .

Доказательство . Если остатки от деления на одинаковы у чисел и , а также у и , то и тоже имеют одинаковые остатки при делении на .

Таким образом, отношение сравнимости есть отношение эквивалентности.

Теорема 5 . Если и произвольное целое число, то

.

Доказательство . Если , то , , , .

Теорема 6 . Если и 1 , то .

Доказательство . Если , то | , | , но тогда условие дает | , т.е. .

Теорема 7 . Если и произвольное натуральное число, то .

Доказательство . Если , то | ,| ,.

Теорема 8 . Если , где и произвольные натуральные числа, то.

Доказательство . Если , то | , | ,

натуральное (, тогда | , .

Теорема 9 . Если , , то и .

Доказательство . Если и , то и . Получим, что

Теорема 9' . Если , то .

Теорема 10 . Если и , то .

Доказательство . Если и , то и . Тогда по транзитивности сравнений получим, что .

Теорема 10' . Если , то

.

Доказательство . Последовательно применяя теорему 7, получим:

.

Теорема 11 . Если , то при любом целом ,.

Доказательство . При утверждение верно по теореме 2, а при оно верно согласно теореме 10', если и .

Переход от сравнений , к сравнениям

, ,

будем называть соответственно сложением (вычитанием), умножением, возведением в степень сравнений.

Так как из сравнения следует , то из сравнений и следует также, что и .

Теорема 12 . Если и произвольный многочлен с целыми коэффициентами, то .

Доказательство . Если , то, согласно теоремам 7 и 11, имеем:

при .

По теореме 9', получаем ,

т.е. .

Теорема 12' . Если и многочлен с целыми коэффициентами, то

.

Теорема 13 . Любое слагаемое левой или правой части сравнения можно перенести с противоположным знаком в другую часть.

Доказательство . Ввиду симметричности отношения сравнения достаточно рассмотреть случай, когда дано сравнение . Складывая это сравнение со сравнением , получаем .

Следствие . В левой и правой частях сравнения можно добавлять или отбрасывать одно и то же слагаемое.

Теорема 14 . В сравнении можно отбрасывать или добавлять слагаемые, делящиеся на модуль.

Доказательство . Если и , т.е. , то, складывая эти сравнения, получаем . Аналогично из и получаем .

Поскольку левую и правую части сравнения можно менять местами, утверждение верно и для слагаемых правой части.

Теорема 15 . Если и , то .

Доказательство . Если , то . Из , в силу транзитивности отношения делимости получаем , .

Теорема 16 . Если , то множество общих делителей и совпадает с множеством общих делителей и . В частности,

Доказательство . Если , то , , , любой общий делитель чисел и является общим делителем чисел и , и, наоборот, если и , то .

Поскольку пара и пара имеют одни и те же общие делители, то и .

Теорема 17 . Если , , то , где .

Доказательство . Если , , то , то и, согласно свойствам наименьшего общего кратного,.

2. Сравнения первой степени с одной переменной

2.1 Основные понятия

Определение 1 . Сравнением первой степени с одной переменной называется сравнение вида

где

Будем говорить, что целое число удовлетворяет сравнению (2.1), если верное сравнение.

Теорема 1 . Если целое число удовлетворяет сравнению (*), то и весь класс по состоит из чисел, удовлетворяющих этому сравнению.

Доказательство . Имеем: , отсюда получим, что . Обозначим через разность , то есть . Следовательно, . А так как число удовлетворяет сравнению (2.1), то сравнение

является верным. Кроме того,

Получим

Но тогда по свойству транзитивности из (2.2) и (2.3) получим, что

,

то есть удовлетворяет сравнению (2.1), поэтому весь класс , состоит из чисел, удовлетворяющих сравнению (2.1). Теорема 1 доказана.

Определение 2 . Решением сравнения (2.1) называется класс вычетов по , которые при подстановке в сравнение обращают его в верное сравнение.

Число решений сравнения по это число решений этого сравнения в какой-либо полной системе вычетов по модулю .

Примеры.

1) . Полная система наименьших неотрицательных вычетов по модулю 7: (так как классы вычетов будут ).

Если , то , следовательно, не удовлетворяет сравнению.

Если , то , следовательно, не удовлетворяет сравнению.

Если , то , следовательно, не удовлетворяет сравнению.

Если , то , следовательно, удовлетворяет сравнению, а поэтому класс вычетов по является решением сравнения.

Если , то , следовательно, не удовлетворяет сравнению.

Если , то , следовательно, не удовлетворяет сравнению.

Если , то , следовательно, не удовлетворяет сравнению.

Таким образом, сравнение имеет одно решение или, в другом виде, .

Ответ: .

2).

Классы вычетов по mod 10: . Полная система наименьших по абсолютной величине вычетов по mod 10: {0, 1, 2, 3, 4, 5, -4, -3, -2, -1}. Проверим для каждого из этих чисел, будет ли выполнено условие . Имеем:

Получили, что ни одно из чисел, взятых из полной системы вычетов, не удовлетворяет сравнению, следовательно, данное сравнение не имеет решения.

Ответ: .

2.2 Теорема о неразрешимости сравнения

Теорема 1 . Пусть дано сравнение

, . Тогда сравнение (2.4) не имеет решения.

Доказательство . От противного. Предположим, что существует решение: класс вычетов по mod m. Тогда удовлетворяет сравнению, то есть верное сравнение. Отсюда получим, что

Из условия теоремы: следует, что

Поэтому из (2.5) и (2.6) получим, что и , отсюда следует, что . Получили противоречие: так как сделали неправильное предположение. Отбросив его, получим, что сравнение (2.4) не имеет решения. Теорема 1 доказана.

2.3 Теорема о разрешимости сравнения

Рассмотрим сравнение:

где , , . Если и то сравнение не имеет решения.

Пусть теперь , тогда будем иметь:

Поэтому получим: . Так как по определению НОД число , то из последнего сравнения получим:

Таким образом, полагая в (1), что НОД, мы пришли к сравнению такого же вида, но с условием: . Исследуем этот случай.

Теорема 1 . Пусть дано сравнение (2.7) и НОД. Тогда сравнение (2.7) имеет единственное решение.

Доказательство. Так как НОД, то класс вычетов по mod m принадлежит мультипликативной группе классов вычетов, взаимно простых с mod m. Поэтому (по свойству группы) уравнение имеет единственное решение , где класс вычетов по mod m, взаимно простых с m. Значит, для , но тогда , отсюда . Обозначим через класс вычетов no mod m, тогда получим, что для следовательно, , a верное сравнение, то есть класс является решением сравнения (2.7). Это решение единственно, так как существует единственный класс . Теорема 1 доказана.

Пример 1 . НОД (5,9) = 1, следовательно, сравнение имеет одно решение. Найдем его способом «подбора», то есть перебирая все числа из полной системы вычетов по mod m : {0, 1, 2, 3, 4, 5, б, 7, 8} (m = 9 ).

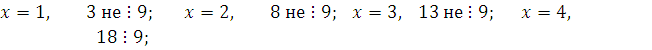
следовательно, удовлетворяет сравнению, поэтому решением будет класс вычетов по mod m или, по-другому, .

А так как данное сравнение имеет 1 решение, то остальные числа : 5, 6, 7, 8 проверять уже не надо.

Ответ: .

Заметим, что для нахождения решения сравнения первой степени с одной переменной (если оно есть) существует несколько способов:

1) подбора;

2) преобразования коэффициентов;

3) Эйлера (с помощью функции Эйлера);

4) цепных дробей.

Если модуль m является простым числом, то есть , число не делится на , то сравнение имеет единственное решение. Следовательно, множество классов вычетов образует поле по отношению сложения и умножения классов вычетов. Его обозначают через

Пример 2 . Вычислить остаток при делении на 15.

Решение . 1 способ. Сравнение для применения теоремы Эйлера сократим на 3 (очевидно, .

Так как , то по теореме Ферма показатель 99 можно уменьшить по модулю 4. Получаем, что из следует:

.

Умножаем на 3 обе части сравнения и модуль: , т.е.

.

Аналогично вычисляем . Отсюда почленным сложением сравнений найдем: . Затем, возводя в 100-ю степень обе части сравнения, получаем .

Ответ: 1.

2 способ. Сравнение рассмотрим отдельно по модулям 3 и 5 (делители 15). Так как и , то

,

.

Среди целых чисел от 0 до 14 (возможные остатки при делении на 15) только 1, 6, 11 сравнимы с 1 по модулю 5. А среди этих трех только 1 сравнима с 1 по модулю 3, т.е. . Тогда .

3 способ. Число не делится на 3 (первое слагаемое делится, а второе не делится) и не делится на 5. Так как 3 и 5 есть простые числа, то с ними взаимно просто и взаимно просто с 15. По теореме Эйлера

,

Ответ: 1.

Пример 3 . Разложить в цепную дробь. Проверить разложение, свернув цепную дробь последовательным вычислением подходящих дробей.

Решение . Найдём элементы цепной дроби как частные в алгоритме Евклида:

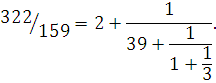
Сделаем сокращённую запись:

Пусть обозначает элемент цепной дроби, ю подходящую дробь, подходящей дроби. Будем вычислять подходящие дроби по рекуррентной формуле

,

используя схему:

Как видно, последняя подходящая дробь совпадает с исходным числом.

Замечание. Непосредственное сворачивание конечной цепной дроби «снизу вверх» обычно громоздко:

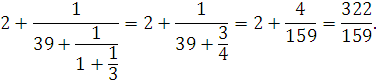
Задачи для самостоятельного решения .

Задача 1 . Сократите дробь , применяя алгоритм Евклида.

Задача 2 . Сколько натуральных чисел взаимно просто с 520 и не превосходит это число? (решить с помощью функции Эйлера)

Задача 3 . Решить сравнение

Задача 4 . Найти все целочисленные решения уравнения

2.4 Метод преобразования коэффициентов

Теорема 1 . Пусть дано сравнение:

НОД и Тогда класс вычетов по модулю m является решением сравнения (2.8).

Доказательство . Так как НОД, то сравнение имеет одно решение. Кроме того, Возьмем целое число , , тогда , следовательно, получим сравнение: , которое является верным сравнением.

Поэтому целое число удовлетворяет сравнению, а, значит, класс вычетов по модулю m является решением сравнения. Теорема 1 доказана.

Примеры.

1)

НОД, поэтому сравнение имеет единственное решение.

.

Найдем такое целое число k , чтобы делилось на 5. Например, . Тогда получим: , .

Проверка. , 18 делится на 9, поэтому при подстановке в сравнение вместо переменной значения 4, получим верное сравнение, следовательно, число 4 удовлетворяет сравнению, поэтому класс целых чисел, содержащий число 4, является решением сравнения.

Ответ:

2)

НОД, следовательно, сравнение имеет одно решение.

(при будет )

,

Ответ: .

2.6 Метод Эйлера

Получим метод решения сравнения

с помощью функции Эйлера.

Теорема 1 . Пусть дано сравнение (2.9), . Тогда класс вычетов

по модулю m является решением сравнения (2.9), где функция Эйлера.

Доказательство . Так как , то по теореме Эйлера имеет место сравнение где функция Эйлера

Выберем , тогда при подстановке его вместо в сравнение (2.9) и, учитывая, что

получим сравнение

которое является верным в силу теоремы Эйлера. Следовательно, удовлетворяет сравнению (2.9), а класс вычетов

по модулю m является решением сравнения, или, по-другому, решение сравнения (2.9). Теорема 1 доказана.

Примеры.

1)

, следовательно, сравнение имеет одно решение,

Преобразуем произведение . простое число, то . Поэтому

,

Ответ: .

2) .

, поэтому сравнение имеет одно решение.

1-й способ – способ подбора. Полная система наименьших по абсолютной величине вычетов по модулю 34: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 25, 26, 27, 28, 29, 30, 31, 32, 33}.

Проверим, какое из этих чисел удовлетворяет сравнению, то есть . Это будет , так как . Следовательно, решение сравнения.

Ответ: .

2-й способ – способ преобразования коэффициентов.

, k

Найдем такое целое число , при котором . Например, , тогда .

,решение сравнения.

Ответ:

3-й способ – метод Эйлера (с помощью функции Эйлера).

Упростим произведение

решение сравнения.

Ответ:

3. Сравнения высших степеней

3.1 Основные понятия

Определение 1. Сравнением n -й степени с одной переменной называется сравнение вида

где многочлен с целыми коэффициентами:

причем, .

Целое число удовлетворяет сравнению (3.1), если сравнение является верным сравнением.

Теорема 1 . Пусть дано сравнение (3.1) и целое число удовлетворяет сравнению (3.1). Тогда весь класс по mod m состоит из чисел, удовлетворяющих сравнению (3.1).

Доказательство . Число удовлетворяет сравнению (3.1), следовательно, верное сравнение. Для любого всегда . Но тогда по свойству сравнений , поэтому по транзитивности получим, что , отсюда следует, что число удовлетворяет сравнению (3.1). А так как произвольное из , то, следовательно, весь класс вычетов по mod m состоит из чисел, удовлетворяющих сравнению (3.1). Теорема 1 доказана.

Определение 2. Решением сравнения (3.1) называется класс вычетов по модулю m , состоящий из чисел, удовлетворяющих сравнению (3.1).

Если класс mod m является решением сравнения (3.1), то будем говорить, что класс удовлетворяет сравнению (3.1). Числом решений сравнения (3.1) называется число классов вычетов по mod m , удовлетворяющих сравнению (3.1).

Задача нахождения чисел, удовлетворяющих сравнению (3.1), сводится к нахождению классов, удовлетворяющих уравнению

Действительно:

· так как верно, то

· обратно, если , то , следовательно,

Чтобы решить сравнение , можно

1) взять любую полную систему вычетов по mod m :

2) вычислить

3) взять те числа , при которых сравнение является верным, то есть Соответствующие классы , дадут все решения сравнения.

Удобнее брать полную систему наименьших по абсолютной величине вычетов по mod . Если сравнение имеет несколько решений , то эти решения можно записывать в виде (то есть принимает любые значения, сравнимые с одним из чисел ) вместо записи

Примеры.

1) (mod 11).

классы вычетов по mod 11.

2)

Сравнение не имеет решения.

3)

Ответ:

Задача нахождения решения сравнения проще, чем рассматриваемая в курсе алгебры задача нахождения решения уравнения . Так как решая уравнение в некотором бесконечном множестве (R, С) нельзя перебрать все числа . А решая сравнение , ищем решение в конечном кольце Z_m классов вычетов по mod m . Следовательно, с помощью конечного числа операций можно найти все решения. Но надо заметить, что при больших m будут громоздкие вычисления, поэтому надо изучить способы, позволяющие определить число решений, а иногда и способы нахождения решения с помощью возможно меньшего числа операций.

3.2 Сравнения вида

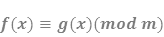
Рассмотрим сравнение с одной переменной вида

где , , коэффициенты при старшем члене и не делятся на m.

Определение 1. Решением сравнения (3.3) называется класс вычетов по mod m , состоящий из чисел, удовлетворяющих этому сравнению.

Теорема 1. Пусть и многочлены с целыми коэффициентами и целое число удовлетворяет сравнению (3.3). Тогда весь класс вычетов (mod m ) состоит из чисел, удовлетворяющих этому сравнению.

Доказательство.

1) Так как число удовлетворяет сравнению (3.3), то оно удовлетворяет сравнению , где .

2) mod m будет , следовательно, , поэтому число удовлетворяет сравнениюто есть сравнению . Следовательно, число удовлетворяет сравнению (3.3). Таким образом, класс вычетов состоит из чисел, удовлетворяющих сравнению (3.3). Теорема 1 доказана.

Определение 2 . Два сравнения

и

называются эквивалентными, если множество чисел, удовлетворяющих одному из них, совпадает с множеством чисел, удовлетворяющих другому сравнению.

Если и сравнения (3.4) и (3.5) имеют одни и те же решения, то получим два эквивалентных сравнения по .

Эквивалентные сравнения могут иметь разную степень.

Пример.

Решение первого сравнения: , решением второго сравнения тоже будет класс вычетов . Следовательно, они эквивалентны. Но степени их различны (степень первого сравнения равна 1, степень второго – 3).

3.3 Теоремы об эквивалентных сравнениях

Теорема 1. Пусть дано сравнение

где .

Тогда имеют место следующие утверждения:

1) Если к обеим частям сравнения (3.6) прибавить любой многочлен то получится сравнение, эквивалентное сравнению (3.6).

2) Если обе части сравнения (3.6) умножить на одно и то же целое число, взаимно простое с модулем, то получится сравнение, эквивалентное сравнению (3.6).

3) Если обе части сравнения и модуль умножить на одно и то же натуральное число , то получится сравнение, эквивалентное сравнению (3.6).

Доказательство.

1) Пусть класс вычетов но модулю решение сравнения (3.6), то есть для сравнение

2)

является верным сравнением, следовательно, сравнение

где , тоже верно. Поэтому класс вычетов по модулю является решением сравнения

Обратное также верно: если решение сравнения (3.9), то для , будет верно сравнение (3.8), а, следовательно, верно сравнение (3.7), поэтому является решением сравнения (3.6).

Таким образом, сравнения (3.6) и (3.9) эквивалентны.

3) Пусть класс вычетов по – решение сравнения (3.6), тогда для , получим верное сравнение . Возьмем целое число , взаимно простое с модулем: . Умножим последнее сравнение почленно на , получим верное сравнение:

отсюда получим, что класс вычетов по модулю решение сравнения

Обратно, если класс вычетов по модулю решение сравнения (3.11), то для верно сравнение (3.10), следовательно, будет верно и сравнение:

(заметим, что , так как , в противном случае было бы: ). Поэтому класс вычетов по модулю решение сравнения (3.6).

Таким образом, сравнения (3.6) и (3.11), где , будут эквивалентными.

3) Пусть класс вычетов по модулю решение сравнения (3.6), тогда для верно сравнение , а, значит, верно и сравнение

4)

для любого натурального числа , поэтому класс вычетов по модулю решение сравнения

Обратно, если класс вычетов по модулю решение сравнения (3.13), то для верно сравнение (3.12), но тогда по свойству сравнений верно сравнение: , поэтому класс вычетов по модулю решение сравнения (3.6). Следовательно, сравнения (3.6) и (3.13) эквивалентны. Теорема доказана.

В дальнейшем сравнение (3.6) можно заменить эквивалентным сравнением:

где Теорема 1 доказана.

Теорема 2. Пусть даны сравнения 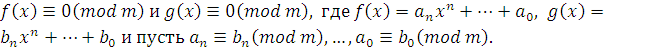Тогда сравнения эквивалентны.

Доказательство . Умножим почленно верные сравнения на некоторое целое число:

Сложим почленно полученные сравнения, тогда получим сравнение:

отсюда получим, что . Но тогда и . Следовательно, сравнения и эквивалентны. Теорема 2 доказана.

Заметим, из доказанной теоремы, в частности, следует, что сравнение заменится эквивалентным, если отбросить (или добавить) слагаемое с коэффициентами, делящимися на модуль.

3.4 Сравнения по простому модулю с одним неизвестным

Переходя от сравнений 1-й степени к сравнениям более высоких степеней, целесообразно сначала рассмотреть тот случай, когда модуль – простое число. В этом случае имеется ряд весьма важных теорем, которые, вообще говоря, неверны для составных модулей. Вместе с тем теория сравнений по простому модулю является основой, на которой строится изучение сравнений по составному модулю.

Во всей этой главе буквой будем обозначать модуль, представляющий собой простое число.

Теорема 1. Если , то сравнение

может быть заменено эквивалентным сравнением с коэффициентом при старшем члене, равном единице.

Доказательство. Рассмотрим сравнение 1-й степени ; поскольку то и сравнение имеет решение. Найдем число , удовлетворяющее этому сравнению, т.е. такое, что .

Тогда сравнение эквивалентно сравнению

,

а следовательно, сравнению

,

где .

Пример 1. Заменить сравнение

эквивалентным сравнением с коэффициентом при старшем члене, равным 1.

Решаем сравнение и находим . Данное нам сравнение эквивалентно сравнению

т.е. сравнению .

Теорема 2. Если и многочлены с целыми коэффициентами, то сравнения по простому модулю

эквивалентны.

Доказательство. Пусть удовлетворяет сравнению (3,15), т.е. . Поскольку при любом согласно теореме Ферма , то

.

Пользуясь той же теоремой Ферма, получаем, что если удовлетворяет сравнению (3,16), то , и, таким образом, сравнения (3,15) и (3,16) эквивалентны.

Из этой теоремы непосредственно вытекает следующая.

Теорема 3. Сравнение по простому модулю , степень которого больше, чем этот модуль или равна ему, может быть заменено эквивалентным сравнением степени, меньшей .

Доказательство. Пусть многочлен с целыми коэффициентами степени . При делении на ), частное и остаток будут также многочленами с целыми коэффициентами:

,

где степень меньше степени , т.е. меньше, чем . Согласно предыдущей теореме, сравнения и эквивалентны.

Пример 2. Сравнение заменить эквивалентным сравнением степени, меньшей чем 7.

Решение. Мы получим эквивалентное сравнение, если заменим на , на , на . Таким образом, заданное сравнение эквивалентно сравнению

т.е. сравнению .

Теорема 4. Если многочлены с целыми коэффициентами: , и все коэффициенты делятся на простое число , то любое решение сравнения

является решением, по крайней мере, одного из сравнений:

Доказательство. Пусть решение сравнения (3.17), т.е. . Поскольку все коэффициенты делятся на , будем также иметь , поэтому

Из сравнимости произведения с нулем по модулю следует, что по крайней мере один из этих множителей сравним с нулем по этому модулю, т.е. решение по крайней мере одного из сравнений (3.18).

Пример 3. В сравнении левую часть можно представить в виде , и мы находим все решения этого сравнения, решая сравнения: , , т.е. и . Все эти четыре класса удовлетворяют нашему сравнению.

Для составных модулей эта теорема неверна. Например, сравнению

удовлетворяет класс , не являющийся решением ни одного из сравнений:

,

Теорема 5. Сравнение степени по простому модулю с коэффициентом при старшем члене, не делящимся на , может иметь не больше чем решений.

Доказательство. Утверждение теоремы верно при . Действительно, в этом случае мы имеем сравнение 1-й степени: , где , т.е. , а такое сравнение имеет в точности одно решение. Применим теперь для доказательства теоремы метод полной математической индукции.

Предположим, что утверждение теоремы верно для всех многочленов () – й степени со старшими коэффициентами, не делящимися на простой модуль . Возьмем теперь произвольный многочлен – й степени:

,

где , и рассмотрим сравнение

Если это сравнение не имеет ни одного решения, то число решений меньше чем .

Если же это сравнение имеет решения, то возьмем любое число , удовлетворяющее ему, и разделим на . Согласно теореме Безу будем иметь:

.

Коэффициенты многочлена -й степени могут быть найдены по схеме Горнера и представляют собой целые числа, причем .

Поскольку удовлетворяет сравнению (3.19), , то все решения (3,19) находятся среди решений сравнений и , удовлетворяя либо одному из них, либо обоим.

Сравнение имеет одно решение, а сравнение представляет собой сравнение ( ) – й степени по простому модулю с коэффициентом при старшем члене , не делящемся на , и, по предположению, может иметь не больше чем решений. Таким образом, сравнение (5) имеет не больше, чем , т.е. не больше чем решений.

Согласно принципу математической индукции справедливость теоремы доказана.

Пример 4. удовлетворяет сравнению Найти все решения этого сравнения.

Очевидно, что вместе с классом этому сравнению удовлетворяет и класс . Коэффициент при старшем члене не делится на простой модуль , поэтому сравнение не может иметь больше двух решений.

Ответ . .

Для составных модулей эта теорема неверна. Сравнение степени по составному модулю с коэффициентом при старшем члене, не делящемся на модуль или даже взаимно простом с модулем, может иметь больше чем решений. Например, сравнение имеет 4 решения: .

Теорема 6. Если сравнение степени по простому модулю имеет больше чем решений, то все коэффициенты сравнения делятся на .

Доказательство. Возьмем любое простое число . Если сравнение имеет больше чем одно решение, то , т.е. . Таким образом, при теорема верна. Предположим, что утверждение теоремы верно для многочленов степени, меньшей чем , т.е. предположим, что число решений сравнения степени, меньшей чем , может превосходить степень сравнения только тогда, когда все коэффициенты делятся на модуль .

Возьмем любое сравнение степени :

имеющее больше чем решений. В таком сравнении делится на , а тогда сравнение

эквивалентное сравнению (3.20), также имеет больше чем решений.

В сравнении (3.21), степень которого меньше чем , а число решений превосходит степень согласно предположению, все коэффициенты должны делиться на , т.е. . Поскольку уже раньше было установлено, что , утверждение теоремы верно для . Согласно принципу математической индукции справедливость теоремы доказана.

Теорема 7. Пусть многочлен с целыми коэффициентами и свободным членом , где простое число, причем . Сравнение имеет решений тогда и только тогда, когда все коэффициенты остатка от деления на кратны .

Доказательство. Пусть , где и многочлены с целыми коэффициентами, причем степень меньше чем .

1) Докажем достаточность условия. Пусть коэффициенты делятся на .

Обозначим через и соответственно число решений сравнений

Сравнение по теореме Ферма имеет решений. Каждое из этих решений является решением хотя бы одного из сравнений: (3.22) или (3.23), т.е.

Сравнение (3.23) степени имеет коэффициент при старшем члене, равный единице, так что и, следовательно,

.

Поскольку при этом , получаем , т.е. из делимости коэффициентов на следует, что число решений сравнения (3.22) равно .

2) Докажем необходимость условия. Пусть сравнение (3.22) имеет решений. Если решение сравнения (3.22), то и вместе с тем, поскольку , то , а, следовательно, согласно теореме Ферма, , так что

Таким образом, каждое из решений сравнения (3.22) является решением сравнения , степень которого меньше чем . Следовательно, все коэффициенты делятся на .

Пример 5. Сравнению удовлетворяют классы и . Имеет ли это сравнение еще одно решение?

Делим на , находим:

так что и, следовательно, это сравнение имеет три решения.

3.5 Сравнения по простому модулю с несколькими неизвестными

Некоторые из рассмотренных нами теорем можно легко обобщить на случай сравнений с несколькими неизвестными вида:

где многочлен с целыми коэффициентами, а простое число.

Теорема 1. Если в левой части сравнения (3.24) некоторые из неизвестных встречаются в виде степени с показателем , то сравнение (3.24) можно заменить эквивалентным сравнением, в котором степень каждого из неизвестных не превосходит .

Доказательство. Сравнение (3.24) эквивалентно сравнению

где произвольный многочлен с целыми коэффициентами.

Если среди слагаемых есть член вида

где , то мы можем, взяв

,

заменить его членом , затем и т.д.

Если где , то в показателе для можно отбросить и получить эквивалентное сравнение, в котором слагаемое будет заменено на Проделав такие операции для всех слагаемых по отношению к каждому из неизвестных, входящему с показателем , получим сравнение, эквивалентное первоначальному, в котором степень по отношению к каждому неизвестному будет не больше чем .

Теорема 2. Если сравнение степень которого по каждому неизвестному меньше чем , удовлетворяется при всех целых , то все коэффициенты многочлена делятся на .

Доказательство. Проведем индукцию по числу неизвестных . При утверждение теоремы верно. Предположим, что утверждение теоремы верно при , и возьмем произвольное тождественное сравнение , степень которого по каждому неизвестному меньше чем . Если наибольший показатель степени неизвестного , то сравнение можно представить в виде:

где все многочлены с целыми коэффициентами, степени которых по каждому неизвестному меньше чем . Если вместо подставить любые целые числа, то получим тождественное сравнение с неизвестной степени . Все коэффициенты этого сравнения: должны при любых значениях делиться на . Поскольку согласно предположению для многочленов от аргументов утверждение теоремы верно, все коэффициенты этих многочленов, а следовательно, и многочлена должны делиться на .

Согласно принципу полной математической индукции утверждение теоремы верно для любого числа аргументов.

4. Системы сравнений

4.1 Системы сравнений первой степени

Систему сравнений первой степени с одним и тем же неизвестным, но с разными модулями, запишем в общем виде так:

Общий способ (способ последовательного решения) состоит в том, что сначала находится из первого сравнения, где – наименьший неотрицательный или абсолютно наименьший вычет по модулю и берется класс чисел

удовлетворяющих первому сравнению.

Затем это значение подставляется во второе сравнение, что дает

откуда находится опять в виде класса чисел и подставляется в равенство (.

В результате получается значение в виде класса чисел, удовлетворяющих первым двум сравнениям системы. Дальше это значение подставляется в третье сравнение системы, так же находится , затем находится и подставляется в четвертое сравнение системы и т.д.

Заметим, что можно идти и несколько иным путем: сначала решается каждое из сравнений системы и представляется в виде:

а затем поступают описанным способом.

Если окажется, что хотя бы одно из сравнений системы (4.1) не имеет решения или сравнение относительно в описанном способе неразрешимо, то система (4.1) не имеет решения.

Если для сравнений системы (4.1) и то, сокращая члены и модуль каждого сравнения на получаем систему:

эквивалентную (4.1).

Сравнения этой системы можно решить относительно и свести решение системы (4.3) к решению системы:

Если в системе (4.2) модули попарно просты, то решение ее можно находить не указанным выше общим способом, а по формуле:

где и есть решения сравнений:

Решением системы будет:

Этим способом можно решать и систему (4.4), если модули попарно просты.

Пример 1 . Решить систему сравнений:

Классы вычетов по : при имеем:

1) , следовательно, удовлетворяет первому сравнению системы,

2) , следовательно, удовлетворяет второму сравнению системы.

Поэтому класс вычетов является решением системы. Можно записать этот класс иначе: прибавив к модуль 9, получим, что

Итак, данная система сравнений имеет решение

Заключение

В работе изложены основы теории сравнений. Задача данной курсовой работы разработка учебного пособия, которое содержит достаточный теоретический и практический материал.

В данной работе достаточно полно изложены основные моменты теории, они иллюстрируются примерами, которые позволяют глубже понять рассматриваемые вопросы.

Материал курсовой работы может быть использован как при изучении соответствующего курса теории чисел, так и для спецкурсов по алгебре, в частности, для тех специальностей, на которых нет курса теории чисел, уже на младших курсах обучения.

Приведенный список литературы позволяет при необходимости рассмотреть некоторые более сложные моменты теории сравнений и их приложений.

Литература

1. Бухштаб А.А. Теория чисел. – М.: Просвещение, 1960. – 376 с.

2. Алгебра и теория чисел: Уч. пособие. под ред. Н.Я. Виленкина. – М.: Просвещение, 1984. – 192 с. (гл. 3).

3. Вахитова Е.В. Теория сравнений и ее приложения. – Стерлитамак: Изд-во СГПИ, 2000. – 414 с.

4. Фаддеев Д.К., Соминский И.С. Сборник задач по высшей алгебре. – М.: Наука, 1984. – 288 с.

5. Лельчук М.П., Полевченко И.И., Радьков А.М., Чеботаревский Б.Д. Практические занятия по алгебре и теории чисел. – Минск: Высш. Школа, 1986. – 302 с. (Занятия 46–51).

6. Шнеперман Л.Б. Сборник задач по алгебре и теории чисел. – Мн.: Высш. шк., – 1982. – 223 с.

7. Михелович Ш.Х. Теория чисел. М.: Высшая Школа, 1967. – 335 с.

8. Грибанов П.И., Титов П.И. Сборник упражнений по теории чисел. М. Просвещение 1964.

9. Александров В.А., Горшенин С.М. Задачник-практикум по теории чисел. М.: Просвещение 1960. – 48 с.