| Скачать .pptx |
Презентация: Геометрическая пирамида и ее проекция
Презентацию готовили
¨ Дасиева Роза,
¨ Набоко Михаил,
¨ Ибрагимова Карина,
¨ Егизбаева Айнура,
¨ Асанова Эльвира,
¨ Ускенбаева Мадия.
О слове пирамида.
Пирамида.
Слово «пирамида» в геометрию ввели греки,
которые, как полагают, заимствовали его
у египтян, создавших самые знаменитые
пирамиды в мире. Другая теория выводит
этот термин из греческого слова «пирос»
(рожь) – считают, что греки выпекали хлебцы,
имевшие форму пирамиды.
Что же такое пирамида?
Пирамида - многогранник, у которого основание- многоугольник, боковые грани- треугольники, имеющие общую вершину.
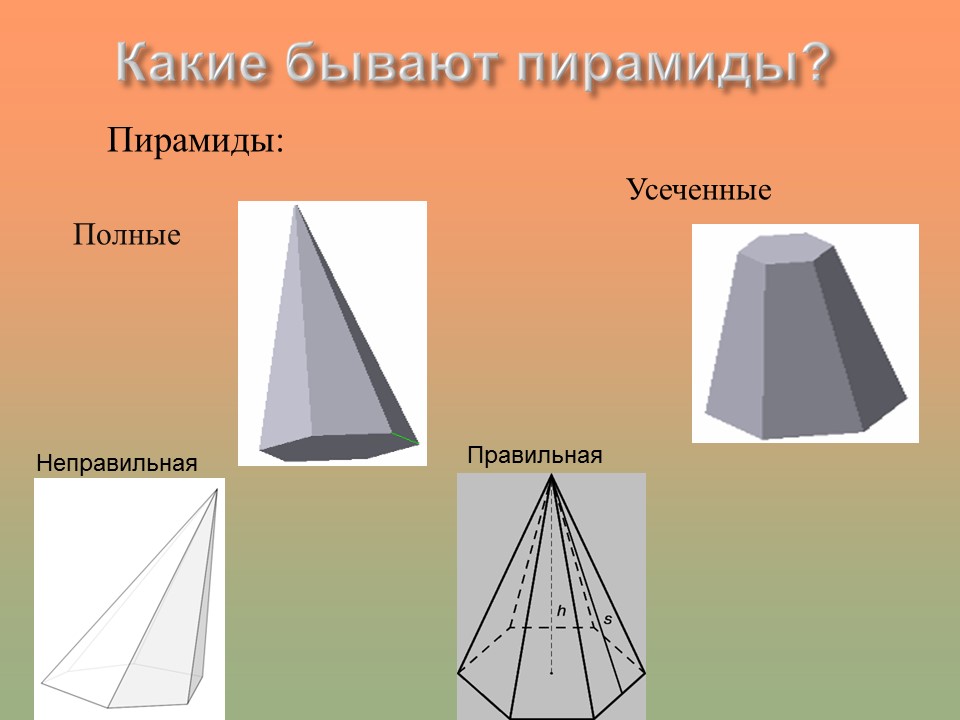
Пирамиды:
Полные
От чего зависит вид пирамиды?
Вид пирамиды зависит от многоугольника, который лежит в основании.
Проекция пирамиды
¨ Пирамида треугольная
¨ Пирамида – это многогранник, одна из граней которого – произвольный n – угольник A1 A2 …An , а остальные грани – треугольники с общей вершиной.
Этот n – угольник A1 A2 …An называется основанием пирамиды.
¨ Треугольные грани называются боковыми гранями.
¨ Общая вершина всех боковых граней называется вершиной пирамиды.
¨ Отрезки, соединяющие вершину пирамиды с вершинами основания называются боковыми рёбрами.
¨ Объединение боковых граней пирамиды называется её боковой поверхностью.
¨ Перпендикуляр, проведённый из вершины пирамиды к плоскости основания, называется высотой пирамиды.
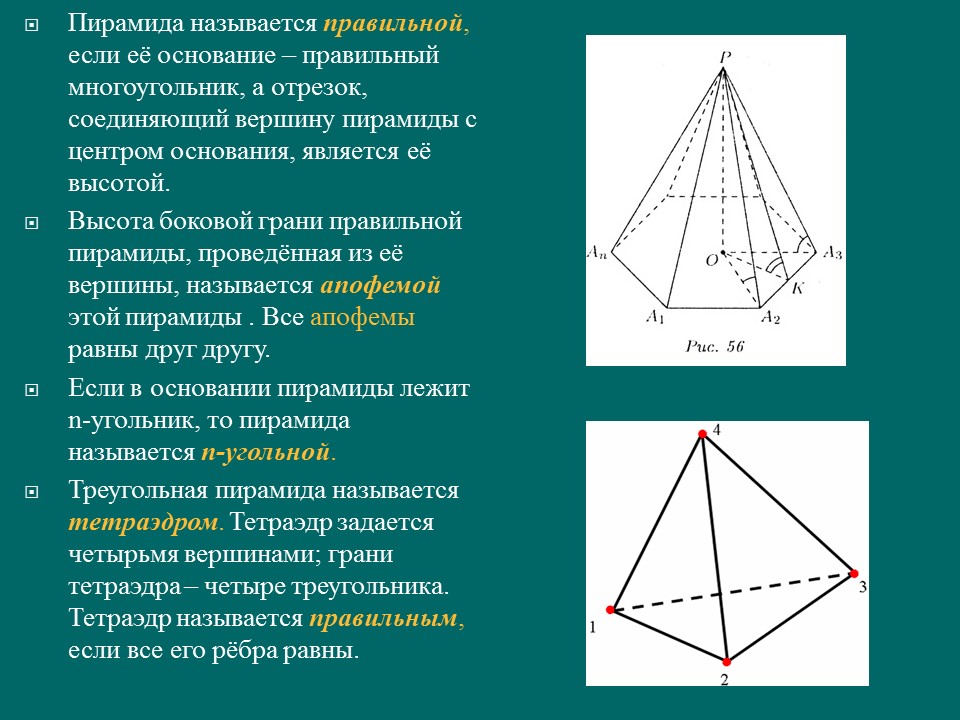
¨ Пирамида называется правильной , если её основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является её высотой.
¨ Высота боковой грани правильной пирамиды, проведённая из её вершины, называется апофемой этой пирамиды . Все апофемы равны друг другу.
¨ Если в основании пирамиды лежит n-угольник, то пирамида называется n-угольной .
¨ Треугольная пирамида называется тетраэдром . Тетраэдр задается четырьмя вершинами; грани тетраэдра – четыре треугольника. Тетраэдр называется правильным , если все его рёбра равны.
Свойства пирамиды
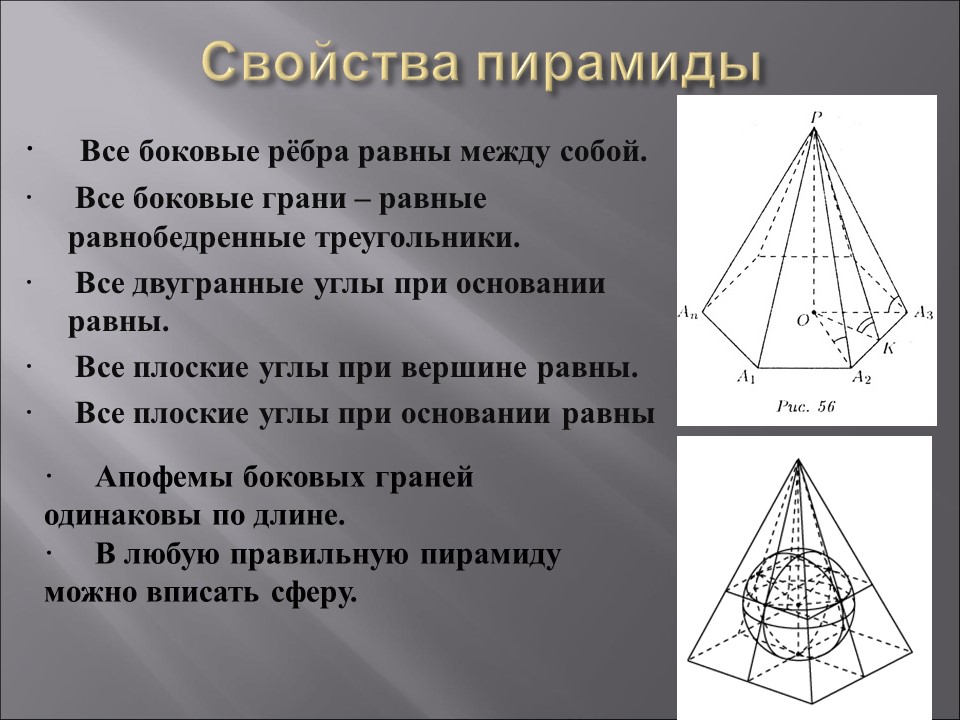
· Все боковые рёбра равны между собой.
· Все боковые грани – равные равнобедренные треугольники.
· Все двугранные углы при основании равны.
· Все плоские углы при вершине равны.
· Все плоские углы при основании равны
Площадь пирамиды
¨ Площадью полной поверхности пирамиды называется сумма площадей всех её граней.
Sполн =Sбок +Sосн
Обьём пирамиды
¨ Объём пирамиды
V=(1/3)*Sосн *h,
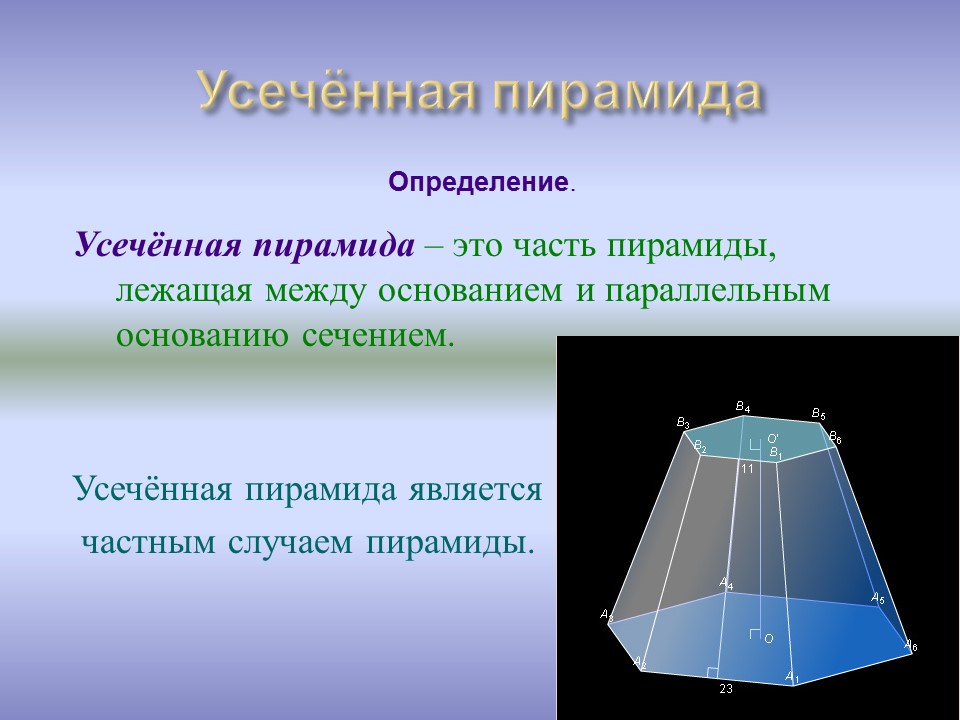
Усечённая пирамида
Усечённая пирамида – это часть пирамиды, лежащая между основанием и параллельным основанию сечением.
Усечённая пирамида является
частным случаем пирамиды.
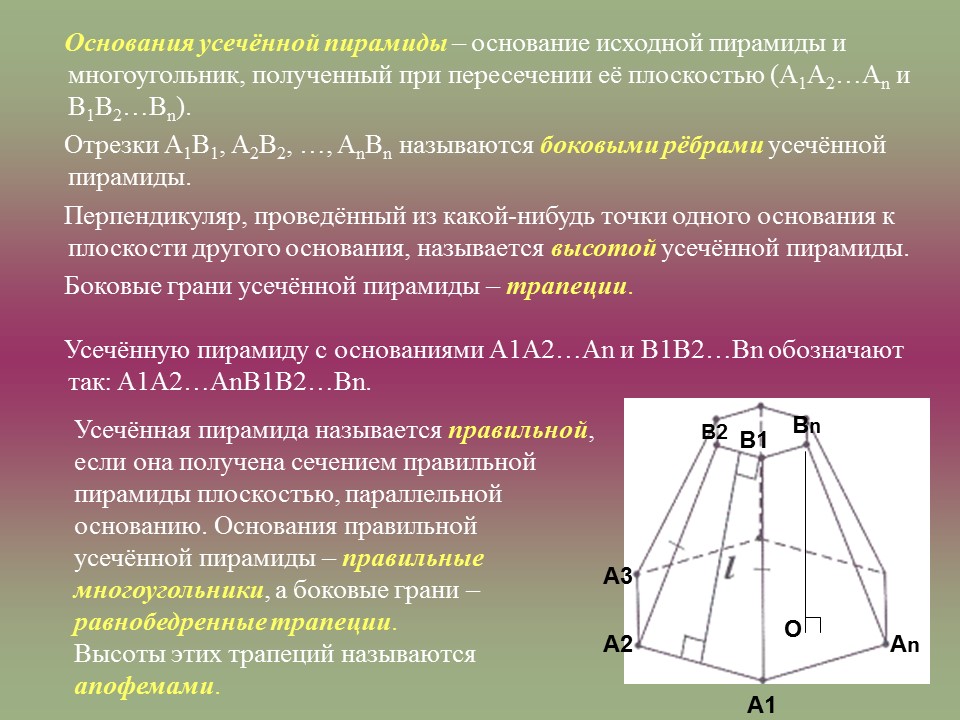
Основания усечённой пирамиды – основание исходной пирамиды и многоугольник, полученный при пересечении её плоскостью (A1 A2 …An и B1 B2 …Bn ).
Отрезки A1 B1 , A2 B2 , …, An Bn называются боковыми рёбрами усечённой пирамиды.
Перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания, называется высотой усечённой пирамиды.
Боковые грани усечённой пирамиды – трапеции .
Усечённую пирамиду с основаниями A1A2…An и B1B2…Bn обозначают так: A1A2…AnB1B2…Bn.
Свойства усечённой пирамиды.
¨ 1. Боковые рёбра и высота пирамиды делятся секущей плоскостью на пропорциональные отрезки.
¨ 2. В сечении получ ает ся многоугольник, подобный многоугольнику, лежащему в основании.
¨ 3. Площади сечения и основания будут относится между собой, как квадраты их расстояний от вершины пирамиды.
Площадь поверхности правильной усечённой пирамиды:
S=(1/2)*m*(P+P1 ), где m – апофема, P- периметр оснований, P 1 - периметр боковой поверхности.
Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему:
Sбок =1/2*(Рв +Рн )* m, где m – апофема, Рв , Рн – периметр верхнего и нижнего оснований
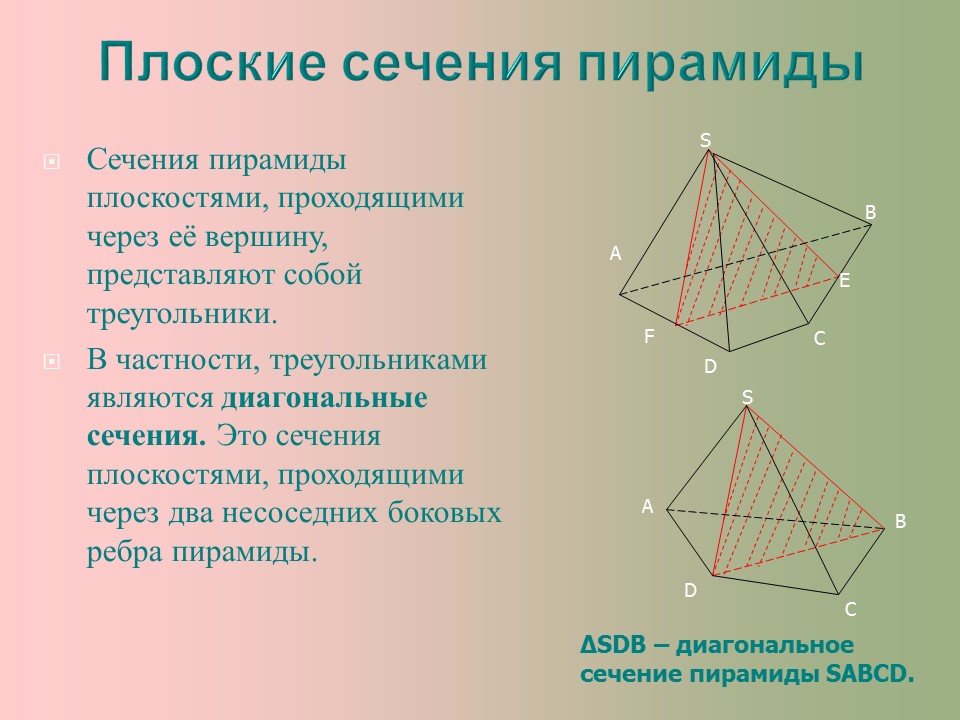
Плоские сечения пирамиды
¨ Сечения пирамиды плоскостями, проходящими через её вершину, представляют собой треугольники.
¨ В частности, треугольниками являются диагональные сечения. Это сечения плоскостями, проходящими через два несоседних боковых ребра пирамиды.
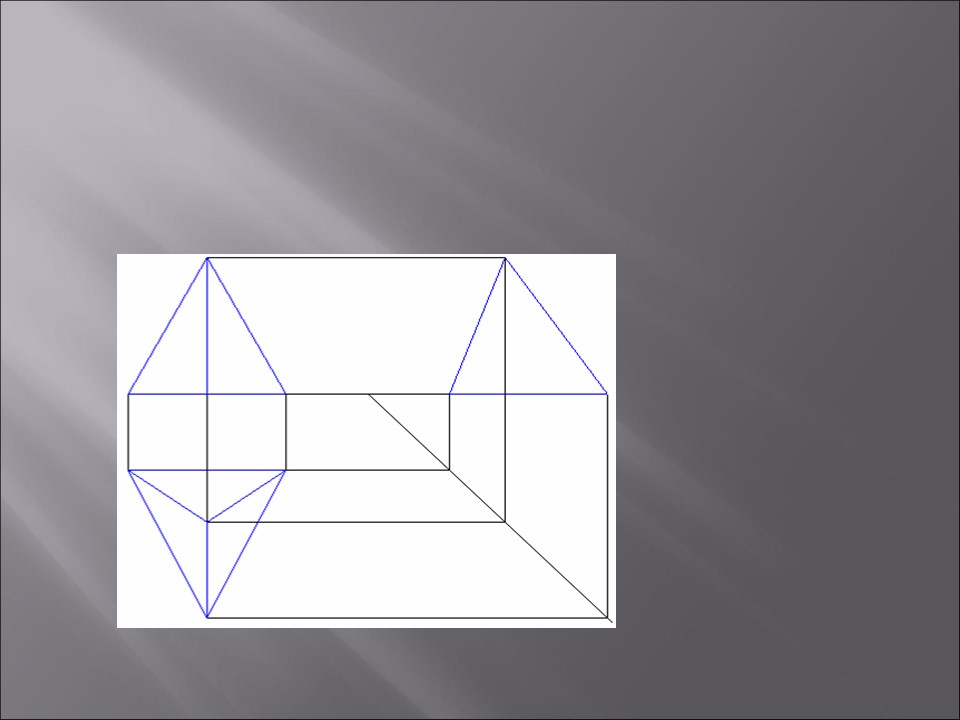
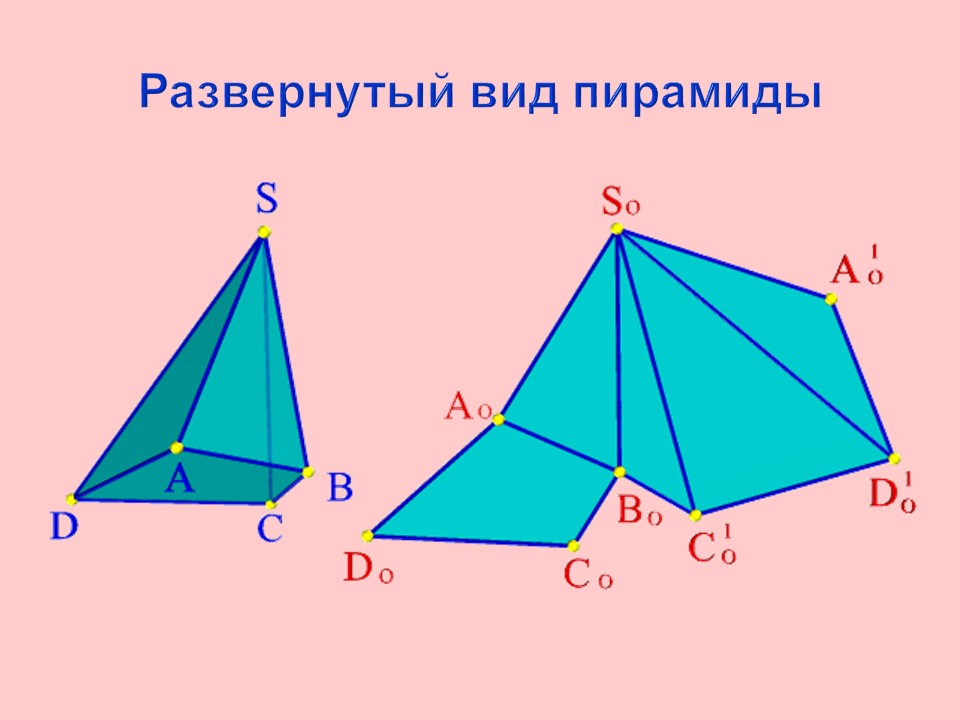
Развернутый вид пирамиды