| Скачать .docx | Скачать .pdf |
Книга: Решение систем линейных алгебраических уравнений для больших разреженных матриц
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГO
ОБРАЗОВАНИЯ
“ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ”
В.А.Еремеев
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ ДЛЯ БОЛЬШИХ РАЗРЕЖЕННЫХ МАТРИЦ
(учебно-методическое пособие)
Ростов-на-Дону
2008
В.А.Еремеев. Решение систем линейных алгебраических уравнений для больших разреженных матриц: Учебно-методическое пособие. – г.Ростов-на-Дону, 2008 г. – 39 с.
В данном пособии в концентрированном виде содержится информация о решении систем линейных алгебраических уравнений для разреженных матриц большой размерности. Пособие состоит из четырех основных модулей:
1. задачи линейной алгебры с разреженными матрицами на примере дискретизации уравнения Пуассона;
2. векторные и матричные нормы;
3. итерационные методы;
4. методы подпространств Крылова.
Пособие предназначено для преподавания дисциплин в рамках магистерской образовательной программы “Математическое моделирование и компьютерная механика”.
Пособие также предназначено для студентов и аспирантов факультета математики, механики и компьютерных наук, специализирующихся в области математического моделирования, вычислительной математики и механики твердого деформируемого тела.
Пособие подготовлено в рамках гранта ЮФУ K-07-T-41.
Содержание
1 Задачи линейной алгебры с разреженными матрицами на примере дискретизации уравнения Пуассона 4
1.1 Решение уравнения −x 00 = f (t ) . . . . . . . . . . . . . . . 4
1.2 Решение уравнения Пуассона . . . . . . . . . . . . . . . . 6
2 Векторные и матричные нормы 11
2.1 Векторные нормы . . . . . . . . . . . . . . . . . . . . . . 11
2.2 Матричные нормы . . . . . . . . . . . . . . . . . . . . . . 13
2.3 Связь векторных и матричных норм . . . . . . . . . . . 15
3 Итерационные методы 19
3.1 Определения и условия сходимости итерационных методов 19
3.2 Метод простой итерации . . . . . . . . . . . . . . . . . . . 23
3.3 Метод Якоби . . . . . . . . . . . . . . . . . . . . . . . . . 24
3.4 Метод Гаусса-Зейделя . . . . . . . . . . . . . . . . . . . . 25
3.5 Метод последовательной верхней релаксации (SOR) . . . 26
3.6 Метод симметричной последовательной верхней релак-
сации (SSOR) . . . . . . . . . . . . . . . . . . . . . . . . . 27
4 Методы подпространств Крылова 30
4.1 Инвариантные подпространства . . . . . . . . . . . . . . 30
4.2 Степенная последовательность и подпространства Кры-
лова . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
4.3 Итерационные методы подпространств Крылова . . . . . 33
Заключение 38
Литература 38
Дополнительная литература 39
1 Задачи линейной алгебры с разреженными матрицами на примере дискретизации уравнения Пуассона
Основным источником задач линейной алгебры для матриц большой размерности являются задачи, получаемые в результате дискретизации краевых задач математической физики. Далее рассмотрим два примера, иллюстрирующих особенности получаемых матричных задач.
1.1 Решение уравнения −x 00 = f (t )
Рассмотрим простейшую краевую задачу
−x 00 = f (t ), x (0) = x (1) = 0.
Для дискретизации этой краевой задачи воспользуемся методом конечных разностей. Введем равномерную сетку на единичном отрезке
ti = hi, i = 0,...n + 1, h = 1/ (n + 1)
так, чтобы t 0 = 0, tn +1 = 1. Используем обозначения
xi = x (ti ), fi = f (ti ).
Для дискретизации второй производной воспользуемся центральной конечной разностью
![]() ,
,
которая аппроксимирует x 00 (ti ) c точностью O (h 2 ). Тогда исходная краевая задача сводится к системе линейных алгебраических уравнений (СЛАУ) относительно
−xi −1 + 2xi − xi +1 = h 2 fi (i = 1,...,n )
или c учетом краевых условий x 0 = xn +1 = 0
2x 1 − x 2 = = h 2 f 1 ,
−x 1 + 2x 2 − x 3 = h 2 f 2 ,
![]() ,
,
![]() .
.
Эту СЛАУ можно записать также в матричном виде
A x = b,
где
2 −1 A = 0 |
−1 0 2 −1 −1 2 |
... ... ... ... |
0 0 0 |
0 0 0 , |
0 0 0 ... −1 2
x 1 x 2 x 3 , x = ... xn |
b 1 b 2 b 3 b = ... b n |
Обратим внимание на следующие свойства матрицы A .
• A – разреженная матрица, она трехдиагональная;
• A – симметричная и, более того, положительно определенная. Это свойство она унаследовала от свойств оператора исходной краевой задачи;
• Структура A достаточно простая, ее элементы вычисляются по простым формулам. Следовательно, для ее хранения в памяти компьютера нет необходимости использовать типы данных, предназначенные для хранения заполненных матриц.
Обсудим размерность полученной СЛАУ. Предположим, что требуемая точность аппроксимации равна ² = 10−6 . Поскольку ² ∼ h 2 , то
![]() −3
, т.к. h
∼ √²
. Т.е. требуемый шаг сетки нужно выбрать порядка 10 мы имеем матрицу размерности 103
× 103
. На практике, размерность должна быть выше, чтобы удовлетворить большей точности.
−3
, т.к. h
∼ √²
. Т.е. требуемый шаг сетки нужно выбрать порядка 10 мы имеем матрицу размерности 103
× 103
. На практике, размерность должна быть выше, чтобы удовлетворить большей точности.

0 1
Рис. 1: Конечно-разностная сетка. Естественная нумерация узлов.
1.2 Решение уравнения Пуассона Рассмотрим более сложную краевую задачу
−∆u (x,y ) = f (x,y ), u |Γ = 0,
где u = u (x,y ) – неизвестная функция, f (x,y ) – известная, заданные на единичном квадрате (x,y ) ∈ Ω = [0, 1]×[0, 1]}, Γ = ∂ Ω – граница Ω. Введем на Ω равномерную сетку, так что координаты узлов даются формулами xi = hi, yi = hi, i = 0,...N + 1, h = 1/ (N + 1).
Используем обозначения
u i,j = u (x i ,y j ), f i,j = f (x i ,y j ).
Для дискретизации вторых производных в операторе Лапласа ∆ воспользуемся формулами для центральной конечной разности
 ,
,
Таким образом, исходная краевая задача сводится к СЛАУ
−u i −1,j + 4u i,j − u i +1,j − u i,j −1 − u i,j +1 = h 2f i,j (1) относительно ui,j . Для того, чтобы свести ее к стандартному виду A x = b, необходимо преобразовать ui,j к выражению с одним индексом, т.е. перенумеровать каким-то образом. Выбор нумерации влияет, вообще говоря, на структуру матрицы A .
Рассмотрим случай N = 3. Соответствующая сетка показана на рис. 1, где использована естественная нумерация внутренних узлов. Полые кружки соответствуют граничным узлам, в которых известно значение функции, а сплошные – внутренним.
Если преобразовать конечно-разностное уравнение (1) в матричное уравнение A x = b, вводя вектор неизвестных по правилу u 1, 1 = x 1, u 1, 2 = x 2, u 1, 3 = x 3, u 2, 1 = x 4,..., u 3, 3 = x 9,
| то матрица A принимает вид | ||||||||
| | −1 0 0 4 −1 0 −1 0 0 |
0 −1 0 −1 4 −1 0 −1 0 |
0 0 −1 0 −1 4 0 0 −1 |
0 0 0 −1 0 0 4 −1 0 |
0 0 0 0 −1 0 0 4 −1 |
0 0 0 0 0 −1 0 −1 4 |
||
4 −1 0 −1 A = 0 0 0 0 0 |
−1 4 −1 0 −1 0 0 0 0 |
0 −1 4 0 0 −1 0 0 0 |
||||||
Видно, что A является симметричной ленточной разреженной матрицей с диагональным преобладанием.
В результате нужно отметить, что в целом, матрица A обладает теми же свойствами, что и в случае одномерной, задачи, хотя ее структура может не быть ленточной, что зависит от способа нумерации узлов сетки
Обсудим размерность полученной СЛАУ. Предположим как и ранее, что требуемая точность аппроксимации равна ² = 10−6 . Поскольку ² ∼ h 2 , то требуемый шаг сетки нужно выбрать порядка 10−3 , т.к.
![]() √ 3
× 103
= 106
. Таh
∼ ²
. Число узлов здесь оказывается равным 10 кому же числу равно число неизвестных n
. Таким образом, мы имеем матрицу размерности 106
× 106
.
√ 3
× 103
= 106
. Таh
∼ ²
. Число узлов здесь оказывается равным 10 кому же числу равно число неизвестных n
. Таким образом, мы имеем матрицу размерности 106
× 106
.
Нетрудно догадаться, что если рассмотреть, не квадрат, а куб, то число неизвестных будет примерно равно n = 109 . В расчетной практике встречаются задачи, где нужно определять не одну функцию, а несколько. Например, в гидродинамике при учете теплопереноса имеем четыре скалярных неизвестных (три компоненты поля скорости и поле температуры). Если рассматривать конечно-разностную аппроксимацию этой задачи с точностью ² = 10−6 , то получим размерность n = 4 · 109 .
Рассмотренные выше два примера показывают характерные источники задач линейной алгебры, приводящие к СЛАУ с большими разреженными матрицами. Естественно, что при решении таких СЛАУ необходимо развивать специальные методы вычислительной алгебры.
Рассмотрим другую нумерацию узлов, показанную на рис. 2. Здесь использовано так называемое красно-черное разбиение (или чернобелое). Вначале нумеруются узлы, сумма индексов которых – четное число, а потом узлы, сумма индексов которых дает нечетное число. Таким образом, вектор переменных вводится по правилу вектор неизвестных по правилу
u 1, 1 = x 1, u 1, 3 = x 2, u 2, 2 = x 3, u 3, 1 = x 4, u 3, 3 = x 5
– это красные неизвестные, а
u 1, 2 = x 6, u 2, 1 = x 7, u 2, 3 = x 8, u 3, 2 = x 9
– черные неизвестные.

0 1
Рис. 2: Конечно-разностная сетка. Красно-черное разбиение.
Соответствующая красно-черному разбиению матрица дается формулой
4 0 0 0 0 4 0 0 0 0 4 0 0 0 0 4 A = 0 0 0 0 −1 −1 −1 0 −1 0 −1 −1 0 −1 −1 0 |
0 0 0 0 4 0 0 −1 |
−1 −1 0 0 −1 0 −1 0 −1 −1 −1 −1 0 −1 0 −1 0 0 −1 −1 4 0 0 0 0 4 0 0 0 0 4 0 0 0 0 4 |
| 0 0 −1 −1 −1 | ||
Видно, что A является симметричной блочной (состоящей из четырех блоков) разреженной матрицей с диагональным преобладанием.
ТЕСТ РУБЕЖНОГО КОНТРОЛЯ № 1
1. Если исходная краевая задача порождает самосопряженный оператор, то какого вида матрицу следует ожидать после дискретизации? (выберите один из ответов)
(a) диагональную;
(b) верхнюю треугольную;
(c) трехдиагональную; (d) симметричную.
2. Зависит ли структура матрицы от способа нумерации узлов (выберите один из ответов)
(a) зависит;
(b) не зависит;
(c) не зависит, если оператор краевой задачи самосопряженный; (d) не зависит, если матрица ленточная.
3. Выберите из списка все разреженные матрицы
(a) диагональная;
(b) ленточная;
(c) нижняя треугольная; (d) теплицева.
4. При аппроксимации конечными разностями второго порядка двумерного уравнения Лапласа потребовалась точность 10−10 . Каков порядок матрицы соответствующей СЛАУ получится, т.е. размерность n ? (выберите один из ответов)
(a) 10−10 ;
(b) 1010 ;
(c) 105 ;
(d) 10100 .
2 Векторные и матричные нормы
Напомним некоторые основные определения и утверждения из линейной алгебры. В данном пособии мы будем иметь дело с квадратными вещественными матрицами размерности n × n .
2.1 Векторные нормы
Определение 1. Пусть V – векторное пространство над полем F (R или C). Функция k · k: V → R является векторной нормой, если для всех x, y ∈ V выполняются следующие условия:
(1) kxk ≥ 0 (неотрицательность);
(1a) kxk = 0 тогда и только тогда, когда x = 0 (положительность);
(2) kc xk = |c |kxk для всех чисел c ∈ F (абсолютная однородность);
(3) kx + y| ≤ kxk + kyk (неравенство треугольника).
Это привычные свойства евклидовой длины на плоскости. Евклидова длина обладает и другими свойствами, независимыми от приведенных аксиом (например, выполнено тождество параллелограмма). Подобные дополнительные свойства оказываются несущественными для общей теории норм и поэтому не причисляются к аксиомам.
Функцию, для которой выполнены аксиомы (1), (2) и (3), но не обязательно (1а), называют векторной полунормой. Это более общее понятие, чем норма. Некоторые векторы, отличные от нулевого, могут иметь нулевую длину в смысле полунормы.
Определение 2. Пусть V – векторное пространство над полем F (R или C). Функция (x, y): Vx V → F является скалярным произведением, если для всех x, y, z ∈ V следующие условия:
(1) (x, x) ≥ 0 (неотрицательность);
(1a) (x, x) = 0 тогда и только тогда, когда x = 0 (положительность);
(2) (x + y, z) = (x, z) + (y, z) (аддитивность); (3) (c x, y) = c (x, y) для всех чисел c ∈ F (однородность);
![]()
(4) (x, y) = (y, x) для любых x, y (эрмитовость).
Примеры векторных норм. В конечномерном анализе используются так называемые `p -нормы
 .
.
Наиболее распространенными являются следующие три нормы
![]() ;
;
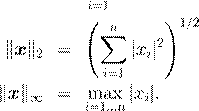 (евклидова норма);
(евклидова норма);
Естественно, что существует бесконечно много норм. Например, нормой также является выражение max{kxk1 + kx||2 } или такое
kxkT = kT xk,
где T – произвольная невырожденная матрица.
Имеет место теорема, с теоретической точки зрения показывающая достаточность только одной нормы
Теорема 1. В конечномерном пространстве все нормы эквивалентны, т.е. для любых двух норм k · kα , k · kβ и для любого x выполняется неравенство
kxkα ≥ C (α,β,n )kxkβ
где C (α,β,n ) – некоторая постоянная, зависящая от вида норм и от размерности матрицы n .
Для норм k · k1 , k · k2 , k · k∞ константа C (α,β,n ) определяется таблицей
| α \β | 1 | 2 √ |
∞ |
| 1 | 1 | n | n √ |
| 2 | 1 | 1 | n |
| ∞ | 1 | 1 | 1 |
Проверим выполнение некоторых из неравенств.
Очевидно, что kxk1 ≤ n kxk∞ . Это следует из неравенства
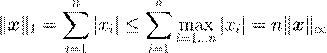 ,
,
которое получается, если в kxk1 заменить компоненты на максимальное значение. Неравенство достигается, если xi = xm ax , т.е. все компоненты равны друг другу. Тем самым это неравенство является точным, поскольку иногда становится равенством.
Проверку остальных неравенств оставляем читателю (см. также
[10]).
Несмотря на теоретическую эквивалентность норм, с практической точки зрения норма вектора большой размерности n может отличаться от другой нормы того же вектора в n раз. Поэтому выбор нормы при больших n имеет значение с практической точки зрения.
Геометрические свойства норм k·k1 , k·k2 , k·k∞ могут быть прояснены в случае R2 . Графики уравнений kxk1 = 1, kxk2 = 1, kxk∞ = 1 показаны на рис. 3. .
2.2 Матричные нормы
Обозначим пространство квадратных матриц порядка n через Mn .
Определение 3. Функция k·k, действующая из Mn в Rn , называется матричной нормой, если выполнены следующие свойства

Рис. 3: Графики уравнений kxk1 =1, kxk2 =1, kxk∞ =1.
1. kA k ≥ 0, kA k = 0 ⇔ A = 0;
2. kλ A k = |λ |kA k;
3. kA + B k ≤ kA k + kB k (неравенство треугольника);
4. kAB k ≤ kA kkB k (кольцевое свойство).
Если последнее свойство не выполнено, то такую норму будем называть обобщенной матричной нормой.
Приведем примеры наиболее распространенных матричных норм.
1. ![]() – максимальная столбцовая норма;
– максимальная столбцовая норма;
2. ![]() – максимальная строчная норма;
– максимальная строчная норма;
3. kA kM = n max |aij |;
i,j =1..n
4. kA k2 = max νi – спектральная норма. Здесь νi – сингулярные i =1..n
числа матрицы A , т.е. νi 2 – собственные числа матрицы AA T ;
5.  – евклидова норма;
– евклидова норма;
6. ![]() норма.
норма.
Как и в случае векторных норм, все матричные нормы эквивалентны. Использование различных норм связано с удобством использования, а также с тем фактом, что матриц большой размерности значения нормы могут отличаться весьма значительно.
2.3 Связь векторных и матричных норм
Выше были даны примеры векторных и матричных норм, введенные независимо друг от друга. Вместе с тем, эти два понятия могут быть связаны при помощи двух понятий.
Определение 4. Матричная норма k · k называется согласованной с векторной нормой k · k, если для любой A ∈ Mn и любого x ∈ V выполняется неравенство
kA xk ≤ kA kkxk.
Заметим, что в этом неравенстве знак нормы относится к разным нормам – векторным и матричной.
Определение 5. Матричная норма называется подчиненной (операторной, индуцированной) соответствующей векторной норме, если она определена равенством
kA k = max kA xk.
kxk=1
Понятие операторной матричной нормы является более сильным, чем подчиненной:
Теорема 2. Операторная норма является подчиненной соответствующей матричной норме.
Доказательство. Действительно, из определения следует,
kA xk ≤ kA kkxk.
![]()
Следствие 2.3.1. Операторная норма единичной матрицы равна единице:
kE
k = 1.
Доказательство. Действительно, kE
k = max kE
xk = 1.
![]() kxk=1
kxk=1
Существует ряд утверждений, связывающих введенные матричные и векторные нормы.
1. Матричная норма k · k1 являются операторной нормой, соответствующей векторной норме k · k1 .
2. Матричная норма k · k∞ являются операторной нормой, соответствующей векторной норме k · k∞ .
3. Спектральная матричная норма k·k2 являются операторной нормой, соответствующей евклидовой векторной норме k · k2 .
4. Матричные нормы k·kE , k·kM , k·k` 1 не являются операторными.
5. Матричная норма k · k2 согласована с векторной нормой k · k2 .
6. Матричная норма k·kM согласована с векторными нормами k·k1 , k · k∞ , k · k2 .
ТЕСТ РУБЕЖНОГО КОНТРОЛЯ № 2
1. Вычислите нормы k · k1 , k · k∞ , k · kM , k · k` 1 матриц
(a)

![]()
![]()
 ...
0 0
...
0 0
... 0 0
A ... 0 0 ;
..
0 0 0−1 2
(b)
41 0 1 0 0 0 0 0
−1 4 −1 0 1 0 0 0 0
01 4 0 01 0 0 0
−1 0 0 4 1 0 −1 0 0
A = 01 01 0 −1 0 ;

![]() 0 01 0 1 4 0 0 −1
0 01 0 1 4 0 0 −1
0 0 0 1 0 0 4 0 0
0 0 0 0 1 0 −1 4 −1 0 0 0 0 0 −1 0 −1 4
(c)
4 0 0 0 0 −1 −1 0 0
0 4 0 0 0 −1 0 −1 0
0 0 4 0 0 −1 −1 −1 −1
0 0 0 4 0 0 −1 0 −1
A = 0 0 0 0 4 0 0 −1 −1 .
−1 −11 0 0 4 0 0 0
−1 01 0 0 4 0 0
0 −11 0 1 0 0 4 0
0 01 0 0 0 4
2. Если матричная норма является согласованной, то можно ли построить соответствующую ей векторную норму, чтобы она стала операторной? (выберите один из ответов)
(a) нельзя;
(b) можно;
(c) можно, если матрица симметрична; (d) можно для евклидовой нормы.
3. Если матричная норма k · k является операторной, то (выберите правильные ответы)
(a) она согласована;
(b) положительна;
(c) kE k = 1;
(d) kE k = n .
4. Операторная норма единичной матрицы равна (выберите один из ответов)
(a) чему угодно;
(b) единице; (c) n ;
(d) n 2 .
5. Согласованная норма единичной матрицы равна (выберите один из ответов)
(a) чему угодно;
(b) единице; (c) n ;
(d) n 2 .
3 Итерационные методы
3.1 Определения и условия сходимости итерационных методов
Различают прямые и итерационные методы решения систем линейных алгебраических уравнений (СЛАУ). Прямые методы получают решение за конечное число шагов, причем, если предположить, что это решение может быть получено в точной арифметике (когда нет ошибок округления), то это решение является точным. Итерационные методы, вообще говоря, всегда дают приближенное решение, для получения точного решения необходимо бесконечное число шагов. Интерес к итерационным методам связан как раз с решением СЛАУ с матрицами большой размерности. Прямые методы для таких матриц не дают требуемой точности. В случае разреженных матриц большой размерности итерационные методы дают заметный выигрыш в точности, быстродействии и экономии памяти.
Определение 6. Итерационный метод дается последовательностью
x(k +1) = G k x(k ) + gk
или
³ ´
x(k +1) = x(k ) + Q −k 1 b − A x(k ) .
G k называется матрицей перехода, а Q k – матрицей расщепления, x(0) предполагается известным начальным приближением.
Определение 7. Метод называется стационарным, если матрица перехода G k (матрица расщепления Q k ) и не зависят от номера итерации k .
Далее ограничимся рассмотрением стационарных итерационных методов
x(k +1) = G x(k ) + g, G = E − Q −1A , g = Q −1b. (2)
В результате выполнения итерационного метода по начальному приближению строится последовательность
x(0),
x(1),
x![]()
Рассмотрим погрешность k -й итерации. Пусть x(∞) – точное решение исходной задачи, т.е.
A x(∞) = b.
С другой стороны, x(∞) должно удовлетворять уравнению
x(∞) = G x(∞) + g.
Тогда погрешность k -й итерации дается формулой εk = x(k ) −x(∞) .
Установим для εk итерационую формулу. Имеем соотношения
x(1) = G x(0) + g, x(2) = G x(1) + g, x(3) = G x(2) + g,
x![]() G
x(k
)
+ g,
G
x(k
)
+ g,
...
Вычтем из них уравнение x(∞) = G x(∞) + g. Получим
| ε(1) | = | G ε(0), |
| ε(2) | = | G ε(1), |
| ε(3) | = | G ε(2), |
![]() ,
,
...
Выражая все через погрешность начального приближения ε(0) , получим
| ε(1) | = | G ε(0), |
| ε(2) | = | G ε(1) = G 2ε(0), |
| ε(3) | = | G ε(2) = G 2ε(1) = G 3ε(0), |
![]() ,
,
...
Таким образом, получаем формулу для погрешности на k -й итерации, которой будем пользоваться в дальнейшем:
ε(k ) = G k ε(0). (3)
Рассмотрим сходимость итерационного метода (2). Поскольку сходимость метода состоит в том, чтобы погрешность убывала, нужно исследовать сходимость к нулю последовательности ε(k ) . Для анализа сходимости нам потребуется понятие спектрального радиуса.
Определение 8. Спектральным радиусом матрицы G называется максимальное по модулю собственное число матрицы G :
ρ (G ) = max |λi (G )|. i =1...n
Обратим внимание, что в этом определении участвуют все собственные числа, т.е. вещественные и комплексные.
Теорема 3 (Достаточное условие сходимости). Для сходимости итерационного метода достаточно выполнения неравенства
kG k < 1.
Доказательство. Доказательство повторяет доказательство принципа сжимающих отображений, поскольку эта теорема является частным случаем этого принципа. ![]()
Отметим, что для сходимости достаточно выполнение неравенства для какой-то одной нормы. Это условие является легко проверяемым, хотя лишь достаточным. Необходимое и достаточное условие сходимости является проверяется более сложным образом и дается следующим утверждением.
Теорема 4 (Необходимое и достаточное условие сходимости). Для сходимости итерационного метода необходимо и достаточно выполнения неравенства
ρ (G ) < 1.
Доказательство. Из соображений краткости, ограничимся случаем, когда собственные векторы матрицы G образуют базис в Rn . Это всегда так, например, если G – симметрична. Очевидно, что сходимость итерационного метода эквивалентная сходимости к нулю последовательности {ε(k ) }.
1. Докажем достаточность. Пусть ρ (G ) < 1. Рассмотрим произвольное начальное приближение и разложим его по базису собственных векторов
![]() .
.
Тогда
![]() .
.
По условиям теоремы все собственные числа по модулю меньше единицы, поэтому c учетом |λi |k | → 0 при k → ∞ (i = 1, 2,...,n ) выполняются соотношения kε(k )k = kλ k 1ε (0)1 e1 + ... + λ kn ε (0)n en k ≤
≤ |λ 1 |k |ε (0) 1 | + ... + |λn |k |ε (0) n | → 0, k → ∞.
2. Докажем необходимость. Пусть итерационный метод сходитсяпри любом начальном приближении. Предположим противное, т.е. что ρ (G ) ≥ 1. Это значит, что существует как минимум один собственный вектор e, такой, что G e = λ e c |λ | ≡ ρ (G ) ≥ 1. Выберем начальное приближение так: ε(0) = e. Тогда имеем
ε(k ) = G k ε(0) = λ k e.
Поскольку |λ | ≥ 1, последовательность {ε(k ) } не сходится к нулю при данном начальном приближении, т.к. kε(k ) k = |λ |k ≥ 1. Полученное противоречие и доказывает необходимость.
![]()
Важным свойством итерационного метода является его симметризуемость. В частности, она используется для его ускорения (т.е. модификации, позволяющей достичь той же точности за меньшее число итераций).
Определение 9. Итерационный метод является симметризуемым, если существует такая невырожденная матрица W (матрица симметризации), что W (E − G )W −1 является симметричной и положительно определенной.
Для симметризуемого метода выполняются свойства:
1. собственные числа матрицы перехода G вещественны;
2. наибольшее собственное число матрицы G меньше единицы;
3. множество собственных векторов матрицы перехода G образует базис векторного пространства.
Для симметризуемого метода всегда существует так называемый экстраполированный метод, который сходится всегда, независимо от сходимости исходного метода. Он дается формулой x(k +1) = G γ x(k ) + gγ , G γ = γ G + (1 − γ )E , gγ = γ g.
Оптимальное значение параметра γ определяется соотношением
![]() ,
,
где M (G ) и m (G ) – максимальное и минимальное собственные числа G .
Рассмотрим далее классические итерационные методы.
3.2 Метод простой итерации
Метод простой итерации является простейшим примером итерационных методов. Он дается формулой x(k +1) = (E − A )x(k ) + b, G = E − A , Q = E .
Сходится при M (A ) < 2.
Для симметричной положительно определенной матрицы A ) симметризуем и экстраполированный метод имеет вид
x![]() .
.
3.3 Метод Якоби
Метод Якоби определяется формулой
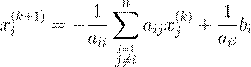 .
(4)
.
(4)
Запишем его в матричных обозначениях (в безиндексном виде). Представим матрицу A в виде
A = D − CL − CU ,
где D – диагональная матрица, C L – верхняя треугольная, а C U – нижняя треугольная. Если A имеет вид
a 11 a 12 a 13 ... a 1n
a 21 a 22 a 23 ... a 2n
A = a 31 a 32 a 33 ... a 3n ,
... ...
a n 1 a n 2 a n 3 ... a nn
то D , C L и C U даются формулами
D,
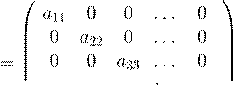 ...
..
...
..
0 0 0 ... ann
0 0 0 ... 0 0 a 12 a 13 ... a 1n
a 21 0 0 ... 0 0 0 a 23 ... a 2n
![]() C
C
![]() .
.
Используя матричные обозначения, формулу метода Якоби можно записать так: x(k +1) = B x(k ) + g,
где матрица перехода B дается формулой
B = D−1 (CU + CL ) = E − D−1 A
а g = D −1 b.
Достаточным условием сходимости метода Якоби является диагональное преобладание. Если A – положительно определенная симметричная матрица, то метод Якоби симметризуем.
3.4 Метод Гаусса-Зейделя
Запишем последовательность формул метода Якоби более подробно
= −a 31x (1k ) − a 32x (2k ) − ... − a 3n x (2k ) + b 3, ... |
|
Если посмотреть внимательно на них, то видно, что при вычислении последних компонент вектора x(k +1) уже известны предыдущие компоненты x(k +1) , но они не используются. Например, для последней компоненты имеется формула
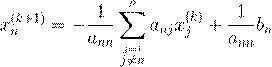 .
.
В ней в левой части присутствует n
− 1 компонент ![]() предыдущей итерации, но к этому моменту уже вычислены компоненты текущей итерации
предыдущей итерации, но к этому моменту уже вычислены компоненты текущей итерации ![]() . Естественно их использовать при вычислении
. Естественно их использовать при вычислении ![]() . Перепишем эти формулы следующим образом, заменяя в левой части уравнений компоненты x(k
)
на уже найденные компоненты x(k
+1)
:
. Перепишем эти формулы следующим образом, заменяя в левой части уравнений компоненты x(k
)
на уже найденные компоненты x(k
+1)
:
| a 11x (1k +1) | |
= −a 31x (1k +1) − a 32x (2k +1) − ... − a 3n x (2k ) + b 3, ... |
|
Эти формулы лежат в основе метода Гаусса–Зейделя:
 .
(5)
.
(5)
В матричном виде метод Гаусса–Зейделя записывается таким образом:
x(k +1) = Lx(k ) + g,
где L = (E − L )−1 U , g = (E − L )−1 D −1 b, L = D −1 C L , U = D −1 C U .
В общем случае метод несимметризуем.
Есть интересный исторический комментарий [Д2]: метод был неизвестен Зейделю, а Гаусс относился к нему достаточно плохо.
Замечание. Хотя для положительно определенных симметричных матриц метод Гаусса-Зейделя сходится почти в два раза быстрее метода Якоби, для матриц общего вида существуют примеры, когда метод Якоби сходится, а метод Гаусса-Зейделя расходится.
3.5 Метод последовательной верхней релаксации (SOR) Дается формулами
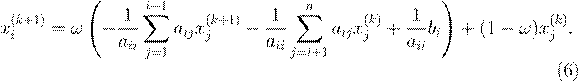
Здесь ω – параметр релаксации, ω ∈ [0, 2]. При ω > 1 говорят о верхней релаксации, при ω < 1 – о нижней, а при ω = 1 метод SOR сводится к методу Гаусса–Зейделя. Удачный выбор параметра релаксации позволяет на порядки понизить число итераций для достижения требуемой точности.
Матричная форма (6) имеет вид
x(k +1) = Lω x(k ) + gω ,
где Lω = (E − ω L )−1 (ω U + (1 − ω )E ), gω = (E − ω L )−1 ω D −1 b.
В общем случае метод несимметризуем. Сходимость гарантирована для положительно определенной симметричной матрицы.
3.6 Метод симметричной последовательной верхней релаксации (SSOR)
Этот метод по числу итераций сходится в два быстрее, чем предыдущий, но итерации являются более сложными и даются соотношениями

![]() ;
;

![]() 1;
1;
Здесь ω – параметр релаксации, ω ∈ [0, 2].
Если A – положительно определенная симметричная матрица, то метод SSOR симметризуем.
Упражнение. Найдите матрицу перехода.
ТЕСТ РУБЕЖНОГО КОНТРОЛЯ № 2
1. Проверьте сходимость предыдущих методов для матриц
(a)
A
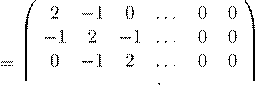 ;
;
 |
0 0 0 0 |
−1 0 0 0 |
0 −1 0 0 |
−1 0 −1 0 |
4 0 0 4 0 −1 −1 0 |
0 0 4 −1 |
 |
|
| (c) | 0 4 |
0 0 |
0 0 |
0 0 | −1 −1 −1 0 | 0 −1 |  |
![]()

![]()
 0 0 0
0 0 0
(b)
41 0 −1 0 0 0 0 0
−1 4 −1 0 −1 0 0 0 0
01 4 0 01 0 0 0
−1 0 0 4 −1 0
A = 01 0 −1 41 0 ;
0 0 4 0 0 −1 −1 −1 −1 0 0 0 4 0 0 −1 0 −1
A 0 0 0 0 4 0 0 −1 −1 .
−1 −1 0 0 4 0 0 0
1 0 −1 −1 0 0 4 0 0
−1 −1 0 −1 0 0 4 0
0 0 −1 −1 −1 0 0 0 4
2. A является симметричной и положительно определенной. Какие из методов являются симметризуемыми?
(a) простой итерации;
(b) Якоби;
(c) Гаусса–Зейделя;
(d) SOR;
(e) SSOR.
3. Необходимым и достаточным условием сходимости итерационного метода является
(a) положительная определенность матрицы перехода G ;
(b) симметричность матрицы перехода G ;
(c) неравенство kG k < 1;
(d) неравенство ρ (G ) < 1.
4. Матрица симметризации – это
(a) симметричная матрица;
(b) единичная матрица;
(c) такая матрица W , что W (E −G )W −1 – положительно определенная и симметричная матрица;
(d) такая матрица W , что W (G −E )W −1 – положительно определенная и симметричная матрица.
5. При ω = 1 метод SOR переходит в метод (выберите один из ответов)
(a) Якоби;
(b) SSOR;
(c) простой итерации; (d) Гаусса–Зейделя.
6. Параметр релаксации ω лежит в диапазоне (выберите один из ответов)
(a) [0, 1];
(b) [0, 2]; (c) (0, 2);
(d) [−1, 1].
4 Методы подпространств Крылова
4.1 Инвариантные подпространства
Для понижения размерности исходной задачи воспользуемся понятием инвариантного подпространства.
Определение 10. Подпространство L инвариантно относительно матрицы A , если для любого вектора x из L вектор A x также принадлежит L.
Примером инвариантного подпространства, является подпространство, образованное линейными комбинациями нескольких собственных векторов A .
Предположим, что нам известен базис L, образованный векторами q1 , q2 , ..., qm , m ≤ n . Образуем из этих векторов матрицу Q = [q1 , q2 ,..., qm ] размерности n ×m . Вычислим AQ . Это матрица также размерности n ×m , причем ее столбцы есть линейные комбинации q1 , q2 , ... qm . Другими словами, столбцы AQ принадлежат инвариантному подпространству L. Указанные столбцы удобно записать в виде
QC , где C – квадратная матрица размерности m ×m . Действительно,
AQ = A [q1 , q2 ,... qm ].
Вектор A qi ∈ L, следовательно, A qi представим в виде линейной комбинации q1 , q2 , ... qm :
A qi = ci 1 q1 + ci 2 q2 + ... + cim qm , i = 1,...,m.
Таким образом, выполняется равенство
AQ = QC . (8)
Матрица C называется сужением A на подпространстве L. Более наглядно (8) можно представить в виде
n m m m
| A | Q | = | Q |
C m
n
Рассмотрим случай, когда q1 , q2 , ..., qm – ортонормированы. Тогда
QT Q = Em ,
где E m – единичная матрица размерности m ×m . Из (8) вытекает, что
C = Q T AQ .
Рассмотрим решение СЛАУ
C y = d,
где d ∈ Rm . Умножая это уравнение на Q слева получим, что
QC y = AQ y = Q d.
То есть вектор Q y является решением исходной задачи, если b = Q d. Таким образом, знание инвариантного подпространства позволяет свести решение СЛАУ для матрицы A к двум СЛАУ меньшей размерности, которые могут быть решены независимо друг от друга. Проблема состоит в том, что априори инвариантные подпространства матрицы A неизвестны. Вместо инвариантных подпространств можно использовать “почти” инвариантные подпространства, например, подпространства Крылова.
4.2 Степенная последовательность и подпространства Крылова
Определение 11. Подпространством Крылова Km (b) называется подпространство, образованное всеми линейными комбинациями векторов степенной последовательности
b, A b, A 2 b, ..., A m −1 b,
то есть линейная оболочка, натянутая на эти векторы
Km (b) = span(b, A b, A 2 b, ..., A m −1 b).
Рассмотрим свойства степенной последовательности
b, A b, A 2 b, A 3 b,... A k b,...,
где b – некоторый произвольный ненулевой вектор.
Рассмотрим случай, когда A – симметричная матрица. Следовательно, ее собственные векторы ek образуют базис в Rn . Соответствующие собственные числа A обозначим через λk :
A ek = λk ek .
Для определенности примем, что λk упорядочены по убыванию:
|λ 1 | ≥ |λ 2 | ≥ ... ≥ |λn |.
Произвольный вектор b можно представить в виде разложения по ek :
b = b 1 e1 + b 2 e2 + ... + bn en .
Имеют место формулы:
b = b 1 e1 + b 2 e2 + ... + bn en ,
A
b = λ
1
b
1
e1
+ λ
2
b
2
e2
+ ...
+ λn
bn
en
,
A
![]() ,
,
...
A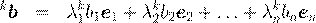 ,
,
...
Сделаем дополнительное предположение. Пусть |λ 1 | > |λ 2 |. Другими словами, λ 1 – максимальное собственное число по модулю: λ 1 = λ max . Тогда A k b можно записать следующим образом:
A
![]() .
(9)
.
(9)
Поскольку все ![]() , то если b
1
6= 0, то все слагаемые в скобках в уравнении (9) кроме первого будут убывать при k
→ ∞:
, то если b
1
6= 0, то все слагаемые в скобках в уравнении (9) кроме первого будут убывать при k
→ ∞:
![]() при k
→ ∞.
при k
→ ∞.
Кроме того, также выполняется соотношение
||A k b|| → |λ 1 |k |b 1 | при k → ∞.
Таким образом, при возрастании k члены степенной последовательности поворачиваются таким образом, что оказываются параллельными собственному вектору emax ≡ e1 , соответствующему максимальному по модулю собственному значению λ max .
4.3 Итерационные методы подпространств Крылова
Подпространства Крылова обладают замечательным свойством: если A – симметрична и если последовательно строить ортонормированный базис в Km (b) m = 1, 2,...n , то вектора базиса для Kn (b) образуют такую ортогональную матрицу Q , что выполняется равенство
Q T AQ = T , (10)
где T является трехдиагональной матрицей
α 1 β 1 0 ··· 0
β 1 α 2 β 2 ...
T = 0... β 1 α 3 ...
... ... βn −1
0 ··· β n −1 α n
Если A – несимметричная матрица, то вместо (10) получаем
Q T AQ = H , (11)
где H – матрица в верхней форме Хессенберга, т.е. имеет структуру
× × H = 0 ... 0 |
× × × × × × ... ··· |
··· × ... ... ... × × × |
(крестиком помечены ненулевые элементы).
Ясно, что если построено представление (10) или (11), то решение СЛАУ A x = b можно провести в три шага. Например, если выполнено
(10), то решение A x = b эквивалентно трем СЛАУ
| Q z = b, | (12) |
| T y = z, | (13) |
| Q T x = y, | (14) |
причем системы (12) и (14) решаются элементарно, поскольку обратная к ортогональной матрице Q является транспонированная Q T . Система (13) также решается гораздо проще исходной, поскольку T – трехдиагональная матрица, для которых развиты быстрые и эффективные методы решения СЛАУ.
Рассмотрим алгоритм, приводящий симметричную матрицу A к трехдиагональному виду.
Алгоритм Ланцоша. v = 0; β 0 = 1; j = 0;
while βj 6= 0 if j 6= 0
for i = 1..n
t = wi ; wi = vi /βj ; vi = −βj t end
end
v = +A w
j = j + 1; αj = (w, v); v = v − αj w; βj := kvk2 end
Для приведения матрицы к трехдиагональному виду нужна только процедура умножения матрицы на вектор и процедура скалярного произведения. Это позволяет не хранить матрицу как двумерный массив.
Алгоритм Ланцоша может быть обобщен на случай несимметричных матриц. Здесь матрица A приводится к верхней форме Хессенберга H . Компоненты H обозначим через hi,j , hi,j = 0 при i < j − 1.
Соответствующий алгоритм носит названия алгоритма Арнольди.
Алгоритм Арнольди. r = q1 ; β = 1; j = 0;
while β 6= 0
h j +1,i = β ; qj +1 = rj /β ; j = j + 1 w = A qj ; r = w for i = 1..j
hij = (qi , w); r = r − hij qi
end
β = krk2 if j < n
h j +1,j = β
end
end
Определенным недостатком алгоритмов Ланцоша и Арнольди является потеря ортогональности Q в процессе вычислений. СУществет ряд реализаций этих алгоритмов, преодолевающих этот недостаток, и делающих эти методы весьма эффективными для решения СЛАУ с большими разреженными матрицами.
ТЕСТ РУБЕЖНОГО КОНТРОЛЯ № 4
1. Что такое инвариантное подпространство? (выберите один из ответов)
(a) линейная оболочка, натянутая на столбцы матрицы A ;
(b) подпространство, не изменяющееся при действии на него матрицы A ;
(c) нульмерное-подпространство; (d) подпространство Крылова.
2. Что такое степенная последовательность? (выберите один из ответов)
(a) последовательность E , A , A 2 , A 3 , ...;
(b) последовательность b, A b, A 2 b, A 3 b, ...;
(c) последовательность 1, x , x 2 , x 3 , ...; (d) последовательность 1, 2, 4, 8, ....
3. Недостатком метода Ланцоша является (выберите один из ответов)
(a) медленная сходимость;
(b) потеря ортогонализации;
(c) невозможность вычисления собственных векторов; (d) необходимость вычисления степеней.
4. В методе Ланцоша используются
(a) подпространства Крылова;
(b) линейная оболочка, натянутая на столбцы матрицы A ;
(c) подпространство, образованное собственными векторами матрицы A ;
(d) подпространство, образованное собственными векторами матрицы Q T AQ .
5. Метод Ланцоша приводит матрицу к
(a) диагональной;
(b) трехдиагональной;
(c) верхней треугольной;
(d) верхней треугольной в форме Хессенберга.
6. Метод Ланцоша применим для матриц
(a) диагональных;
(b) трехдиагональных;
(c) симметричных; (d) произвольных.
7. Метод Арнольди приводит матрицу к
(a) диагональной;
(b) трехдиагональной;
(c) верхней треугольной;
(d) верхней треугольной в форме Хессенберга.
8. Метод Арнольди применим для матриц
(a) диагональных;
(b) трехдиагональных;
(c) симметричных; (d) произвольных.
Заключение
Выше дано описание некоторых методов решения систем линейных алгебраических уравнений для симметричных разреженных матриц большой размерности.
При написании данного пособия в основном использовались материалы [3, 4, 7, 9, 10]. Более подробные сведения о можно получить в приведенной ниже основной и дополнительной литературе.
ЛИТЕРАТУРА
[1] В. В. Воеводин. Вычислительные основы линейной алгебры. М.: Наука, 1977. 304 с.
[2] В. В. Воеводин, Ю. А. Кузнецов. Матрицы и вычисления. М.: Наука, 1984. 320 с.
[3] Дж. Голуб, Ч. Ван Лоун. Матричные вычисления. М.: Мир, 1999. 548 с.
[4] Дж. Деммель. Вычислительная линейная алгебра. Теория и приложения. М.: Мир, 2001. 430 с.
[5] Х. Д. Икрамов. Численные методы для симметричных линейных систем. М.: Наука, 1988. 160 с.
[6] Б. Парлетт. Симметричная проблема собственных значений. Численные методы. М.: Мир, 1983. 384 с.
[7] C. Писсанецки. Технология разреженных матриц. М.: Мир, 1988. 410 с.
[8] Дж. Х. Уилкинсон. Алгебраическая проблема собственных значений. М.: Наука, 1970. 564 с.
[9] Л. Хейнгеман, Д. Янг. Прикладные итерационные методы. М.: Мир, 1986. 448 с.
[10] Р. Хорн, Ч. Джонсон. Матричный анализ. М.: Мир, 1989. 655 с.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
[Д1] Х. Д. Икрамов. Несимметричная проблема собственных значений. М.: Наука, 1991. 240 с.
[Д2] Дж. Райс. Матричные вычисления и математическое обеспечение. М.: Мир, 1984. 264 с.
[Д3] Y. Saad. Numerical Methods for Large Eigenvalue Problems. Halsted Press: Manchester, 1992. 347 p.
[Д4] Дж. Форсайт, К. Молер. Численное решение систем линейных алгебраических уравнений. М.: Мир, 1969. 167 с.