| Скачать .docx | Скачать .pdf |
Реферат: Математика 10 класс Бевз стандарт

Пе ред мо ва
На у ку ма те ма ти ку мож на розг ля да ти з різних то чок зо ру. Одні ба чать у ній на сам пе ред своє рід ний інстру мент для на у ковців, інжен ерів і техн ік ів. Бо за допомогою математичного моделювання можна порівняно легко і швидко розв’язувати дуже важливі прикладні проблеми, які іншими методами розв’язувати надто дорого або неможливо. Ось що гов ор ил и про ма те ма ти ку відомі лю ди:
«У вив чен ня при ро ди ма те ма ти ка робить най біль ший вне сок» (Прокл, V ст.).
«Той, хто не знає ма те ма ти ки ... не мо же пізна ти світ» (Р. Бек он, XIII ст.).
«Лю ди, які зас воїли ве ликі прин ци пи ма те ма ти ки, ма ють на один орг ан чутт я більш е, ніж прості смертні» (Ч. Дарвін, ХІХ ст.).
 Ма те ма ти ка не тіль ки ко рис ний інстру мент чи засіб, а й знач на час ти на за галь но людсь кої куль тури. Як що істо рик опи сує тільк и війни і рев ол юції, діяльність царів, полк ов одців і митців, йог о іст ор ія неповн а, одн обічна. Ноmо sаріеns – люд и- на мисл яч а. Том у історія людства пер ед усім має містит и опис и діяльн ості кращ их мисл ит елів, зокр ем а й мат ем ат иків. Чи від оме вам найбіль ше відкрит тя XVII ст.? Во но сто суєть ся ма те ма ти ки. А чи мо же істо рик об ми на ти най важ ливіші від крит тя? Які найістотніші зміни відбу ли ся в другій по ло вині XX ст.? Ство рен ня швид кодію чих елект рон них об чис лю валь них ма шин (ЕОМ), а на їх ос нові – комп’ютерів. Комп’юте ри зація на ук и і вир обн иц тв а безп ер ечн о внос ить у розв ит ок людства зміни наб аг ат о важл ивіші й ваг оміші, ніж зміни урядів, ло- кальні війни і будь9що інше. Щоб прав ильн о опис ат и цю епох у, істор ик має сказ ат и про створ енн я ЕОМ і комп’ютерів, а для ць о го він по ви нен хоч тро хи зна ти історію ма те ма ти ки.
Ма те ма ти ка не тіль ки ко рис ний інстру мент чи засіб, а й знач на час ти на за галь но людсь кої куль тури. Як що істо рик опи сує тільк и війни і рев ол юції, діяльність царів, полк ов одців і митців, йог о іст ор ія неповн а, одн обічна. Ноmо sаріеns – люд и- на мисл яч а. Том у історія людства пер ед усім має містит и опис и діяльн ості кращ их мисл ит елів, зокр ем а й мат ем ат иків. Чи від оме вам найбіль ше відкрит тя XVII ст.? Во но сто суєть ся ма те ма ти ки. А чи мо же істо рик об ми на ти най важ ливіші від крит тя? Які найістотніші зміни відбу ли ся в другій по ло вині XX ст.? Ство рен ня швид кодію чих елект рон них об чис лю валь них ма шин (ЕОМ), а на їх ос нові – комп’ютерів. Комп’юте ри зація на ук и і вир обн иц тв а безп ер ечн о внос ить у розв ит ок людства зміни наб аг ат о важл ивіші й ваг оміші, ніж зміни урядів, ло- кальні війни і будь9що інше. Щоб прав ильн о опис ат и цю епох у, істор ик має сказ ат и про створ енн я ЕОМ і комп’ютерів, а для ць о го він по ви нен хоч тро хи зна ти історію ма те ма ти ки.
Дехт о з учнів гов ор ить: «Мені не потрібна мат ем ат ик а, бо я не зби ра ю ся бути ма те ма ти ком». Подібна ар гу мен тація анітро хи не кращ а так ої: «Мені не потрібен авт ом обіль, бо я не збир а- ю ся бути шо фе ром».
Ма те ма ти ка – це своєрідна мо ва, засіб спілку ван ня. Чи ж мо же філо лог ефек тив но досліджу ва ти різні мо ви, не ма ю чи уяв лен ня про су час ну ма те ма тич ну мо ву та її історію?
Мат ем ат ик а – осн ов а баг атьо х нау к, поч ин аю ч и від філос оф ії й аж до кос мо гонії. А ще во на – логічний тренінг мис ли тель ної діяльн ості для фахівців з будь9якої гал узі знань. Не вип адк ов о ба га то ма те ма тиків доб ре ви я ви ли се бе і в інших га лу зях. На п рик лад, Піфа гор, Р. Де карт, Б. Пас каль – філо со фи, О. Хайям – по ет, П. Фер ма – юрист, І. Кеп лер – бо гос лов, Г. Лейбніц –
3
магістр філос офії, докт ор прав а, юрист, дипл ом ат. Цей спис ок мож на про дов жу ва ти.
Справжній ма те ма тик має не тіль ки на один «ор ган чут тя» біль ше від зви чай ної лю ди ни, він має та кож знач но біль ше «сту пенів сво бо ди». З три вимірно го прос то ру йо му зовсім не важ ко пе рей ти в чо ти ри вимірний чи в будь9який n 9ви мір ний або в простір Бан ах а, Гільб ерт а, Клейн а тощ о. А кожн ий із цих прост орів – дивн ий своєр ідн ий світ, баг атш ий і корисніший від світів, виг ад ан их фант аст ам и. Мат ем ат ик а та її історія настільк и баг аті, що справжній філос оф, істор ик, будь9який гум анітарій у них мо же знай ти чи ма ло ціка во го й ко рис но го.
У ць о му підруч ни ку про по нуєть ся інтег ро ва ний курс ма те ма ти ки. До нь о го вхо дять най важ ливіші те ми з ариф ме ти ки, ал геб ри, по чатків аналізу та з ге о метрії.
Окр емі тем и ви вже знаєте з поп ер едніх класів, а більшість – зовсім нові. На ма гай те ся опа ну ва ти їх. Чи та ю чи те орію, ос нов ну ува гу звер тай те на сло ва, над ру ко вані кур си вом і жир ним шриф том. Кур си вом виділе но терміни, наз ви по нять. Жир ним шриф том над ру ко ва но важ ливі тверд жен ня, те о ре ми.
 Зна ти ма те ма ти ку – це на сам пе ред уміти ко рис ту ва тися нею. Учит ис я кор ист ув ат ис я мат ем ат ичн им и знанн ям и най- к ра ще під час розв’язу ван ня за дач. У підруч ни ку є за дачі до кож ної те ми, до кож но го па раг ра фа – різних рівнів склад ності. Зад ачі і вправ и в підручн ик у поділен о на: «Вик он айт е ус9 но», рівень А, рівень Б і «Вправи для повт ор енн я». Завд ан- ня, ре ко мен до вані для до машньої ро бо ти, виділено коль о ром. У кожно му па раг рафі підруч ни ка є руб ри ка «Ви ко наємо ра зом», у якій подано зад ачі з розв’язан нями. Ра ди мо перег ля ну ти їх, перш ніж ви ко ну ва ти до машнє зав дан ня.
Зна ти ма те ма ти ку – це на сам пе ред уміти ко рис ту ва тися нею. Учит ис я кор ист ув ат ис я мат ем ат ичн им и знанн ям и най- к ра ще під час розв’язу ван ня за дач. У підруч ни ку є за дачі до кож ної те ми, до кож но го па раг ра фа – різних рівнів склад ності. Зад ачі і вправ и в підручн ик у поділен о на: «Вик он айт е ус9 но», рівень А, рівень Б і «Вправи для повт ор енн я». Завд ан- ня, ре ко мен до вані для до машньої ро бо ти, виділено коль о ром. У кожно му па раг рафі підруч ни ка є руб ри ка «Ви ко наємо ра зом», у якій подано зад ачі з розв’язан нями. Ра ди мо перег ля ну ти їх, перш ніж ви ко ну ва ти до машнє зав дан ня.
Цікаві до пов нен ня до ос нов но го ма теріалу містять ся в руб ри ках «Істо ричні відо мості».
Для узаг альн енн я і сист ем ат из ації вивч ен ог о мат еріалу призначено рубрики «Гол овн е в розділі» і «Сам остійна ро- бо та».
У до дат ках для тих, хто хо че дізна ти ся біль ше, про по ну ють ся тем и для робіт творч ог о хар акт ер у і спис ок відповідної літе- ра ту ри.
Мат ем ат ик у можн а порівнят и з вел ик им і барв истим квітни ком, у яко му ко жен мо же дібра ти собі бу кет за сма ком. Зроз уміло, щоб зроб ит и це, сперш у треб а ввійти в цей квітник. Лас ка во про си мо!
Ав тори

§ 1. Дійсні числа
Важ ли ву роль у ма те ма тиці відігра ють чис ла. Найп ростіші з них – на ту ральні чис ла 1, 2, 3, 4, 5, ..., які вик ор ист ов ую ть під час лічби. Вон и бул и відомі ще в доістор ичні час и. Зроз уміло, що наз ив ал и і зап ис ув ал и їх раніше не так, як теп ер.
 Не слід ото тож ню ва ти чис ла із циф ра ми. Циф ри – це знач ки, яки ми поз на ча ють чис ла. На ту раль них чи сел існує безліч, а цифр – тільк и дес ять: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Такі цифр и на- зи ва ють арабсь ки ми або індійсь ки ми. Іноді чис ла поз на ча ють так ож римськ им и цифр ам и І, V, X, L, С, D, М, які відповідаю ть числ ам 1, 5, 10, 50, 100, 500 і 1000. Напр икл ад, числ о 1998 римсь ки ми циф ра ми за пи суєть ся так: МСМХСVIII. Як що ти сяч ба га то, їх відок рем лю ють від оди ниць літерою m
. За пис XXVIIm
ССLХХХІV оз на чає чис ло 27284.
Не слід ото тож ню ва ти чис ла із циф ра ми. Циф ри – це знач ки, яки ми поз на ча ють чис ла. На ту раль них чи сел існує безліч, а цифр – тільк и дес ять: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Такі цифр и на- зи ва ють арабсь ки ми або індійсь ки ми. Іноді чис ла поз на ча ють так ож римськ им и цифр ам и І, V, X, L, С, D, М, які відповідаю ть числ ам 1, 5, 10, 50, 100, 500 і 1000. Напр икл ад, числ о 1998 римсь ки ми циф ра ми за пи суєть ся так: МСМХСVIII. Як що ти сяч ба га то, їх відок рем лю ють від оди ниць літерою m
. За пис XXVIIm
ССLХХХІV оз на чає чис ло 27284.
Існую ть спеціальні позн ач енн я чис ел в азб уці Морз е. А в рельєфно9точ ко во му шрифті Брай ля циф ри поз на ча ють різни ми конфігур аціями точ ок (мал. 1).
Зга даємо, як на зи ва ють і поз на ча ють ве ликі чис ла:
мілья рд – 1 000 000 000 = 109 ; трильйон – 1 000 000 000 000 = 1012 ; квадр ильйон – 1 000 000 000 000 000 = 1015 ; квінтильйон – 1 000 000 000 000 000 000 = 1018 .
У різних країнах вел икі числ а наз ив аю ть по9різном у. Наприкл ад, трильйон ом у США, Франції наз ив аю ть числ о 1012 , а в Англії, Німечч ині 1018 . Ми слов ам и «мілья рд» і «більйон» наз ив аємо одн е й те сам е числ о 109 , а в Німечч ині більйо ном прий ня то на зи ва ти чис ло 1012 . Вар то звер ну ти ува гу та кож на те, що ми чис ло 0 не вва жаємо на ту раль ним, а в Італії, Франції та де я ких інших країнах 0 відно сять до на ту раль них чи сел.
Мал. 1
не про хо дить, 1 – про хо дить. Уявіть, нап рик лад, блок з де ся ти лам по чок. Як що в нь о му увімкне но тіль ки пер шу, п’яту, восьм у і дев’яту ламп очк и (мал. 2), то вваж аю ть, що позн а- чено чис ло 1000100110. Пе рек лю ча ти такі бло ки, тоб то «за писув ат и і вит ир ати» числ а, а отж е, дод ав ат и і віднімат и їх, мож на за ти сячні част ки се кун ди. Удос ко на лю ючи такі «су ма то ри», фахівці ство ри ли швид ко діючі елект ронні об чис лювальні ма ши ни. Об’єднав ши ЕОМ з те левізо ра ми, ство ри ли комп’ю тери. В ос нові ць о го – за пис чис ла тіль ки дво ма циф рами!

Крім нат ур альн их, відомі так ож числ а цілі, раціональні, дійсні та інші. Мно жи на цілих чи сел
містить усі на ту ральні числ а, усі прот ил ежні їм числ а і 0, тобт о це числ а ..., –5, –4, –3, –2, –1, 0, 1, 2, 3, 4, 5, ... .
|
|
|
|
|
|
|
|
|
|
|
![]()
Мал. 2
Цілі чис ла ра зом з дро бо ви ми ут во рю ють мно жи ну ра ціо нальн их чис ел
. Раціональн им наз ив аю ть кожн е числ о, яке мож на по да ти у виг ляді дро бу ![]() , де m
– чис ло ціле, а n
– на ту9 раль не. Кож не раціональ не чис ло мож на за пи са ти у виг ляді скінченн ог о або нескінченн ог о періодичн ог о дес ятк ов ог о дроб у.
, де m
– чис ло ціле, а n
– на ту9 раль не. Кож не раціональ не чис ло мож на за пи са ти у виг ляді скінченн ог о або нескінченн ог о періодичн ог о дес ятк ов ог о дроб у.
 Існую ть числ а, відмінні від раціональн их. Напр икл ад, обч ис9 лю ючи зна чен ня діста ють нескінченні не пе ріо дичні
Існую ть числ а, відмінні від раціональн их. Напр икл ад, обч ис9 лю ючи зна чен ня діста ють нескінченні не пе ріо дичні
Ці числ а – не раціональні.
Чис ла, які зоб ра жа ють ся нескінчен ни ми не періодич ни ми де сят ко ви ми дро ба ми, на зи ва ють ірраціональ ни ми . Ірра ціо нальн ий – знач ить не раціональн ий (лат . ir відповідає за пе ре чу вальній частці не ).
Ірраціональ ни ми на зи ва ють чис ла, які не мож на ви ра зи ти у виг ляді відно шен ня двох цілих чи сел. Усі раціональні й ір ра ціональні чис ла ра зом на зи ва ють дійсни ми чис ла ми . Кож но му дійсно му чис лу на ко ор ди натній прямій відповідає єди на точк а і кожній точці коо рдин атн ої прям ої – єдин е дійсне числ о.
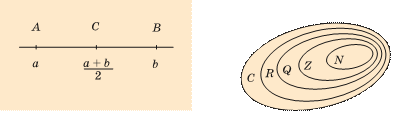
Уявіть, що на ко ор ди натній пря мій поз на че но дві довільні точ ки А і В з раціональ ни ми ко ор ди на та ми а і b (мал. 3). Скіль ки на відрізку АВ існує то чок з раціональ ни ми коор ди на та ми? Безліч. А то чок з ірра ціональ ни ми ко ор ди на та ми? Знач но біль ше, ніж з раціональн им и!
Множ ин и нат ур альн их, цілих, раціональн их, дійсних і комплек с них чи сел поз на ча ють відпо відно літерами N , Z , Q , R , С . Кожн а із цих множ ин нескінченн а і є підмнож ин ою (част ин ою) нас туп ної мно жи ни (мал. 4). То му будь9яке на ту раль не чис ло можн а вваж ат и водн оч ас і цілим, і раціональн им, і дійсним, і навіть компл ек сн им (про комплексні числа читайте на с. 78).
Мно жи ну R дійсних чи сел та кож на зи ва ють чис ло вою пря мою, а її еле мен ти (чис ла) – точ ка ми чис ло вої пря мої.
Мал. 3 Мал. 4
ПІФА ГОР СА МОСЬ КИЙ
(бл. 580–500 рр. до н. е.)
 Давньо гр ецьк ий мат ем ат ик, філос оф. Орг а- нізув ав свою школ у (піфаг ор ейськ ий сою з), яка бу ла вод но час і релігійним братством, і політичн ою партією. Досліджув ав пробл ем и те орії чи сел, ге о метрії, гар монії, аст ро номії. Вва жав, що все виз на ча ють чис ла. Досліджу вав різні ви ди чи сел: парні, три кутні, квад ратні, дос ко налі, дружні то що. Ви я вив, що сто ро на квад ра та і йо го діаго наль не ма ють спіль ної міри.
Давньо гр ецьк ий мат ем ат ик, філос оф. Орг а- нізув ав свою школ у (піфаг ор ейськ ий сою з), яка бу ла вод но час і релігійним братством, і політичн ою партією. Досліджув ав пробл ем и те орії чи сел, ге о метрії, гар монії, аст ро номії. Вва жав, що все виз на ча ють чис ла. Досліджу вав різні ви ди чи сел: парні, три кутні, квад ратні, дос ко налі, дружні то що. Ви я вив, що сто ро на квад ра та і йо го діаго наль не ма ють спіль ної міри.
Дійсні чис ла мож на порівню ва ти.
З двох дод атн их дійсних чис ел більш е те, у яког о ціла част и- на більш а. Якщ о цілі част ин и рівні, більш им вваж аєтьс я те чис ло, у яко го пер ший з не од на ко вих де сят ко вих знаків біль ший, а всі по пе редні од на кові.
Прикл ад и. 1,4148... > 1,4139... ; –1,4162... < –1,4139... ; –0,0674... < 0,00176... .
Розг ля не мо де які влас ти вості мно жи ни дійсних чи сел. Мно жи на дійсних чи сел R нескінчен на, не містить ні най мен шо го, ні найбіль шо го чис ла. Мно жи ни N , Z і Q є її підмно жи на ми. Як і множ ин а Q , множ ин а дійсних чис ел скрізь щіль на , тобт о для будь9яких двох різних дійсних чис ел завжд и можн а назв ат и так е третє дійсне числ о, яке більш е за одн е з дан их, але менш е за друг е. Це випл ив ає з тог о, що кол и a < b , то
![]()
 ПЕРЕВІРТЕ СЕБЕ
ПЕРЕВІРТЕ СЕБЕ
1. Як поз на ча ють на ту ральні чис ла? На ведіть прик ла ди.
2. На ведіть прик лад не де сят ко вої сис те ми чис лен ня.
3. Які ви знаєте наз ви для ве ли ких чи сел? За пишіть кіль ка ве ли ких чис ел та назвіть їх.
4. Назвіть най мен ше на ту раль не чис ло. Чи існує найбіль ше на ту раль не чис ло?
5. Які числ а наз ив аю ть цілим и? Як позн ач аєтьс я множ ин а цілих чис ел?
6. Як на зи ва ють ся цілі до датні чис ла?
7. Назвіть ціле числ о, яке більш е від найбільш ог о цілого від’ємног о чис ла, але мен ше від най мен шо го до дат но го ціло го чис ла.
8. Сфор му люй те оз на чен ня раціональ но го чис ла. Як поз на чаєть ся мно жи на раціональ них чи сел?

Відповідь. 4 століття.
![]() За у ва жен ня. На трад иційній осі час у відсутні нульо в ий вік і нуль о вий рік, то му во на відрізняєть ся від ма те ма тич ної чис ло вої осі. І якщ о одн а подія відбул ася в m
9му році до н. e., а друг а – в n
9му році н. e., то між ци ми подіями пройш ло не m
+ n
, а m
+ n
– 1 років.
За у ва жен ня. На трад иційній осі час у відсутні нульо в ий вік і нуль о вий рік, то му во на відрізняєть ся від ма те ма тич ної чис ло вої осі. І якщ о одн а подія відбул ася в m
9му році до н. e., а друг а – в n
9му році н. e., то між ци ми подіями пройш ло не m
+ n
, а m
+ n
– 1 років.
2. До ведіть, що між будь9яки ми дво ма раціональ ни ми чис ла ми а і b на числ овій прямій існує безліч раціональн их чис ел.
![]() Розв’язанн я. Не хай а
< b
. Тоді 2а
< а
+ b
і а
+ b
< 2b
, звідси Якщ о а
і b
раціональні, то числ о
Розв’язанн я. Не хай а
< b
. Тоді 2а
< а
+ b
і а
+ b
< 2b
, звідси Якщ о а
і b
раціональні, то числ о ![]() також
також
 раціональн е. Позн ач ивш и йог о літерою m
, так сам о пер екон у9 ємося, що числ о так ож раціональн е і т. д.
раціональн е. Позн ач ивш и йог о літерою m
, так сам о пер екон у9 ємося, що числ о так ож раціональн е і т. д.
3.
По дай те у виг ляді де сят ко во го дро бу: ![]()
![]() Розв’язанн я. Щоб пе рет во ри ти зви чай ний дріб у де сят ко вий, потрібно чи сель ник да но го дро бу поділи ти на йо го зна мен ник. Маємо:
Розв’язанн я. Щоб пе рет во ри ти зви чай ний дріб у де сят ко вий, потрібно чи сель ник да но го дро бу поділи ти на йо го зна мен ник. Маємо:
![]()
Відповідь. а) 1,125; б) 0, 363636...; в) 1,1666... .
4. Більш е чи менш е від мілья рд а числ о 230 ?

2. Яке з тверджень правильне:
а) кожне натуральне число є дійсним;
б) кожне ціле число є дійсним;
в) кожне раціональне число є дійсним;
г) кожне ірраціональне число є дійсним;
ґ) не кожне дійсне число є раціональним;
д) не кожне дійсне число є ірраціональним?
3. Укажіть правильні твердження:
а) 2π – число дійсне; б) –π – число ірраціональне;
в) 1 + π – число ірраціональне; г) π : 2π – число раціональне.
4. Чи правильні схеми на малюнках 6 і 7?


5. Які із записів правильні?
а) –3 ∈ N
; б) 0 ∈ R
; в) 0,5 ∈ Z
; г) ![]()
ґ) –7 ∈ Q
; д) ![]() е)
е) ![]() є) 0,333 ∈ Q
.
є) 0,333 ∈ Q
.
6. Чи правильні твердження:
а) будь9яке натуральне число є раціональним;
б) будь9яке натуральне число є дійсним;
в) будь9яке ціле число є натуральним;
г) будь9яке раціональне число є цілим;
ґ) будь9яке ірраціональне число є дійсним?
7. Для будь9яких дійсних чисел а , b , с правильні рівності а + b = b + а , а + (b + с ) = (а + b ) + с , аb = bа , а (bс ) = (аb )с , (а + b )с = ас + bс .
Які закони дій виражають ці рівності?
8. На скільки число 3 більше від –2? А від 2?
9.
Назвіть кілька раціональних чисел. Чи є раціональними чис9 ла 5; –3; ![]() 0; 2,01?
0; 2,01?
10. Назвіть кілька дійсних чисел, які не є раціональ ними. Як називаються такі числа?
À ![]()
11. Запишіть число, яке має 38 мільярдів, 7 тисяч і 5 один иць.
12. Скільки хвилин пройшло від початку нашої ери до сьогодні?
13. Серце здорової людини робить у середньому 70 скорочень за хвилину. Скільки разів воно скорочується протягом 70 років?
14. Обчисліть:
а) 432 ⋅ (567 – 202) + 1001 : 13 + 28;
б) (43 ⋅ 19 – 26 928 : 33) ⋅ (16 112 : 53 – 304).
15. Знайдіть суму всіх натуральних чисел, менших від 100.
16. Розгляньте рівності. Чи правильні вони? Які законо мір ності ви помітили? Спробуйте продовжити записи.
а) 1 + 9 ⋅ 0 = 1, б) 1 + 8 ⋅ 1 = 9,
2 + 9 ⋅ 1 = 11, 2 + 8 ⋅ 12 = 98,
3 + 9 ⋅ 12 = 111; 3 + 8 ⋅ 123 = 987.
17. Запишіть римськими цифрами число:
а) 47; б) 109; в) 1999; г) 2009.
18. Подайте у вигляді звичайного дробу числа:

24. З поданих нижче чисел випишіть: а) цілі; б) іррац іон альні.
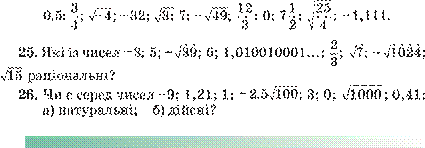 Á
Á
27. Числа 10 111, 1 101 110, 10 000 000 записано у двійковій системі. Запишіть їх у десятковій системі числення.
28. Спробуйте знайти суму й різницю чисел 1 011 101 і 110100, записаних у двійковій системі числення.
29. Уявіть, що якась жінка М на початку нашої ери наро- дила двох дочок, кожна з яких до 33 років народила також не менше двох дочок, а кожна з них – також не менше двох дочок і т. д. Скільки нащадків жінки М жило б за таких умов у наші дні? Чи могло б таке бути?
30. Задумайте будь9яке трицифрове число. Допишіть до ньо- го таке саме, щоб утворилося шестицифрове число. Поділіть це шестицифрове число на 13, знайдену частку – на 11, а нову частку – на задумане трицифрове число. Я знаю, яке число ви одержали в результаті. На основі чого я безпомилково можу вгадати результат?
31. Поет Віргілій народився в 70 р. до н. е. У якому році тре- ба було відзначати 20009річчя з дня його народження?
32. За візантійською хронологією від створення світу до Різдва Христового пройшло 5508 років. У літописі зазначає ться, що якась подія відбулася 7168 року. Про який рік ідеться?
33. Видатний український математик Михайло Пилипович Кравчук народився 27 вересня 1892 року, а помер 9 березня 1942 року. Скільки років прожив наш співвітчизник? Скільки часу пройшло від дня його народження дотепер?
34. З’ясуйте роки життя видатних українських математиків М.В. Остроградського, В.Я. Буняковського, Г.Ф. Вороного і за цими даними складіть і розв’яжіть задачі.
 36.
Один учень говорить, що число не, а другий, що раціональне. Хто з них має рацію?
36.
Один учень говорить, що число не, а другий, що раціональне. Хто з них має рацію?
37. Чи правильно, що сума двох раціональних чисел є число раціональне? А чи завжди сума двох ірраціональних чисел є число ірраціональне?
38. Чи правильно, що сума, різниця, добуток і частка двох дійсних чисел – числа дійсні?
39. Чи може бути раціональним числом:
а) сума ірраціональних чисел;
б) різниця ірраціональних чисел;
в) добуток ірраціональних чисел;
г) степінь ірраціонального числа;
ґ) частка двох ірраціональних чисел?
Відповідь обґрунтуйте.

41. Розв’яжіть рівняння:
а) х 2 – 7х + 6 = 0; б) х 2 – 4х – 21 = 0.
42. Спростіть вираз:
а) (х – 5)(2х + 3) + 7х ; б) (3а – 2)(а + 4) – 3а 2 .
 § 2. Обчислення
§ 2. Обчислення
Як ви вже знаєте, числа можна записувати в різних видах. Відповідно й обчислення можна здійснювати по9різному. Якщо дані числа раціональні, то дії над ними можна виконувати в звичайних або десяткових дробах – усно, письмово чи за до по мо гою калькуляторів. Якщо серед даних чисел є й ірраціо нальні, то обчислення можна вести у вигляді перетворень ірраціо наль них виразів або за допомогою десяткових наближень.
Для додавання і множення дійсних чисел а , b , с справ джу ються такі закони:
а + b = b + а – переставний закон додавання; (а + b ) + с = а + (b + с ) – сполучний закон додаванн я; а ⋅ b = b ⋅ а – переставний закон множення;
(а ⋅ b ) ⋅ с = а ⋅ (b ⋅ с ) – сполучний закон множення;
(а + b ) ⋅ с = а ⋅ с + b ⋅ с – розподільний закон множ ення.
ОБЧИСЛЕННЯ
Віднімання означується як дія, обернена додаванню, ділен- ня – як дія, обернена множенню.
У множині раціональних чисел Q завжди виконуються дії додавання, віднімання, множення і ділення (за винятк ом ділення на 0). Виконуваністю дії ділення множина Q істотно відрізняється від множини цілих чисел Z , у якій ця дія вико- нується не завжди.
На практиці, розв’язуючи прикладні задачі, обчислення ви конують не з абстрактними числами, а з числами, які вираж аю ть значення конкретних величин (маси, відстані, часу, швидк ості, площі, об’єму тощо). Існують різні одиниці вимірюв ання цих та інших величин. Для кількісної характерис тики однієї ве личини можна викор ис товувати різні одиниці вимір ювання. Наприклад, у метричній системі довж ин у вимір юють у кіло- мет рах, метрах, санти мет рах, міліметрах. Щоб порівнювати і вик он увати дії над значеннями величин, пот рібно вміти пере- творювати одні одиниці виміру на інші. Для цього корис туються формулами або спеціальними таб ли цями. Наприклад:
![]()
1га = 100 ар = 10 000 м2 ;
1 л = 1 дм3 = 1000 см3 = 0,001 м3 .
Розв’язуючи прикладні задачі, переважно мають справу не з точними, а з наближеними значеннями величин. Щоб мати найменшу похибку в таких розрахунках, слід дотримуватися такого правила округлення.
Якщо число округлюють до деякого розряду, то всі наступні за цим розрядом цифри відкидають. Якщо перша з відкинутих цифр 0, 1, 2, 3 або 4 (5, 6, 7, 8 або 9), то останню цифру, що залишається, не змінюють (збільшують на 1).
 Розв’язуючи прикладні задачі, ірраціональні числа звич айн о округлюють, відкидаючи їх нескінченні «хвости» дес ятков их зна- ків. Наприклад, якщо треба знайти значення суми чисел π і з точністю до тисячних, пишуть:
Розв’язуючи прикладні задачі, ірраціональні числа звич айн о округлюють, відкидаючи їх нескінченні «хвости» дес ятков их зна- ків. Наприклад, якщо треба знайти значення суми чисел π і з точністю до тисячних, пишуть:
Аналогічно можна знайти наближене значення добутку даних дійсних чисел:
Тепер науковцям часто доводиться виконувати обчислення над числами, записаними в стандартному вигляді.
Запис числа у вигляді а ⋅ 10n , де 1 а < 10, n – ціле, на зи вають стандартним виглядом числа . Число n у такому записі називають порядком даного числа .
Запишемо в стандартному вигляді числа, якими вира жа ються маси Землі, Місяця і маленької мурашки.
5 980 000 000 000 000 000 000 т = 5,98 ⋅ 1021 т,
73 500 000 000 000 000 000 т = 7,35 ⋅ 1019 т, 0,0000015 кг = 1,5 ⋅ 10–6 кг.
Числа, записані в стандартному ви гля ді, можна додавати, від ні мати, множити і ділити. Наприклад, якщо а = 4,2 ⋅ 105 і b = 1,5 ⋅ 105 , то а + b = 4,2 ⋅ 105 + 1,5 ⋅ 105 = (4,2 + 1,5) ⋅ 105 = 5,7 ⋅ 105 ; а – b = 4,2 ⋅ 105 – 1,5 ⋅ 105 = (4,2 – 1,5) ⋅ 105 = 2,7 ⋅ 105 ; а ⋅ b = 4,2 ⋅ 105 ⋅ 1,5 ⋅ 105 = (4,2 ⋅ 1,5) ⋅ 105 ⋅ 105 = 6,3 ⋅ 1010 ; а : b = (4,2 ⋅ 105 ) : (1,5 ⋅ 105 ) = 4,2 : 1,5 = 2,8.
В останньому прикладі застосовано основну властивість відношення.
 Питання про обчислення в математиці здавна було одним з найважливіших, а в окремі періоди – і найважчим. Відомий вчений середньовіччя Беда Достойний писав: «У світі є чимало важких речей, але немає нічого важчого за чотири дії арифм е- тики». Оскільки теперішніх алгоритмів дій навіть над натуральними числами тоді люди не знали, одні рахували, користуючися ква солинами, кісточками слив чи ка мінцями, інші – «на лі ніях». На малюнку 8, узятому з книжки ХVІ ст., муза Арифметика спо сте рігає, як ді ють два обчислювачі: один на абаці, другий – користую чись пером.
Питання про обчислення в математиці здавна було одним з найважливіших, а в окремі періоди – і найважчим. Відомий вчений середньовіччя Беда Достойний писав: «У світі є чимало важких речей, але немає нічого важчого за чотири дії арифм е- тики». Оскільки теперішніх алгоритмів дій навіть над натуральними числами тоді люди не знали, одні рахували, користуючися ква солинами, кісточками слив чи ка мінцями, інші – «на лі ніях». На малюнку 8, узятому з книжки ХVІ ст., муза Арифметика спо сте рігає, як ді ють два обчислювачі: один на абаці, другий – користую чись пером.
Коли з’явились арифмометри, стали і їх використовувати. З вин ай- денням ЕОМ і особливо мікрокаль куляторів навіть найскладніші об- числення стали доступні багатьом.
Сучасні комп’ютерні технології дають змогу автоматизувати процес обчислення. Доступною і простою для виконання різного роду обчисл ень є
Мал. 8 програма Excel, якою оснащено су часні комп’ютери.
 ПЕРЕВІРТЕ СЕБЕ
ПЕРЕВІРТЕ СЕБЕ
1. Які арифметичні дії вам відомі?
2. Які дії завжди можливі в множині натуральних чисел? А в множи- нах Z , Q , R ?
3. Які ви знаєте закони дій? Сформулюйте їх.
4. Чому не можна ділити на 0?
5. Що ви розумієте під сумою двох ірраціональних чисел? А під їх добутком?

![]() Р о з в ’ я з а н н я. Перетворимо звичайні дроби в десяткові, виконаємо від по від ні дії в чисельнику і знаменнику, а потім поділимо чисельн ик на знаменник. Маємо:
Р о з в ’ я з а н н я. Перетворимо звичайні дроби в десяткові, виконаємо від по від ні дії в чисельнику і знаменнику, а потім поділимо чисельн ик на знаменник. Маємо:
![]()
2. Рекомендовані розміри футбольного поля 115 × 75 ярдів. Якою буде площа такого поля у м2 ?
![]() Р о з в ’ я з а н н я. Ярд (англ. yard
) – британська одиниця ви мі рювання відстані.
Р о з в ’ я з а н н я. Ярд (англ. yard
) – британська одиниця ви мі рювання відстані.
1 ярд = 3 фути = 36 дюймів = 0,9144 м,
115 ярдів = 115 ⋅ 0,9144 = 105,156 ≈ 105 (м), 75 ярдів = 75 ⋅ 0,9144 = 68,58 ≈ 69 (м).
Площа футбольного поля 105 ⋅ 69 ≈ 7245 (м2 ).
3. На фарбування 7,5 м2 підлоги потрібно 0,75 кг фарби. Скільки фарби потрібно, щоб пофарбувати підлогу, розміри якої 3,2 м і 4,5 м?
![]() Р о з в ’ я з а н н я. Площа підлоги, яку потрібно пофарбувати, 3,2 ⋅ 4,5 = 14,4 (м2
). Маса фарби пропорційна площі підлоги, тому маємо пропорцію 7,5 м2
: 14,4 м2
= 0,75 : х
. Звідси х
= 1,44 кг.
Р о з в ’ я з а н н я. Площа підлоги, яку потрібно пофарбувати, 3,2 ⋅ 4,5 = 14,4 (м2
). Маса фарби пропорційна площі підлоги, тому маємо пропорцію 7,5 м2
: 14,4 м2
= 0,75 : х
. Звідси х
= 1,44 кг.
![]()
| Обчисліть (43, 44) . |
|
| 43. а) 23,5 ⋅ 10, б) 47,96 ⋅ 100, |
в) 12,077 ⋅ 1000, |
| 0,08 ⋅ 10; 10 005 : 100; |
0,0036 ⋅ 1000. |
| 44. а) 345 ⋅ 0,1, б) 29,5 ⋅ 0,01, |
в) 345,8 ⋅ 0,001, |
| 2,3 ⋅ 0,1; 3,7 ⋅ 0,01; |
67,981 : 0,001. |
45. Знайдіть значення виразу зручним способом:
а) 3,72 ⋅ 2,41 – 2,72 ⋅ 2,41; б) 2,252 – 0,252 ;
в) 5, 27 ⋅ 1,45 + 4,73 ⋅ 1,45; г) 0,04 – 10,22 .
46. Назвіть числа, позначені крапками:
| 1 м = ... см; |
1 м = ... дм; 1 см = ... мм; |
| 1 м2 = ... дм2 ; |
1 м2 = ... см2 ; 1 дм2 = ... см2 ; |
| 1 т = ... ц; |
1 ц = ... кг; 1 кг = ... г; |
| 1 год = ... хв; |
1 хв = ... с; 1 год = ... с. |
47. Знайдіть суму всіх цілих чисел:
а) від –10 до 10; б) від –30 до 32; в) від 28 до 32.
48. На скільки сума чисел 4,35 і 2,3 більша за їх різницю?
À ![]()
49. Обчисліть зручним способом:
а) 24,1 ⋅ 1,4 + 24,1 ⋅ 1,01 – 24,1 ⋅ 1,41;
б) 1,3 ⋅ 37 + 1,3 ⋅ 63 + 2,3 ⋅ 74 + 2,3 ⋅ 26. Виконайте ділення (50–51) .
50. а) 250 кг : 50 кг; б) 6 ц : 75 кг;
в) 8 грн. : 40 к.; г) 7 грн. 20 к. : 80 к.
51. а) 8 м : 40 см; б) 3 м 20 см : 80 см;
в) 3 год : 45 хв; г) 5 год 20 хв : 16 хв.
52. Знайдіть невідомий член пропорції:

53. Поділіть число 600 на частини, пропорційні числам 2, 5 і 8.
54. Знайдіть середнє арифметичне і середнє геометричне чи- сел 2 і 18.
55.
Знайдіть суму, різницю, добуток і частку чисел 4,2 і ![]()
56. Продовжте обчислення, подані нижче.
57.


66. Автомобіль їхав протягом а год зі швидкістю 72 км/год і b год зі швидкістю 84 км/год. Скільки кілометрів він проїхав?
Обчисліть, якщо:
а) а
= 3 і b
= 2,5; б) а
= 1,3 і b
= 3,5; в) ![]()
67. Відстань від Сонця до Землі дорівнює 1,5 ⋅ 108 км. За який час світло проходить цей шлях, якщо швидкість світла дорів нює 3 ⋅ 105 км/год?
68. Для фарбування підлоги площею 12,5 × 4,2 м2 витрачено 5,78 кг фарби. Скільки потрібно фарби для фарбування підлоги в кімнаті площею 5,2 × 4,6 м2 ?
69. Масу коня можна визначити за формулою так: маса (кг) = = обхват грудної клітки (см) × 6 – 620. Знайдіть масу коня, обх ват грудної клітки якого наближено дорівнює: а) 180 см; б) 200 см; в) 220 см.
70. Масу коня можна визначити за іншою формулою: маса (кг) = = обхват грудної клітки (см) × K , де K = 2,7 (для легких коней), K = 3,1 (для середніх) і K = 3,5 (для великих коней). Обчисліть масу коня, обхват грудної клітки якого наближено дорівнює: а) 180 см; б) 200 см; в) 220 см. Порівняйте результати з отри- маними в попередній задачі.
71. Циркова арена у формі круга з’явилась у Лондоні в кінці XVIII ст. Її діаметр – 42 фути – було обрано таким чином, щоб для вершника, який скаче на коні, створ ювалася оптимальна відцентрова сила. Знайдіть площу циркової арени (у м2 ) і дов- жину її кола (у м). Результати округліть до десятих.
 Знайдіть значення виразу зручним способом (72–75)
.
Знайдіть значення виразу зручним способом (72–75)
.

74. а) 750 ⋅ 550 – (3525 – 1)(3525 + 1);
б) 830 ⋅ 930 + (1 – 7215 )(1 + 7215 ).
75. а) (3232 – 2)(3232 + 2) – 864 ⋅ 464 ;
б) (3 + 548 )(3 – 548 ) + 616 ⋅ 916 .
76. Порівняйте значення величин:
а) 5 км/год і 5 м/с; б) 1250 хв і 25 год;
в) 4 дюйми і 10 см; г) 500 г і 1 фунт.
Обчисліть (77–79) .
 78.
78.
79.
83. В основі басейну для водного поло – прямок утн ик з роз- мірами 25 м і 15 м. Яку найменшу кількість літрів води має містити басейн, якщо відомо, що мінімальна глибина такого басейну має бути 1,8 м?
84. Ділянка електричного кола складається з трьох послі- довно з’єднаних резисторів, які мають опори R 1 ≈ 3,869 Ом, R 2 ≈ 4,455 Ом, R 3 ≈ 1,61 Ом. Знайдіть загальний опір на ділянці цього кола. Результат округліть до сотих.
85. Турист на човні рухався спочатку проти течії річки, а потім за течією. Який шлях він пройшов загалом, якщо швидкість човна в стоячій воді – 25 км/год, швидкість течії річки 2 км/год, час руху за течією t з , а проти течії t п ? Обчисліть за умови:
а) t п = 30 хв, t з = 1 год 10 хв; б) t п = 15 хв, t з = 50 хв.
86.
Вартість обладнання – А
грн., а вартість його капіт аль- ного ремонту – r
. До капітального ремонту обладнання працює n
років, а з ремонтом – m
років. Відомо, що капітальний ремонт є рентабельним, якщо ![]()
Визначте, в якому випадку капітальний ремонт обладнання буде рента бельним:
а) А = 1200 грн., r = 300 грн., n = 3 роки, m = 4 роки;
б) А = 2100 грн., r = 800 грн., n = 6 років, m = 10 років;
в) А = 3500 грн., r = 2000 грн., n = 12 років, m = 20 років;
г) А = 6000 грн., r = 2500 грн., n = 10 років, m = 20 років.
87. На деякий момент часу зафіксовано курси валют, подані в таблиці.
| Назва |
Курс НБУ |
Комерційний курс |
| 1 долар США |
7,64 |
7,831 |
| 1 євро |
10,73 |
10,96 |
| 1 російський рубль |
0,25 |
0,26 |
Знайдіть суму грошей у національній валюті, за курсом НБУ і комерційним, якщо в наявності було:
а) 21,3 євро, 231,3 дол., 135 руб., 12 375,5 грн.;
б) 91,5 євро, 321,5 дол., 35 руб., 1237 грн.;
в) 71,2 євро, 23 дол., 535 руб., 92 375,5 грн.
![]()
88. Одне з двох натуральних чисел на 5 більше за інше. Знай діть ці числа, якщо їх добуток дорівнює 266.
89. Раціональним чи ірраціональним є число?
![]()
90. Знайдіть 12 % від числа: а) 45; б) 2,5.
91. Знайдіть число, 15 % якого дорівнює: а) 300; б) 0,6.
 § 3. Відсоткові розрахунки
§ 3. Відсоткові розрахунки
Багатьом фахівцям часто доводиться виконувати обчис ленн я за умови, якщо деякі значення виражено у відсотках. Коротко їх називають відсотковими розрахунками .
Нагадаємо, що відсоток – це сота частина. 1 % = 0,01, 10 % = 0,1, 100 % = 1.
Примітка. Відсотки часто називають процентами, а зам ість «скільки відсотків» іноді кажуть «який відсоток».
Існує три основні види задач на відсотки:
1 знаходження відсотків від числа ;
2 знаходження числа за відсотками ;
3 знаходження відсоткового відношення двох чисел.
Розглянемо приклади таких задач.
1 ![]() Потрібно зорати поле, площа якого дорівнює 300 га. За перший день трактористи виконали 40 % завдання. Скільки гектарів зорали вони за перший день?
Потрібно зорати поле, площа якого дорівнює 300 га. За перший день трактористи виконали 40 % завдання. Скільки гектарів зорали вони за перший день?
2 За перший день трактористи зорали 120 га, що стан овить 40 % поля. Знайдіть площу всього поля.
3 Потрібно зорати поле, площа якого дорівнює 300 га. За перший день трактористи зорали 120 га. Скільки відс отків усього поля вони зорали за перший день?

![]() Спробуйте розв’язати кожну із цих задач кількома способ ам и, замінивши 40 % дробом 0,4 чи
Спробуйте розв’язати кожну із цих задач кількома способ ам и, замінивши 40 % дробом 0,4 чи
Такі задачі зручно розв’язувати способом пропорції . Офор м люват и розв’язання сформульованих задач можна так:
300 га – 100 %, х га – 40 %.
120 га – 40 %, х га – 100 %.
![]() 3 300 га – 100 %,
3 300 га – 100 %,
120 га – х %.
Крім трьох основних видів задач, існують також склад ніші задачі на відсотки. Насамперед це задачі, в яких ідеться про збільшення чи зменшення чого9небудь на кільк а відсотків, і обернені до них. Розв’язуючи такі задачі, уточнюйте насам -
перед про відсотки від чого саме йдеться. Про це в задачі прямо не говориться, але існують домовлен ості про розуміння тих чи інших висловлювань.
Для прикладу розглянемо задачу.
Задача. Спочатку ціну на товар підвищили на 10 %, а потім знизили на 10 %. Як змінилася ціна на цей товар у результаті двох переоцінок?
Зверніть увагу на те, що перший раз ідеться про 10 % від початкової ціни, а другий раз – про 10 % від підвищен ої ціни.
А вони не однакові.
![]() Р о з в ’ я з а н н я. Нехай спочатку товар коштував а
грн.
Р о з в ’ я з а н н я. Нехай спочатку товар коштував а
грн.
Після підвищення ціни на 10 % він став коштувати а грн. + + 0,1а грн., або 1,1а грн.
10 % від підвищеної ціни становлять (1,1а ⋅ 0,1) грн., або 0,11а грн. Після зниження вартості товар став коштув ати (1,1а – – 0,11а ) грн., або 0,99а грн.
Отже, спочатку товар коштував а грн., а після двох пер ео ці- нок став коштувати 0,99а грн., тобто на 0,01а грн. менше. Це становить 0,01а : а = 0,01, або 1 %.
Відповідь. Після двох переоцінок початкова ціна товар у знизилася на 1%.
Особливо часто доводиться розв’язувати задачі на відсотки бухгалтерам і працівникам банків. Розглянемо для прикладу задачі, пов’язані з нарахуванням відсоткових грошей.
Прості відсотки – це нарахування відсотків лише на поч ат- ково інвестовану суму.
Наприклад, на початку року вкладник розміщує на рахунку в банку суму Р під відсоток r . Через рік він одержить суму Р 1 , яка дорівнює початковому вкладу (Р ) плюс нараховані від сотки:

Тут Р – сума початкового вкладу, Рn – сума вкладу через n років.
Нарахування за схемою простих відсотків застосовується, як правило, в короткострокових фінансових операціях, коли після кожного інтервалу нарахування кредитору виплачують ся відсотки, а також у будь9яких інших випадках за домов ле ністю сторін, що беруть участь в операції.
У довгострокових фінансово9кредитних угодах частіше використовують складні відсотки – їх нараховують не тільки на основну суму, а й на нараховані раніше відсотки. У цьому випадку кажуть, що відбувається капіталізація відсотків у міру їх нарахування.
Припустимо, що вкладник дав ощадбанку під 9 % річних 1000 грн. Це – початковий капітал . Через рік банк нарахує вкладнику за це 90 грн. відсоткових грошей (9 % від 1000 грн.). Після цього на рахунку вкладника стане 1090 грн., оскільки 1000 (1 + 0,09) = 1090. За другий рік відсоткових грошей йому нарах ують уже 9 % від 1090 грн.; нарощений капітал вклад9 ника після двох років дорівнюватиме 1000 (1 + 0,09)2 грн. Зрозуміло, що через n років нарощений капітал становитиме 1000 (1 + 0,09)n грн.
Взагалі, вкладений в ощадбанк початковий капітал А 0 під р % річних через n років перетвориться в нарощений капітал:
![]()
Це формула складних відсотків . За цією формулою можна розв’язувати також задачі, не пов’язані з нарощенням капіт алу.
Відсоткові гроші за неповний рік нараховують пропорційно до числа днів. Наприклад, якщо 350 грн., віддані під 11 % річн их, були в банку 183 дні, тобто ![]() року, то за це вкладник одерж ить
року, то за це вкладник одерж ить
![]() (грн.). Нарощений капітал вкладника дорівню-
(грн.). Нарощений капітал вкладника дорівню-
вати ме 369,25 грн.
Подібні до поняття відсотка проміле і проба.
Проміле – це одна тисячна (1 ‰ = 0,001). Наприклад, роз- чин солі, концентрація якого 5 проміле, – це розчин, 1000 г якого містять 5 г солі.
Пробами характеризують сплави дорогоцінних металів. Так, золото 8759ї проби – це сплав, 1000 г якого містять 875 г чистого золота.
Примітка. До переходу на метричну систему мір (1918 р.) пробою називалося дещо інше. У старих підручниках ариф метики пояснювалося: «Проба означає, скільки вагових частин чистого металу міститься в 96 вагових частинах сплаву». Тоді пробою називали кількість золотників чистого металу, які містяться в одному фунті сплаву. А 1 фунт дорівнював 96 зо лотникам. Сплав, який тепер називають золотом 7509ї проби, рані ше називали золотом 729ї проби. А в багатьох англомовних країн ах його і тепер називають золотом 189ї проби.
Проби дорогоцінних металів, з яких виготовляють різн і вироби, не довільні. В Україні законом установлено такі проби:
• для золота – 375, 500, 583, 750, 958;
• для срібла – 800, 875, 916.
 ПЕРЕВІРТЕ СЕБЕ
ПЕРЕВІРТЕ СЕБЕ
1. Що таке відсоток? А відсоток числа?
2. Що таке відсоткове відношення двох чисел?
3. Назвіть три основні види задач на відсотки.
4. Як знайти кілька відсотків від числа?
5. Як знайти число за відсотками?
6. Як знайти відсоткове відношення двох чисел?
7. Яким способом зручно розв’язувати задачі на відсотки?
![]()
1. Під час перевірки вологість зерна дорівнювала 16 %. 2 ц цього зерна просушили, після чого воно втратило 20 кг. Ви знач те вологість зерна після просушування.
![]() Розв’язання. 2 ц = 200 кг (мал. 9).
Розв’язання. 2 ц = 200 кг (мал. 9). ![]()
|
|
|
|
1) Скільки вологи містили 200 кг зерна до просушування?
200 ⋅ 0,16 = 32 (кг).
2. Скільки вологи містило зерно піс- ля просушування?
32 – 20 = 12 (кг).
3. Якою стала маса всього зерна після просушування?
200 – 20 = 180 (кг).
4.
Якою стала вологість зерна після ![]()
![]() просушування?
просушування?
12 : 180 = 0,0666... ≈ 6,7 (%). Мал. 9
2. На малюнку 10 наведено діаграму вікового складу укра- їнців, які жили в 1897 р. в Росії. Скільки відсотків від усього

Мал. 10
українського населення становили тоді діти віком до 10 років? А скільки діти і молодь до 20 років? Скільки новонароджених не доживало до 10 років?
![]() Розв’язання. Хлопчиків до 10 років тоді було близько 31 %, стільки ж і дівчаток. Отже, дітей до 10 років було трохи більше 30 %.
Розв’язання. Хлопчиків до 10 років тоді було близько 31 %, стільки ж і дівчаток. Отже, дітей до 10 років було трохи більше 30 %.
Молоді від 10 до 20 років було близько 22 %. Отже, разом з дітьми вони становили приблизно 52 %. Людей старшого віку було близько 48 %.
Оскільки діти віком до 10 років становили приблизно 31 % усіх українців, а молодь від 10 до 20 років – близько 22 %, то не доживали до 109річного віку близько 30 % усіх дітей.
3. До 10 кг 39відсоткового розчину солі долили 5 л води. На скільки відсотків зменшилася концентрація розчину?
![]() Розв’язання. Наявний розчин мав 10 ⋅ 0,03 = 0,3 (кг) солі. 5 л води мають масу 5 кг. Маса утвореного розчину 15 кг, він містить 0,3 кг солі. Знайдемо його концентрацію.
Розв’язання. Наявний розчин мав 10 ⋅ 0,03 = 0,3 (кг) солі. 5 л води мають масу 5 кг. Маса утвореного розчину 15 кг, він містить 0,3 кг солі. Знайдемо його концентрацію.
0,3 : 15 = 0,02, 0,02 = 2 %, 3 % – 2 % = 1 %.
Відповідь. Відсоткова концентрація розчину зменшилася на 1 %.
![]()
92. Знайдіть 10 % від числа: 180; 6000; 40; 8; 0,75.
93. Знайдіть число, 50 % якого дорівнюють: 8; 20; 18 000; 1.
94. Виразіть у відсотках відношення:
9 : 100; 6 : 10; 7 : 20; 13 : 10;
: 100; 6 : 10; 7 : 20; 13 : 10;
96. Скільки відсотків становлять:
а) 3 см відносно 12 см; б) 5 см відносно 1 дм;
в) 80 г відносно 1 кг; г) 5 хв відносно 1 год;
ґ) 0,1 м відносно 1 м; д) 0,1 г відносно 1 кг;
е) 2 с відносно 1 год; є) 3 ц відносно 1 т?
97.
 Скільки відсотків площі всього квадрата становить площа його зафарбованої частини (мал. 11)?
Скільки відсотків площі всього квадрата становить площа його зафарбованої частини (мал. 11)?
98. На скільки відсотків змінилося значення велич ин и, якщо воно: а) збільшилося вдвічі; б) збільши лося втричі; в) зменшилося вдвічі;
г) зменшилося в чотири рази; г) зменшилося в Мал. 11 п’ять разів?
99. У скільки разів збільшилося значення величини, якщо воно збільш ил ося на: а) 300 %; б) 50 %; в) 200 %; г) 150 %?
À ![]()
100. Із 120 випускників фінансового коледжу 20 % було направлено на роботу в банки, а 25 % – у заклади торгівлі. Скільки випускників ще не працевлаштовано?
101. У три цистерни розлили 30 000 т нафти. У першій цистерні 35 % усієї нафти, у другій – 40 %. Скільки тонн нафти міститься в третій цистерні?
102. Три баржі перевозили деякий вантаж. Перша перевезла30 % усього вантажу, друга – 25 % усього вантажу, а третя решту 55 т. Яка маса всього вантажу?
103. У 109А класі 24 учні і 25 % з них протягом навчального року не пропустили жодного заняття. У 109Б класі 25 учнів і 20 % з них не пропустили жодного заняття протягом нав чаль ного року. Який відсоток учнів обох класів, які постійно відві- ду вали заняття?
104. З 20 000 клієнтів банку триста звернулись із скаргами. Який відсоток клієнтів банку, задоволених його роботою?
105. Сторони прямокутника дорівнюють 12 см і 15 см. Знай- діть р % його площі, якщо:
а) р = 18; б) р = 30; в) р = 125.
106. Довжина однієї сторони трикутника дорівнює 6 м, а сума двох інших становить 150 % цієї сторони. Знайдіть периметр трикутника.
107. З молока виходить 10 % сиру. Скільки молока треба, щоб вийшло 50 кг сиру?
108. Із цукрових буряків виходить 15 % цукру. Скільки бу ряків потрібно переробити, щоб вийшло 3 т цукру?
109. Пошта обслуговує 3000 пенсіонерів. 1020 з них – чоло віки, решта – жінки. На скільки відсотків кількість жінок пенсіонерок перевищує кількість пенсіонерів чоловіків?
110. На склад центрального банку надійшло 95 найменувань бланків, які використовують центральний банк та його відд і- лення. 20 % найменувань використовують тільки відділення. Скільки найменувань бланків використовує центральний банк?
111. Латунь – сплав 60 % міді і 40 % цинку. Скільки міді і цинку треба сплавити, щоб вийшло 200 кг латуні?
112. Бронза – сплав міді й олова. Скільки відсотків олова в бронзовому злитку, який містить 33 кг міді і 17 кг олова?
113. Англійську мову вивчають 165 студентів першого курсу фізико9математичного інституту педагогічного університету, що становить 75 % усіх першокурсників. Скільки всього першокурсників навчається на фізматі?
Ðîçäië
114. Страхова компанія обслужила 63 особи, що становить 15 % від усіх клієнтів. Скільки клієнтів має страхова компан ія? 115. Який відсоток доби становлять 500 хвилин?
116. Сума коштів у 2000 гривень інвестована в десятирічний трастовий фонд під простий річний відсоток у 16 %. Якою буде величина капіталу в кінці десятиріччя?
117. Підприємству надано 50 000 грн. у кредит на шість місяців за ставкою 18% річних. Яку суму підприємство має повер нути банку через півроку?
Á ![]()
118. Малина під час сушіння втрачає 75 % своєї маси. Скіль ки свіжої малини потрібно висушити, щоб мати 5 кг сушеної?
119. З молока виходить 20 % вершків, а з вершків – 25 % масла. Скільки треба молока, щоб одержати 100 кг масла?
120. Руда містить 60 % заліза. З неї виплавляють чавун, який містить 98 % заліза. Із скількох тонн руди виплавляють 200 т чавуну?
121. Кам’яне вугілля містить у середньому 80 % вуглецю, а торф – 56 %. Скільки потрібно взяти торфу, щоб маса вуглецю в ньому була такою, як у 2 т вугілля?
122. Власник магазину підвищив ціну на чоловічі краватки на 25 %, але, як з’ясувалось, його товар перестали купувати за такими високими цінами, і йому довелося знизити нові ціни на 25 %. Ціна краватки тепер становить 126 грн. Якою була початкова ціна краватки?
123. Ціну на товар знизили спочатку на 20 %, а потім ще на 15 %, і в результаті він став коштувати 53,8 грн. Якою була початкова ціна товару?
124. В одному мішку крупи на 2 % менше, ніж у другому. На скільки відсотків у другому мішку крупи більше, ніж у першому?
125. У 109му класі хлопців на 25 % більше, ніж дівчат. На скільк и відсотків дівчат у цьому класі менше, ніж хлопців?
126. Ціна краму спочатку знизилася на 5 %, а потім ще раз на 10 %. На скільки відсотків змінилася вона після двох переоцінок?
127. Ціна на автомобіль спочатку знизилась на 15 %, а потім підвищилася на 10 %. Як змінилася ціна на автомобіль після цих двох переоцінок?
128. Випуск цукерок на кондитерській фабриці за перший рік зріс на 5 %, а за другий – на 8 %. Як зріс випуск продукції на заводі за ці два роки?
129. Площа поверхні Землі становить 510,1 млн км2 , з них 149,2 млн км2 – суходіл. На скільки відсотків площа поверхні Землі, покрита водою, перевищує площу суходолу?
130. За 15 м тканини одного виду та 20 м другого заплатили 2208 грн. Скільки заплачено за тканину кожного виду, коли відомо, що ціна одного метра тканини першого виду на 12 % більша від ціни одного метра тканини другого виду?
131. Підприємець купує на заводі труби зі знижкою 10 % від їхньої оптової ціни, а продає їх за роздрібною, яка вища від оптової на 10 %. Який відсоток прибутку має підприємець?
132. Борошно подешевшало на 14 %. Скільки кілограмів його можна купити за ті самі гроші, за які раніше купували 150 кг?
133. Раніше 3 кг рису коштували стільки, скільки тепер коштують 2 кг. На скільки відсотків подорожчав рис?
134. Свіжі гриби містять 95 % води, а сухі – 12 %. Скільки вийде сухих грибів з 22 кг свіжих?
135. Свіжі гриби містять 90 % води, а сухі – 12 %. Скільки треба висушити свіжих грибів, щоб одержати 25 кг сухих?
136. Вологість свіжих грибів дорівнювала 99 %. Коли гриби підсушили, їх вологість зменшилася до 98 %. Як змінилася маса грибів?
137. Скільки грамів води потрібно додати до 50 г 359від сот кової соляної кислоти, щоб отримати 109відсоткову кислоту?
138. До 8 кг 709відсоткового розчину кислоти долили 2 кг води. Визначте відсоткову концентрацію нового розчину.
139. Скільки потрібно змішати 109відсоткового і 159відсот кового розчинів солі, щоб мати 25 кг 129відсоткового розчину? 140. Скільки золота 3759ї проби треба сплавити з 30 г золота 7509ї проби, щоб одержати сплав золота 5009ї проби?
141. Будівельна компанія взяла в банку кредит 1 250 000 грн. на 3 роки під простих 15 %. Визначте: а) скільки гривень ком панія поверне банку через 3 роки; б) який прибуток одержить банк?
142. Підприємець вніс до банку 15 000 грн. під складні 16 % річних. Якою буде сума його вкладу через 4 роки?
143. На вклад у розмірі 100 000 грн. строком на 5 років банк нараховує 20 % річних. Яка сума буде на рахунку в кінці строку, якщо нар ахування відсотків здійснюється за схемою:
а) простих відсотків; б) складних відсотків?
144. На скільки відсотків число 2,5 ⋅ 108 більше за число:
а) 5 ⋅ 107 ; б) 1,5 ⋅ 108 ; в) 7,5 ⋅ 107 ?
145. Дано два вирази:
 На скільки відсотків значення першого з них більше від зна9 чення другого, якщо:
На скільки відсотків значення першого з них більше від зна9 чення другого, якщо:
![]()
146. Розв’яжіть нерівність:
а) 2х + 3 > 5(х – 12); б) х 2 – 4х > (х – 1)( х + 1). 147. Винесіть спільний множник за дужки:
а) 6а (х – 2) + 8b (х – 2) + 4с (2 – х );
б) х 3 (2х + 3) + 3(2х 3 + 3х 2 ) + 3х 3 (3 + 2х ). 148. Побудуйте графіки функцій:
а) у = –х 2 ; б) у = 2х 2 ; в) у = х 2 – 4; г) у = (х + 1)2 .
![]()
Варіант 1
1. Зап ишіть п’ять цілих чис ел, які не є нат ур альн им и.
2.
 У скільк и разів числ о 5 більш е від числ а
У скільк и разів числ о 5 більш е від числ а
3.
Чи є се ред чи сел (![]() – 1)2
, (
– 1)2
, ( ![]() )2
– 1, чис ло?
)2
– 1, чис ло?
4. Обч исліть: а) (0,36 + 1,64)(0,36 – 1,64); б)
5. Знайдіть: а) 20 % від числ а 35; б) числ о, 35 % яког о дор ів- нює 70.
Варіант 2
1. Зап ишіть п’ять раціональн их чис ел, які не є нат уральн им и.
2.
![]() У скільк и разів числ о менш е від числ а 6?
У скільк и разів числ о менш е від числ а 6?
3. Чи є сер ед чис ел – 12 , ( – 1)2 , (
4.
 Обч исліть: а) (1,73 + 0,27)(1,73 – 0,27); б)
Обч исліть: а) (1,73 + 0,27)(1,73 – 0,27); б)
5. Знайдіть: а) 25 % від числ а 40; б) числ о, 40 % яког о дор ів- нює 80.
 § 4. Числові функції
§ 4. Числові функції
Одн е з найважл ивіших пон ять мат ем ат ик и – функція. З її до по мо гою мо де лю ють і досліджу ють різно манітні про це си, що від бува ють ся нав ко ло нас. Пов то ри мо ос новні відо мості про функцію, які ви знаєте з поп ер едніх класів.
Як що кож но му зна чен ню змінної х з де я кої мно жи ни D відповідає єди не зна чен ня змінної у , то та ку відповідність на зи ва ють функцією .
 При ць о му х на зи ва ють не за леж ною змінною
, або ар гу мен том
, у
– за леж ною змінною
,
або функцією
.
При ць о му х на зи ва ють не за леж ною змінною
, або ар гу мен том
, у
– за леж ною змінною
,
або функцією
.
Усі зна чен ня, які мо же на бу ва ти ар гу мент функції, на зи ва ють об лас тю виз на чення дан ої функції і позн ач аю ть літе9рою D .
Мно жи ну всіх зна чень у , яких мо же на бу ва ти функція, на зи ва ють її об лас тю зна чень і поз на ча ють літерою Е (мал. 12). Мал. 12
Дві функції вваж аю тьс я різним и, якщ о в них різні обл асті виз на чен ня або пра ви ла відповідності. Нап рик лад, функціяу = х 2 , зад ан а на проміжку [–3; 3], і функція у = х 2 , за да на на R , різні. А зад ані на R функції у = 1 – х 2 і у = (1 – х )(1 + х ) одн ак ові, оскільки вир аз и 1 – х 2 і (1 – х )(1 + х ) то тож но рівні.
Дві функції на зи ва ють ся рівни ми, як що їх об ласті виз на чен ня од на кові і в кожній точці об ласті виз на чен ня во ни ма ють рівні знач енн я. Рівним и є, напр икл ад, такі пар и функцій:
![]()
Щоб за да ти функцію, до сить заз на чи ти її об ласть виз на чен ня і прав ил о відповідності.
Задавати функції можна різними спос обами. Часто їх задаю ть формулами . Наприклад, відпо відність між довжиною а сторони квадрата і його площею S можна задати формулою S = а 2 .
Відповідність між радіусом r кола і довжиною С кола можна задати формулою С = 2πr .
Відповідність між значеннями змінної х і значеннями вираз у 2х – 1 можна задати формулою у = 2х – 1.
Зад анн я функції форм ул ою зручн е тим, що дає можл ивість зна хо ди ти зна чен ня функції для довіль но го зна чен ня ар гу мен ту. Та ке за дан ня функції до сить еко ном не: здебіль шо го фор му ла займ ає один ряд ок.
Якщ о функцію зад аю ть форм ул ою і нічог о не кажуть про об ласть її виз на чен ня, то вва жа ють, що ця об ласть – мно жи на всіх зна чень змінної, при яких фор му ла має зміст. Нап рик лад, об ласть виз на чен ня функції у
= 2х
– 1 – множ ин а всіх дійсних чис ел, а функції ![]() – множ ин а всіх дійсних чис ел, крім 1,
– множ ин а всіх дійсних чис ел, крім 1,
ос кіль ки на 0 діли ти не мож на.
За да ва ти функції мож на і у виг ляді таб лиці . Нап рик лад, функцію у = 2х – 1 для пер ших де ся ти на ту раль них зна чень х мож на за да ти у виг ляді та кої таб лиці:
| х |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| у |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
Тут:
• обл асть визн ач енн я: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
• обл асть знач ень: {1, 3, 5, 7, 9, 11, 13, 15, 17, 19}.
Табл ичн ий спосіб зад анн я функції зручн ий тим, що для пев- них зна чень ар гу мен ту до таб лиці вже за не се но відповідні зна чен ня функції, то му не тре ба ро би ти будь9яких об чис лень. Не з руч ний він тим, що таб ли ця зай має біль ше місця. До то го ж, як прав ил о, містить знач енн я функції не для всіх знач ень арг ум ен- ту, а тіль ки для де я ких.
Функцію можн а зад ав ат и і слов есн о . Напр икл ад, якщ о кожн о- му ціло му чис лу пос та ви ти у відповідність йо го квад рат, то одер жим о функцію, обл аст ю визн ач енн я якої є множ ин а цілих чис ел, а обл аст ю знач ень – множ ин а нат ур альн их чис ел і числ о нуль.
Час то функції за да ють у виг ляді графіків, по бу до ва них у де кар товій сис темі ко ор ди нат.
Графіком функції наз ив аєтьс я множ ин а всіх точ ок коо рди нат ної пло щи ни, абс ци си яких дорівню ють зна чен ням ар гу мен ту, а ор ди на ти – відповідним зна чен ням функції.
Напр икл ад, на мал юнк у 13 зобр аж ен о графік функції у
= 2х
– 3, зад ан ої на відрізку [–1; 5], а на мал юнк у 14 – гра9 фік функції ![]() на відрізку [1; 6].
на відрізку [1; 6].
Ма ю чи графік функції, мож на для будь9яко го зна чен ня ар гум ент у (з обл асті визн ач енн я) вказ ат и відповідне знач енн я функції. Для прик ла ду знай де мо зна чен ня функції ![]() , як що х
= 4, кор ист ую ч ись поб уд ов ан им графіком. Шук аємо на осі х
точк у з абсц ис ою 4, на графіку знах од им о точк у М
з абсц ис ою 4, а на осі орд ин ат – орд ин ат у точк и М
; вон а дорівнює 1,5. Отж е, ко рис ту ю чись графіком функції, мож на склас ти таб ли цю її знач ень, тобт о графік зад ає функцію. Графічний спосіб
за дан ня
, як що х
= 4, кор ист ую ч ись поб уд ов ан им графіком. Шук аємо на осі х
точк у з абсц ис ою 4, на графіку знах од им о точк у М
з абсц ис ою 4, а на осі орд ин ат – орд ин ат у точк и М
; вон а дорівнює 1,5. Отж е, ко рис ту ю чись графіком функції, мож на склас ти таб ли цю її знач ень, тобт о графік зад ає функцію. Графічний спосіб
за дан ня

функції зручн ий своєю нао чністю. Дивл яч ись на графік, одр аз у мож на з’ясу ва ти влас ти вості функції, яку він за дає. Зок ре ма, мож на вста но ви ти такі її ха рак те рис ти ки:
• об ласть виз на чен ня і об ласть зна чень функції;
• при яких зна чен нях ар гу мен ту зна чен ня функції до датні, при яких – від’ємні, при яких дорівнюю ть нул ю;
• на яких проміжках функція зрос тає , а на яких спа дає .
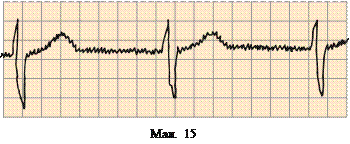
Існую ть прил ад и – терм огр аф и, які самі кресл ять графік тем- пер ат ур и. Графіком функції є так ож кардіогр ам а, накр есл ен а кардіогр аф ом (мал. 15). «Чит аю ч и» так ий графік, лікар діагн ос- тує роб от у серц я хвор ог о. Взаг алі, баг атьо м фахівцям треб а вміти «чи та ти» різні графіки.
 Чи за дає функцію графік, зоб ра же ний на мал юнк у 16? Ні, оскільки на ць о му графіку од но му зна чен ню ар гу мен ту х
(нап рик лад, х
= 3) від повідають три різних зна чен ня у
. А згід но з оз на чен ням функцією вва жаєть ся тіль ки та ка відповід ність, при якій одн ом у знач енн ю арг ум ент у х
відпо ві дає єди не зна чен ня функ ції у
.
Чи за дає функцію графік, зоб ра же ний на мал юнк у 16? Ні, оскільки на ць о му графіку од но му зна чен ню ар гу мен ту х
(нап рик лад, х
= 3) від повідають три різних зна чен ня у
. А згід но з оз на чен ням функцією вва жаєть ся тіль ки та ка відповід ність, при якій одн ом у знач енн ю арг ум ент у х
відпо ві дає єди не зна чен ня функ ції у
.
Існує баг ат о різних видів функц ій.
Дея кі з них ви вже знає те: Мал. 16
• у = kх – прям а проп орційність (k ≠ 0);
• у = kх + b – лінійна функція;
• ![]() – обер не на про порційність (k
≠ 0);
– обер не на про порційність (k
≠ 0);
• у = ах 2 + bх + с – квадр ат ичн а (або квадр атн а) функція (a ≠ 0). Графіки найуж ив аніших функцій под ан о в табл иці 1.
Щоб буд ув ат и графіки складніших функцій, вик ор ист ов ую ть такі пра ви ла.
• Графіки функцій y = f (х ) і y = –f (х ) сим етр ичні відносн о осі х .
• Щоб по бу ду ва ти графік функції y
= kf
(х
), де k
> 0, треб а графік функції y
= f
(х
) розт ягн ут и від осі х
у k
разів, якщ о k
> 1, або стисн ут и йог о в ![]() разів до осі х
, якщ о 0 < k
< 1.
разів до осі х
, якщ о 0 < k
< 1.
Таб ли ця 1
| y = x
|
y = x 2 графік – парабола
|
|
D (y ) = (– ∞; 0) ∪ (0; +∞) E (y ) = (– ∞; 0) ∪ (0; +∞) |
y = x 3 графік – кубічна парабола
|
|
|
|
• Щоб побудувати графік функції y
=f
(kх
), де k
> 0, треба графік функції y
= f
(х
) розтягнути від осі y
в ![]() разів, якщо 0 < k
< 1, або стиснути його в k
разів, якщо k
> 1.
разів, якщо 0 < k
< 1, або стиснути його в k
разів, якщо k
> 1.
• Щоб одерж ат и графік функції y = f (х ) + n , треб а графік функції y = f (х ) пе ре нес ти на n один иць у напр ямі осі у , як що n > 0, або на |n| один иць у прот ил ежн ом у напр ямі, якщ о n < 0.
• Щоб одерж ат и графік функції y = f (х – m ), дос ить графік функції y = f (х ) пе ре нес ти на m один иць у напр ямі осі х , як що m > 0, або на |m| оди ниць у про ти леж но му нап рям і, як що m < 0.

Прик ла ди по бу до ви графіків у = х 2 , у = 2х 2 , у = –2х 2 по да но на ма люн ку 17, а графіків у = х 2 , у = (х – 3,5)2 , у = (х – 3,5)2 + 3 – на ма люн ку 18.
Термін «функція» ввів у математику Г.В. Лейбніц.
ЛЕЙБНІЦ ГОТФРІД ВІЛЬГ ЕЛЬМ
(1646–1716)
 Вид атн ий німецьк ий учен ий. За освітою юрист, прац юв ав бібліотек ар ем, історіогр аф ом, орг анізув ав Берлінськ у акад емію нау к, досліджув ав проб ле ми політич ної еко номії, мо воз на в ства, хі мії, ге о логії, констру ю вав об чис лю вальні ма ши ни. Ос но во по лож ник сим волічної логіки, один з творців мат ем ат ичн ог о аналізу. Ввів терміни: «функція», «абс ци са», «орд ин ат а», логічну сим- воліку, знак и множ енн я і ділен ня (крап ку і дво к рап ку) та ін.
Вид атн ий німецьк ий учен ий. За освітою юрист, прац юв ав бібліотек ар ем, історіогр аф ом, орг анізув ав Берлінськ у акад емію нау к, досліджув ав проб ле ми політич ної еко номії, мо воз на в ства, хі мії, ге о логії, констру ю вав об чис лю вальні ма ши ни. Ос но во по лож ник сим волічної логіки, один з творців мат ем ат ичн ог о аналізу. Ввів терміни: «функція», «абс ци са», «орд ин ат а», логічну сим- воліку, знак и множ енн я і ділен ня (крап ку і дво к рап ку) та ін.
«Після Лейбніца, ма буть, уже не бу ло лю ди ни, яка повністю охоп лю ва ла б усе інте лек ту аль не жит тя сво го ча су».
Н. Вінер
ПЕРЕВІРТЕ СЕБЕ
1. Що так е функція? Як позн ач аю ть функції?
2. Що та ке ар гу мент функції, об ласть виз на чен ня функції?
3. Як мож на за да ва ти функцію?
4. Назвіть осн овні вид и функцій. Які їх графіки?
5. За да но графік функції у = f (х ). Як по бу ду ва ти графік функції:
а) у = аf (х ); б) у = f (х ) + b ; в) у = f (х + а )?
6. Які функції на зи ва ють рівни ми? А нерівни ми? На ведіть прик ла ди.
 Розв’язання. а) Про а налізуємо функцію
Розв’язання. а) Про а налізуємо функцію
Змінна х
мож е наб ув ат и будь9яких знач ень, крім тих, при яких знам енн ик дроб у ![]() дорівнює нул ю. Щоб їх знайт и, розв ’яже9
дорівнює нул ю. Щоб їх знайт и, розв ’яже9
мо рівнянн я 9 – х 2 = 0, (3 – х )(3 + х ) = 0, звідcи х 1 = 3, х 2 = –3.
От же, об ласть виз на чен ня функції – мно жи на дійсних чи сел, крім х = 3.
![]() D
(y
) = (–∞; –3) (–3; 3) ∪(3; +∞).
D
(y
) = (–∞; –3) (–3; 3) ∪(3; +∞).
![]() б) Розг ля не мо функцію . Ви ко наємо то тожні
б) Розг ля не мо функцію . Ви ко наємо то тожні
перетв ор енн я: отж е, ![]()
При будь9яких зна чен нях змінної х вираз (1 – х )2 0, а то му обл асть виз н ач енн я функції – уся множ ин а дійсних чис ел.
D (y ) = R .
2. Чим різнятьс я графіки функцій

 Розв’язання. Праві част ин и да9
Розв’язання. Праві част ин и да9
вир аз має числ ові значенн я при всіх дійсних зна чен нях х , а дру гий – при
всіх, крім х = 3. То му графік пер шої Мал. 19 функції – прям а, а друг ої – прям а без однієї точк и (мал. 19).

150. Як на зи ваєть ся графік функції, за да ної фор му лою:
а) у = 3х + 1; б) у = х 2 ; в) у = 3; г) у = х –1 ?
151. Графік якої з функцій про хо дить че рез по ча ток ко ор ди нат:
а) у = –5х ; б) у = 3х – 2; в) у = 2х 2 ; г) у = х (х – 2)?
152. Які з функцій, за да них фор му ла ми у = 15 – х , у = |х|, у = 3(х – 2), у = х 2 + 5, не можуть мати від’ємних значень.
153. Чи є пло ща кру га функцією йо го радіуса? А йо го діа мет ра?
154. Чи є об’єм куб а функцією довж ин и йог о ребр а? Спро- буйте за да ти цю функцію фор му лою.
À ![]()
155. За дай те фор му лою функцію, яка ви ра жає пло щу квад ра та че рез йо го пе ри метр Р .
156.
 По бу дуй те графік функції, яка ви ра жає за лежність пе ри мет ра пра виль но го три кут ни ка від дов жи ни йо го сто ро ни. 157.
На мал юнк у 20 зобр аж ен о графік функції. Один учень ствер джує, що цю функцію мож на за да ти фор му лою
По бу дуй те графік функції, яка ви ра жає за лежність пе ри мет ра пра виль но го три кут ни ка від дов жи ни йо го сто ро ни. 157.
На мал юнк у 20 зобр аж ен о графік функції. Один учень ствер джує, що цю функцію мож на за да ти фор му лою ![]() інший – що гра фіку відповідає форм ул а у
= |х
|. Хто з них прав ий?
інший – що гра фіку відповідає форм ул а у
= |х
|. Хто з них прав ий?
158. У США осн овн ою один иц ею дов жи ни вва жаєть ся ярд, який до9
Мал. 20
рівнює ![]() м. Зад айт е форм ул ою
м. Зад айт е форм ул ою
за лежність дов жи ни L , вир аж ен ої в метр ах, від числ а ярдів l .
159. «Про чи тай те» графік зміни ат мос фер но го тис ку, зоб ра же ний на ма люн ку 21.
160. На мал юнк у 22 зобр аж ен о графіки рух у двох електр о- поїздів. Про а налізуй те ці ру хи: скіль ки зу пи нок ро бив ко жен поїзд; ко ли во ни зустріли ся; скіль ки ча су три ва ла кож на зу пин ка?

161. Знайдіть f (–2), f (–1), f (0), f (1), f (2), як що функцію за да но фор му лою:
а) f
(x
) = 3x
– 1; б) f
(x
) = 2x
2
+ 3; в) ![]()
162. Функцію за да но фор му лою у = –0,5х + 2. Знайдіть зна чен ня функції, яке відповідає зна чен ню ар гу мен ту, що дорів нює –24; –10; 0; 5. При яком у знач енні арг ум ент у знач енн я функції дорівнює –6; 0; 5; 7,5?
163. Знайдіть зна чен ня функції, за да ної фор му лою:
а) у = 8x – 5, яке відповідає знач енн ю арг ум ент у, що дорівн ює
–2; 0; 1,5; 12; 25;
б) ![]() , яке відповідає знач енн ю арг ум ент у, що дорівн ює
, яке відповідає знач енн ю арг ум ент у, що дорівн ює
–8; –1; 0; 1; 20.
164. Функцію за да но фор му лою у = 0,25х – 1. Зап овніть таб- ли цю.
| x |
–10 |
–5 |
|||||
| y |
–2 |
–1 |
0 |
1 |
1,5 |
4 |
25 |
165.
Функцію зад ан о форм ул ою ![]() на обл асті визн ач ен9 ня D
= {–4; –2,75; –1; 1,25; 4; 11}. За дай те її таб лич но і гра фічно.
на обл асті визн ач ен9 ня D
= {–4; –2,75; –1; 1,25; 4; 11}. За дай те її таб лич но і гра фічно.
166. Функцію за да но таб ли цею.
| x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| y |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
За дай те її фор му лою. Укажіть її об ласть виз на чен ня й об ласть зна чень.
167. У яких точк ах графік функції у = х 2 – 3х пе ре ти нає:
а) вісь у ; б) вісь х ?
168. Знайдіть об ласть виз на чен ня функції:

169. Функцію у = х 2 зад ан о на проміжку [–2; 5]. Знайдіть її об ласть зна чень.
170. Знайдіть об ласть виз на чен ня функції у = х 3 , якщ о її об- ласть знач ень [–8; 27].

172.
![]()
173. Ма са по рожньої боч ки 40 кг, а ма са 1 л бен зи ну 0,8 кг. Ви разіть фор му лою за лежність ма си m боч ки з бен зи ном від об’єму V бенз ин у в ній. Чи є ця зал ежність лінійною функцією?
174. Пря мо кут ний па ра ле лепіпед зі сто ро на ми ос но ви а см, b см і вис от ою 6 см має об’єм, що дорівнює 72 см3 . Ви разіть фор му лою за лежність b від а .
175. Щоб по ши ти од ну со роч ку, потрібно 2,5 м тка ни ни. За пишіть фор му лу для об чис лен ня за лиш ку тка ни ни після по шит тя х со ро чок, як що в су вої 200 м тка ни ни. Яких зна чень мо же на бу ва ти х ?
176. Знайдіть зна чен ня ар гу мен ту, при яко му:
а) зна чен ня функції у = –3х + 2 дорівнює –7; 0; 5;
б) знач енн я функції дорівнює –20; 2; ;

![]() в) зна чен ня функції у
= х
(х
– 3) дорівнює –2; 0; 10;
в) зна чен ня функції у
= х
(х
– 3) дорівнює –2; 0; 10;
г) знач енн я функції дорівнює – ; 0; 1,4.
177. За дай те фор му лою функцію, як що:
а) знач енн я функції на 4 більші від знач ень арг ум ент у;
б) знач енн я функції на 9 менші від знач ень арг ум ент у;
в) знач енн я функції втричі більші від знач ень арг ум ент у;
г) зна чен ня функції про ти лежні зна чен ням ар гу мен ту;
ґ) зна чен ня функції обер нені до зна чень ар гу мен ту.
178.
Функцію за да но фор му лою ![]() , де –7 х
< 1. За- повніть таб ли цю.
, де –7 х
< 1. За- повніть таб ли цю.
| x |
–7 |
–3 |
–2 |
–1 |
|
0 |
|
| y |
По бу дуй те графік цієї функції.
179.
Функцію за да но фор му лою ![]() , де 1 х
< 6. Поб у9 дуйт е графік цієї функції, склавш и споч атк у табл иц ю її знач ень.
, де 1 х
< 6. Поб у9 дуйт е графік цієї функції, склавш и споч атк у табл иц ю її знач ень.
180. Відо мо, що графік лінійної функції про хо дить че рез точ ки А (–2; 1) і B (3; 6). Зад айт е цю функцію форм ул ою.
181. За дай те фор му лою обер не ну про порційність, графік якої про хо дить че рез точ ку А (3; 4).
182. Чи прох од ить графік функції у = х 2 – 5х + 6 чер ез точк у А (0; 5)? А чер ез точк у В (5; 6)?
183. Чи прав ильн о, що графік функції у = х 2 – 4х + 5 відріз- ня єть ся від графіка функції у = х 2 – 4х тіль ки тим, що йо го зміщен о на 5 один иць угор у вздовж осі у ?
184. По бу дуй те графік функції у = х 2 – 4х + 4. 185. По бу дуй те графік функції у = х 2 + 4х – 2.
По бу дуй те в одній сис темі ко ор ди нат графіки функцій (186– 188) .

190*. Вваж аю ть, що при загл ибл енні на кожні 30,5 м внут- рішня тем пе ра ту ра Землі підви щуєть ся на 1 °С. На глиб ині 5 м вон а дорівнює 15 °С. За дай те за лежність тем пе ра ту ри t від гли би ни h . Яка темп ер ат ур а на глиб ині 1 км? А на глиб ині 3 км?
191. Чим різнять ся по нят тя «графік функції» і «графік рів няння»? На ведіть прик ла ди.
![]()
192. Рoзв’яжіть рівнян ня:
а) 3x 2 – 5х + 2 = 0; б) х 2 + 6х + 6 = 0; в) 5х 2 – х + 1 = 0.
193. З двох роз чинів солі – 109відсот ко во го і 159відсот ко во го – тре ба ут во ри ти 40 г 129відсот ко во го роз чи ну. Скіль ки грамів кож но го роз чи ну потрібно взя ти?
194. Спростіть ви раз, як що а , b , с – до датні чис ла:
![]()

 E
(y
) = [0; +∞)
E
(y
) = [0; +∞)
 E
(y
) = R
E
(y
) = R
 E
(y
) = [0; +∞)
E
(y
) = [0; +∞)