| Скачать .pdf |
Реферат: Решение системы линейных уравнений методом Крамера и с помощью расширенной матрицы
1 Нелинейные уравнения
Рассматривается задача нахождения значений переменной x = x*, для которых справедливо равенство
f(x) = 0. (1)
В этом уравнениии f(x) - некоторая нелинейная функция x.
Если такие значения существуют, то они называются корнями
уравнения (1). Корень называется простым, если
 и кратным, если
и кратным, если
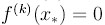 для k = 1,..., n - 1, а
для k = 1,..., n - 1, а
 . Целое
n
назывется кратностью корня.
. Целое
n
назывется кратностью корня.
1.1 Отделение корней
Под отделением корней уравнения (1) понимают определение достаточно узкого интервала (a, b) , в котором лежит корень уравнения. Основой отделения корней служит Теорема 1 (Первая теорема Больцано-Коши). Пусть функция определена и непрерывна в замкнутом промежутке [a, b] , на концах которого она принимает значения разных знаков. Тогда между a и b найдется хотя бы одна точка c , в которой функция обращается в нуль: f ( c ) = 0 , a < c < b. Если функция f ( x ) монотонна в этом интервале, то внутри его лежит только один корень уравнения f ( x ) = 0 . Алгоритм отделения можно реализовать следующим образом

1.2 Метод бисекций
Метод бисекций(метод деления пополам) основан на следующем итерационном процессе: интервал
a, b
, на котором  делится пополам -
делится пополам -
 и вычисляется
и вычисляется
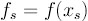 . Если
. Если
 , то
, то
 Далее выполняется следующий шаг, и т.д.
На i-м шаге приближенным значением корня служит полусумма
(a + b)/2,
оценкой погрешности - полуразность
(b - a)/2.
Метод бисекций можно описать следующим алгоритмом
(В приводимых ниже алгоритмах используется только одна серия итераций. Нужно их модифицировать, используя структуры из файла it_gen.pdf)
Далее выполняется следующий шаг, и т.д.
На i-м шаге приближенным значением корня служит полусумма
(a + b)/2,
оценкой погрешности - полуразность
(b - a)/2.
Метод бисекций можно описать следующим алгоритмом
(В приводимых ниже алгоритмах используется только одна серия итераций. Нужно их модифицировать, используя структуры из файла it_gen.pdf)

1.3 Метод хорд
В методе хорд вместо деления отрезка (a, b) пополам используется линейная интерполяция граничных значений функции f(x) .
Следующая контрольная точка находится из уравнения
.
Следующая контрольная точка находится из уравнения
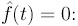
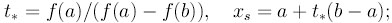

Метод бисекций и метод хорд нельзя использовать в многомерном случае!
1.4 Метод установления
Идея этого метода состоит в переходе от нелинейного уравнения (1) к обыкновенному дифференциальному уравнению
Это уравнение должно обладать устойчивым предельным стационарным
состоянием, чтобы при 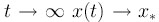 . Тогда приближенное решение
уравнениия (2) с помощью устойчивого численного метода дает (для достаточно больших
t) хорошее приближение к решению (1).
Простейшим алгоритмом будет метод Эйлера, являющийся вариантом
метода простой итерации
. Тогда приближенное решение
уравнениия (2) с помощью устойчивого численного метода дает (для достаточно больших
t) хорошее приближение к решению (1).
Простейшим алгоритмом будет метод Эйлера, являющийся вариантом
метода простой итерации


Для погрешности
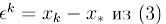 получается следующее уравнение
получается следующее уравнение
 Представив
Представив
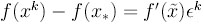 , получим соотношение
, получим соотношение

 должна
находиться в области
должна
находиться в области
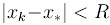 , в которой первая производная ограничена и сохраняет свой знак. Тогда выбор параметра
, в которой первая производная ограничена и сохраняет свой знак. Тогда выбор параметра
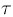 , удовлетворяющего
условиям,
, удовлетворяющего
условиям,
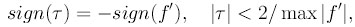
обеспечивает сходимость метода установления.
1.5 Метод Ньютона
Метод Ньютона для уравнения (1) записывается в виде
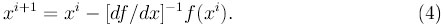
Определение:
говорят, что функция
 , если
, если
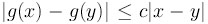 для
всех
для
всех
 .
.
Теорема
(о сходимости метода Ньютона).
Пусть
 где
D
- открытый интервал , а
R
- вещественная ось,
и пусть
где
D
- открытый интервал , а
R
- вещественная ось,
и пусть
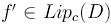 . Предположим, что для некоторого
. Предположим, что для некоторого
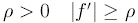 при всех
при всех
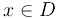 . Если уравнение
f(x) = 0
имеет решение, то существует
некоторое
. Если уравнение
f(x) = 0
имеет решение, то существует
некоторое
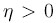 , такое, что если
, такое, что если
 , то последовательность,
задаваемая формулой
, то последовательность,
задаваемая формулой
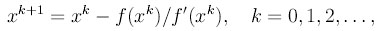
существует и сходится к
x*. Более того, для
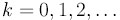

Замечание 1.
Как следует из теоремы, при
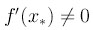 сходимость квадратичная. Если же
сходимость квадратичная. Если же
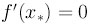 , то только линейная.
, то только линейная.
Замечание 2.
Для сходимости метода Ньютона начальное приближение
x0
должно быть достаточно близко к корню. Если же расстояние
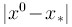 велико, то метод Ньютона может вообще не сходиться.
велико, то метод Ньютона может вообще не сходиться.
Метод Ньютона можно реализовать следующим алгоритмом

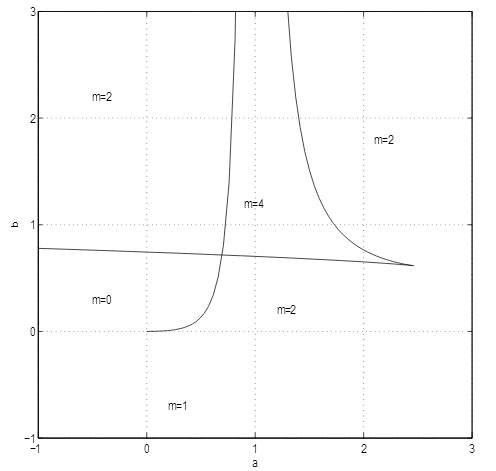
Рис. 1: Разбиение плоскости параметров уравнения 
1.6 Тестовое уравнение
1. В качестве 1-го тестового используется уравнение
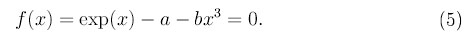
В зависимости от значений параметров a, b это уравнение может иметь m = 0,1,2,4 корня. Для исследования знака 1-й производной функции f(x) полезно находить корни уравнения
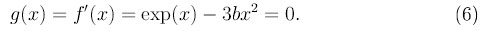
На рисунке 1 показано разбиение плоскости параметров a, b на подобласти с различным числом корней уравнения (5). 2. В качестве 2-го тестового используется уравнение

Это уравнение имеет единственный корень
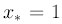 бесконечной кратности
(
бесконечной кратности
(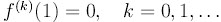 ). Первая производная
). Первая производная
 для
x <
1
и
для
x <
1
и 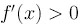 для
x > 1
.
для
x > 1
.
1.7 Компьютерные эксперименты
1. Для функции уравнения (5) с параметрами a = 1.15, b = 1.25 найти границы корней. Для функции уравнения (6) с параметром b = 1.25 найти границы корней и ее знаки на всей вещественной оси.
Контрольная информация:
Функция f(x): корни(приближенно)
x1 = -0.83 , x2 = 0.14 , x3 = 1.20 , x4 = 5.14Функция
 : знаки и корни
: знаки и корни

2. Описанными выше методами(бисекций, хорд, установления, Ньютона) для значений
 найти корни функции (5) со значениями
a = 1.15, b = 1.25. Для этих корней составить
таблицы зависимости числа итераций от
найти корни функции (5) со значениями
a = 1.15, b = 1.25. Для этих корней составить
таблицы зависимости числа итераций от 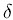 .
.
3. Методом установления попытаться найти корень функции (5), беря
значения параметра
 , для которых нет сходимости. Каким образом проявляется расходимость итерационного процесса ?
, для которых нет сходимости. Каким образом проявляется расходимость итерационного процесса ?
4. Метод Ньютона: в случае корня кратности 2 метод Ньютона сходится линейно,т.е.существенно медленнее, чем в случае простого корня. Проверить, будет ли модифицированный метод Ньютона
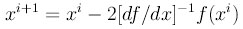
иметь для корня кратности 2 ту же скорость сходимости, что и стандартный метод для простого корня. Для проверки использовать уравнение

Для значения  найти корень этого уравнения простым и
модифицированным методом Ньютона. Сравнить число итераций.
найти корень этого уравнения простым и
модифицированным методом Ньютона. Сравнить число итераций.