| Скачать .docx | Скачать .pdf |
Реферат: Матрицы Метод Гаусса
КОСТРОМСКОЙ ФИЛИАЛ ВОЕННОГО УНИВЕРСИТЕТА РХБ ЗАЩИТЫ
Кафедра «Автоматизации управления войсками»
Только для преподавателей
"Утверждаю"
Начальник кафедры № 9
полковник ЯКОВЛЕВ А.Б.
«____»______________ 2004 г.
доцент СМИРНОВА А.И.
"МАТРИЦЫ. МЕТОД ГАУССА"
ЛЕКЦИЯ № 2 / 3
Обсуждено на заседании кафедры № 9
«____»___________ 2003г.
Протокол № ___________
Кострома, 2003
C одержание
Введение
1. Действия над матрицами.
2. Решение систем линейных уравнений методом Гаусса.
Заключение
Литература
1. В.Е. Шнейдер и др., Краткий курс высшей математики,том I, гл.2,§6, 7.
2. В.С. Щипачев, Высшая математика, гл. 10, § 1, 7.
ВВЕДЕНИЕ
На лекции рассматривается понятие матрицы, действия над над матрицами, а также метод Гаусса для решения систем линейных уравнений. Для частного случая, так называемых квадратных матриц, можно вычислять определители, понятие о которых рассмотрено на предыдущей лекции. Метод Гаусса является более общим, чем рассмотренный ранее метод Крамера решения линейных систем. Разбираемые на лекции вопросы используются в различных разделах математики и в прикладных вопросах.
1-ый учебный вопрос ДЕЙСТВИЯ НАД МАТРИЦАМИ
ОПРЕДЕЛЕНИЕ 1. Прямоугольная таблица из m , n чисел, содержащая m – строк и n – столбцов, вида:

называется матрицей размера m ´ n
Числа, из которых составлена матрица, называются элементами матрицы.
Положение элемента а i j в матрице характеризуются двойным индексом:
первый i – номер строки;
второй j – номер столбца, на пересечении которых стоит элемент.
Сокращенно матрицы обозначают заглавными буквами: А, В, С…
Коротко можно записывать так: ![]()
ОПРЕДЕЛЕНИЕ 2. Матрица, у которой число строк равно числу столбцов, т.е. m = n , называется квадратной.
Число строк (столбцов) квадратной матрицы называется порядком матрицы.
ПРИМЕР.

ЗАМЕЧАНИЕ 1. Мы будем рассматривать матрицы, элементами которых являются числа. В математике и ее приложениях встречаются матрицы, элементами которых являются другие объекты, например, функции, векторы.
ЗАМЕЧАНИЕ 2. Матрица – специальное математическое понятие. С помощью матриц удобно записывать различные преобразования, линейные системы и т.д., поэтому матрицы часто встречаются в математической и технической литературе.
ОПРЕДЕЛЕНИЕ 3. Матрица размера 1 ´ n , состоящая из одной строки, называется матрицей – строкой.
Матрица размера т ´ 1, состоящая из одного столбца, называется матрицей – столбцом.
ОПРЕДЕЛЕНИЕ 4. Нулевой матрицей называют матрицу, все элементы которой равны нулю.
Рассмотрим квадратную матрицу порядка n :
 побочная диагональ
побочная диагональ

главная диагональ
Диагональ квадратной матрицы, идущая от верхнего левого элемента таблицы к правому нижнему, называется главной диагональю матрицы (на главной диагонали стоят элементы вида а i i ).
Диагональ, идущая от правого верхнего элемента к левому нижнему, называется побочной диагональю матрицы .
Рассмотрим некоторые частные виды квадратных матриц.
1) Квадратная матрица называется диагональной , если все элементы, не стоящие на главной диагонали, равны нулю.

2) Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной . Обозначается:
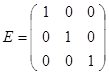
3) Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю:


верхняя нижняя
треугольная матрица треугольная матрица
Для квадратной матрицы вводится понятие: определитель матрицы . Это определитель, составленный из элементов матрицы. Обозначается:
![]()
Ясно, что определитель единичной матрицы равен 1: ½Е ½ = 1
ЗАМЕЧАНИЕ. Неквадратная матрица определителя не имеет.
Если определитель квадратичной матрицы отличен от нуля, то матрица называется невырожденной , если определитель равен нулю, то матрица называется вырожденной.
ОПРЕДЕЛЕНИЕ 5. Матрица, полученная из данной заменой ее строк столбцами с теми же номерами, называется транспонированной к данной.
Матрицу, транспонированную к А , обозначают АТ .
ПРИМЕР.
![]()

2 ![]() 3 3
3 3 ![]() 2
2
ОПРЕДЕЛЕНИЕ. Две матрицы одного и того же размера называются равными, если равны все их соответственные элементы.
Рассмотрим действия над матрицами.
СЛОЖЕНИЕ МАТРИЦ.
Операция сложения вводится только для матриц одинакового размера.
ОПРЕДЕЛЕНИЕ 7. Суммой двух матриц А = (а i j ) и В = ( bi j ) одинакового размера называется матрица С = (с i j ) того же размера, элементы которой равны суммам соответствующих элементов слагаемых матриц, т.е. с i j = a i j + b i j
Обозначается сумма матриц А + В.
ПРИМЕР.

УМНОЖЕНИЕ МАТРИЦ НА ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО
ОПРЕДЕЛЕНИЕ 8. Чтобы умножить матрицу на число k , надо умножить на это число каждый элемент матрицы :
если А= (а i j ), то k · A = (k · a i j )
ПРИМЕР.
![]()
СВОЙСТВА СЛОЖЕНИЯ МАТРИЦ И УМНОЖЕНИЯ НА ЧИСЛО
1. Переместительное свойство: А + В = В + А
2. Сочетательное свойство: ( А + В ) + С = А + ( В + С )
3. Распределительное свойство: k · ( A + B ) = k A + k B , где k – число
УМНОЖЕНИЕ МАТРИЦ
Матрицу А назовем с о г л а с о в а н н о й с матрицей В , если число столбцов матрицы А равно числу строк матрицы В , т.е. для согласованных матриц матрица А имеет размер m ´ n , матрица В имеет размер n ´ k . Квадратные матрицы согласованы, если они одного порядка.
ОПРЕДЕЛЕНИЕ 9. Произведением матрицы А размера m ´ n на матрицу В размера n ´ k называется матрица С размера m ´ k , элемент которой а i j , расположенный в i –ой строке и j – ом столбце, равен сумме произведений элементов i – ой строки матрицы А на соответствующие элементы j – столбца матрицы В, т.е.
c i j = a i 1 b 1 j + a i 2 b 2 j +……+ a i n b n j
Обозначим: С = А · В.
Если  то
то

Произведение В
´ А
не имеет смысла, т.к. матрицы ![]() не согласованы.
не согласованы.
ЗАМЕЧАНИЕ 1. Если А ´ В имеет смысл, то В ´ А может не иметь смысла.
ЗАМЕЧАНИЕ 2. Если имеет смысл А ´ В и В ´ А , то, вообще говоря
А ´ В ¹ В ´ А , т.е. умножение матриц не обладает переместительным законом.
ЗАМЕЧАНИЕ 3. Если А – квадратная матрица и Е – единичная матрица того же порядка, то А ´ Е = Е ´ А = А .
Отсюда следует, что единичная матрица при умножении играет роль единицы.
ПРИМЕРЫ . Найти , если можно, А ´ В и В ´ А .
1. 
Решение : Квадратные матрицы одного и того же второго порядка согласованы в томи другом порядке, поэтому А ´ В и В ´ А существуют.

2. 
Решение : Матрицы А и В согласованы

Матрицы В и А не согласованы, поэтому В ´ А не имеет смысла.
Отметим, что в результате перемножения двух матриц получается матрица, содержащая столько строк, сколько их имеет матрица–множимое и столько столбцов, сколько их имеет матрица-множитель .
СВОЙСТВА УМНОЖЕНИЯ МАТРИЦ
1. Сочетательное свойство: А ´ ( В ´ С ) = (А ´ В ) ´С
2. Распределительное свойство: (А + В) ´ С = А ´ С + В ´С
Можно показать, что , если А и В – две квадратные матрицы одного порядка с определителями ½ А ½ и ½ В ½, то определитель матрицы С = А ´ В равен произведению определителей перемножаемых матриц, т.е.
½С ½ = ½ А ½ ½ В ½
Отметим следующий любопытный факт. Как известно, произведение двух отличных от нуля чисел не равно нулю. Для матриц подобное обстоятельство может и не иметь места, т.е. произведение двух ненулевых матриц может оказаться равным нуль - матрице .
Действие "деление" для матриц не вводится. Для квадратных невырожденных матриц вводится обратная матрица. С понятием обратной матрицы можно познакомиться в рекомендуемой литературе.
2 – ой учебный вопрос РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ
УРАВНЕНИЙ МЕТОДОМ ГАУССА
Метод Гаусса (или метод последовательного исключения неизвестных) применим для решения систем линейных уравнений, в которых число неизвестных может быть либо равно числу уравнений, либо отлично от него.
Система т линейных уравнений с п неизвестными имеет вид:

x 1 , x 2 , …, xn – неизвестные.
ai j - коэффициенты при неизвестных.
bi - свободные члены (или правые части)
Система линейных уравнений называется совместной , если она имеет решение, и несовместной , если она не имеет решения.
Совместная система называется определенной , если она имеет единственное решение и неопределенной , если она имеет бесчисленное множество решений.
Две совместные системы называются равносильными , если они имеют одно и то же множество решений.
К элементарным преобразованиям системы отнесем следующее:
1. перемена местами двух любых уравнений;
2. умножение обеих частей любого из уравнений на произвольное число, отличное от нуля;
3. прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число.
Элементарные преобразования переводят систему уравнений в равносильную ей.
Элементарные преобразования системы используются в методе Гаусса.
Для простоты рассмотрим метод Гаусса для системы трех линейных уравнений с тремя неизвестными в случае, когда существует единственное решение:
Дана система:
 ( 1 )
( 1 )
1-ый шаг метода Гаусса.
На первом шаге исключим неизвестное х1
из всех уравнений системы (1), кроме первого. Пусть коэффициент ![]() . Назовем его ведущим элементом. Разделим первое уравнение системы (1) на а11
.
Получим уравнение:
. Назовем его ведущим элементом. Разделим первое уравнение системы (1) на а11
.
Получим уравнение:
![]() ( 2 )
( 2 )
где ![]()
Исключим х1 из второго и третьего уравнений системы (1). Для этого вычтем из них уравнение (2), умноженное на коэффициент при х1 (соответственно а 21 и а 31 ).
Система примет вид:
 ( 3 )
( 3 )
Верхний индекс (1) указывает, что речь идет о коэффициентах первой преобразованной системы.
2-ой шаг метода Гаусса.
На втором шаге исключим неизвестное х2
из третьего уравнения системы (3). Пусть коэффициент ![]() . Выберем его за ведущий элемент и разделим на него второе уравнение системы (3), получим уравнение:
. Выберем его за ведущий элемент и разделим на него второе уравнение системы (3), получим уравнение:
![]() ( 4 )
( 4 )
где 
Из третьего уравнения системы (3) вычтем уравнение (4), умноженное на ![]() Получим уравнение:
Получим уравнение:
![]()
Предполагая, что ![]() находим
находим

В результате преобразований система приняла вид:
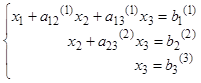 (5)
(5)
Система вида (5) называется треугольной .
Процесс приведения системы (1) к треугольному виду (5) (шаги 1 и 2) называют прямым ходом метода Гаусса .
Нахождение неизвестных из треугольной системы называют обратным ходом метода Гаусса.
Для этого найденное значение х3 подставляют во второе уравнение системы (5) и находят х2 . Затем х2 и х3 подставляют в первое уравнение и находят х1 .
В общем случае для системы т линейных уравнений с п неизвестными проводятся аналогичные преобразования. На каждом шаге исключается одно из неизвестных из всех уравнений, расположенных ниже ведущего уравнения.
Отсюда другое называние метода Гаусса – метод последовательного исключения неизвестных.
Если в ходе преобразований системы получается противоречивое уравнение вида 0 = b , где b ¹ 0, то это означает, что система несовместна и решений не имеет.
В случае совместной системы после преобразований по методу Гаусса, составляющих прямой ход метода, система т линейных уравнений с п неизвестными будет приведена или к треугольному или к ступенчатому виду.
Треугольная система имеет вид:

Такая система имеет единственное решение, которое находится в результате проведения обратного хода метода гаусса.
Ступенчатая система имеет вид:

Такая система имеет бесчисленное множество решений. Чтобы найти эти решения, во всех уравнениях системы члены с неизвестными х k +1 , … , xk переносят в правую часть. Эти неизвестные называются свободными и придают им произвольные значения. Из полученной треугольной системы находим х 1 , … , xk , которые будут выражаться через свободные неизвестные. Подробнее об этом можно узнать в рекомендуемой литературе.
Рассмотренный метод Гаусса легко программируется на ЭВМ и является более экономичным (по числу действий), чем другие методы.
ЗАКЛЮЧЕНИЕ
Рассмотренные на лекции матрицы являются удобным инструментом для записи различных математических преобразований и широко используется в научно-технической литературе. Метод Гаусса позволяет решать любые линейные системы, он находит широкое применение и содержится в пакетах стандартных программ для ЭВМ.
доцент Смирнова А.И.