| Скачать .docx | Скачать .pdf |
Дипломная работа: Система дифференциальных уравнений с постоянными коэффициентами
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ
НАБЕРЕЖНОЧЕЛНИНСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ
Математический факультет
Кафедра математического анализа
Козлова Любовь Владимировна
Система дифференциальных уравнений с постоянными коэффициентами
/дипломная работа/
Работа завершена:
Студентка группы 721
Козлова Л.В.
(подпись)
Рекомендуется к защите:
Научный руководитель, профессор
Хайруллин Р.С.
(подпись)
Допускается к защите:
Зав. кафедрой, профессор
Габбасов Н.С.
(подпись)
Набережные Челны
2002
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
ГЛАВА I. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ АНАЛИЗА
§ 1. Дифференциальное уравнение первого порядка
§ 2. Формулировка теоремы существования и единственности
§ 3. Сведение обшей системы дифференциальных уравнений к нормальной
§ 4. Некоторые сведения о линейных дифференциальных уравнениях
ГЛАВА II. Линейные уравнения с постоянными Коэффициентами.
§ 5. Линейное однородное уравнении с постоянными коэффициентами (случай простых корней)
§6. Линейное однородное уравнение с постоянными коэффициентами (случаи кратных корней)
§ 7. Линейное неоднородное уравнение с постоянными коэффициентами
§ 8. Метод исключения
§9. Нормальная линейная однородная система с постоянными коэффициентами
§ 10. Автономные системы дифференциальных уравнений и их фазовые пространства
§ 11. Фазовая плоскость линейной однородной системы с постоянными коэффициентами
ГЛАВА III. теоремы существования
§ 12. Доказательство теоремы существования и единственности для одного уравнения
§13. Доказательство теоремы существования и единственности для нормальной системы уравнений
§ 14. Понятие о теории устойчивости Ляпунова. Поведение траектории дифференциального уравнения в окрестности особой точки
ГЛАВА IV. ПРАКТИЧЕСКИЯ СХЕМА РЕШЕНИЯ СИСТЕМЫ ДИФФЕРЕНЦАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
ЗАКЛЮЧЕНИЕ
ЛИТЕРАТУРА
ПРИЛОЖЕНИЕ
ВВЕДЕНИЕ
Данная работа посвящена теме: «Системы дифференциальных уравнений с постоянными коэффициентами»
Многие процессы химической технологии описываются системами дифференциальных уравнений - начиная от кинетических исследований и заканчивая химическими технологическими процессами. В основу математических способов описания процессов положены системы дифференциальных уравнений и системы линейных алгебраических уравнений. Эти уравнения описывают материальные и тепловые балансы объектов химической технологии, а так же структуры потоков технических веществ в этих аппаратах.
Системы обыкновенных дифференциальных уравнений с постоянными коэффициентами представляют собой большой и важный класс обыкновенных дифференциальных уравнений, решающихся до конца при помощи элементарных функций. Ввиду того, что решение этих уравнений принципиально не представляет больших трудностей, часто, считают, что они не имеют сколько-нибудь значительного интереса для теории, и в учебниках им обычно отводит место простого примера к общей теория линейных уравнений. Между тем линейные уравнения с постоянными коэффициентами имеют многочисленные технические применения, так как работа весьма многих технических объектов достаточно адекватным образом описывается этими уравнениями. Именно технические применения выдвигают ряд новых задач теоретического характера в теории линейных уравнений с постоянными коэффициентами. Решению этих теоретических задач посвящено немало работ, имеющих прикладную направленность.
Данная работа состоит из четырех глав.
Первая глава посвящена в первую очередь определению тех понятий, которые будут изучаться в дальнейшем. Что такое система обыкновенных дифференциальных уравнений, что называется ее решением и как много этих решении существует - таковы главные вопросы, на которые дается ответ в этой главе. Количество решений определяется теоремами существования и единственности, которые здесь не доказываются, а только формулируются. Доказательство этих и ряда других теорем того же типа дается в третьей главе, а до этого сформулированные в первой главе теоремы многократно используются, чем выясняется их значение.
Во второй главе используются обычные для инженерной практики операционные обозначения, которые очень удобны для решения систем уравнений методом исключения. Кроме того, в эту главу включено исследование фазовой плоскости линейных систем второго порядка, которому предшествует изучение фазовых пространств автономных систем. Фазовые пространства автономных систем также находят важные приложения в технике.
В третьей главе доказываются теоремы существования и единственности сформулированные в первой главе, также здесь дается понятие о теории устойчивости Ляпунова.
Работа очень многих механических, электрических и другого вида устройств (машин, приборов и т.п.) описывается системами обыкновенных дифференциальных уравнений. Система обыкновенных дифференциальных уравнений имеет всегда бесконечное множество решений, и для задания одного определенного решения нужно указать его начальные значения. Для полного понимания какого-либо устройства желательно иметь хорошее представление о фазовом пространстве системы уравнений, описывающей работу этого устройства. При этом важнее всего знать все устойчивые решения этой системы уравнений.
В четвертой главе данной решена система пяти дифференциальных уравнений с постоянными коэффициентами и исследована устойчивость решения этой системы уравнений.
ГЛАВА I . НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ АНАЛИЗА
§ 1. Дифференциальное уравнение первого порядка
Дифференциальными уравнениями называются такие уравнения, в которых неизвестными являются функции одного или нескольких переменных, причем в уравнения входят не только сами функции, но и их производные. Если неизвестными функциями являются функции многих переменных, то уравнения называются уравнениями в частных производных, в противном случае, т. е. при рассмотрении функций только одного независимого переменного, уравнения называются обыкновенными дифференциальными уравнениями.
Так как в ряде физических применений независимым переменным, от которого зависят неизвестные искомые функции, является время, которое принято обозначать через t, то всюду в дальнейшем независимое переменное будет обозначаться через t. Неизвестные функции будут обозначаться через x, y, z и т. д. Производные функции по t будут, как правило, обозначаться так: ![]() ,
,  и т. д. В тех случаях, когда это неудобно или невозможно, мы будем указывать порядок производной верхним индексом в скобках; например,
и т. д. В тех случаях, когда это неудобно или невозможно, мы будем указывать порядок производной верхним индексом в скобках; например,  .
.
В первую очередь мы займемся рассмотрением одного дифференциального уравнения первого порядка, т. е. уравнения, в которое, входит лишь первая производная неизвестной функции. Уравнение это может быть записано в виде:
![]() (1)
(1)
Здесь t - независимое переменное, x - его неизвестная функция, ![]() - ее производная, а F - заданная функция трех переменных. Функция F может быть задана не для всех значений ее аргументов; поэтому говорят об области B задания функции F. Здесь имеется в виду множество В точек координатного пространства трех переменных
- ее производная, а F - заданная функция трех переменных. Функция F может быть задана не для всех значений ее аргументов; поэтому говорят об области B задания функции F. Здесь имеется в виду множество В точек координатного пространства трех переменных ![]() . Решением уравнения (1) называется такая функция
. Решением уравнения (1) называется такая функция ![]() независимого переменного t, определенная на некотором интервале
независимого переменного t, определенная на некотором интервале ![]() (случаи
(случаи ![]() не исключаются), что при подстановке ее вместо x в соотношение (1) мы получаем тождество на всем интервале
не исключаются), что при подстановке ее вместо x в соотношение (1) мы получаем тождество на всем интервале ![]() . Интервал
. Интервал ![]() называется интервалом определения решения
называется интервалом определения решения ![]() . Очевидно, что подстановка
. Очевидно, что подстановка ![]() в соотношение (1) возможна лишь тогда, когда функция
в соотношение (1) возможна лишь тогда, когда функция ![]() на всем интервале
на всем интервале ![]() имеет первую производную (и, в частности, непрерывна). Для того чтобы подстановка
имеет первую производную (и, в частности, непрерывна). Для того чтобы подстановка ![]() в соотношение (1) была возможна, необходимо также, чтобы при произвольном значении переменного t из интервала
в соотношение (1) была возможна, необходимо также, чтобы при произвольном значении переменного t из интервала ![]() точка с координатами
точка с координатами ![]() принадлежала множеству В, на котором определена функция F.
принадлежала множеству В, на котором определена функция F.
Соотношение (1) связывает три переменные величины ![]() . В некоторых случаях оно определяет переменное
. В некоторых случаях оно определяет переменное ![]() как однозначную неявную функцию независимых переменных
как однозначную неявную функцию независимых переменных ![]() . В этом случае дифференциальное уравнение (1) равносильно дифференциальному уравнению вида
. В этом случае дифференциальное уравнение (1) равносильно дифференциальному уравнению вида
![]() (2)
(2)
Дифференциальное уравнение (2) называется разрешенным относительно производной; оно в некоторых отношениях более доступно для изучения, чем общее дифференциальное уравнение (1). Именно уравнения, разрешенные относительно производной, мы и будем теперь рассматривать. Мы не будем уже считать, что соотношение (2) получено в результате разрешения относительно ![]() уравнения вида (1), а будем исходить из функции
уравнения вида (1), а будем исходить из функции ![]() как из заданной функции двух независимых переменных
как из заданной функции двух независимых переменных ![]() .
.
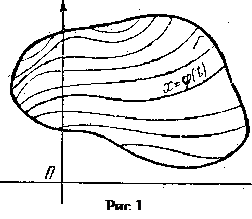
Для того чтобы пользоваться наглядными геометрическими представлениями, мы введем в рассмотрение координатную плоскость Р переменных t и х. При этом t как независимое переменное мы будем откладывать по оси абсцисс, а х как зависимое переменное - по оси ординат. Функция f, определяющая дифференциальное уравнение (2), может быть задана не для всех значений своих аргументов t и х, или, говоря геометрическим языком, не во всех точках плоскости Р, а лишь в точках некоторого множества Г плоскости Р (рис.1). Относительно множества Г мы в дальнейшем всегда будем предполагать, что оно является открытым. Это значит, что наряду с каждой точкой р в Г входит и некоторый круг положительного радиуса с центром в р. Относительно функции f будет предполагаться, что как она сама, так и ее частная производная ![]() являются непрерывными функциями пары переменных
являются непрерывными функциями пары переменных ![]() на всем множестве Г. Решение
на всем множестве Г. Решение ![]() уравнения (2) будем геометрически изображать в плоскости Р в виде кривой с уравнением
уравнения (2) будем геометрически изображать в плоскости Р в виде кривой с уравнением ![]() . Кривая эта в каждой точке имеет касательную и полностью проходит в открытом множестве Г; она называется интегральной кривой дифференциального уравнения (2).
. Кривая эта в каждой точке имеет касательную и полностью проходит в открытом множестве Г; она называется интегральной кривой дифференциального уравнения (2).
Теорема существования и единственности
Известно, какую большую роль в алгебре играют теоремы, отвечающие на вопрос о том, сколько решений имеет та или другая система алгебраических уравнении. В теории дифференциальных уравнений важным теоретическим вопросом является вопрос о том, насколько много решений имеет дифференциальное уравнение. Оказывается, что каждое дифференциальное уравнение имеет бесконечное множество решений, и потому приходится ставить вопрос не о числе решений, а о том, как можно описать совокупность всех решении данного дифференциального уравнения. Ответ на этот вопрос дает теорема существования и единственности (теорема 1), которая в этом параграфе приводится без доказательства. Доказательство будет дано значительно позже (см. §12).
Теорема 1. Пусть ![]() - дифференциальное уравнение. Будем предполагать, что функция
- дифференциальное уравнение. Будем предполагать, что функция ![]() задана на некотором открытом множестве Г плоскости Р переменных.
задана на некотором открытом множестве Г плоскости Р переменных. ![]() . Относительно функции f будем предполагать, что она сама и ее частная производная
. Относительно функции f будем предполагать, что она сама и ее частная производная ![]() являются непрерывными функциями, на всем открытом множестве Г. Теорема утверждает
являются непрерывными функциями, на всем открытом множестве Г. Теорема утверждает
1) для всякой точки ![]() множества Г найдется решение
множества Г найдется решение ![]() уравнения (3), удовлетворяющее условию
уравнения (3), удовлетворяющее условию
![]() (4)
(4)
2) если два решения ![]() и
и ![]() уравнения (3) совпадают хотя бы для одного значения
уравнения (3) совпадают хотя бы для одного значения ![]() , т. е. если
, т. е. если
![]()
то решения эти тождественно равны для всех тех значений переменного t, для которых они оба определены.
Числа ![]() называют начальными значениями для решения
называют начальными значениями для решения ![]() , а соотношение (4) — начальным условием для этого решения. Говорят также, что решение
, а соотношение (4) — начальным условием для этого решения. Говорят также, что решение ![]() удовлетворяет начальному условию (4) или же что оно имеет начальные значения
удовлетворяет начальному условию (4) или же что оно имеет начальные значения ![]() . Утверждение, что решение
. Утверждение, что решение ![]() удовлетворяет начальному условию (4) (или имеет начальные значения
удовлетворяет начальному условию (4) (или имеет начальные значения![]() ), предполагает, что интервал
), предполагает, что интервал ![]() определения решения
определения решения ![]() содержит точку
содержит точку ![]() .
.
Таким образом, теорема 1 утверждает, что координаты любой точки ![]() множества Г являются начальными значениями для некоторого решения уравнения (3) и что два решения с общими начальными значениями совпадают.
множества Г являются начальными значениями для некоторого решения уравнения (3) и что два решения с общими начальными значениями совпадают.
Геометрическое содержание теоремы 1 заключается в том, что через каждую точку ![]() множества Г проходит одна и только одна интегральная кривая уравнения (3) (см. рис. 1).
множества Г проходит одна и только одна интегральная кривая уравнения (3) (см. рис. 1).
Говоря, что через каждую точку ![]() множества Г проходит «только одна» интегральная кривая, мы допускаем некоторую неточность. В самом деле, решением уравнения (3) называется функция
множества Г проходит «только одна» интегральная кривая, мы допускаем некоторую неточность. В самом деле, решением уравнения (3) называется функция ![]() , заданная на вполне определенном интервале
, заданная на вполне определенном интервале ![]() . Наряду с этой функцией может существовать функция
. Наряду с этой функцией может существовать функция ![]() , также удовлетворяющая уравнению (3) и имеющая те же начальные значения
, также удовлетворяющая уравнению (3) и имеющая те же начальные значения ![]() , но заданная на другом интервале
, но заданная на другом интервале ![]() . Вторая часть теоремы 1 утверждает лишь, что функции
. Вторая часть теоремы 1 утверждает лишь, что функции ![]() и
и ![]() совпадают там, где они обе определены, но вовсе на утверждает, что интервалы их определения
совпадают там, где они обе определены, но вовсе на утверждает, что интервалы их определения![]() и
и ![]() одинаковы.
одинаковы.

Если один из интервалов, например ![]() , полностью содержит другой, то мы будем говорить, что решение
, полностью содержит другой, то мы будем говорить, что решение ![]() , заданное на интервале
, заданное на интервале ![]() является продолжением решения
является продолжением решения ![]() . Естественно сосредоточить все внимание на тех решениях, которые нельзя продолжить ни вправо, ни влево. Такие решения мы будем называть непродолжаемыми. Нетрудно доказать, что каждое решение может быть продолжено до непродолжаемого и притом единственным способом. Если теперь подразумевать под интегральной кривой график непродолжаемого решения, то утверждение том, что через каждую точку
. Естественно сосредоточить все внимание на тех решениях, которые нельзя продолжить ни вправо, ни влево. Такие решения мы будем называть непродолжаемыми. Нетрудно доказать, что каждое решение может быть продолжено до непродолжаемого и притом единственным способом. Если теперь подразумевать под интегральной кривой график непродолжаемого решения, то утверждение том, что через каждую точку ![]() проходит единственная интегральная кривая, становится точным.
проходит единственная интегральная кривая, становится точным.
Каждое решение ![]() уравнения (3) мы интерпретировали геометрически в виде графика функции
уравнения (3) мы интерпретировали геометрически в виде графика функции ![]() . Дадим теперь геометрическую интерпретацию самого уравнения (3). Через каждую точку
. Дадим теперь геометрическую интерпретацию самого уравнения (3). Через каждую точку![]() множества Г проведем прямую
множества Г проведем прямую ![]() с угловым коэффициентом
с угловым коэффициентом ![]() . Мы получаем поле направлений, соответствующее уравнению (3), что и дает геометрическую интерпретацию этого уравнения.
. Мы получаем поле направлений, соответствующее уравнению (3), что и дает геометрическую интерпретацию этого уравнения.
Связь между геометрической интерпретацией уравнения и геометрической интерпретацией его решений заключается в том (рис. 2), что любая интегральная кривая ![]() в каждой своей точке
в каждой своей точке ![]() касается прямой
касается прямой ![]() .
.
Примеры:
1. Для того чтобы проиллюстрировать значение теоремы 1 (в данном случае второй ее части), решим дифференциальное уравнение
![]() (5)
(5)
где ![]() - действительное число. Здесь
- действительное число. Здесь
![]()
так что функция ![]() в действительности зависит лишь от переменного х. Множество точек, на котором определена функция
в действительности зависит лишь от переменного х. Множество точек, на котором определена функция ![]() , в данном случае совпадает со всей плоскостью Р. Как сама функция
, в данном случае совпадает со всей плоскостью Р. Как сама функция ![]() , так и ее производная
, так и ее производная ![]() являются непрерывными функциями переменных t и x во всей плоскости Р. Таким образом, теорема 1 к уравнению (5) применима. Непосредственной подстановкой в уравнение (5) проверяется, что каждая функция
являются непрерывными функциями переменных t и x во всей плоскости Р. Таким образом, теорема 1 к уравнению (5) применима. Непосредственной подстановкой в уравнение (5) проверяется, что каждая функция
![]() , (6)
, (6)
где с — произвольное действительное число, является решением уравнения (5). Решение это непродолжаемо, так как оно задано уже на всей прямой ![]() . Покажем, что, придавая всевозможные значения числу с, мы получим все решения уравнении (5). Пусть
. Покажем, что, придавая всевозможные значения числу с, мы получим все решения уравнении (5). Пусть ![]() - произвольное решение этого уравнения. Покажем, что при надлежащем выборе числа с мы имеем
- произвольное решение этого уравнения. Покажем, что при надлежащем выборе числа с мы имеем![]() . Пусть
. Пусть ![]() - некоторая точка интервала существования решения
- некоторая точка интервала существования решения ![]() и
и ![]() . Положим
. Положим ![]() . Тогда решения
. Тогда решения ![]() и
и ![]() уравнения (5) имеют одинаковые начальные значения
уравнения (5) имеют одинаковые начальные значения ![]() и потому в силу второй части теоремы 1 совпадают. Таким образом, формула (6) исчерпывает совокупность всех решений дифференциального уравнения (5).
и потому в силу второй части теоремы 1 совпадают. Таким образом, формула (6) исчерпывает совокупность всех решений дифференциального уравнения (5).
§ 2. Формулировка теоремы существования и единственности
В §1 было рассмотрено одно дифференциальное уравнение первого порядка, причем была сформулирована теорема существования и единственности для этого уравнения. Теория обыкновенных дифференциальных уравнений имеет дело и с более общими системами уравнений. Обычно система обыкновенных дифференциальных уравнений состоит из стольких уравнений, сколько в нее входит неизвестных функций; при этом все неизвестные функции являются функциями одного и того же независимого переменного. Во всех случаях теорема существования и единственности является основным теоретическим положением, дающим возможность подойти к изучению данной системы дифференциальных уравнений.
Теорема существовании и единственности формулируется и доказывается применительно к системе уравнений, по внешнему виду имеющей несколько частный тип. В действительности же к этой системе уравнений сводятся системы сравнительно общего типа. Системы дифференциальных уравнений того частного тина, о котором здесь идет речь, мы будем называть в дальнейшем нормальными.
Система
![]()
![]() (1)
(1)
обыкновенных дифференциальных уравнений называется нормальной. В этой системе t —независимое переменное, ![]() — неизвестные функции; этого переменного, а
— неизвестные функции; этого переменного, а ![]() — функции от
— функции от ![]() переменных, заданные на некотором открытом множестве Г пространства размерности
переменных, заданные на некотором открытом множестве Г пространства размерности ![]() , в котором координатами точки являются числа
, в котором координатами точки являются числа ![]() . В дальнейшем всегда будет предполагаться, что функции
. В дальнейшем всегда будет предполагаться, что функции
![]()
![]() (2)
(2)
непрерывны на открытом множестве Г; точно так же будет предполагаться, что и их частные производные

![]() (3)
(3)
существуют и непрерывны на множестве Г. Следует заметить, что частные производные (3), непрерывность которых предполагается, берутся только по переменным ![]() , а не по независимому переменному t.
, а не по независимому переменному t.
Решением системы уравнений (1) называется система непрерывных функций
![]() ,
, ![]() (4)
(4)
определенных на некотором интервале ![]() и удовлетворяющих системе (1). Интервал
и удовлетворяющих системе (1). Интервал ![]() называется интервалом определения решения (4) (случаи
называется интервалом определения решения (4) (случаи![]() ,
, ![]() не исключаются). Считается, что система функций (4) удовлетворяет системе уравнений (1), если при подстановке в соотношение (1) вместо
не исключаются). Считается, что система функций (4) удовлетворяет системе уравнений (1), если при подстановке в соотношение (1) вместо ![]() функций (4) соотношения (1) превращаются в тождества по t на всем интервале
функций (4) соотношения (1) превращаются в тождества по t на всем интервале ![]() . Для возможности этой подстановки необходимо, чтобы функции (4) имели производные в каждой точке интервала
. Для возможности этой подстановки необходимо, чтобы функции (4) имели производные в каждой точке интервала ![]() и чтобы правые части уравнений (1) были определены для всех подставляемых в них значений аргументов. Таким образом, точка с координатами
и чтобы правые части уравнений (1) были определены для всех подставляемых в них значений аргументов. Таким образом, точка с координатами
![]()
должна принадлежать, множеству Г для всех значений t на интервале ![]() .
.
Дадим теперь формулировку теоремы существовании и единственности для нормальной системы (1). (Доказательство будет приведено в § 13.)
Теорема 2. Пусть (1) — нормальная система обыкновенных дифференциальных уравнений. Здесь правые части уравнений (1) определены на некотором открытом множестве Г, а функции (2) и (3) непрерывны на этом множестве. Оказывается, что для каждой точки
![]() (5)
(5)
множества Г существует решение
![]() ,
, ![]() (6)
(6)
системы (1), определенное на некотором интервале, содержащем точку ![]() , и удовлетворяющее условиям:
, и удовлетворяющее условиям:
![]() ;
; ![]() (7)
(7)
Далее, оказывается, что если имеются два каких-либо решения
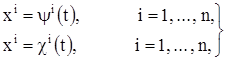 (8)
(8)
системы (1), удовлетворяющих условиям
![]()
![]() (9)
(9)
причем каждое решение определено на своем собственном интервале значений переменного t, содержащем точку ![]() то решения эти совпадают всюду, где они оба определены.
то решения эти совпадают всюду, где они оба определены.
Значения (5) называются начальными для решения (6), а соотношения (7) называются начальными условиями для этого решения. Мы будем говорить в дальнейшем, что решение (6) имеет начальные значения (5) или удовлетворяет начальным условиям (7).
Таким образом, теорему существования и единственности для нормальной системы кратко можно формулировать так:
Каковы бы ни были начальные значения (5), всегда существует решение системы (1) с этими начальными значениями, определенное на некотором интервале, содержащем точку ![]() . Далее, если имеются два решения с одинаковыми начальными значениями (5), каждое из которых определено на своем интервале, содержащем
. Далее, если имеются два решения с одинаковыми начальными значениями (5), каждое из которых определено на своем интервале, содержащем ![]() , то эти решения совпадают на общей части этих интервалов.
, то эти решения совпадают на общей части этих интервалов.
Введем здесь понятие непродолжаемого решения.
А) Пусть
![]() ,
, ![]() (10)
(10)
- решение системы уравнений (1), определенное на интервале ![]() , и
, и
![]() ,
, ![]() (11)
(11)
- решение той же системы уравнений (1), определенное на интервале ![]() . Мы будем говорить, что решение (11) является продолжением решения (10), если интервал
. Мы будем говорить, что решение (11) является продолжением решения (10), если интервал ![]() содержит интервал
содержит интервал ![]() (т.е.
(т.е. ![]() ) и решение (10) совпадает с решением (11) на интервале
) и решение (10) совпадает с решением (11) на интервале ![]() . В частности, мы будем считать, что решение (11) является продолжением решения (10) и в том случае, когда оба решения полностью совпадают, т. е.
. В частности, мы будем считать, что решение (11) является продолжением решения (10) и в том случае, когда оба решения полностью совпадают, т. е. ![]() . Решение (10) будем называть непродолжаемым, если не существует никакого отличного от него решения, являющегося его продолжением.
. Решение (10) будем называть непродолжаемым, если не существует никакого отличного от него решения, являющегося его продолжением.
Сформулируем теперь еще одну теорему существования.
Теорема 3. Пусть
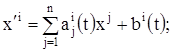
![]() (12)
(12)
- нормальная линейная система уравнений. Здесь коэффициенты ![]() и свободные члены
и свободные члены ![]() являются непрерывными функциями независимого переменного i, определенными на некотором интервале
являются непрерывными функциями независимого переменного i, определенными на некотором интервале ![]() . Оказывается, что для любых начальных значений
. Оказывается, что для любых начальных значений
![]() (13)
(13)
существует решение системы (12) с этими начальными значениями, определенное на всем интервале ![]() .
.
В частности, если коэффициенты и свободные члены системы (12) определены на всей прямой, т. е. если ![]() , то для любых начальных значений существует решение системы (12), определенное на всем бесконечном интервале
, то для любых начальных значений существует решение системы (12), определенное на всем бесконечном интервале ![]() .
.
Решения нормальной системы (1) интерпретируются геометрически в виде интегральных кривых (n+1)-мерном пространстве с координатами ![]() . Уравнения интегральной кривой имеют вид:
. Уравнения интегральной кривой имеют вид:
![]() ,
, ![]() (14)
(14)
где (14) есть решение системы.
Сама система (1) интерпретируется с помощью поля направлений в (n+1)-мерном пространстве.
Примеры
1. Решим нормальную линейную систему уравнений
![]() (15)
(15)
Множеством Г для нее является все трехмерное пространство с координатами ![]() Непосредственно проверяется, что система функций
Непосредственно проверяется, что система функций
![]() (16)
(16)
где ![]() и
и ![]() — произвольные постоянные, представляет собой решение системы (15). Для того чтобы попадать, что, выбирая надлежащим образом постоянные
— произвольные постоянные, представляет собой решение системы (15). Для того чтобы попадать, что, выбирая надлежащим образом постоянные ![]() и
и ![]() , можно получить по формуле (16) произвольное решение, зададимся начальными значениями
, можно получить по формуле (16) произвольное решение, зададимся начальными значениями ![]() покажем, что среди решений (16) имеется решение с этими начальными значениями. Мы получаем для постоянных
покажем, что среди решений (16) имеется решение с этими начальными значениями. Мы получаем для постоянных ![]() и
и ![]() условия
условия
![]() (17)
(17)
Пусть ![]() и
и ![]() - полярные координаты точки
- полярные координаты точки ![]() , так что
, так что
![]()
Тогда уравнения (17) переписываются в виде:
![]()
Полагая
![]()
мы, очевидно, выполним условия (17). Таким образом, через каждую точку ![]() проходит решение, задаваемое формулой (16).
проходит решение, задаваемое формулой (16).
В силу теоремы 2 (единственность) формула (16) охватывает совокупность всех решений.
2. Покажем, что если правые части (2) системы уравнений (1) k раз непрерывно дифференцируемы, т. е. имеют непрерывные производные порядка k (включая смешанные) по всем переменным ![]() , то (k+1)-я производная решения (4) системы (1) существует и непрерывна.
, то (k+1)-я производная решения (4) системы (1) существует и непрерывна.
В самом деле, для решения (4) имеет место тождество:
![]()
![]() (18)
(18)
Если правые части (2) имеют непрерывные первые производные, то правая часть тождества (18) имеет непрерывную производную по t, и потому функция ![]() существует и непрерывна. Дифференцируя написанное тождество (18) k раз, мы последовательно убедимся в существовании и непрерывности всех производных порядков 2, 3,..., k+1 функций
существует и непрерывна. Дифференцируя написанное тождество (18) k раз, мы последовательно убедимся в существовании и непрерывности всех производных порядков 2, 3,..., k+1 функций ![]() .
.
§ 3. Сведение обшей системы дифференциальных уравнений к нормальной
В предыдущем параграфе была сформулирована теорема существования и единственности для нормальной системы дифференциальных уравнений. Здесь будет показано, каким образом весьма общие системы дифференциальных уравнений сводятся к нормальным системам дифференциальных уравнений, и тем самым будет установлена теорема существования и единственности для этих общих систем уравнений.
Дадим сначала понятие о системе дифференциальных уравнений в общем виде.
В случае одной неизвестной функции х независимого переменного t обычно рассматривается одно уравнение, которое можно записать в виде:
![]() (1)
(1)
Здесь t — независимое переменное, х — его неизвестная функция, а F - заданная функция n+2 переменных. Функция F может быть задана не для всех значений ее аргументов, поэтому говорят об области В задания функции F. Здесь имеется в виду открытое множество В координатного пространства размерности n+2, в котором координатами точки являются переменные ![]() . Если максимальный порядок производной, входящей в дифференциальное уравнение, равен n, то говорят, что имеется уравнение n-го порядка. Решением уравнения (1) называется такая непрерывная функция
. Если максимальный порядок производной, входящей в дифференциальное уравнение, равен n, то говорят, что имеется уравнение n-го порядка. Решением уравнения (1) называется такая непрерывная функция ![]() независимого переменного t, определенная на некотором интервале
независимого переменного t, определенная на некотором интервале ![]() , что при подстановке ее вместо х в уравнение (1) мы получаем тождество по t на интервале
, что при подстановке ее вместо х в уравнение (1) мы получаем тождество по t на интервале ![]() . Очевидно, что подстановка
. Очевидно, что подстановка ![]() в соотношение (1) возможна лишь тогда, когда функция
в соотношение (1) возможна лишь тогда, когда функция ![]() на всем интервале своего существования
на всем интервале своего существования ![]() имеет производные до порядка n включительно. Для того чтобы подстановка
имеет производные до порядка n включительно. Для того чтобы подстановка ![]() в соотношение (1) была возможна, необходимо также, чтобы точка, имеющая координаты
в соотношение (1) была возможна, необходимо также, чтобы точка, имеющая координаты ![]() , принадлежала множеству В определения функции F при произвольном t интервала
, принадлежала множеству В определения функции F при произвольном t интервала ![]() .
.
Если имеются две неизвестные функции одного независимого переменного, то рассматриваются два дифференциальных уравнения, вместе образующих систему уравнений. Система эта может быть написаны в виде:
 (2)
(2)
Здесь t - независимое переменное, х и у — две его неизвестные функции, F и G - две функции, каждая от ![]() переменных, заданные в некотором открытом множестве В. Если максимальный порядок производной функции х, входящей в систему (2), равен
переменных, заданные в некотором открытом множестве В. Если максимальный порядок производной функции х, входящей в систему (2), равен ![]() , м максимальный порядок производной функции у, входящей в систему (2), равен
, м максимальный порядок производной функции у, входящей в систему (2), равен ![]() , то число
, то число ![]() называется порядком системы (2) относительно х, число
называется порядком системы (2) относительно х, число ![]() — порядком системы (2) относительно у, а число
— порядком системы (2) относительно у, а число ![]() называется порядком системы (2). Решением системы (2) называется пара непрерывных функций
называется порядком системы (2). Решением системы (2) называется пара непрерывных функций ![]() и
и ![]() , заданных на некотором интервале
, заданных на некотором интервале ![]() и обладающих тем свойством, что при подстановке их в соотношения (2) мы приходим к тождествам по t на всем интервале
и обладающих тем свойством, что при подстановке их в соотношения (2) мы приходим к тождествам по t на всем интервале ![]() . Как и в случае одного уравнения, предполагаются выполненными условия, дающие возможность делать подстановку
. Как и в случае одного уравнения, предполагаются выполненными условия, дающие возможность делать подстановку ![]() ,
, ![]() , в систему (2).
, в систему (2).
Аналогично определяются системы дифференциальных уравнений с тремя и большим числом неизвестных функций от одного независимого переменного. Если неизвестными функциями системы дифференциальных уравнении являются функции ![]() , а наивысший порядок производной функции
, а наивысший порядок производной функции ![]() , входящей в систему, равен
, входящей в систему, равен ![]() то число
то число ![]() называется порядком системы относительно
называется порядком системы относительно ![]() , а число
, а число ![]() называется порядком системы. Таким образом, нормальная система (1) §2 имеет порядок n.
называется порядком системы. Таким образом, нормальная система (1) §2 имеет порядок n.
Если соотношение (1) может быть разрешено относительно ![]() , то уравнение (1) переписывается в виде:
, то уравнение (1) переписывается в виде:
![]() (3)
(3)
Точно так же, если система (2) может быть разрешена относительно величин ![]() и
и ![]() , то эта система может быть переписана в виде:
, то эта система может быть переписана в виде:
 (4)
(4)
Уравнение (3) и система (4) называются разрешенными относительно высших производных. Аналогично определяются разрешенные относительно высших производных системы с произвольным числом неизвестных функций. В частности, нормальная система (1) § 2 является разрешенной относительно высших производных.
Покажем теперь, что всякая имеющая порядок n система дифференциальных уравнений, разрешенная относительно высших производных. сводится к нормальной системе порядка n. Для начала покажем, как одно уравнение порядка n сводится к нормальной системе порядка n.
А) Пусть
![]() (5)
(5)
- одно дифференциальное уравнение порядка n, разрешенное относительно высшей производной. Здесь t — независимое переменное, у — неизвестная функция переменного t. Далее, ![]() есть заданная функция n+1 переменных
есть заданная функция n+1 переменных ![]() , определенная в некотором открытом множестве Г координатного пространства размерности n+1. Относительно функции
, определенная в некотором открытом множестве Г координатного пространства размерности n+1. Относительно функции ![]() мы будем предполагать, что она непрерывна на множестве Г и что ее частные производные
мы будем предполагать, что она непрерывна на множестве Г и что ее частные производные

(где предполагается, что ![]() ) также непрерывны на множестве Г. Для замены уравнения (5) нормальной системой уравнений вводятся новые неизвестные функции
) также непрерывны на множестве Г. Для замены уравнения (5) нормальной системой уравнений вводятся новые неизвестные функции ![]() независимого переменного t при помощи равенств
независимого переменного t при помощи равенств
![]() (6)
(6)
Оказывается, что уравнение (5) эквивалентно системе
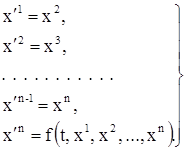 (7)
(7)
Из этого в силу теоремы 2 следует, что для каждой точки ![]() множества Г существует решение
множества Г существует решение ![]() уравнения (5), удовлетворяющее начальным условиям
уравнения (5), удовлетворяющее начальным условиям
![]()
или, как говорят, решение с начальными значениями
![]() (8)
(8)
Далее, любые два решения с начальными значениями (8) совпадают на общей части их интервалов определения. Если уравнение (5) линейно, т. е. функция f линейна относительно переменных ![]() , а коэффициенты ее определены и непрерывны на интервале
, а коэффициенты ее определены и непрерывны на интервале ![]() , то для любых начальных значений
, то для любых начальных значений ![]() , где
, где ![]() имеется решение
имеется решение ![]() , определенное на всем интервале
, определенное на всем интервале ![]() .
.
Докажем, что уравнение (5) эквивалентно системе (7). Допустим, что функция у удовлетворяет уравнению (5), и докажем, что функции ![]() , определенные соотношениями (6), удовлетворяют системе (7). Дифференцируя соотношения (6), вводящие новые неизвестные функции
, определенные соотношениями (6), удовлетворяют системе (7). Дифференцируя соотношения (6), вводящие новые неизвестные функции ![]() , получаем:
, получаем:
![]() (9)
(9)
![]() (10)
(10)
Заменяя правые части соотношений (9) на основе соотношений (6), а правую часть соотношения (10) на основании уравнения (5), которому функция у удовлетворяет, мы получаем систему (7). Допустим, что, наоборот, функции ![]() удовлетворяют системе (7); примем тогда
удовлетворяют системе (7); примем тогда ![]() за у покажем, что функция у удовлетворяет уравнению (5). Полагая в первом из уравнении системы (7)
за у покажем, что функция у удовлетворяет уравнению (5). Полагая в первом из уравнении системы (7) ![]() получаем
получаем ![]() . Заменяя во втором из уравнений (7)
. Заменяя во втором из уравнений (7) ![]() через
через ![]() , получаем
, получаем ![]() . Продолжая это построение дальше, мы приходим к соотношениям (6). Наконец, заменяя в последнем из уравнений системы (7) каждую функцию
. Продолжая это построение дальше, мы приходим к соотношениям (6). Наконец, заменяя в последнем из уравнений системы (7) каждую функцию ![]() в силу формул (6), получаем уравнение (5) для у.
в силу формул (6), получаем уравнение (5) для у.
Так как функция f определена на множестве Г, то правые части системы (7) также определены на множестве Г при условии замены координат по формулам (6). Для системы (7) выполнены условия теоремы 2 на множестве Г. Таким образом, можно произвольно выбрать начальные значения ![]() в множестве Г. Эти начальные значения в силу замены (6) превращаются в начальные значения
в множестве Г. Эти начальные значения в силу замены (6) превращаются в начальные значения
![]()
для уравнения (5).
Если уравнение (5) линейно, то система (7) также линейна. Из этого в силу теоремы 3 вытекает заключительная часть предложения А). Таким образом, предложение А) доказано.
Прием, описанный в предложении А), дает возможность привести к нормальной системе произвольную систему дифференциальных уравнений, разрешенную относительно высших производных.
§4. Некоторые сведения о линейных дифференциальных уравнениях
Система дифференциальных уравнений называется линейной, если все неизвестные функции и их производные, вместе взятые, входят в уравнения системы линейно. Таким образом, система линейных уравнений самого общего вида может быть записана в форме
![]() (1)
(1)
Здесь ![]() - неизвестные функции независимого переменного t, а коэффициенты
- неизвестные функции независимого переменного t, а коэффициенты ![]() и свободные члены
и свободные члены ![]() уравнений являются функциями t. Если все свободные члены системы (1) тождественно равны нулю, то система называется однородной. Каждой линейной системе соответствует однородная линейная система, получающаяся из нее отбрасыванием свободных членов. Таким образом, линейной системе (1) соответствует линейная однородная система
уравнений являются функциями t. Если все свободные члены системы (1) тождественно равны нулю, то система называется однородной. Каждой линейной системе соответствует однородная линейная система, получающаяся из нее отбрасыванием свободных членов. Таким образом, линейной системе (1) соответствует линейная однородная система
![]() (2)
(2)
Отметим несколько непосредственно проверяемых свойств линейных систем. При их формулировке будет предполагаться, что все коэффициенты и свободные члены линейной системы определены и непрерывны на интервале ![]() ; все рассматриваемые решения будут предполагаться заданными на всем интервале
; все рассматриваемые решения будут предполагаться заданными на всем интервале ![]() .
.
А) Если ![]() и
и ![]() ;
; ![]() - два решения линейной однородной системы (2), а
- два решения линейной однородной системы (2), а ![]() и
и ![]() - два произвольных числа, то система функций
- два произвольных числа, то система функций
![]()
также представляет собой решение однородной системы (2). Аналогичное утверждение справедливо также для трех и большего числа решений однородной системы (2).
Б) Если ![]() и
и ![]() ;
; ![]() - два решения линейной системы (1), то система функций
- два решения линейной системы (1), то система функций
![]()
представляет собой решение однородной системы (2). Далее, если ![]() ,
, ![]() , есть решение однородной системы уравнений (2), а
, есть решение однородной системы уравнений (2), а ![]() ;
; ![]() , есть решение системы уравнений (1), то система функций
, есть решение системы уравнений (1), то система функций
![]()
представляет собой решение линейной системы (1).
В) Допустим, что свободные члены системы линейных уравнений (1) представлены в виде сумм:
![]()
рассмотрим наряду с системой (1) две системы уравнений:
![]() (3)
(3)
![]() (4)
(4)
Если ![]() ,
, ![]() , есть решение системы (3), а
, есть решение системы (3), а ![]() ,
, ![]() , есть решение системы (4), то система функций
, есть решение системы (4), то система функций
![]()
представляет собой решение системы (1).
ГЛАВА II . Линейные уравнения с постоянными коэффициентами.
§ 5. Линейное однородное уравнении с постоянными коэффициентами (случай простых корней)
В этом и следующем параграфах будет решено линейное однородное уравнение с постоянными коэффициентами порядка n, т. е. уравнение
![]() (1)
(1)
где z есть неизвестная функция независимого переменного t, а коэффициенты ![]() суть постоянные числа (действительные или комплексные). Сначала будут найдены все комплексные решения этого уравнения, а затем (в случае, когда коэффициенты
суть постоянные числа (действительные или комплексные). Сначала будут найдены все комплексные решения этого уравнения, а затем (в случае, когда коэффициенты ![]() действительны) из них будут выделены действительные решения. Уравнение (1) можно записать в виде:
действительны) из них будут выделены действительные решения. Уравнение (1) можно записать в виде:
![]() (2)
(2)
так что к нему применима теорема существования и единственности. В дальнейшем будет использована лишь единственность, так как решения уравнения (2) будут найдены явно и тем самым существование их будет установлено; единственность же будет использована для доказательства того, что найдены все решения.
В инженерных применениях обыкновенных дифференциальных уравнений с постоянными коэффициентами важную роль играет операционное исчисление. Мы используем здесь символические (или, иначе, операционные) обозначения, лежащие в основе операционного исчисления. Суть этих обозначений заключается в том, что производная по времени t, от произвольной функции ![]() обозначается не через
обозначается не через ![]() , а через
, а через ![]() , так что буква р, стоящая слева от функции, является символом дифференцирования по t. Если позволить себе применить к символу дифференцирования р некоторые алгебраические действия, то мы приходим к обозначению
, так что буква р, стоящая слева от функции, является символом дифференцирования по t. Если позволить себе применить к символу дифференцирования р некоторые алгебраические действия, то мы приходим к обозначению
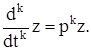
Пользуясь этим обозначением, мы можем написать
![]()
Если теперь в правой части последнего равенства позволить себе вынести за скобку функцию z, то мы получаем равенство
![]()
Таким образом, мы приходим к формальному определению.
А) Пусть
![]()
- произвольный многочлен относительно символа р с постоянными коэффициентами (действительными или комплексными) и z — некоторая действительная или комплексная функция действительного переменного t. Положим:
![]() (3)
(3)
Если ![]() и
и ![]() суть два произвольных многочлена относительно символа р (или, как говорят, оператора дифференцирования р), а
суть два произвольных многочлена относительно символа р (или, как говорят, оператора дифференцирования р), а ![]() — функции переменного t, то, как легко видеть, мы имеем тождества
— функции переменного t, то, как легко видеть, мы имеем тождества
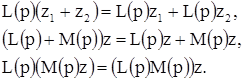
В силу введенных обозначений уравнение (1) может быть записано в виде:
![]() (4)
(4)
где
![]()
Б) Пусть ![]() — произвольный многочлен относительно символа р. Тогда
— произвольный многочлен относительно символа р. Тогда
![]() (5)
(5)
Докажем формулу (5). Мы имеем
![]()
Из этого следует, что ![]() . Отсюда формула (5) вытекает непосредственно (см. (3)).
. Отсюда формула (5) вытекает непосредственно (см. (3)).
Из формулы (5) следует, что функция ![]() тогда и только тогда является решением уравнения (4), когда число
тогда и только тогда является решением уравнения (4), когда число ![]() есть корень многочлена
есть корень многочлена ![]() . Многочлен
. Многочлен ![]() называется характеристическим многочленом уравнения (4). В том случае, когда он не имеет кратных корней, совокупность всех решений уравнения (4) описывается следующей теоремой.
называется характеристическим многочленом уравнения (4). В том случае, когда он не имеет кратных корней, совокупность всех решений уравнения (4) описывается следующей теоремой.
Теорема 4. Предположим, что характеристический многочлен ![]() уравнения
уравнения
![]() (6)
(6)
(см. (1) и (4)) не имеет кратных корней, и обозначим его корни через
![]()
Положим:
![]() (7)
(7)
Тогда при любых комплексных постоянных ![]() функция
функция
![]() (8)
(8)
является решением уравнения (6). Решение это является общим в том смысле, что каждое решение уравнении (6) может быть получено по формуле (8) при надлежащем выборе констант ![]() . При этом константы
. При этом константы ![]() (называемые постоянными интегрирования) однозначно определяются для каждого данного решения z.
(называемые постоянными интегрирования) однозначно определяются для каждого данного решения z.
Заметим, что функции (7) определены на всей числовой прямой ![]() .
.
Примеры
1. Найдем все комплексные решения уравнения
![]()
Его можно записать в виде (6), где
![]()
Непосредственно проверяется, что р = - 1 есть корень характеристического многочлена L(р). Разделив L(р) на р+1, получаем:
![]()
откуда находим еще два корня ![]() . Таким образом, корнями многочлена L(р) являются числа
. Таким образом, корнями многочлена L(р) являются числа
![]()
В силу теоремы 4 общее комплексное решение рассматриваемого уравнения имеет вид:
![]()
2. Будем считать, что система решений (7) удовлетворяет условиям
![]() (9)
(9)
и положим:
![]()
где ![]() - действительные функции. Будем, далее, считать, что числа
- действительные функции. Будем, далее, считать, что числа ![]() удовлетворяют условиям
удовлетворяют условиям
![]() (10)
(10)
и положим:
![]()
где ![]() — действительные числа. При этих обозначениях общее действительное решение уравнения (6) записывается в виде:
— действительные числа. При этих обозначениях общее действительное решение уравнения (6) записывается в виде:
![]()
где
![]()
суть произвольные действительные числа.
§6. Линейное однородное уравнение с постоянными коэффициентами (случаи кратных корней)
Если характеристический многочлен
![]()
уравнения
![]() (1)
(1)
(см. § 5, А)) имеет кратные корни, то среди функций вида ![]() нельзя найти n различных решений уравнения (1). Для нахождения в этом случае решений другого вида можно воспользоваться следующим наводящим соображением. Пусть
нельзя найти n различных решений уравнения (1). Для нахождения в этом случае решений другого вида можно воспользоваться следующим наводящим соображением. Пусть ![]() и
и ![]() — два различных действительных корня характеристического многочлена L(р); тогда функция
— два различных действительных корня характеристического многочлена L(р); тогда функция 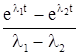 является решением уравнения (1). Если теперь предположить, что при изменении коэффициентов многочлена L (р) число
является решением уравнения (1). Если теперь предположить, что при изменении коэффициентов многочлена L (р) число ![]() стремится к
стремится к ![]() , то это решение переходит (в пределе) в функцию
, то это решение переходит (в пределе) в функцию ![]() , о которой естественно предположить, что они являются решением уравнения (1) и случае, если
, о которой естественно предположить, что они являются решением уравнения (1) и случае, если ![]() , есть двукратный корень многочлена L (р). Аналогично мы приходим к догадке, что если
, есть двукратный корень многочлена L (р). Аналогично мы приходим к догадке, что если ![]() есть k-кратный корень характеристического многочлена L (р), то решениями уравнения (1) являются все функции:
есть k-кратный корень характеристического многочлена L (р), то решениями уравнения (1) являются все функции:
![]() .
.
Распространяя эту догадку на случай комплексных кратных корней, мы приходим к предположению о справедливости нижеследующей теоремы (являющейся обобщением теоремы 4):
Теорема 5. Пусть
![]() (2)
(2)
— линейное однородное уравнение порядка n с постоянными коэффициентами. Пусть, далее, ![]() - совокупность всех попарно различных корней характеристического многочлена L(р) уравнения (2), причем корень
- совокупность всех попарно различных корней характеристического многочлена L(р) уравнения (2), причем корень ![]() имеет кратность
имеет кратность ![]() , так что
, так что ![]() . Положим:
. Положим:
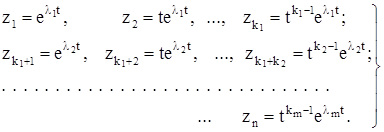 (3)
(3)
Тогда все функции (3) являются решениями уравнения (2), так что при любых комплексных постоянных ![]() функция
функция
![]() (4)
(4)
также является решением этого уравнения. Решение это является общим в том смысле, что каждое решение уравнения (2) может быть получено по формуле (4) при надлежащем выборе констант ![]() . При этом константы
. При этом константы ![]() однозначно определяются для каждого данного решения z.
однозначно определяются для каждого данного решения z.
Заметим, что функции (3) определены на всей числовой прямой ![]() .
.
Отметим одно очевидное следствие теоремы 5.
А) Каждое решение z(t) уравнения (2) может быть записано в виде:
![]()
где ![]() есть многочлен степени, не превосходящей числа
есть многочлен степени, не превосходящей числа ![]() ,
, ![]() . При этом многочлены
. При этом многочлены ![]() определены однозначно решением z(t), так как их коэффициенты являются константами интегрирования
определены однозначно решением z(t), так как их коэффициенты являются константами интегрирования ![]() , которые в силу теоремы 5 определены решением z(t) однозначно.
, которые в силу теоремы 5 определены решением z(t) однозначно.
Если коэффициенты уравнения (2) действительны, то перед нами стоит задача выделения из совокупности комплексных решений уравнения (2) его действительных решений.
Б) Будем считать, что коэффициенты характеристического многочлена L(р) уравнения (2) действительны. Пусть ![]() — некоторый корень многочлена L(р) кратности k; тогда при
— некоторый корень многочлена L(р) кратности k; тогда при ![]() функция
функция ![]() является решением уравнения (2). Если корень
является решением уравнения (2). Если корень ![]() действительный, то функция
действительный, то функция ![]() действительна, если же корень
действительна, если же корень ![]() комплексный, то наряду с решением
комплексный, то наряду с решением ![]() имеется комплексно-сопряженное ему решение
имеется комплексно-сопряженное ему решение ![]() , так как
, так как ![]() есть корень кратности k многочлена L(р). Таким образом, в системе решений (3) наряду с каждым комплексным решением имеется сопряженное с ним решение. Для того чтобы решение (4) было действительным, необходимо и достаточно, чтобы коэффициенты при действительных решениях были действительными, а коэффициенты у попарно сопряженных комплексных решений были попарно сопряжены.
есть корень кратности k многочлена L(р). Таким образом, в системе решений (3) наряду с каждым комплексным решением имеется сопряженное с ним решение. Для того чтобы решение (4) было действительным, необходимо и достаточно, чтобы коэффициенты при действительных решениях были действительными, а коэффициенты у попарно сопряженных комплексных решений были попарно сопряжены.
Примеры
1. Решим уравнение
![]()
Уравнение это может быть записано в виде (2), где характеристический многочлен L(р) имеет вид:
![]()
Корнями этого многочлена служат числа
![]()
имеющие кратности ![]() Поэтому в силу теоремы 5 система решений (3) для рассматриваемого уравнения имеет вид:
Поэтому в силу теоремы 5 система решений (3) для рассматриваемого уравнения имеет вид:
![]()
Общее решение дается формулой
![]()
2. Решим уравнение
![]()
Характеристический многочлен равен ![]() ; его корнями (двукратными) являются числа
; его корнями (двукратными) являются числа ![]() . Общее решение рассматриваемого уравнения записывается в виде:
. Общее решение рассматриваемого уравнения записывается в виде:
![]()
§7. Линейное неоднородное уравнение с постоянными коэффициентами
Здесь будет дано решение линейного уравнения с постоянными коэффициентами со свободным членом специального вида, являющимся так называемым квазимногочленом.
А) Квазимногочленом будем называть всякую функцию F(t), которую можно записать в виде:
![]() (1)
(1)
где ![]() суть некоторые комплексные числа, а
суть некоторые комплексные числа, а ![]() — многочлены от t. Из предложения А) § 6 следует, что каждое решение линейного однородного уравнения с постоянными коэффициентами является квазимногочленом. Можно доказать, что и обратно, каждый квазимногочлен является решением некоторою линейного однородного уравнения с постоянными коэффициентами. Если какие-нибудь два числа последовательности
— многочлены от t. Из предложения А) § 6 следует, что каждое решение линейного однородного уравнения с постоянными коэффициентами является квазимногочленом. Можно доказать, что и обратно, каждый квазимногочлен является решением некоторою линейного однородного уравнения с постоянными коэффициентами. Если какие-нибудь два числа последовательности ![]() совпадают между собой, например, если
совпадают между собой, например, если ![]() , то члены суммы (1), соответствующие этим числам, можно объединить и заменить членом
, то члены суммы (1), соответствующие этим числам, можно объединить и заменить членом ![]() . Таким образом, запись (1) всегда можно привести к такому виду, что числа
. Таким образом, запись (1) всегда можно привести к такому виду, что числа ![]() , входящие в нее, попарно различны. Отметим, что сумма и произведение двух произвольных квазимногочленов также есть квазимногочлен; далее, если к произвольному квазимногочлену применить произвольный оператор L(p), то мы вновь получим квазимногочлен.
, входящие в нее, попарно различны. Отметим, что сумма и произведение двух произвольных квазимногочленов также есть квазимногочлен; далее, если к произвольному квазимногочлену применить произвольный оператор L(p), то мы вновь получим квазимногочлен.
Таким образом, в настоящем параграфе будет рассматриваться уравнение
![]() (2)
(2)
где F(t) есть некоторый квазимногочлен. Наряду с уравнением (2) рассмотрим соответствующее однородное уравнение
![]() (3)
(3)
Нижеследующее предложение непосредственно вытекает из замечания Б) § 4.
Б) Если ![]() есть некоторое решенме уравнения (2), то произвольное z того же уравнения может быть записано в виде:
есть некоторое решенме уравнения (2), то произвольное z того же уравнения может быть записано в виде:
![]()
где u есть некоторое решение уравнения (3).
Так как произвольное решение однородного уравнения мы отыскивать уже умеем, то дело сводится, таким образом, к отысканию одного решения или, как говорят, частного решения уравнения (2) в случае, когда F(t) есть квазимногочлен. Так как, далее, каждый квазимногочлен записывается в виде (1), то в силу замечания В) § 4 дело сводится к отысканию частного решения уравнения (2) в случае, когда ![]() где f(t) - многочлен. Для этого случая решение отыскивается в нижеследующей теореме.
где f(t) - многочлен. Для этого случая решение отыскивается в нижеследующей теореме.
Во избежание недоразумений отметим, что в дальнейшем под многочленом степени r мы будем понимать функцию вида ![]() , не предполагая непременно, что старший коэффициент
, не предполагая непременно, что старший коэффициент ![]() отличен от нуля.
отличен от нуля.
Теорема 6. Рассмотрим неоднородное уравнение
![]() (4)
(4)
в котором f(t) есть многочлен степени r относительно t, а ![]() - комплексное число. Пусть k = 0, если
- комплексное число. Пусть k = 0, если ![]() . Оказывается, что существует частное решение уравнения (4), имеющее вид:
. Оказывается, что существует частное решение уравнения (4), имеющее вид:
![]() (5)
(5)
где g(t) есть многочлен степени r относительно t. Коэффициенты многочлена g(t) можно найти методом неопределенных коэффициентов.
§ 8. Метод исключения
До сих пор мы занимались решением одного линейного уравнения с постоянными коэффициентами. Оказывается, однако, что весьма общую систему линейных уравнений с постоянными коэффициентами можно в некотором смысле свести к одному уравнению. Сведение это осуществляется методом исключения, аналогичным тому, который употребляется в теории линейных алгебраических (не дифференциальных) уравнений. Здесь будет дано изложение этого метода и сделаны некоторые выводы из него.
Мы будем рассматривать систему уравнений
![]() (1)
(1)
здесь ![]() - неизвестные функции независимого переменного t, а
- неизвестные функции независимого переменного t, а ![]() — заданные функции времени t. Каждый символ
— заданные функции времени t. Каждый символ ![]() представляет собой многочлен с постоянными коэффициентами относительно оператора дифференцирования р, так что один член
представляет собой многочлен с постоянными коэффициентами относительно оператора дифференцирования р, так что один член ![]() представляет собой линейную комбинацию с постоянными коэффициентами относительно функции
представляет собой линейную комбинацию с постоянными коэффициентами относительно функции ![]() и ее производных. Число уравнений системы (1) равно числу неизвестных функции.
и ее производных. Число уравнений системы (1) равно числу неизвестных функции.
Порядок системы (1) относительно неизвестной функции ![]() обозначим через
обозначим через ![]() , так что общий порядок системы (1) определяется формулой
, так что общий порядок системы (1) определяется формулой ![]() . Ставя задачу решения системы (1), мы, естественно, должны предполагать, что каждая неизвестная функция
. Ставя задачу решения системы (1), мы, естественно, должны предполагать, что каждая неизвестная функция ![]() имеет все производные до порядка
имеет все производные до порядка ![]() включительно; предположение о существовании производных более высоких порядков не вытекает из постановки задачи.
включительно; предположение о существовании производных более высоких порядков не вытекает из постановки задачи.
Применяя к системе (1) метод исключения, мы будем предполагать, что каждая из неизвестных функций ![]() имеет достаточное число производных, точно так же, как и каждая из функций
имеет достаточное число производных, точно так же, как и каждая из функций ![]() . Делая эти допущения, мы, с одной стороны, сужаем класс рассматриваемых решений (предположение о достаточной дифференцируемости неизвестных функций), а, с другой стороны, сужаем класс рассматриваемых уравнений (предположение о достаточной дифференцируемости функций
. Делая эти допущения, мы, с одной стороны, сужаем класс рассматриваемых решений (предположение о достаточной дифференцируемости неизвестных функций), а, с другой стороны, сужаем класс рассматриваемых уравнений (предположение о достаточной дифференцируемости функций ![]() ). Первое из этих ограничений можно снять, доказав, что если
). Первое из этих ограничений можно снять, доказав, что если ![]() есть решение системы (1) и если правые части
есть решение системы (1) и если правые части ![]() имеют достаточное число производных, то каждая из функций
имеют достаточное число производных, то каждая из функций ![]() имеет достаточное число производных (см. примеры 3 и 4).
имеет достаточное число производных (см. примеры 3 и 4).
Перейдем к изложению метода исключения.
А) Рассмотрим матрицу
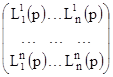 (2)
(2)
системы уравнений (1). Каждый элемент ![]() матрицы (2) есть многочлен относительно р. Таким образом, можно вычислить детерминант D(р) матрицы (2) и ее миноры. Алгебраическое дополнение элемента
матрицы (2) есть многочлен относительно р. Таким образом, можно вычислить детерминант D(р) матрицы (2) и ее миноры. Алгебраическое дополнение элемента ![]() матрицы (2) (т. е. минор этого элемента, взятый с надлежащим знаком) обозначим через
матрицы (2) (т. е. минор этого элемента, взятый с надлежащим знаком) обозначим через ![]() . Из курса высшей алгебры известно, что имеет место тождество:
. Из курса высшей алгебры известно, что имеет место тождество:
 (3)
(3)
где ![]() есть так называемый символ Кронекера:
есть так называемый символ Кронекера:
![]()
Умножая уравнение (1) на многочлен ![]() (т.е. производя ряд дифференцирований, умножений на числа и сложений) и суммируя затем по j, мы получаем равенство
(т.е. производя ряд дифференцирований, умножений на числа и сложений) и суммируя затем по j, мы получаем равенство
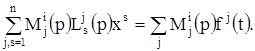 (4)
(4)
(При переходе от равенств (1) к равенству (4) мы использовали существование достаточно большого числа производных у функций ![]() и
и ![]() .) В силу (3) равенство (4) можно переписать в виде
.) В силу (3) равенство (4) можно переписать в виде
 (5)
(5)
Полученная нами система уравнений (5) (![]() ) обладает тем свойством, что каждая неизвестная функция
) обладает тем свойством, что каждая неизвестная функция ![]() входит лишь в одно уравнение (5). Мы доказали, таким образом, что если система функций
входит лишь в одно уравнение (5). Мы доказали, таким образом, что если система функций ![]() представляет собой решение системы (1), то каждая отдельная функция
представляет собой решение системы (1), то каждая отдельная функция ![]() является решением уравнения (5).
является решением уравнения (5).
Не следует думать, однако, что если для каждого номера i выбрать произвольным образом решение ![]() уравнения (5) и затем составить систему функций
уравнения (5) и затем составить систему функций ![]() , то полученная система функций будет решением системы (1). Для того чтобы найти общее решение
, то полученная система функций будет решением системы (1). Для того чтобы найти общее решение ![]() системы (1), нужно найти общее решение
системы (1), нужно найти общее решение ![]() каждого уравнения (5),
каждого уравнения (5), ![]() , составить систему функций
, составить систему функций ![]() и затем выяснить, при каких условиях (при каких соотношениях между постоянными интегрирования) эта система функций удовлетворяет системе уравнений (1).
и затем выяснить, при каких условиях (при каких соотношениях между постоянными интегрирования) эта система функций удовлетворяет системе уравнений (1).
Сделаем теперь некоторые выводы из метода исключения. Формулируем прежде всего результат, полученный в предложении А), для случая однородной системы уравнений
![]() (6)
(6)
Б) Если система функций ![]() представляет собой решение системы (6), то каждая отдельная функция
представляет собой решение системы (6), то каждая отдельная функция ![]() , входящая в это решение, удовлетворяет уравнению
, входящая в это решение, удовлетворяет уравнению
![]()
где D(p) — детерминант матрицы ![]() системы (6).
системы (6).
Покажем теперь, как, пользуясь методом исключения, следует решать, однородную систему уравнений (6).
Систему (6) перепишем в векторной форме
![]() (7)
(7)
где ![]() - матрица системы (6), а
- матрица системы (6), а ![]() .
.
В) Допустим, что детерминант D(p) системы (6) не обращается тождественно в нуль, и пусть ![]() — корень многочлена D(p), имеющий кратность k. Будем искать решение уравнения (8), имеющее вид:
— корень многочлена D(p), имеющий кратность k. Будем искать решение уравнения (8), имеющее вид:
![]() (8)
(8)
г7де ![]() — вектор, компоненты
— вектор, компоненты
![]() (9)
(9)
которого являются многочленами степени k - 1 относительно t с неопределенными коэффициентами. Каждое решение вида (8) уравнения (7) мы будем называть соответствующим корню ![]() .
.
Подставляя предполагаемое решение (8) в уравнение (7), мы получим:
![]()
После сокращения на ![]() это дает:
это дает:
![]() (10)
(10)
Таким образом, вектор (8) тогда и только тогда является решением уравнения (8), когда многочлены (9) удовлетворяют условию (10). Переписывая векторное уравнение (10) в координатной форме, получим n соотношений:
![]() (11)
(11)
Левая часть каждого соотношения (11) представляет собой многочлен степени k - 1 относительно t, коэффициенты которого являются линейными однородными функциями коэффициентов многочленов (9). Приравнивая нулю коэффициент при каждой степени t в каждом из соотношений (11), мы получим систему линейных однородных уравнений относительно коэффициентов многочленов (9). Эта система эквивалентна уравнению (10).
Таким образом, изложенный метод сводит задачу отыскания решений вида (8) к решению некоторой линейной однородной системы алгебраических уравнений. Из сказанного видно, что решения вида (8) определены на всем бесконечном интервале ![]() .
.
Вопрос о том, как отыскать все решения уравнения (7), решается нижеследующей теоремой:
Теорема 7. Допустим, что детерминант D(p) системы (6) не обращается тождественно в нуль, и пусть ![]() - совокупность всех различных корней многочлена D(p). Тогда произвольное решение х уравнения (7), может быть записано в виде:
- совокупность всех различных корней многочлена D(p). Тогда произвольное решение х уравнения (7), может быть записано в виде:
![]() (12)
(12)
где ![]() — некоторое решение уравнения (7), соответствующее корню
— некоторое решение уравнения (7), соответствующее корню ![]() (см. В)). Отсюда, в частности, следует, что каждое решение уравнения (7), определено для всех значений t.
(см. В)). Отсюда, в частности, следует, что каждое решение уравнения (7), определено для всех значений t.
Доказательство. Допустим, что ![]() - некоторое решение уравнения (7) определенное на интервале
- некоторое решение уравнения (7) определенное на интервале ![]() ; покажем, что на этом интервале оно может быть записано в виде (12). В силу предложения Б), каждая функция
; покажем, что на этом интервале оно может быть записано в виде (12). В силу предложения Б), каждая функция ![]() , на интервале
, на интервале ![]() удовлетворяет уравнению
удовлетворяет уравнению
![]()
и потом в силу предложения А) § 6 может быть записана на этом интервале в виде:
![]() (13)
(13)
Здесь ![]() есть многочлен степени
есть многочлен степени ![]() , где
, где ![]() — кратность корня
— кратность корня ![]() .
.
Таким образом, каждое решение х уравнения (7) на интервале своего определения ![]() записывается в виде:
записывается в виде:
![]() (14)
(14)
где ![]() — вектор, компоненты которого являются многочленами степени
— вектор, компоненты которого являются многочленами степени ![]() . Для доказательства теоремы 7 нам достаточно показать теперь, что каждое слагаемое
. Для доказательства теоремы 7 нам достаточно показать теперь, что каждое слагаемое ![]() в правой части равенства (14) есть решение уравнения (7). Для доказательства этого подставим решение (14) в уравнение (7). Мы получим:
в правой части равенства (14) есть решение уравнения (7). Для доказательства этого подставим решение (14) в уравнение (7). Мы получим:
 (15)
(15)
Так как числа ![]() попарно различны, то из равенства (15) следует:
попарно различны, то из равенства (15) следует:
![]()
или, иначе,
![]()
Но это и значит, что ![]() есть решение уравнения (7).
есть решение уравнения (7).
Итак, теорема 7 доказана.
Пример
Решим методом исключения систему уравнений
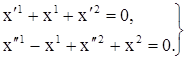
Перепишем ее в символической форме:
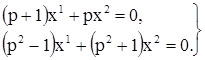
Детерминант системы, как легко видеть, равен ![]() ; он имеет двукратный корень
; он имеет двукратный корень ![]() . Согласно теореме 7 решение системы следует искать в виде:
. Согласно теореме 7 решение системы следует искать в виде:

Подстановка этих функций в первое уравнение дает (после сокращения на ![]() ):
):
a + c – ct – d = 0,
откуда

Те же соотношения для коэффициентов получаются и при подстановке во второе уравнение системы. Таким образом, общее решение рассматриваемой системы записывается в виде:
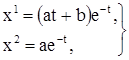
где a и b - произвольные постоянные.
§9. Нормальная линейная однородная система с постоянными коэффициентами
В этом параграфе решается система уравнений
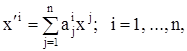 (1)
(1)
с постоянными коэффициентами. Эта система может быть решена методом исключения, здесь она решается путем приведения матрицы ![]() к жордановой форме. В случае, когда все собственные значения матрицы А различны, возможность приведения ее к жордановой, т.е. в данном случае диагональной, форме представляет собой весьма элементарный алгебраический факт. В общем случае возможность приведения матрицы А к жордановой форме относиться к наиболее сложным результатам курса линейной алгебры.
к жордановой форме. В случае, когда все собственные значения матрицы А различны, возможность приведения ее к жордановой, т.е. в данном случае диагональной, форме представляет собой весьма элементарный алгебраический факт. В общем случае возможность приведения матрицы А к жордановой форме относиться к наиболее сложным результатам курса линейной алгебры.
Обычно приведение матрицы А к жордановой форме для решения системы (1) используется путем линейного преобразования неизвестных функций ![]() . Другой способ, по существу также опирающийся на приведение матрицы А к жордановой форме, изложен в этом параграфе.
. Другой способ, по существу также опирающийся на приведение матрицы А к жордановой форме, изложен в этом параграфе.
В этом параграфе мы не будем делать различия между матрицей А и соответствующим ей преобразованием А в пространстве векторов ![]() , так как базис меняться не будет.
, так как базис меняться не будет.
Случай простых корней характеристического уравнения
А) Система дифференциальных уравнений (1) в векторной форме переписывается в виде:
![]() (2)
(2)
Здесь ![]() , а вместо системы
, а вместо системы ![]() неизвестных функций введен неизвестный вектор
неизвестных функций введен неизвестный вектор
![]() ;
;
под производной ![]() вектора х понимается вектор
вектора х понимается вектор ![]() . Если h есть собственный вектор матрицы А с собственным значением
. Если h есть собственный вектор матрицы А с собственным значением ![]() т.е. если
т.е. если
![]()
то векторная функция х, определяемая соотношением
![]() ,
,
является решением уравнения (2).
Последнее утверждение проверяется путем подстановки ![]() в соотношение (2).
в соотношение (2).
Теорема 8. Пусть
![]() (3)
(3)
- такая система дифференциальных уравнений (см. А.)), что собственные значения ![]() матрицы А попарно различны, и пусть
матрицы А попарно различны, и пусть
![]()
- соответствующие собственные векторы этой матрицы. Положим:
![]() (4)
(4)
Тогда векторная функция
![]() (5)
(5)
где ![]() – константы, является решением уравнения (3), и всякое решение уравнения (3) задается этой формулой.
– константы, является решением уравнения (3), и всякое решение уравнения (3) задается этой формулой.
Доказательство. В силу предложения А) каждая функция ![]() представляет собой решение уравнения (3), и потому в силу предложения А) §4 формула (5) всегда дает решение уравнения (3). Докажем теперь, что всякое решение уравнения (3) может быть записано в виде (5). Пусть
представляет собой решение уравнения (3), и потому в силу предложения А) §4 формула (5) всегда дает решение уравнения (3). Докажем теперь, что всякое решение уравнения (3) может быть записано в виде (5). Пусть ![]() - произвольное решение уравнения (3). В силу теоремы 3 решение
- произвольное решение уравнения (3). В силу теоремы 3 решение ![]() можно считать заданным на всей бесконечной прямой
можно считать заданным на всей бесконечной прямой ![]() . Таким образом, решение это определено и при t = 0. Положим
. Таким образом, решение это определено и при t = 0. Положим ![]() . Пусть
. Пусть
![]()
- разложение вектора ![]() по векторам базиса
по векторам базиса ![]() . Тогда решение х, определяемое формулой (5), очевидно, удовлетворяет начальным условиям
. Тогда решение х, определяемое формулой (5), очевидно, удовлетворяет начальным условиям
![]()
Тем же начальным условиям ![]() удовлетворяет и решение
удовлетворяет и решение ![]() ; таким образом, в силу теоремы единственности (см. теорему 2),
; таким образом, в силу теоремы единственности (см. теорему 2), ![]() .
.
Итак, теорема 8 доказана.
В случае, если матрица ![]() , задающая уравнение (3), действительна, перед нами встает задача выделения из всех решений (5) действительных решений.
, задающая уравнение (3), действительна, перед нами встает задача выделения из всех решений (5) действительных решений.
Б) Будем считать, что матрица ![]() , задающая уравнение (3), действительна, и выберем векторы
, задающая уравнение (3), действительна, и выберем векторы ![]() таким образом, чтобы действительным собственным значениям соответствовали действительные векторы, а комплексно сопряженным – комплексно сопряженные. Тогда в системе решений (4) каждому действительному собственному значению будет соответствовать действительное решение, а каждым двум комплексно сопряженным собственным значениям будут соответствовать комплексно сопряженные решения. Оказывается, что решение (5) тогда и только тогда действительно, когда константы, стоящие при действительных решениях, действительны, а константы, стоящие при комплексно сопряженных решениях, сопряжены.
таким образом, чтобы действительным собственным значениям соответствовали действительные векторы, а комплексно сопряженным – комплексно сопряженные. Тогда в системе решений (4) каждому действительному собственному значению будет соответствовать действительное решение, а каждым двум комплексно сопряженным собственным значениям будут соответствовать комплексно сопряженные решения. Оказывается, что решение (5) тогда и только тогда действительно, когда константы, стоящие при действительных решениях, действительны, а константы, стоящие при комплексно сопряженных решениях, сопряжены.
Общий случай
Перейдем теперь к решению системы (1) в общем случае (матрица ![]() может иметь кратные собственные значения). Разбор этого случая опирается на весьма нетривиальную и сложно доказуемую алгебраическую теорему о приведении матрицы к жордановой форме.
может иметь кратные собственные значения). Разбор этого случая опирается на весьма нетривиальную и сложно доказуемую алгебраическую теорему о приведении матрицы к жордановой форме.
В) Запишем систему (1) в векторной форме
![]() (6)
(6)
и пусть
![]()
- некоторая серия с собственным значением ![]() относительно матрицы А, так что выполнены соотношения
относительно матрицы А, так что выполнены соотношения
![]()
Введем последовательность векторных функций, положив:
 (7)
(7)
Оказывается тогда, что векторные функции
![]() (8)
(8)
являются решениями уравнения (6), причем
![]() (9)
(9)
Таким образом, каждой серии из k векторов соответствует система из k решений.
Для доказательства того, что векторные функции (8) являются решениями уравнения (6), укажем два тождества относительно векторных функций (7). Тождества эти следующие:
![]()
![]()
В этих соотношениях принято ![]() . Оба они проверяются непосредственно путем проведения элементарных вычислений. При помощи этих тождеств непосредственно проверяется, что функции (8) являются решениями уравнения (6). Действительно, мы имеем:
. Оба они проверяются непосредственно путем проведения элементарных вычислений. При помощи этих тождеств непосредственно проверяется, что функции (8) являются решениями уравнения (6). Действительно, мы имеем:
![]()
Перейдем теперь к формулировке и доказательству теоремы, дающей решение системы (1) в общем случае.
Теорема 9. Пусть
![]() (10)
(10)
- векторная запись системы (1). Существует базис ![]() , состоящий из серий относительно матрицы А. Для определенности будем считать, что
, состоящий из серий относительно матрицы А. Для определенности будем считать, что ![]() есть серия с собственным значением
есть серия с собственным значением ![]() ;
; ![]() есть серия с собственным значением
есть серия с собственным значением ![]() ; и т.д. В силу предложения В) каждой из серий соответствует система решений, так что мы можем выписать следующие решения уравнения (10):
; и т.д. В силу предложения В) каждой из серий соответствует система решений, так что мы можем выписать следующие решения уравнения (10):
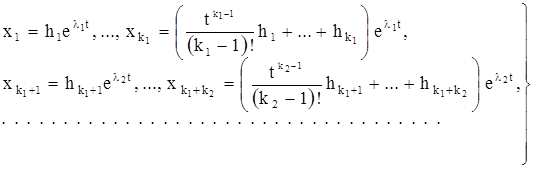 (11)
(11)
Оказывается, что формула
![]() (12)
(12)
где ![]() – константы, всегда дает решение уравнения (10) и что каждое решение уравнения (10) описывается формулой (12).
– константы, всегда дает решение уравнения (10) и что каждое решение уравнения (10) описывается формулой (12).
Доказательство. Так как функции ![]() являются решениями уравнения (10) (см. В)), то в силу предложения А) §4 формула (12) всегда дает решение уравнения (10). Покажем, что всякое решение уравнения (10) при надлежащем подборе констант
являются решениями уравнения (10) (см. В)), то в силу предложения А) §4 формула (12) всегда дает решение уравнения (10). Покажем, что всякое решение уравнения (10) при надлежащем подборе констант ![]() записывается в виде (12). Пусть
записывается в виде (12). Пусть ![]() - произвольное решение уравнения (10). В силу теоремы 3 решение
- произвольное решение уравнения (10). В силу теоремы 3 решение ![]() можно считать заданным на всей прямой
можно считать заданным на всей прямой ![]() , и потому вектор
, и потому вектор ![]() определен. Разложим этот вектор по базису
определен. Разложим этот вектор по базису ![]() :
:
![]()
Если теперь подставить найденные константы ![]() в соотношение (12), то мы получим решение
в соотношение (12), то мы получим решение ![]() , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям
![]()
(см. (9)). Таким образом, решения ![]() и
и ![]() имеют общие начальные значения и потому совпадают.
имеют общие начальные значения и потому совпадают.
Итак, теорема 9 доказана.
Теперь нам осталось выделить из решений, заданных формулой (12), действительные решения в случае, когда матрица ![]() действительна. Делается это совершенно так же, как и в случае простых корней характеристического уравнения.
действительна. Делается это совершенно так же, как и в случае простых корней характеристического уравнения.
§ 10. Автономные системы дифференциальных уравнений и их фазовые пространства
Здесь будет дана геометрическая интерпретация автономной системы уравнений в виде фазового пространства этой системы. Эта интерпретация существенно отличается от геометрической интерпретации системы уравнений, указанной в §§ 1, 2 и правильнее должна называться не геометрической, а кинематической, так как в этой интерпретации каждому решению системы уравнений ставится в соответствие не кривая в пространстве, а движение точки по кривой. Кинематическая интерпретация (фазовое пространство) в некоторых отношениях более выразительна, чем геометрическая (система интегральных кривых).
Автономные системы
Система обыкновенных дифференциальных уравнений называется автономной, если в нее явно не входит независимое переменное (или, как мы будем говорить, время) t. Это значит, что закон изменения неизвестных функций, описываемый системой уравнений не меняется с течением времени, как это обычно и бывает с физическими законами. Очень легко доказывается, что если
![]()
есть решение некоторой автономной системы уравнений, то
![]()
где с — константа, также есть решение той же автономной системы уравнений. Проведем доказательство этого факта на примере нормальной автономной системы уравнений,
А) Пусть
![]() (1)
(1)
- автономная нормальная система уравнений порядка n и
![]()
- векторная ее запись. Автономность системы (1) заключается в том, что функции ![]() являются функциями переменных
являются функциями переменных ![]() и не зависят от времени t. Относительно функций
и не зависят от времени t. Относительно функций ![]() мы будем предполагать, что они определены на некотором открытом множестве
мы будем предполагать, что они определены на некотором открытом множестве ![]() пространства размерности n, где координатами точки являются переменные
пространства размерности n, где координатами точки являются переменные ![]() . Мы будем предполагать, что функции
. Мы будем предполагать, что функции ![]() и их частные производные первого порядка непрерывны на множестве
и их частные производные первого порядка непрерывны на множестве ![]() . Оказывается, что если
. Оказывается, что если
![]() (2)
(2)
решение уравнения (1), то
![]() (3)
(3)
также есть решение системы (1).
Из правила дифференцирования сложной функции вытекает соотношение
![]() (4)
(4)
Действительно,
Докажем теперь, что (3) есть решение системы (1). Так как (2) есть решение, то мы имеем тождества
![]()
Заменяя в этих тождества t через t + c, мы получаем:
![]()
Из этого в силу (4) и (3) вытекает
![]()
Перейдем теперь к кинематической интерпретации решений системы (1). Формально речь будет идти об интерпретации в n – мерном пространстве, но для наглядности разумно представлять себе случай плоскости (n = 2).
Б) Каждому решению
![]() (5)
(5)
автономной системы (1) поставим в соответствие движение точки в n-мерном пространстве, задаваемое уравнениями (5), где ![]() — координаты точки в пространстве, а t — время. В процессе своего движения точка описывает некоторую кривую — траекторию движения. Если сопоставить решению (5) не процесс движения, а траекторию движения точки, то мы получим менее полное представление о решении, поэтому желательно на траектории указать хотя бы направление движения. Оказывается, что если наряду с решением (5) имеется другое решение
— координаты точки в пространстве, а t — время. В процессе своего движения точка описывает некоторую кривую — траекторию движения. Если сопоставить решению (5) не процесс движения, а траекторию движения точки, то мы получим менее полное представление о решении, поэтому желательно на траектории указать хотя бы направление движения. Оказывается, что если наряду с решением (5) имеется другое решение
![]() (6)
(6)
то траектории, соответствующие этим решениям, либо не пересекаются в пространстве, либо совпадают. Именно, если траектории имеют хотя бы одну общую точку, т. е.
![]() (7)
(7)
то
![]() где
где ![]() (8)
(8)
Последние равенства показывают, что траектории, описываемые первым и вторым решениями, совпадают между собой, но первое решение описывает ту же самую траекторию, что и второе, с «запозданием» на время с. Если точка, соответствующая первому решению, достигла некоторого положения на траектории в момент времени t + c, то точка, соответствующая второму решению, уже побывала в том положении в момент времени t.
Для того чтобы вывести из равенства (7) тождество (8), рассмотрим наряду с решением (5) решение
![]() (9)
(9)
(см. А)). Из равенства (7) при ![]() следует равенство
следует равенство
![]()
Таким образом, решения (6) и (9) системы (1) имеют общие начальные условия (а именно, значения в момент времени ![]() ) и потому в силу теоремы единственности совпадают, так что мы имеем:
) и потому в силу теоремы единственности совпадают, так что мы имеем:
![]()
Положения равновесия и замкнутые траектории
Поставим вопрос о том, может ли траектория, изображающая решение системы, пересекать себя.
В) Пусть
![]() (10)
(10)
некоторое решение системы (1). Допустим, что имеет место равенство
![]() (11)
(11)
где числа ![]() и
и ![]() , конечно, принадлежат интервалу
, конечно, принадлежат интервалу ![]() определения решения (10). Оказывается, что при этом условии решение (10) может быть продолжено на весь бесконечный интервал
определения решения (10). Оказывается, что при этом условии решение (10) может быть продолжено на весь бесконечный интервал ![]() . Поэтому мы сразу будем считать, что само решение (10) определено на этом интервале
. Поэтому мы сразу будем считать, что само решение (10) определено на этом интервале ![]() . Оказывается далее, что возможны два следующих взаимно исключающих случая.
. Оказывается далее, что возможны два следующих взаимно исключающих случая.
1) Для всех значений t имеет место равенство
![]()
где ![]() есть точка множества
есть точка множества ![]() , не зависящая от t. Таким образом, в этом случае точка
, не зависящая от t. Таким образом, в этом случае точка ![]() в действительности не движется при изменении t, а стоит на месте. Само решение (10) и точка
в действительности не движется при изменении t, а стоит на месте. Само решение (10) и точка ![]() в этом случае называются положением равновесия системы (1).
в этом случае называются положением равновесия системы (1).
2) Существует такое положительное число Т, что при произвольном t имеют место равенства
![]()
но при ![]() хотя бы для одного
хотя бы для одного ![]() имеет место неравенство
имеет место неравенство
![]()
В этом случае решение (10) называется периодическим с периодом Т, а траектория, описываемая решением (10), называется замкнутой траекторией, или циклом.
Докажем предложение В). Как было отмечено в предложении Б) из равенств (11) следуют тождества
![]() (12)
(12)
При этом функции ![]() также представляют решение системы (1) (см. А)). Это решение и первоначальное решение (10) совпадают там, где они оба определены (теорема 2). Если объединить эти два решения, мы получим новое решение с большим интервалом существования, чем исходное, а именно, с интервалом
также представляют решение системы (1) (см. А)). Это решение и первоначальное решение (10) совпадают там, где они оба определены (теорема 2). Если объединить эти два решения, мы получим новое решение с большим интервалом существования, чем исходное, а именно, с интервалом ![]() при с>0 и
при с>0 и ![]() при с<0. Так как
при с<0. Так как ![]() и
и ![]() равноправны, то знак величины с можно изменить, так что решение можно продолжить, на интервал
равноправны, то знак величины с можно изменить, так что решение можно продолжить, на интервал ![]() . Так как, кроме того, для продолженного решения равенство (11) по-прежнему выполнено, то к нему опять можно применить указанный способ расширения интервала существования, и потому мы можем продолжить решение (10) на всю бесконечную прямую с сохранением для него тождества (12).
. Так как, кроме того, для продолженного решения равенство (11) по-прежнему выполнено, то к нему опять можно применить указанный способ расширения интервала существования, и потому мы можем продолжить решение (10) на всю бесконечную прямую с сохранением для него тождества (12).
Каждое число с, для которого выполнено тождество (12), будем называть периодом решения (10); множество всех периодов решения (10) обозначим через F. Множество F есть некоторое множество чисел. Установим некоторые его свойства. Заменяя в соотношении (12) t через t - с, получаем ![]() . Таким образом, если с есть период, то — с также есть период. Допустим, что
. Таким образом, если с есть период, то — с также есть период. Допустим, что ![]() и
и ![]() — периоды, т. е.
— периоды, т. е.
![]()
Тогда
![]()
Таким образом, если ![]() и
и ![]() суть периоды, то
суть периоды, то ![]() также есть период. Допустим, что
также есть период. Допустим, что ![]() есть последовательность периодов, сходящаяся к некоторому числу
есть последовательность периодов, сходящаяся к некоторому числу ![]() ; тогда мы имеем
; тогда мы имеем
![]()
Так как функции ![]() непрерывны, то при
непрерывны, то при ![]() мы получаем:
мы получаем:
![]()
т.е. мы видим, что ![]() также есть период, так что множество F замкнуто.
также есть период, так что множество F замкнуто.
Так как число с в равенстве (12) отлично от нуля ![]() , то множество F содержит числа, отличные от нуля. Из установленных свойств множества F легко выводится, что для него есть только две возможности: 1) множество F совпадает с множеством всех действительных чисел; 2) в множестве F имеется минимальное положительное число Т, и тогда F состоит из всех целочисленных кратных числа Т. Докажем, что действительно имеются только эти две возможности. Так как множество F вместе с каждым числом с содержит число – с и так как в F имеются числа, отличные от нуля, то в F имеются положительные числа.
, то множество F содержит числа, отличные от нуля. Из установленных свойств множества F легко выводится, что для него есть только две возможности: 1) множество F совпадает с множеством всех действительных чисел; 2) в множестве F имеется минимальное положительное число Т, и тогда F состоит из всех целочисленных кратных числа Т. Докажем, что действительно имеются только эти две возможности. Так как множество F вместе с каждым числом с содержит число – с и так как в F имеются числа, отличные от нуля, то в F имеются положительные числа.
Допустим, что в множестве F нет наименьшего положительного числа, т. е. что для произвольного положительного числа ![]() имеется положительный период с<
имеется положительный период с<![]() . Из доказанных свойств множества F следует (так как с есть период), что все числа mc, где m — целое, также являются периодами. Так как с<
. Из доказанных свойств множества F следует (так как с есть период), что все числа mc, где m — целое, также являются периодами. Так как с<![]() , то для произвольного действительного числа
, то для произвольного действительного числа ![]() можно подобрать такое целое m, что
можно подобрать такое целое m, что ![]() . Таким образом, произвольное число
. Таким образом, произвольное число ![]() является предельным для множества F, и потому, ввиду замкнутости множества F, это множество совпадает с множеством всех действительных чисел.
является предельным для множества F, и потому, ввиду замкнутости множества F, это множество совпадает с множеством всех действительных чисел.
Допустим теперь, что F не есть множество всех действительных чисел. В силу доказанного, в F имеется тогда наименьшее положительное число Т. Пусть с — произвольный период. Можно тогда выбрать такое целое число m, что ![]() . Допустим, что
. Допустим, что ![]() ; тогда
; тогда ![]() есть отличный от нуля период, а это невозможно, так как
есть отличный от нуля период, а это невозможно, так как ![]() , что противоречит минимальности числа Т. Итак, доказано, что каждое число с из F может быть записано в виде c = mТ, где m — целое число.
, что противоречит минимальности числа Т. Итак, доказано, что каждое число с из F может быть записано в виде c = mТ, где m — целое число.
Теперь уже легко проверить, что если F есть множество всех действительных чисел, то имеет место случай 1), а если F не есть множество действительных чисел, то имеет место случай 2). Таким образом, предложение В) доказано.
Кратко предложение В) можно сформулировать, сказав, что имеется три сорта траекторий: 1) положение равновесия; 2) периодические траектории (циклы); 3) траектории без самопересечений. Естественно считать, что последний случай является «наиболее общим».
Из теоремы 2 следует, что через каждую точку области ![]() задания системы (1) проходит траектория, изображающая решение системы.
задания системы (1) проходит траектория, изображающая решение системы.
Таким образом, вся область ![]() заполнена траекториями, причем, согласно Б), траектории эти попарно не пересекаются. Среди всех траекторий особо выделяются самопересекающиеся, которые являются либо положениями равновесия, либо циклами. Эти два сорта траекторий имеют весьма важное значение.
заполнена траекториями, причем, согласно Б), траектории эти попарно не пересекаются. Среди всех траекторий особо выделяются самопересекающиеся, которые являются либо положениями равновесия, либо циклами. Эти два сорта траекторий имеют весьма важное значение.
Такова кинематическая интерпретация решений автономной системы уравнений. Сама система уравнений также допускает геометрическую интерпретацию.
Фазовые пространства
Г) Поскольку автономная система уравнений (1) определена на открытом множестве ![]() , каждой точке
, каждой точке ![]() множества
множества ![]() поставлена в соответствие последовательность из n чисел, именно последовательность:
поставлена в соответствие последовательность из n чисел, именно последовательность:
![]()
Эти числа можно рассматривать как компоненты вектора ![]() , проведенного в n-мерном пространстве и выходящего из точки
, проведенного в n-мерном пространстве и выходящего из точки ![]() . Таким образом, автономной системе ставится в соответствие геометрический образ — векторное поле, заданное на открытом множестве
. Таким образом, автономной системе ставится в соответствие геометрический образ — векторное поле, заданное на открытом множестве ![]() . В каждой точке
. В каждой точке ![]() множества
множества ![]() определен вектор
определен вектор ![]() , выходящий из этой точки. Связь между геометрической интерпретацией решений и геометрической интерпретацией самой системы уравнений заключается в следующем. Пусть
, выходящий из этой точки. Связь между геометрической интерпретацией решений и геометрической интерпретацией самой системы уравнений заключается в следующем. Пусть ![]() - произвольная точка множества
- произвольная точка множества ![]() . В силу геометрической интерпретации системы уравнений этой точке поставлен в соответствие выходящий из нее вектор
. В силу геометрической интерпретации системы уравнений этой точке поставлен в соответствие выходящий из нее вектор ![]() . Далее, в силу теоремы 2 существует решение
. Далее, в силу теоремы 2 существует решение ![]() системы (1), удовлетворяющее начальным условиям
системы (1), удовлетворяющее начальным условиям
![]()
В силу кинематической интерпретации решению ![]() соответствует в пространстве движение точки, описывающее траекторию, причем в момент времени
соответствует в пространстве движение точки, описывающее траекторию, причем в момент времени ![]() движущая точка проходит через положение
движущая точка проходит через положение ![]() в пространстве. Оказывается, что векторная скорость точки, описывающей решение
в пространстве. Оказывается, что векторная скорость точки, описывающей решение ![]() , в момент ее прохождения через положение
, в момент ее прохождения через положение ![]() совпадает с вектором
совпадает с вектором ![]() . Именно это совпадение и выражается системой уравнений (1) при
. Именно это совпадение и выражается системой уравнений (1) при
![]()
Пространство размерности n, в котором интерпретируются решения автономной системы (1) в виде траекторий и сама автономная система (1) в виде векторного поля, называется фазовым пространством системы (1). Траектории называются фазовыми траекториями, векторы ![]() называются фазовыми скоростями. Связь между обеими интерпретациями заключается в том, что скорость движения точки по траектории в каждый момент времени совпадает с фазовой скоростью, заданной в том месте пространства, где в этот момент находится движущаяся точка.
называются фазовыми скоростями. Связь между обеими интерпретациями заключается в том, что скорость движения точки по траектории в каждый момент времени совпадает с фазовой скоростью, заданной в том месте пространства, где в этот момент находится движущаяся точка.
Рассмотрим теперь положения равновесия с точки зрения фазовых скоростей.
Д) Для того чтобы точка ![]() множества
множества ![]() была положением равновесия системы (1), т. е. чтобы имелось решение
была положением равновесия системы (1), т. е. чтобы имелось решение ![]() системы, для которого
системы, для которого
![]() (13)
(13)
необходимо и достаточно, чтобы фазовая скорость ![]() в точке
в точке ![]() была равна нулю. Таким образом, для отыскания всех положений равновесия системы (1) нужно решить систему уравнений
была равна нулю. Таким образом, для отыскания всех положений равновесия системы (1) нужно решить систему уравнений
![]()
Эта система представляет собой не систему дифференциальных уравнений, а, как говорят, систему конечных уравнений (производные в нее не входят).
Для доказательства утверждения Д) допустим, что ![]() есть положение равновесия, т. е. что имеется решение
есть положение равновесия, т. е. что имеется решение![]() , для которого выполнены соотношения (13), и подставим в систему (1) это решение. Так как производная постоянной равна нулю, то подстановка дает
, для которого выполнены соотношения (13), и подставим в систему (1) это решение. Так как производная постоянной равна нулю, то подстановка дает
![]()
Таким образом, вектор ![]() фазовой скорости действительно обращается в нуль, в точке
фазовой скорости действительно обращается в нуль, в точке ![]() . Допустим, что, обратно, вектор
. Допустим, что, обратно, вектор ![]() фазовой скорости обращается в нуль в точке
фазовой скорости обращается в нуль в точке ![]() , т. е. что
, т. е. что ![]() и покажем, что в этом случае равенства (13) определяют решение системы (1). Подстановка дает
и покажем, что в этом случае равенства (13) определяют решение системы (1). Подстановка дает
![]()
равенства эти выполнены, так как слева стоит производная константы, а справа — нуль.
Е) Геометрическая интерпретация решения (2) системы уравнений (1), указанная в §2, ставит в соответствие этому решению кривую К в (n + 1)-мерном пространстве переменных ![]() , определяемую системой уравнений (2). Здесь t является одной из координат в пространстве R. Переход к интерпретации в n-мерном фазовом пространстве S переменных
, определяемую системой уравнений (2). Здесь t является одной из координат в пространстве R. Переход к интерпретации в n-мерном фазовом пространстве S переменных ![]() заключается в том, что мы перестаем считать величину t координатой точки, а считаем ее параметром. Таким образом, фазовая траектория L получается из кривой К в результате проектирования пространства R на пространство S в направлении оси t.
заключается в том, что мы перестаем считать величину t координатой точки, а считаем ее параметром. Таким образом, фазовая траектория L получается из кривой К в результате проектирования пространства R на пространство S в направлении оси t.
Геометрическую наглядность это проектирование приобретает при n = 2. В этом случае пространство R трехмерно, а пространство S представляет собой плоскость (см. пример 4).
Примеры
1. Рассмотрим автономное дифференциальное уравнение
![]() (14)
(14)
первого порядка, правая часть которого непрерывна и имеет непрерывную производную на всей прямой Р изменения переменного х. Предположим дополнительно, что нули функции f(x) или, что то же самое, положения равновесия уравнения (14), не имеют предельных точек. В этом предположении положения равновесия разбивают прямую Р на систему ![]() интервалов. Каждый интервал (a, b) системы
интервалов. Каждый интервал (a, b) системы ![]() обладает тем свойством, что на нем функция f (x) не обращается в нуль, а каждый конец a или b его является либо нулем функции f (x), либо равен
обладает тем свойством, что на нем функция f (x) не обращается в нуль, а каждый конец a или b его является либо нулем функции f (x), либо равен ![]() . Таким образом, система
. Таким образом, система ![]() состоит из конечного или счетного числа конечных интервалов и не более чем двух полубесконечных интервалов или же содержит только один бесконечный в обе стороны интервал
состоит из конечного или счетного числа конечных интервалов и не более чем двух полубесконечных интервалов или же содержит только один бесконечный в обе стороны интервал ![]() . Пусть (a, b) - некоторый интервал системы
. Пусть (a, b) - некоторый интервал системы ![]() ,
, ![]() - точка этого интервала и
- точка этого интервала и ![]() ,
, ![]() , - непродолжаемое решение уравнения (14) с начальными значениями 0,
, - непродолжаемое решение уравнения (14) с начальными значениями 0, ![]() . Допустим для определенности, что
. Допустим для определенности, что ![]() ; тогда оказывается, что
; тогда оказывается, что
![]() при
при ![]() , (15)
, (15)
![]() (16)
(16)
Далее, если число а, или соответственно b, конечно, то число ![]() или соответственно
или соответственно ![]() , бесконечно. Таким образом (рис. 3), каждый интервал (a, b) представляет собой одну-единственную фазовую траекторию уравнения (14).
, бесконечно. Таким образом (рис. 3), каждый интервал (a, b) представляет собой одну-единственную фазовую траекторию уравнения (14).
Докажем соотношения (15), (16). Из предположения ![]() следует, что на интервале (a, b) функция f (x) положительна и потому каждая точка этого интервала, описывая фазовую траекторию, движется слева направо. Таким образом, при возрастающем t точка
следует, что на интервале (a, b) функция f (x) положительна и потому каждая точка этого интервала, описывая фазовую траекторию, движется слева направо. Таким образом, при возрастающем t точка ![]() может покинуть интервал (a, b), лишь перейдя его правый конец b. Допустим, что это происходит при некотором
может покинуть интервал (a, b), лишь перейдя его правый конец b. Допустим, что это происходит при некотором ![]() ; тогда при
; тогда при ![]() имеем
имеем ![]() , а это значит, что две различные траектории
, а это значит, что две различные траектории ![]() и x = b пересекаются, что невозможно. Точно так же доказывается, что точка
и x = b пересекаются, что невозможно. Точно так же доказывается, что точка ![]() не может покинуть интервал (a,b) при убывающем t. Таким образом, соотношение (15) доказано.
не может покинуть интервал (a,b) при убывающем t. Таким образом, соотношение (15) доказано.
Допустим теперь, что ![]() и пусть
и пусть ![]() — решение уравнения (14) с начальными значениями 0, с. Так как f (с)> 0, то при некотором отрицательном значении
— решение уравнения (14) с начальными значениями 0, с. Так как f (с)> 0, то при некотором отрицательном значении ![]() имеем
имеем ![]() , а это значит, что две различные траектории
, а это значит, что две различные траектории ![]() и
и ![]() пересекаются, что невозможно. Таким образом, доказано, что
пересекаются, что невозможно. Таким образом, доказано, что ![]() . Точно так же доказывается и соотношение
. Точно так же доказывается и соотношение ![]() .
.
Допустим, наконец, что ![]() , и покажем, что тогда
, и покажем, что тогда ![]() . Допустим противоположное, именно, что
. Допустим противоположное, именно, что ![]() . Определим тогда функцию
. Определим тогда функцию ![]() , положив
, положив ![]() при
при ![]() и
и ![]() при
при ![]() . Очевидно, что функция
. Очевидно, что функция ![]() непрерывна и удовлетворяет уравнению (14), а это невозможно, так как тогда пересекаются две различные траектории
непрерывна и удовлетворяет уравнению (14), а это невозможно, так как тогда пересекаются две различные траектории ![]() и
и ![]() . Полученное противоречие показывает, что
. Полученное противоречие показывает, что ![]() . Точно так же доказывается, что при
. Точно так же доказывается, что при ![]() имеем
имеем ![]() .
.
Пусть b — произвольное положение равновесия уравнения (14), а (a, b) и (b, c) — два интервала системы ![]() , примыкающие к нему (соответственно слева и справа). Каждый из интервалов (a, b), (b, c) представляет собой одну траекторию. Если обе точки, описывающие траектории (a, b) и (b, c), приближаются (при возрастании t) к положению равновесия b, то положение равновесия b называется устойчивым (рис. 4, а). Если обе точки, описывающие траектории (a, b) и (b, c), удаляются от точки b, то положение равновесия b называется неустойчивым (рис 4, б). Если по одной из траекторий точка приближается, а по другой удаляется, то положение равновесия b называется полуустойчивым (рис. 4, в). Для того чтобы положение равновесия b было устойчивым, необходимо и достаточно, чтобы функция f (x) была положительна на интервале (a, b) и отрицательна на интервале (b, c). Для того чтобы положение равновесия b было неустойчивым, необходимо и достаточно, чтобы функция f (х) была отрицательна на интервале (a, b) и положительна на интервале (b, c). Для того чтобы положение равновесия b было полуустойчиво, необходимо и достаточно, чтобы функция f (х) имела один и тот же знак на обоих интервалах (a, b) и (b,c).
, примыкающие к нему (соответственно слева и справа). Каждый из интервалов (a, b), (b, c) представляет собой одну траекторию. Если обе точки, описывающие траектории (a, b) и (b, c), приближаются (при возрастании t) к положению равновесия b, то положение равновесия b называется устойчивым (рис. 4, а). Если обе точки, описывающие траектории (a, b) и (b, c), удаляются от точки b, то положение равновесия b называется неустойчивым (рис 4, б). Если по одной из траекторий точка приближается, а по другой удаляется, то положение равновесия b называется полуустойчивым (рис. 4, в). Для того чтобы положение равновесия b было устойчивым, необходимо и достаточно, чтобы функция f (x) была положительна на интервале (a, b) и отрицательна на интервале (b, c). Для того чтобы положение равновесия b было неустойчивым, необходимо и достаточно, чтобы функция f (х) была отрицательна на интервале (a, b) и положительна на интервале (b, c). Для того чтобы положение равновесия b было полуустойчиво, необходимо и достаточно, чтобы функция f (х) имела один и тот же знак на обоих интервалах (a, b) и (b,c).
Допустим, что ![]() ; тогда знак функции f (х) вблизи точки b совпадает со знаком величины
; тогда знак функции f (х) вблизи точки b совпадает со знаком величины ![]() . Отсюда следует, что при
. Отсюда следует, что при ![]() положение равновесия b уравнения (14) устойчиво, а при
положение равновесия b уравнения (14) устойчиво, а при ![]() оно неустойчиво.
оно неустойчиво.
2. Рассмотрим уравнение
![]() (17)
(17)
где f (x) есть периодическая функция с непрерывной первой производной. Для определенности будем считать, что период ее равен ![]() . Все сказанное в примере 1 относительно уравнения (14) остается правильным и для уравнения (17), так как уравнение (17) является частным случаем уравнения (14). Однако, для того чтобы учесть специфику уравнения (17) (периодичность функций f (x)) разумно считать, что фазовым пространством уравнения (17) является не прямая, а окружность К радиуса единица, на которой выбрано некоторое начало отсчета 0 и направление обхода (например, против часовой стрелки). Каждому числу х поставим в соответствие точку
. Все сказанное в примере 1 относительно уравнения (14) остается правильным и для уравнения (17), так как уравнение (17) является частным случаем уравнения (14). Однако, для того чтобы учесть специфику уравнения (17) (периодичность функций f (x)) разумно считать, что фазовым пространством уравнения (17) является не прямая, а окружность К радиуса единица, на которой выбрано некоторое начало отсчета 0 и направление обхода (например, против часовой стрелки). Каждому числу х поставим в соответствие точку ![]() окружности К, отложив от начала отсчета против часовой стрелки дугу длины х (рис. 5). При этом всем числам
окружности К, отложив от начала отсчета против часовой стрелки дугу длины х (рис. 5). При этом всем числам ![]() (k – целое число) будет соответствовать на окружности одна и та же точка
(k – целое число) будет соответствовать на окружности одна и та же точка ![]() . Так как f(
. Так как f(![]() ) = f(x), то можно положить f(
) = f(x), то можно положить f(![]() ) = f(x), и функция f оказывается заданной на окружности К.
) = f(x), и функция f оказывается заданной на окружности К.
Уравнение (17) задает теперь движение точки ![]() по окружности К. Если x(t) есть некоторое решение уравнения (17), то соответствующая числу x(t) точка
по окружности К. Если x(t) есть некоторое решение уравнения (17), то соответствующая числу x(t) точка ![]() (t) движется по окружности К. Если
(t) движется по окружности К. Если ![]() — такая точка на окружности К, что f (
— такая точка на окружности К, что f (![]() ) = 0, то существует такое решение x(t) уравнения (17), что
) = 0, то существует такое решение x(t) уравнения (17), что ![]() , и
, и ![]() есть положение равновесия уравнения (17). Допустим для простоты, что положения равновесия уравнения (17) на окружности К не имеют предельных точек: тогда их имеется лишь конечное число или нет вовсе (рис. 6). Положения равновесия разбивают окружность на конечную систему
есть положение равновесия уравнения (17). Допустим для простоты, что положения равновесия уравнения (17) на окружности К не имеют предельных точек: тогда их имеется лишь конечное число или нет вовсе (рис. 6). Положения равновесия разбивают окружность на конечную систему ![]() интервалов. Если положений равновесия вовсе нет, то система
интервалов. Если положений равновесия вовсе нет, то система ![]() содержит лишь один «интервал» (окружность). Если имеется лишь одно положение равновесия
содержит лишь один «интервал» (окружность). Если имеется лишь одно положение равновесия ![]() , то система
, то система ![]() также содержит лишь один интервал, состоящий из всех точек окружности К за исключением точки
также содержит лишь один интервал, состоящий из всех точек окружности К за исключением точки ![]() . В первом случае интервал вовсе не имеет концов, во втором оба его конца совпадают. Пусть I — некоторый интервал системы
. В первом случае интервал вовсе не имеет концов, во втором оба его конца совпадают. Пусть I — некоторый интервал системы ![]() и x(t) — некоторое решение уравнения (17) с начальными значениями 0,
и x(t) — некоторое решение уравнения (17) с начальными значениями 0, ![]() , где
, где ![]() есть точка, интервала I. Решение x(t) всегда определено для всех значении t, и точка
есть точка, интервала I. Решение x(t) всегда определено для всех значении t, и точка ![]() принадлежит интервалу I. Если интервал I имеет концы (один или два), то точка пробегает интервал I и определенном направлении, причем каждая точка интервала I проходится решением
принадлежит интервалу I. Если интервал I имеет концы (один или два), то точка пробегает интервал I и определенном направлении, причем каждая точка интервала I проходится решением ![]() один раз. Если интервал I совпадает со всей окружностью, то, отправившись из положения
один раз. Если интервал I совпадает со всей окружностью, то, отправившись из положения ![]() , точка через некоторое время Т вернется в нее, так что
, точка через некоторое время Т вернется в нее, так что ![]() . В этом случае
. В этом случае ![]() периодически зависит от числа t с периодом Т. Соответствующее движению
периодически зависит от числа t с периодом Т. Соответствующее движению ![]() числовое решение x(t) уравнения (17) удовлетворяет условию
числовое решение x(t) уравнения (17) удовлетворяет условию
![]()
Из этого примера видно, что фазовым пространством системы уравнений не всегда целесообразно считать эвклидово координатное пространство, а иногда приходится считать более сложное геометрическое образование. Ниже, в примере 3, мы столкнемся с этим обстоятельством в более сложной обстановке, чем в этом примере.
3. Рассмотрим систему уравнений
![]() (18)
(18)
где функции ![]() являются периодическими относительно обоих аргументов с периодами
являются периодическими относительно обоих аргументов с периодами ![]() :
:
![]()
Как всегда, будем предполагать, что функции ![]() непрерывны и имеют непрерывные частные производные первого порядка. Ввиду периодичности функций
непрерывны и имеют непрерывные частные производные первого порядка. Ввиду периодичности функций ![]() разумно считать, что фазовым пространством системы (18) является не плоскость, а более сложное геометрическое образование, именно, поверхность тора или, как говорят, тор (рис. 7). Опишем эту поверхность.
разумно считать, что фазовым пространством системы (18) является не плоскость, а более сложное геометрическое образование, именно, поверхность тора или, как говорят, тор (рис. 7). Опишем эту поверхность.
Рис. 7.
В трехмерном эвклидовом пространстве с декартовыми координатами х, у, z выберем в плоскости х, z окружность K радиуса единица с центром в точке (2, 0, 0). Примем на этой окружности за начало отсчета точку с координатами (3, 0, 0). Тогда каждому числу х будет поставлена в соответствие точка ![]() окружности К (см. пример 2). Будем теперь вращать плоскость (х, z) в пространстве (х, у, z) вокруг оси z. Описываемая при этом вращении окружностью К поверхность Р представляет собой тор. Пусть
окружности К (см. пример 2). Будем теперь вращать плоскость (х, z) в пространстве (х, у, z) вокруг оси z. Описываемая при этом вращении окружностью К поверхность Р представляет собой тор. Пусть ![]() — некоторая точка окружности К. В результате поворота плоскости (х, z) на угол
— некоторая точка окружности К. В результате поворота плоскости (х, z) на угол ![]() , исчисляемый в радианах, точка
, исчисляемый в радианах, точка ![]() перейдет в некоторую точку р, тора Р (рис. 7). Если сделать поворот не на угол
перейдет в некоторую точку р, тора Р (рис. 7). Если сделать поворот не на угол ![]() , а на угол
, а на угол ![]() , то мы придем к той же точке р тора Р. Таким образом, точка р тора Р однозначно определяется двумя циклическими координатами
, то мы придем к той же точке р тора Р. Таким образом, точка р тора Р однозначно определяется двумя циклическими координатами ![]() , и каждой паре циклических координат
, и каждой паре циклических координат ![]() соответствует на торе одна вполне определенная точка. Мы видим, таким образом, что функции
соответствует на торе одна вполне определенная точка. Мы видим, таким образом, что функции ![]() можно считать заданными не на плоскости, а на поверхности тора Р:
можно считать заданными не на плоскости, а на поверхности тора Р:
![]()
Пусть теперь ![]() — некоторое решение системы (18). Ставя в соответствие каждому из чисел
— некоторое решение системы (18). Ставя в соответствие каждому из чисел ![]() и
и ![]() циклические координаты
циклические координаты ![]() и
и ![]() , мы получаем точку
, мы получаем точку ![]() тора Р. Таким образом, каждое решении
тора Р. Таким образом, каждое решении ![]() системы (18) может быть изображено движением точки по тору, причем закон движения в каждый момент времени определяется той точкой
системы (18) может быть изображено движением точки по тору, причем закон движения в каждый момент времени определяется той точкой ![]() тора, через которую траектория в этот момент проходит. Это объясняется тем, что функции
тора, через которую траектория в этот момент проходит. Это объясняется тем, что функции ![]() заданы на торе. Таким образом, весь тор Р оказывается покрытым траекториями, каждые две из которых либо не пересекаются либо совпадают. В частности, если траектория пересекает самое себя, то она либо замкнута, либо является положением равновесия.
заданы на торе. Таким образом, весь тор Р оказывается покрытым траекториями, каждые две из которых либо не пересекаются либо совпадают. В частности, если траектория пересекает самое себя, то она либо замкнута, либо является положением равновесия.
Изображение, фазовых траекторий системы (18) не на плоскости, а на поверхности тора отражает специфическое свойство системы (18) (периодичность функций ![]() ) и удобно при ее изучении.
) и удобно при ее изучении.
4. Каждое решение автономной системы уравнений
![]()
записывается в виде:
![]() (19)
(19)
где r и ![]() — константы. Система уравнений (19) определяет в трехмерном пространстве R переменных t, х, у винтовую спираль при
— константы. Система уравнений (19) определяет в трехмерном пространстве R переменных t, х, у винтовую спираль при ![]() и прямую линию (именно, ось t) при r = 0.
и прямую линию (именно, ось t) при r = 0.
В фазовой плоскости S переменных х и у та же система уравнений (19) определяет окружность при ![]() и точку (положение равновесия) при r = 0. Переход от кривых в пространстве R к кривым плоскости S осуществляется проектированием в направлении оси t на координатную плоскость ху.
и точку (положение равновесия) при r = 0. Переход от кривых в пространстве R к кривым плоскости S осуществляется проектированием в направлении оси t на координатную плоскость ху.
5. Каждое решение неавтономной системы уравнений
![]()
записывается в виде:
![]() (20)
(20)
где a и b — константы. Из общей теории известно (единственность решения), что в трехмерном пространстве R переменных t, х, у две кривые, определяемые системой уравнении (20), либо не пересекаются, либо совпадают. Для того, чтобы получить проекцию кривой, определяемой системой (20), на плоскость S переменных х, у, следует из системы (20) исключить t. Производя это исключение, получаем:
![]()
Это уравнение определяет на плоскости ху параболу с осью, направленной вдоль положительной полуоси х и вершиной в точке (а, b). Две такие параболы: одна с вершиной в точке ![]() , а другая с вершиной в точке
, а другая с вершиной в точке ![]() — не пересекаются лишь в случае, если
— не пересекаются лишь в случае, если ![]() . Если же
. Если же ![]() , то соответствующие параболы пересекаются (в одной точке). Пересечение траекторий происходит потому, что исходная система дифференциальных уравнений неавтономна. Поэтому изображение решений на плоскости ху в случае неавтономной системы нецелесообразно.
, то соответствующие параболы пересекаются (в одной точке). Пересечение траекторий происходит потому, что исходная система дифференциальных уравнений неавтономна. Поэтому изображение решений на плоскости ху в случае неавтономной системы нецелесообразно.
§ 11. Фазовая плоскость линейной однородной системы с постоянными коэффициентами
Здесь будут построены фазовые траектории на фазовой плоскости системы
 (1)
(1)
или в векторной форме
![]() (2)
(2)
с постоянными действительными коэффициентами ![]() . При этом нам придется разобрать, несколько различных случаев, так как фазовая картина траекторий системы существенно зависит от значении коэффициентов.
. При этом нам придется разобрать, несколько различных случаев, так как фазовая картина траекторий системы существенно зависит от значении коэффициентов.
Следует заметить, что начало координат (точка (0, 0)) всегда является положением равновесия системы (1). Это положение равновесия тогда и только тогда является единственным, когда детерминант матрицы ![]() отличен от нуля, или, что то же, оба собственных значения этой матрицы отличны от нуля.
отличен от нуля, или, что то же, оба собственных значения этой матрицы отличны от нуля.
Допустим, что собственные значения матрицы А действительны, различны и отличны от нуля. Тогда, как это следует из результатов § 9 (теорема 8) произвольное действительное решение уравнения (2) можно записать в виде:
![]() (3)
(3)
Здесь ![]() и
и ![]() — действительные линейно независимые собственные векторы матрицы А;
— действительные линейно независимые собственные векторы матрицы А; ![]() и
и ![]() — его действительные собственные значения, а
— его действительные собственные значения, а ![]() и
и ![]() — действительные константы. Решение (3) разложим по базису
— действительные константы. Решение (3) разложим по базису ![]() , положив
, положив
![]() (4)
(4)
тогда мы будем иметь:
![]() (5)
(5)
Координаты ![]() на фазовой плоскости Р системы (1) вообще говоря, не являются прямоугольными, поэтому отобразим аффинно фазовую плоскость Р на вспомогательную плоскость Р* таким образом чтобы при этом векторы
на фазовой плоскости Р системы (1) вообще говоря, не являются прямоугольными, поэтому отобразим аффинно фазовую плоскость Р на вспомогательную плоскость Р* таким образом чтобы при этом векторы ![]() ,
, ![]() перешли во взаимно ортогональные единичные векторы плоскости Р*, направленные соответственно по оси абсцисс и оси ординат (рис. 8). Точка
перешли во взаимно ортогональные единичные векторы плоскости Р*, направленные соответственно по оси абсцисс и оси ординат (рис. 8). Точка ![]() плоскости Р перейдет при этом отображении в точку с декартовыми прямоугольными координатами
плоскости Р перейдет при этом отображении в точку с декартовыми прямоугольными координатами ![]() в плоскости Р*. Таким образом, траектория заданная, параметрическими уравнениями (5) а плоскости Р перейдет в траекторию (которую мы также назовем фазовой), заданную теми же уравнениями в прямоугольных координатах плоскости Р*. Мы начертим сперва траектории, заданные уравнениями (5) в плоскости Р*, и затем отобразим их обратно в плоскость Р.
в плоскости Р*. Таким образом, траектория заданная, параметрическими уравнениями (5) а плоскости Р перейдет в траекторию (которую мы также назовем фазовой), заданную теми же уравнениями в прямоугольных координатах плоскости Р*. Мы начертим сперва траектории, заданные уравнениями (5) в плоскости Р*, и затем отобразим их обратно в плоскость Р.


Рис. 8.
Наряду с фазовой траекторией (5) в плоскости Р* имеется траектория, задаваемая уравнениями
![]() (6)
(6)
а также траектория, задаваемая уравнениями
![]() (7)
(7)
Траектория (6) получается из траектории (5) зеркальным отражением относительно оси абсцисс, а траектория (7) — относительно оси ординат. Таким образом, указанные два зеркальных отображения оставляют картину траекторий на плоскости Р* инвариантной. Из этого видно, что если вычертить траектории в первом квадранте, то уже легко представить себе всю фазовую картину в плоскости Р*.
Отметим что при ![]() мы получаем движение точки, описывающее положение равновесия (0, 0). При
мы получаем движение точки, описывающее положение равновесия (0, 0). При ![]() получаем движение, описывающее положительную полуось абсцисс, при
получаем движение, описывающее положительную полуось абсцисс, при ![]() получаем движение, описывающее положительную полуось ординат. Если
получаем движение, описывающее положительную полуось ординат. Если ![]() , то движение, описывающее положительную полуось абсцисс, протекает в направлении к началу координат, если же
, то движение, описывающее положительную полуось абсцисс, протекает в направлении к началу координат, если же ![]() , то движение это имеет противоположное направление от начала координат. В первом случае точка движется, неограниченно приближаясь к началу координат, во второй — неограниченно удаляясь в бесконечность. То же справедливо и относительно движения, описывающего положительную полуось ординат. Если
, то движение это имеет противоположное направление от начала координат. В первом случае точка движется, неограниченно приближаясь к началу координат, во второй — неограниченно удаляясь в бесконечность. То же справедливо и относительно движения, описывающего положительную полуось ординат. Если ![]() и
и ![]() положительны, то движение точки протекает в первой четверти, не выходя на ее границу.
положительны, то движение точки протекает в первой четверти, не выходя на ее границу.
Дальнейшее, более детальное описание фазовой плоскости проведем отдельно для нескольких случаев - в зависимости от знаков чисел ![]() .
.
А) Узел. Допустим, что оба числа ![]() и
и ![]() отличны от нуля и имеют один знак, причем
отличны от нуля и имеют один знак, причем
![]() (8)
(8)
Разберем сперва случай, когда ![]() ,
, ![]() .
.
При этих предположениях движение по положительной полуоси абсцисс направлено к началу координат, точно так же, как движение по положительной полуоси ординат. Далее, движение по произвольной траектории внутри первого квадранта состоит в асимптотическом приближении точки к началу координат, причем траектория при этом касается оси абсцисс в начале координат. При t, стремящемся к ![]() , точка движется так, что абсцисса и ордината ее бесконечно возрастают, но возрастание ординаты сильнее, чем возрастание абсциссы, т. е. движение идет в направлении оси ординат. Эта фазовая картина называется устойчивом узлом (рис. 9, а). Если наряду с неравенством (8) выполнены неравенства
, точка движется так, что абсцисса и ордината ее бесконечно возрастают, но возрастание ординаты сильнее, чем возрастание абсциссы, т. е. движение идет в направлении оси ординат. Эта фазовая картина называется устойчивом узлом (рис. 9, а). Если наряду с неравенством (8) выполнены неравенства
![]()
то траектории остаются прежними, но движение по ним направлено в противоположном направлении. Мы имеем неустойчивый узел (рис. 9, б).

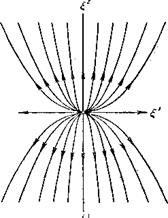
а) Рис. 9. б)
![]()
Б) Седло. Допустим, что числа ![]() и
и ![]() имеют противоположные знаки. Для определенности предположим, что
имеют противоположные знаки. Для определенности предположим, что ![]() . В этом случае движение по положительной полуоси абсцисс идет к началу координат, а движение по положительной полуоси ординат — от начала координат. Траектории, лежащие внутри первого квадранта, напоминают по своему виду гиперболы, а движения по ним происходят в направлении к началу вдоль оси абсцисс, и в направлении от начала вдоль оси ординат. Эта фазовая картина называется седлом (рис. 10).
. В этом случае движение по положительной полуоси абсцисс идет к началу координат, а движение по положительной полуоси ординат — от начала координат. Траектории, лежащие внутри первого квадранта, напоминают по своему виду гиперболы, а движения по ним происходят в направлении к началу вдоль оси абсцисс, и в направлении от начала вдоль оси ординат. Эта фазовая картина называется седлом (рис. 10).
Рисунки 9, а, б и 10 дают картину траекторий на вспомогательной фазовой плоскости Р*. Расположение траекторий на фазовой плоскости Р получается из этого с помощью аффинного преобразования и зависят от положения собственных векторов (см., например, рис. 11 и 12).
Рассмотрим теперь случай, когда собственные значения матрицы А комплексны. В этом случае они комплексно сопряжены и могут быть обозначены через ![]() и
и ![]() , причем
, причем ![]() . Собственные векторы матрицы А могут быть выбраны сопряженными, так что их можно обозначить через h и
. Собственные векторы матрицы А могут быть выбраны сопряженными, так что их можно обозначить через h и ![]() . Положим:
. Положим:
![]()
где ![]() и
и ![]() — действительные векторы. Векторы
— действительные векторы. Векторы ![]() и
и ![]() линейно независимы, так как в случае линейной зависимости между ними мы имели бы линейную зависимость между h и
линейно независимы, так как в случае линейной зависимости между ними мы имели бы линейную зависимость между h и ![]() . Итак, векторы
. Итак, векторы ![]() и
и ![]() можно принять, за базис фазовой плоскости Р уравнения (2).
можно принять, за базис фазовой плоскости Р уравнения (2).
Произвольное действительное решение уравнения (2) можно записать в виде:
![]() (9)
(9)
где с — комплексная константа. Пусть
![]()
тогда мы имеем:
![]()
Отобразим аффинно фазовую плоскость Р на вспомогательную плоскость Р* комплексного переменного ![]() так, чтобы вектор
так, чтобы вектор ![]() перешел в единицу, а вектор
перешел в единицу, а вектор ![]() - в i; тогда вектору
- в i; тогда вектору ![]() будет соответствовать комплексное число
будет соответствовать комплексное число ![]() . В силу этого отображения фазовая траектория (9) перейдет в фазовую траекторию на плоскости Р*, описываемую уравнением
. В силу этого отображения фазовая траектория (9) перейдет в фазовую траекторию на плоскости Р*, описываемую уравнением
![]() (10)
(10)
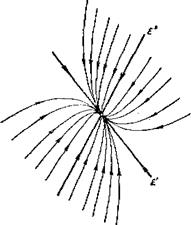

Рис. 11. Рис. 12.
В) Фокус и центр. Перепишем уравнение (10) в полярных координатах, положив
![]()
Таким образом, получаем:
![]()
это есть уравнение движения точки в плоскости Р*. При ![]() каждая траектория оказывается логарифмической спиралью. Соответствующая картина на плоскости Р называется фокусом. Если
каждая траектория оказывается логарифмической спиралью. Соответствующая картина на плоскости Р называется фокусом. Если ![]() , то точка при возрастании t асимптотически приближается к началу координат, описывая логарифмическую спираль. Это – устойчивый фокус (рис. 13, а). Если
, то точка при возрастании t асимптотически приближается к началу координат, описывая логарифмическую спираль. Это – устойчивый фокус (рис. 13, а). Если ![]() , то точка уходит от начала координат в бесконечность, и мы имеем неустойчивый фокус (рис. 13, б). Если число
, то точка уходит от начала координат в бесконечность, и мы имеем неустойчивый фокус (рис. 13, б). Если число ![]() равно нулю, то каждая фазовая траектория, кроме положения равновесия (0,0), замкнута, и мы имеем так называемый центр (рис. 14).
равно нулю, то каждая фазовая траектория, кроме положения равновесия (0,0), замкнута, и мы имеем так называемый центр (рис. 14).
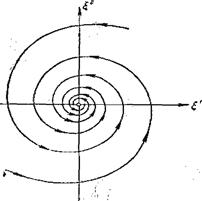

а) Рис. 13 б)
Рисунки 13 и 14 дают картину во вспомогательной фазовой плоскости; в плоскости Р картина аффинно искажается (см., например, рис. 15 и 16).
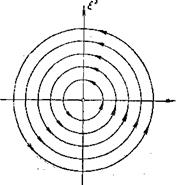
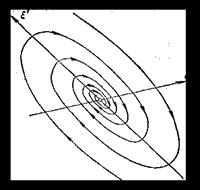
Рис. 14. Рис. 15.
![]()
Выше мы рассматривали так называемые невырожденные случаи: корни ![]() и
и ![]() различны и отличны от нуля. Малое изменение элементов матрицы
различны и отличны от нуля. Малое изменение элементов матрицы ![]() не меняет в этих предположениях общего характера поведения фазовых траекторий. Исключение составляет случай центра: при малом изменении элементов матрицы
не меняет в этих предположениях общего характера поведения фазовых траекторий. Исключение составляет случай центра: при малом изменении элементов матрицы ![]() равенство
равенство ![]() может нарушиться, и центр перейдет в устойчивый или неустойчивый фокус.
может нарушиться, и центр перейдет в устойчивый или неустойчивый фокус.
ГЛАВА III . теоремы существования
§ 12. Доказательство теоремы существования и единственности для одного уравнения
В этом параграфе будет дано доказательство сформулированной в § 1 теоремы 1 существования и единственности для одного уравнения первого порядка
![]() (1)
(1)
правая часть которого определена и непрерывна вместе со своей частной производной ![]() на некотором открытом множестве Г плоскости Р переменных t, х. Доказательство теоремы 2, приводимое в следующем параграфе, представляет собой усложнение доказательства теоремы 1 и содержит его как частный случай. Доказательство теорем 1 и 2 проводится методом последовательных приближений, принадлежащим Пикару и применяемым в анализе при доказательстве многих теорем существования. Этот метод является одновременно методом приближенного вычисления решения и потому имеет большую практическую ценность. В некоторых случаях метод последовательных приближений может быть истолкован как метод сжатых отображений.
на некотором открытом множестве Г плоскости Р переменных t, х. Доказательство теоремы 2, приводимое в следующем параграфе, представляет собой усложнение доказательства теоремы 1 и содержит его как частный случай. Доказательство теорем 1 и 2 проводится методом последовательных приближений, принадлежащим Пикару и применяемым в анализе при доказательстве многих теорем существования. Этот метод является одновременно методом приближенного вычисления решения и потому имеет большую практическую ценность. В некоторых случаях метод последовательных приближений может быть истолкован как метод сжатых отображений.
Основные идеи доказательства
Первым шагом при доказательстве теоремы 1 методом последовательных приближений является переход от дифференциального уравнения к интегральному, который мы формулируем в виде отдельного предложения.
А) Пусть ![]() — некоторое решение уравнения (1), определенное на интервале
— некоторое решение уравнения (1), определенное на интервале ![]() , так что выполнено тождество
, так что выполнено тождество
![]() (2)
(2)
и пусть
![]() (3)
(3)
- некоторое начальное условие, которому это решение удовлетворяет. Оказывается, что тогда для функции ![]() на всем интервале
на всем интервале ![]() выполнено интегральное тождество
выполнено интегральное тождество
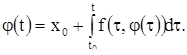 (4)
(4)
Обратно если для некоторой непрерывной функции ![]() на интервале
на интервале ![]() выполнено тождество (4), то функция
выполнено тождество (4), то функция ![]() дифференцируема, является решением уравнения (1) и удовлетворяет начальному условию (3). Кратко говоря интегральное уравнение (4), эквивалентно дифференциальному уравнению (2) вместе с начальным условием (3).
дифференцируема, является решением уравнения (1) и удовлетворяет начальному условию (3). Кратко говоря интегральное уравнение (4), эквивалентно дифференциальному уравнению (2) вместе с начальным условием (3).
Докажем это. Допустим сначала, что выполнено соотношение (4). Заменяя в нем переменное t его значением ![]() , получаем:
, получаем: ![]() . Таким образом, из (4) вытекает (3). Далее, правая часть тождества (4) очевидно дифференцируема по t, а потому дифференцируема по t и левая его часть. В результате дифференцирования тождества (4), получаем тождество (2).
. Таким образом, из (4) вытекает (3). Далее, правая часть тождества (4) очевидно дифференцируема по t, а потому дифференцируема по t и левая его часть. В результате дифференцирования тождества (4), получаем тождество (2).
Допустим теперь, что выполнены соотношения (2) и (3). Интегрируя соотношение (2) в пределах от ![]() до t, получаем:
до t, получаем:

В силу соотношения (3) из последнего равенства получаем (4).
Таким образом, предложение А) доказано.
Введем теперь некоторые обозначения, используемые ниже при доказательстве теоремы 1.
Б) Пусть ![]() - такая непрерывная функция, определенная на некотором отрезке
- такая непрерывная функция, определенная на некотором отрезке ![]() , что ее график расположен в открытом множестве Г, и
, что ее график расположен в открытом множестве Г, и ![]() - некоторая точка отрезка
- некоторая точка отрезка ![]() . Тогда, пользуясь правой частью тождества (4), можно функции
. Тогда, пользуясь правой частью тождества (4), можно функции ![]() поставить в соответствие функцию
поставить в соответствие функцию ![]() , определенную также на отрезке
, определенную также на отрезке ![]() , при помощи равенства
, при помощи равенства
 (5)
(5)
(график функции ![]() , конечно, уже может не проходить в множестве Г). Таким образом, правую часть тождества (4) можно рассматривать как оператор, ставящий в соответствие функции
, конечно, уже может не проходить в множестве Г). Таким образом, правую часть тождества (4) можно рассматривать как оператор, ставящий в соответствие функции ![]() функцию
функцию ![]() . Обозначая этот оператор одной буквой А, мы запишем соотношение (5) в виде формулы
. Обозначая этот оператор одной буквой А, мы запишем соотношение (5) в виде формулы
![]() (6)
(6)
Пользуясь оператором А, интегральное уравнение (4) можно записать в виде:
![]() (7)
(7)
В) Пусть, ![]() - некоторая непрерывная функция, определенная на отрезке
- некоторая непрерывная функция, определенная на отрезке ![]() . Нормой
. Нормой ![]() этой функции называется максимум ее модуля
этой функции называется максимум ее модуля
![]()
Если ![]() и
и ![]() - две непрерывные функции, заданные на отрезке
- две непрерывные функции, заданные на отрезке ![]() , то норма
, то норма ![]() их разности
их разности ![]() является неотрицательным числом, оценивающим, насколько сильно отличаются эти функции друг от друга. Если число
является неотрицательным числом, оценивающим, насколько сильно отличаются эти функции друг от друга. Если число ![]() мало, то функции
мало, то функции ![]() и
и ![]() «близки» друг к другу. Равенство
«близки» друг к другу. Равенство ![]() = 0 имеет место тогда и только тогда, когда функции
= 0 имеет место тогда и только тогда, когда функции ![]() и
и ![]() тождественно совпадают. Пользуясь понятием нормы, легко можно формулировать известное из курса анализа условие равномерной сходимости последовательности непрерывных функций. Пусть
тождественно совпадают. Пользуясь понятием нормы, легко можно формулировать известное из курса анализа условие равномерной сходимости последовательности непрерывных функций. Пусть
![]() (8)
(8)
- последовательность непрерывных функций, заданных на отрезке ![]() . Последовательность (8) равномерно сходится к функции
. Последовательность (8) равномерно сходится к функции ![]() , определенной на том же отрезке
, определенной на том же отрезке ![]() , если
, если
![]()
Для того, чтобы последовательность (8) равномерно сходилась, достаточно, чтобы имели место неравенства
![]()
где числа ![]() образуют сходящийся ряд.
образуют сходящийся ряд.
Прежде чем перейти к детальному проведению доказательства теоремы 1, изложим кратко суть метода последовательных приближений, применяемого для решения уравнения (7). Строится последовательность
![]() (9)
(9)
непрерывных функций, определенных на некотором отрезке ![]() , который содержит внутри себя точку
, который содержит внутри себя точку ![]() . Каждая функция последовательности (9) определяется через предыдущую при помощи равенства
. Каждая функция последовательности (9) определяется через предыдущую при помощи равенства
![]() (10)
(10)
Если график функции ![]() , проходит в множестве Г, то функция
, проходит в множестве Г, то функция ![]() , равенством (10) определяется, но для того, чтобы могла быть определена следующая функция
, равенством (10) определяется, но для того, чтобы могла быть определена следующая функция ![]() , нужно, чтобы и график функции
, нужно, чтобы и график функции ![]() проходил в множестве Г. Этого, как мы покажем, удается достичь, выбрав отрезок
проходил в множестве Г. Этого, как мы покажем, удается достичь, выбрав отрезок ![]() достаточно коротким. Далее, также за счет уменьшения длины отрезка
достаточно коротким. Далее, также за счет уменьшения длины отрезка ![]() , можно достичь того, чтобы для последовательности (9) выполнялись неравенства
, можно достичь того, чтобы для последовательности (9) выполнялись неравенства
![]() (11)
(11)
где 0<k<1. Из неравенства (11) следуют неравенства
![]()
и, таким образом, последовательность (9) равномерно сходится (см. В)). Далее уже легко устанавливается, что предел ![]() последовательности (9) удовлетворяет уравнению (7).
последовательности (9) удовлетворяет уравнению (7).
Ту же конструкцию можно описать несколько иным способом – в форме метода сжатых отображений. Выберем некоторое семейство ![]() функций, заданных на отрезке
функций, заданных на отрезке ![]() (причем
(причем ![]() ), так, чтобы графики этих функций проходили в множестве Г. Допустим еще, что в отношении оператора А семейство
), так, чтобы графики этих функций проходили в множестве Г. Допустим еще, что в отношении оператора А семейство ![]() удовлетворяет следующим двум условиям: 1) применяя оператор А к любой функции семейства
удовлетворяет следующим двум условиям: 1) применяя оператор А к любой функции семейства ![]() , мы вновь получаем функцию семейства
, мы вновь получаем функцию семейства ![]() ; 2) существует такое число k, 0<k<1, что для двух произвольных функций
; 2) существует такое число k, 0<k<1, что для двух произвольных функций ![]() и
и ![]() семейства
семейства ![]() выполнено неравенство
выполнено неравенство
![]()
В этом смысле отображение А является сжатым (правильнее было бы сказать «сжимающим»).
Легко видеть, что если для семейства ![]() выполнены формулированные условия, то, исходя из произвольной его функции
выполнены формулированные условия, то, исходя из произвольной его функции ![]() , мы по индуктивной формуле (10) получим бесконечную последовательность (9), удовлетворяющую условию (11), и, как было отмечено выше, равномерно сходящуюся к решению уравнения (7).
, мы по индуктивной формуле (10) получим бесконечную последовательность (9), удовлетворяющую условию (11), и, как было отмечено выше, равномерно сходящуюся к решению уравнения (7).
Перейдем теперь к доказательству теоремы 1 на основе изложенных соображений.
Доказательство теоремы 1
Начальные значения ![]() и
и ![]() искомого решения уравнения (1) являются координатами точки
искомого решения уравнения (1) являются координатами точки ![]() , лежащей в множестве Г. Выберем прежде всего какой-либо прямоугольник П с центром в точке
, лежащей в множестве Г. Выберем прежде всего какой-либо прямоугольник П с центром в точке ![]() со сторонами, параллельными осям, целиком вместе со своей границей содержащихся в множестве Г (рис. 17). Длину горизонтальной (параллельной оси t) стороны прямоугольника П обозначим через 2q, а длину вертикальной стороны – через 2а. Таким образом, точка
со сторонами, параллельными осям, целиком вместе со своей границей содержащихся в множестве Г (рис. 17). Длину горизонтальной (параллельной оси t) стороны прямоугольника П обозначим через 2q, а длину вертикальной стороны – через 2а. Таким образом, точка ![]() тогда и только тогда принадлежит прямоугольнику П, когда выполнены неравенства:
тогда и только тогда принадлежит прямоугольнику П, когда выполнены неравенства:
![]() ,
, ![]() (12)
(12)
Так как прямоугольник П есть замкнутое множество, содержащееся в Г, то непрерывные на нем функции f ![]() и
и ![]() ограничены, и потому существуют такие положительные числа М и К, что для t и x, удовлетворяющих условиям (12), выполнены неравенства
ограничены, и потому существуют такие положительные числа М и К, что для t и x, удовлетворяющих условиям (12), выполнены неравенства
![]() ,
, 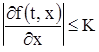 (13)
(13)
Наряду с прямоугольником П будем рассматривать более «узкий» прямоугольник ![]() , определяемый неравенствами
, определяемый неравенствами
![]() ,
, ![]() (14)
(14)
где
![]()
(см. рис. 17). Более точно число r определим далее. Обозначим через ![]() семейство всех непрерывных функций, заданных на отрезке
семейство всех непрерывных функций, заданных на отрезке ![]() , графики которых проходят в прямоугольнике
, графики которых проходят в прямоугольнике ![]() . Таким образом, функция
. Таким образом, функция ![]() , определенная на отрезке
, определенная на отрезке ![]() , тогда и только тогда принадлежит семейству
, тогда и только тогда принадлежит семейству ![]() , когда для любого t, принадлежащего этому отрезку, выполнено неравенство
, когда для любого t, принадлежащего этому отрезку, выполнено неравенство
![]() (15)
(15)
Постараемся теперь выбрать число r таким образом, чтобы были выполнены следующие два условия:
а) Если функция ![]() принадлежит семейству
принадлежит семейству ![]() , то функция
, то функция ![]() (см. (5), (6)) также принадлежит семейству
(см. (5), (6)) также принадлежит семейству ![]() .
.
б) Существует такое число ![]() что для любых двух функций
что для любых двух функций ![]() и
и ![]() семейства
семейства ![]() имеет место неравенство
имеет место неравенство
![]() (16)
(16)
Рассмотрим условие а). Для того чтобы функция ![]() принадлежала семейству
принадлежала семейству ![]() необходимо и достаточно, чтобы при
необходимо и достаточно, чтобы при ![]() было выполнено неравенство
было выполнено неравенство
![]()
В силу (5) и (13) мы имеем:

Из этого видно, что при
![]() (17)
(17)
условие а) выполнено.
Рассмотрим теперь условие б). Мы имеем:
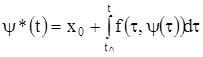 ,
,
 .
.
Вычитая второе равенство из первого, получаем:
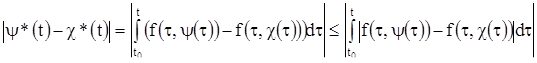 (18)
(18)
Оценим теперь последнее подынтегральное выражение, пользуясь формулой Лагранжа и вторым из неравенств (13):
 ; (19)
; (19)
здесь ![]() – число, заключенное между
– число, заключенное между ![]() и
и ![]() и, следовательно, удовлетворяющее неравенству
и, следовательно, удовлетворяющее неравенству ![]() . Из (18) и (19) следует:
. Из (18) и (19) следует:
![]()
Таким образом, условие б) выполнено, если число ![]() меньше единицы, т. е. если
меньше единицы, т. е. если
![]() (20)
(20)
Итак, если число r удовлетворяет неравенствам (14), (17) и (20), то для семейства ![]() выполнены условия а) и б). В дальнейшем будем считать число r выбранным таким образом, что неравенства (14), (17) и (20) для него выполнены.
выполнены условия а) и б). В дальнейшем будем считать число r выбранным таким образом, что неравенства (14), (17) и (20) для него выполнены.
Построим теперь последовательность
![]() (21)
(21)
функций, определенных на отрезке ![]() , положив:
, положив:
![]() (22)
(22)
![]() (23)
(23)
Так как функция (22) принадлежит семейству ![]() , то и все функции последовательности (21) принадлежат этому же семейству (см. условие а)). Далее, мы имеем (см. (15)):
, то и все функции последовательности (21) принадлежат этому же семейству (см. условие а)). Далее, мы имеем (см. (15)):
![]()
В силу (16) получаем:
![]() ,
,
откуда
![]()
Таким образом, и силу В), последовательность (21) равномерно сходится на отрезке ![]() к некоторой непрерывной функции
к некоторой непрерывной функции ![]() . Так как все функции последовательности (21) принадлежат семейству
. Так как все функции последовательности (21) принадлежат семейству ![]() то и функция
то и функция ![]() принадлежит ему (см. (15)). Покажем, что функция
принадлежит ему (см. (15)). Покажем, что функция ![]() удовлетворяет уравнению (7). Для этого заметим, что последовательность
удовлетворяет уравнению (7). Для этого заметим, что последовательность
![]()
равномерно сходится к функции ![]() ; действительно, мы имеем:
; действительно, мы имеем:
![]() .
.
Переходя в соотношении (23) к пределу при ![]() , получаем:
, получаем:
![]()
Итак, существование решения ![]() уравнения (1), удовлетворяющего начальному условию (3), доказано; при этом установлено, что решение
уравнения (1), удовлетворяющего начальному условию (3), доказано; при этом установлено, что решение ![]() определено на интервале
определено на интервале ![]() , где r – произвольное число, удовлетворяющее неравенствам (14), (17) и (20).
, где r – произвольное число, удовлетворяющее неравенствам (14), (17) и (20).
Перейдем теперь к доказательству единственности. Пусть ![]() и
и ![]() - два решения уравнения (1) с общими начальными значениями
- два решения уравнения (1) с общими начальными значениями ![]() ,
, ![]() и
и ![]() — интервал, являющийся пересечением интервалов существования решений
— интервал, являющийся пересечением интервалов существования решений ![]() и
и ![]() ; очевидно, что
; очевидно, что ![]() . Покажем, что если решения
. Покажем, что если решения ![]() и
и ![]() совпадают в некоторой точке
совпадают в некоторой точке ![]() интервала
интервала ![]() , то они совпадают и на некотором интервале
, то они совпадают и на некотором интервале ![]() , где r – достаточно малое положительное число. Положим
, где r – достаточно малое положительное число. Положим ![]() ; тогда величины
; тогда величины ![]() ,
, ![]() могут быть приняты за начальные значения обоих решений
могут быть приняты за начальные значения обоих решений ![]() и
и ![]() . В этом смысле точка
. В этом смысле точка ![]() ничем не отличается от точки
ничем не отличается от точки ![]() , и поэтому мы сохраним за точкой
, и поэтому мы сохраним за точкой ![]() обозначение
обозначение ![]() : это позволит нам сохранить и другие прежние обозначения. Переходя от дифференциального уравнения (1) к интегральному уравнению (4), мы получаем для обеих функций
: это позволит нам сохранить и другие прежние обозначения. Переходя от дифференциального уравнения (1) к интегральному уравнению (4), мы получаем для обеих функций ![]() и
и ![]() интегральные равенства, которые в операторной форме могут быть записаны в виде:
интегральные равенства, которые в операторной форме могут быть записаны в виде:
![]() . (24)
. (24)
Выберем теперь, как и прежде, в открытом множества Г прямоугольник П с центром в точке ![]() , а затем прямоугольник
, а затем прямоугольник ![]() таким образом, чтобы число r кроме неравенств (14), (17), (20) удовлетворяло еще тому условию, что при
таким образом, чтобы число r кроме неравенств (14), (17), (20) удовлетворяло еще тому условию, что при ![]() функции
функции ![]() и
и ![]() определены и удовлетворяют неравенствам
определены и удовлетворяют неравенствам
![]()
Это возможно, так как функции ![]() и
и ![]() непрерывны. Тогда функции
непрерывны. Тогда функции ![]() и
и ![]() , рассматриваемые на отрезке
, рассматриваемые на отрезке ![]() , входят в семейство
, входят в семейство ![]() , и, следовательно, в силу неравенства (16) и соотношений (24) получаем:
, и, следовательно, в силу неравенства (16) и соотношений (24) получаем:
![]() ,
,
а это возможно только тогда, когда ![]() , т.е. когда функции
, т.е. когда функции ![]() и
и ![]() совпадают на отрезке
совпадают на отрезке ![]() .
.
Докажем теперь, что функции ![]() и
и ![]() совпадают на всем интервале
совпадают на всем интервале ![]() . Допустим противоположное, именно, что существует точка
. Допустим противоположное, именно, что существует точка ![]() интервала
интервала ![]() , для которой
, для которой ![]() . Ясно, что
. Ясно, что ![]() . Для определенности будем считать, что
. Для определенности будем считать, что ![]()
Обозначим через N множество всех тех точек ![]() отрезка
отрезка ![]() , для которых
, для которых ![]() , и докажем, что множество N замкнуто. В самом деле, пусть
, и докажем, что множество N замкнуто. В самом деле, пусть ![]() – последовательность точек множества N, сходящаяся к некоторой точке
– последовательность точек множества N, сходящаяся к некоторой точке ![]() . Тогда
. Тогда ![]() , и потому, в силу непрерывности функций
, и потому, в силу непрерывности функций ![]() и
и ![]() ,
,
![]() ,
,
т.е. точка ![]() также принадлежит множеству N.
также принадлежит множеству N.
Обозначим через ![]() точную верхнюю грань множества N. Так как N замкнуто, то
точную верхнюю грань множества N. Так как N замкнуто, то ![]() принадлежит этому множеству, т. е.
принадлежит этому множеству, т. е. ![]() ; следовательно,
; следовательно, ![]() . Но тогда, в силу ранее доказанного, функции
. Но тогда, в силу ранее доказанного, функции ![]() и
и ![]() должны совпадать на некотором интервале
должны совпадать на некотором интервале ![]() , и точка
, и точка ![]() не может быть точной верхней гранью множества N. Таким образом, мы пришли к противоречию.
не может быть точной верхней гранью множества N. Таким образом, мы пришли к противоречию.
Итак, теорема 1 доказана.
Пример
Для весьма простого уравнения ![]() найдем решение методом последовательных приближений. Решение будем искать с начальными значениями
найдем решение методом последовательных приближений. Решение будем искать с начальными значениями ![]()
Соответствующее интегральное уравнение запишется в виде: 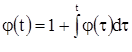
Будем строить теперь последовательность ![]()
Мы имеем:
![]() ,
,
 ,
,
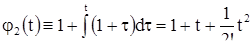 ,
,
 ,
,
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
![]() ,
,
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Пределом этой последовательности (равномерно сходящейся на любом отрезке числовой оси) является функция ![]() .
.
§13. Доказательство теоремы существования и единственности для нормальной системы уравнений
Здесь будет доказана сформулированная и §2 теорема 2 существования и единственности для нормальной системы уравнений
![]() (1)
(1)
правые части ![]() которые вместе с их частными производными
которые вместе с их частными производными  определены и непрерывны на некотором открытом множестве Г пространства переменных
определены и непрерывны на некотором открытом множестве Г пространства переменных ![]() . Полагая
. Полагая
![]() , (2)
, (2)
![]() ,
,
мы перепишем систему (1) в векторной форме:
![]() . (3)
. (3)
Доказательство будет проводиться в векторной форме методом последовательных приближений, и будет представлять собой почти буквальное повторение доказательства теоремы 1, данного в предыдущем параграфе.
Вспомогательные предложения
Для того чтобы непринужденно пользоваться векторными обозначениями, установим прежде всего некоторые естественные определения и простые неравенства для векторов и векторных функций.
Длина или модуль ![]() вектора (2), как известно, определяется формулой
вектора (2), как известно, определяется формулой
![]() .
.
Известно и без труда доказывается, что если х и у суть два вектора, то имеет место неравенство
![]() .
.
Из этого неравенства следует аналогичное неравенство и для произвольного числа векторов ![]() именно:
именно:
![]() (4)
(4)
Пусть ![]() — непрерывная векторная функция действительного переменного t, т. е. вектор, координаты которого являются непрерывными функциями переменного t. Если функция
— непрерывная векторная функция действительного переменного t, т. е. вектор, координаты которого являются непрерывными функциями переменного t. Если функция ![]() определена на интервале
определена на интервале ![]() , то при
, то при ![]() на том же интервале можно определить векторную функцию
на том же интервале можно определить векторную функцию
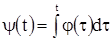 ,
,
задав компоненты ![]() вектора
вектора ![]() формулами
формулами
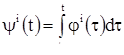 ;
;
при этом имеет место неравенство
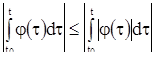 . (5)
. (5)
Установим еще одно неравенство для векторной функции
![]()
векторного переменного х, заданной на выпуклом множестве ![]() пространства переменных
пространства переменных ![]() . Предположим, что имеют место неравенства:
. Предположим, что имеют место неравенства:
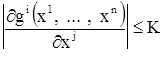 ,
,
где К — положительное число. Оказывается тогда, что для двух любых точек х и у множества ![]() выполнены неравенства
выполнены неравенства
![]() . (6)
. (6)
Так же, как при доказательстве теоремы 1, от дифференциального уравнения (3) перейдем к интегральному.
А) Пусть ![]() — некоторое решение дифференциального уравнения (3), так что выполнено тождество
— некоторое решение дифференциального уравнения (3), так что выполнено тождество
![]() (7)
(7)
и пусть
![]() (8)
(8)
— начальное условие, которому это решение удовлетворяет. Оказывается, что совокупность соотношений (7) и (8) эквивалентна одному соотношению
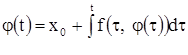 (9)
(9)
Докажем это. Допустим, что выполнено интегральное тождество (9). Подставляя в него ![]() , получаем равенство (8), а дифференцируя его по t, получаем тождество (7). Допустим теперь, что выполнены соотношения (7) и (8). Интегрируя соотношение (7) в пределах от
, получаем равенство (8), а дифференцируя его по t, получаем тождество (7). Допустим теперь, что выполнены соотношения (7) и (8). Интегрируя соотношение (7) в пределах от ![]() и
и ![]() и принимай во внимание соотношение (8), мы получаем соотношение (9).
и принимай во внимание соотношение (8), мы получаем соотношение (9).
Б) Пользуясь правой частью тождества (9), каждой векторной функции ![]() , график которой проходит в множестве Г, поставим в соответствие функцию
, график которой проходит в множестве Г, поставим в соответствие функцию ![]() , положив:
, положив:
 . (10)
. (10)
Кратко, в операторной форме то же соотношение запишем в виде:
![]() . (11)
. (11)
Уравнение (9) теперь может быть записано в виде:
![]() . (12)
. (12)
В) Пусть ![]() — непрерывная векторная функция, заданная на отрезке
— непрерывная векторная функция, заданная на отрезке ![]() . Определим норму
. Определим норму ![]() этой функции, положив:
этой функции, положив:
![]()
Пользуясь понятием нормы, можно формулировать определение равномерной сходимости последовательности
![]() (13)
(13)
непрерывных векторных функций, заданных на отрезке ![]() . Последовательность (13) векторных функций равномерно сходится к непрерывной функции
. Последовательность (13) векторных функций равномерно сходится к непрерывной функции ![]() , заданной на том же отрезке
, заданной на том же отрезке ![]() , если
, если
![]() .
.
Для того чтобы последовательность (13) равномерно сходилась, достаточно, чтобы были выполнены неравенства
![]()
где числа ![]() образуют сходящийся ряд.
образуют сходящийся ряд.
Прейдем теперь к доказательству теоремы 2.
Доказательство теоремы 2
Так как точка ![]() принадлежит открытому множеству Г, то существуют такие положительные числа q и a, что все точки
принадлежит открытому множеству Г, то существуют такие положительные числа q и a, что все точки ![]() , удовлетворяющие условиям
, удовлетворяющие условиям
![]() , (14)
, (14)
лежат в множестве Г. Так как множество П, состоящее из всех точек ![]() удовлетворяющих условиям (14), замкнуто и ограничено (рис.18), то. непрерывные функции
удовлетворяющих условиям (14), замкнуто и ограничено (рис.18), то. непрерывные функции
![]() и
и  ,
, ![]()
ограничены на нем, т. е. существуют такие положительные числа М и К, что
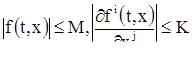 ,
, ![]() (15)
(15)
на множестве П.
Наряду с множеством П рассмотрим содержащееся в нем множество ![]() определяемое неравенствами
определяемое неравенствами
![]() ,
,
где
![]() (16)
(16)
(рис. 18). Обозначим через ![]() семейство всех непрерывных векторных функций, заданных на отрезке
семейство всех непрерывных векторных функций, заданных на отрезке ![]() , графики которых проходят в
, графики которых проходят в ![]() . Таким образом, функция
. Таким образом, функция ![]() , определенная на отрезке
, определенная на отрезке ![]() , тогда и только тогда принадлежит семейству
, тогда и только тогда принадлежит семейству ![]() когда
когда

Рис. 18.
для любого t, принадлежащего этому отрезку, выполнено неравенство
![]() (17)
(17)
Постараемся выбрать теперь число r таким образом, чтобы были выполнены следующие два условия:
а) Если функция ![]() принадлежит семейству
принадлежит семейству ![]() , то функция
, то функция ![]() (см. (10), (11)) также принадлежит семейству
(см. (10), (11)) также принадлежит семейству ![]() .
.
б) Существует такое число ![]() , что для любых двух функций
, что для любых двух функций ![]() семейства
семейства ![]() , имеет место неравенство
, имеет место неравенство
![]() (18)
(18)
Рассмотрим условие а). Для того чтобы функция ![]() принадлежала семейству
принадлежала семейству ![]() , необходимо и достаточно, чтобы при
, необходимо и достаточно, чтобы при ![]() было выполнено неравенство:
было выполнено неравенство:
![]() .
.
В силу (10), (5) и (15) мы имеем:
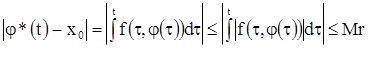 .
.
Из этого видно, что при
![]() (19)
(19)
условие а) выполнено.
Рассмотрим теперь условие б). Мы имеем:
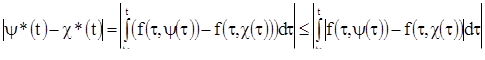 . (20)
. (20)
Оценим теперь последнее подынтегральное выражение, пользуясь неравенствами (6) и (15):
![]() . (21)
. (21)
Из (20) и (21) следует
![]()
Таким образом, условие б) выполнено, если
![]() , (22)
, (22)
где ![]() .
.
Итак, если число r удовлетворяет неравенствам (16), (19), (22) (которые мы в дальнейшем будем считать выполненными), то для семейства ![]() выполнены условия а) и б).
выполнены условия а) и б).
Построим теперь последовательность векторных функций
![]() ,
, ![]()
![]() (23)
(23)
определенных на отрезке ![]() , положив
, положив
![]() (24)
(24)
Так как функция ![]() принадлежит семейству
принадлежит семейству ![]() , то и все функции последовательности (23) принадлежат этому же семейству (см. условие а)). Далее, мы имеем (см. (17)):
, то и все функции последовательности (23) принадлежат этому же семейству (см. условие а)). Далее, мы имеем (см. (17)):
![]()
В силу (18) получаем:
![]() ,
,
отсюда
![]() . (25)
. (25)
Таким образом, в силу В) последовательность (23) равномерно сходится к некоторой непрерывной функции ![]() , принадлежащей семейству
, принадлежащей семейству ![]() . Покажем, что функция
. Покажем, что функция ![]() удовлетворяет уравнению (12). Для этого заметим, что последовательность
удовлетворяет уравнению (12). Для этого заметим, что последовательность
![]()
Равномерно сходится к функции ![]() ; действительно, мы имеем (см. (18))
; действительно, мы имеем (см. (18))
![]() .
.
Переходя в соотношении (24) к приделу при ![]() , получаем:
, получаем:
![]() .
.
Итак, существование решении ![]() уравнения (3), удовлетворяющего начальному условию (8), доказано; при этом установлено, что решение
уравнения (3), удовлетворяющего начальному условию (8), доказано; при этом установлено, что решение ![]() определено на интервале
определено на интервале ![]() , где r – произвольное число; удовлетворяющее неравенствам (16), (19), (22).
, где r – произвольное число; удовлетворяющее неравенствам (16), (19), (22).
Перейдем теперь к доказательству единственности. Пусть ![]() и
и ![]() - два решения уравнения (3) с общими начальными значениями
- два решения уравнения (3) с общими начальными значениями ![]() и
и ![]() — интервал, являющийся пересечением интервалов существования решений
— интервал, являющийся пересечением интервалов существования решений ![]() и
и ![]() ; очевидно, что
; очевидно, что ![]() . Покажем, что если решения
. Покажем, что если решения ![]() и
и ![]() совпадают в некоторой точке
совпадают в некоторой точке ![]() интервала
интервала ![]() , то они совпадают и на некотором интервале
, то они совпадают и на некотором интервале ![]() , где r – достаточно малое положительное число. Положим
, где r – достаточно малое положительное число. Положим ![]() ; тогда величины
; тогда величины ![]() могут быть приняты за начальные значения обоих решений
могут быть приняты за начальные значения обоих решений ![]() и
и ![]() . В этом смысле точка
. В этом смысле точка ![]() ничем не отличается от точки
ничем не отличается от точки ![]() и потому мы сохраним за точкой
и потому мы сохраним за точкой ![]() обозначение
обозначение ![]() ; это позволит нам сохранить и другие прежние, обозначения. Переходя от дифференциального уравнения (3) к интегральному уравнению (9), мы получаем для обеих функций
; это позволит нам сохранить и другие прежние, обозначения. Переходя от дифференциального уравнения (3) к интегральному уравнению (9), мы получаем для обеих функций ![]() и
и ![]() интегральные равенства, которые в операторной форме могут быть записаны в виде:
интегральные равенства, которые в операторной форме могут быть записаны в виде:
![]() . (26)
. (26)
Выберем теперь, как и прежде, в множестве Г множество П с центром в точке ![]() (см, неравенства (14)), содержащееся в Г, а затем множество
(см, неравенства (14)), содержащееся в Г, а затем множество ![]() таким образом, чтобы число r, кроме неравенств (16), (19), (22), удовлетворяло еще тому условию, что при
таким образом, чтобы число r, кроме неравенств (16), (19), (22), удовлетворяло еще тому условию, что при ![]() функции
функции ![]() и
и ![]() определены и удовлетворяют неравенствам:
определены и удовлетворяют неравенствам:
![]() ,
, ![]() .
.
Это возможно, так как функции ![]() и
и ![]() непрерывны. Тогда функции
непрерывны. Тогда функции ![]() и
и ![]() , рассматриваемые на, отрезке
, рассматриваемые на, отрезке ![]() , входят в семейство
, входят в семейство ![]() и, следовательно, в силу неравенства (18) и соотношений (26), получаем:
и, следовательно, в силу неравенства (18) и соотношений (26), получаем:
![]() ,
,
а это возможно только тогда, когда ![]() , т.е. когда функций
, т.е. когда функций ![]() и
и ![]() совпадают на отрезке
совпадают на отрезке ![]() .
.
Докажем теперь, что функции ![]() и
и ![]() совпадают на всем интервале
совпадают на всем интервале ![]() . Допустим противоположное, именно, что существует точка
. Допустим противоположное, именно, что существует точка ![]() интервала
интервала ![]() , для которой
, для которой ![]() . Ясно, что
. Ясно, что ![]() . Для определенности будем считать, что
. Для определенности будем считать, что ![]() . Обозначим через N множество всех тех точек
. Обозначим через N множество всех тех точек ![]() отрезка
отрезка ![]() , для которых
, для которых ![]() , и докажем, что множество N замкнуто. В самом деле, пусть
, и докажем, что множество N замкнуто. В самом деле, пусть ![]() — последовательность точек множества N, сходящаяся к некоторой точке
— последовательность точек множества N, сходящаяся к некоторой точке ![]() . Тогда
. Тогда ![]() , и потому, в силу непрерывности функций
, и потому, в силу непрерывности функций ![]() и
и ![]() ,
,
![]() ,
,
т.е. точка ![]() также принадлежит множеству N.
также принадлежит множеству N.
Обозначим через ![]() точную верхнюю грань множества N. Так как N замкнуто, то
точную верхнюю грань множества N. Так как N замкнуто, то ![]() принадлежит этому множеству, т. е
принадлежит этому множеству, т. е ![]() ; следовательно,
; следовательно, ![]() . Но тогда, в силу ранее доказанного, функции
. Но тогда, в силу ранее доказанного, функции ![]() и
и ![]() должны совпадать на некотором интервале
должны совпадать на некотором интервале ![]() , и точка
, и точка ![]() не может быть точной верхней гранью множества N. Таким образом, мы пришли к противоречию.
не может быть точной верхней гранью множества N. Таким образом, мы пришли к противоречию.
Итак, теорема 2 доказана.
§ 14. Понятие о теории устойчивости Ляпунова. Поведение траектории дифференциального уравнения в окрестности особой точки
Во многих задачах механики и техники бывает важно знать не конкретные значения решения при данном конкретном значении аргумента, а характер поведения решения при изменении аргумента и, в частности, при неограниченном возрастании аргумента. Например, бывает важно знать, являются ли решения, удовлетворяющие данным начальным условиям, периодическими, приближаются ли они асимптотически к какой-либо известной функции и т.д. Этими вопросами занимается качественная теория дифференциальных уравнений.
Одним из основных вопросов качественной теории является вопрос об устойчивости решения или об устойчивости движения; этот вопрос был подробно исследован знаменитым русским математиком А.М. Ляпуновым (1857-1918).
Пусть дана система дифференциальных уравнений
![]() . (1)
. (1)
Пусть ![]() и
и ![]() - решения этой системы, удовлетворяющие начальным условиям
- решения этой системы, удовлетворяющие начальным условиям
![]() (1’)
(1’)
Пусть далее, ![]() и
и ![]() - решения уравнения (1), удовлетворяющие начальным условиям
- решения уравнения (1), удовлетворяющие начальным условиям
![]() (1”)
(1”)
Решения ![]() и
и ![]() , удовлетворяющие уравнениям (1) и начальным условиям (1’), называются устойчивыми по Ляпунову при
, удовлетворяющие уравнениям (1) и начальным условиям (1’), называются устойчивыми по Ляпунову при ![]() , если для каждого как угодно малого
, если для каждого как угодно малого ![]() можно указать
можно указать ![]() такое, что при всех значениях
такое, что при всех значениях ![]() будут выполняться неравенства
будут выполняться неравенства
![]() (2)
(2)
если начальные данные удовлетворяют неравенствам
![]() (3)
(3)
Выясним смысл этого определения. Из неравенств (2) и (3) следует, что при малых изменениях начальных условий мало отличаются соответствующие решения при всех положительных значениях ![]() . Если система дифференциальных уравнений является системой, описывающей некоторое движение, то в случае устойчивости решений характер движений мало изменяется при малом изменении начальных данных.
. Если система дифференциальных уравнений является системой, описывающей некоторое движение, то в случае устойчивости решений характер движений мало изменяется при малом изменении начальных данных.
Рассмотрим, далее, систему линейных дифференциальных уравнений
![]() (4)
(4)
Будем предполагать, что коэффициенты ![]() постоянные, при этом очевидно, что
постоянные, при этом очевидно, что ![]() есть решение системы (4), в чем убеждаемся непосредственной подстановкой. Исследуем вопрос о том, каким условиям должны удовлетворять коэффициенты системы, чтобы решение
есть решение системы (4), в чем убеждаемся непосредственной подстановкой. Исследуем вопрос о том, каким условиям должны удовлетворять коэффициенты системы, чтобы решение ![]() было устойчиво. Это исследование проводится так.
было устойчиво. Это исследование проводится так.
Дифференцируем первое уравнение и исключаем ![]() и
и ![]() на основании уравнений системы:
на основании уравнений системы:
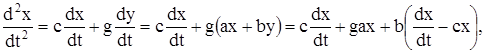
или
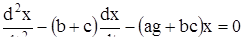 . (5)
. (5)
Характеристическое уравнение дифференциального уравнения (5) имеет вид
![]() (6)
(6)
Это уравнение принято записывать в виде определителя
 (7)
(7)
Обозначим корни характеристического уравнения (7) через ![]() и
и ![]() . Как мы увидим ниже, устойчивость или неустойчивость решений системы (4) определяется характером корней
. Как мы увидим ниже, устойчивость или неустойчивость решений системы (4) определяется характером корней ![]() и
и ![]() .
.
Рассмотрим все возможные случаи.
I. Корни характеристического уравнения действительные, отрицательные и различные: ![]() . Из уравнения (5) находим
. Из уравнения (5) находим
![]()
Зная х, из первого уравнения (4) находим у. Таким образом, решение системы (4) имеет вид:
![]()
 (8)
(8)
Если g = 0 и ![]() , то уравнение (5) мы составим для функции у. Найдя у, из второго уравнения системы (4) находим х. Структура решений (8) сохранится. Если же g = 0, а=0, то решение системы уравнений принимает вид:
, то уравнение (5) мы составим для функции у. Найдя у, из второго уравнения системы (4) находим х. Структура решений (8) сохранится. Если же g = 0, а=0, то решение системы уравнений принимает вид:
![]() (8’)
(8’)
Анализ характера решений в этом случае производится проще.
Подберем  и
и  так, чтобы решения (8) удовлетворяли начальным условиям
так, чтобы решения (8) удовлетворяли начальным условиям
![]()
Решение, удовлетворяющее начальным условиям, будет
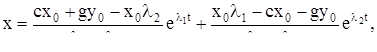
 (9)
(9)
Из последних равенств следует, что при любом ![]() можно выбирать
можно выбирать ![]() и
и ![]() столь малыми, что для всех t > 0 будет
столь малыми, что для всех t > 0 будет ![]() , так как
, так как ![]() .
.
Отметим, что в данном случае
![]() (10)
(10)
В случае решений (9) особая точка называется устойчивым узлом (рис.9 а). Говорят, что точка, неограниченно приближается к особой точке при ![]() .
.
II. Корни характеристического уравнения действительные, положительные, различные: ![]() . В этом случае решения выражаются также формулами (8) и соответственно (9). Но в данном случае при как угодно малых
. В этом случае решения выражаются также формулами (8) и соответственно (9). Но в данном случае при как угодно малых ![]() и
и ![]() будет
будет ![]() при
при ![]() , так как
, так как ![]() и
и ![]() при
при ![]() . На фазовой плоскости особая точка – неустойчивый узел: при
. На фазовой плоскости особая точка – неустойчивый узел: при ![]() точка на траектории удаляется от точки покоя х = 0, у = 0 (рис. 9 б).
точка на траектории удаляется от точки покоя х = 0, у = 0 (рис. 9 б).
III. Корни характеристического уравнения действительные, разных знаков, например, ![]() . Из формул (9) следует, что при как угодно малых
. Из формул (9) следует, что при как угодно малых ![]() и
и ![]() , если
, если ![]() , будет
, будет ![]() при
при ![]() . Решение неустойчиво. На фазовой плоскости особая точка называется седлом (рис. 10).
. Решение неустойчиво. На фазовой плоскости особая точка называется седлом (рис. 10).
IV. Корни характеристического уравнения комплексные с отрицательной действительной частью: ![]() . Решение системы (4) будет
. Решение системы (4) будет
![]()
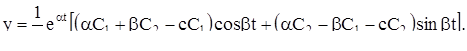 (11)
(11)
Если ввести обозначение
![]()
то уравнения (11) можно переписать в виде
![]()
 (12)
(12)
где ![]() и
и ![]() - произвольные постоянные, которые определяются из начальных условий
- произвольные постоянные, которые определяются из начальных условий ![]() ,
, ![]() при t = 0, причем
при t = 0, причем

откуда находим
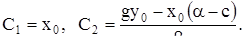 (13)
(13)
Снова заметим, что если g=0, то вид решения будет несколько иной, но характер анализа не изменится. Очевидно, что при любом ![]() при достаточно малых
при достаточно малых ![]() и
и ![]() будут выполняться соотношения
будут выполняться соотношения
![]() .
.
Решение устойчиво. В данном случае при ![]()
![]() и
и ![]() ,
,
неограниченное число раз меняя знаки. На фазовой плоскости особая точка называется устойчивым фокусом (рис. 13 а).
V. Корни характеристического уравнения комплексные с положительной действительной частью: ![]() . В этом случае решение также выразится формулами (11), где
. В этом случае решение также выразится формулами (11), где ![]() . При любых начальных условиях
. При любых начальных условиях ![]() и
и ![]()
![]() и при
и при ![]() величины
величины ![]() и
и ![]() могут принимать как угодно большие значения. Решение неустойчиво. На фазовой плоскости особая точка называется неустойчивым фокусом. Точка по траектории неограниченно удаляется от начала координат (рис. 13 б).
могут принимать как угодно большие значения. Решение неустойчиво. На фазовой плоскости особая точка называется неустойчивым фокусом. Точка по траектории неограниченно удаляется от начала координат (рис. 13 б).
VI. Корни характеристического уравнения чисто мнимые: ![]() . Решение (11) в этом случае примут вид
. Решение (11) в этом случае примут вид
![]()
 (14)
(14)
Постоянные ![]() и
и ![]() определяются по формулам (13):
определяются по формулам (13):
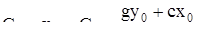 (15)
(15)
Очевидно, что при любом ![]() и при всех достаточно малых
и при всех достаточно малых ![]() и
и ![]() будет
будет ![]() при любом t. Решение устойчиво. Здесь х и у – периодические функции от t.
при любом t. Решение устойчиво. Здесь х и у – периодические функции от t.
Чтобы произвести анализ интегральных кривых на фазовой плоскости, целесообразно первое из решений (14) записать в в следующем виде (см. (12)):
![]()
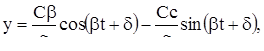 (16)
(16)
где С, ![]() - произвольные постоянные. Из выражений (16) следует, что х и у – периодические функции от t. Исключаем параметр t из уравнений (16):
- произвольные постоянные. Из выражений (16) следует, что х и у – периодические функции от t. Исключаем параметр t из уравнений (16):
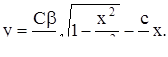
Освобождаясь от радикала, получим
 (17)
(17)
Это семейство кривых 2-го порядка (кривые действительные), зависящих от произвольной постоянной С. Каждая из них не имеет неограниченно удаленных точек. Следовательно, это семейство эллипсов, окружающих начало координат (при с=0 оси эллипсов параллельны осям координат). Особая точка называется центром (рис. 14).
VII. Пусть ![]() . Решение (8) в этом случае принимает вид
. Решение (8) в этом случае принимает вид
![]()
 (18)
(18)
Очевидно, что при любом ![]() и при достаточно малых
и при достаточно малых ![]() и
и ![]() будет
будет ![]() , при t > 0. Следовательно, решение устойчиво.
, при t > 0. Следовательно, решение устойчиво.
VIII. Пусть ![]() . Из формул (18) или (8’) следует, что решение неустойчиво, так как
. Из формул (18) или (8’) следует, что решение неустойчиво, так как ![]() при
при ![]() .
.
IX. Пусть ![]() . Решение будет
. Решение будет
![]()
 (19)
(19)
Так как ![]() и
и ![]() при
при ![]() , то для любого
, то для любого ![]() можно подобрать
можно подобрать ![]() и
и ![]() такие (путем выбора
такие (путем выбора ![]() и
и ![]() ), что будет
), что будет ![]() при любом t > 0. Следовательно, решение устойчиво. При этом
при любом t > 0. Следовательно, решение устойчиво. При этом ![]() и
и ![]() при
при ![]() .
.
Заметим, что в случае 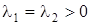 форма решения (18) сохраняется, но при
форма решения (18) сохраняется, но при 
![]() .
.
Решение неустойчиво.
X. Пусть ![]() . Тогда
. Тогда
 (20)
(20)
Откуда видно, что ![]() и
и ![]() при
при ![]() . Решение неустойчиво.
. Решение неустойчиво.
Чтобы дать общий критерий устойчивости решения системы (4), поступим следующим образом.
Запишем корни характеристического уравнения в форме комплексных чисел:
![]()
(в случае действительных корней ![]() и
и ![]() ).
).
![]()
Возьмем плоскость ![]() комплексной переменной и будем изображать корни характеристического уравнения точками на этой плоскости. Тогда на основании рассмотренных случаев условие устойчивости решения системы (4) можно сформулировать следующим образом.
комплексной переменной и будем изображать корни характеристического уравнения точками на этой плоскости. Тогда на основании рассмотренных случаев условие устойчивости решения системы (4) можно сформулировать следующим образом.
Если ни один из корней ![]() характеристического уравнения (6) не лежит справа от мнимой оси, причем хотя бы один корень отличен от нуля, то решение устойчиво; если же хотя бы один корень лежит справа от мнимой оси или оба корня равны нулю, то решение неустойчив (рис.19).
характеристического уравнения (6) не лежит справа от мнимой оси, причем хотя бы один корень отличен от нуля, то решение устойчиво; если же хотя бы один корень лежит справа от мнимой оси или оба корня равны нулю, то решение неустойчив (рис.19).
А.М. Ляпунов исследовал вопрос об устойчивости решений систем уравнений при довольно общих предположениях относительно вида этих уравнений.
В теории колебаний часто рассматривают уравнение
 (21)
(21)
Обозначим
![]() (22)
(22)
Тогда получаем систему уравнений
![]() (23)
(23)
Фазовой плоскостью для этой системы будет плоскость ![]() . Траектории на фазовой плоскости дают геометрическое изображение зависимости скорости
. Траектории на фазовой плоскости дают геометрическое изображение зависимости скорости ![]() от координаты х и наглядно качественно характеризуют изменение х и
от координаты х и наглядно качественно характеризуют изменение х и ![]() . Если точка х = 0,
. Если точка х = 0, ![]() = 0 является особой точкой, то она определяет положение равновесия.
= 0 является особой точкой, то она определяет положение равновесия.
Так, например, если особая точка системы уравнений есть центр, т. е. Траектории на фазовой плоскости представляют собой замкнутые линии, окружающие начало координат, то движения определяемые уравнением (21), - незатухающие колебательные движения. Если особая точка фазовой плоскости есть фокус (при этом ![]() при
при ![]() ), то движения, определяемые уравнением (21), - затухающие колебания. Если особая точка есть узел или седло (и это единственная особая точка), то
), то движения, определяемые уравнением (21), - затухающие колебания. Если особая точка есть узел или седло (и это единственная особая точка), то ![]() при
при ![]() . В этом случае движущаяся материальная точка уходит в бесконечность.
. В этом случае движущаяся материальная точка уходит в бесконечность.
Если уравнение (21) линейное вида  , то система (23) имеет вид
, то система (23) имеет вид
![]()
Это система вида (4). Точка х = 0, ![]() = 0 есть особая точка, она определяет положение равновесия. Отметим, что переменная ч – не обязательно механическое перемещение точки. Она может иметь различный физический смысл, например, обозначать величину, характеризующую электрические колебания.
= 0 есть особая точка, она определяет положение равновесия. Отметим, что переменная ч – не обязательно механическое перемещение точки. Она может иметь различный физический смысл, например, обозначать величину, характеризующую электрические колебания.
ГЛАВА IV . ПРАКТИЧЕСКИЯ СХЕМА РЕШЕНИЯ СИСТЕМЫ ДИФФЕРЕНЦАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Найти общее решение системы дифференциальных уравнений.
 (1)
(1)
Решение. Будем искать частное решение системы в следующем виде:
![]() (2)
(2)
Требуется определить постоянные ![]() и k так, чтобы функции
и k так, чтобы функции ![]() удовлетворяли системе уравнений (1). Подставляя их в систему (1), получим
удовлетворяли системе уравнений (1). Подставляя их в систему (1), получим
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() .
.
Сократим на ![]() . Перенося все члены в одну сторону и собирая коэффициенты при
. Перенося все члены в одну сторону и собирая коэффициенты при ![]() , получим систему уравнений
, получим систему уравнений
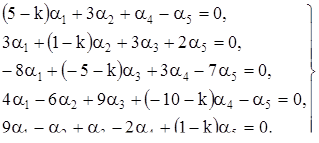 (3)
(3)
Выберем ![]() и k такими чтобы удовлетворялась система (3). Эта система есть система линейных однородных алгебраических уравнений относительно
и k такими чтобы удовлетворялась система (3). Эта система есть система линейных однородных алгебраических уравнений относительно ![]() . Составим определитель системы (3):
. Составим определитель системы (3):
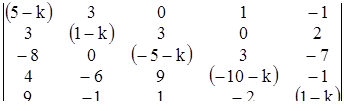 (4)
(4)
Нетривиальные решения (2) мы получим только при таких k , при которых определитель (4) обращается в ноль. Мы приходим к уравнению пятого порядка для определения k:
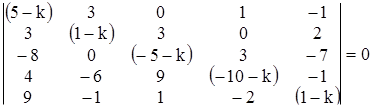 ,
,
или
![]() .
.
Находим корни этого уравнения, используя математическую программу Mach Cad
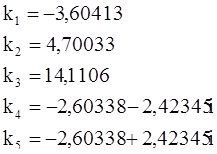
Для каждого корня ![]() (i=1, 2, 3, 4, 5) напишем систему (3) и определим коэффициенты
(i=1, 2, 3, 4, 5) напишем систему (3) и определим коэффициенты ![]() . Можно показать, что один из них произвольный, его можно считать равным единице.
. Можно показать, что один из них произвольный, его можно считать равным единице.
Для корня ![]() составим систему (3):
составим систему (3):
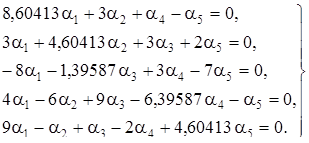
Пусть ![]() =1, тогда получаем систему:
=1, тогда получаем систему:

Решим эту систему с помощью программы реализующей метод Гаусса (см. приложение.)
Программа решения систем линейных уравнений по методу Гаусса
Введите порядок матрицы системы (max. 10)
> 4
Введите расширенную матрицу системы
A 1 2 3 4 b
1 8.6 3 0 1 1
2 3 4.6 3 0 -2
3 -8 0 -1.4 3 7
4 4 -6 9 -6.4 1
Результат вычислений по методу Гаусса
![]() 1 = 2.4834281139E-01
1 = 2.4834281139E-01
![]() 2 = -1.6215428632E+00
2 = -1.6215428632E+00
![]() 3 = 1.5713562455E+00
3 = 1.5713562455E+00
![]() 4 = 3.7288804116E+00
4 = 3.7288804116E+00
Таким образом, используя формулу (2) получаем для корня ![]() решение системы (1):
решение системы (1):
![]()
Для корня ![]() составим систему (3):
составим систему (3):
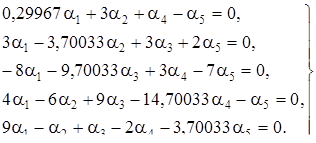
Пусть ![]() =1, тогда получаем систему:
=1, тогда получаем систему:
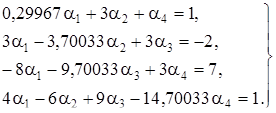
Решим эту систему с помощью программы реализующей метод Гаусса (см. приложение.)
Программа решения систем линейных уравнений по методу Гаусса
Введите порядок матрицы системы (max. 10)
> 4
Введите расширенную матрицу системы
A 1 2 3 4 b
1 0.3 3 0 1 1
2 3 -3.7 3 0 -2
3 -8 0 -9.7 3 7
4 4 -6 9 -14.7 1
Результат вычислений по методу Гаусса
![]() 1 = 1.2357323071E+01
1 = 1.2357323071E+01
![]() 2 = 5.8924432138E-01
2 = 5.8924432138E-01
![]() 3 = -1.2297255075E+01
3 = -1.2297255075E+01
![]() 4 = -4.4749298856E+00
4 = -4.4749298856E+00
Таким образом, используя формулу (2) получаем для корня ![]() решение системы (1):
решение системы (1):
![]()
Для корня ![]() составим систему (3):
составим систему (3):
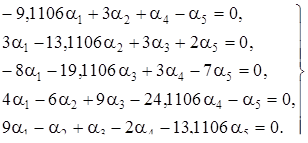
Пусть ![]() =1, тогда получаем систему:
=1, тогда получаем систему:
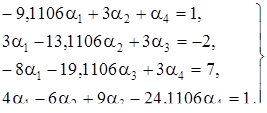
Решим эту систему с помощью программы реализующей метод Гаусса (см. приложение.)
Программа решения систем линейных уравнений по методу Гаусса
Введите порядок матрицы системы (max. 10)
> 4
Введите расширенную матрицу системы
A 1 2 3 4 b
1 -9.1 3 0 1 1
2 3 -13.1 3 0 -2
3 -8 0 -19.1 3 7
4 4 -6 9 -24.1 1
Результат вычислений по методу Гаусса
![]() 1 = -1.1863988144E-01
1 = -1.1863988144E-01
![]() 2 = 4.5529392393E-02
2 = 4.5529392393E-02
![]() 3 = -3.5073275152E-01
3 = -3.5073275152E-01
![]() 4 = -2.0434711016E-01
4 = -2.0434711016E-01
Таким образом, используя формулу (2) получаем для корня ![]() решение системы (1):
решение системы (1):
![]()
Для корня ![]() составим систему (3):
составим систему (3):
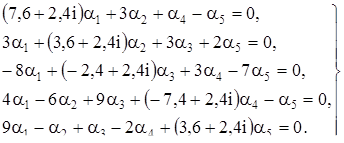
Пусть ![]() =1, тогда получаем систему:
=1, тогда получаем систему:

Решив эту систему методом Гаусса, получим:
![]()
Таким образом, используя формулу (2) получаем для корня ![]() решение системы (1):
решение системы (1):
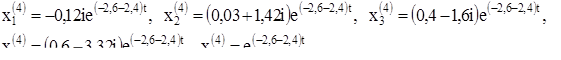
Для корня ![]() составим систему (3):
составим систему (3):
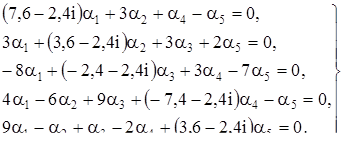
Пусть ![]() =1, тогда получаем систему:
=1, тогда получаем систему:

Решив эту систему методом Гаусса, получим:
![]()
Таким образом, используя формулу (2) получаем для корня ![]() решение системы (1):
решение системы (1):
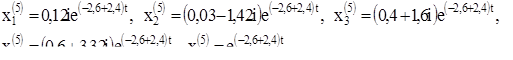
Выпишем комплексное решение
![]()
![]()




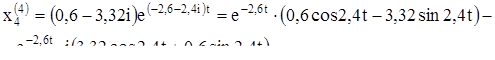
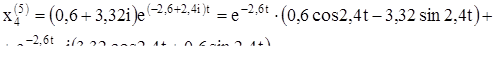
![]()
![]()
Решением будут действительные и мнимые части:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Теперь можем написать общее решение

Исследуем устойчивость решения системы (1). Корни характеристического уравнения

Для того, чтобы решение было устойчивым необходимо чтобы все действительные части корней характеристического уравнения были отрицательными. В данном случае ![]() положительные. Отсюда делаем вывод, что решение системы (1) неустойчиво.
положительные. Отсюда делаем вывод, что решение системы (1) неустойчиво.
ЗАКЛЮЧЕНИЕ
В ходе исследовательской работы были рассмотрены линейные однородные и неоднородные уравнения с постоянными коэффициентами, системы линейных однородных дифференциальных уравнений с постоянными коэффициентами и один из методов их решения – метод исключения. Также были рассмотрены автономные системы дифференциальных уравнений и их фазовые пространства. Было проведено исследование фазовой плоскости линейных систем второго порядка. В работе приведены доказательства теорем существования и единственности как для одного уравнения, так и для нормальной системы уравнений. В ходе исследовательской работы было рассмотрено лишь понятие об устойчивости решений, не были рассмотрены важнейшие теоремы устойчивости, что является темой для дальнейшего исследования. В каждом параграфе приведены примеры, что значительно облегчает понимание темы.
Характерным для данной работы является то, что многие важные утверждения и их доказательства приведены в виде предложений или примеров, обозначенных А), Б), и т.д. Поэтому при изучении некоторых тем игнорирование этих примеров нежелательно, так как они используются при доказательстве основных теорем.
В практической части работы было найдено общее решение системы дифференциальных уравнений

При решении этой системы была использована программа Mach Cad, составлена программа реализующая метод Гаусса на языке программирования Паскаль. При исследовании решения системы было выяснено, что решение системы не устойчиво.
ЛИТЕРАТУРА
1. Видаль П. Нелинейные импульсные системы: Монография: Пер. с фр. – М.: энергия, 1994. – 336с.
2. Гукасов Н.А. Механика жидкости и газа: Учеб. пособие для вузов. – М.: 1996. – 443с.
3. Камке Э. Справочник по обыкновенным дифференциальным уравнениям: – 5-е изд. – М.: Наука, Главная редакция физико-математической литературы, 1976. – 576с.
4. Мудров А.Е.Численные методы для ПЭВМ на языках Паскаль, Фортран и Бейсик. МП “Раско”, Томск, 1991 г.
5. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов, т.2: Учеб. пособие для втузов. – 13-е изд. – М.: Наука, Главная редакция физико-математической литературы, 1985. – 560 с.
6. Понтрягин Л.С. Обыкновенные дифференциальные уравнения: – 4-е изд. – М.: Наука, Главная редакция физико-математической литературы, 1974. – 332с.
7. Турчак Л. И. Основы численных методов: Учеб. пособие. – М.: Наука. Гл. ред. физ.-мат. лит, 1987.
8. Численные методы: Учеб. пособие для студентов физ.-мат. спец. пед. ин-тов/ Под ред. В. М. Заварыкин, В. Г. Житомирский, М. П. Лапчик. – М.: Просвещение, 1990.
ПРИЛОЖЕНИЕ
Описание алгоритма. В данной программе реализован метод Гаусса со схемой частичного выбора.
В переменную n вводится порядок матрицы системы. С помощью вспомогательной процедуры ReadSystem в двумерный массив a и одномерный массив b вводится c клавиатуры расширенная матрица системы, после чего оба массива и переменная n передаются функции Gauss. В фукции Gauss для каждого k-го шага вычислений выполняется поиск максимального элемента в k-м столбце матрицы начинаяя с k-й строки. Номер строки, содержащей максимальный элемент сохраняеется в переменной l. В том случае если максимальный элемент находится не в k-й строке, строки с номерами k и l меняются местами. Если же все эти элементы равны нулю, то происходит прекращение выполнения функции Gauss c результатом false. После выбора строки выполняется преобразование матрицы по методу Гаусса. Далее вычисляется решение системы и помещается в массив x. Полученное решение выводится на экран при помощи вспомогательной процедуры WriteX.
Листинг программы
Uses CRT;
Const
maxn = 10;
Type
Data = Real;
Matrix = Array[1..maxn, 1..maxn] of Data;
Vector = Array[1..maxn] of Data;
{ Процедура ввода расширенной матрицы системы }
Procedure ReadSystem(n: Integer; var a: Matrix; var b: Vector);
Var
i, j, r: Integer;
Begin
r := WhereY;
GotoXY(2, r);
Write('A');
For i := 1 to n do begin
GotoXY(i*6+2, r);
Write(i);
GotoXY(1, r+i+1);
Write(i:2);
end;
GotoXY((n+1)*6+2, r);
Write('b');
For i := 1 to n do begin
For j := 1 to n do begin
GotoXY(j * 6 + 2, r + i + 1);
Read(a[i, j]);
end;
GotoXY((n + 1) * 6 + 2, r + i + 1);
Read(b[i]);
end;
End;
{ Процедура вывода результатов }
Procedure WriteX(n :Integer; x: Vector);
Var
i: Integer;
Begin
For i := 1 to n do
Writeln('x', i, ' = ', x[i]);
End;
{ Функция, реализующая метод Гаусса }
Function Gauss(n: Integer; a: Matrix; b: Vector; var x:Vector): Boolean;
Var
i, j, k, l: Integer;
q, m, t: Data;
Begin
For k := 1 to n - 1 do begin
{ Ищем строку l с максимальным элементом в k-ом столбце}
l := 0;
m := 0;
For i := k to n do
If Abs(a[i, k]) > m then begin
m := Abs(a[i, k]);
l := i;
end;
{ Если у всех строк от k до n элемент в k-м столбце нулевой,
то система не имеет однозначного решения }
If l = 0 then begin
Gauss := false;
Exit;
end;
{ Меняем местом l-ую строку с k-ой }
If l <> k then begin
For j := 1 to n do begin
t := a[k, j];
a[k, j] := a[l, j];
a[l, j] := t;
end;
t := b[k];
b[k] := b[l];
b[l] := t;
end;
{ Преобразуем матрицу }
For i := k + 1 to n do begin
q := a[i, k] / a[k, k];
For j := 1 to n do
If j = k then
a[i, j] := 0
else
a[i, j] := a[i, j] - q * a[k, j];
b[i] := b[i] - q * b[k];
end;
end;
{ Вычисляем решение }
x[n] := b[n] / a[n, n];
For i := n - 1 downto 1 do begin
t := 0;
For j := 1 to n-i do
t := t + a[i, i + j] * x[i + j];
x[i] := (1 / a[i, i]) * (b[i] - t);
end;
Gauss := true;
End;
Var
n, i: Integer;
a: Matrix ;
b, x: Vector;
Begin
ClrScr;
Writeln('Программа решения систем линейных уравнений по методу Гаусса');
Writeln;
Writeln('Введите порядок матрицы системы (макс. 10)');
Repeat
Write('>');
Read(n);
Until (n > 0) and (n <= maxn);
Writeln;
Writeln('Введите расширенную матрицу системы');
ReadSystem(n, a, b);
Writeln;
If Gauss(n, a, b, x) then begin
Writeln('Результат вычислений по методу Гаусса');
WriteX(n, x);
end
else
Writeln('Данную систему невозможно решить по методу Гаусса');
Writeln;
End.